2. 中石油西部钻探工程公司克拉玛依钻井公司;
3. 中国石油大学(北京)机械与储运工程学院
2. CNPC Xibu Drilling Engineering Company Limited;
3. College of Mechanical and Transportation Engineering, China University of Petroleum(Beijing)
0 引言
连续管具有许多技术优点和作业优势,广泛应用于钻井、完井、修井、测试、增产、采油和采气等石油工程方面。连续管在下井过程中要经过多次弯曲和矫直动作,并承受相应的内压等作用,在这些复杂载荷作用下,连续管会产生显著的几何变形[1]。刚生产的连续管截面近乎理想圆,椭圆度很小(≤0.5%),随着在滚筒上缠绕和卸绕,由于塑性变形使得理想圆的连续管椭圆化,缠绕的次数越多,椭圆度越大[2]。在较大内压作用下,连续管周向应力使其直径增加;在循环弯曲载荷的作用下,连续管发生疲劳,使其屈服强度下降;在内压和循环弯曲载荷的共同作用下,连续管直径迅速增大[3]。钟守炎等[4]在连续管在内压作用下直径增长模型的建立研究中提到连续管在高压下直径增长剧烈,用户采用6%作为其最大直径增长值,而在高压下,在疲劳试验中通常会看到直径增长超过20%,直径增长将引起连续管与设备不兼容现象。王海涛等[5]以三参数幂函数能量法(3SE)和梁弯曲理论为基础,分析了连续管卷曲低周疲劳寿命预测计算公式,研究出连续管在滚筒上缠绕及其他载荷作用下的椭圆度、直径增长、壁厚变化和累积塑性应变等因素及其对连续管寿命的影响,对连续管的应用有重要意义[5]。
笔者对连续管现场载荷和试验中加载的载荷进行分析和比较,并通过有限元模拟连续管在不同加载形式时的卷绕矫直过程,探寻目前试验中连续管弯曲椭圆度等参数与现场数据不吻合的原因,同时分析在不同工况下卷绕时连续管各参数变化情况和破坏形式,以期为高效使用连续管和设计性能优良的连续管作业机提供理论基础。
1 连续管疲劳失效形式分析在连续管的使用过程中,主要的疲劳失效形式有:连续管开裂、穿孔,连续管椭圆度太大以及连续管直径增长过大(鼓包)等。连续管开裂或穿孔将直接导致连续管无法正常工作。连续管椭圆化对其通过注入头的能力有影响,椭圆度太大连续管无法通过井口下入井中,同时影响密封和设备夹紧[6],更重要的是其对连续管抵抗外压的能力有很大影响,若椭圆化严重,则连续管的挤毁抗力将大大降低[7];直径增长过大(鼓包)将引起连续管与设备不兼容现象,容易造成连续管的严重失效[8];在缠绕过程中,塑性应变在不断累积增加,当累积塑性应变达到一定程度时,便会由于低周疲劳产生微小裂纹并随着缠绕的进行而不断扩展。连续管开裂和穿孔由低周疲劳引起。连续管在不断卷绕矫直过程中,反复的塑性变形使得材料产生微裂纹并不断扩展,最后连续管开裂。累积塑性应变可以描述这种损伤。文献[9]认为,累积塑性应变达到475%,将发生疲劳断裂。连续管在滚筒上缠绕和卸绕,由于塑性变形使得连续管椭圆化。在轴向应力、环向应力和径向应力这3轴应力作用下,连续管直径会增大;随着疲劳循环次数的增加,管体直径将变大,同时伴随着壁厚的减小[10]。
2 连续管卷绕矫直载荷分析目前,国内外研究者对承受弯曲和相应内压作用的连续管疲劳失效进行了试验和理论计算。试验研究中多采用连续管专用疲劳试验机来测试其疲劳寿命。试验机通过油缸提供双向拉力使连续管试样在已知半径的弯曲模具上拉弯或矫直[11]。这样的弯曲方式在连续管的一端只加载了端面切向载荷。
2.1 连续管的弯矩分析假设连续管材料为理想弹塑性,屈服应力为σy,连续管弯曲半径为RG,弹性区高度y按式(1)计算。连续管在弯曲后产生弹塑性应变,弹性区域上的应力正比于中性轴的距离,而塑性区域的应力大小均为σy。

计算弯矩时,按对称原理只需计算 1/4 的区域。其中弹性区域分成2个区域(扇形区域和三角区域),塑性区域分成2个区域(三角区域和扇形区域),如图1所示。弯矩计算式为:
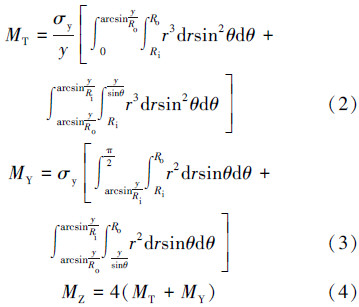
|
| 图 1 连续管弯曲弹性区与塑性区示意图 Fig.1 Schematic of elasticity zone and plasticity zone of coiled tubing bending |
为了比较连续管专用疲劳试验机加载的载荷与连续管在现场作业中载荷的差别,重点考察与疲劳试验机弯曲程度相当的连续管的截面切向载荷。
2.2.1 疲劳试验机载荷分析外径 50.8 mm、壁厚4.78 mm、钢级CT90连续管在直径2 m滚筒上缠绕所需弯矩MZ为6.3 kN·m(由式(4)计算得到),设试件为1 m长,使连续管试件中间截面(0.5 m处)达到此弯矩时该截面切向力为12.6 kN,则此截面切向应力为18.2 MPa。
2.2.2 连续管现场载荷分析现场作业时,连续管通过注入器从井中起出后,经导向架再到滚筒卷绕,滚筒离导向架之间有一段距离。除了轴向拉力外,在悬垂部分连续管的重力会在滚筒上的排管器产生弯矩。为计算该弯矩的大小,设导向架到滚筒的距离为16 m左右,滚筒与导向架之间有高度差,在10 m左右。运用有限元梁单元建立连续管悬垂段模型,在右端加载3.8 kN拉力,变形如图2所示。左端有3.3 kN左右的轴向力和1.1 kN·m的弯矩作用。
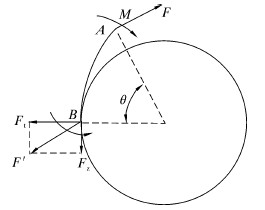
|
| 图 2 连续管在滚筒缠绕受力图 Fig.2 Forces on the coiled tubing during winding on the roller |
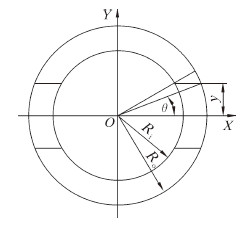
连续管滚筒缠绕受力如图2所示,与文献[12]相比,多计算了排管器A处的弯矩M的作用。设A点到滚筒中心1.6 m,松弛角θ为60°,则此时接触点B弯矩为6.4 kN·m,略大于试验机的弯矩。此端面切向力Ft为2.8 kN,切向应力4.1 MPa,疲劳试验机加载方式产生的截面切向应力是现场产生的截面切向应力的4.4倍。
3 加载方式对连续管卷绕矫直变形的影响分析通过上述连续管载荷分析可知,疲劳试验机加载方式产生的切向应力是现场产生的截面切向应力的4.4倍。这种差别会对连续管的变形产生何种影响?笔者采用有限元计算和试验以及现场检测结果比较进行分析。
3.1 连续管加切向载荷弯曲运用有限元建立连续管卷绕矫直模型,为了研究连续管反复弯曲现象,建立弯曲模和矫直模辅助分析。考虑到问题的对称性,有限元建模时,将连续管建立成 1/2 对称模型,连续管模型取足够长,保证分析中研究对象不受加载方式的影响。建立50.8 mm×4.78 mm,滚筒直径3 m的连续管在滚筒上缠绕模型,弯曲模和矫直模采用一次单元并固定其节点全部自由度。连续管加载时,一端对称和固定一个节点,另一端用单元压力的方式加载端面切向载荷和拉伸载荷,如图3所示,逐步进行比例加载使连续管弯曲直至连续管中间有一段应力均匀,贴靠于弯曲模为止,再改变切向载荷的方向使之贴靠于矫直模,然后放松,连续管回到初始位置。将上述计算过程重复进行,研究连续管在多次弯曲矫直后各参数指标的变化。
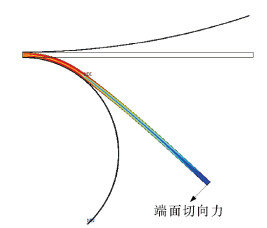
|
| 图 3 连续管加端面切向载荷弯曲示意图 Fig.3 Schematic of bending of coiled tubing with the tangential load on the end |
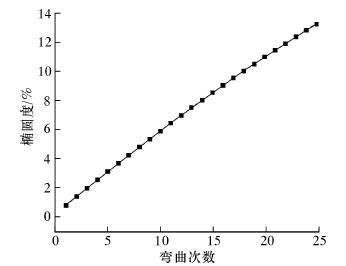
将此模型计算结果与何春生等人在专用连续管疲劳寿命装置上对连续管进行的疲劳寿命试验得到的不同循环次数下连续管椭圆度和壁厚变化值进行比较,试验结果与模型计算结果吻合[13],在15次弯曲后其椭圆度都在8.7%左右,如图4所示。然而,在对现场工作的连续管进行测量后发现,15次下井后连续管椭圆度仅有0.7%~1.3%,见文献[14]。
|
| 图 4 有限元计算的连续管在端面切向载荷作 用下弯曲椭圆度随弯曲次数变化曲线 Fig.4 The effects of bending number on the bending ovality of coiled tubing with the tangential load on the end calculated by FEM |
按疲劳试验机加载方式,在连续管端部加切向载荷弯曲,试验和数值模拟时其椭圆度等参数都与现场检测数据不吻合。由第2章的载荷分析可以知道,现场的载荷截面切向应力很小。采用同样的连续管有限元模型,但是在油管端部以加载弯矩载荷为主,配合拉伸和切向应力,计算出的连续管椭圆度和壁厚减薄数据与现场得到的数据比较接近,在15次弯曲后其椭圆度为1.1%。因此可以推定连续管在实际弯曲中主要载荷是弯矩,切向载荷所占比例较小。这与上述连续管载荷分析中计算的数据符合。
4 疲劳失效分析连续管的弯曲过程用上述三维实体模型进行研究,但计算量大,对大量不同几何尺寸、弯曲直径和材料参数的连续管弯曲寿命分析时,耗时较长。如果是纯弯曲,考虑对称性,采用二维广义平面应变单元,则大大减小了计算工作量[9]。
单元广义平面应变选项为每个单元引入了3个新的自由度,内部自动创2个节点,用于解决广义平面应变单元轴向载荷、位移、弯曲载荷和转角等的加载。运用广义平面应变单元建立50.80 mm×4.78 mm、CT90钢级连续管弯曲模型,运用广义平面应变单元加载选项加载使其弯曲半径达到预定值,研究连续管弯曲半径在2~3 m间变化时其相关参数的变化情况。
在循环卷绕矫直计算中,根据连续管用户要求和连续管材料的性质对连续管施加3个约束条件:连续管椭圆度在8.0%以下[15],累积塑性应变在475%以下,直径增长率在6%以下[4]。这3个条件分别为连续管椭圆度极限、累积塑性应变极限和直径增长极限,在连续管弯曲中,如果任意一个参数达到极限,就认为失效。
压力的增加对直径的增长有很大影响,内压的增加会导致直径增长率迅速增大,在压力为80.0 MPa时,4或5次弯曲,连续管直径增长便会超过用户要求;累积塑性应变在内压不高时受压力影响不大;椭圆度在压力变化,特别是高压时无特别规律,在低压力,循环次数少,大约20次以内,随循环次数增加呈线性增加,在循环次数较多时,呈非线性规律,压力稍微增加时,相同弯曲次数椭圆度反而减小,但压力太大,椭圆度又会迅速增加。在无内压或压力很低时,主要是椭圆度和累积塑性应变使连续管变差,对外径50.8 mm、壁厚4.78 mm的CT90连续管,弯曲半径1 m及以下时,连续管椭圆度会迅速增大,抵抗外挤压能力急剧减弱,甚至无法与设备兼容;在弯曲半径较大时,主要是累积塑性应变使连续管破坏。在压力较高时主要是连续管直径增长率迅速增大(鼓包),使连续管无法与设备兼容,壁厚大大减薄,无法满足预定的工作要求而损坏。
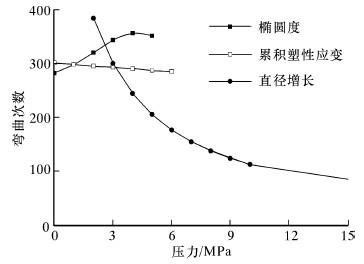
以弯曲直径2 m、承受内压0.0~90.0 MPa的连续管弯曲为例,达到椭圆度极限、累积塑性应变极限和直径增长极限的连续管的弯曲次数与其承受的内压的关系如图5所示。从图中可以看出,在椭圆度达到极限时,连续管可弯曲次数随着压力的增加略有增加;在累积塑性应变达到极限时,连续管可弯曲次数随着压力的增加缓慢降低;在直径增长达到极限时,连续管可弯曲次数随着压力的增加迅速下降。故连续管可弯曲次数随着压力的增加开始略有增加,然后比较平稳,随后迅速下降,与实际中连续管弯曲破坏规律符合[16]。
|
| 图 5 达到椭圆度、累积塑性应变和直径增 长极限的连续管弯曲次数与内压的关系 Fig.5 The relation between the bending number of times and internal pressure of coiled tubing with the ovality,cumulative bending plastic strain and diameter expansion limit |
(1)连续管疲劳试验机试验和现场作业中连续管卷绕时所受载荷不一致,前者截面切向应力差是后者的4.4倍。两者截面切向应力的差异导致反复卷绕矫直中连续管椭圆度的变化有较大差异。试验结果和现场测试结果支持这一结论,有限元分析同样支持这一结论。
(2)连续管加内压时卷绕矫直的数值模拟揭示连续管卷绕矫直失效形式与内压的大小有关。在无内压或压力很低时,主要是椭圆度失效;随着内压的增大,累积塑性应变较大,可能使连续管开裂;在弯曲半径较大时,主要是累积塑性应变使连续管破坏;在内压较高时,连续管直径增长率迅速增大(出现鼓包),连续管壁厚减薄,无法满足预定的工作要求而失效。
| [1] | 李磊,王鹏,申昭熙,等.连续管在内压和循环弯曲作用下的试验研究[J].石油机械, 2011,39(1):5-7. |
| [2] | 董昌乐,聂翠平,韩新利,等.基于有限元法对小椭圆度连续管挤毁压力研究[J].石油矿场机械,2010,39(11):22-24. |
| [3] | 郭兆光.连续管疲劳的力学试验分析[J].油气井测试,2012,21(5):15-16. |
| [4] | 钟守炎,刘明尧,Yang Y S.连续管在内压作用下直径增长模型的建立[J].石油机械,1999,27(2):34-37. |
| [5] | 王海涛,李相方.连续管卷曲低周疲劳寿命预测[J].石油机械,2008,36(11):25-27,31. |
| [6] | 于润桥,廖城,夏桂锁,等.基于涡流传感器的连续管椭圆度在线检测技术研究[J].科学技术与工程,2014,14(10):38-41. |
| [7] | 王优强,张嗣伟.连续管的挤毁压力分析[J].石油矿场机械,1999,28(2):37-40. |
| [8] | Yang Y S,Gao C.Development of a coiled tubing diametral growth model[C]//SPE Rocky Mountain Regional Meeting.SPE,1999. |
| [9] | Sisak W J,Crawford D J.The fatigue life of coiled tubing[C]//SPE/IADC Drilling Conference.SPE,1994. |
| [10] | 李晓秋,樊建春,范磊,等.大位移塑性变形下连续管直径增长规律研究[J].中国安全生产科学技术,2013,9(5):25-28. |
| [11] | Behenna F R,Myrick D D,Stanley R K.Field valid- ation of a coiled tubing fatigue model[C]//SPE/ICoTA Coiled Tubing Conference and Exhibition.SPE,2003. |
| [12] | 施志辉,范佳,许立,等.连续管在滚筒上缠绕的力学研究[J].大连交通大学学报,2011,32(5):50-52. |
| [13] | 何春生,刘巨保,岳欠杯,等.基于椭圆度及壁厚参数的连续管低周疲劳寿命预测[J].石油钻采工艺,2013,35(11):15-18. |
| [14] | Stanley R K.Results of recent inspections performed on coiled tubing[C]//SPE/ICoTA Coiled Tubing Roundtable.SPE,1999. |
| [15] | Zheng A S.Improved model for collapse pressure of oval coiled tubing[C]//SPE/ICoTA coiled tubing Roundtable.SPE,1999. |
| [16] | 朱小平.连续管在弯曲和内压共同作用下的疲劳寿命分析[J].钻采工艺,2004,27(4):73-75. |




