0 引言
叶片圆盘泵是实现海底钻井液举升双梯度钻井技术的关键装备,被安放在水下或海底,举升钻井液至钻井船[1, 2]。叶片圆盘泵叶轮由前、后2个平行盖板构成,盖板上均带有径向直叶片,形成有叶区和无叶区,具有无堵塞、抗冲击和耐磨损等优点[3]。叶轮的高速旋转、叶轮和蜗壳的动静干涉等都会引起泵内流场的压力脉动,进而诱发振动产生噪声;泵内压力脉动还将加剧叶轮径向力波动,导致泵轴和密封环的失效;泵出口压力脉动还可能引起钻井液返回管线的共振,严重影响钻井作业安全和效率。
叶片圆盘泵作为一种新型泵,目前的研究工作主要是定常计算条件下性能预测、流场分析及叶轮优化设计等,泵内压力脉动特性及非定常条件下叶轮所受径向力变化规律尚不明确[4, 5, 6, 7]。因此开展叶片圆盘泵压力脉动相关研究对于了解其瞬态特性,提高其运行稳定性具有重要意义。数值模拟方法是研究泵内流场压力脉动的重要手段,施卫东等[8]分析了高比转速斜流泵内部非定常压力脉动时域和频域特性。程效锐等[9]对螺旋离心泵内压力脉动和叶轮轴向力、径向力变化进行了研究。刘厚林等[10]重点分析了双蜗壳泵隔舌等特定区域的压力脉动和叶轮径向力变化规律。目前尚无叶片圆盘泵压力脉动特性的数值研究文献报道。
笔者应用Fluent软件,对叶片圆盘泵内部流场进行了三维非定常数值计算,在外特性试验验证的基础上,分析了设计工况下叶轮内压力、蜗壳内压力、扬程脉动情况,以及叶轮径向力变化规律和影响因素,以期为叶片圆盘泵瞬态特性的深入研究及结构优化提供理论依据。
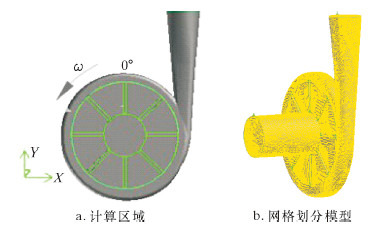
1 计算模型与数值方法 1.1 计算区域及网格划分数值计算所用叶片圆盘泵每个圆盘上叶片数目为8,设计流量Q=200 m3/h,设计扬程H=124 m,转速n=2 900 r/min。计算区域是由进口延长段、叶轮和蜗壳3部分组成的全流道,计算区域网格划分如图1所示。
|
| 图 1 叶片圆盘泵计算区域及网格划分 Fig.1 Computational domain and mesh generation of the disc pump with radial straight blade |
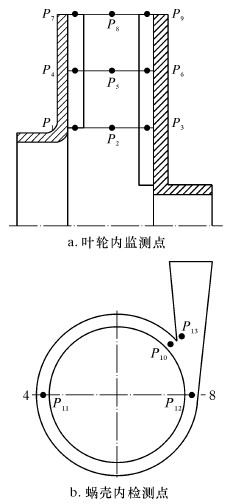
为分析叶片圆盘泵内部不同位置的压力脉动,在计算区域内布置如图2所示的13个监测点,获取各监测点压力瞬时值。其中,点P1~P9分布在叶轮内,且点P1、P4和P7均布在前盖板叶片中线;点P3、P6和P9均布在后盖板叶片中线;点P2、P5和P8分布在叶轮无叶区中截面。点P1、P2、和P3,点P4、P5和P6,点P7、P8和P9分别位于同一半径处。点P10~P13位于蜗壳内,且均处在蜗壳中截面,点P10、P13分别位于隔舌两侧,点P11和P12分别位于蜗壳第4和8断面中心。
|
| 图 2 泵内压力监测点位置 Fig.2 Positions of pump pressure monitoring point |
采用Simple方法求解不可压缩时均Navier-Stokes方程,选用RNG κ-ε湍流模型进行封闭[9, 10, 11]。考虑到数据精度和有效性,采用二阶中心差分格式离散扩散项,对流项离散采用二阶迎风格式。采用速度入口和自由出流出口条件;流道内与流体相接触的壁面上均采用无滑移壁面条件,壁面附近采用标准壁面函数。采用滑移网格技术在叶轮内动、静计算域之间,叶轮计算域与固定的蜗壳计算域之间分别设置数据传递交界面。设定时间步长为3.448 28×10-4 s,即叶轮旋转6°,计算收敛精度均设置为10-4,每个物理时间步长上的计算均收敛。计算结果表明,叶轮转动5个周期后扬程曲线开始呈周期性变化,选取第6个周期的计算结果进行分析。
2 性能预测与试验验证以清水为介质对计算模型进行5种(0.4Q、0.6Q、0.8Q、1.0Q和1.2Q)工况下的非定常计算,取第6个周期不同时间步计算结果的平均值作为叶片圆盘泵扬程和效率预测值。计算公式如下:
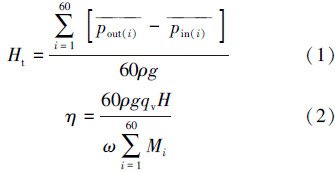
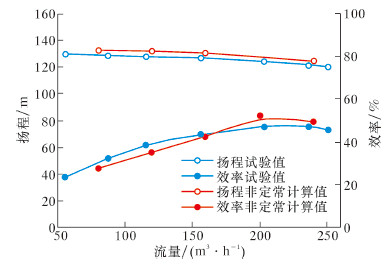
叶片圆盘泵性能曲线计算值与试验值对比如图3所示。
|
| 图 3 叶片圆盘泵性能曲线试验值与计算值对比 Fig.3 Performance curve of experimental results and calculation results |
水力性能试验装置、试验条件、试验方法及试验数据的获得都符合GB/T 3215—2005回转动力泵水力性能验收试验1级和2级的规定,试验精度达到国家标准的1级精度。
从图3可以看出,在大流量变化范围内,叶片圆盘泵预测曲线与试验曲线很接近。扬程计算值略高于试验值,相对误差不超过3.5%,设计流量点为2.6%;在小流量点效率计算值与试验值偏差稍大,相对误差不超过10%,设计流量点为6.5%。总体来看,计算模型能准确地预测该叶片圆盘泵的外特性,这也证实数值计算模型和方法的正确性,为进一步的压力、扬程脉动和叶轮径向力分析提供了参考。
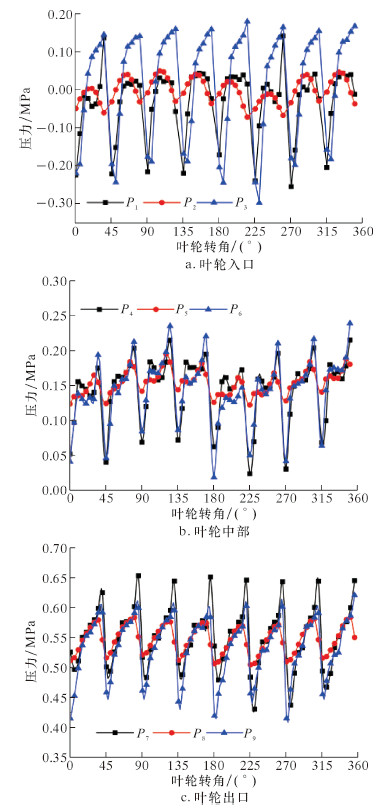
3 泵内压力脉动和扬程脉动分析 3.1 叶轮内压力脉动图4为叶轮转动1周叶轮内不同半径处监测点静压脉动曲线。
|
| 图 4 设计工况下叶轮内监测点静压脉动曲线 Fig.4 Static pressure fluctuation at the monitoring points on the pump impeller under designed conditions |
为方便说明,横坐标用叶轮转角表示,1°代表5.747 13×10-5 s。整体上看,叶轮内所有监测点压力都呈现周期性变化,脉动周期与叶片通过隔舌周期相同,可见叶片与隔舌干涉作用对叶轮内压力脉动起主导作用。分析有叶区内监测点压力脉动曲线可知,在同一半径处,前、后盖板有叶区内监测点压力脉动曲线基本一致;在叶轮入口处,前盖板有叶区内监测点压力脉动幅值略低于后盖板内监测点压力脉动幅值,如图4a所示;在叶轮中部,如图4b所示,前、后盖板有叶区内监测点压力脉动曲线已基本接近;而叶轮出口处,前盖板监测点压力脉动幅值略高于后盖板内监测点,如图4c所示。分析无叶区监测点压力脉动曲线可知,无叶区监测点压力脉动幅值均小于有叶区内监测点压力脉动幅值,其中P5监测点距离叶轮入口和出口均较远,受叶轮入口流体流动和叶片与隔舌干涉影响均较小,压力脉动幅值最小。
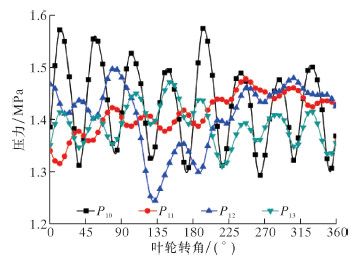
3.2 蜗壳内压力脉动叶轮转动1周蜗壳内不同位置监测点总压脉动曲线如图5所示。从图可以看出,蜗壳内不同位置监测点压力也有明显脉动,脉动周期与叶轮内监测点脉动周期相同,但相比叶轮内部,蜗壳内监测点压力脉动较为紊乱。这表明蜗壳内压力脉动除受叶片与隔舌的干涉作用外,还受到其他因素较大的影响。隔舌附近点P10和P13压力脉动周期性比点P11和P12更明显,蜗壳进口处点P10压力脉动幅值大于点P13,4个监测点中距离隔舌最远的点P11压力脉动幅值最小。由此可见,叶轮与蜗壳的动、静干涉作用在蜗壳处最为强烈,随着监测点与隔舌相对距离的增大,干涉作用逐渐减弱,压力脉动幅值随之减小。
|
| 图 5 设计工况下蜗壳内监测点总压脉动曲线 Fig.5 Total pressure fluctuation at the monitoring points on the pump volute under designed conditions |
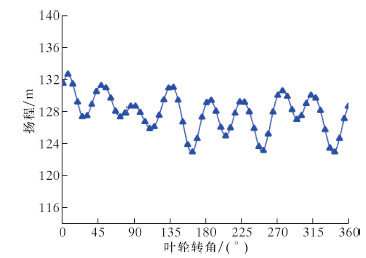
为分析泵外特性脉动规律,计算得到叶轮转动1周内扬程波动曲线,如图6所示。从图可以看出,叶轮转动1个周期,扬程波动曲线分别有8个波峰和波谷,与叶轮叶片数目对应,8个周期脉动幅值不同,但均维持在平均扬程的±5%以内;当叶轮转角在22.5°偶数倍附近时,隔舌处于相邻2叶片中间位置扬程处于极大值点;当叶轮转角在22.5°奇数倍附近时,叶片转至隔舌处扬程处于极小值点。这是因为叶片转至隔舌位置时,叶片与隔舌形成狭窄流道,随着叶轮转动流体对隔舌头部和该叶片冲击的加强,加剧隔舌附近流体能量下降,形成低压区域,且此时叶轮出口与扩散管入口接触面积大,因此流量大、扬程低;隔舌处于相邻2叶片中间时,没有叶片阻挡,隔舌附近流动相对较宽,无明显压降,且此时叶轮出口与扩散管入口接触面积小,因此流量小、扬程高。
|
| 图 6 设计工况下扬程脉动曲线 Fig.6 Pump head fluctuation curve under designed conditions |
叶轮径向力计算采用出口压力法,即根据数值模拟结果,得到叶轮出口与蜗壳耦合面的静压分布,假定在耦合面的每个网格节点附近静压均匀分布,则可以认为作用在每个网格节点上的面积相等。先求解耦合面上每一个节点上受到的作用力,然后通过力的分解合成定理,分别计算在X轴和Y轴方向的作用力,最后求得总作用力的大小和方向[12]。
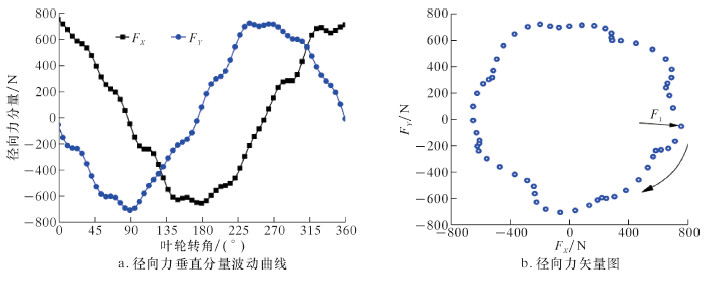
分别计算设计工况下叶轮转动1周内每个时间步叶轮所受径向力,结果如图7所示。其中,图7a表示径向力垂直分量随时间变化曲线,图7b为径向力矢量图,表示径向力在大小和方向上的变化。从图7a可以看出,径向力2分量呈正弦规律变化,周期与叶轮转动周期相同。从图7b可以看出,因泵叶轮采用轴对称结构设计,叶轮受到的径向力平均值仅为680 N,比同等工况下其他类型离心泵叶轮径向力小很多,且径向力随着叶轮旋转也呈现出不稳定性,但波动范围不超过15%,近似呈圆形分布;此外,径向力方向沿圆周方向周期性变化,F1为叶轮位于初始位置时径向力,圆弧箭头方向为径向力随时间变化方向,与叶轮转动方向相反。以上分析结果表明,叶轮周期性转动是径向力方向变化的主要原因,泵内压力波动对叶片圆盘泵径向力数值变化影响较小。
|
| 图 7 设计工况下叶轮径向力 Fig.7 The impeller radial force under designed conditions |
(1)泵内监测点压力脉动周期取决于叶轮叶片数目,前、后盖板有叶区内监测点压力脉动规律基本相同,无叶区压力脉动幅值小于有叶区压力脉动幅值;隔舌附近压力脉动幅值最大,且蜗壳入口侧大于出口侧。
(2)叶片圆盘泵扬程具有明显脉动,应引起足够重视。扬程脉动周期与监测点压力脉动周期相同,当叶片转至隔舌时扬程为极小值,隔舌处于相邻2叶片中间位置时扬程为极大值。
(3)叶轮所受径向力变化周期与叶轮转动周期相同,径向力2垂直分量呈正弦规律变化,轴对称叶轮结构使其所受径向力数值整体很小,且径向力变化方向与叶轮转动方向相反。
(4)通过分析压力和径向力波动产生的原因可知,旋转叶片与静止蜗壳隔舌间的动静干涉作用是叶片圆盘泵压力和扬程的主要脉动源,而叶轮周期性地转动是引起叶轮所受径向力变化的主要因素。在保证水力性能的前提下,建议适当减少叶片数目以减小压力脉动;泵串联工作时,可使各运转叶轮间偏离一定角度,减小泵组扬程脉动,提高机组稳定性。
| [1] | 陈国明,殷志明,许亮斌,等.深水双梯度钻井技术研究进展[J].石油勘探与开发,2007,34(2):246-251. |
| [2] | Dowell J D.Deploying the world's first commercial dual gradient drilling system[R].SPE137319-MS,2010. |
| [3] | Pacello J,Hanas P.Disc pump-type pump technology for hard-to-pump applications[C]//17th International Pump Users Symposium.Houston,Texas:[s.n.],2000:69-80. |
| [4] | 周昌静,陈国明,徐群,等.固液圆盘泵固相体积分数分布数值模拟[J].石油机械,2010,38(8):30-33. |
| [5] | 周昌静,陈国明,徐群,等.圆盘泵流动规律研究[J].流体机械,2010,38(10):44-47. |
| [6] | 尹树孟,陈国明,周昌静,等.圆锥圆盘泵固液两相流动及泵外特性数值分析[J].石油机械,2011,39(10):26-28,38. |
| [7] | 陈永超,陈国明,尹树孟,等.叶片圆盘泵叶轮结构流固耦合强度分析[J].石油机械,2012,40(12):98-101. |
| [8] | 施卫东,邹萍萍,张德胜,等.高比转速斜流泵内部非定常压力脉动特性[J].农业工程学报,2011,27(4):147-152. |
| [9] | 程效锐,李仁年,黎义斌,等.螺旋离心泵瞬态特性的数值分析[J].机械工程学报,2013,49(8):186-192. |
| [10] | 刘厚林,任芸,谈明高,等.双流道泵内压力脉动的CFD计算及测试[J].排灌机械工程学报,2010,28(4):277-281. |
| [11] | 侯树强,王灿星,林建忠.叶轮机械内部流场数值模拟研究综述[J].流体机械,2005,33(5):30-34. |
| [12] | 赵万勇,张亮,雒军.双吸离心泵径向力数值分析[J].排灌机械,2009,27(4):205-209. |




