0 引 言
钻进过程中对钻井管柱振动信号的组成及变化规律进行认识,可以为管柱振动信号的解释提供有力参考,同时也能极大地增强信号解释的科学性,提高信号识别能力,促进信号处理技术的进步与革新。
对于井下管柱的振动研究,学者们或是给出了振动数学规律方程[1],或是给出了振动特性分析[2,3],但都没有从信号的基本组成与时域结构出发进行管柱振动信号时域特征的分析研究。为了了解管柱内部信号传递的过程与规律性以及各种信号的组成,笔者通过建立信号传递过程模型,采用仿真方法开展详细研究,并利用实测信号对该方法的可行性与可靠性进行验证。
1 管柱轴向振动传播效应钻井过程中,钻柱在井中的运动状态由钻柱本体、钻井液、井壁或井底几大部分相互作用决定。在钻进过程中,钻柱在地面设备的驱动下处在内、外均有钻井液流动的环境中,局限于井筒的有限空间里,遭受着井底岩石的反作用力[4]。钻柱振动包括轴向振动、扭转振动、横向振动和粘滑振动,同时钻柱承受着冲撞动载作用,这些振动在复杂、不确定的边界条件下耦合在一起,形成具有显著随机特征的动态系统。但在整个钻井过程中,钻柱承受的主要振动还是轴向振动[5,6]。为此,笔者以管柱的轴向振动作为研究对象。
钻柱对声波信号低衰减的传播特性,使其成为连接井底与地面的信息通道,钻头振动通过钻柱传递至地面。同时,钻柱具有特殊的几何结构和机械特性,在信号传播过程中存在独特的传播效应[7,8]。钻杆接头在钻柱中周期性出现,导致振动波沿钻柱传播过程中除了衰减外还会引起带阻效应,降低了振动传播的群速度,增大了信号分辨难度。
波在钻柱中沿纵向传播过程中,遇到波阻变化时就会发生透反射,其表达式为[6]:

式中,ZL为杆波阻,ZH为接头波阻,ρ为材料密度,c为波的传播速度,AL为杆的横截面积,AH为接头的横截面积。
钻杆接头处反射系数λ和透射系数μ计算式分别为:
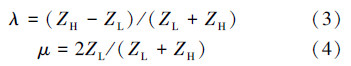
由此可确定透射振幅和反射振幅分别为:

式中,ARj、ARg、ATg分别为接头处的入射源振幅、反射信号振幅和透射信号振幅。
若只考虑波的透射与反射,则有:

另外,在自由端处,空气的波阻无限趋近于0,即ZL趋于0,此时没有透射,只有反射,并且是全反射,即λ=1,μ=0。
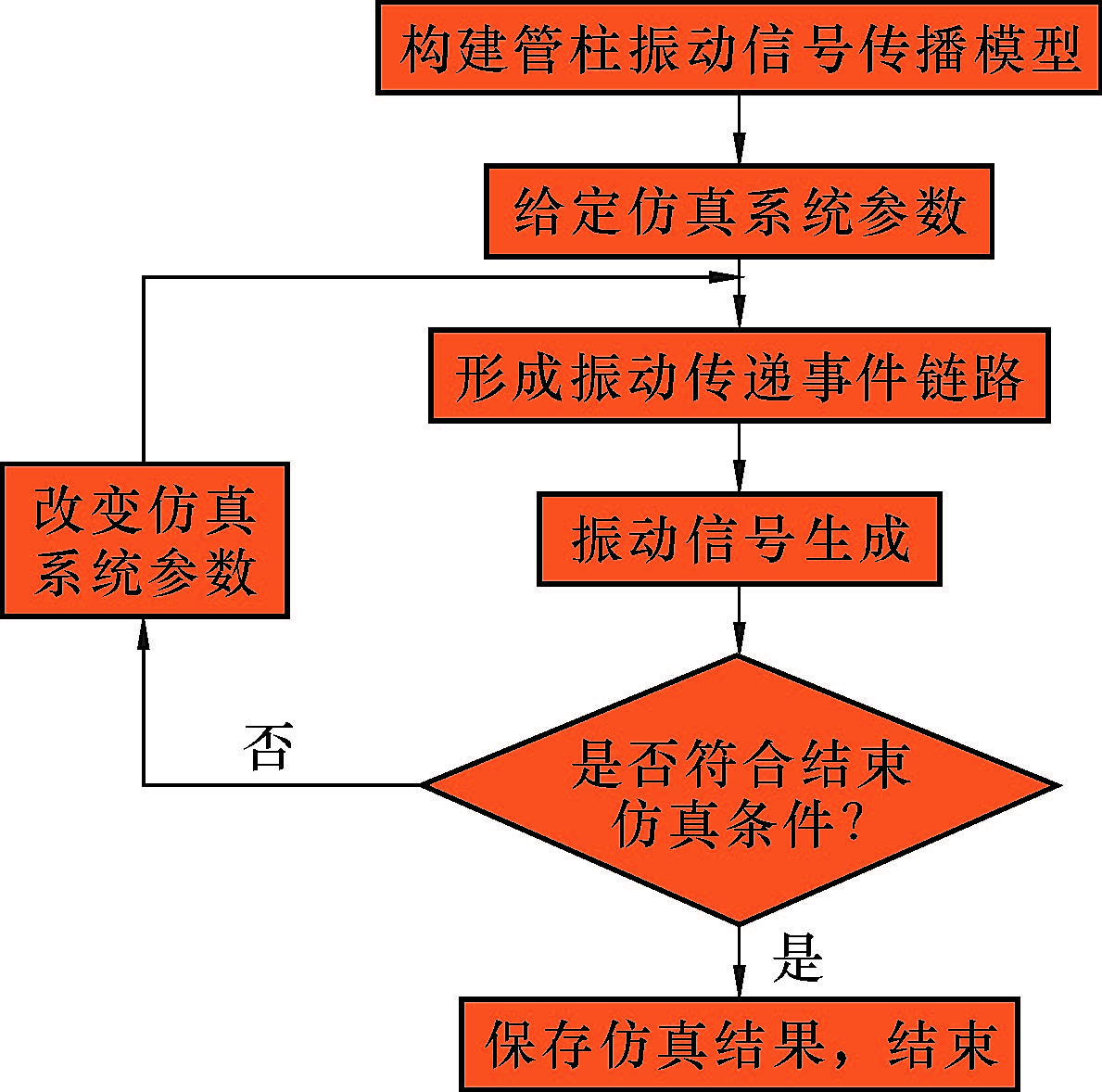
2 管柱振动信号仿真软件开发 2.1 管柱振动仿真流程设计为了实现管柱振动的系统仿真,笔者基于Windows平台,利用Delphi开发工具开发了管柱振动系统仿真处理软件,实现不同条件下管柱振动信号传播规律性的系统分析。管柱振动信号系统仿真流程如图1所示。
|
| 图 1 管柱振动信号系统仿真流程 Fig.1 Simulation process of drill string vibration signal system |
图1中的“管柱振动信号传播模型”为冲击振动信号在管柱中进行反射和透射传播的一维纵向振动模型,模型不考虑管柱的散逸损失,因此式(7)成立。
对于实际的钻柱振动问题,钻柱内部的声波传播速度非常快,达到5 990 m/s,以一个10 m长的单根为例,撞击振动源和传感器都在单根的中部,即使撞击振动源的持续时间只有几个毫秒,传感器在1 s时间内接收到的振动信号实际上也是由两端反射590多次的旅行波与撞击首波叠加而成的信号,信号混叠不可避免,信号成分非常复杂。但即便如此,理论上也可以从实测管柱振动信号中提取得到撞击振动源信号,并解析得到管柱的结构信息。为了降低管柱振动仿真难度,笔者对通过多次透反射后,信号振幅与源信号比降低到一定程度的信号进行截断处理,在仿真过程中只记录没有被截断的透反射信号,形成振动传递事件链路。在仿真过程中,不同的测点可以形成不同的振动传递事件链路。
开展管柱纵向振动仿真实际上就是针对不同的管柱结构和参数、不同的撞击位置,获得不同测点的振动传递事件链路的过程,利用这一链路可以确定具体的时域振动信号。反之,可以通过这一链路来解析具体的振动撞击源信号以及管柱的结构等信息,以便实现振动信号的检测、识别与井下故障诊断。
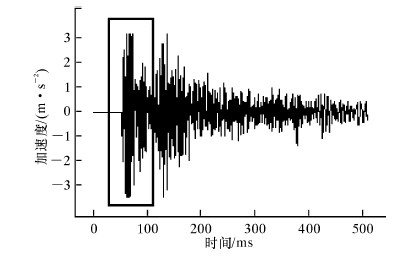
3 管柱振动信号仿真系统分析 3.1 原始撞击信号设计为了尽可能地仿真振动波在管柱中的传播现象,笔者采用实测撞击信号来开展相关研究。图2是从声振测量系统中得到的敲击信号,采用文献[8]中的方法进行模式滤波处理,以便获取管柱的敲击源信号。
|
| 图 2 实测管柱振动信号 Fig.2 Measured drill string vibration signal |
管柱仿真系统基本参数:弹性模量260 GPa,管材密度7.8 g/cm3,泊松比0.35,传播速度5 990 m/s,仿真时间3 s,仿真步长0.000 1s,敲击位置在管柱4.5 m处,敲击时间0 s,敲击方向为垂向,敲击强度1,反射系数0.005,透射系数0.995,截止数值5.0×10-4,采样率1.0×104,传感器位置在管柱4.5 m处,管柱数量300根。
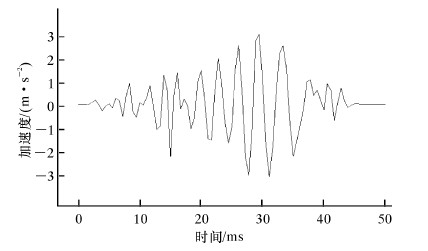
将图2方框内的信号进行模式滤波处理,并在三维空间显示,同时对滤波子波进行信号重构就得到图3的结果。笔者将图3作为敲击仿真源信号来开展管柱振动的波动仿真。
|
| 图 3 重构激励信号时域图 Fig.3 Time-domain diagram of the reconstruction of the excitation signal |
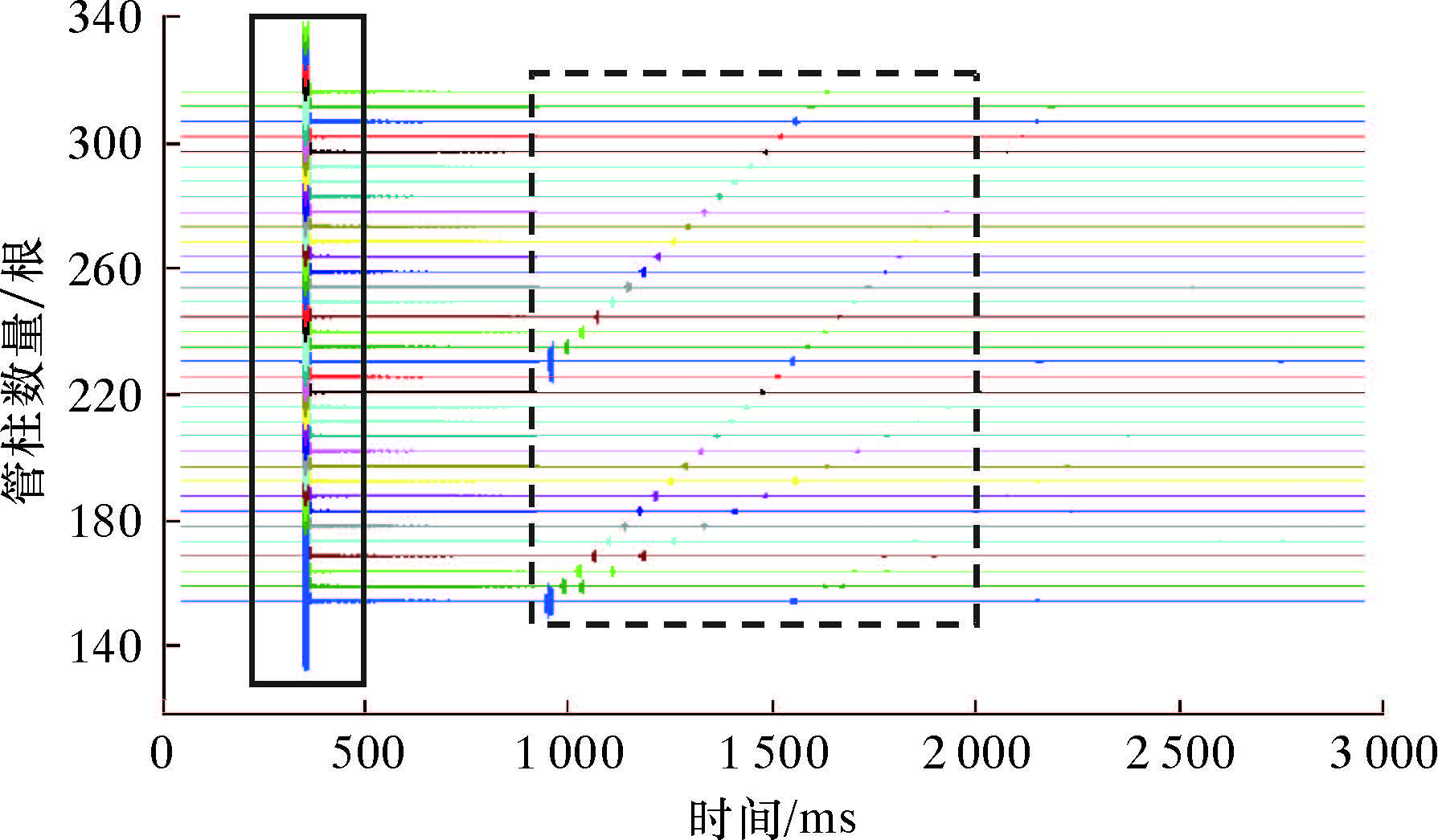
分析管柱振动仿真信号可以发现,管柱振动信号大体上可以分成2类:①结构类信号。该类信号由管柱特定的组成结构决定,在保持传播速度和测量位置不变的条件下,这些信号往往在特定的时刻出现,例如图4所示的实线矩形框中信号。对此类信号进行研究可以大体确定管柱的基本结构与组成。②传递类信号。该类信号是管柱结构的随体响应,往往随管柱结构及其参数的变化而发生相应变化。对此类信号进行分析可以确定管柱和测量系统的变化,例如图4虚线矩形框内的信号。
|
| 图 4 管柱数量仿真结果 Fig.4 The effect of the number drill pipe on the simulation results |
(1)敲击位置对结构类振动信号的影响。图4是保持其他参数不变,敲击位置在管柱1 500 m处,而管柱数量以5根为步长从160根变化至320根的仿真结果。 图4左端振动最强烈的那部分信号由3部分组成:①敲击直达波的透射信号;②与该透射波到达端部后时差约1.586 ms的反射信号;③强度很弱的、对应传感器所在管柱本体两端的多次透射和反射传播信号。其中按时间排列的前10个传播信号见表1。表中振动传递事件链路S[]中的数字为透反射信号到达传感器的顺序编号。因此,撞击信号可以表示为:
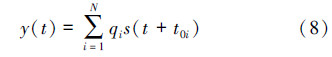
| 序号 | 来源 | 源位置 | 传播 方向 | 信号强度 | 到达时间/ ms | 信号源 |
| 1 | 透射 | 9.5 | 反向 | 0.770 549 | 0.081 886 | S[2] |
| 2 | 反射 | 0.0 | 正向 | 0.770 549 | 0.083 472 | S[2] |
| 3 | 反射 | 9.5 | 反向 | 0.003 853 | 0.083 055 | S[3] |
| 4 | 反射 | 0.0 | 正向 | 0.003 853 | 0.084 641 | S[3] |
| 5 | 透射 | 9.5 | 反向 | 0.003 814 | 0.086 227 | S[5] |
| 6 | 反射 | 0.0 | 正向 | 0.003 814 | 0.087 813 | S[5] |
| 7 | 透射 | 9.5 | 反向 | 0.003 776 | 0.089 399 | S[7] |
| 8 | 反射 | 0.0 | 正向 | 0.003 776 | 0.090 985 | S[7] |
| 9 | 透射 | 9.5 | 反向 | 0.003 739 | 0.092 571 | S[9] |
| 10 | 反射 | 0.0 | 正向 | 0.003 739 | 0.094 157 | S[9] |
式中,N为合成信号的数量,即在计算时段达到传感器的透射和反射信号数量;qi是第i个信号到达传感器时的信号强度;t0i是传感器接收到第i个信号的时间;s(t)是图3所示的波形信号。
由于传感器位置和敲击位置没有改变,在不同管柱数量下第1个直达波到达传感器的时间,以及该直达波在端部反射后经过传感器的时间均保持不变,所以图4振动信号的时域结构也保持不变。
研究还表明,当管柱信号传播速度保持不变时,在同一位置或不同位置处检测得到的结构类信号时域结构保持不变。但是在敲击位置下移到接近管柱底端的过程中,如果底部的反射信号和直达波信号发生重叠干扰,则信号的时域结构会发生很大改变。
图5是传感器固定在管柱4.5 m处,敲击位置以200 m为步长从1 m变化至3 000 m的部分仿真结果。由图可见,信号的幅值随传感器与敲击位置的相对距离呈明显的反比变化,传播的时间也随着该距离的增大而线性增大。随着距离的增大,信号衰减十分明显。
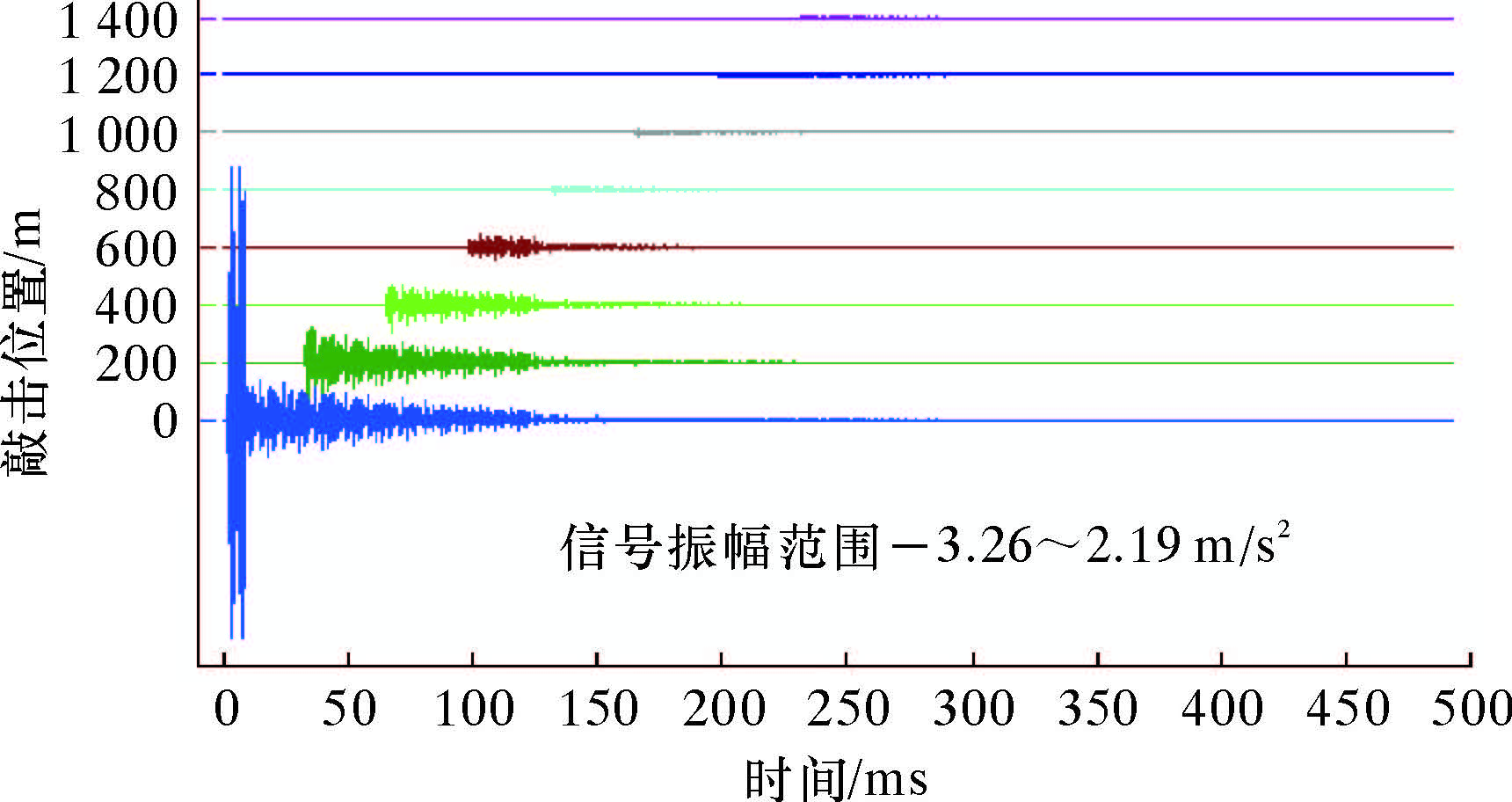
|
| 图 5 敲击位置变化的仿真信号时域图 Fig.5 The effect of the impact position on the time-domain of the simulated signal |
(2)传感器位置对结构类信号的影响。与图5情况相对应的是敲击位置不变,而传感器位置发生变化时,管柱振动信号的测试结果。图6是传感器位置从管柱1 m处开始以50 m的步长变化至管柱5 000 m的部分仿真结果,仿真时敲击位置固定在4.5 m处。由图可见,图5和图6几乎相同。信号幅值随传感器与敲击位置的相对距离呈明显的反比关系,随着距离增大,信号衰减非常大,并且每段信号都有2次明显的冲击波,第1次为敲击源透射波,第2次为管柱顶部反射波,2次冲击波发生的时间随管柱反射端部与传感器之间的距离大致成正比关系。
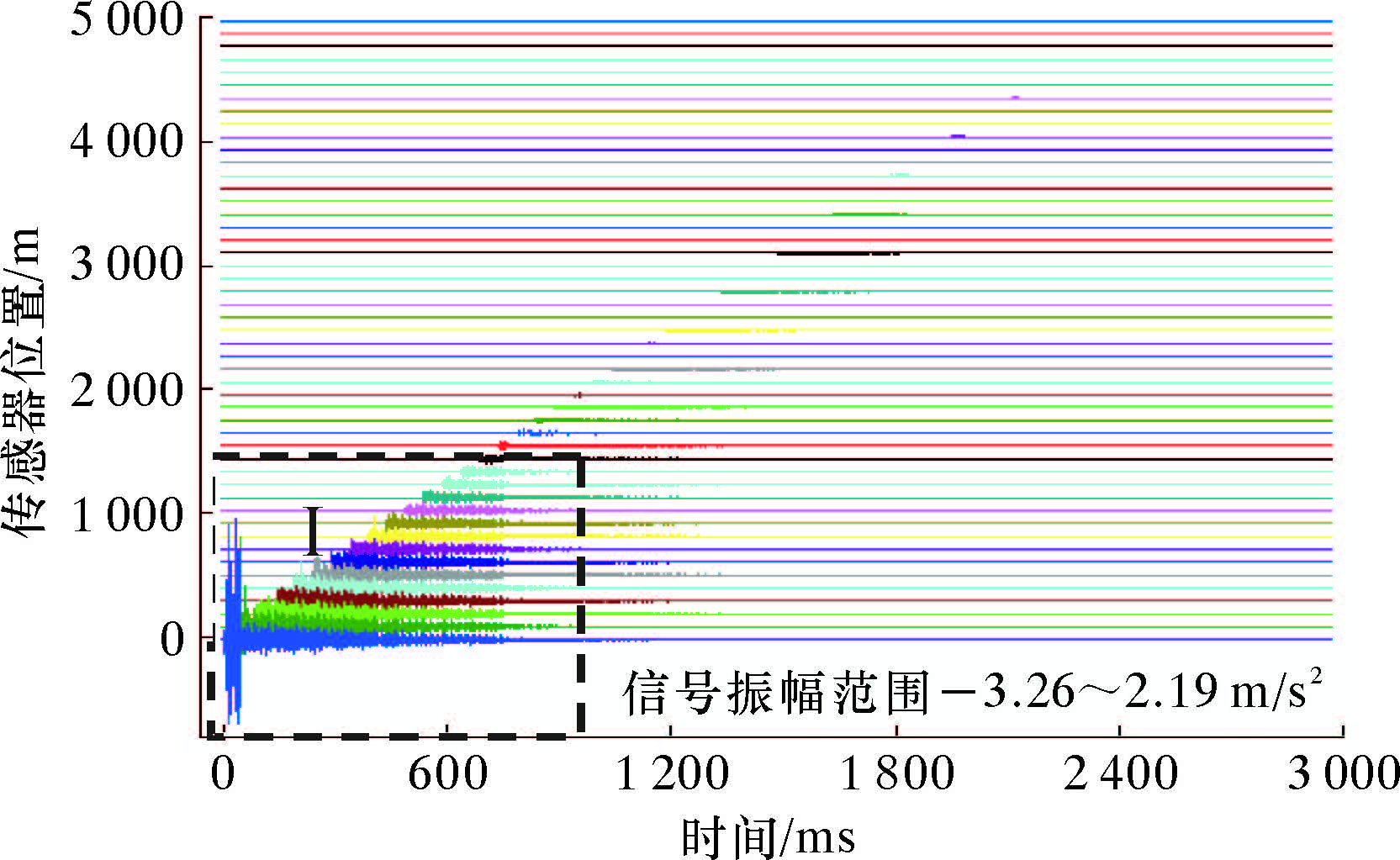
|
| 图 6 传感器位置变换时仿真信号时域图 Fig.6 The effect of the sensor position on the time-domain of the simulated signal |
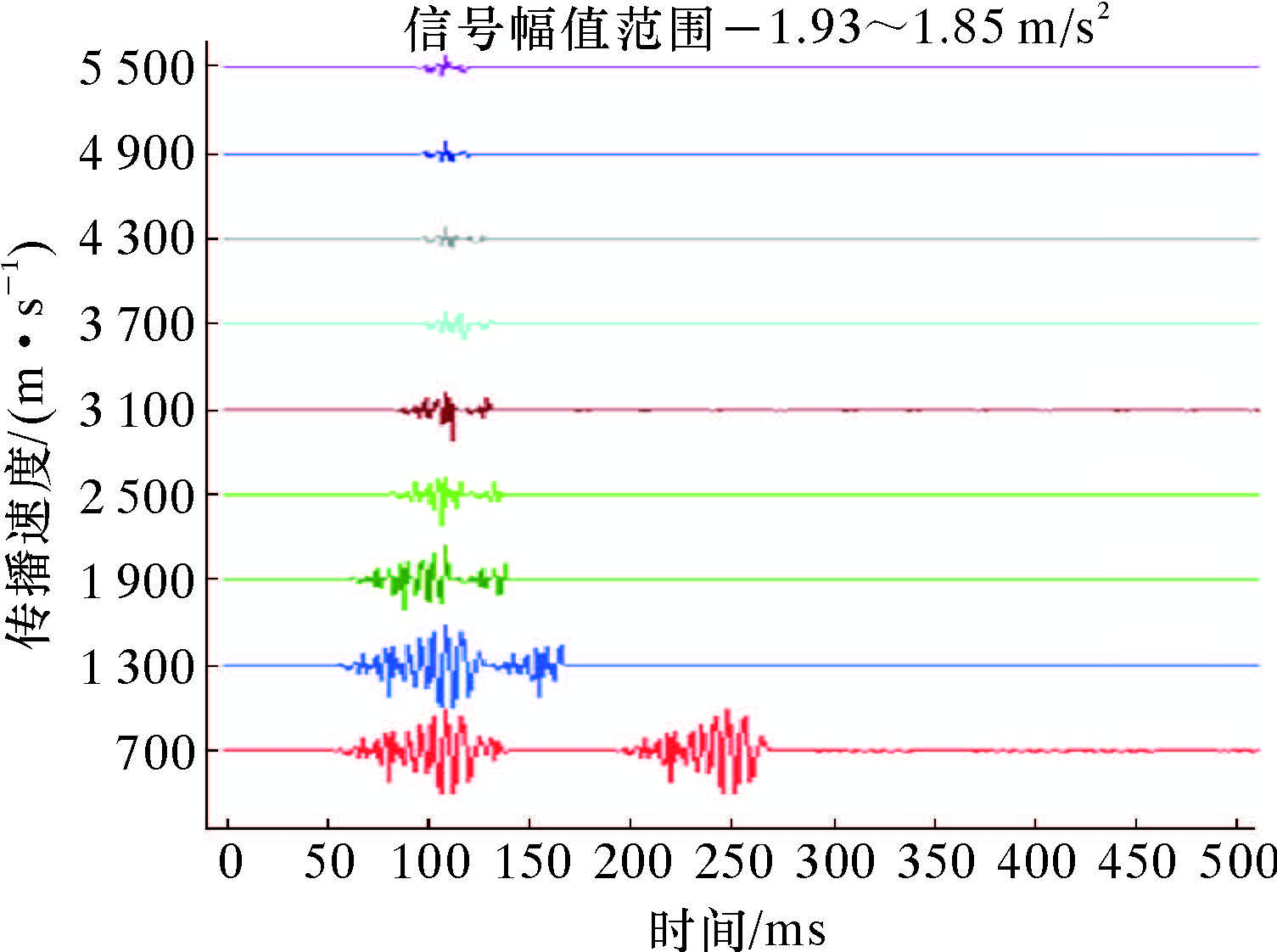
(3)传播速度对结构类振动信号的影响。仿真结果表明,传播速度不仅影响振动波达到传感器的时间,而且对测量得到的结构类信号的波形也会产生很大影响。图7是不同传播速度下结构类振动信号的仿真结果。
|
| 图 7 不同传播速度下结构类信号的变化 Fig.7 The effect of the transmission velocity on structural signal |
当传播速度很低(700 m/s)时,透射波和反射波没有发生时域重叠,是2个各自分离的信号。但随着传播速度的增大,不仅直达的透射波和反射波发生重叠,而且大量的多次透射波和反射波也叠加到传感器中,使得检测得到的信号波形和幅度都发生了很大变化。
表2是当传播速度为700和1 810 m/s时,大约在0.5 s时间段内,参与叠加的透射信号和反射信号。从表可以看出,在700 m/s的低速阶段,只有19个透射信号和反射信号参与叠加;但当传播速度提高到1 810 m/s时,大约有200个透射信号和反射信号参与叠加,导致结构类信号的波形发生很大改变。
| 传播速度700 m/s | 传播速度1 810 m/s | ||||
| 序号 | 来源 | 强度 | 序号 | 来源 | 强度 |
| 1 | 透射 | 0.590 776 9 | 1 | 透射 | 0.590 776 9 |
| 2 | 反射 | 0.590 776 9 | 2 | 反射 | 0.590 776 9 |
| 3 | 透射 | 0.002 953 9 | 3 | 透射 | 0.002 953 9 |
| 4 | 反射 | 0.002 953 9 | 4 | 反射 | 0.002 953 9 |
| 5 | 反射 | 0.002 953 9 | 5 | 反射 | 0.002 953 9 |
| 6 | 反射 | 0.002 953 9 | 6 | 反射 | 0.002 953 9 |
| … | … | … | … | … | … |
| 17 | 反射 | 0.002 866 4 | 190 | 反射 | 0.001 862 6 |
| 18 | 反射 | 0.002 866 4 | 191 | 透射 | 0.001 844 0 |
| 19 | 透射 | 0.002 837 8 | 192 | 透射 | 0.001 844 0 |
(4)透射系数和反射系数对结构类振动信号的影响。只有在接头的反射系数很小和透射系数较大的情况下,才能实现振动信号在管柱内的有效传递。因此,当井下装有减振器等配件时,会给钻头和BHA振动信号解释带来不利影响。如果将传感器装在受敲击管柱上,则透射系数以0.05的步长从0.05变化至0.95的仿真结果如图8所示。

|
| 图 8 透反射系数变化仿真信号时域图 Fig.8 The effect of the transmission and reflection coefficient on the time-domain of the simulated signal |
从图8可以看到,反射系数对信号结构具有明显的影响,在同一衰减系数下,信号的时间曲线大致呈抛物线状分布,抛物线的中轴线处透射系数和反射系数相等,即λ=μ=0.5。然而在轴线下半部分曲线发生了偏差,如图中I段虚线所示,这是由透射信号和反射信号在传播过程中存在时差造成的。
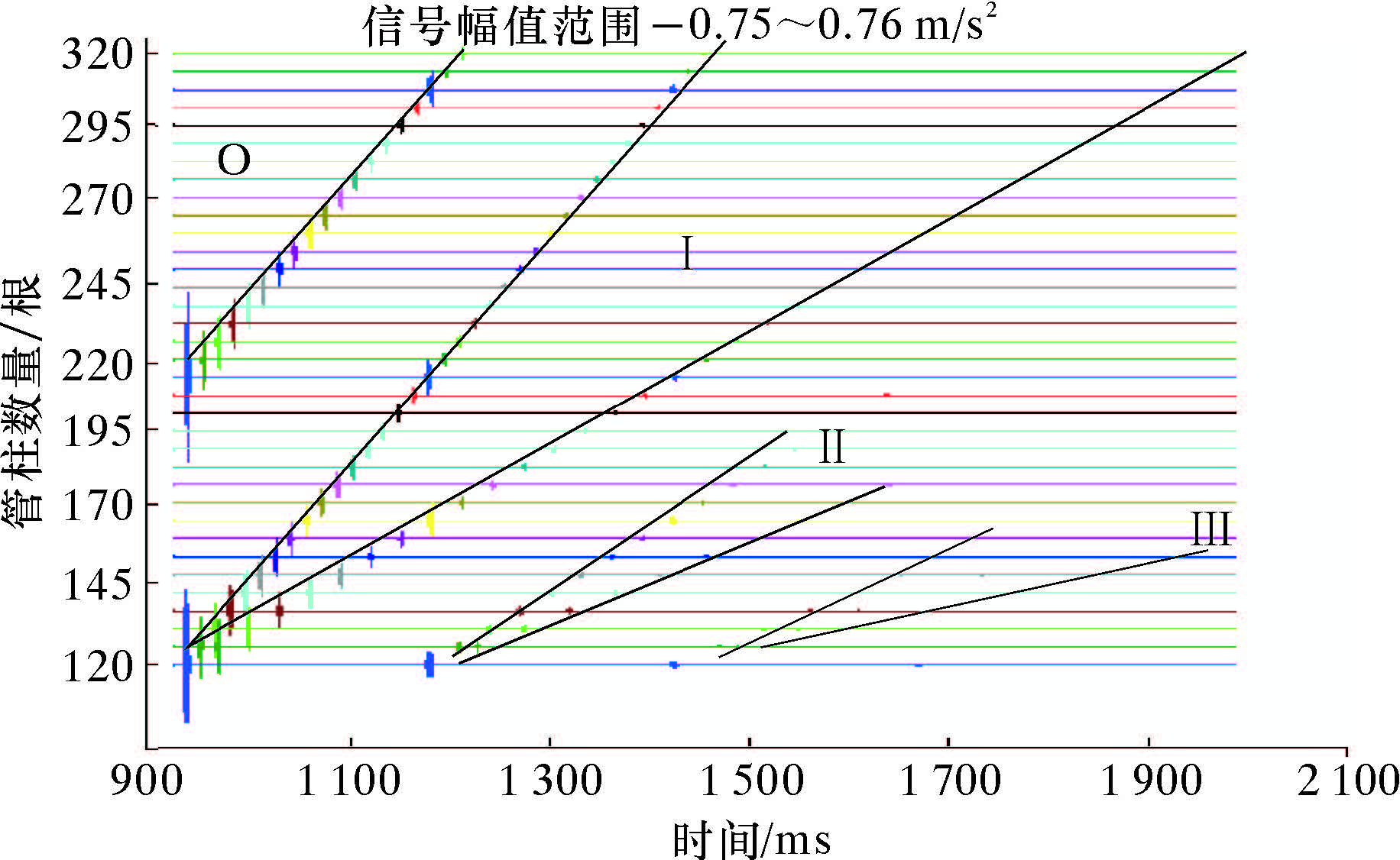
3.2.3 传递类振动信号的影响因素分析(1)管柱数量对传递类信号的影响。从图4可以看出,左端的第1次冲击信号为敲击源信号在离传感器最近管端直达波的透射和反射信号。将虚线框内的信号段放大,即从第2次激励波开始信号随时间呈明显的规律性变化,如图9所示。
|
| 图 9 区域信号放大图 Fig.9 The enlarged regional signal |
从图9可以看到,Ⅰ、Ⅱ、Ⅲ 3个区域信号均呈分叉式变化。经分析,这3个区的信号波形其实就是两端冲击波反射信号在传感器中的叠加,对于由160个单根组成的管柱,就是图中最下方的仿真结果。由于敲击位置为1 500 m,接近管柱底部,所以由敲击位置向2个不同方向传递的信号经过时差的传播之后,又在传感器处产生重叠。但随着管柱数量的增加,一端与传感器的距离逐渐增大,导致图9中的信号间隔呈线性的规律逐渐增强。同时,根据以上分析可知,信号会以该规律不断重复,即在后边的时段内出现Ⅳ、Ⅴ等区域信号。
图9中还存在着O区域信号,该段信号刚好出现在第17段,此时增加的管柱数量刚好为原先的1倍,即320根。实际上,每个区2条直线的交叉点为管柱两端透反射信号的时间交汇点位置。由于管柱数量变化,振动波到达管柱两端的传递时间不同,导致2条直线出现分叉,只要保持对振动信号有足够高的分辨率,就能获得这种分叉的周期特征。利用图9的信号波形特征可以很好地确定井下管柱的长度(或数量),并计算得到发射声振源的深度。
(2)传播速度对传递类信号的影响。图10a是敲击位置和测量位置均在管柱4.5 m处,仿真时间为3.0 s,其他因素不变时,波的传播速度由小变大的仿真结果。从图可以看出,振动波的分布从左到右大致分为3个区。在第1区的信号段主要是敲击激励直达波和0 m处管柱顶端的反射波,另外还包含多次的接头透射波和反射波。当传播速度很小时,直达透射波和端部反射波处于分裂状态,如1区下半部分所示。由波的传递原理可知,在不同速度下1区信号的透射波实际上也按曲线分布,只是此次仿真敲击位置和传感器位置相同,故传播时差为0。图中2、3区域的信号也属于特有的结构类信号,是管柱振动信号在传播过程中产生共振叠加的结果。

|
| 图 10 波的传播速度变化仿真信号时域图 Fig.10 The effect of the wave propagation velocity on the time-domain of the simulated signal |
改变敲击位置,以扩大敲击位置与传感器的相对距离,仿真结果如图10b所示。由于距离的增大,图10a中1区内重叠的信号部分在图10b中被明显地拆分开,由于仿真时间有限,图中只能显示部分信号。根据以上分析可以得出,利用振动法判断井下故障时,只要信号幅值在可辨识范围内,延长采样时间就有利于信号的分离与判别。
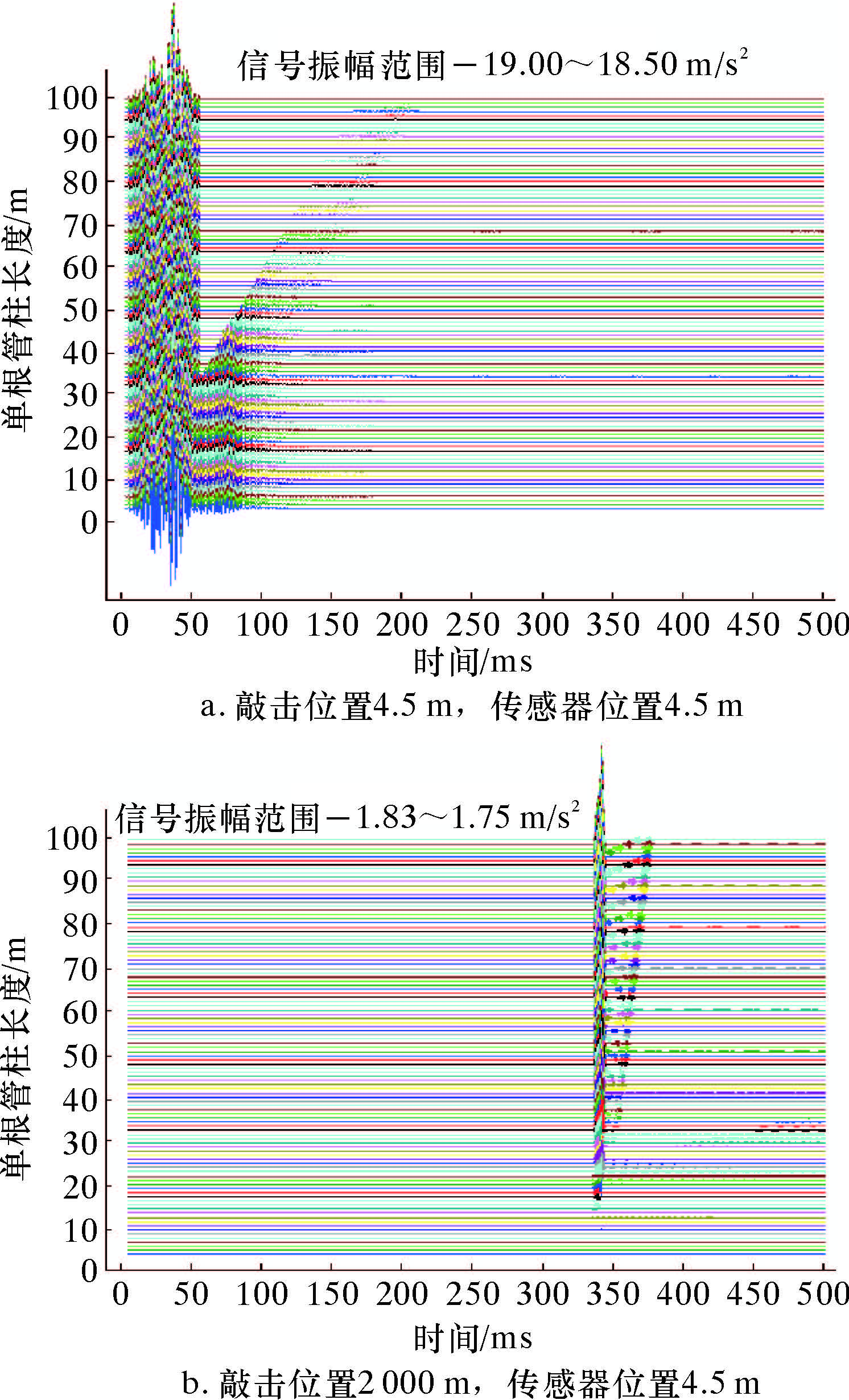
(3)单根管柱长度对传递类信号的影响。图11a是敲击位置在管柱4.5 m处,传感器处于管柱4.5 m处时,管柱长度由1 m以1 m为步长变化至100 m的信号时域图。从图可以发现,随着单根管柱长度增大,在起初阶段信号的分布相似;当管柱长度达到32 m时,信号开始分裂,并以一定的斜率变化。当敲击位置改变为管柱2 000 m处时,在管柱长度也为32 m时,信号开始分裂,并以一定的斜率变化,如图11b所示。
|
| 图 11 管柱长度变化振动信号仿真结果 Fig.11 The effect of the drill string length on the vibration signal simulation results |
在一定的采样率下,能够分辨的管柱长度变化存在一个下限值。低于该值时,相邻接头振动波的传播间隔时间过短,低于传感器的采样时间间隔,故波以叠加为主,仿真得到的每一个信号波形相似,但数值不同。也就是说,只有当采集系统的采样率高于信号变化时差时才可以将波形合理分辨,并能显现自身的传播规律。因此对于现场的管柱,应根据实际管长与管柱材料,选择合适的信号采集器与传感器,以便合理采样。
3.3 管柱振动信号分析步骤由前面的管柱振动信号系统仿真分析可知,为了对管柱振动信号进行科学的现场测试与分析,应从结构类信号开始研究。具体而言,可以分为以下几个步骤:
(1)找到管柱振动的直达波及其合成信号;
(2)结合研究对象的物理性质以及结构参数,详细研究直达波及其混叠信号波形,由此来揭示研究对象的本质特征;
(3)从采集信号中截取不同时间段的结构类信号,并按照时间对应尽可能一致的原则,将信号汇总排列在一起;
(4)采用文献[9,10]介绍的模式滤波法和最优频率匹配法等,从汇总排列的信号段中排除噪声干扰,对管柱振动信号进行分离、分类以及合理的归类处理;
(5)从归类后的分离信号中找出传递类信号,以便获取管柱在井眼内运动的各种有用信息。
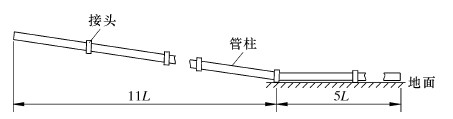
4 结果验证 4.1 试验装置的构建与信号的采集鉴于钻井现场的约束,笔者采用室内模拟试验。试验采用AWA6290A声振信号同步采集仪,采样率为10 kHz,管柱布置与传感器分布如图12所示。
|
| 图 12 管柱试验测试系统示意图 Fig.12 Schematic of the drill string test system |
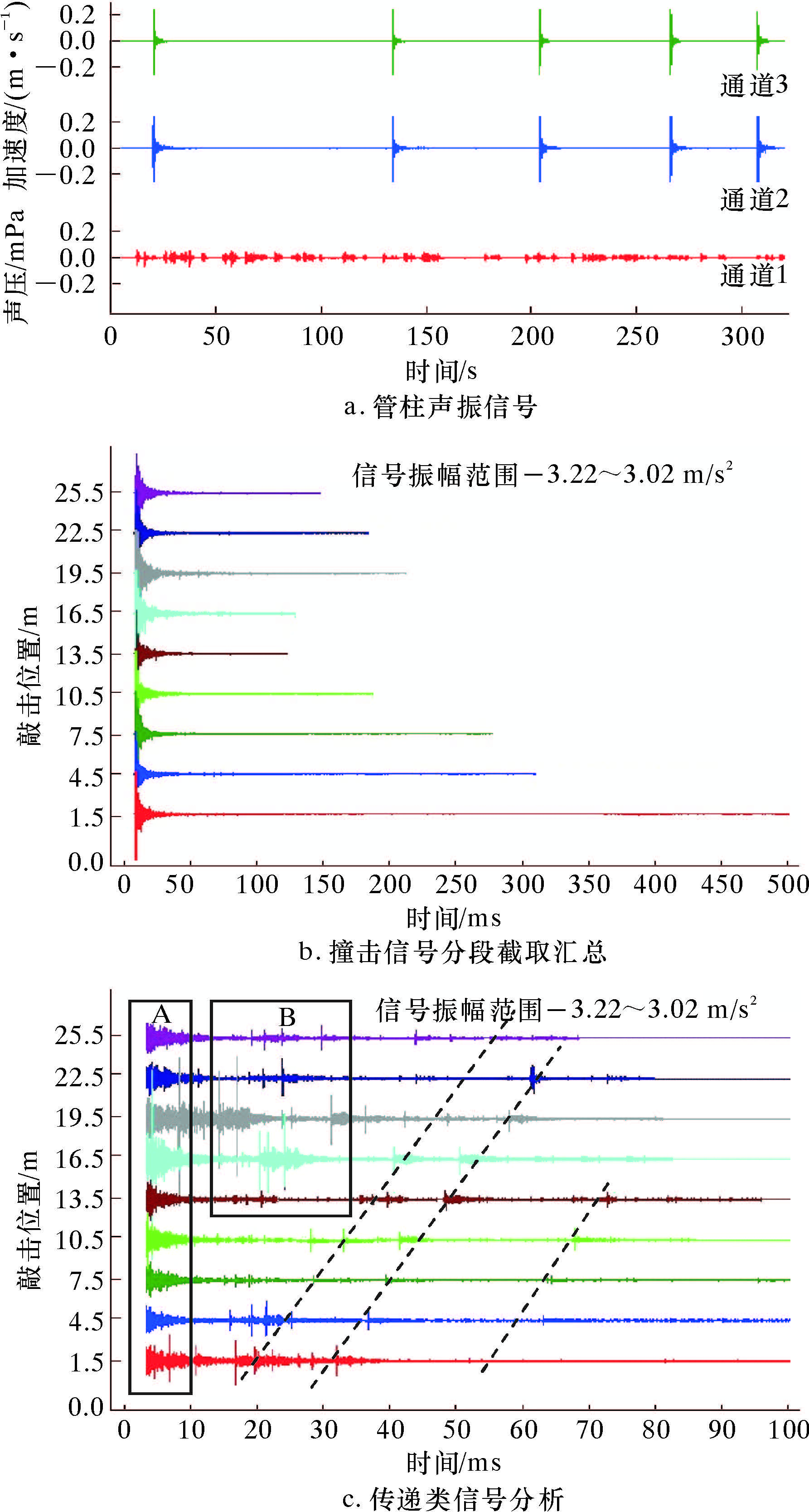
试验中,采用16根、长L=3 m的空心碳素钢管来模拟钻井管柱,每2根管柱之间采用同质材料接头连接。通过人为采点敲击,测得2个通道的振动信号和1个通道的声信号,如图13a所示。
|
| 图 13 实测多通道信号时域图 Fig.13 The measured multi-channel signal time-domain diagram |
图13a的直达波信号很容易分辨,就是振动极为强烈的撞击信号。因文章篇幅有限,并结合验证试验的可操作性,采用敲击位置因素进行本次验证。数据源采用上述试验所获得的通道2振动信号。试验过程中进行了9次敲击,时间间隔比较长,均为2 s以上,因此每次振动信号具有非常明显的独立性。从采集信号中分段截取这9段信号,汇总显示如图13b所示。对这些信号的前0.1 s部分进行放大,以便进行传递类信号分析,结果如图13c所示。
从图13c可以发现,现场试验所获得的波形比仿真信号复杂。但不管怎样,如果以敲击后的首个到达传感器的强烈振动信号为起点进行汇总排列,就可以得到图13c的结果。显然图中实线框A为结构类信号,是多次透射信号和反射信号叠加的结果。比较汇总信号传播后期的波形发现,存在明显的、按照图中虚线传播规律变化的小幅撞击振动,即管柱的传递类信号。因此,可以利用前面介绍的方法来确定振动系统的物理特征参数。进一步的研究发现,B区内信号实则为管柱自身振动引起的振动波。试验中敲击位置变大的过程中,经过了从管柱顶部到中部,再由中部至顶部的变化,由此引起的管柱自身晃动也由弱变强再变弱,B区域信号的分布及幅值变化很好地反映了这一变化。
由以上分析可知,管柱振动信号由敲击信号通过一定的方式叠加而成,可以利用实测振动信号的波形分析来获得实际的敲击信号、管柱振动的反射系数和透射系数,以及管柱系统的结构特征。也就是说,本研究也为新的管柱振动信号解释方法的创立创造了一定条件。
5 结 论(1)管柱振动信号在传播的过程中存在着多次透射和反射,由此形成各种复杂的信号结构。通过建立管柱振动系统模型,编制软件实现了管柱振动的系统仿真,获得了信号振动的系统特征与规律性。
(2)管柱的系统仿真分析结果表明,在管柱内的振动传播存在明显的多次波效应,传播过程存在着衰减效应。管柱振动信号波形大体上分为2类,即结构类信号和传递类信号。结构类信号在时域上往往在特定的时刻出现,而传递类信号往往随测量系统的变化而相应变化。
(3)结构类信号与管柱的组成及物理参数相关,也与管柱的共振相联系。在管柱物理参数不变的情况下,可以利用结构类信号来确定管柱的几何结构以及撞击信号的源特征。通过分析传递类信号的变化规律,可以获得管柱长度、敲(撞)击位置、传播速度、透射系数及反射系数等有用信息。
(4)通过信号的系统仿真研究,提出了开展管柱振动信号测试分析的步骤和方法,并利用室内管柱振动试验验证了该方法的有效性。
笔者的研究为新的管柱振动信号解释方法的创立创造了一定条件,也为井下管柱的故障诊断、定位,管柱系统特性参数的确定以及信号分析提供了依据。
| [1] | 李子丰,张少南,李敬媛.定向水平井杆(管)柱纵向振动的数学模型[J].石油机械,1993,21(7):47-52. |
| [2] | 梁政,邓雄,余孝林.高温高压深井测试管柱横向振动分析[J].油气井测试,1999,8(4):5-11. |
| [3] | 牛成成,张辉,李善伟,等.深水作业管柱横向振动特性计算[J].内蒙古石油化工,2012(22):23-25. |
| [4] | 朱才朝,冯代辉,陆波,等.钻柱结构与井壁岩石互作用下系统耦合非线性动力学研究[J].机械工程学报,2007,43(5):145-149. |
| [5] | 李子丰,张永贵,侯绪田,等.钻柱纵向和扭转振动分析[J].工程力学,2004,21(6):203-209. |
| [6] | 刘德顺,李夕兵,朱萍玉.冲击机械动力学与反演设计[M].北京:科学出版社,2007. |
| [7] | 宿雪,葛洪魁,杨微,等.钻柱振动录井的研究现状及发展趋势[J].石油机械,2009,37(5):15-19. |
| [8] | 崔士波,葛洪魁,陆斌,等.钻柱振动信号特征及多次波成像[J].地球物理学进展,2010,25(2):714-720. |
| [9] | 吕苗荣,王茜.模式滤波法分离井场振动信号的应用实践[J].噪声与振动控制,2010(2):107-110. |
| [10] | 吕苗荣,李梅.工频干扰振动信号的建模与分离处理[J].噪声与振动控制,2012(4):158-162. |



