2. 北京林业大学水土保持学院重庆缙云山三峡库区森林生态系统国家定位观测研究站, 100083, 北京
-
项目名称
- 国家自然科学基金“降雨条件下植物根系动态固土护坡效应研究”(31971726);北京林业大学热点追踪项目“重庆缙云山森林火灾调查和灾后植被恢复重建研究“(2022BLRD11)
-
第一作者简介
- 李通(1991—), 男, 博士。主要研究方向: 水土保持工程。E-mail: 1142618421@qq.com
-
通信作者简介
- 王云琦(1979—), 女, 博士, 教授, 博士生导师。主要研究方向: 水土保持工程。E-mail: wangyunqi@bjfu.edu.cn
-
文章历史
-
收稿日期:2022-11-04
修回日期:2023-02-22
2. 北京林业大学水土保持学院重庆缙云山三峡库区森林生态系统国家定位观测研究站, 100083, 北京
2. Three-Gorges Reservoir Area (Chongqing) Forest Ecosystem Research Station, School of Soil and Water Conservation, Beijing Forestry University, 100083, Beijing, China
降雨诱发的浅层边坡失稳为我国山地灾害最常见形式之一。这种侵蚀现象往往发生在数米之内的坡面浅层,其单个规模不大,但在流域内密集分布,发生频率高。其造成的松散碎屑往往是泥石流的主要物源,潜在危害和土壤流失巨大[1]。当前已对降雨浅层滑坡的孕灾机理有了统一认识:1)降雨入渗导致的浅表层土体基质吸力丧失,土体强度降低[1-3];2)土体在降雨中饱和度升高,总容重变大,下滑力变化导致稳定性降低,最终导致塑性破坏和失稳[4-5]。边坡稳定性和侵蚀机理的研究一直是世界性课题。
长期以来对滑坡的研究以易发性和安全分析为主要目的,大致分为2类:1)早期基于空间监测的滑坡灾害和气象数据在统计学上的关联性研究,建立临界降雨阈值模型如E-D模型、I-D模型等,随着人工智能飞速发展,近期基于机器学习和深度学习的滑坡易感性分析也成为新的热点;2)基于力学原理的边坡稳定性分析,定义其稳定系数为上覆滑体抗滑力与下滑力的比值,表征当前土体的状态相对于临界滑动的强度和安全储备,如常见的极限平衡或有限元分析。尽管2类方法在区域尺度和分析精度上各有优势,成为了滑坡灾害研究的得力工具,但对滑坡可能产生的侵蚀量即“潜在重力侵蚀”的估计和预测相对重视较弱。“潜在重力侵蚀”一旦由未然转化为已然,其碎屑体势必成为土壤流失甚至泥石流灾害的主要物源。相比之下,回归力学本质的有限单元法根据有滑坡侵蚀过程的分析和量化。针对以滑坡为主的潜在侵蚀量的模拟方法和计算流程依然为当前水土保持领域重力侵蚀计算中有待完善的工作。
针对降雨型边坡稳定分析的有限元模拟技术已基本成熟,国内外专家提出的孔隙水压力-土体应力耦合方法也已形成较为完善的计算流程,并在ABAQUS、ANASYS、PLAXIS、Geo-studio等岩土软件中广泛应用,模拟所得的潜在滑动面或整体安全系数有助于指导欠稳定边坡加固工程的实施或灾害预警。实现降雨过程中边坡剪切破坏方量的模拟和预测,所用方法至少应同时满足:1)适用于3D情境非均质土的应力-变形模拟;2)满足非饱和土多孔介质流固耦合分析要求;3)失效范围的判别提取和量化。
现在被广泛采纳的稳定性分析方法以极限平衡法和有限元强度折减法为主,以Geo-studio平台为代表的极限平衡法Morgenstern-Price法[6-7]可提供安全系数小于1的边坡失稳范围,当前软件依然为单宽度平面应变模型,当考虑土体侧向异质性时单宽滑弧不能映射至三维真实滑动面,无法满足侵蚀量的预测。而基于有限元法的强度折减法将黏聚力和摩擦角的等比折减系数作为土体的强度储备参数和边坡稳定系数[8-10],可将等效塑性应变带作为滑坡体范围,其在整体稳定性分析上的优势越来越受到科研工作者的青睐。但无论是基于折减计算收敛性或是基于塑性带贯通的失效判据,都无法给出明确的土体失效范围,因为折减系数要么大于1,要么不收敛。受限于单个时间节点稳态计算的效率,也不适合较高时间分辨率的侵蚀量的瞬态模拟。
近年来除传统有限元强度折减和极限平衡法外,新一类的边坡稳定分析方法-局部稳定系数标量场法应运而生,类似于极限平衡的概念,定义为空间任意点的Mohr-Coulomb抗剪强度和剪应力比值,作为标量场求解[1]。一方面,它延用极限平衡中稳定系数的概念,且避开了滑动面假定的步骤;另一方面它兼顾了有限元方法中应力和变形的考虑,具有三维空间分析和瞬态分析的潜力。按是否考虑非饱和效应列举,以总应力分析的研究。如:杨涛等[11]通过在位移等值面上定义点安全系数的方法,建立FLAC3D局部稳定分析模型,并验证其可靠性;闵江涛等[12]采用ANAYS复刻了杨涛等的分析方法,分析多层土坡稳定性;宋林波等[13]和齐兵等[14]将点安全系数法拓展至三维,分别分析了基坑和工程坡地的三维点安全系数云图。以非饱和有效应力分析的研究如: 鲁宁[15]通过自定义局部稳定系数(local factor of safety, LFS)在HILLSLOPE(FS2D)中模拟了降雨边坡的局部稳定性;以此为模板,Shao等[16]分析了降雨-优先流对边坡稳定的影响;Moradi等[17]分析了基岩形态对边坡渗流与稳定的影响;Dou等[18]分析了土层界面效应对边坡渗流稳定的影响。尽管如此,上述应用案例的主要目的为边坡安全方面,目前鲜有侵蚀量量化的案例可供参考。
综上,3类边坡稳定性分析方法的特点对比见表 1,可知LFS法具有实现降雨过程中边坡土体潜在重力侵蚀量瞬态量化的潜力。本研究拟采用有限元软件COMSOL Multiphysics综合边坡水文与高等土力学知识,对降雨诱发的浅层滑坡过程进行模拟,并对若干降雨时间节点的潜在剪切破坏方量进行积分量化。研究中所用思路和方法为探索性研究,有助于未来岩土模拟计算程序的进一步开发,也可为相关工作者提供降雨滑坡敏感土壤潜在侵蚀计算的便利。
| 表 1 3类稳定性分析方法对比 Tab. 1 Comparison of 3 stability analysis methods |
数值模拟试验采用流固耦合思路,在建立初始地应力-重力-基质吸力平衡条件的基础上对渗流场和应力场同时求解,其应力平衡原理[15-18]为
| $ \nabla(\sigma)+\gamma(\theta) b=0 \text { 。} $ | (1) |
式中: σ为应力张量,kPa;γ(θ)为增湿土重度,kN/m3;b为体力单位矢量。
根据Bishop有效应力原理[19]:
| $ \sigma^{\prime}=\sigma-\chi p_{\mathrm{w}} \text { 。} $ | (2) |
式中:σ′为有效应力,kPa;pw为孔隙水压力或基质吸力,kPa;χ为基质吸力系数,量纲为1,以饱和度取值。
土体渗流场采用Richards方程[20]描述,
| $ \frac{\partial \theta(h)}{\partial t}=\nabla K(h) \nabla H+W。$ | (3) |
式中:θ(h)为含水方程;h为压力水头,m;K(h)为非饱和水力传导率,m/s;H为水头,m;W为源项。
含水方程和相对渗透性采用Mualem和van-Genuchten[21]方程描述:
| $ S_{\mathrm{e}}=\frac{\theta(h)-\theta_{\mathrm{r}}}{\theta_{\mathrm{s}}-\theta_{\mathrm{r}}}=\left(\frac{1}{1+(\alpha|h|)^n}\right)^m ; $ | (4) |
| $ K(h)=K_s S_{\mathrm{e}}^1\left(1-\left(1-S_e^{\frac{1}{m}}\right)^m\right)^2 \text { 。} $ | (5) |
式中:Se为饱和度,量纲为1;θs、θr分别为饱和含水率和残余含水率,量纲为1;Ks为饱和水力传导率, m/s;α、m和n为拟合参数;l为经验值取0.5。
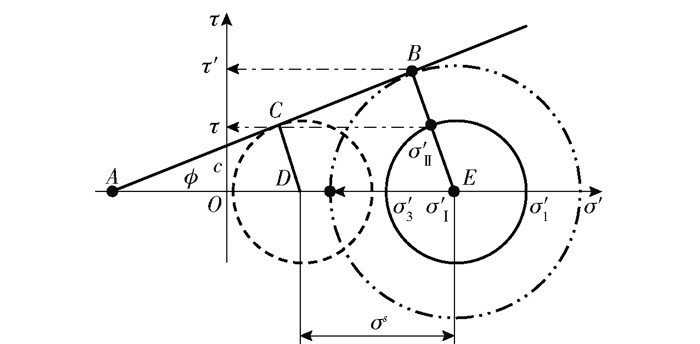
1.2 基于局部稳定系数的潜在破坏方量计算Lu等[1, 15]将局部稳定系数LFS的标量定义为边坡某一点处潜在破坏的应力与当前摩尔应力的比值,库伦应力可以通过莫尔圆平移使其与摩尔库伦包络线相切而确定(图 1),其表达式为
| $ L_{\mathrm{FS}}=\frac{\cos \phi^{\prime}}{\sigma_{\mathrm{Ⅱ}}^{\prime}}\left(c^{\prime}+\sigma_{\mathrm{Ⅰ}}^{\prime} \tan \phi^{\prime}\right) 。$ | (6) |
式中:c′为排水条件下黏聚力,kPa;ϕ′为内摩擦角,°;σ′Ⅰ和σ′Ⅱ分别为土体的平均有效应力和有效偏应力,kPa;即:
| $ \sigma_{\mathrm{Ⅰ}}^{\prime}=\frac{\sigma_1^{\prime}+\sigma_3^{\prime}}{2}=\frac{\sigma_1+\sigma_3}{2}-\sigma_{\mathrm{s}} ; $ | (7) |
| $ \sigma_{\mathrm{Ⅱ}}^{\prime}=\frac{\sigma_1^{\prime}-\sigma_3^{\prime}}{2}=\frac{\sigma_1-\sigma_3}{2} ; $ | (8) |
| $ \sigma_s=\chi\left(u_a-u_w\right) \text { 。} $ | (9) |
式中:σ′1和σ′3分别为土体的第1、3有效主应力,kPa;σs为非饱和吸应力,kPa。
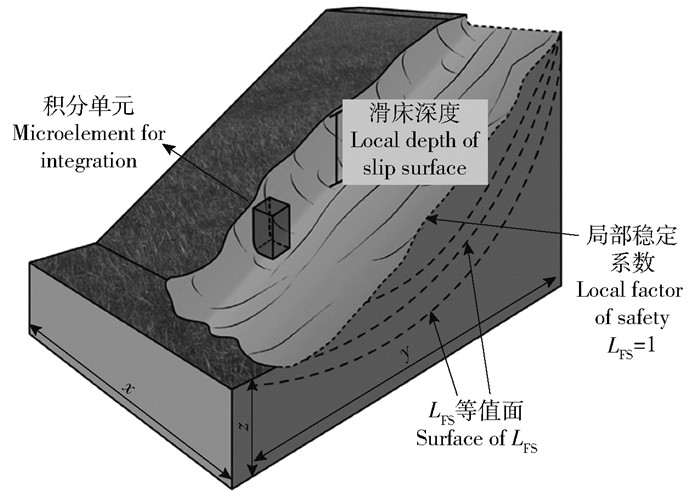
对局部稳定系数标量场进行进一步处理,以LFS≤1等值线包络区域作为潜在破坏区域,如图 2所示,通过空间积分[22]计算潜在侵蚀方量(potential gravity erosion,PGE)
| $ P_{\mathrm{GE}}=\iiint_{L_{\mathrm{FS}}<1} \mathrm{d} x \mathrm{d} y \mathrm{d} z。$ | (10) |
|
图 2 潜在重力侵蚀量计算示意图 Fig. 2 Illustration of the PGE volume calculation |
为探讨上述LFS法模拟3D边坡的可靠性,同时采用广为认可的强度折减法(strength reduction method,SRD)[8-10]计算滑动位置,等比折减原理为:
| $ \left(\begin{array}{l} c_{\mathrm{m}}=c^{\prime} / F_{\mathrm{OS}} \\ \varphi_{\mathrm{m}}=\arctan \left(\tan \varphi^{\prime} / F_{\mathrm{OS}}\right) \end{array}\right.。$ | (11) |
式中: cm为临界状态黏聚力,kPa;φm为临界状态内摩擦角,(°);FOS为折减系数, 即边坡的整体稳定系数。
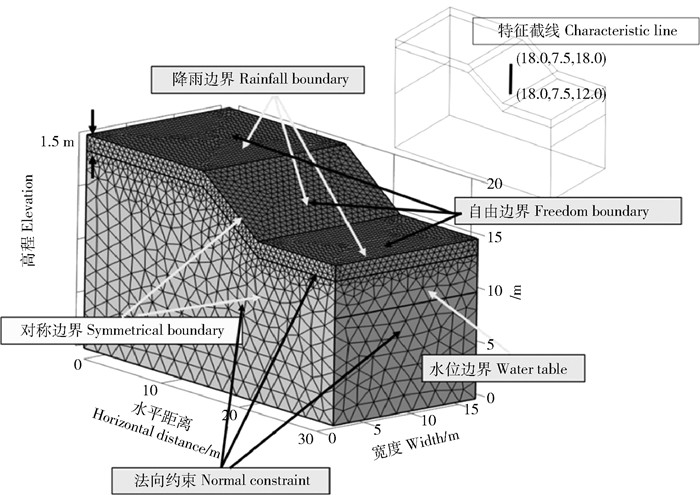
1.4 计算流程与示例为研究降雨过程中边坡的整体稳定性变化及局部稳定性变化,并实现所述潜在侵蚀方量即剪切失效土体体积的量化计算,笔者设计坡高5 m、坡度35°的均质土坡模型,为排除边坡周围约束及排水条件对目标范围的影响[9]。经多次试算,坡顶及坡脚宽度15和10 m,坡脚以下空间扩大至15 m,最终确定尺寸如图 3所示。力学边界中,4围采用法向约束,底面全约束,坡面自由;渗流边界中,左右两侧采用10 m水头控制地下水位,前后2面及底部为不透水边界,坡面为流量边界,单位流量设置为80 mm/d,时长5 d模拟连续暴雨情境。渗流和变形的求解均采用自由四面体网格,由于上表面受降雨影响,水力梯度变化较大,单独剖分1.5 m深度进行网格加密处理,单元8万4 202个,网格顶点数1万5 662个。用于监测和分析土层数据的特征截线位置及坐标见图 2右上角。边坡土体简化为均质,力学及水力参数见表 2。
|
图 3 边坡模型边界条件及网格剖分示意 Fig. 3 Boundary conditions and mesh physics generalization of slope model |
| 表 2 边坡模型力学及水力参数 Tab. 2 Mechanical and hydraulic parameters of slope model |
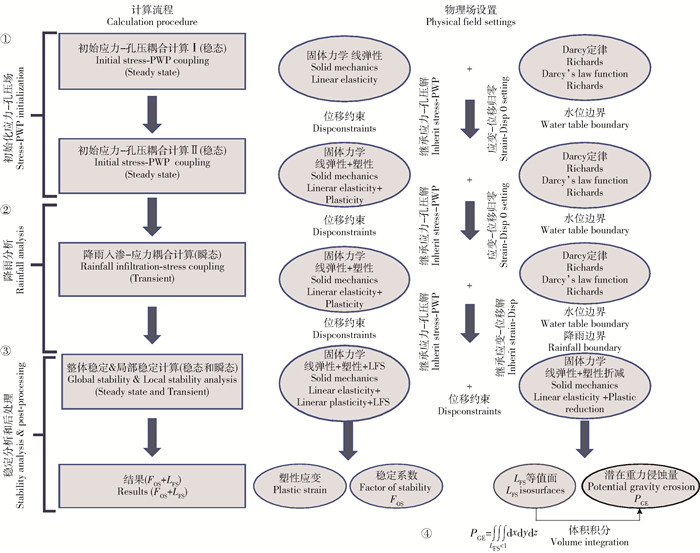
计算思路和模拟流程如图 4所示,分4步进行:1)首先在稳态条件下进行初始孔压和应力的求解;2)其次在瞬态条件下施加降雨边界,进行降雨过程中孔压变化条件下边坡有效应力和变形的求解;3)然后对第2步中各个时间节点进行强度折减,计算边坡整体稳定性,其实质为稳态分析;4)最后继承降雨过程中的孔隙水压力解和有效应力解,采用自定义变量LFS的方法计算边坡的局部稳定性,其实质为步骤2瞬态解的后处理过程,进一步地,将LFS≤1等值面包络区域作为潜在侵蚀区域,自定义intop (expr)函数通过体积积分得到潜在侵蚀方量。步骤1中所得到初始地应力导入步骤3后得瞬态降雨计算的初始位移为4.18×10-7 m,远在mm级以下,地应力平衡效果良好。求解过程中对上一步骤解的继承和调用采用软件算符withsol (expr)实现,如对步骤2中应力和应变的调用表示为:withsol 2 (σij),withsol 2 (eij)。
|
图 4 COMSOL中的计算思路及模拟流程 Fig. 4 Calculation procedure and simulation step diagram in COMSOL |
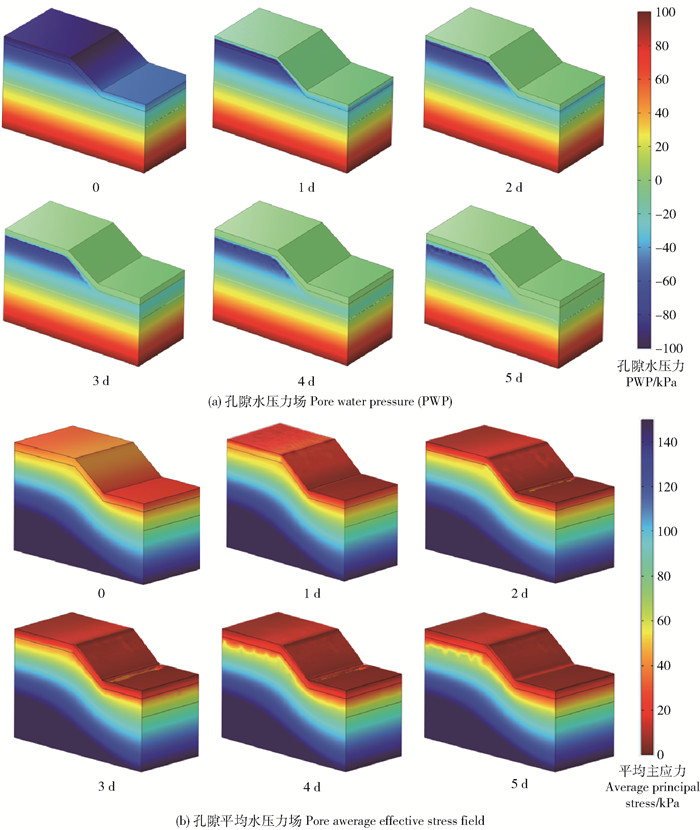
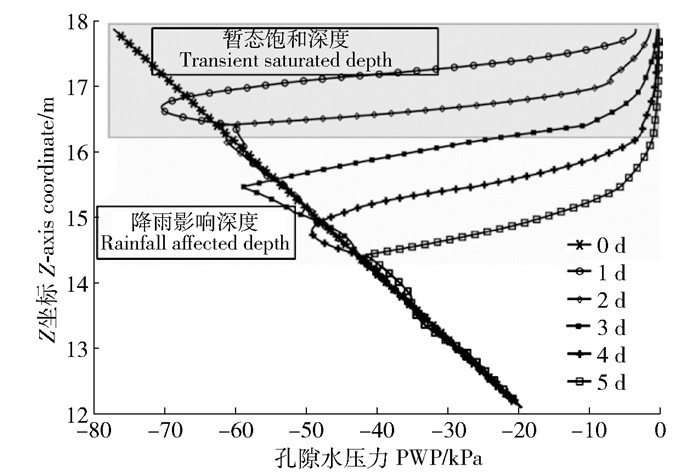
模拟降雨情境下边坡孔隙水压力变化(图 5a),初始状态下边坡孔压随高程线性分布,从坡底至坡顶由100 kPa均匀变化至-100 kPa,随降雨进行,表层有较快的孔压变化,因为地下水位位于坡脚下5 m,模拟所用渗透性函数的孔径参数较小,土体非饱和渗透性随高程变化不明显,整个上下坡位湿润锋基本平行于坡面向下层发展,降雨5 d时入渗深度约为3.5 m,表层暂态饱和深度约2 m,孔压接近0的近饱和状态(图 6),表层基质吸力基本丧失,整个降雨过程中地下水位无明显变化。
|
图 5 降雨过程中边坡孔隙水压力场和平均主应力场变化 Fig. 5 Temporal change of pore water pressure field and average effective stress field of slope during rainfall |
|
图 6 降雨过程中边坡特征截线孔隙水压力变 Fig. 6 Temporal change of PWP at characteristic line during rainfall |
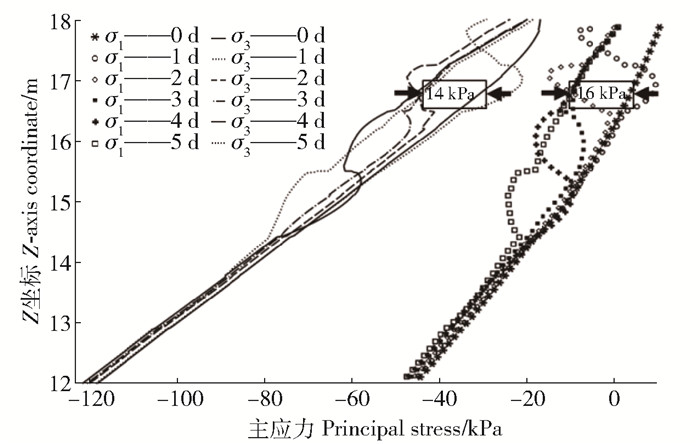
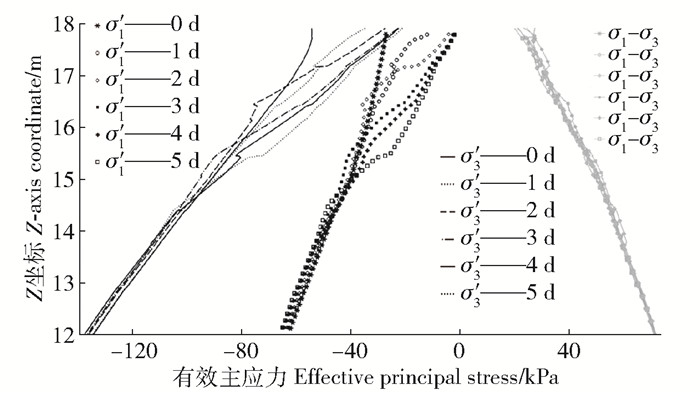
模拟降雨情境下边坡平均有效主应力变化云图如图 5b所示,初始状态下边坡平均有效主应力受重力场影响,空间内呈现随深度增大,由深至浅层转向平行于坡面的分布规律,从坡底最深处至坡面由204 kPa变化至16.9 kPa。随5 d降雨进行,表层平均有效主应力有明显降低,最值范围变为206~1.86 kPa,在近坡面位置的低应力带厚度增大,坡脚处有轻微应力集中。为了解主应力的变化详情,绘制特征截线上第1、第3主应力结果如图 7。COMSOL中压力为负,因此本研究第1、3主应力排序与绝对值大小相反,可知,降雨前2个主应力随深度呈近似线性增大趋势,与云图相符,随降雨进行,2个主应力呈逐层增大,5 d分别增大约14 kPa和16 kPa,该变化由重力效应引起。纳入基质吸力作用,有效应力结果见图 8。可知有效主应力受降雨的影响浅层土大于深层,表现为浅层的大幅度降低和深层的极小幅度增高。该变化趋势由降雨入渗过程中的基质吸力消散和湿润增载2种效应共同引起,机理见式(1)和(2)。偏差应力σ1-σ3随降雨时间变化不大,随时间变化趋势也不单调,降雨入渗对截线位置土体剪切行为的影响过程比较复杂。
|
图 7 降雨过程中边坡特征截线上主应力变化云图 Fig. 7 Temporal change of principal stress at characteristic line during rainfall |
|
图 8 降雨过程中边坡特征截线有效主应力变化云图 Fig. 8 Temporal change of effective principal stress at characteristic line during rainfall |
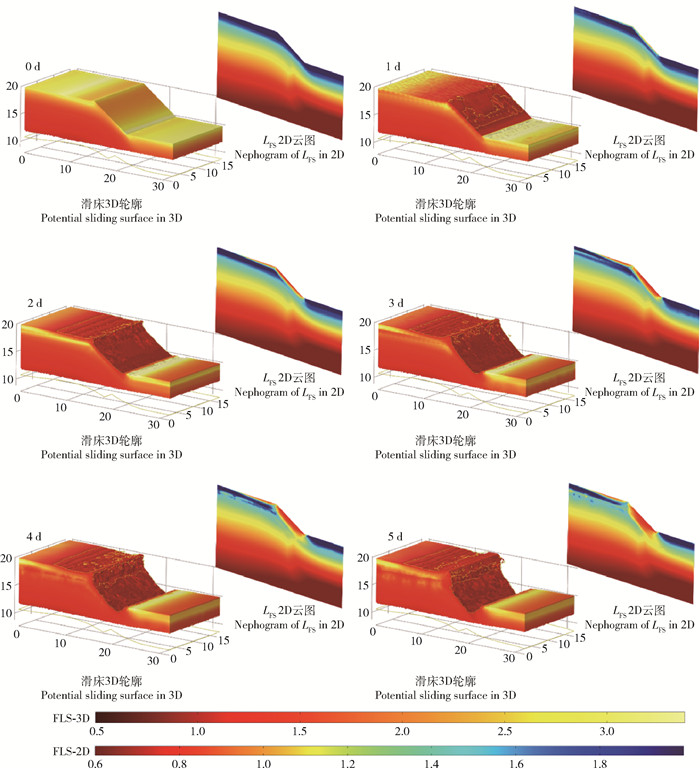
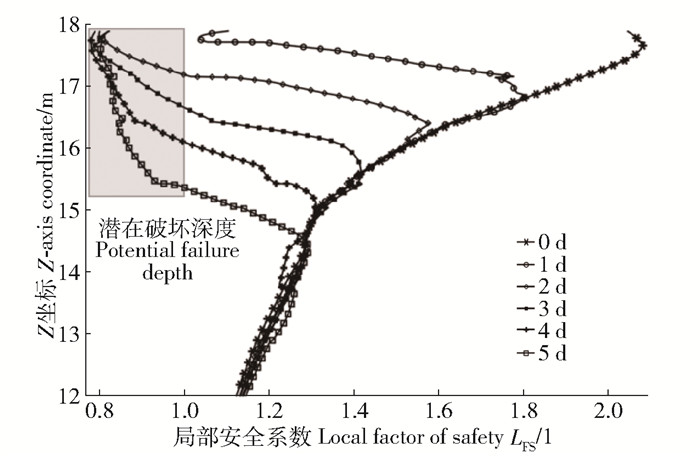
图 9为降雨过程中边坡中部截面LFS云图(右上)及三维潜在滑床的轮廓(左下),该滑床由LFS云图移除LFS≤1等值面包络土体单元后得到。由图可知,在降雨初期边坡表层LFS整体大于1处于稳定状态,随降雨进行坡顶及坡面上的LFS逐渐降低,该趋势从表层向深层土体蔓延。降雨1 d内未发现LFS≤1的区域,即无潜在滑床出现。降雨2 d后已经出现了较浅的表层破坏,滑床几乎平行于坡面,深度小于1 m,随后,滑床的深度逐渐增大,且在下坡位至坡脚发展速度更大,逐渐演变为深层的圆弧状滑动面。图 10为三维特征截线上LFS随土层深度的变化,可知,特征截线上的LFS随降雨时间延长逐日降低,在第2天出现LFS≤1的情况,深度约0.86 m。
|
图 9 降雨过程中边坡中部纵截面LFS (右上)及滑床3D轮廓(左下)变化 Fig. 9 Temporal development of LFS at middle cross-section of slope (upper right) and 3D sliding surface (lower left) during rainfall |
|
图 10 降雨过程中边坡特征截线上LFS变化图 Fig. 10 Temporal development of LFS at characteristic line during rainfall |
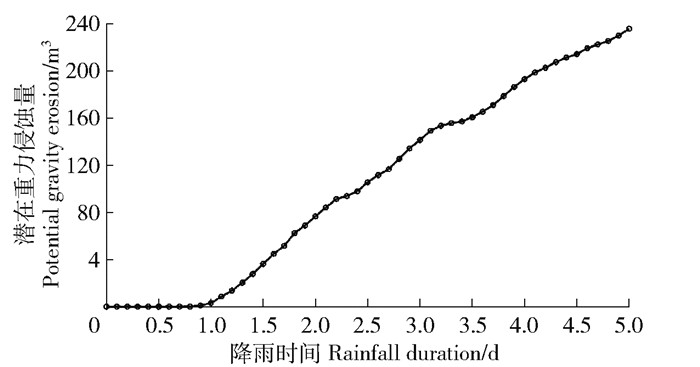
结合结果2.2中边坡LFS标量场数据,对LFS≤1的区域即剪应力大于土体抗剪强度的土体体积进行积分,时间分辨率为0.1 d,所得结果如图 11所示,边坡的潜在侵蚀量大概出现在降雨1 d,随后持续增大,降雨5 d的潜在剪切破坏量接近230 m3,结合图 6和图 10分析可知降雨过程中,当暂态饱和深度达到一定程度后便会出现潜在侵蚀量,之后随着降雨影响深度的逐渐增大,潜在侵蚀量持续增大,坡脚潜在侵蚀最为严重,说明本研究思路和方法可满足预测降雨性浅层边坡潜在侵蚀方量的计算。
|
图 11 降雨过程中边坡潜在重力侵蚀量随时间变化 Fig. 11 Quantified potential gravity erosion of slope during rainfall |
对滑坡过程的反演和预测是防灾减灾工作的前沿课题[23-24],以2018年10—11月金沙江白格流域2次滑坡事件为例,相关研究者们从不同角度反演和预测该滑坡的运动趋势,如,许强等[24]通过遥感影像结合位移监测技术分析2次滑动的形成和发展;周礼等[25]采用PFC3D颗粒流软件模拟反演了2次滑坡的发生、运动、堆积过程,并预测了滑体未来运动路径和堆积范围;Yang等[26]则采用Sentinel-2时间序列数据,对植被扰动范围-位移影像识别,发现未来滑体具有气象和植被高度相关的年周期现象(夏季加速移动、冬季低速移动),模拟和监测成果达到了高度吻合。也有研究者采用模型实验和数值模拟结合的方式探讨了滑坡发生机制和规模,沈冬成[27]通过采用三维激光扫描法量化了实体模型在降雨过程中的滑动方量。以上研究均为对“已然”事件的分析和预测,而本研究的“潜在重力侵蚀量”为边坡滑动前可能造成的土体流失,为对“未然”事件的理论求解,其研究结果的论证可依靠降雨过程中实体模型的变形过程监测来实现。滑坡的发生一般经历初始变形、等速变形和加速变形3个阶段[23]。因此未来研究中可依靠进入加速变形阶段的土体方量监测来实现“PGE”的试验验证。
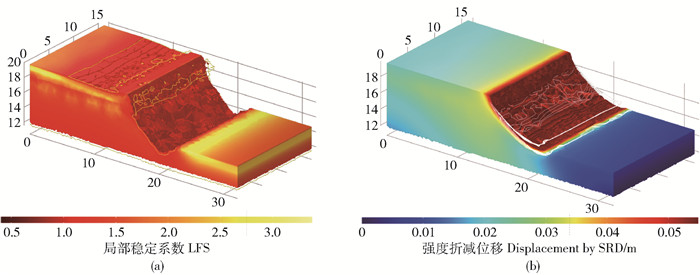
物理模型虽然为最可信的验证方式,但存在试验周期长,成本高,边界尺寸效应和变量难以控制的挑战,因此部分学者采用了数值模拟验证的方法。鲁宁等[15]通过2D边坡LFS计算滑动面位置与极限平衡法的对比论证了其细微差别和可靠性。本研究将对3D模型下LFS法计算边坡滑床和SRD进行对比,考虑SRD的计算耗时(1.6 h/次),仅以降雨第5天结果做详细比较。图 12a为结果2.2中基于LFS第5天滑床轮廓。图 12b为第5天强度折减的总位移云图,折减系数FOS=1.46,为方便比较,移除0.55 m位移等面(对应等效塑性应变为0.02~0.04,白色表面等值线)上方土体。2图以同等变形比例显示,对比可知两者具有较为吻合的滑动位置和规模。强度折减法中FOS=1.46>1,对应的塑性应变和位移等值面难以捕捉和提取,不能作为潜在侵蚀量计算的依据。LFS法的滑动深度略大于强度折减法,滑床轮廓也更陡峭,说明LFS法模拟的3D边坡滑动模式较为可信。
|
图 12 为LFS法(a)和强度折减法(b)计算的滑床对比图 Fig. 12 Comparison of slide surface geometry in two methods (LFS in (a) and SRD in (b)) |
二者存的差异根源在于对土体失效准则的不同,LFS法,仅采用了Mohr-Coulomb准则,一旦剪应力大于临界强度峰值即判别为失效,不再考虑塑性变形,而强度折减中匹配塑性分析匹配Drucker-Prager屈服准则,考虑了塑性发展。这也是降雨第5天强度折减法计算边坡土体强度依然具有1.46倍安全储备,而LFS法计算的滑床位置局部稳定系数为1的原因。总体而言,强度折减法具有更严谨的计算结果,LFS法则具有更好的计算效率和更保守的计算结果,可满足进一步积分计算边坡潜在侵蚀量的条件。
3.2 应用及建议研究中图 5~图 7系列结果展示降雨过程中潜在重力侵蚀的力学原理:降雨过程中,当暂态饱和深度达到一定程度后便会出现潜在侵蚀量,之后随着降雨影响深度的逐渐增大,潜在侵蚀量持续增大,图 9形象展示了滑床持续变深的过程,坡脚潜在侵蚀最为严重。当坡面存在裂隙,或遭遇持续降雨径流等不利条件影响时,这些处于临界剪切状态的土体可能发生剥离和搬运,形成真实侵蚀量,模拟结果与认知相符。考虑实际研究需求,结合图 4所示模拟流程,则整个降雨滑坡潜在侵蚀量的预测应包括以下步骤:
1) 实地地形、土壤、水文勘察。获取必要的DEM数据,土层力学水力参数,水位、降雨数据等如表 2;
2) 渗流-应力耦合模型构建。根据主要矛盾对实际问题简化,建立耦合模型,如图 3;
3) LFS等值面提取。自定义LFS标量场,将孔压场和主/偏应力场后处理为LFS标量场,如图 9;
4) 几何体切割积分。采用LFS等值面对几何实体切割,并定义积分算子进行体积积分,如图 9和图 11。
值得强调的是,本研究的建模算例仅作为机理解释和方法的探索,因此,在边坡几何设置和边界条件设置方面都做了简化,仅可代表普通的边坡单元的失效情境。首先,复杂地形和土层条件建模需要更精细的网格单元和更高的计算成本,这也是当前研究中人们对精度要求和计算机算力的主要矛盾;其次,边坡模型的4围仅采用法向位移的约束条件,这样有利于初始应力场的建立,但当分析目标的空间范围有限时,还应采用完全约束才符合客观实际[28]。最后,降雨的边界条件采用第2类边界条件,模拟降雨无积水,完全入渗的情况,当降雨强度过大,或者土体入渗能力很弱时,如进气值过小或饱和渗透系数较小时,则应考虑采用第3类边界条件,允许流量和压力边界随降雨的自动转化[29-30]。
COMSOL Multiphysics为标准化的多物理场耦合仿真软件,其灵活的PDE和函变量定义功能和强大的求解能力为本研究提供便利。本研究中对滑坡体潜在重力侵蚀量PGE的求解思路和方法不局限于软件的选取,同样可在Abaqus和Flac3D等类似有限元分析软件中实现,可为更复杂物理场景如裂隙损伤、大孔隙渗流、流固气三相耦合、冻融等条件下的滑坡侵蚀量化提供参考。
4 结论1) 暴雨过程中暂态饱和达到一定深度后坡面出现潜在重力侵蚀,随着降雨影响深度的增大,潜在重力侵蚀量PGE持续增大,形成由浅渐深的潜在滑床,坡脚处潜在侵蚀最严重。
2) LFS法可实现与强度折减法较为吻合的滑床轮廓,且计算效率更高,结果更保守,可获得准确的临界失效范围。
3) 降雨型坡潜在重力侵蚀量模拟流程为:(1)实地地形、土壤、水文勘察,(2)渗流-应力耦合模型构建,(3)LFS等值面提取,(4)几何体切割和体积积分。
| [1] |
LU Ning, GONATHON W G. Hillslope hydrology and stability[M]. Cambridge, UK: Cambridge University Press, 2013: 369.
|
| [2] |
NG C W W, SHI Q. A numerical investigation of the stability of unsaturated soil slopes subjected to transient seepage[J]. Computers and Geotechnics, 1998, 22(1): 1. DOI:10.1016/S0266-352X(97)00036-0 |
| [3] |
XU Qianjun, ZHANG Limin. The mechanism of a railway landslide caused by rainfall[J]. Landslides, 2010, 7: 149. DOI:10.1007/s10346-010-0195-y |
| [4] |
WANG Xinhao, MA Chao, WANG Yunqi, et al. Effect of root architecture on rainfall threshold for slope stability: Variabilities in saturated hydraulic conductivity and strength of root-soil composite[J]. Landslides, 2020, 17(8): 1965. DOI:10.1007/s10346-020-01422-6 |
| [5] |
DAI Zhisheng, MA Chao, MIAO Lyu, et al. Initiation conditions of shallow landslides in two man-made forests and back estimation of the possible rainfall threshold[J]. Landslides, 2022, 19(5): 1031. DOI:10.1007/s10346-021-01823-1 |
| [6] |
MORGENSTERN N R, PRICE V E. The analysis of the stability of general slip surfaces[J]. Geotechnique, 1965, 15(1): 79. DOI:10.1680/geot.1965.15.1.79 |
| [7] |
ZHU D Y, LEE C F, QIAN Q H, et al. A concise algorithm for computing the factor of safety using the Morgenstern Price method[J]. Canadian Geotechnical Journal, 2005, 42(1): 272. DOI:10.1139/t04-072 |
| [8] |
GRIFFITHS D V, LANE P A. Slope stability analysis by finite elements[J]. Geotechnique, 1999, 49(3): 387. DOI:10.1680/geot.1999.49.3.387 |
| [9] |
郑颖人, 赵尚毅. 有限元强度折减法在土坡与岩坡中的应用[J]. 岩石力学与工程学报, 2004, 23(19): 3381. ZHENG Yingren, ZHAO Shangyi. Application of strength reduction FEM in soil and rock slope[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(19): 3381. DOI:10.3321/j.issn:1000-6915.2004.19.029 |
| [10] |
孔郁斐, 宋二祥, 杨军, 等. 降雨入渗对非饱和土边坡稳定性的影响[J]. 土木建筑与环境工程, 2013, 35(6): 16. KONG Yufei, SONG Erxiang, YANG Jun, et al. Rainfall's effect on the stability of unsaturated slopes[J]. Journal of Civil, Architectural & Environmental Engineering, 2013, 35(6): 16. |
| [11] |
杨涛, 孙立娟, 成启航, 等. 基于位移等值面的边坡点安全系数分析[J]. 铁道学报, 2018, 40(6): 115. YANG Tao, SUN Lijuan, CHENG Qihang, et al. Analysis of slope point safety factor based on displacement isosurface[J]. Journal of The China Raillway Society, 2018, 40(6): 115. |
| [12] |
闵江涛, 赵强. 基于点安全系数法的边坡稳定性评价[J]. 杨凌职业技术学院学报, 2020, 19(1): 10. MIN Jiangtao, ZHAO Qiang. The slope stability evaluation based on point safety factor method[J]. Journal of Yangling Vocational & Technical College, 2020, 19(1): 10. |
| [13] |
宋林波, 丁增志, 罗智勇, 等. 基坑转角处三维空间效应对稳定性影响分析[J]. 路基工程, 2021, 4(4): 120. SONG Linbo, DING Zengzhi, LUO Zhiyong, et al. Study on influence of 3D spatial effect at foundation pit corner on stability[J]. Subgrade Engineering, 2021, 4: 120. |
| [14] |
齐兵, 杨官润, 陈治炜, 等. 边坡点安全系数计算方法比较及应用研究[J]. 路基工程, 2021, 219(6): 88. QI Bing, YANG Guanrun, CHEN Zhiwei, et al. Comparison and application research on calculation methods of side slope point safety factoer[J]. Subgrade Engineering, 2021, 219(6): 88. |
| [15] |
LU Ning, SENER-KAYA B, WAYLLACE A, et al. Analysis of rainfall-induced slope instability using a field of local factor of safety[J]. Water Resources Research, 2012, 48(9): W9524. |
| [16] |
SHAO Wei, BOGAARD T A, BAKKER M, et al. Quantification of the influence of preferential flow on slope stability using a numerical modelling approach[J]. Hydrology and Earth System Sciences, 2015, 19(5): 2197. |
| [17] |
MORADI S, HUISIMAN J A, CLASS H, et al. The effect of bedrock topography on timing and location of landslide initiation using the local factor of safety concept[J]. Water, 2018, 10(10): 1290. |
| [18] |
DOU Zhi, LIU Yimin, ZHANG Xueyi, et al. Influence of layer transition zone on rainfall-induced instability of multilayered slope[J]. Lithosphere, 2021, 2021: 2277284. |
| [19] |
BISHOP A W. The principle of effective stress[J]. Tecnisk Ukeblad, 1960, 39: 859. |
| [20] |
RICHARDS L A. Capillary conduction of liquids through porous mediums[J]. Physics, 1931, 1(5): 318. |
| [21] |
VAN GENUCHTEN M T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils[J]. Soil Science Society of America Journal, 1980, 44(5): 892. |
| [22] |
TEMGOUAA G T, KOKUTSE N K, KAVAZOVIC Z. Influence of forest stands and root morphologies on hillslope stability[J]. Ecological Engineering, 2016, 95: 622. |
| [23] |
许强, 汤明高, 徐开祥, 等. 滑坡时空演化规律及预警预报研究[J]. 岩石力学与工程学报, 2008, 27(6): 1104. XU Qiang, TANG Minggao, XU Kaixiang, et al. Research on space-time evolution laws and early warning-prediction of landslides[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(6): 1104. |
| [24] |
许强, 郑光, 李为乐, 等. 2018年10月和11月金沙江白格两次滑坡-堰塞堵江事件分析研究[J]. 工程地质学报, 2018, 26(6): 1534. XU Qiang, ZHENG Guang, LI Weile, et al. Study on successive landslides damming events on Jinsha River Baige Village on October 11 and November 3, 2018[J]. Journal of Engineering Geology, 2018, 26(6): 1534. |
| [25] |
周礼, 范宣梅, 许强, 等. 金沙江白格滑坡运动过程特征数值模拟与危险性预测研究[J]. 工程地质学报, 2019, 27(6): 1395. ZHOU Li, FAN Xuanmei, XU Qiang, et al. Numerical simulation and hazard prediction on movement process characteristics of Baige landslide in Jinsha River[J]. Journal of Engineering Geology, 2019, 27(6): 1395. |
| [26] |
YANG Wentao, WANG Yujie, WANG Yunqi, et al. Retrospective deformation of the Baige landslide using optical remote sensing images[J]. Landslides, 2019, 17: 659. |
| [27] |
沈冬成. 降雨诱发根土复合坡体失稳特征研究[D]. 成都: 成都理工大学, 2020: 24. SHEN Dongcheng. Research on instability characteristics of root soil composite slope caused by rainfall[D]. Chengdu: Chengdu University of Technology, 2020: 24. |
| [28] |
ZHANG Ke, CAO Ping, LIU Ziyao, et al. Simulation analysis on three-dimensional slope failure under different conditions[J]. Transactions of Nonferrous Metals Society of China, 2011, 21(11): 2490. |
| [29] |
CHUI T F M, FREYBERG D L. Implementing hydrologic boundary conditions in a multiphysics model[J]. Journal of Hydrologic Engineering, 2009, 14(12): 1374. |
| [30] |
窦智, 刘一民, 周志芳, 等. 基于单、双重渗透介质降雨边界处理的改进[J]. 岩土力学, 2022, 43(3): 789. DOU Zhi, LIU Yimin, ZHOU Zhifang, et al. Improvement of rainfall boundary treatment based on single and double permeable media[J]. Rock and Soil Mechanics, 2022, 43(3): 789. |
 2024, Vol. 22
2024, Vol. 22