-
项目名称
- 国家自然科学基金“基于气候空间上限列线的栓皮栎幼苗高温叠加干旱胁迫机制研究”(31370621)
-
第一作者简介
- 王谦(1963—),男,博士,教授。主要研究方向:农林生态。E-mail:wangqianhau@163.com
-
通信作者简介
- 陈景玲(1964—),女,副教授。主要研究方向:农林生态。E-mail:chenjingling5@163.com
-
文章历史
-
收稿日期:2022-08-03
修回日期:2023-10-10
干旱缺水影响植物正常生长,生态系统就会破坏,受损生态系统的恢复也会因水分缺乏而变得困难。在山地还直接导致水土流失加速。干旱使土壤水分缺乏导致植物水分吸收不足、蒸腾作用受阻,光合作用降低[1],进而影响非结构性碳积累和结构器官建成。了解植物受干旱胁迫影响,首先要测定土壤水分含量,其次是植物对水分变化的响应,以及生态系统主要植物对水分需求的量值,即植物受旱响应指标[2]。植物对水分胁迫有一定耐受力,不同程度的干旱对植物产生危害程度不一。所以,了解土壤水分的动态变化和植物的响应程度,需要长时间系统的土壤水分监测。
土壤水分监测,主要有土钻法、挖掘法、中子仪法、微根管法,以及时域反射仪法等方法。土钻法原理简单,测定数据准确,但测定效率低;中子仪法可连续多次测定,获得土壤水分动态,但仪器价格高;电容式传感器可多点连续测定,测量土壤水分效率高,但数据准确性不高。这些方法还存在一个共同问题是因布点数量有限,获得的数据有限。研究发现,感知植物叶温可以了解土壤水分,它能较好地被无人机和遥感平台利用[3-4]。
植物的叶温与气温不同,叶温和气温之差称为叶气温差(或冠气温差)。叶气温差的大小与土壤水分有较好的相关规律[5],这使遥感大面积获知土壤水分成为现实。1981年由Jackson等提出作物水分胁迫指数(crop water stress index,CWSI)理论模型,后经过很多学者进一步完善[6-7]。CWSI模型在农业、林业、园林、生态等很多领域起到很大的作用,但该模型的下基线确定不准确。尽管研究CWSI模型的学者都确定其下基线[8-9],但理论参数不易确定,或经验方法的理论依据不足,使确定下基线及由此得到的CWSI模型诊断结果不能令人满意[10]。笔者以栓皮栎(Quercus variabilis)为对象,通过叶片表面能量平衡分析,确定CWSI模型下基线。为精确控制和测定土壤水分,采用盆栽法。为消除单花盆种植的边际效应,将花盆按小区布置,边缘加保护行。叶温测定采用热电偶法,以获得更准确的叶温,确定准确的下基线。
1 材料与方法 1.1 试验材料试验在河南农业大学林学院试验基地进行。2020年9月下旬开始进行栓皮栎育苗,装盆土壤为粉壤土。试验土壤的土壤特征参见文献[2]中表1中的C样点土壤。<2 μm、2~50 μm和50 μm~2 mm粒径比例分别为0.3%、52.4%和47.3%。项目组多年用该样点土壤进行试验研究,已测定花盆土壤田间持水量为33%(体积比例,全文土壤湿度均为体积比例)。凋萎湿度为9.6%(以叶绿素荧光参数绝对量子效率Fv/Fm开始下降为标志测得,参见文献[2])。试验开始日期为2021年5月17日,2021年10月30日结束。选择1块3 m×2 m的样地,分成6个样点,每个样点面积1 m2,在每个样点放置1年生盆栽栓皮栎幼苗,外围放置2排花盆为保护行。全部样地保证其太阳辐射条件,幼苗生长良好。每株幼苗至少3片以上成熟叶片时开始试验。此时测得平均株高25.0 cm、平均地径2.5 mm、成熟叶片平均叶长9.3 cm、平均叶宽2.8 cm。全部试验在成熟叶片上完成。
1.2 试验方法用干湿参考面法确定叶气温差与环境因子的关系。在叶片上下表面涂抹凡士林,完全阻断蒸腾作用为干参考面;对栓皮栎土壤充分供水,使叶片蒸腾作用不受土壤水分限制,此时的叶片作为湿参考面。具体试验方法,将6盆试验幼苗花盆编号,分为2组,每组3盆,每盆随机选取3片健康成熟叶片并做标记,第1组充分供水后叶片不做任何处理,每日晚上浇水保证充分供水,第2组所标记的叶片均匀涂抹上凡士林(叶子正反面均涂抹),不浇水,选取晴朗无风无云天气为典型天气,08:00使用Y X- 0232型多通道热电偶温度仪对标记叶片进行叶温监测,将热电偶探头接触叶片背部,并用特制的鹅颈管固定装置固定叶片,使其防止风摆动的影响,每30s自动读取数据,17:00结束试验。
1.3 上基线的确定对干参考面连续测定叶温tc干(℃)和气温ta(℃),用干参考面无蒸腾影响下的叶温减去气温,即得到干参考面叶气温差Δt干(℃),其计算式为
| $ \Delta t_{\text {干 }}=t_{c \mp}-t_{\mathrm{a}} \text { 。} $ | (1) |
形成Δt干的时间序列,与太阳辐射时间序列回归,得到Δt干与太阳辐射的线性回归方程,即CWSI经验模型中的上基线。其计算式为
| $ \Delta t_{\text {干 }}=a Q+b 。$ | (2) |
式中:Q为太阳辐射,W/m2;a和b为线性回归系数。
1.4 能量收支分析与下基线的确定根据下垫面能量收支平衡方程
| $ \Delta Q=R+P+L E。$ | (3) |
式中:ΔQ为叶片吸收的热量,W/m2;R为辐射平衡,W/m2;P为叶表面对流换热,W/m2;L为水的蒸发潜热,J/mmol,它是随气温略有变化的常数,即L=44.98-0.041 94ta;E为叶片蒸腾量,mmol/(m2·s);L与E的乘积为蒸腾潜热,W/m2。
对于稳态过程(晴朗无风无云的典型天气,可认为是稳态的),叶温随能量收支变化而变化,叶表面没有热量积累,则有
| $ R+P+L E=0。$ | (4) |
对干参考面,叶表面对流换热P干(W/m2)可以用对流换热公式表达
| $ P_{\text {干 }}=k \Delta t_{\text {干}}。$ | (5) |
式中k为对流换热系数,W/m2。
类似的,对湿参考面,叶表面对流换热
| $ P_{\text {湿 }}=k \Delta t_{\text {湿 }}。$ | (6) |
式中Δt湿为湿参考面叶气温差,℃。
即
| $ \Delta t_{\text {湿 }}=t_{\mathrm{c} \text { 湿 }}-t_{\mathrm{a} \text { 。}} $ | (7) |
式中tc湿为叶片湿参考面温度,℃。
对干参考面
| $ R_{\text {干 }}+k \Delta t_{\text {干 }}+L E_{\text {干 }}=0 \text { 。} $ | (8) |
式中:R干为干参考面辐射平衡,W/m2;E干为干参考面蒸腾量,mmol/(m2·s)。
对湿参考面
| $ R_{\text {湿 }}+k \Delta t_{\text {湿 }}+L E_{\text {湿 }}=0 \text { 。} $ | (9) |
式中:R湿为湿参考面辐射平衡,W/m2;E湿为湿参考面蒸腾量,mmol/(m2·s)。
干参考面无蒸腾,即LE干为0。干湿参考面的太阳辐射平衡相同,即R干=R湿。2式相减,有
| $ k\left(\Delta t_{\text {湿 }}-\Delta t_{\text {干 }}\right)+L E_{\text {湿 }}=0 \text { 。} $ | (10) |
即
| $ k\left(\Delta t_{\text {湿 }}-\Delta t_{\text {干 }}\right)=-L E_{\text {湿 }}。$ | (11) |
式右边为湿参考面蒸腾产生的潜热消耗量,在充分供水条件下,与空气饱和水汽压差V(kPa)有关;式左边为因此产生的P湿和P干的差,变换上式,得
| $ \Delta t_{\text {湿 }}-\Delta t_{\text {干 }}=-\frac{L}{k} E_{\text {湿 }}。$ | (12) |
式左边为因湿参考面蒸腾,叶气温差比干参考面降低的部分,它相当于消除Q影响时,Δt湿降低,因为Δt湿<Δt干,所以它是负值,可用Δt湿干表示,即
| $ \Delta t_{\text {湿干 }}=\Delta t_{\text {湿 }}-\Delta t_{\text {干 }}。$ | (13) |
式中Δt湿干为湿参考面叶气温差与干参考面叶气温差的差值,℃。
结合式(1)和(7),有
| $ \begin{array}{l} \Delta t_{\text {湿干 }}=\Delta t_{\text {湿 }}-\Delta t_{\text {干 }}=\left(t_{\text {c湿 }}-t_{\mathrm{a}}\right)- \\ \;\; \;\; \;\; \;\; \left(t_{\mathrm{c} \mp}-t_{\mathrm{a}}\right)=t_{\mathrm{c} \text { 湿 }}-t_{\mathrm{c} 干} 。\end{array} $ | (14) |
因LE湿与V有关,可写成V的函数,f(V),则有
| $ \Delta t_{\text {湿干 }}=-f(V) \text { 。} $ | (15) |
上式即为统计计算无Q影响,充分供水时植物叶片充分蒸腾情况下叶气温差与的V关系的方程式。
计算V所需的微气象数据为ta、空气湿度H(%)等。在试验场地内采用RR-1008小气候梯度自动监测系统测量获得, 每30 s监测1次,与叶温测量频率保持一致。V可由下式得到:
| $ V=0.610\;78 {\rm{e}}^{\frac{17.27 t_{\rm{a}}}{t_{\rm{a}}+237.3}}\left(1-\frac{H}{100}\right) 。$ | (16) |
实际测定时,同时连续测定tc干、tc湿和ta,用Δt湿减去Δt干,形成Δt湿干的时间序列。它与V的时间序列一一对应,将Δt湿干与V回归,则可得到没有Q影响时,Δt湿与V的关系,即CWSI经验模型中的下基线。其表达公式如下:
| $ \Delta t_{\text {湿干 }}=m V+n {\text {。}} $ | (17) |
式中m,n为线性回归系数。
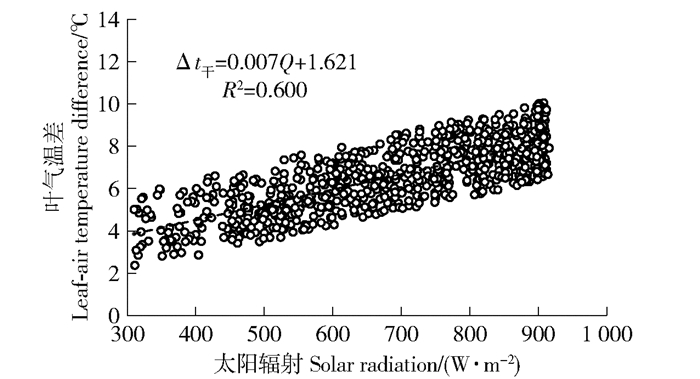
2 结果与分析 2.1 栓皮栎CWSI模型上基线将3d晴朗天气观测得到的Δt干的时间序列,和用自动气象站测定的对应时刻的Q,将Δt干的时间序列与Q的时间序列一一对应,将Δt干与Q回归,得到式(2)的回归系数a和b,进行相关统计得到图 1。
|
Δt干:Dry reference surface leaf temperature difference,℃;Q:solar radiation, W/m2. 图 1 栓皮栎干参考面叶气温差与太阳辐射的关系 Fig. 1 Relationship between solar radiation and leaf-air temperature difference of Quercus variabilis dry reference surface |
图 1为栓皮栎Δt干与Q之间的线性关系,由图可知栓皮栎Δt干与Q表现出较好的线性正相关关系,即Δt干随着Q的增大而增大。其回归方程为Δt干=0.007Q+1.621,决定系数为0.600。
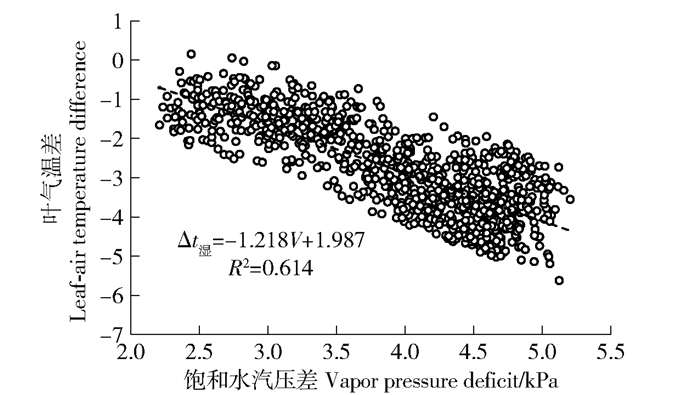
2.2 栓皮栎CWSI模型下基线用前述试验方法测定得到Δt湿的时间序列,用自动气象站测得的ta和H,根据式(16)计算出V。Δt湿的时间序列同V的时间序列一一对应,将Δt湿与V回归,确定式(17)的m、n系数,并进行相关统计得到图 2。
|
Δt湿:Wet reference surface leaf temperature difference, ℃; V:vapor pressure deficit, kPa. 图 2 栓皮栎湿参考面叶气温差与饱和水气压差的关系 Fig. 2 Relationship between vapor pressure deficit (VPD) and leaf-air temperature difference of Quercus variabilis wet reference surface |
图 2为栓皮栎修正后的Δt湿与V之间的线性关系,由图可知修正后的Δt湿与V表现出较好的线性关系,拟合度高,为负相关关系,即消除Q影响的Δt湿随V的增大而降低,决定系数为0.614,修正后的Δt湿与V的线性回归方程为Δt湿=-1.218V+1.987。
2.3 栓皮栎的CWSI和土壤水分诊断根据前述Δt干与Q的线性回归方程,以及湿参考面仅由蒸腾作用产生的Δt湿与V的线性回归方程,即栓皮栎的上基线和下基线,代入CWSI经验模型中,可得栓皮栎修正下基线后的CWSI(用I表示)经验模型,为
| $ I=\frac{t_{\mathrm{ca}}-(-1.218 V+1.987)}{(0.007 Q+1.621)-(-1.218 V+1.987) }。$ | (18) |
式中tca为实际应用中所测量的叶气温差,℃。
于1.1试验材料的样地中,重新随机选取3盆试验幼苗并标记盆号。每次选1盆用作土壤水分诊断验证,选取3片健康叶片并做标记。每天08:00至17:00监测叶温,并每日测定花盆质量,直至试验幼苗叶片完全干枯。全部监测试验结束后,将标记花盆内土壤全部取出烘干,并计算出花盆每日体积含水量(V水/V土,%),即土壤湿度θ(%)。这样可以得到从田间持水量到凋萎湿度、干旱致死叶片完全干枯的θ梯度的叶气温差序列。
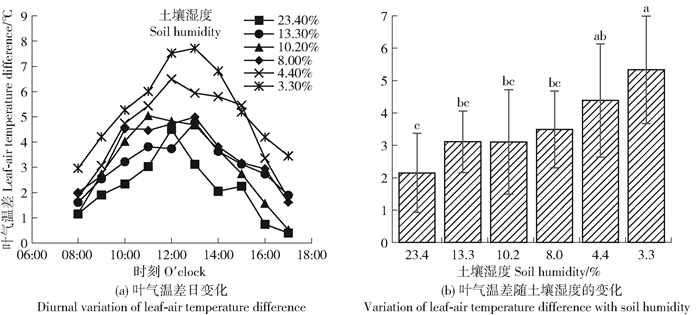
统计3个叶片的tca的平均值,不同θ时tca的日变化如图 3a。从图 3a可以看出各θ下,均为每日早晚叶气温差较小,中午叶气温差较大;而且10:00—14:00时不同θ之间tca差异较大。所以,中午时段适于用叶气温差法的CWSI模型进行土壤水分诊断。3个叶片的tca方差较小,如5月26日θ为8%时,3片叶片tca的方差为0.65,说明tca测定较稳定。不同θ时的tca日均值及其方差如图 3b。从图 3b可以看出,不同θ的tca差异显著,尤其是θ降低到凋萎湿度以下(<9.6%)时,差异显著(P<0.05)。这样的特点也有利于用叶气温差法关于I的模型进行土壤水分诊断。因为土壤干旱,即土壤水分低,是农林植物种植最关心的。从图 3b还可以看出,不同θ时全天测定的tca的方差比较大。这是因为tca有日变化。所以,不用全天tca的平均值进行土壤水分的诊断,而是用正午时段的某时刻的tca进行土壤水分诊断更准确。
|
图 3 土壤水分诊断的叶气温差和土壤湿度 Fig. 3 Leaf-air temperature difference and soil moisture for soil moisture diagnosis |
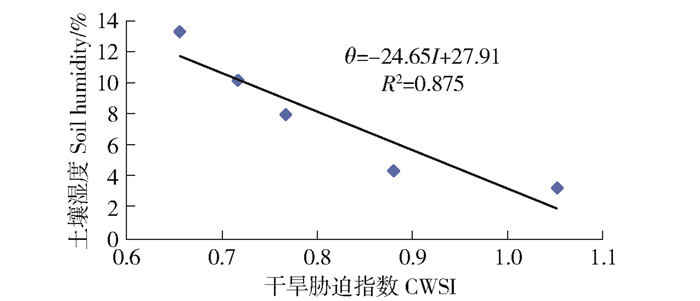
对比中午时段试验数据,发现每日12:00时左右测得的tca和Q、H数据,计算出的I值与θ关系最密切。用每日12:00时实测的tca,根据I的模型(式18)计算不同θ阶段的I值,与实测的θ数据点图,如图 4。进行线性回归,得I与θ的关系方程如图 4中所示,其关系系数为0.875,通过0.01信度的相关显著性检验。即只要测定栓皮栎的叶温和ta和H,根据构建关于I的模型(式18),就能较准确地诊断栓皮栎的θ。诊断公式为θ=-24.65I+27.91。
|
θ:Soil moisture, %; I: crop water stress index,dimension is 1. 图 4 栓皮栎干旱胁迫指数与土壤湿度之间的关系 Fig. 4 Relationship between CWSI of Quercus variabilis and soil moisture content |
本研究砂壤土和粉壤土条件下的栓皮栎幼苗的干旱胁迫指标为: >13%无干旱, >10%~13%轻度干旱, >8%~10%中度干旱, >5%~8%重度干旱[19]。图 4直线对应的θ为2%~12%。θ为12%时对应轻度干旱,I约为0.65;θ为8%~10%时对应中度干旱,I为0.75~0.8;θ为5%~8%对应重度干旱,I为0.80~0.95。文献[2]的研究还指出,当θ<5%时,栓皮栎幼苗叶绿素荧光的最大量效率Fv/Fm降低为0,光系统Ⅱ损伤失去光合能力,幼苗枯死。所以I>0.95时,幼苗胁迫致死。
3 讨论Payero等[11]研究CWSI模型上下基线,认为太阳辐射是主要因子,与本研究结果一致。赵福年等[10, 12]发现施氮和作物生长也影响下基线。Testi等[13]认为受太阳辐射影响,模型基线有日变化,但没有量化。Yazar等[14]研究认为气象因素的差异是影响CWSI模型上下基线的最主要因子,Jensen等[15]认为辐射和风速使CWSI模型基线的回归性较差,在本研究中得到印证,推荐在12:00时测定叶气温差和气象数据,进行CWSI计算。而且发现风对叶温影响较大,因此推荐静风或微风时进行测定。
Idso等[16]建立了26种不同作物物种的下基线,发现晴天下基线截距明显大于多云天气,但单纯的经验模型没有很强的适用性。Taghvaeian等[17]建立的玉米的CWSI模型下基线呈环形,不能很好地展现叶气温差与VPD的相关关系。Alderfasi等[18]研究计算出的冬小麦CWSI模型中的下基线与Howell等[19]得出的下基线有很大程度上的不同,表现为基线斜率的不同,且下基线截距前者明显小于后者,相关性也不同。综合来看,纯经验模型下基线的不确定性给CWSI模型的推广带来了一定的局限[10]。
笔者根据能量平衡原理对CWSI模型中的下基线进行改进。CWSI模型包括经验模型和理论模型。经验模型的参数简单,但考虑的因子数量不足,影响模型应用;理论模型的线性回归关系复杂,难以进行试验验证。所以两者都具有一定的局限性[8-9]。本研究由前人的纯经验下基线上升为半经验半理论的下基线,是综合二者的特点的优化。
4 结论1) 通过能量平衡方程的热量收支计算方法可以更准确确定叶气温差与VPD的关系,进而优化CWSI模型。
2) 对于栓皮栎,用干湿参考面法修正了CWSI经验模型下基线,计算得出栓皮栎下基线的线性回归方程为Δt湿=-1.218V+1.987,通过干参考面法确定了CWSI经验模型中的上基线为Δt干=0.007Q+1.621。并求出优化下基线后的栓皮栎CWSI经验模型:
| $ I=\frac{t_{\mathrm{ca}}-(-1.218 V+1.987)}{(0.007 Q+1.621)-(-1.218 V+1.987) }。$ |
3) 用栓皮栎叶气温差结合太阳辐射和空气湿度θ诊断土壤水分的模型为θ=-24.65I+27.91。
4) 用本研究相同的方法构建不同作物的CWSI模型和土壤水分诊断模型,可以根据遥感叶温和气象站的太阳辐射、气温和空气湿度诊断不同农作物或林木植物的土壤湿度。
| [1] |
陈景玲, 王佩舒, 刘琳奇, 等. 光温条件和土壤湿度对栓皮栎幼苗蒸腾潜热和叶温的影响[J]. 中国水土保持科学, 2017, 15(1): 62. CHEN Jingling, WANG Peishu, LIU Linqi, et al. Impacts of radiation, temperature and soil moisture on hidden heat of transpiration and leaf temperature of Quercus variabilis seedlings[J]. Science of Soil and Water Conservation, 2017, 15(1): 62. DOI:10.16843/j.sswc.2017.01.008 |
| [2] |
王谦, 李明蔚, 李强, 等. 基于栓皮栎幼苗叶绿素荧光参数的不同质地土壤干旱胁迫指标[J]. 中国水土保持科学, 2021, 19(2): 27. WANG Qian, LI Mingwei, LI Qiang, et al. Drought stress indexes of soil with different texture based on chlorophyll fluorescence parameters of Quercus variabilis seedlings[J]. Science of Soil and Water Conservation, 2021, 19(2): 27. DOI:10.16843/j.sswc.2021.02.004 |
| [3] |
张立元. 基于无人机遥感的大田玉米水分胁迫监测研究[D]. 陕西杨凌: 西北农林科技大学, 2022: 128. ZHANG Liyuan. Monitoring maize water stress based on UAV remote sensing data[D]. Yangling, Shaanxi: Northwest A&F University, 2022: 128. |
| [4] |
刘婵, 范兴科. 基于冠层叶气温差的温室土壤水分诊断[J]. 干旱地区农业研究, 2012, 30(1): 90. LIU Chan, FAN Xingke. Diagnosis of soil moisture in greenhouse based on canopy leaf-air temperature difference[J]. Agricultural Research in the Arid Areas, 2012, 30(1): 90. |
| [5] |
IDSO S B, JACKSON R D, PINTER P J, et al. Normalizing the stress-degree-day parameter for environmental variability[J]. Agricultural Meteorology, 1981, 24: 45. DOI:10.1016/0002-1571(81)90032-7 |
| [6] |
JACKSON R D, KUSTAS W P, CHOUDHURY B J. A reexamination of the crop water stress index[J]. Irrigation Science, 1988, 9(4): 309. DOI:10.1007/BF00296705 |
| [7] |
JACKSON R D, IDSO S B, REGINATO R J, et al. Canopy temperature as a crop water stress indicator[J]. Water Resources Research, 1981, 17(4): 1133. DOI:10.1029/WR017i004p01133 |
| [8] |
张立元, 牛亚晓, 韩文霆, 等. 大田玉米水分胁迫指数经验模型建立方法[J]. 农业机械学报, 2018, 49(5): 233. ZHANG Liyuan, NIU Yaxiao, HAN Wenting, et al. Establishing method of crop water stress index empirical model of field maize[J]. Transactions of the CSAM, 2018, 49(5): 233. |
| [9] |
赵福年, 张虹, 陈家宙, 等. 玉米作物水分胁迫指数(CWSI)基线差异原因初探[J]. 中国农学通报, 2013, 29(6): 46. ZHAO Funian, ZHANG Hong, CHEN Jiazhou, et al. Preliminary investigation on difference of crop water stress index baseline for maize[J]. Chinese Agricultural Science Bulletin, 2013, 29(6): 46. |
| [10] |
赵福年, 王瑞君, 张虹, 等. 基于冠气温差的作物水分胁迫指数经验模型研究进展[J]. 干旱气象, 2012, 30(4): 522. ZHAO Funian, WANG Ruijun, ZHANG Hong, et al. Advances in crop water stress index empirical model research based on canopy and atmosphere temperature difference[J]. Journal of Arid Meteorology, 2012, 30(4): 522. |
| [11] |
PAYERO J O, NEALE C M U, WRIGHT J L. Non-water-stressed baselines for calculating crop water stress index (cwsi) for alfalfa and tall fescue grass[J]. Transactions of the ASAE, 2005, 48(2): 653. DOI:10.13031/2013.18329 |
| [12] |
赵福年, 陈家宙, 张虹. 施氮水平对红壤区夏玉米水分胁迫指数下基线的影响[J]. 中国农业气象, 2012, 33(2): 215. ZHAO Funian, CHEN Jiazhou, ZHANG Hong. Effect of nitrogen fertilization level on the low baseline of crop water stress index for summer maize in red soil[J]. Chinese Journal of Agrometeorology, 2012, 33(2): 215. |
| [13] |
TESTI L, GOLDHAMER D A, INIESTA F, et al. Crop water stress index is a sensitive water stress indicator in pistachio trees[J]. Irrigation Science, 2008, 26(5): 395. DOI:10.1007/s00271-008-0104-5 |
| [14] |
YAZAR A, HOWELL T A, DUSEK D A, et al. Evaluation of crop water stress index for LEPA irrigated corn[J]. Irrigation Science, 1999, 18(4): 171. DOI:10.1007/s002710050059 |
| [15] |
JENSEN H E, SVENDSEN H, JENSEN S E, et al. Canopy-air temperature of crops grown under different irrigation regimes in a temperate humid climate[J]. Irrigation Science, 1991, 12(2): 181. |
| [16] |
IDSO S B. Non-water-stressed baselines: A key to measuring and interpreting plant water stress[J]. Agricultural Meteorology, 1982, 27(1-2): 59. DOI:10.1016/0002-1571(82)90020-6 |
| [17] |
TAGHVAEIAN S, CHÁVEZ J L, HANSEN N C. Infrared thermometry to estimate crop water stress index and water use of irrigated maize in northeastern Colorado[J]. Remote Sensing, 2012, 4(11): 3619. DOI:10.3390/rs4113619 |
| [18] |
ALDERFASI A A, NIELSEN D C. Use of crop water stress index for monitoring water status and scheduling irrigation in wheat[J]. Agricultural Water Management, 2001, 47(1): 69. DOI:10.1016/S0378-3774(00)00096-2 |
| [19] |
HOWELL T A, MUSICK J T, TOLK JA. Canopy temperature of irrigated winter wheat[J]. Transactions of the Asae, 1986, 29(6): 1692. DOI:10.13031/2013.30375 |
 2024, Vol. 22
2024, Vol. 22 
