文章快速检索     高级检索
  中国水土保持科学   2024, Vol. 22 Issue (2): 81-89.  DOI: 10.16843/j.sswc.2022202
0

引用本文 

宋克鹏, 李一帆, 曲思仪, 周帆, 王彬, 王盛萍. 黄土高原沟壑区典型流域不同算法土壤侵蚀集成模拟比较[J]. 中国水土保持科学, 2024, 22(2): 81-89. DOI: 10.16843/j.sswc.2022202.
SONG Kepeng, LI Yifan, QU Siyi, ZHOU Fan, WANG Bin, WANG Shengping. Ensemble simulation for soil erosion of a typical watershed in the gully region of Loess Plateau on the basis of different algorithms[J]. Science of Soil and Water Conservation, 2024, 22(2): 81-89. DOI: 10.16843/j.sswc.2022202.

项目名称

国家重点研发计划项目课题“典型工程区水资源植被承载力与防护林体系优化配置技术研究与示范”(2022YFF1302501)；水专项项目课题“密云水库水源地保护和监管集成技术示范”(2017ZX07108-002)

第一作者简介

宋克鹏(1996—)，男，硕士研究生。主要研究方向：土壤侵蚀与水土保持。E-mail: 1251753783@qq.com

通信作者简介

王盛萍(1978—)，女，副教授。主要研究方向：生态水文，土壤侵蚀防治。E-mail: wangshp418@126.com

文章历史

收稿日期：2022-10-08
修回日期：2023-12-11
Contents              Abstract              Full text              Figures/Tables              PDF
黄土高原沟壑区典型流域不同算法土壤侵蚀集成模拟比较
宋克鹏 1,2, 李一帆 1, 曲思仪 1, 周帆 1, 王彬 3, 王盛萍 1     
1. 华北电力大学水利与水电工程学院，102206，北京;
2. 华北电力大学环境科学与工程学院，102206，北京;
3. 北京林业大学水土保持学院，100083，北京
收稿日期：2022-10-08; 修回日期：2023-12-11
项目名称：国家重点研发计划项目课题“典型工程区水资源植被承载力与防护林体系优化配置技术研究与示范”(2022YFF1302501)；水专项项目课题“密云水库水源地保护和监管集成技术示范”(2017ZX07108-002)
第一作者简介：宋克鹏(1996—)，男，硕士研究生。主要研究方向：土壤侵蚀与水土保持。E-mail: 1251753783@qq.com
通信作者简介：王盛萍(1978—)，女，副教授。主要研究方向：生态水文，土壤侵蚀防治。E-mail: wangshp418@126.com
摘要：为探究集成模拟技术对减少不同模型模拟土壤侵蚀的不确定性，以黄土高原昕水河流域为研究对象，采用Bates-Granger(BG)集成、等权重集成和Granger-Ramanathan集成技术，对广泛运用的Morgan-Morgan-Finney(MMF)、修正土壤流失方程(RUSLE)和中国土壤流失方程(CSLE)等进行集成模拟。集成模拟以流域出口泥沙观测进行率定，并根据纳什系数(NSE)、相关系数(R)、均方根误差(RMSE)进行模型模拟评价。结果表明：1)对于单一模型而言，MMF模拟效果在多数情况下优于CSLE和RUSLE模拟效果；2) 集成模拟可显著改善土壤侵蚀模型模拟效果，集成模拟前后，模型评价指标如NSE、R、RMSE分别提高23.6%、15.8%、46.4%；3) 不同集成模拟中BG集成算法在模型不确定性方面更加稳定、可靠。研究认为，在基于经验性模型开展流域土壤侵蚀模拟时，可以采用集成模拟技术进一步提升其模拟性能。
关键词：土壤侵蚀模型    集成模拟    Bates-Granger    Granger-Ramanathan    等权重    黄土高原流域    
Ensemble simulation for soil erosion of a typical watershed in the gully region of Loess Plateau on the basis of different algorithms
SONG Kepeng 1,2, LI Yifan 1, QU Siyi 1, ZHOU Fan 1, WANG Bin 3, WANG Shengping 1     
1. School of Water Resources and Hydropower Engineering, North China Electric Power University, 102206, Beijing, China;
2. School of Environmental Science and Engineering, North China Electric Power University, 102206, Beijing, China;
3. School of Soil and Water Conservation, Beijing Forestry University, 100083, Beijing, China
Abstract: [Background] The Loess Plateau is one of the most severely eroded areas in the world, and quantification of soil erosion has been an important research work in the Loess Plateau of China.Although there exist many different soil erosion models for simulating soil erosion, few studies have used ensemble models to simulate soil erosion. [Methods] To investigate whether ensemble simulation can effectively improve soil erosion simulation, this study used the techniques of Bates-Granger (BG), equal weight (EW) and Granger-Ramanathan (GR) to integrate three widely used empirical-based soil erosion models, being Morgan-Morgan-Finney (MMF), Revised Universal Soil Loss Equation (RUSLE), and Chinese Soil Loss Equation (CSLE), respectively, for simulating soil erosion and sediment yield of a loess watershed, i.e., Xinshui River watershed.The training period (1991-2000) was for estimating the weight of each model, and the testing period (2001-2005) was for examining the applicability of the various ensemble approaches.The model performance was evaluated in terms of Nash coefficient (NSE), correlation coefficient (R), and root mean square error (RMSE), by against the measured sediment yield at the outlet of the watershed.Uncertainties of the model simulation were also evaluated by means of confidence interval. [Results] 1) The three individual models differed in their performances, with MMF performing the best compared with the other two.2)Ensemble techniques greatly improved the performance of soil erosion simulation, and reduced uncertainties among various modelling tools.Comparing the best ensemble simulation with the best individual model, performances of NSE, R, and RMSE were improved by 23.6%, 15.8%, and 46.4%, respectively.3)BG technique provided more accurate predictions than the other methods did, the width of the confidence interval for BG technique smaller than that of the others, indicating a more stable and reliable performance. [Conclusions] The performance of the widely used empirical soil erosion models (e.g., RUSLE, CSLE) could be further enhanced by using the technique of ensemble simulation combined with uncertainty analysis in their applications.
Keywords: soil erosion models    ensemble simulation    Bates-Granger    Granger-Ramanathan    equal weight    Loess Plateau watershed    

土壤侵蚀不仅导致土壤质量退化、土壤有机质含量流失、农业减产、沉积物堆积[1]，还导致山洪、泥石流等自然灾害发生[2]。有效模拟土壤侵蚀是流域及区域侵蚀防治的的重要研究内容之一[3]。当前已开发有大量的土壤侵蚀模型可广泛应用于不同尺度土壤侵蚀及产沙模拟，例如：Morgan-Morgan-Finney model (MMF)[4]、修正土壤通用流失方程(Revised Universal Soil Loss Equation, RUSLE)[5]、中国土壤流失方程(Chinese Soil Loss Equation, CSLE)[6]等。但当前的多模型模拟研究仍存在较多不确定性。近年，通过模型集成，组合多个模型以显著降低单个模型预测不确定性的思想，引起研究者广泛关注[7]。

集成模拟技术通常在大气和水文研究领域很常见[8]，但在土壤侵蚀研究中应用较少。已有研究表明，集成模拟技术预测比许多领域中的单个模型更准确的拟合观察结果[9]。不同单模型预测存在多样性，使用集成模拟技术可以有效改进单模型输出的不确定性 [10-12]。

笔者基于3种常用经验性土壤侵蚀模型(MMF、CSLE和RUSLE)，采用不同模型集成技术：Bates-Granger(BG)集成[13]、等权重模型集成、以及Granger-Ramanathan集成[14]，对黄土高原昕水河流域土壤侵蚀进行集成模拟，探讨集成模拟技术相对单一模型是否显著改善或提高土壤侵蚀模型模拟性能，并比较不同集成模拟技术在应用于土壤侵蚀模型模拟预测时是否存在显著差异。

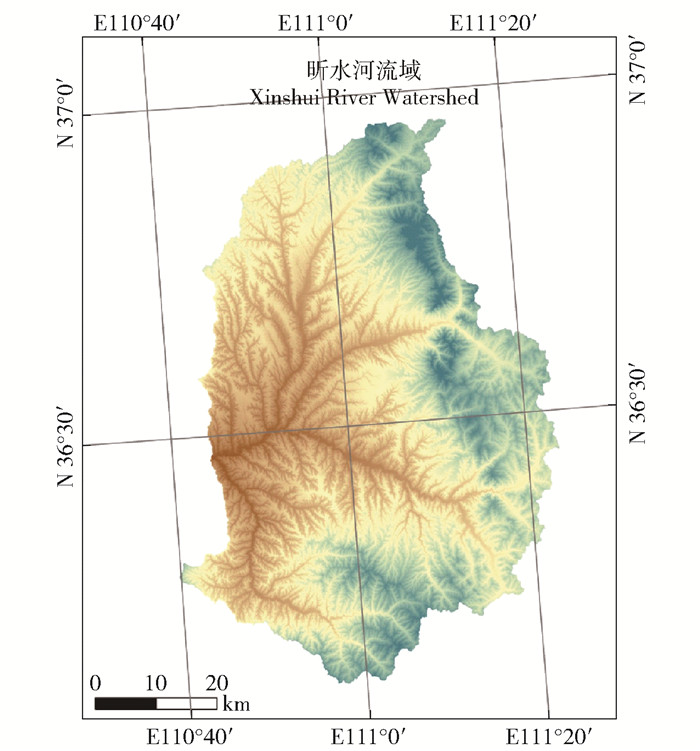
1 研究区概况

昕水河流域位于山西省吕梁山南端(E 110°30′~ 111°27′，N 36°36′~36°55′)。流域总面积3 992 km2，干流全长135 km，流经黄土丘陵沟壑区，河流含沙量高，在大宁县注入黄河(图 1)。研究区气候类型为半湿润大陆性季风气候，流域多年平均降水量为515.8 mm，年平均气温在9~12℃之间，年平均潜在蒸发量为1 073.7 mm，年平均输沙量约为1 280万t。流域植被丰富，土地利用包括阔、针叶林、灌木林、农田、耕地、草地和建设用地。流域内有黄土残塬沟壑区、土石山区、河谷区3种地貌类型区。河谷区主要土壤类型为黄土状褐土性土和草甸褐土；残塬沟壑丘陵区主要为褐土性土；土石山地区多为淋溶性土、山地褐土。

图 1 研究区地理位置 Fig. 1 Geographical location of the study area
2 材料与方法 2.1 数据收集

研究所用降雨数据为昕水河流域内6个雨量站1991—2005年的逐日降水数据；泥沙数据由流域内大宁水文站实测得到。气象数据资料下载于中国气象数据网(http://data.cma.cn/)；数字高程模型(Digital Elevation Model，DEM)下载于中国地理空间数据云(https://www.gscloud.cn/)，分辨率30 m×30 m；土壤类型数据来源世界土壤数据库(HWSD，https://harmonized-world-soil-database-v12)，比例尺1 ∶100万。基于FAO-90土壤数据库标准，对土壤类型进行分类，最终得到黏粒、沙粒、粉粒含量，用以计算RUSLE模型中的土壤可蚀性因子K等。

流域同期土地利用数据下载于美国地质勘探局(https://earthexplorer.usgs.gov)，分辨率30 m×30 m。解译后根据GB/T 21010—2017《土地利用现状分类》进行分类(具体包括：耕地、草地、林地、灌木林地、建筑用地及居民区、水域)，共下载1990、1995、2000和2005年4期土地利用数据。

2.2 土壤侵蚀模型 2.2.1 RUSLE模型

RUSLE源自USLE[15]，由Renard[5]提出，是目前应用最广泛的经验模型之一。方程如下：

$ A=R K L S C P_{\circ} $ (1)

式中：A为年土壤侵蚀率，t/hm2; R为降雨侵蚀力因子，MJ·mm/(hm2 ·h)；K为土壤可蚀性因子t·hm2·h/(MJ·hm2·mm)；L为坡长因子；S为坡度因子；C为植被覆盖管理因子；P为水土保持措施因子。L、S、C、P量纲均为1。

降雨侵蚀力因子

$ R=0.562 P_1-8.12 \text { 。} $ (2)

式中P1为年降水量，mm。

土壤可蚀性因子(K)：由世界土壤数据库(Harmonized World Soil Database，HWSD)进行分类, 根据侵蚀土地生产力影响评价模型(erosion productivity impact calculator，EPIC)模型计算得到。

坡长因子

$ L=\left(\frac{\lambda}{22.13}\right)^m \text { 。} $ (3)

式中：m为坡长效应指数；λ为栅格单元投影长度，m。m的取值请参考文献[16]。

坡度因子

$ S= \begin{cases}10.8 \sin \theta+0.03 & \left(\theta<5^{\circ}\right) \\ 16.8 \sin \theta+0.05 & \left(5^{\circ} \leqslant \theta<10^{\circ}\right) 。\\ 21.9 \sin \theta-0.96 & \left(\theta \geqslant 10^{\circ}\right)\end{cases} $ (4)

式中θ为坡面倾斜角度。

植被覆盖因子(C)：基于归一化植被指数(normalized difference vegetation index，NDVI)计算得到。

水土保持因子(P)：根据RUSLE模型推荐值，耕地为0.1；草地为0.55；灌木林地为0.01；林地为0.5；水体及建设用地为0。

2.2.2 CSLE模型

中国土壤流失方程(CSLE)基于USLE发展而来[6]。模型考虑中国土壤侵蚀特征和常用水土保护措施[17]。根据我国实际情况，CSLE将水土保持实践要素分为生物防治、工程防治和耕作管理3个子要素。其他因子(R、K、L、S)则与RUSLE意义相同[18]。CSLE模型表示如下：

$ A=R K L S B E T。$ (5)

式中：B为生物量控制因子；E为工程措施因子；T为耕作措施控制因子；B、E、T量纲均为1。

生物措施因子(B)：与植被覆盖管理因子(C)赋值一致。

工程措施因子(E)：根据CSLE文献赋值，梯田E =0.16；截流沟E =0.161[17]。

耕作措施因子(T)：≥0~2°取0.1；≥2°~6°取0.221；≥6°~15°取0.305；≥15°~20°取0.575；≥20°~25°取0.735；≥25°取0.8[17]。

2.2.3 MMF模型

MMF模型由Morgan等[4]于1984年开发，是基于物理过程的经验模型，用于模拟坡面尺度的年土壤侵蚀量[19]。笔者主要采用Morgan &Duzant版本[20]进行模拟：

$ G=(F+H)\left(1-D_{\text {ep }} / 100\right) 。$ (6)

式中：G为年输沙量, t；F为年降雨剥蚀量t；H为年径流冲刷量，t；Dep为沉积率，量纲为1。其中，对于F、H、Dep的确定，需要对土壤类型黏粒、沙粒、粉粒含量及理化性质，降雨强度、植被高度、坡度、植被覆盖度、土壤分散率、径流速度等计算或赋值得到[21-22]，因篇幅原因，具体计算步骤请参考Morgan &Duzant版本[20]。

上述模型模拟潜在土壤侵蚀分布以后，结合泥沙输移比估算流域出口侵蚀产沙。其中，泥沙运输比参考陈浩[23]对黄河上、中、下游流域泥沙输移的相关研究，设置昕水河流域泥沙输移比为0.89。

2.3 模型集成

将不同的模拟结果集成计算统一的方法被称为模型集成[24]。不同集成模拟技术计算权重的方法不同[25]，笔者运用Bates-Granger(BG)算法、等权重法、Granger-Ramanathan(GR)算法对前述土壤侵蚀模型进行集成模拟。

2.3.1 Bates-Granger(BG)算法

BG算法由Bates等[13]提出。通过1/σi2对集成模型成员进行加权，其中1/σi2是其预测方差；k为模型数量，k=3。假设模型预测是无偏预测，此时模拟预测具有最小RMSE，权重为最优[26]。BG算法的权重采用式(7)进行估计：

$ W_i=\frac{1 / \sigma_i^2}{\sum\limits_{i=1}^k 1 / \sigma_i^2} 。$ (7)

式中：Wi为各模型权重；1/σi2为模型i的预测方差；k为模型数量，k=3。

2.3.2 Granger-Ramanathan(GR)算法

GR算法基于多元线性回归模型系数的普通最小二乘(Ordinary Least Square，OLS)估计权重[14]。从本质上讲，GR算法涉及多元线性回归模型拟合，根据训练期(1991—2000)模拟结果，与观测值进行相应预测回归[27]，拟合模型为：

$ Y=W_0+\left(W_1 W_2\right)+\left(W_2 X_2\right)+\left(W_3 X_3\right) 。$ (8)

式中：Y为研究区观测值；X1、X2、X3分别为MMF、RUSLE、CSLE在训练期(1991—2000)相应的预测结果，采用最小二乘法求解得到参数W0、W1、W2、W3。这种情况下权重W1、W2、W3的和不一定等于1，W0为截距项，是观测值和单个模型预测之间的偏差修正项。

2.4 模拟性能评价

研究以1991—2000作为训练期，用以训练产生集成模型。2001—2005则作为验证期，用以验证集成模型模拟效果。模拟性能主要采用以下指标进行评价：纳什系数(Nash-sutclife efficiency，NSE)(式(9))[28]，相关系数(R)(式(10))[29]，均方根误差(Root mean squared error，RMSE)(式(11))[30]。

$ \mathrm{NSE}=1-\frac{\sum\limits_{i=1}^I\left(Q_i-M_{\mathrm{i}}\right)^2}{\sum\limits_{i=1}^I\left(Q_i-\bar{Q}_0\right)^2} \text {; } $ (9)
$ R=\frac{\sum\limits_{i=1}^I\left(Q_i-\bar{Q}_0\right)\left(M_i-\bar{M}_0\right)}{\sqrt{\sum\limits_{i=1}^I\left(Q_i-\bar{Q}_0\right)^2} \cdot \sqrt{\sum\limits_{i=1}^I\left(M_i-\bar{M}_0\right)^2}} ; $ (10)
$ \operatorname{RMSE}=\left(\frac{\sum\limits_{i=1}^I\left(Q_{\mathrm{i}}-M_i\right)^2}{I}\right)^{1 / 2} 。$ (11)

式中：Qi为第i年泥沙观测值；Mi为模型模拟值，Q0为观测值的总平均；M0为模拟值的总平均；i为训练时间；I为训练(或测试)的总时间，a。NSE取值-∞~1。当NSE>0.50时，认为侵蚀产沙模拟性能可以接受，越接近1，表示模型性能越好[28]。R取值0~1，越接近1，表示模拟结果与观测结果趋势变化越相似[29]。RMSE越小，模拟值与观测值越接近，模拟误差越小[30]。

2.5 不确定性分析

研究采用置信区间量化分析集成模型模拟结果的不确定性。置信区间由统计量的置信上限和置信下限为上下边界构成，可用以揭示真实值在一定概率下落在测量结果周围的程度，反映集成结果的可信程度[31]，其表达式如下：

$ \left(\bar{x}-t_{\alpha / 2} s / \sqrt{n}, \bar{x}+t_{\alpha / 2} s / \sqrt{n}\right) 。$ (12)

式中：x为整体均值；s为标准偏差；n为样本数量。研究中置信度设置为95%，故α=0.05。

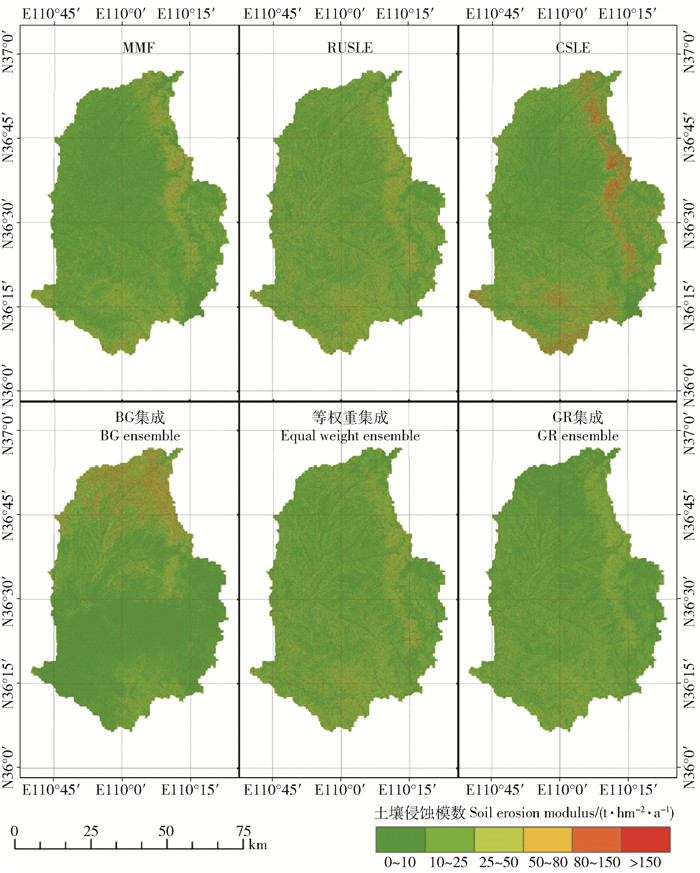
3 结果与分析 3.1 各型模拟结果比较

如图 2所示，整体来看，3个单一模型模拟结果都比较相似。土壤侵蚀严重的区域主要分布在流域的东部区域，结合土地利用类型进行对比发现，耕地在这一区域的面积比例较大。以MMF为例，流域土地利用类型耕地、草地、林地、灌木林地对应的多年平均侵蚀模数分别为24.19、10.47、8.19和8.03 t/hm2。3个模型均呈现土壤侵蚀随土地利用类型的不同而具有明显差异的特点。从坡度分级来看，不同坡度(＜5°，≥5°~15°，≥15°~25°，≥25°)的多年平均侵蚀模数分别为4.38、9.45、18.96和24.37 t/hm2。随着坡度的增加，土壤侵蚀也逐渐增大。

MMF: Morgan-Morgan-Finney model. RUSLE: Revised universal soil loss equation. CSLE: Chinese soil loss equation. The same below. 图 2 1991—2005 MMF、RUSLE、CSLE、BG集成、等权重集成、GR集成平均土壤侵蚀量空间分布 Fig. 2 Spatial distribution of the average soil erosion simulation estimated by MMF, RUSLE, CSLE, BG ensemble, equal weight ensemble, and GR ensemble over 1991 to 2005

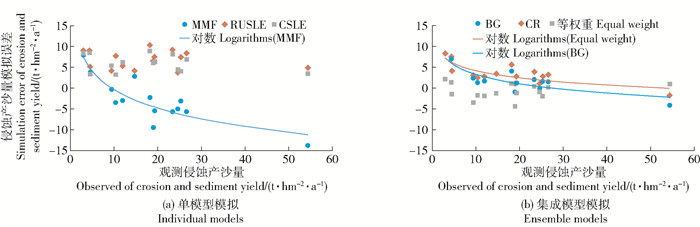
整个模拟阶段，各模型均能较好模拟侵蚀产沙的年际动态变化趋势。由表 1可见，各模型R值均＞0.8。其中，CSLE的R值高达0.89，但从NSE以及RMSE来看，其性能并不是最优。比较MMF、RUSLE、CSLE 3个模型，MMF模型较其他2个模型性能要好。结合图 3误差分布图来看，MMF模型模拟误差呈现一定变化趋势(R2=0.54)，侵蚀产沙量误差较多分布在-5~0 t/hm2(图 3a)，普遍低估侵蚀产沙量；RUSLE、CSLE侵蚀产沙量误差散点未体现显著变化趋势，但集中在5~10 t/hm2，普遍高估侵蚀产沙量。总体来看，成员模型中MMF要优于其他模型，CSLE模型虽然有效改进侵蚀产沙年际动态变化趋势的模拟，但其侵蚀产沙量的模拟效果与MMF仍有差距，而RUSLE模拟效果则最不理想。

表 1 集成模型与单模型统计分析 Tab. 1 Statistical analysis for individual models and various ensemble models
实线表示拟合趋势线。 The solid line indicates the fitted regression line. 图 3 土壤侵蚀产沙模型模拟误差与观测散点图 Fig. 3 Scatter plot of the errors of soil erosion sediment model simulation against the observations
3.2 集成模型模拟分析

集成模拟显著改善模型模拟性能，但不同集成算法其模拟性能仍具有一定差异。由表 1可见，在训练期，BG模型表现最优；GR模型在NSE、R方面与BG模型相当，但其RMSE性能较逊；等权重模型模拟性能较差。在测试阶段，BG模型仍表现稳定，模拟性能最优；GR模型次之；等权重模型尽管其R稍稍有所提升，但关于NSE、RMSE方面的模拟性能仍然逊于其他模型。

由图 3误差分布图来看，GR集成模型的模拟误差集中分布在0刻线周围，且并无显现任何趋势(图 3b)，但平均模拟误差稍大，为1.61 t/hm2；等权重模型模拟误差展现有显著变化趋势(R2=0.62)：模型模拟在枯水年份侵蚀产沙较少时误差较大，随着产沙量的增大，误差逐渐减少；此外，模型整体平均模拟误差最大，为3.60 t/hm2。BG模型模拟误差虽体现有一定变化趋势(R2=0.73)，但模型整体平均模拟误差亦最小，为1.58 t/hm2，且较多散点分布于0值周围。综合来看，BG集成模型较其他集成模型的模拟误差较小，性能较好。

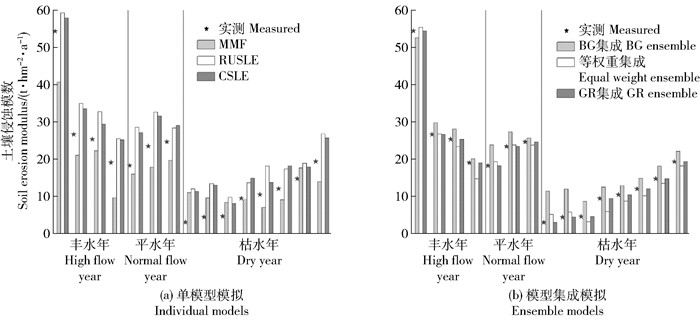
比较集成模拟与单一模型模拟性能(表 1)，在NSE、R、RMSE方面，所有集成模型的表现都优于单一模型，这与POURGHASEMI等[32]的研究结果一致，即集成模型模拟可有效提高模型模拟性能。根据GB/T 50095—1998《水文基本术语和符号标准》[33]流域年径流量分为丰水年、平水年、枯水年。由图 4可以看出，单一模型相对侵蚀产沙观测的误差变化较大。其中，MMF在枯水年(1997—2002、2004、2005)模拟平均误差为(3.99±2.24)t/hm2，相对较小；而丰水年(1993、1994、1996、2003)模拟平均误差为(7.78±4.64)t/hm2，呈现上升趋势；平水年(1991、1992、1995)为(4.32±2.31)t/hm2，误差变化较为平缓，介于两者之间。RUSLE、CSLE仅在个别丰水年(1993、2003)模拟误差较小外，其他年份无论丰水年还是枯水年，其误差变化始终较大。反观集成模拟，无论是在丰水年、平水年、枯水年，其模拟值与实测值更加接近，BG集成、GR集成，以及等权重集成各模型模拟平均误差仅为2.31、2.38以及3.60 t/hm2。

图 4 昕水河流域侵蚀产沙模拟在不同降水水平年份对比 Fig. 4 Yearly comparision of erosion and sediment simulation at different precipitation levels in Xinshui River watershed
3.3 模型不确定性分析

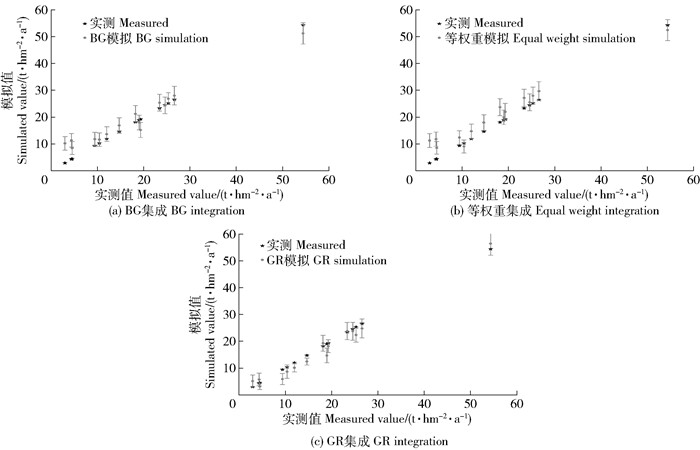
图 5为不同集成模型模拟结果及其置信区间分布(α=0.05)。BG集成模拟总体更为可靠、稳健，73%的实测值可有效落在BG集成模拟95%置信区间范围内。而等权重模拟则仅有60%的实测值可落在其95%置信区间内；GR模拟则有67%的实测值落在其95%置信区间内。比较各集成模型置信区间的变幅，BG集成的置信区间变幅为2.85±0.20；等权重集成的置信区间变幅为4.95±0.19；GR集成的置信区间变幅为4.43±0.56。BG集成模拟置信区间变幅较其他2种集成模拟要小，表明其数值模拟的不确定性较其他集成模型的要小。综上所述，BG集成相对另外2种集成方法，能提供跟准确的预测结果，在不确定性方面也更加稳定、可靠。

图 5 集成模型模拟土壤侵蚀产沙及其不确定性 Fig. 5 Soil erosion and sediment yield simulated by various ensemble models as well as the uncertainties against the observations
4 结论与讨论

1) 集成模拟可以一定程度增加单模型模拟的预测精度，集成前后NSE、R、RMSE分别提高23.6%、15.8%、46.4%。原因是BG集成与GR集成模拟分别采用方差加权以及普通最小二乘(OLS)估计权重，将实测值与单一模型模拟值进行比较训练，最终依据每个模型不同的预测精度赋予不同的权重，精度高的模型分配的权重也就相应较高，具有合理的科学依据。等权重集成方法仅仅对模型进行简单的平均权重分配，忽略对模型的质量判断，集成模拟时其模拟性能提升较少。因此，BG集成、GR集成方法对于侵蚀产沙预测的模拟应用较为值得考虑。

2) 3个单一模型模拟的土壤侵蚀量具有一定差异，其中MMF更加接近流域真实土壤侵蚀状况，原因是RUSLE、CSLE均为传统经验模型，虽然其对模型输入数据要求较少，方便操作。但模型没有考虑泥沙输移的问题，对于泥沙输移的细节描述有很大欠缺。MMF模型较这2个模型具有一些物理意义，考虑水相、沙相2个阶段，同时考虑泥沙输移和沉降的过程。物理过程模型在模型精度方面具有一定的优势，未来的研究中，集成物理过程模型可以作为一个新的尝试。

3) 通过比较3种集成方法的置信区间，笔者发现BG集成、GR集成相较于等权重集成有着更高的置信度。使用不同的统计方法为集合成员分配权重，但最近的研究发现，根据集水区的性质动态及时调整权重可能有利于提高集成置信度[34]。由于涉及模型不确定性的来源很广，土壤侵蚀模型集成的应用仅提供模型不确定性的部分量化。未来，如何利用集成方法更大程度减少模型预测的不确定性将尤为重要。

研究表明，集成建模可显著降低模型模拟的不确定性。不同集成模型中，BG集成较等权重、GR集成效果更优。研究认为，在运用广泛应用的经验型土壤侵蚀模型(如RUSLE、CSLE)时，有必要以集成模拟的方法策略减少模型模拟不确定性。此外，今后的研究将进一步结合概率分布量化确定集成模型中各参数的不确定性。

5 参考文献
[1]
史志华, 刘前进, 张含玉, 等. 近十年土壤侵蚀与水土保持研究进展与展望[J]. 土壤学报, 2020, 57(5): 1117.
SHI Zhihua, LIU Qianjin, ZHANG Hanyu, et al. Progress and prospects of soil erosion and soil conservation research in the past decade[J]. Acta Pedologica Sinical, 2020, 57(5): 1117.
[2]
谢怡凡, 姚顺波, 丁振民, 等. 退耕还林和地理特征对土壤侵蚀的关联影响: 以陕西省107个县区为例[J]. 生态学报, 2022, 42(1): 301.
XIE Yifan, YAO Shunbo, DING Zhenmin, et al. Associated effects of forest restoration and geographical features on soil erosion in 107 counties and districts in Shaanxi province[J]. Acta Ecologica Sinica, 2022, 42(1): 301.
[3]
张勇. 晋北侵蚀区土壤侵蚀潜在危险度评价研究[J]. 亚热带水土保持, 2014, 26(2): 1.
ZHANG Yong. Study on the evaluation of potential risk of soil erosion in the erosion zone of northern Jin[J]. Subtropical Soil and Water Conservation, 2014, 26(2): 1.
[4]
MORGAN R P C, MORGAN D D V, FINNEY H J. A predictive model for the assessment of soil erosion risk[J]. Journal of Agricultural Engineering Research, 1984, 30: 245. DOI:10.1016/S0021-8634(84)80025-6
[5]
RENARD K G. Predicting soil erosion by water: a guide to conservation planning with the Revised Universal Soil Loss Equation (RUSLE)[M]. United States Government Printing, 1997: 1.
[6]
LIU Baoyuan, ZHANG Keli, XIE Yun. An empirical soil loss equation[J]. Proceedings-Process of Soil Erosion and Its Environment Effect, 2002, 2: 21.
[7]
EEKHOUT J P C, MILLARES A, MARTÍNEZ A, et al. A process-based soil erosion model ensemble to assess model uncertainty in climate-change impact assessments[J]. Land Degradation & Development, 2021, 32(7): 2409.
[8]
颜停霞, 许金朵, 林晨, 等. OpenMI技术在水文模型集成中的研究进展[J]. 南水北调与水利科技, 2016, 14(5): 13.
YAN Tingxia, XU Jinduo, LIN Chen, et al. Research progress of OpenMI technology in hydrological model integration[J]. South-to-North Water Transfers and Water Science & Technology, 2016, 14(5): 13.
[9]
WAGENA M B, BHATT G, BUELL E, et al. Quantifying model uncertainty using Bayesian multi-model ensembles[J]. Environmental Modelling & Software, 2019, 117: 89.
[10]
BOOMER K M B, WELLER D E, JORDANT E, et al. Using multiple watershed models to predict water, nitrogen, and phosphorus discharges to the Patuxent Estuary 1[J]. JAWRA Journal of the American Water Resources Association, 2013, 49(1): 15. DOI:10.1111/j.1752-1688.2012.00689.x
[11]
DUAN Qingyun, AJAMI N K, GAO Xiaogang, et al. Multi-model ensemble hydrologic prediction using Bayesian model averaging[J]. Advances in Water Resources, 2007, 30(5): 1371. DOI:10.1016/j.advwatres.2006.11.014
[12]
WILLCOCK S, HOOFTMAN D A P, BLANCHARD R, et al. Ensembles of ecosystem service models can improve accuracy and indicate uncertainty[J]. Science of The Total Environment, 2020, 747: 2.
[13]
BATES J M, GRANGER C W J. The combination of forecasts[J]. Journal of the Operational Research Society, 1969, 20(4): 451. DOI:10.1057/jors.1969.103
[14]
GRANGER C W J, RAMANATHAN R. Improved methods of combining forecasts[J]. Journal of Forecasting, 1984, 3(2): 197. DOI:10.1002/for.3980030207
[15]
WISCHMEIER W H, SMITH D D. Predicting rainfall erosion losses: A guide to conservation planning[M]. Department of Agriculture, Science and Education Administration, 1978: 1.
[16]
江忠善, 郑粉莉, 武敏. 中国坡面水蚀预报模型研究[J]. 泥沙研究, 2005(4): 1.
JIANG Zhongshan, ZHENG Fenli, WU Min. Water erosion prediction model for slopes in China[J]. Journal of Sediment Research, 2005(4): 1.
[17]
符素华, 刘宝元, 周贵云, 等. 坡长坡度因子计算工具[J]. 中国水土保持科学, 2015, 13(5): 105.
FU Suhua, LIU Baoyuan, ZHOU Guiyun, et al. A tool for calculating slope length and slope factor[J]. Science of Soil and Water Conservation, 2015, 13(5): 105.
[18]
沈子雅, 杨志, 李建国, 等. 基于CSLE模型的宁夏黄土地区水土保持措施因子研究[J]. 中国水土保持, 2021(7): 53.
SHEN Ziya, YANG Zhi, LI Jianguo, et al. Research on soil and water conservation measures based on CSLE model in Ningxia loess area[J]. Soil and Water Conservation in China, 2021(7): 53.
[19]
JAIN P, RAMSANKARAN R. GIS-based modelling of soil erosion processes using the modified-MMF (MMMF) model in a large watershed having vast agro-climatological differences[J]. Earth Surface Processes and Landforms, 2018, 43(10): 2064. DOI:10.1002/esp.4372
[20]
MORGAN R P C, DUZANT J H. Modified MMF (Morgan-Morgan-Finney) model for evaluating effects of crops and vegetation cover on soil erosion[J]. Earth Surface Processes and Landforms: The Journal of the British Geomorphological Research Group, 2008, 33(1): 95.
[21]
穆兴民, 李朋飞, 高鹏, 等. 土壤侵蚀模型在黄土高原的应用述评[J]. 人民黄河, 2016, 38(10): 100.
MU Xingmin, LI Pengfei, GAO Peng, et al. A review on the application of soil erosion models in the Loess Plateau[J]. Yellow River, 2016, 38(10): 100.
[22]
张莉, 苗连朋, 温仲明. 基于MMF模型估算植被与降雨变化对水沙的影响: 以延河流域为例[J]. 自然资源学报, 2015, 30(3): 446.
ZHANG Li, MIAO Lianpeng, WEN Zhongming. Estimating the effect of vegetation and rainfall changes on water and sand based on MMF model: An example from the Yanhe River Basin[J]. Journal of Natural Resources, 2015, 30(3): 446.
[23]
陈浩. 黄土丘陵沟壑区流域系统侵蚀与产沙关系[J]. 地理学报, 2000, 55(3): 354.
CHEN Hao. Relationship between erosion and sand production in a watershed system in the loess hills and gullies[J]. Acta Geographica Sinica, 2000, 55(3): 354.
[24]
李新, 程国栋, 康尔泗, 等. 数字黑河的思考与实践3:模型集成[J]. 地球科学进展, 2010, 25(8): 851.
LI Xin, CHENG Guodong, KANG Ersi, et al. Reflections and practices on the digital Heihe River 3:Model integration[J]. Advances in Earth Science, 2010, 25(8): 851.
[25]
韦林, 段凯, 刘效东, 等. 基于多源数据与多模型集成的流域人为蒸散发变异评估[J]. 水利学报, 2022, 53(4): 433.
WEI Lin, DUAN Kai, LIU Xiaodong, et al. Assessment of anthropogenic evapotranspiration variability in watersheds based on multi-source data and multi-model integration[J]. Journal of Hydraulic Engineering, 2022, 53(4): 433.
[26]
DIKS C G H, VRUGT J A. Comparison of point forecast accuracy of model averaging methods in hydrologic applications[J]. Stochastic Environmental Research and Risk Assessment, 2010, 24(6): 809. DOI:10.1007/s00477-010-0378-z
[27]
张晓峒. 回归系数OLS, GLS估计量分布的收敛速度分析[J]. 南开经济研究, 2002(5): 3.
ZHANG Xiaodong. Analysis of the convergence rate of the distribution of regression coefficients OLS, GLS estimators[J]. Nankai Economic Studies, 2002(5): 3.
[28]
李鑫, 王颖苗. 水文模拟优化算法不确定性对流域水资源评估的影响[J]. 水资源开发与管理, 2020(8): 43.
LI Xin, WANG Yingmiao. Impact of uncertainty in hydrological simulation optimization algorithm on water resources assessment in river basins[J]. Water Resources Development and Management, 2020(8): 43.
[29]
吴子怡, 谢平, 桑燕芳, 等. 基于相关系数的水文序列分段趋势识别方法[J]. 水力发电学报, 2019, 38(7): 77.
WU Ziyi, XIE Ping, SANG Yanfang, et al. A correlation coefficient-based method for segmentation trend identification of hydrological series[J]. Journal of Hydroelectric Engineering, 2019, 38(7): 77.
[30]
漠草. 回归的均方根误差[J]. 数理统计与管理, 1983(4): 25.
MO Cao. Root mean square error in regression[J]. Journal of Applied Statistics and Management, 1983(4): 25.
[31]
梁骏, 宋松柏. 水文设计值置信区间估计研究[J]. 西北农林科技大学学报(自然科学版), 2016, 44(10): 221.
LIANG Jun, SONG Songbai. Research on confidence interval estimation of hydrological design values[J]. Journal of Northwest A&F University (Natural Science Edition), 2016, 44(10): 221.
[32]
POURGHASEMI H R, YOUSEFI S, KORNEJADY A, et al. Performance assessment of individual and ensemble data-mining techniques for gully erosion modeling[J]. Science of the Total Environment, 2017, 609: 764. DOI:10.1016/j.scitotenv.2017.07.198
[33]
蓝云龙. 湟水民和站丰、平、枯水年划分初探[J]. 水利科技与经济, 2007(12): 899.
LAN Yunlong. Huangshui Minhe station abundant, flat, dry water year division[J]. Water Conservancy Science and Technology and Economy, 2007(12): 899.
[34]
REGONDA S K, RAJAGOPALAN B, CLARK M, et al. A multimodel ensemble forecast framework: Application to spring seasonal flows in the Gunnison River Basin[J]. Water Resources Research, 2006, 42(9): 12.