2. 北京林业大学水土保持学院水土保持国家林业局重点实验室, 100083, 北京;
3. 北京林业大学水土保持学院, 100083, 北京
中国水土保持科学  2023, Vol. 21 2023, Vol. 21  Issue (2): 107-116. DOI: 10.16843/j.sswc.2023.02.013 Issue (2): 107-116. DOI: 10.16843/j.sswc.2023.02.013 |
黄土高原水土流失严重、滑坡高发,频繁的自然灾害给人民的生命和财产带来巨大的安全风险。传统的土木工程措施加固斜坡或边坡不仅耗资大,也不利于自然生态环境的修复。大量研究表明,植物根系能够有效固持土壤,减少水土流失及浅层滑坡的发生[1-2];因此,量化根系对土体的加强作用、评价根系对边坡稳定性的影响至关重要。在过去40年里,国内外学者对根系固土效果的量化进行了大量研究,而现有研究方法大部分是将根系对土体的增强作用转化为单一的附加黏聚力(cr)[3-4]。根土复合体的黏聚力(c)为素土黏聚力(cs)与根系附加黏聚力cr之和,即c=cs+cr。目前确定cr的理论模型有很多,其中应用最为广泛的模型为Wu[5]模型和纤维束模型[6],以及在此基础上发展的优化模型[7]。
表征cr的计算模型简化根系对边坡稳定性的影响,易于分析含根边坡的稳定性。多数学者[8-10]依据此类模型探究cr的影响因素和变化规律。然而,此类模型建立在大量简化和假设的基础上,均以单根或简单根束为研究对象,cr仅被认为是根系抗拉强度及含根率的函数。事实上,根系的物理特性(形态、直径、长度等),以及土体的物理性质(含水率、弹性模量等)都会对根土复合体的力学性质产生较为复杂的影响[9]。根系的存在提高根土复合体的刚度,使边坡在较小的变形下发生显著的应力重分布[11]。以Wu模型为代表的cr计算模型由于过于简化,忽视了此类因素的变化。数值方法,如有限元法等,具有分析根系形态、根土接触等问题的能力。但是针对坡面数量庞大的根系进行建模和计算,工作量无疑巨大,时间显著延长[2, 12]。因此,开发更加科学和完善的根系固土研究思路和计算模型,将有助于更加精准地理解根系固土机理。
事实上,黄土高原广泛分布的人工林在空间上呈现周期排布。受复合材料力学启发,边坡上具有周期密布根系的土层可以视为天然纤维增强复合材料,通过均匀化理论思想可以获得根土复合体的等效力学参数[13]。均匀化理论中的代表体元(representative volume element,RVE)法可以将复合材料细观量和宏观量联系起来,在细观尺度上能详细地捕捉纤维增强材料的局部构造特征、组分性能等因素,从而高效准确地预测复合材料的宏观力学参数[14]。通过引入RVE法进行根系固土力学研究,有助于从宏细观尺度分析根土特性和根系形态对根土复合体宏观力学性质的影响。目前,根土复合体均匀化理论的研究刚刚起步,缺乏根土复合体三维本构关系和强度的研究[13, 15]。
研究根土复合体的等效力学性能有2类基本参数。一是根土复合体屈服前的弹性参数,即根系的存在对根土复合体弹性参数的影响,Wu模型等传统模型所采用的弹性参数仍为素土弹性参数,不能考虑根系的存在对根土复合体弹性模量的改变量。二是根土复合体的屈服强度准则,虽然Wu模型等传统模型主要集中研究这方面,然而都没有在弹性参数变化的基础上考虑cr的增加;因此,笔者以黄土高原人工造林树种刺槐(Robinia pseudoacacia)为例,通过RVE法直接建立根土复合体三维本构关系,量化根系对土体的增强作用;通过不同埋根方式的直剪试验及反复剪切试验验证RVE法理论结果;最后通过数值模拟阐明RVE法获得的根土复合体等效力学参数用于评价边坡稳定性的可行性。研究成果从周期复合材料的视角为我国黄土高原根系固土机制研究提供新的研究思路。
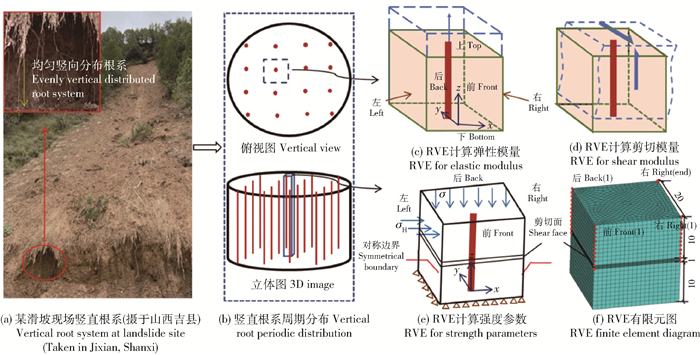
1 材料与方法 1.1 研究地点及材料参数2021年10月,山西省出现大范围强降雨,临汾等地区先后发生多起滑坡、崩塌等地质灾害,其中尤以蒲县、大宁和吉县等地最为严重。作者赴现场调研发现,根系的存在有力减缓了浅表层滑坡发生的可能,从坡面破坏形态可以看出,根系抗拉作用分担部分土体剪切力,起到固持土体的作用(图 1a)。
|
图 1 RVE法计算根土复合体等效力学参数模型概化图 Fig. 1 Generalized model of equivalent mechanical parameters of root-soil composite calculated by RVE method |
本研究刺槐根系及土壤均采集于山西吉县森林生态系统国家野外科学观测研究站。依据国家标准G B-T 50123—2019 《土工试验方法标准》测定土壤物理力学性质,由于研究区刺槐根系已积累大量数据,故根的力学性质、土的弹性模量主要由文献[16]确定,cs和φ由直剪试验得到,根土材料参数见表 1。
| 表 1 材料参数 Tab. 1 Material properties |
受地形和气候的影响,黄土高原造林护坡植物的根系竖长且发达,侧根相对较少,多数根(包括侧根)深深扎入土壤中,植物根系整体上呈竖直周期性分布(图 1a)。因此,根土复合体可以视为周期分布的长纤维复合材料,相较于边坡尺度,根系为细观量,含根坡面整体可以看作由单根及根周土组成的RVE重复构成(图 1b)。根据均匀化理论,对选取出的RVE施加周期边界条件,RVE所具有的力学性质代表了整个坡面的等效力学性质。因此,仅需构造典型的RVE即能代表整个坡面进行等效力学性能的研究,极大简化计算模型。以RVE为计算对象,能以较小的计算量建立微观RVE和根土复合体之间跨尺度的力学关系,进而获得根土复合体的等效力学性能。
RVE利用有限元法求解,具有考虑根系形态、根土接触等因素的潜力。而本研究基于研究区植物生长特点,在RVE模型中,仅研究竖直根系,暂不考虑含复杂分支根系的工况。根系简化为排列在土壤中的圆形纤维,锚固在土壤中,根土界面不发生相对位移[3]。摩尔-库伦强度准则表达式简洁,主要参数为c和φ,被广泛应用于土体强度分析中,根土复合体与相应土体有类似的力学特征;因此,为简洁表述根土复合体的强度求解方法,依然采用该准则描述土和根土复合体的抗剪强度。
1.2.1 根土复合体等效弹性参数RVE法的计算过程与微结构的绝对尺度无关。等效弹性参数计算过程中,代表体元采用量纲为1尺寸。周期边界的施加需根据求解方向上的均匀化参数特性,通过在有限元软件中建立节点到节点的线性约束方程及位移边界条件实现。计算不同方向上的弹性参数时,按照所需计算弹性张量性质,设定该分量方向上的应变值为特定值,其余方向满足位移连续。以计算纵向(沿根长向)弹性模量Ez和yz面内剪切模量Gyz为例,代表体元边界应满足以下线性约束方程。
计算Ez时:
| $ U_{{\text {上, 左, 前 }}}=U_{{\text {下, 右, 后 }}} ; $ | (1) |
| $ V_{{\text {上, 左, 前 }}}=V_{{\text {下, 右, 后 }}} ; $ | (2) |
| $ W_{{\text {上 }}}-W_{{\text {下 }}}=W_{{\text {设定值 }}} ; $ | (3) |
| $ W_{{\text {左, 前 }}}=W_{{\text {右, 后 }}}。$ | (4) |
计算Gyz时:
| $ U_{{\text {上, 左, 前 }}}=U_{{\text {下, 右, 后 }}} ; $ | (5) |
| $ V_{{\text {上, 左 }}}=V_{{\text {下, 右 }}} ; $ | (6) |
| $ V_{{\text {前 }}}-V_{{\text {后 }}}=V_{{\text {设定值 }}} ; $ | (7) |
| $ W_{{\text {左, 前 }}}=W_{{\text {右, 后 }}} ; $ | (8) |
| $ W_{{\text {上 }}}-W_{{\text {下 }}}=W_{{\text {设定值 }}}。$ | (9) |
式中:Ez为z方向的弹性模量,N/m2;Gyz为yz平面内的剪切模量,N/m2;U, V, W分别为沿x,y和z方向的位移分量,m,W设定值和V设定值为设定的微小值,均为0.01[17];下角标前-后、左-右和上-下分别为图 1c中的对应面。
相应的,在求解其余的横向(垂直根长向)弹性模量Ex和Ey时,计算时参照Ez;xy和xz面内剪切模量Gxy和Gxz的计算则参照Gyz,即相应的角标进行轮换可得到。
由图 1c和图 1d中代表体元的几何特性可知,根土复合体计算模型至少含有2个对称面,因此,根土复合体为正交各向异性材料,其应变-应力关系为:
| $ \left[\begin{array}{c}\varepsilon_1 \\ \varepsilon_2 \\ \varepsilon_3 \\ \gamma_{23} \\ \gamma_{31} \\ \gamma_{12}\end{array}\right]=\left[\begin{array}{cccccc}S_{11} & S_{12} & S_{13} & 0 & 0 & 0 \\ S_{21} & S_{22} & S_{23} & 0 & 0 & 0 \\ S_{31} & S_{32} & S_{33} & 0 & 0 & 0 \\ 0 & 0 & 0 & S_{44} & 0 & 0 \\ 0 & 0 & 0 & 0 & S_{55} & 0 \\ 0 & 0 & 0 & 0 & 0 & S_{66}\end{array}\right]\left[\begin{array}{c}\sigma_1 \\ \sigma_2 \\ \sigma_3 \\ \tau_{23} \\ \tau_{31} \\ \tau_{12}\end{array}\right]。$ | (10) |
式中:ε为主应变;γ为切应变;S为柔度系数,m/N;σ为主应力,N/m2; τ为切应力,N/m2。下标1代表x,2代表y,3代表z,S44为yz(即23)平面内的柔性系数,S55为zx(即31)平面内的柔度系数,S66为xy(即12)平面内的柔性系数。
对于正交各向异性材料,若坐标方向为材料弹性模量的主方向时,正应力只引起线应变,剪应力只引起剪应变,2者互不耦合。因此,根据不同方向上的弹性参数求解需求,对RVE分别进行3次单向拉伸和3次纯剪切,如图 1c和1d所示,通过提取RVE在对应位移边界表面上产生的边界应力,即可由式(10)求解根土复合体等效柔度系数矩阵,根据胡克定律及泊松比定义,最终得到弹性参数与柔度系数矩阵S之间的转化关系,实现3维弹性参数求解,见式(11)。
| $ \left\{\begin{array}{l}E_x=\frac{1}{S_{11}} \quad E_y=\frac{1}{S_{22}} \quad E_z=\frac{1}{S_{33}} \\ v_{y z}=-\frac{S_{23}}{S_{33}} \quad v_{x z}=-\frac{S_{13}}{S_{33}} \quad v_{x y}=-\frac{S_{12}}{S_{22}} \\ G_{x z}=\frac{1}{S_{44}} \quad G_{y z}=\frac{1}{S_{55}} \quad G_{x y}=\frac{1}{S_{66}}\end{array}\right.。$ | (11) |
式中υ为泊松比,量纲为1。
通过ABAQUS CAE插件Easy PBC[17],实现RVE法周期边界和位移边界条件的施加,以及等效弹性参数的求解。
1.2.2 根土复合体等效强度参数RVE的抗剪强度的求解借助直剪试验的力学思想,通过自编程序对RVE施加周期边界后进行直剪加载求解。RVE直剪加载的模型与计算等效弹性参数时略有不同,如图 1e和1f所示,RVE分为上下2个部分,中间添加厚度为1 mm的薄层模拟剪切面。根系直径为1.7 mm,根长为20 mm。土体采用实体单元,由于根系较细,在直剪试验过程中仅承受拉力,因此根系设置为受拉不抗压。材料参数如表 1所示。
RVE直剪加载过程中,用应力条件代替垂直加载设备,位移边界条件代替剪切的位移约束。下部土体边界条件为:4个侧面添加对称边界,底部约束z方向位移。RVE中,薄层及上部土体侧面施加周期边界,顶面自由。周期边界的线性约束方程为:
| $ U_{{\text {前, 左 }}}=U_{{\text {后, 右 }}} ; $ | (12) |
| $ V_{{\text {前, 左 }}}=V_{{\text {后, 右 }}}。$ | (13) |
式中下角标前、后、左、右为图 1e的4个侧面。对于直角边线上的点,即图 1f标注的点,需满足以下约束方程:
| $ U_{{\text {右 }}(1), {\text { 后 }}(1) {\text {, 右(end) }}}=U_{{\text {前(1), 前 }}(1) {\text {, 后 }}(1)} ; $ | (14) |
| $ V_{{\text {右 }}(1), {\text { 后 }}(1) {\text {, 右 }}({\text { end }})}=V_{{\text {前 }}(1) {\text {, 前 }}(1), {\text { 后(1) }}} 。$ | (15) |
式中:下角标(1)为相应面的线上起始点,(end)为组成相应面的线上结束点。
根据直剪试验规范G B-T 50123—2019要求,对顶面分别施加σ=100、200、300和400 kPa的垂直荷载,在上部土体的左侧施加σH=100 kPa的应力模拟推动作用,分40步进行求解。提取剪切面上的剪应力和剪切位移,得到剪应力-剪切位移曲线以及黏聚力c和内摩擦角φ。
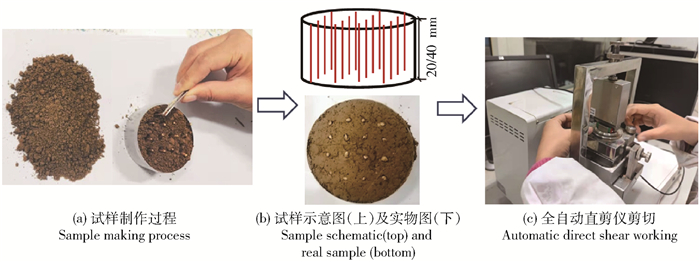
1.3 刺槐根土复合体直剪试验为验证RVE法理论计算根土复合体等效力学参数的可靠性,根据国家标准G B-T 50123—2019,采用重塑土进行制样,使用北京华勘公司的全自动直剪仪对素土及含根土进行直剪及反复剪切试验(往复剪5次,每次剪切至2 mm),剪切速率为1 mm/min。限于论文篇幅,仅配置含水率为20%的试样。等效弹性和强度参数计算中,由于利用周期边界条件,仅使用边长为20 mm(或量纲为1)RVE。为验证理论计算结果的准确性,在61.8 mm的直剪盒中,构造4排×4列均匀等距分布的根系,根系的平均直径为1.7 mm。为使根系和土壤有足够的联结长度,设置40 mm竖根与20 mm竖根2种含根试样,试样高度及根系分布如图 2所示。
|
图 2 直剪试验制样及试验过程 Fig. 2 Sample preparation and test process of direct shear test |
在试样制备过程中,称取相应质量的土壤并全部压入环刀中,以保证制作的试样具有相同的紧实度。为保证根系与土壤紧密结合,先将一半的土逐层倒入环刀中,保持比较松散的状态下,将根系垂直均匀插入土中,用手按实,再逐层放入另一半土按实,最后进行相同次数击实以保证根土复合体的密实度。为尽量减少采用重塑土制样造成的根土原生胶结面的削弱,试件覆保鲜膜静置24 h后再进行直剪。
1.4 边坡稳定性评价为了阐明RVE法评价造林边坡稳定性的可行性,采用Wu模型[5]和RVE法分别计算边坡表面含根土层(厚度为2 m)的力学参数,其中Wu模型仅能得到根土复合体的cr,RVE法能得到等效弹性(表 2)和强度参数(见2.3)。Wu模型和RVE法计算得到的安全系数与根土复合体试验结果计算得到的安全系数进行对比。由于黄土抗剪强度随深度增加,因此底层土的黏聚力设置为表层素土的2倍[18]。边坡坡度为30°,坡长为12.4 m,边坡宽度为1个RVE厚度,厚度方向测面采用对称边界(用于模拟无限扩展的多排根系),左右2侧面采用x向约束,模型底部采用固结约束,坡面自由,仅受重力作用。采用强度折减法计算边坡安全系数,通过数值迭代计算是否收敛作为边坡失稳临界状态的标准[19]。
| 表 2 根土复合体本构参数 Tab. 2 Constitutive parameters of root-soil composite |
通过RVE法得到20%含水率下根土复合体的等效弹性参数如表 2所示。数据说明,根系的存在使各向同性土体转变为正交各向异性根土复合材料,对各个方向的弹性模量均有提升作用,尤其增强纵向弹性模量Ez(提高35%),而对横向弹性模量Ex、Ey和剪切模量增强作用较小。
在沿纤维方向,变形和受力主要由根系承担,根的弹性模量大于土的弹性模量,在纵向受力时根系能发挥抗拉作用,因此根土复合体的纵向弹性模量增加较明显。根土复合体横向受拉变形主要是土体的变形,横向弹性模量Ex、Ey增加不明显。在剪切作用下,根系和土体同时发生剪切,以土体剪切为主,根系对土体的增强作用有限,剪切模量提升不明显。以上结果表明,根系对土体弹性参数的影响不可忽略。
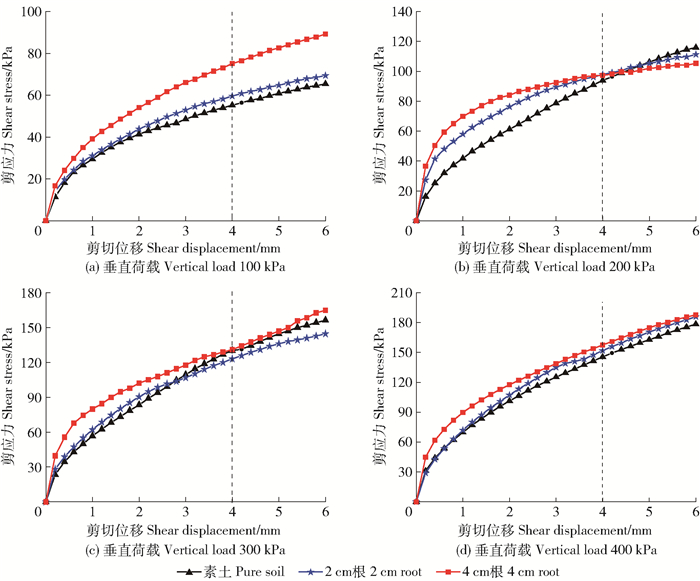
2.2 根土复合体剪应力-剪切位移曲线不同垂直荷载下不同试样的剪应力与剪切位移关系曲线如图 3所示。从图中可以看出,在同一垂直荷载下,不同试样的剪应力值不相同,含20 mm竖直根的根土复合体相较于素土增强作用较小,甚至出现剪切力小于素土的情况。这是由于试样高度较小(即根土接触长度较短),剪切作用下根会随着土体发生同步倾斜,无法发挥根系的抗拉作用;因此,笔者增加试样高度,采用40 mm竖直根的试样,增加根土接触长度,发挥根系的抗拉作用,得到的根土复合体剪应力总体上高于素土工况。以下的讨论以含40 mm竖直根的根土复合体和素土为例。
|
图 3 素土及不同含根土体剪应力与剪切位移关系 Fig. 3 Relationship between shear stress and shear displacement of pure soil and root-soil composite |
从图 3中可以看出,素土及根土复合体在不同荷载下剪应力与剪切位移的变化趋势基本一致。在剪切位移较小时,剪应力呈线性增长,剪应力-剪切位移关系近似为弹性。随着剪切位移的增加,剪应力呈现明显地非线性增长,增长速率逐渐减缓并有趋向于稳定的趋势。对比图 3a~3d,素土及根土复合体的剪应力均随垂直荷载的增加而增大。
在剪切位移较小时,根土复合体的剪切力-剪切位移曲线的斜率比素土工况更大,说明根系的存在提高了土体的弹性模量。根据G B-T 50123—2019,当剪应力与剪切位移关系曲线无明显峰值点时,取剪切位移4 mm对应的剪应力作为抗剪强度。由图 3可知,根系的存在增强了土体的抗剪强度。从剪应力-剪切位移曲线分析可知,根系的存在不仅能够提高土体抗剪强度,对弹性模量的提高同样不可忽视。
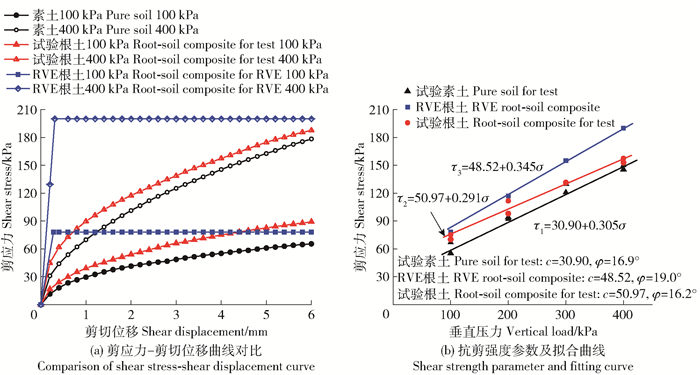
2.3 根土复合体剪切强度的理论与试验图 4a为基于RVE法计算得到的根土复合体剪应力-剪切位移曲线以及相应的直剪试验结果。图 4b为垂直荷载σ与抗剪强度τ(即剪切位移等于4 mm处的剪应力)的拟合曲线,其中τ1、τ2和τ3分别表示素土、根土复合体试验(重复2次)和RVE法理论抗剪强度。根土复合体试验与RVE法理论计算得到的c和φ仅分别相差2.45 kPa和3°。与素土相比,根土复合体的黏聚力提升较大,为20.07 kPa,内摩擦角变化不大。试验中根土复合体含根率AR/A=1.2%,根据Wu模型计算得到cr=1.2T(AR./A)=244.8 kPa,此时基于Wu模型得到的c=cs+cr=275.7 kPa,比试验结果高估约5倍,先前的研究曾指出Wu模型高估抗剪强度达2.70~9.28倍[8],这与本试验结果一致。因此,笔者提出的RVE法在计算根系对土体增强作用较Wu模型更加准确。
|
图 4 根土复合体的抗剪强度理论值与试验结果对比 Fig. 4 Comparison between theoretical shear strength and experimental results of root-soil composite |
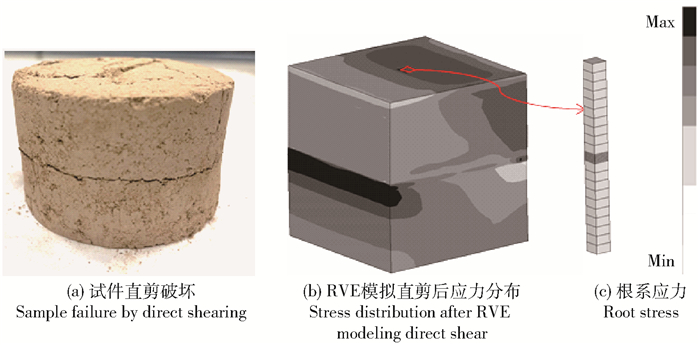
图 5为试件剪切后的形态与RVE直剪后应力和形变图。从图中可以看出试件和RVE模型破坏形态一致,即剪切破坏均发生在剪切面处。此外,RVE模型还能提取代表体元任意点处的应力状态以及根系应力分布。图 5c说明根系通过发挥抗拉作用对土体的变形起到抑制,分担了土体的部分剪力,因而起到了固土及延迟土体破坏的效果。相比于试验,RVE模型在揭示根-土相互作用方面更直观。
|
图 5 试样直剪与RVE模拟直剪结果的对比 Fig. 5 Comparison of sample direct shear and RVE modeling direct shear |
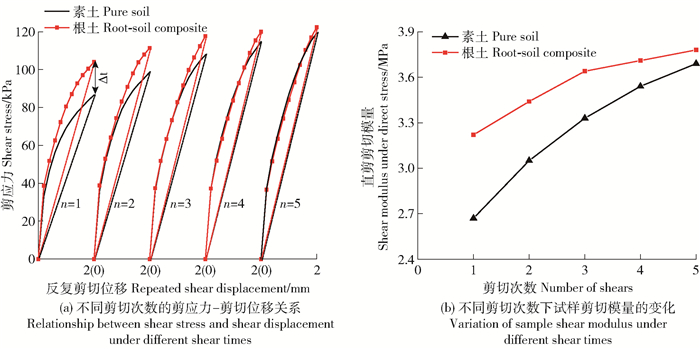
为验证RVE法计算根土复合体等效弹性参数的准确性,笔者以根土复合体剪切模量Gxz为例,通过根土复合体反复剪切试验,验证RVE法计算根系增强土体弹性参数的准确性。素土及根土复合体反复剪切试验的应力-位移关系如图 6a所示。可见,以割线斜率表征剪切模量,根土复合体的剪切弹性模量高于素土弹性模量。随着剪切次数n的增加,素土及根土复合体的剪切模量均有所提升,素土与根土复合体的剪切模量差值越来越小,并趋近于定值,这是由于反复剪过程中土体不断被压密。
|
图 6 试验反复剪切曲线 Fig. 6 Shear curves under repeated shear tests |
经过反复剪后,素土与根土复合体的剪切模量变化收窄并趋于稳定,此时根土之间的结合更加紧密且接近自然状态。第5次剪切后,根土复合体的剪切模量为3.78 MPa,素土的剪切模量为3.69 MPa,根的加入使素土剪切模量值提升2.38%。由表 2可知,根据RVE法计算,根系使土体剪切模量提升2.16%,RVE法计算结果与试验得到的提升率十分接近,验证RVE法在评估根土复合体弹性参数的准确性。在试样经过反复剪和不断被压实的过程中,根土复合体与素土的剪应力差值Δτ逐渐减小,即试验验证了根系对土体的增强作用随着土体弹性模量的增加而减小。虽然在反复剪切过程中,素土和根土复合体的试验剪切模量均高于理论计算采用的剪切模量,但是根土复合体的剪切模量试验提升率与RVE法结果一致。试验剪切模量偏大是由于试样受到直剪盒的约束,侧向变形受到限制。
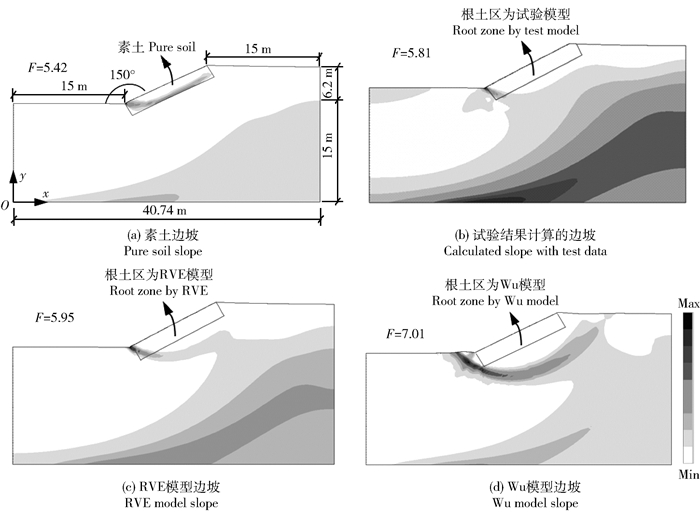
2.5 RVE法在造林边坡稳定性分析中的应用将RVE法计算得到的根土复合体等效力学参数应用于边坡稳定性分析中,并与传统Wu模型的边坡稳定性计算结果进行对比。同时采用素土和根土复合体试验结果分析边坡稳定性。不同方法得到的边坡安全系数F及等效塑性应变云图如图 7所示。素土边坡的安全系数最小(F=5.42),试验结果计算得到的边坡安全系数为F=5.81,提升7.20%。RVE法边坡安全系数为F=5.95,提升9.78%。Wu模型边坡的安全系数提升较大(F=7.01,提升29.33%)。
|
图 7 边坡等效塑性应变云图 Fig. 7 Diagram of equivalent plastic strain for different slopes |
3种含根边坡与素土边坡相比安全系数均有所提升,表明根系的存在能够有效提升边坡的稳定性。RVE法与试验结果计算得到的边坡安全系数和等效塑性应变云图都非常接近,说明了RVE法分析边坡稳定性的有效性。RVE法揭示根系的存在提高了土体弹性模量和抗剪强度,因此提升边坡的稳定性。然而,Wu模型过高估计cr,虽然边坡的安全系数同样得到提高,但是存在高估的风险。因此,将RVE法计算结果运用于边坡稳定性评价是可行的。
观察4种工况的等效塑性应变云图可知,素土边坡滑动面较浅。RVE法边坡和试验结果计算的边坡滑动面从坡脚处延伸至边坡内部,穿过根土复合区,根土复合体提升的弹性模量和抗剪强度对滑坡起到了抑制作用。Wu模型边坡的滑动面从根系分布区下部贯通,Wu模型过高估计的cr值造成根土复合区强度过大,滑动面下移,致使安全系数存在高估风险。
3 结论与讨论1) RVE法能预测根土复合体的等效弹性参数,其剪切弹性模量提升率与反复剪试验结果相比,相差仅为0.24%。Wu模型无法评估根土复合体的等效弹性参数,然而弹性参数的变化在边坡稳定性评价中同样值得关注。
2) RVE法能预测根土复合体的强度参数c和φ的变化,根系对土体的增强作用,不仅体现在黏聚力c的增强上,内摩擦角和等效弹性参数同样有变化。根土复合体试验与RVE法理论计算得到的c和φ仅相差2.45 kPa和3°,Wu模型计算的结果比试验结果高估约5倍。
3) RVE法运用到边坡尺度上具有可行性,与素土边坡相比,RVE模型计算得到的边坡安全系数提高9.78%,与试验结果计算的边坡安全系数接近。而Wu模型计算得到的边坡安全系数提高29.33%,Wu模型存在高估边坡稳定性的风险。
笔者所提出的RVE方法,以黄土高原人工林边坡为例,根据植物根系生长特点,假设根系在土中呈周期性分布,研究方法可推广用于其他地区具备相似特点的植被边坡。相对于Wu模型等传统方法,RVE法在研究根土界面类型、土体模型(邓肯-张和修正的剑桥模型等)和根系形态等方面具有潜力,但需要进一步研究。根土复合体的弹性参数和强度参数的试验验证相对比较困难,特别是弹性参数的验证需要精准的设计。笔者尝试采用反复剪的方法验证剪切模量。限于准确测定根土复合体剪切模量较为困难,笔者从剪切模量提升率的角度验证RVE计算结果的准确性。后续可采用真三轴试验等方法验证其他弹性参数,采用原位大型直剪试验等方法验证强度参数。
| [1] |
PHILLIPS C, HALES T, SMITH H, et al. Shallow landslides and vegetation at the catchment scale: A perspective[J]. Ecological Engineering, 2021(173): 106436. |
| [2] |
田佳, 韩磊, 金学娟, 等. 用有限元法研究降雨对青海云杉林边坡稳定性的影响[J]. 中国水土保持科学, 2019, 17(6): 11. TIAN Jia, HAN Lei, JIN Xuejuan, et al. Effect of rainfall on slope stability of Picea crassifolia forest based on finite element method in Qinghai[J]. Science of Soil and Water Conservation, 2019, 17(6): 11. |
| [3] |
MEIJER G J. A generic form of fibre bundle models for root reinforcement of soil[J]. Plant and Soil, 2021(468): 45. |
| [4] |
LIANG T, KNAPPETT J A, LEUNG A, et al. A critical evaluation of predictive models for rooted soil strength with application to predicting the seismic deformation of rooted slopes[J]. Landslides, 2020, 17(1): 93. DOI:10.1007/s10346-019-01259-8 |
| [5] |
WU T H, MCKINNELL III W P, SWANSTON D N. Strength of tree roots and landslides on Prince of Wales Island, Alaska[J]. Canadian Geotechnical Journal, 1979, 16(1): 19. DOI:10.1139/t79-003 |
| [6] |
POLLEN N, SIMON A. Estimating the mechanical effects of riparian vegetation on stream bank stability using a fiber bundle model[J]. Water Resources Research, 2005, 41(7): 226. |
| [7] |
JI Jinnan, MAO Zhun, QU Wenbin, et al. Energy-based fibre bundle model algorithms to predict soil reinforcement by roots[J]. Plant and Soil, 2020, 446(1): 307. |
| [8] |
吕春娟, 陈丽华, 陈卫国, 等. 根土复合体的抗剪特性研究[J]. 灌溉排水学报, 2016, 35(3): 13. LV Chunjuan, CHEN Lihua, CHEN Weiguo, et al. Study on shear performance of soil-root composite[J]. Journal of Irrigation and Drainage, 2016, 35(3): 13. |
| [9] |
ZHU Jinqi, WANG Yunqi, WANG Yujie, et al. How does root biodegradation after plant felling change root reinforcement to soil?[J]. Plant and Soil, 2020, 446(1): 211. |
| [10] |
及金楠, 田佳, 瞿文斌. 基于连续断裂过程的根系黏聚力Wu氏模型修正系数的确定[J]. 林业科学, 2017, 53(11): 170. JI Jinnan, TIAN Jia, QU Wenbin. Determination of correction coefficients of Wu's model of root cohesion based on successive fracture process[J]. Scientia Silvae Sinicae, 2017, 53(11): 170. |
| [11] |
COHEN D, SCHWARZ M. Tree-root control of shallow landslides[J]. Earth Surface Dynamics, 2017, 5(3): 451. |
| [12] |
SWITALA B M, WU W J G. Numerical modelling of rainfall-induced instability of vegetated slopes[J]. Geotechnique, 2018, 68(6): 481. |
| [13] |
黄建坤, 王学林, 及金楠, 等. 基于渐近均匀化理论的黄土高原草本植物固土效果数值分析[J]. 农业工程学报, 2020, 36(9): 168. HUANG Jiankun, WANG Xuelin, JI Jinnan, et al. Numerical simulation of root reinforcement for herbs in Loess Plateau based on asymptotic homogenization theory[J]. Transactions of the CSAE, 2020, 36(9): 168. |
| [14] |
陈玉丽, 马勇, 潘飞, 等. 多尺度复合材料力学研究进展[J]. 固体力学学报, 2018, 39(1): 1. CHEN Yuli, MA Yong, PAN Fei, et al. Research progress in multi-scale mechanics of composite materials[J]. Chinese Journal of Solid Mechanics, 2018, 39(1): 1. |
| [15] |
杨璞, 向志海, 胡夏嵩, 等. 根对土壤加强作用的研究[J]. 清华大学学报: 自然科学版, 2009, 49(2): 305. YANG Pu, XIANG Zhihai, HU Xiasong, et al. Soil reinforcement by vegetation roots[J]. Journal of Tsinghua University: Science and Technology, 2009, 49(2): 305. |
| [16] |
陈丽华, 及金楠, 冀晓东, 等. 林木根系基本力学性质[M]. 北京: 科学出版社, 2012: 121. CHEN Lihua, JI Jinnan, JI Xiaodong, et al. Mechanics of root-soil[M]. Beijing: Science Press, 2012: 121. |
| [17] |
OMAIREY S L, DUNNING P D, SRIRAMULA S. Development of an ABAQUS plugin tool for periodic RVE homogenisation[J]. Engineering with Computers, 2019, 35(2): 567. |
| [18] |
瞿文斌, 及金楠, 陈丽华, 等. 黄土高原植物根系增强土体抗剪强度的模型与试验研究[J]. 北京林业大学学报, 2017, 39(12): 79. QU Wenbin, JI Jinnan, CHEN Lihua, et al. Research on model and test of reinforcing shear strength by vegetation roots in the Loess Plateau of northern China[J]. Journal of Bejing Forestry Unitersity, 2017, 39(12): 79. |
| [19] |
吕庆, 孙红月, 尚岳全. 强度折减有限元法中边坡失稳判据的研究[J]. 浙江大学学报(工学版), 2008, 42(1): 83. LV Qing, SUN Hongyue, SHANG Yuequan. Slope failure criteria of shear strength reduction finite element method[J]. Journal of Zhejiang University (Engineering Science), 2008, 42(1): 83. |