2. 云南省高校高原山地空间信息测绘技术应用工程研究中心, 650000, 昆明;
3. 滇西应用技术大学地球科学与工程技术学院, 671000, 云南大理
中国水土保持科学  2022, Vol. 20 2022, Vol. 20  Issue (5): 109-117. DOI: 10.16843/j.sswc.2022.05.014 Issue (5): 109-117. DOI: 10.16843/j.sswc.2022.05.014 |
近年来,许多国内外学者结合不同分辨率的DEM数据提取地形特征要素,并且根据组合不同地形因子实现对地形特征综合分析,促进高分辨率DEM数据在土地适宜性分析和水土流失分析领域的发展。地形因子是土壤侵蚀模型中的重要变量:我国的黄土高原地区,当陡坡长度在10~60 m范围内,坡长与土壤流失之间的关系与USLE土壤侵蚀经验模型具有很好地近似性,而与RUSLE土壤侵蚀经验模型结果则不太理想[1]。采用数字地形分析方法提取山区坡谱、坡长和坡度因子,探讨3种因子的关系:坡谱信息熵变化范围反映地形起伏由平缓到强烈的变化趋势;坡长和坡度因子平均值介于2.72~18.61之间,在一定程度上表征土壤流失量的大小[2]。
此外,DEM分辨率大小影响着土壤侵蚀模型应用中的地形因子参数精度。DENG等[3]通过对DEM重采样的方式,研究地形因子对DEM分辨率依赖性,得出不同地形因子受DEM分辨率变化的影响不一致,各地形因子间的相关性与DEM分辨率呈线性关系,DEM分辨率降低即地形因子间的相关性降低。李蒙蒙等[4]为研究DEM分辨率对地形因子(LS)提取精度的影响,将30 m分辨率DEM数据进行重采样为7个不同分辨率的DEM,结果表明随着DEM分辨率的降低,坡长和坡度的相关系数呈现降低的趋势。对于构建土壤流失模型,DEM分辨率对LS因子值有重要的影响:在云贵高原区不同等级侵蚀面积随DEM分辨率发生变化,DEM分辨率由5 m降低至50 m,所计算微度侵蚀面积增加49.2%,中度侵蚀面积减小92.5%,轻度增加13.7%[5]。该地区中度土壤侵蚀主要发生在海拔较高区域,同时海拔较高区域也是地形起伏度较大区域,土壤侵蚀分布与地形起伏度分布具有一致性。综合国内外研究现状不难发现,土壤侵蚀与地形有重要关系,土壤侵蚀模数会随着DEM分辨率降低而减小,高精度DEM更为真实描述微地貌形态特征,从而更精确反映土壤侵蚀模数。
对于TCI模型,SHAN等[6]用坡度因子和曲率因子来变化定义地形复杂性,结果表明地形复杂度依赖于DEM精度。王雷等[7]提取的地形TCI模型,有效通过DEM描述黄土丘陵沟壑区的地表形态变化。卢华兴等[8]利用多因子评价方法选取4种局部地形因子并分析融合4种因子最终得到每个格网的地形TCI指标。
笔者以云南禄丰恐龙国家地质公园南缘山区为研究区,基于0.5 m高分辨率DEM,遵循地形因子有效性、易计算性和因子相互独立性原则,选取坡度、地表粗糙度、标准曲率、地表切割度等单地形因子进行加权综合分析,对地形因子通过组合地形复杂度(Terrain Complexity Index, TCI)模型来描述和表达地表形态,以地形表面褶皱和破碎程度的指标判断土壤侵蚀区域。
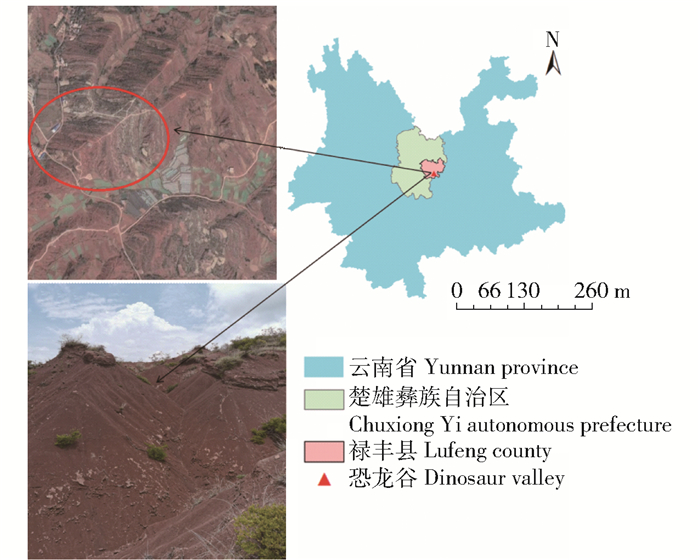
1 研究区概况研究区域位于云南禄丰恐龙国家地质公园南缘山区,隶属云南楚雄彝族自治州, 地理坐标为E 101°38′06″~102°24′34″,N 24°51′33″~25°30′45″。测区范围内地貌类型复杂多样,以构造侵蚀地貌、方山地貌为主,地势东北高,西南低,最高海拔2 200 m,最低海拔1 302 m。测区内存在小型中生代红色沉积盆地,成土母岩由中生代紫色砂页岩和元古代的碳酸盐岩交错分布。受母岩影响,土壤类型呈带分布,紫色土、红壤分布广泛。测区位置如图 1示所示,其中图 1(a)来源于百度地图,图 1(b)为实地踏勘手机拍摄。该区域属亚热带季风性气候,干湿分明,且土壤沙化严重,裸土、裸岩分布广泛。
|
图 1 实验区概况 Fig. 1 Overview of the experimental area |
试验区影像数据通过DJI Phantom 4 RTK进行影像数据采集。首先根据测区实际周边地理环境,交通状况,结合Google earth平台对测区进行航线规划,其次通过前期航线规划以及后期数据质量要求,选择合适的参数设置。鉴于本次数据获取主要面向地形特征分析应用,试验区选取恐龙谷南缘环状山区东北方向的山包,面积0.28 km2。本次飞行参数设置为:航向和旁向重叠度均设80%,平均飞行高度150 m,航测天气条件良好,共采集392张影像,影像平均分辨率为0.07 m。
使用Context Capture Master软件通过集群方式对实测数据进行影像匹配、自动空三等步骤构建密集影像匹配点云。点云需通过滤波处理,将地物点(植被、建筑物、信号塔、高大独立地物等)剔除构建DEM。具体步骤如下:1)应用TerraSolid软件的Terrascan模块中渐进加密不规则三角网(Progressive TIN Densification: PTD)滤波算法,设迭代角6°,迭代距离1.4 m的参数进行滤波处理,得到地面点数据集;2)对于DEM的构建,首先由地面点数据构建不规则三角网,其次选择反距离权重法的像元分配类型和线性函数的填充方法,通过自然领域插值法计算像元值,采样距离选定为0.5、1.0、1.5和2.0,以此构建分辨率为0.5、1.0、1.5及2.0 m的DEM。
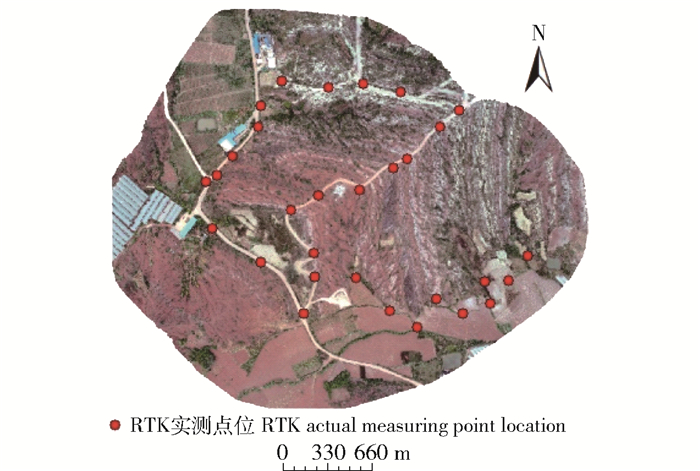
为验证DEM精度,试验首先在野外用RTK采集30个点数据,点位分布叠加到正射影像显示,如图 2示,再分别将0.5、1.0、1.5和2.0 m分辨率DEM高程值赋30个同名点。
|
图 2 实测点位 Fig. 2 Location of actual measuring points |
依据重复测量原理,取观测值的算数平均值作为真值[9-10],即RTK采集野外30个实测点为真值,0.5、1.0、1.5和2.0 m的DEM中选30个同名点的高程值为观测值,分别按式(1)、(2)、(3)和(4)计算相关的误差值,结果保留4位小数(表 1)。
| $d_i=\left(H_i-H_{\text {ture }}\right) ;$ | (1) |
| $M_i=\frac{\sum d_i}{n} ;$ | (2) |
| $S_{\mathrm{D}}=\sqrt{\frac{\sum\left(d_i-M_i\right)^2}{n}} ;$ | (3) |
| $R=\sqrt{\frac{\sum d_i^2}{n}}。$ | (4) |
| 表 1 分析DEM精度指标计算结果 Tab. 1 Calculated results of analytical DEM accuracy metrics |
式中:d为高程误差,m;M为平均误差,m,可平均体现数据集中的误差;SD为标准偏差,m,表示高程误差数据离散程度;R为均方根误差,m,以突显对比值与真值之间离散程度[11];i为4种分辨率序号(i=0.5, 1.0, 1.5, 2.0)。
通过表 1计算结果结合表 2比例尺精度综合分析表明,除2 m分辨率DEM超出7 mm外,其余三者均满足国家1∶500的DEM精度标准。考虑高程值离散程度和与真值误差离散程度,1.5 m分辨率DEM的SD=0.04 m和R=0.040 8 m,与其相比1.0 m分辨率DEM的SD和R略低,分别为0.036 6和0.037 1 m。但0.5 m分辨率DEM的SD和R分别仅为0.016 7和0.017 3,所以后续实验均以0.5 m分辨率DEM为基础进行。
| 表 2 比例尺精度 Tab. 2 Scale accuracy |
TCI模型用于描述和表达地表形态的复杂程度,是评价地形表面褶皱和破碎程度的指标参数,描述地形复杂度基于统计方法有:高程标准差、地形起伏度、等高线密度、沟壑密度等地形因子,基于几何方法描述因子有:形态复杂指数、地表粗糙度、曲率等因子。
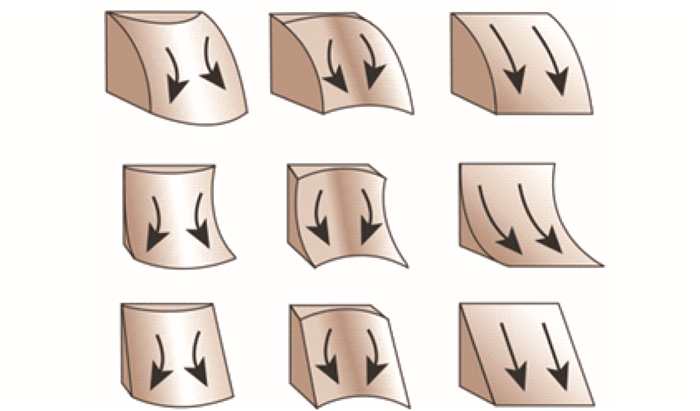
试验区以构造侵蚀地貌为主,构建TCI模型主要选取以下地形因子[12-13]:1)其土壤侵蚀量的大小受地面坡度制约,坡度(Slope)和土壤侵蚀度成正比,受重力侵蚀地区一般坡度值高,所以坡度因子是反映地形复杂度的典型因子;2)地表粗糙度(Surface Roughness)在微地形地貌中把地形表面崎岖程度定为粗糙度,粗糙度客观反映地形表面抗风蚀的能力,具体计算如式(5);3)地表切割深度(Surface Cut Depth)[14]用合适地面点领域范围的高程均值与相同范围内高程最小值相减,按式(6)计算;4)曲率主要包括剖面曲率、平面曲率、全曲率、标准曲率等。曲率反映地形扭曲变化的程度,其中剖面曲率和平面曲率分别沿最大坡度的方向、垂直于最大坡度的方向描述地形的曲面形态,而标准曲率(Standard Curvature)[15-16]是结合剖面和平面曲率,更准确诠释地形变化程度,如图 3所示,来源于ArcGIS官方网址对曲率函数的解释。
| $S_{\mathrm{R}}=1 / \cos \left(S_{\text {lope }} {\rm{ \mathsf{ π} }} / 180\right) ;$ | (5) |
| $S_{\mathrm{CD}}=D_{\text {mean }}-D_{\text {min }}。$ | (6) |
|
源于ArcGIS官方网站https://www.esri.com/en-us/arcgis/products/arcgis-pro/resources From the official ArcGIS website https://www.esri.com/en-us/arcgis/products/arcgis-pro/resources 图 3 标准曲率图 Fig. 3 Standard curvature diagram |
式中:SR为地表粗糙度;Slope为坡度;SCD为地表切割深度;Dmean和Dmin分别为DEM的均值和最小值;量纲均为1。
以0.5 m的高分辨率DEM为基础,基于ArcGIS平台,采用因子分析方法对试验区进行地形复杂度分析。利用统计和几何综合的方法描述地形复杂度指标,针对试验区的特性,选取反映地形本质特征的坡度、地表粗糙度、标准曲率、地表切割深度等地形因子作为评价因子,其中坡度用来描述试验区关于曲面的倾斜程度,地形粗糙度用来表示每个地形表面单元中地表崎岖的复杂程度。通过变异系数法,如式(7)用于确定各项因子权重,通过各地形因子的均值和标准差计算变异系数,单因子变异系数比所有因子变异系数总和,以此确定单因子权重。最后,应用ArcGIS求取TCI指数。
| $P_i=\frac{\frac{S}{\bar{x}}}{\sum\limits_{i=1}^n \frac{S_i}{\bar{x}_i}}。$ | (7) |
式中:Pi为地形因子评价权重;S为地形因子标准差,m;x为地形因子均值,m;i为地形因子数,n=4。
3 单因子指标结果分析 3.1 坡度形态特征分析基于ArcGIS平台的坡度分析,如表 3所示。平缓坡、缓坡和斜坡面积所占比例较为均匀,在20%左右。平缓坡面积比例最大,为25.10%,急陡坡面积比例最小,仅为3.76%。
| 表 3 坡度数据分析 Tab. 3 Analysis of slope data |
针对试验区裸土、裸岩分布广泛的特性,在ArcGIS中使用空间分析,基于坡度提取粗糙度,通过高程值按低、中、高进行分级[17],如表 4所示。低粗糙度比例最大,为74.03%。
| 表 4 地表粗糙度分析 Tab. 4 Surface roughness analysis |
通过ArcGIS输出每个像元的表面曲率,曲率是表面的二阶偏导数,该值是通过将选中像元与8个相邻像元拟合而得。依据表 5分析结果,标准曲率>0面积比例为37.10%,<0面积比例达到67.18%,而表面平滑地区面积比例仅有4.82%。
| 表 5 标准曲率分析 Tab. 5 Standard curvature analysis |
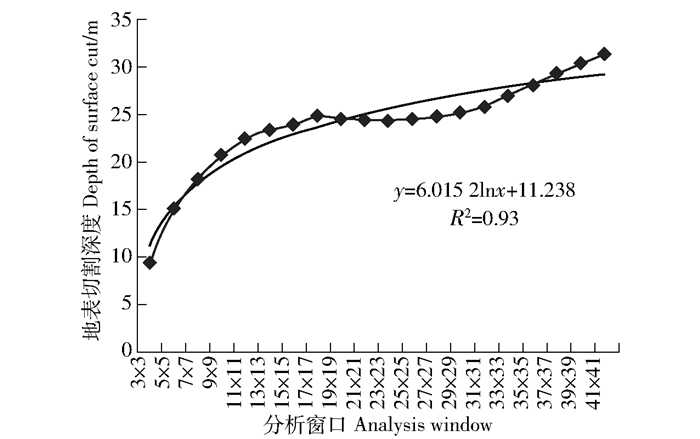
对于地表切割深度,分析最佳窗口是关键步骤[18]。应用ArcGIS的邻域分析,对实验区进行从3×3窗口到41×41窗口的20组数据分析,获得试验区地表切割深度和分析窗口的关系如图 4所示。最大高差法辅助人工作图判断,地表切割度值随窗口大小在拐点5×5—19×19呈现上升趋势,除2个端点区间内整体数值高于拟合函数。在19×19—35×35窗口区间整体数值低于拟合函数,在35×35拐点后又迅速递增。
|
图 4 领域窗口和地表切割深度分析 Fig. 4 Domain window and surface cut depth analysis |
根据表 6的统计数据,结合统计软件可知地表切割深度与网格单元大小与对数方程拟合得到
| $Y=A_0 \ln x+A_{1}。$ | (8) |
| 表 6 地表切割深度分析 Tab. 6 Surface cut depth analysis |
式中:Y为每个网格的平均地势起伏度;x为每个网格的面积;A0和A1为参数。
拟合曲线为Y=6.015 2lnx+11.238,R2=0.93。在5×5、19×19窗口和拟合曲线出现交点,综合考虑试验区面积较小和DEM精度高2个因素,较大窗口会造成DEM模糊,故选取5×5拐点作为最佳窗口并按照Ⅰ、Ⅱ、Ⅲ、Ⅳ等级对该地区地表切割深度进行划分(表 6)。地表切割深度Ⅰ、Ⅱ级所占比例相对更多,分别占总面积的32.54%和31.79%。
4 TCI运用结果分析与验证讨论 4.1 TCI构建结果分析TCI模型进行定量化存在模糊性[19],对此,笔者对4项地形因子先按自然间断点法分级,再进行手动调整,最后以2为步长按低、较低、中、较高和高复杂度分为5级[12, 20],并对其进行赋值。对4项地形因子统一色带,添加注记,分级结果如图 5和表 7所示。
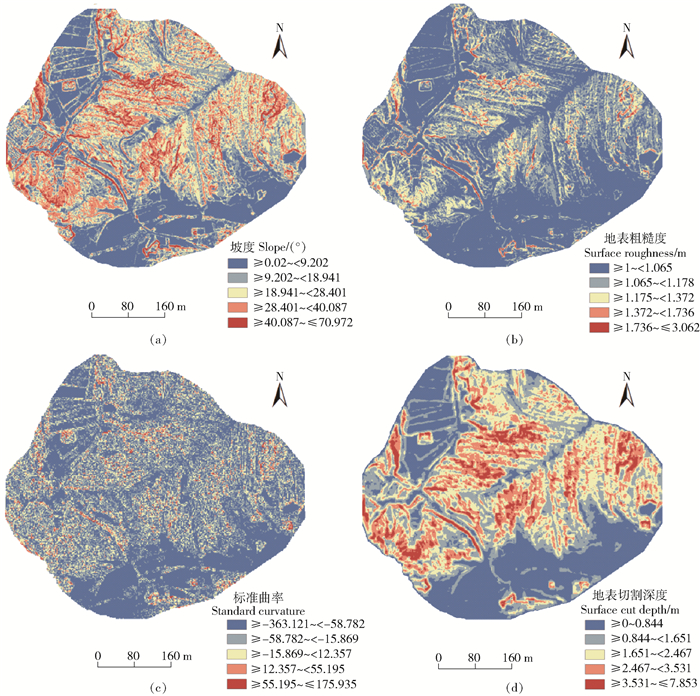
|
图 5 地形复杂度 Fig. 5 Terrain complexity |
| 表 7 地形复杂度因子分级 Tab. 7 Grading of terrain complexity factors |
通过变异系数法计算坡度、地表粗糙度、标准曲率和地表切割深度4项地形因子的权重。经计算,在TCI模型中的权重分别为0.282、0.171、0.259和0.288。构建TCI模型如图 6所示,图中F1、F2和F3标出部分复杂度高的区域,F1、F2为山脊和山谷主要分布区域。该区域复杂度较高不仅因脊-谷区表面崎岖,经实地野外踏勘,试验区裸土、裸岩分布广泛,且红壤和紫色土黏性低。F1、F2区域经雨水冲刷后,脚踩凹陷明显,红壤和紫色土沙化严重。土壤侵蚀是土壤在水力、风力等外力作用下,被剥蚀、破坏和分离的过程。TCI模型中可知,试验区较高和高复杂度区域主要分布于山体两侧,山体两侧凹凸不平说明山体受亚热带季风性气候影响,经风化作用导致土壤受到侵蚀,从而反映出以F1、F2为主的较高和高复杂度区域内水土流失严重。F3为试验区位于试验区东北角,实地踏勘时发现,该区域不仅有沙化严重的红壤和紫色土,且分布着白色碎化的沉积岩。据表 8统计分析表明较高复杂度和高复杂度总体面积比例相对集中,二者总占测区面积的22.95%。
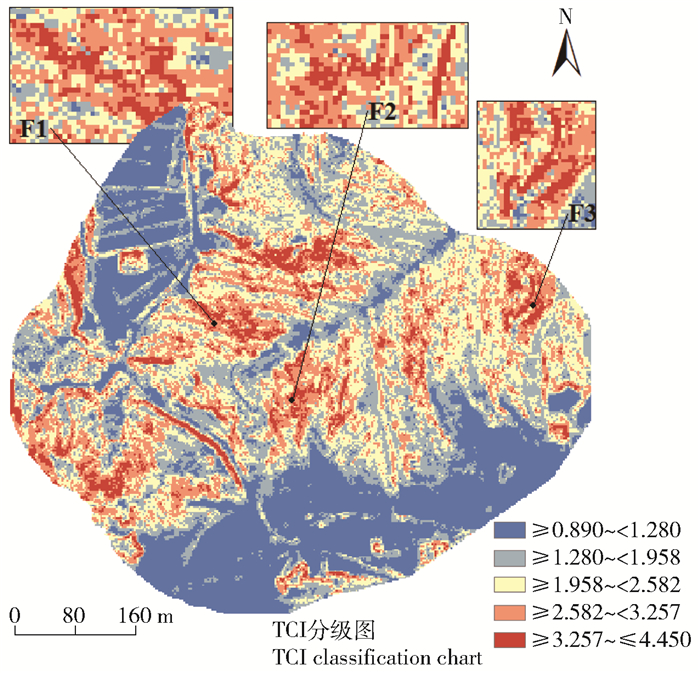
|
F1、F2和F3是复杂度高的区域. F1, F2 and F3 are areas of high complexity. 图 6 TCI分级图 Fig. 6 TCI grading chart |
| 表 8 TCI分级表 Tab. 8 TCI grading scale |
采用可视化对比分析方法[8]验证TCI模型的有效性。依据TCI模型,通过试错法由0~100%调整模型透明度,发现60%透明度模型既能清晰展示模型,在山体阴影和等高线叠加又能较好突出山体和等高线变化趋势,如图 7示。经对比分析可知TCI模型符合等高线变化程度,对于F1和F2区域在TCI模型中为高复杂度区域,等高线走向同样贴合模型。因此,能表明TCI可较好反映地表形态变化。
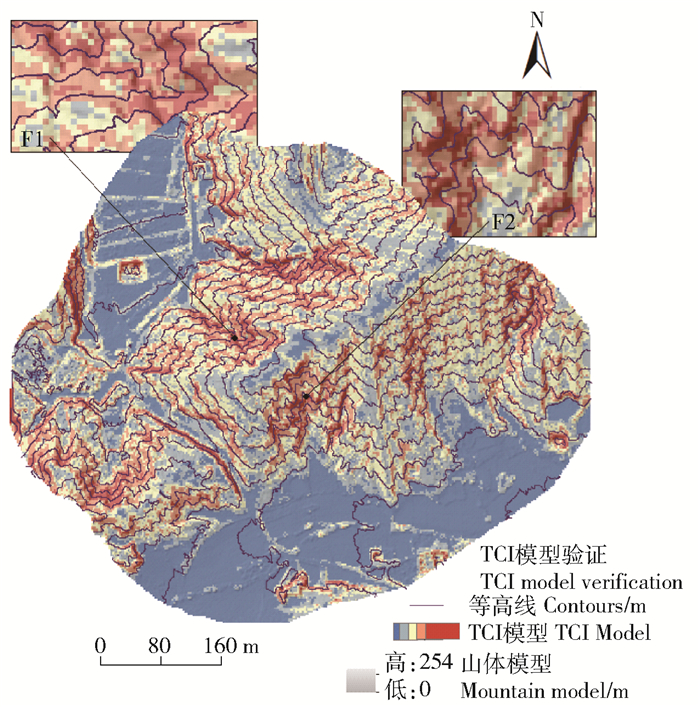
|
F1和F2是复杂度高的区域. F1 and F2 are areas of high complexity. 图 7 TCI模型验证 Fig. 7 TCI model validation |
无人机具有携带轻便、人工成本低的特点,可快速获取高精度DEM。以此为基础,依据对复杂地形地貌进行完整性和适用性的分级处理,结合曲面倾斜度和地表崎岖状况考虑,针对4项地形单因子指标,分别赋予不同权重构建TCI模型。试验研究结果表明:1)依据变异系数计算的各项单因子权重分为0.282、0.171、0.259和0.288;2)TCI模型中复杂度较高的F1、F2区域脊-谷的位置表面崎岖,经实地野外踏勘,试验区裸土、裸岩分布广泛,且红壤和紫色土黏性低;3)结合恐龙谷南缘山区的气候、土壤条件和实地踏勘情况,发现TCI模型中较高复杂、高复杂度区域的土壤受一定程度侵蚀导致水土流失。大面积侵蚀地貌的情况下,以小面积TCI模型快速判断土壤受侵蚀区域主要集中于脊-谷位置。无人机影像构建DEM,相对于其余技术手段,不仅省时省力,且精度相对较高。在大面积侵蚀地貌的情况下,小面积、高精度的DEM构建TCI模型,以地表地形变化结合气候、土壤条件从地表直观角度分析土壤受侵蚀区域,依此为基础快速判断大面积土壤侵蚀区域。基于高分辨率DEM在突出微地貌地形特征的同时相对更符合实地情况反映土壤侵蚀状况。对于TCI模型,可依据不同的地形条件,选取适宜的地形因子。
| [1] |
LIU B Y, NEARING M A, SHI P J, et al. Slope length effects on soil loss for steep slopes[J]. Soil Science Society of America Journal, 2000, 64(5): 1759. DOI:10.2136/sssaj2000.6451759x |
| [2] |
俱战省, 张加兵, 柏子昌. 山区坡谱信息熵与水土流失地形因子关系探讨[J]. 测绘科学, 2019, 44(3): 86. JU Zhansheng, ZHANG Jiabing, BO Zichang. Investigation on relationship between slope spectrum's information entropy and topographical factor influencing soil loss in the mountainous region[J]. Science of Surveying and Mapping, 2019, 44(3): 86. |
| [3] |
DENG Y, WILSON J P, BAUER B O. DEM resolution dependencies of terrain attributes across a landscape[J]. International Journal of Geographical Information Science, 2007, 21(2): 187. DOI:10.1080/13658810600894364 |
| [4] |
李蒙蒙, 赵媛媛, 高广磊, 等. DEM分辨率对地形因子提取精度的影响[J]. 中国水土保持科学, 2016, 14(5): 15. LI Mengmeng, ZHAO Yuanyuan, GAO Guanglei, et al. Effects of DEM resolution on the accuracy of topographic factor derived from DEM[J]. Science of Soil and Water Conservation, 2016, 14(5): 15. DOI:10.16843/j.sswc.2016.05.003 |
| [5] |
周小清. 不同分辨率DEM对地形因子和土壤侵蚀空间分布的影响研究[D]. 北京: 北京林业大学, 2017: 27. ZHOU Xiaoqing. Research on the effects of DEM with different resolutions on terrain factors and the spatial distribution of the soil erosion[D]. Beijing: Beijing Forestry University, 2017: 27. |
| [6] |
SHAN J, ZAHEER M, HUSSAIN E. Study on accuracy of 1-degree DEM versus topographic complexity using gis zonal analysis[J]. Journal of Surveying Engineering, 2003, 129(2): 85. DOI:10.1061/(ASCE)0733-9453(2003)129:2(85) |
| [7] |
王雷, 汤国安, 刘学军, 等. DEM地形复杂度指数及提取方法研究[J]. 水土保持通报, 2004, 24(4): 55. WANG Lei, TANG Guo'an, LIU Xuejun, et al. Research on DEM terrain complexity index and extraction method[J]. Bulletin of Soil and Water Conservation, 2004, 24(4): 55. |
| [8] |
卢华兴, 刘学军, 汤国安. 地形复杂度的多因子综合评价方法[J]. 山地学报, 2012, 30(5): 616. LU Huaxing, LIU Xuejun, TANG Guo'an. Multi-factor comprehensive evaluation method of terrain complexity[J]. Mountain Research, 2012, 30(5): 616. |
| [9] |
KURKOV V M, KISELEVA A S. DEM accuracy research based on unmanned aerial survey data[J]. ISPRS-International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, 2020, XLⅢ-B3-2020. |
| [10] |
蒋广鑫, 谢元礼, 高志远, 等. 中国5类典型区域常用DEM高程精度评价[J]. 水土保持研究, 2020, 27(5): 72. JIANG Guangxing, XIE Yuanli, GAO Zhipeng, et al. Evaluation on elevation accuracy of commonly used DEM in five typical areas of China[J]. Research of Soil and Water Conservation, 2020, 27(5): 72. |
| [11] |
JIANG Ling, LING Dequan, ZHAO Mingwei, et al. Effective identification of terrain positions from gridded DEM data using multimodal classification integration[J]. ISPRS International Journal of Geo-Information, 2018, 7(11): 443. |
| [12] |
何文秀, 石云. 黄土丘陵沟壑区地形复杂度分析[J]. 测绘科学, 2015, 40(10): 146. HE Wenxiu, SHI Yun. Analysis of terrain complexity in loess hilly and gully region[J]. Science of Surveying and Mapping, 2015, 40(10): 146. |
| [13] |
刘春, 孙伟伟, 吴杭彬. DEM地形复杂因子的确定及与地形描述精度的关系[J]. 武汉大学学报(信息科学版), 2009, 34(9): 1014. LIU Chun, SUN Weiwei, WU Hangbin. Terrain complexity factor and its relationship with accuracy of DEM terrain representation[J]. Geomatics and Information Science of Wuhan University, 2009, 34(9): 1014. |
| [14] |
汤国安. 我国数字高程模型与数字地形分析研究进展[J]. 地理学报, 2014, 69(9): 1305. TANG Guo'an. Research progress of digital elevation model and digital terrain analysis in my country[J]. Acta Geographica Sinica, 2014, 69(9): 1305. |
| [15] |
张亮. 矢量等高线曲率的计算方法研究[D]. 北京: 中国科学院研究生院(教育部水土保持与生态环境研究中心), 2014: 32. ZHANG Liang. Research on calculation method of vector contour curvature[D]. Beijing: Graduate School of the Chinese Academy of Sciences (Research Center for Soil and Water Conservation and Ecological Environment, Ministry of Education), 2014: 32. |
| [16] |
陈楠. 剖面曲率精度变化与DEM分辨率关系[J]. 中国矿业大学学报, 2013, 42(1): 147. CHEN Nan. The relationship between the accuracy of profile curvature and DEM resolution[J]. Journal of China University of Mining & Technology, 2013, 42(1): 147. |
| [17] |
张倩宁, 黄泽纯, 徐柱, 等. 一种自适应定权地形复杂度模型[J]. 山地学报, 2017, 35(2): 230. ZHANG Qianning, HUANG Zechun, XU Zhu, et al. An adaptive terrain complexity model with fixed weight[J]. Mountain Research, 2017, 35(2): 230. |
| [18] |
高蜻, 唐丽霞, 谷晓平, 等. 基于ArcGIS的望谟河流域地势起伏度分析[J]. 中国水土保持科学, 2015, 13(4): 9. GAO Qing, TANG Lixia, GU Xiaoping, et al. Analysis of ArcGIS-based relief amplitude of the Wangmo river watershed in Guizhou[J]. Science of Soil and Water Conservation, 2015, 13(4): 9. |
| [19] |
TAROLLI P, FONTANA G D. Hillslope-to-valley transition morphology: New opportunities from high resolution DTMs[J]. Geomorphology, 2009, 113(1). |
| [20] |
牛叔文, 李景满, 李升红, 等. 基于地形复杂度的建设用地适宜性评价: 以甘肃省天水市为例[J]. 资源科学, 2014, 36(10): 2092. NIU Shuwen, LI Jingman, LI Shenghong, et al. Evaluation of suitability of construction land based on terrain complexity: A case study of Tianshui city, Gansu province[J]. Resources Science, 2014, 36(10): 2092. |