RWEQ模型中风因子的改进及应用
巩国丽
1
,
刘鑫
2,
要玲
1,
任丽霞
1,
王敏
3
1. 山西能源学院, 030600, 山西榆次;
2. 生态环境部信息中心, 100029, 北京;
3. 北京维盛沃德科技有限公司, 100029, 北京
收稿日期：2020-04-09; 修回日期：2021-03-13
项目名称：山西能源学院院级科研基金项目"山西省矿产资源开发区生态综合探测分析与治理措施研究"(ZB-2018002);山西省高等学校科技创新项目资助"RWEQ模型的改进及应用"(2020L0728);国家"十二五"科技支撑计划课题"国家尺度生态系统监测与评估技术集成应用系统"(2013BAC03B00);第二次青藏高原综合科学考察研究资助(2019Q2KK1003)
摘要：风是产生土壤风蚀的前提，实地观测的风速是时刻变化的，模型中需要不少于500个的风速值来支撑，而较高时间分辨率的风速数据难以获取，为此很多文章研究风速降尺度拟合的方法，改进修正方程中风因子估算。本文利用二参数韦伯分布函数、日均风速和日最大风速法分别拟合风速，并与实测结果进行对比研究。此外根据修正后的风速值代入RWEQ模型中得到我国北方的风因子空间分布。结果表明：二参数韦伯分布函数拟合风速所求的风蚀力与实测的风速所求的风蚀力存在误差，相对误差值从0.19到0.95，平均相对误差值达到0.52；利用二参数韦伯分布函数拟合所得风蚀力被低估；日均风速和日最大风速法也未能很好地拟合风速，但用该方法拟合风速计算结果风蚀力与实测风速计算结果风蚀力存在相关性，可利用此相关性反推出实测风蚀力；从利用2000-2010年3月份的实测风速拟合所得风因子值来看，我国内蒙古高原上各大沙地的风因子值较高，东北及青藏高原高山地带等地区的风因子值也较高。
关键词：土壤风蚀 RWEQ模型 二参数Weibull分布模型 风速降尺度 风因子
1. Shanxi Institute of Energy, 030600, Yuci, Shanxi, China;
2. Information Center of Ministry of Ecology and Environment, 100029, Beijing, China;
3. Vision World Technology Co., Ltd, 100029, Beijing, China
土壤风蚀是我国北方地区土地退化的主要原因。为了更好地防治区域水土流失，需要定量估算区域风蚀状况及其原因。RWEQ模型是近几年应用比较普遍的能适应大区域定量估算风蚀量的模型。该模型是基于大量野外实验的一种经验模型[1]，在实际测定风力导致的土壤侵蚀量以及当地的气象、地表植被、土壤湿度、地表的结皮和地表的可蚀性等因子的基础上得出的一个经验方程。风是产生风蚀的重要气候驱动力，也是RWEQ模型中最重要的输入数据，风速输入数据的质量对土壤风蚀量的估算结果影响较大。实际的风速时刻在变化，模型中代入不同时段的平均风速会产生不同的模拟结果，如日均风速和月均风速本身存在差异，风因子的计算结果偏差会很大。此外，代入平均风速会使得模型计算所得的风蚀量偏小，因为风蚀量的产生前提是风速大于临界起沙风速，而平均风速可能将瞬间的大于临界起沙的风速过滤掉。为此模型对计算所需风速的时间分辨率要求较高，要求有不少于500个的风速值用以估算模型中的风因子，但除非点位观测，大尺度的风因子值的模拟很难获得高分辨率的风速值。为解决这一问题，有学者利用分形等方式进行风速时间序列的插值研究[2]。模型中也内嵌一个风速生成器，该风速生成器的输入参数为韦伯系数，且很多学者也提到可以采用Weibull分布参数拟合估算风速[3-4]。但也有许多研究[5]表明该方法并不能很好地拟合我国近地面风速。郭中领[6]利用日均、日最大风速拟合法来进行模拟，根据与实测风速计算结果比较，二者存在一定的关系，但其拟合精度仍然需要提高，为此应选择合适的降尺度方法提高日均风速时间分辨率，进而更准确地估算我国风蚀量。
1 数据与方法
1.1 RWEQ模型
该模型可用于定量评估土壤风蚀量(Fryerar D W et al, 1998)，一般用土壤风蚀模数Ls(kg/m2)表示，即单位面积的沙通量。该模型是一种经验模型，与气候因子W、土壤可蚀性E、土壤结皮S、土壤糙度K′和综合植被因子C有关。
|
$
\begin{gathered}
L_{\mathrm{s}}=Q_{x} / x ;
\end{gathered}
$
|
(1) |
|
$
Q_{x}=Q_{\max }\left(1-\mathrm{e}^{\left(\frac{x}{s}\right)^{2}}\right) \\
Q_{\max }=109.8\left(W E S K^{\prime} C\right)。$
|
(2) |
式中：x为地块长度，m；Qx为地块长度x处的沙通量，kg/m；Qmax为风力的最大输沙能力，kg/m；s为关键地块长度，m。
1.2 风速观测数据收集与处理
1) 风速观测数据的收集。笔者利用国家气象信息中心的中国气象数据网(http://data.cma.cn/)下载的2001—2010年内蒙古自治区近10年数据量充足且DEM落差较小的45个国家气象站点的一日四时次的实测风速数据来进行韦伯分布参数拟合，并将计算结果与实测风速进行比较来验证我国北方地区的韦伯分布函数对风速的拟合结果。由于风力侵蚀多发生于春季，本文利用下载的我国北方384个国家气象站点的3月份的风速值代入RWEQ模型计算出风因子值，用来分析我国北方的风蚀驱动力的分布基本特征。
2) 风速观测数据的处理。中国气象数据网下载的风速值为标准高度10 m下的监测值，而模型中所需的风速值为2 m高度下的近地面风速，这就需要在计算前先进行风速值的高度转换。有研究者利用空气动力学粗糙度[7]来估算风速随高度的变化，模型手册中提到利用七分之一定理[8]来转换不同高度的风速值，笔者直接利用Eiliot的转换方法：
|
$
u_{2}=u_{1}\left(g_{2} / g_{1}\right)^{1 / 7}。$
|
(3) |
式中：u1和u2分别为在g1和g2高度处的风速，m/s。
1.3 风因子估算方法对比与验证
1) RWEQ模型中的风因子值估算。笔者利用国家气象信息中心的中国气象数据网(http://data.cma.cn/)下载的2001—2010年内蒙古自治区45个国家气象站点的一日四时次的实测风速数据。由于风力侵蚀多发生于春季，本文选用下载的3月份的风速值分别代入模型和利用韦伯分布函数计算出风因子值，将计算结果进行比较来验证我国北方地区的韦伯分布函数对风速的拟合结果。下载的点状风速数据利用Arcgis软件中的克里金插值法插值为面状数据，根据其他气象站点的风速数据分析，插值结果准确度较高。
研究表明风蚀量与风速的三次方存在相关关系[9-11]。RWEQ中将风因子值表达为：
|
$F=\left(F_{2}-F_{\mathrm{t}}^{2}\right) F_{2}。$
|
(4) |
式中：F为风蚀力，m3/s3；F2为2 m处的风速，Ft为临界起沙风速，部分地区由于地表情况不同，临界起沙风速不同，如塔克拉玛干沙漠等区域的临界起沙风速会偏小，但大部分区域一般为5 m/s。
2) 二参数Weibull分布模型。利用最小二乘法来求取韦伯分布函数的二参数。
韦伯分布的概率分布函数[3-4]为：
|
$
P\left(u \leqslant u_{\mathrm{a}}\right)=1-\exp \left[-\left(\frac{u_{\mathrm{a}}}{C}\right)^{X}\right]。$
|
(5) |
式中：P(u≤ua)为风速u小于给定风速ua的概率；C为尺度参数；X为形状参数。
笔者利用最小二乘法来求取韦伯分布函数的二参数。
将概率分布函数两端取两次对数后，公式变为：
|
$
\ln (-\ln (1-P))=X \ln u_{\mathrm{a}}-X \ln C。$
|
(6) |
为此将ln(-ln(1-P))看做为B，lnua看做A，XlnC看做b时，上式便可写为如下形式：
利用最小二乘法拟合实测风速数据便可求得C、X值。
在风速经过高度转换后，利用最小二乘法求得韦伯分布参数，并利用参数得出拟合风速：
|
$
u=C\left(\ln \left(1-P\left(u \leqslant u_{a}\right)\right)\right)^{\frac{1}{x}}。$
|
(8) |
在此根据模型中的风速值数量要求，设500个间隔概率数(0.002，0.004，…，0.999)。其中将实测数据的静风的概率与利用韦伯分布函数拟合的累积概率比较，当累积概率小于实测数据的静风概率时，将拟合数据设为0。
3) 日均、日最大风速拟合法。郭中领[6]利用日均风速和日最大风速分别提出了风速的降尺度方法，并在此方法基础上，分别计算风蚀力，求得拟合风速计算结果风蚀力与实测风速计算结果风蚀力的关系式。
|
$
\begin{aligned}
W_{\mathrm{n}}=W_{\mathrm{avg}}+\frac{1}{2} W_{\max } \cos \left(\frac{n \pi}{12}\right) ;
\end{aligned}
$
|
(9) |
|
$
W_{\mathrm{n}}=W_{\mathrm{avg}}\left(1+\cos \left(\frac{n \pi}{12}\right)\right)。$
|
(10) |
式中：Wn为拟合的风速；Wavg为日均风速；Wmax为日最大风速，为了满足RWEQ手册中最低风速数据为500的要求，当风蚀力计算时间尺度为月时，n取1~12，由此获取每小时风速值。Wavg和Wmax来源于国家气象信息中心的中国气象数据网(http://data.cma.cn/)下载的地面气候资料日值数据。
1.4 改进风因子在北方地区的模型误差分析
利用误差分析来验证二参数韦伯分布函数是否适用于我国近地层的风速拟合，设用实测数据求得的结果为fr，利用weibull分布函数拟合数据求得的结果为fw，则两者的相对误差E由下列公式求出：
|
$
E=\left|\frac{f_{\mathrm{r}}-f_{\mathrm{w}}}{f_{\mathrm{r}}}\right|。$
|
(11) |
2 结果与分析
2.1 结果验证
结果表明利用二参数韦伯分布函数拟合风速所求的风蚀力与实测的风速所求的风蚀力存在误差，相对误差值从0.19到0.95，平均相对误差值达到0.52。回归分析结果表明二者相关系数达到了0.97，显著性水平P < 0.01。由于风蚀力的计算结果是在风速大于临界起沙风速(一般设为5 m/s)的情况下计算的，为此推测二参数韦伯分布函数没能很好地拟合5 m/s以上的风速值，使得计算结果偏差较大。表 1显示5 m/s以上的风速值的拟合结果误差均值达到0.09，二者的相关系数达到0.82，显著性水平P < 0.01。表示虽然拟合结果存在误差，但是两者具有很好的相关性。
表 1(Tab. 1)
表 1 韦伯风速拟合结果误差分析
Tab. 1 Error analysis of Weibull wind speed fitting results
误差分析
Error analysis |
风蚀力
Wind erosion force |
风速均值
Mean wind speed (>5 m/s) |
相对误差的最大值
Maximum relative error Emax |
0.95 |
0.18 |
相对误差的最小
Minimum relative error Emin |
0.19 |
0.01 |
相对误差均值
Mean relative error Eavg |
0.52 |
0.09 |
相对误差中值
Median relative error Emed |
0.48 |
0.08 |
相关系数
Correlation coefficient R |
0.97 |
0.82 |
显著性水平
Significance level P |
< 0.01 |
< 0.01 |
|
表 1 韦伯风速拟合结果误差分析
Tab. 1 Error analysis of Weibull wind speed fitting results
|
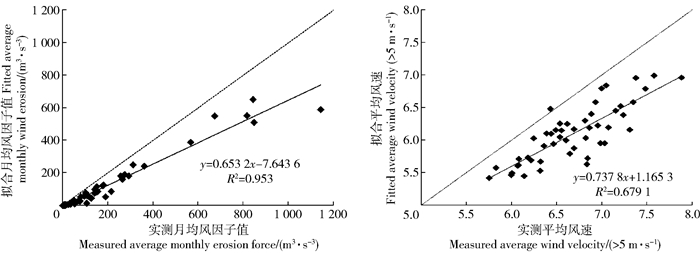
图 1为由实测的风速值和由二参数韦伯分布函数拟合风速计算所得的风蚀力以及平均风速(>5 m/s)的结果比较。结果显示拟合所得风蚀力被低估，斜率达到0.65。同样由于风蚀力是由大于临界起沙的风速值计算而得，为此推算拟合所得的5 m/s以上的风速值结果偏小，对比结果也显示高值风速区(>5 m/s)的拟合结果偏小，斜率为0.74。且Donk等[5]的研究结果也表明利用韦伯分布函数拟合的风速数据可能会被低估，尤其高值风速。
国家气象信息中心的中国气象数据网(http://data.cma.cn/)能够普遍下载的为日均和日最大风速数据，很难满足风蚀力估算对风速的质量要求。而二参数韦伯分布函数拟合结果存在风速值的低估，为此需要选用其他办法来解决此问题，一些经验的方法常用于对日均风速降尺度[12-13]，但这些方法都不能模拟可蚀性的风速数据。本文利用郭中领[6]的日均风速和日最大风速拟合法，求得拟合风速计算结果风蚀力与实测风速计算结果风蚀力的关系式，并判定其拟合的精度。
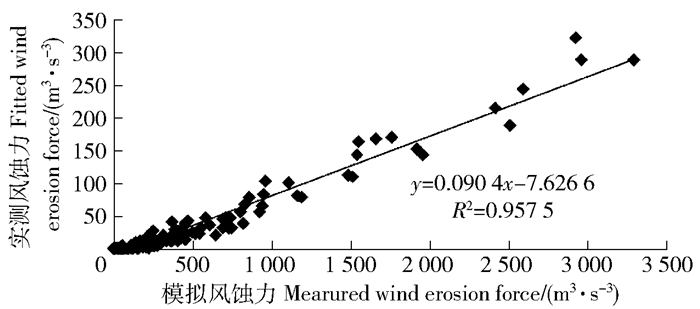
由于中国北方气象站点下载数据多为日均风速，最大风速值缺测数较多，在此情况下本文估算风蚀量多使用了日均风速，在日最大风速满足条件时，也参与了风速拟合。为准确应用于模型，提高风因子估算结果的准确性，根据拟合风速计算结果风蚀力与实测风速计算结果风蚀力的关系式(如图 2中拟合所得的方程)反推得出相对准确的拟合风速的风蚀力，即在实测风速值不够的情况下可利用模拟风速值代入类似图 2的拟合方程进而计算风蚀力，进一步应用于RWEQ估算风蚀量。
2.2 中国北方风因子时空分布与模拟
国家气象信息中心的中国气象数据网(http://data.cma.cn/)中能够下载的风速数据为国家基准站的风速数据，而国家基准站数量偏少，气象观测站点的密集度不够，且分布不均，如很多沙漠区域分布的气象站点数量较少，塔克拉玛干沙漠腹地就只有塔中一个气象站点，而该气象站点的分布区正好是风速较小区，这就影响了塔克拉玛干沙漠区的风蚀量估算精度。同时中国地域辽阔，地形复杂，地表土壤质地等条件不一，不同时期的土地覆被情况也不同，即使是同一覆被条件下，不同土壤质地区的临界起沙风速也不同[14-16]，笔者在利用RWEQ模型计算中，塔克拉玛干沙漠区使用2.5 m/s的临界起沙风速，对于其他区域没能很好地考虑不同土壤质地和不同土地覆被区域的临界起沙风速，统一使用5 m/s，为此需要进一步研究。
由于我国风蚀多发生于植被尚未较好覆盖，风速较大的春季，为此选取3月份作为典型月，求取北方风蚀区的半月风因子值(图 3)。从图可知，内蒙古高原上各大沙地的分布区的风因子值较高，东北及青藏高原高山地带等地区的风因子值也较高。
3 结论
1) Weibull分布模型拟合所得高值风速区(>5 m/s)的风速值偏小，为此不能利用该模型对风速的时间分辨率进行插值进而代入RWEQ模型计算风蚀力。
2) 日均、日最大风速拟合法拟合效果也不尽如意，但该方法所得结果与实测数据所得结果具有很强的相关性，为此可依据模拟与实测的关系式反推风因子。
3) 内蒙古高原上各大沙地分布区的风因子值较高，东北及青藏高原高山地带等地区的风因子值也较高。
4 讨论
1) 反推出的风因子可用于指导风蚀防治，有利于找出风蚀防治的关键区域和关键时间。
2) 鉴于目前实测风蚀量的方法多种多样，有风洞实验法，同位素分析法，插钎法，风蚀盘法等等，各方法不同所获取的实测风蚀量数据本身存在误差，且可获取的实测数据多为点状，区域性的风蚀数据较少，难以对利用反推的风因子带入RWEQ模型估算的风蚀量与实测风蚀量进行对比验证，为此还需进一步研究。
3) 不同土壤质地，不同土地覆被条件下的临界起沙风速不同，大大尺度风因子值估算过程中如何细化分区，获取不同分区的临界起沙风速是需要进一步考虑的。
4) 处于山风口区域的气象站点观测的风速值很高，这往往不代表整个区域的情况，本文是在对山风口气象站点观测数据删除的情况下模拟所得结果，但实际地形复杂区域的风向风速变化很大，这就使得风速插值难度大，有待进一步研究。
5) 国家气象信息中心的中国气象数据网(http://data.cma.cn/)中能够下载的风速数据为国家基准站的风速数据，而国家基准站数量偏少，气象观测站点的密集度不够，有些观测站点所设置的区域正好是风速较高或者较低区，为此如何获取更准确的观测数据是值得进一步研究的。
2021, Vol. 19 
