2. 中国水利水电科学研究院, 100048, 北京
-
项目名称
- 国家重点研发计划项目课题"坡面径流调控与防蚀工程技术"(2018YFC0507002)
-
第一作者简介
- 刘刚(1978-), 男, 博士, 高级实验师。主要研究方向: 土壤侵蚀与土地生产力。E-mail: liugang@bnu.edu.cn
-
通信作者简介
- 焦剑(1983-), 男, 博士, 高级工程师。主要研究方向: 土壤侵蚀与非点源污染。E-mail: 68283847@qq.com
-
文章历史
-
收稿日期:2019-11-18
修回日期:2020-03-18
2. 中国水利水电科学研究院, 100048, 北京
2. China Institute of Hydropower and Water Research, 100048, Beijing, China
地表径流过程是水文循环的重要组成部分。准确预测地表径流,对于土壤侵蚀过程模拟和非点源污染过程分析非常重要。目前,地表径流预报模型按建模方式可分为机理模型和经验模型2大类。机理模型可以较为详细地刻画产汇流物理过程[1-3],但其对于参数率定精度和变量输入要求较高,故限制其广泛应用。对于缺乏基础观测资料的地区,经验模型因结构相对简单、输入数据要求低,具有更强的实用性。20世纪70年代,美国农业部根据本国自然地理特征,研发了径流曲线数模型(soil conservation service-curve number,SCS-CN)。该模型原理清晰简单、对参数和输入变量要求低,已在地表径流预测中得到广泛应用[4]。
SCS-CN模型中有2个重要参数:1)初损率λ,包括产生地表径流之前的地面填洼、截流和下渗;2)径流曲线数CN,该参数为综合指标,量纲为1,体现不同土壤-覆被组合条件下地表产流能力。已有研究表明,CN是该模型中最敏感的参数,仅10%的CN值变化就可导致45%~55%的计算结果误差[5]。自1972年SCS-CN模型手册第一次发表以来,学者们就坡度、土壤特性、土壤前期含水量等因素对CN的影响做了大量研究,进而提出利用坡度和土壤含水率计算CN的方程[6-8]。但是,上述研究一直侧重分析下垫面条件对CN的影响,未充分考虑降雨过程特征对产流过程的影响。SCS-CN模型自使用以来,仅用降雨量一个变量反映降雨特征,可能是造成模拟误差的重要原因之一。为了提升该模型在中国的模拟精度,我国学者自20世纪80年代开始,结合中国的自然地理特征,利用水土保持径流小区观测资料,对模型主要参数进行了修订和优化[6-7, 9-10]。研究表明,即使在同一土壤-覆被条件下,不同降雨产流事件的CN值仍存在显著差异[11-12],但目前尚未提出量化次产流事件间径流曲线数差异的有效方法。
东北黑土区是我国重要的粮食生产基地,因过度开垦和耕作方式粗放,且在相当长的时期内未重视水土保持,目前本区水土流失日益严重,已对粮食安全构成威胁。目前为止,我国对于SCS-CN模型的应用多集中在黄土高原、长江中上游和华北地区。许秀泉等[13]将该模型应用于辽西北地区,但其在东北典型黑土区应用很少。为了提高SCS-CN模型在本区的预报精度,笔者通过量化次降雨过程中雨量在时间上集中程度对地表产流影响,提出在典型黑土区应用SCS-CN模型时,利用量化的降雨过程特征计算次产流径流曲线数CNt的方法;以提高模型预报精度,为本区土壤水蚀过程模拟和水土流失治理提供技术支持。
1 研究区概况鹤北小流域位于黑龙江省黑河市所辖嫩江市鹤山农场内,处于典型黑土区北部,地理坐标为E 125°16′0″~125°121′0″,N 48°59′0″~49°3′0″,属于温带大陆性季风气候,年平均气温0.4 ℃,多年平均降水量534 mm,集中于6—9月。该流域位于小兴安岭南麓,地处小兴安岭向松嫩平原的过渡地带,地形特征为漫川漫岗,坡缓坡长。鹤北小流域面积为27.29 km2,土壤类型为黑土,大部分已开垦为农地,仅有零星分布的草地、林带和居民区。种植农作物主要为大豆、小麦和玉米,尤以大豆为主,田间作业全部实现机械化。
2 材料与方法为分析径流曲线数与降雨特征的关系,在鹤北小流域内九三水土保持试验站选取了7个坡面径流小区(表 1)。各小区坡长均为20 m,土地利用方式分裸地和耕地2种,耕地耕作方式分为顺坡和免耕2种。搜集各小区2003、2004、2006和2007年实测的共138场降雨过程和径流量资料(2005年径流小区观测设施出现故障)进行研究。采用自记雨量计记录降雨过程,其测量精度达0.1 mm。
| 表 1 鹤北小流域径流小区基本情况及径流曲线数 Tab. 1 Features and curve number for plots in Hebei watershed |
径流曲线数模型在降雨产流过程水量平衡(式1)的基础上,对于入渗和产流提出2个基本假定。第1个假定:直接径流和潜在最大径流的比值与入渗量和潜在最大保持量的比值相等(式2);第2个假定:初损量与潜在最大保持量呈线性递增关系(式3)。
| $ P = {I_a} + F + Q; $ | (1) |
| $ Q/(P - {I_a}) = F/S; $ | (2) |
| $ {I_a} = \lambda S 。$ | (3) |
式中:P为降雨量,mm;Ia为初损,mm;F为实际保持量,mm;Q为地表径流量,mm;S为潜在蓄水能力,mm;λ为初损率,依据式(1)~(3),可得出Q的表达式:
| $ \begin{array}{*{20}{c}} {Q = \frac{{{{\left( {P - \lambda S} \right)}^2}}}{{P + \left( {1 - \lambda } \right)S}},\left( {P > \lambda S} \right)}\\ {Q = 0,\left( {P \le \lambda S} \right)} \end{array} $ | (4) |
潜在蓄水能力S采用多年平均径流曲线数CN计算:
| $S = 25\;400/{\rm{CN}} - 254, {\rm{ }}0 \le {\rm{CN}} \le 100 $ | (5) |
在实测获得P和Q后,可利用式(4)和(5)分别反推出式(6)和(7),以计算CN。
| $ \begin{array}{*{20}{c}} {S = }\\ {\frac{{2\lambda P + \left( {1 - \lambda } \right)Q - 4\sqrt {QP{\lambda ^2} + {{\left( {1 - \lambda } \right)}^2}{Q^2} + 4\lambda \left( {1 - \lambda } \right)QP} }}{{2{\lambda ^2}}};} \end{array} $ | (6) |
| $ \begin{array}{*{20}{l}} {{\rm{CN }} = {\rm{ }}25\;400/(254{\rm{ }} + S)} 。\end{array} $ | (7) |
土壤前期湿度条件(antecedent moisture condition, AMC)可依据产流前5 d降雨量划分为3个等级(表 2):AMCⅠ为干旱,AMCⅡ为一般,AMCⅢ为湿润。AMCⅠ、AMCⅡ和AMCⅢ对应的CN值分别为CN1、CN2和CN3。根据查得的CN2利用SCS-CN手册提供的方程计算CN1和CN3。各种土壤-覆被组合条件下的径流曲线数多年平均值(CN)为所有产流事件径流曲线数的算数平均值。
美国土壤保持局依据土壤入渗能力依次减弱的顺序,将土壤划分为A、B、C、D 4大类型[14]。笔者进行水文土壤组划分时采用了Soil Survey Manual[9]中的标准,即根据土壤的饱和导水率(KS)来进行划分,具体的划分标准如表 3所示。各径流小区的饱和导水率通过经验公式(8)计算得到:
| $ {K_{\rm{S}}} = 3.36C + 0.96S + 13.86{O_{\rm{m}}} - 41.58 。$ | (8) |
| 表 3 水文土壤组划分标准 Tab. 3 Division standard for hydrologic soil group |
式中:KS为饱和导水率,mm/h;C为土壤中黏粒质量分数,%;Sd为土壤中砂粒质量分数,%;Om为土壤中有机质质量分数,%。其中的土壤粒级分类标准依照美国制。
2.1.2 利用降雨过程中雨量在时间上集中程度计算次产流径流曲线数的方法研究表明,降雨在时间上的集中程度对于地表产流和土壤侵蚀过程具有重要影响[15]。笔者拟采用降雨过程中最大时段Xmin内的降雨量与次雨量的比值(PX/P)量化雨量在时间上集中程度;其中X为最大时段降雨量对应的时长,min。笔者选取X=5、10、15、20、30、40、50和60,共8个值。根据我国已有研究成果[16-17],结合SCS-CN模型关于初损率取值要求[14],确定λ=0.20。采用式(6)和(7),利用降雨和产流实测资料,计算多年平均径流曲线数的算术平均值CN;同时,分析(PX/P)与次产流径流曲线数CNt与CN比值(CNt/CN)之间的定量关系(式9),进而提出利用降雨在时间上集中程度计算CNt的函数方程:
| $ {\rm{(C}}{{\rm{N}}_t}/{\rm{CN}}) = f({P_X}/P) $ | (9) |
式中PX和P分别为某次降雨过程中最大时段Xmin内的降雨量和次雨量,mm。
因2003年降雨产流的土壤前期湿度包括AMCⅠ、Ⅱ和Ⅲ全部3种类型,故利用各小区2003年降雨产流资料检验以CNt为参数的模型模拟精度。采用Nash模型效率系数Ef[18]、相关系数R和平均相对误差(mean relative error,Re)分析径流深的预测值和实测值差异,分析以CNt为参数的模型模拟效果。
3 结果与分析 3.1 次产流径流曲线数由7个径流小区的土壤级配资料,利用式(8)计算得各径流小区土壤饱和导水率变化于104.70~161.38 mm/h之间,平均为131.48 mm/h。由表 3可见各径流小区水文土壤组类型都是B。
各小区CN变化于74.63~87.97之间,平均为83.27(表 1)。其中,3个裸地小区(2、3和7号)的CN分别为87.97、84.40和83.94,与美国土壤保持局给出的裸地CN取值86较为接近;3个顺坡垄作小区(1、5和6号)的CN分别为84.47、84.86和82.65,高于美国土壤保持局给出的CN值78;免耕小区(4号)的CN为74.63,与美国土壤保持局给出的CN值72较为接近。与美国黑土区相比,东北典型黑土区坡缓坡长,垄作长缓坡耕地的产汇流过程极具特殊性。
各小区CNt在观测期内差异显著,变差系数CV变化于0.085~0.165之间;最大值和最小值的比值变化于1.38~2.24之间,平均为1.81。就土地利用类型而言,裸地各小区CV变化于0.085~0.159之间,平均为0.128;耕地各小区CV变化于0.119~0.173之间,平均为0.151;耕地产流事件中CNt差异略大于裸地。在典型黑土区,若不考虑局地强对流、锋面活动等条件下降雨过程对地表产流影响,仅对径流曲线数单一取值,可能造成显著的径流预报误差。
3.2 次产流径流曲线数与降雨过程特征关系整体而言,(CNt/CN)与(PX/P)呈极显著或显著正相关(表 4)。当10≤X≤40时,两者相关系数更高;其中,当X=20或30时,3个裸地小区(2、3和7号)两者之间相关系数分别达到最大;当X=15或20时,3个顺坡种植小区(1、5和6号)两者之间相关系数分别达到最大;当X=15时,免耕种植小区(4号)两者之间相关系数最大。
| 表 4 (CNt/CN)与(PX/P)之间相关系数 Tab. 4 Correlation coefficient between (CNt/CN)and(PX/P) |
位于黑土层之下的母质层透水性弱,致使水分不易下渗至地下水层[19];夏季降雨集中,雨强较大时,地表产流速率超过入渗速率,易出现超渗产流。按前期土壤湿度条件差异进行分类,条件为AMCⅠ、Ⅱ和Ⅲ的产流事件分别占总产流次数的71.8%、21.7%和6.5%;即产流前地表土壤湿度状况以干旱为主;产流过程中,降雨强度是影响入渗速率和入渗量变化的重要因素。因此,次降雨中最大时段(一般在10~40 min内)降雨量对降雨入渗和产流过程会产生重要影响。
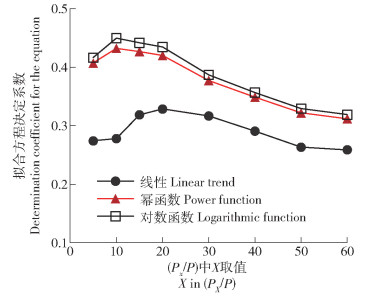
分别拟合所有小区在不同X取值下的(CNt/CN)与(PX/P)之间关系方程。可见幂函数和对数函数方程的决定系数R2明显优于线性方程。随着X值增加,各类方程R2呈先递增后递减的趋势。当X=10时,幂函数和对数函数的R2均达到最大值,分别达0.432和0.450(图 1);对数函数效果略优。因此,可将(P10/P)作为自变量,(CNt/CN)为因变量,建立两者间对数函数关系,进而计算次产流径流曲线数CNt。具体形式如下:
| $ {\rm{C}}{{\rm{N}}_t} = \alpha {\rm{CNln}}({P_{10}}/P) + \beta {\rm{CN}}, {\rm{C}}{{\rm{N}}_t} \le 100{\rm{ }} 。$ | (10) |
|
图 1 (CNt/CN)与(PX/P)之间拟合方程的决定系数 Fig. 1 Determination coefficient for the equation between (CNt/CN)and(PX/P) |
式中:CN为多年平均径流曲线数,α和β为方程参数,各小区α和β取值见表 5。
| 表 5 计算次产流径流曲线数方程的参数取值表 Tab. 5 Parameters for the equation calculating curve number of each runoff event |
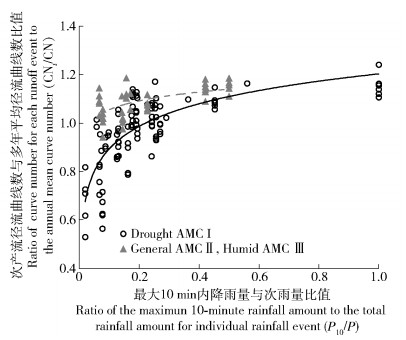
对裸地和顺坡种植条件下(CNt/CN)与(P10/P) 之间函数关系进行进一步分析(图 2),可见拟合的方程趋势线较为接近,但裸地的拟合效果(式11)略优于顺坡种植(式12)。在无植被覆盖的情况下,雨滴打击和径流冲刷作用使裸地地表极易形成细沟,成为坡面产汇流过程中较稳定的汇水路径。顺坡种植垄沟可作为稳定的汇流路径,但垄作坡耕地可人为改变天然坡面汇流路径,且生长期内大豆根茎生长状况存在差异,使坡面产汇流机理更为复杂。
| $ \begin{array}{*{20}{c}} {{\rm{C}}{{\rm{N}}_t} = 0.123{\rm{CNln}}({P_{10}}/P) + 1.214{\rm{CN}}, {\rm{C}}{{\rm{N}}_t} \le 100}\\ {{R^2} = 0.462, P < 0.01} 。\end{array} $ | (11) |
| $ \begin{array}{*{20}{c}} {{\rm{C}}{{\rm{N}}_t} = 0.106{\rm{CNln}}({P_{10}}/P) + 1.187{\rm{CN}}, {\rm{C}}{{\rm{N}}_t} \le 100, }\\ {{R^2} = 0.375, P < 0.01}。\end{array} $ | (12) |
|
图 2 不同土地利用条件下(CNt/CN)与(P10/P)之间关系 Fig. 2 Relationship between (CNt/CN) and (P10/P)for different land uses |
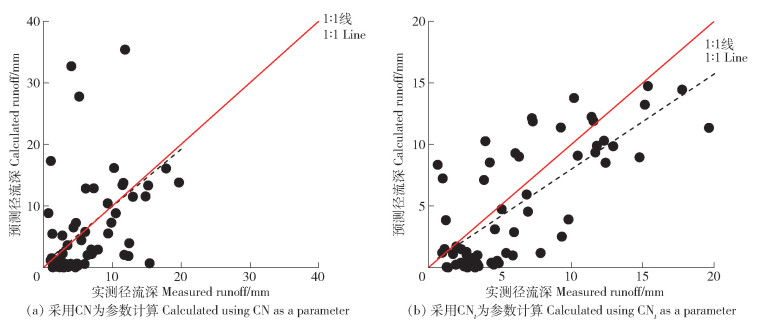
分别将采用CN和CNt为参数的SCS-CN模型的预测径流深和实测径流深做了比较(图 3)。采用CN的SCS-CN模型Ef=-1.63,Re=4.4%,R=0.49;采用CNt的SCS-CN模型Ef=0.47,Re=-18.9%,R=0.77,模型预测值明显更接近于1∶1线。相对于采用CN为参数,采用CNt的SCS-CN模型模拟精度显著提高。
|
图 3 分别采用CN和CNt为参数的SCS-CN模型预测径流和实测径流比较 Fig. 3 Comparison of measured runoff and calculated one by SCS-CN model with the parameter CN and CNt respectively |
1) 各径流小区逐次产流径流曲线数差异显著,其最大值和最小值的比值变化于1.38~2.24之间,平均为1.81。在典型黑土区,若不考虑局地强对流、锋面活动等条件下降雨过程对地表产流影响,仅对径流曲线数单一取值,可能造成显著的径流预报误差。
2) 本文将降雨过程中最大Xmin内的降雨量和次雨量比值(PX/P)作为刻画次降雨过程雨量在时间上集中程度的因子;该因子与次产流径流曲线数和多年平均径流曲线数比值(CNt/CN)间存在极显著正相关。当10≤X≤40时,两者相关程度更高。(P10/P)是对本区CNt影响最显著的降雨过程特征因子,可通过建立(CNt/CN)与(P10/P)之间的对数函数方程,计算CNt。本文给出了裸地和不同耕作方式坡耕地下该方程参数取值。
3) 本区裸地和顺坡种植条件下CNt计算方程形式较为接近,但垄作坡耕地可人为改变天然坡面汇流路径,且生长期内作物根茎生长状况存在差异,可使降雨过程特征因子和CNt关系更为复杂。
| [1] |
VIJI R, PRASANNA P R, ILANGOVAN R. Modified SCS-CN and Green-Ampt methods in surface runoff modelling for the Kundahpallam Watershed, Nilgiris, western Ghats, India[J]. Aquatic Procedia, 2015, 4: 677. DOI:10.1016/j.aqpro.2015.02.087 |
| [2] |
WANG Tao, XU Haili, BAO Weimin. Application of isotopic information for estimating parameters in Philip infiltration model[J]. Water Science and Engineering, 2016, 9(4): 287. DOI:10.1016/j.wse.2017.01.005 |
| [3] |
FADADU M H, SHRIVASTAVA P K, DWIVEDI D K. Application of Horton's infiltration model for the soil of Dediapada (Gujarat), India[J]. Journal of Applied & Natural Science, 2018, 10(4): 1254. |
| [4] |
LI Jun, LIU Changming, WANG Zhonggen, et al. Two universal runoff yield models: SCS vs. LCM[J]. Journal of Geographical Science, 2015, 25(3): 311. DOI:10.1007/s11442-015-1170-2 |
| [5] |
BOUGHTON W C. A review of the USDA SCS curve number method[J]. Australian Journal of Soil Research, 1989, 27(3): 511. DOI:10.1071/SR9890511 |
| [6] |
HUANG Mingbin, JACQUES G, WANG Zhanli, et al. A modification to the soil conservation service curve number method for steep slopes in the Loess Plateau of China[J]. Hydrological Process, 2006, 20(3): 579. DOI:10.1002/hyp.5925 |
| [7] |
HUANG Mingbin, GALLICHAND J, DONG Cuiyun, et al. Use of soil moisture data and curve number method for estimating runoff in the Loess Plateau of China[J]. Hydrological Processes, 2007, 21(11): 1471. DOI:10.1002/hyp.6312 |
| [8] |
DURAN-BARROSO P, GONZALEZ J, VALDES J B. Improvement of the integration of soil moisture accounting into the NRCS-CN model[J]. Journal of Hydrology, 2016, 542(19): 809. |
| [9] |
符素华, 王红叶, 王向亮, 等. 北京地区径流曲线数模型中的径流曲线数[J]. 地理研究, 2013, 32(5): 797. FU Suhua, WANG Hongye, WANG Xiangliang, et al. The runoff curve number of SCS-CN method in Beijing[J]. Geographical Research, 2013, 32(5): 797. |
| [10] |
陈正维, 刘兴年, 朱波. 基于SCS-CN模型的紫色土坡地径流预测[J]. 农业工程学报, 2014, 30(7): 72. CHEN Zhengwei, LIU Xingnian, ZHU Bo. Runoff estimation in hillslope cropland of purple soil based on SCS-CN model[J]. Transactions of the CSAE, 2014, 30(7): 72. |
| [11] |
EL-HAMES A S. An empirical method for peak discharge prediction in ungauged arid and semi-arid region catchment based on morphological parameters and SCS curve number[J]. Journal of Hydrology, 2012, 456(12): 94. |
| [12] |
焦剑, 宋伯岩, 王世雷, 等. 基于改进径流曲线数模型的北京密云坡地径流估算[J]. 农业工程学报, 2017, 33(21): 194. JIAO Jian, SONG Boyan, WANG Shilei, et al. Runoff estimation for hillslope land in Miyun based on improved model of soil conservation service curve number[J]. Transactions of the CSAE, 2017, 33(21): 194. |
| [13] |
许秀泉, 范昊明, 李刚. 径流曲线法在东北半干旱区几种土地利用方式径流估算中的应用与改正[J]. 水土保持学报, 2019, 33(4): 52. XU Xiuquan, FAN Haoming, LI Gang. Application and correction of the SCS-CN method in runoff estimation of several land use patterns in Northeast semi-arid region[J]. Journal of Soil Conservation, 2019, 33(4): 52. |
| [14] |
U S Department of Agriculture-Soil Conservation Service. SCS national engineering handbook, Section 4:Hydrology[M]. Washington D C: U S Department of Agriculture, 1972: 19.
|
| [15] |
WILKEN F, BAURA M, SOMMER M, et al. Uncertainties in rainfall kinetic energy-intensity relations for soil erosion modelling[J]. Catena, 2018(171): 234. |
| [16] |
SHI Zhihua, CHEN Liding, FANG Nufang, et al. Research on the SCS-CN initial abstraction ratio using rainfall-runoff event analysis in the Three Gorges Area, China[J]. Catena, 2009, 77(1): 1. DOI:10.1016/j.catena.2008.11.006 |
| [17] |
FU Suhua, ZHANG Guanghui, WANG Nan, et al. Initial abstraction ratio in the SCS-CN method in the Loess Plateau of China[J]. Transactions of the ASABE, 2011, 54(1): 163. DOI:10.13031/2013.36271 |
| [18] |
NASH J E, SUTCLIFFE J V. River flow forecasting through conceptual models Part I: A discussion of principles[J]. Journal of Hydrology, 1970, 10(3): 282. DOI:10.1016/0022-1694(70)90255-6 |
| [19] |
李发鹏, 李景玉, 徐宗学. 东北黑土区土壤退化及水土流失研究现状[J]. 水土保持研究, 2006, 13(3): 50. LI Fapeng, LI Jingyu, XU Zongxue. The status of black soil degradation and water and soil loss in Northeast China[J]. Research of Soil and Water Conservation, 2006, 13(3): 50. |
 2021, Vol. 19
2021, Vol. 19 
