用有限元法研究降雨对青海云杉林边坡稳定性的影响

引用本文

田佳, 韩磊, 金学娟, 许玲玲, 王晓燕, 董亚宁. 用有限元法研究降雨对青海云杉林边坡稳定性的影响[J]. 中国水土保持科学, 2019, 17(6): 11-18. DOI: 10.16843/j.sswc.2019.06.002.

TIAN Jia, HAN Lei, JIN Xuejuan, XU Lingling, WANG Xiaoyan, DONG Yaning. Effect of rainfall on slope stability of Picea crassifolia forest based on finite element method in Qinghai[J]. Science of Soil and Water Conservation, 2019, 17(6): 11-18. DOI: 10.16843/j.sswc.2019.06.002.

项目名称

国家自然科学基金“贺兰山水土保持功能乔木根系锚固土壤作用与数值模拟研究”（31560232），“宁夏河东沙地典型防护林树种水分来源及水分利用策略研究”（31760236）

第一作者简介

田佳(1982-), 男, 博士, 副教授。主要研究方向:水土保持。E-mail:yuhudie63@qq.com

文章历史

收稿日期：2018-10-23
修回日期：2019-08-08

Contents Abstract Full text Figures/Tables PDF

用有限元法研究降雨对青海云杉林边坡稳定性的影响

田佳 ¹, 韩磊 ², 金学娟 ¹, 许玲玲 ¹, 王晓燕 ¹, 董亚宁 ¹

1. 宁夏大学农学院, 750021, 银川;
2. 宁夏大学环境工程研究院, 750021, 银川

收稿日期：2018-10-23; 修回日期：2019-08-08

项目名称：国家自然科学基金“贺兰山水土保持功能乔木根系锚固土壤作用与数值模拟研究”（31560232），“宁夏河东沙地典型防护林树种水分来源及水分利用策略研究”（31760236）

第一作者简介：田佳(1982-), 男, 博士, 副教授。主要研究方向:水土保持。E-mail:yuhudie63@qq.com

摘要：为研究降雨强度和降雨历时对贺兰山青海云杉林边坡稳定性的影响，通过三轴压缩、饱和渗透等土工试验获取青海云杉林边坡根土复合体的土力学参数，在此基础上建立基于有限元的贺兰山青海云杉林边坡稳定性计算模型。利用该模型分析了青海云杉林边坡与无林边坡（对照）的安全系数和破坏时间随降雨强度、降雨历时、边坡坡度的变化规律，拟合了降雨强度与边坡破坏时间的回归模型。通过降雨条件下青海云杉林边坡和无林边坡破坏时的最大位移、最大塑性应变的分析，量化了贺兰山青海云杉林增强降雨边坡稳定性的程度。研究结果表明：贺兰山青海云杉林与无林边坡的安全系数随降雨历时、降雨强度、边坡坡度的增加而减小。降雨条件下，青海云杉林边坡的破坏时间要显著高于无林边坡（平均高出48.61%），降雨强度与破坏时间的回归关系满足幂函数；青海云杉林的固土护坡作用随降雨强度的增加（从10 mm/h增加到25 mm/h）而减弱（从53.20%降低到45.70%），青海云杉林可以明显提高边坡破坏时的最大位移（提高224.42%）和最大塑性应变（提高95.28%）。综上，青海云杉林显著增强了降雨边坡的稳定性。

关键词：有限元法降雨强度边坡稳定根土复合体数值分析贺兰山

Effect of rainfall on slope stability of Picea crassifolia forest based on finite element method in Qinghai

TIAN Jia ¹, HAN Lei ², JIN Xuejuan ¹, XU Lingling ¹, WANG Xiaoyan ¹, DONG Yaning ¹

1. School of Agriculture, Ningxia University, 750021, Yinchuan, China;
2. Institute of Environmental Engineering, Ningxia University, 750021, Yinchuan, China

Abstract: [Background] Helan Mountain is an ecological barrier and water conservation area of Yinchuan Plain, and it is also a serious area of soil and water loss. The geological disasters, such as debris flow and shallow landslide caused by strong rain intensity, have caused huge economic, cultural and ecological losses in this area. Therefore, the study of slope stability under extreme weather is of great significance to the economic and social development in Helan Mountainous area. [Methods] In order to study the effect of rainfall intensity and duration on the slope stability of Picea crassifolia forest in Helan Mountain, the geomechanical parameters of the root-soil composite of P. crassifolia were obtained by triaxial compression, saturated infiltration and other geotechnical tests. On this basis, the stability calculation model of P. crassifolia forest slope in Helan Mountain was established based on finite element theory and software (ABAQUS). The finite element model for stability calculation of P. crassifolia forest slope was used to calculate the variation of safety factor (F_s) and the duration at failures (t_f) with the rainfall duration under different rainfall intensity (i=10-25 mm/h), and the intensity and duration at failures regression (ID) was fitted. Based on the analysis of maximum displacement (U_max) and maximum plastic strain (PEMAG_max) during the slopes without and with trees failure induced by the rainfall, the degree of slope stability improvement by the root-soil composite of P. crassifolia forest in Helan Mountain was quantified. [Results] 1) The safety factors of the slopes without and with trees decreased with the increase of rainfall duration, rainfall intensity and slope grade. The duration at failures of P. crassifolia forest slope under rainfall was significantly longer than that of the slope without trees (the average increase was 48.61%), and the regression relation between rainfall intensity and duration at failures satisfied the power function (The ID regression model:i=262.4t_f^-0.998, R²=0.999 6 (slope without trees); i=328.7t_f^-0.945, R²=0.999 (slope with trees)). 2) Under rainfall conditions, because of the effect of vegetation, the growth rate of duration at failures were 53.20% (i=10 mm/h), 50.57% (i=15 mm/h), 44.96% (i=20 mm/h) and 45.70% (i=25 mm/h) respectively and the average was 48.61%, however, the effect of root reinforcement on the slope decreased from 53.20% to 45.70%. The P. crassifolia forest obviously increased the maximum displacement U_max (224.42±80.29)% and the maximum plastic strain PEMAG_max(95.28±33.74)% when the slope failed. [Conclusions] The ID regression model, the maximum displacement and the maximum plastic strain of slopes without and with trees are obtained under rainfall, which prove that the P. crassifolia forest in Helan Mountain significantly enhances the slope stability.

Keywords: finite element method rainfall intensity stability of slope root-soil composite numerical analysis Helan Mountain

2016年8月21日18时至22日10时，宁夏贺兰山中北段发生有记录以来最大降雨，16 h降雨量达到239.5 mm^[1]。暴雨引发了部分地区山体浅层滑坡，不仅损坏了公路、房屋等基础设施，而且对贺兰山的生态环境及植被造成了巨大的破坏；此外，贺兰山岩画等文物古迹在滑坡中也遭受了难以估量的损失。因此，研究极端天气下的贺兰山边坡稳定性，对于贺兰山地区的生态和经济社会发展具有重要的意义^[2-3]。青海云杉(Picea crassifolia)作为贺兰山主要的水土保持树种之一，在水源涵养、稳定边坡方面起着十分重要的作用；但是通过查阅相关文献发现国内外对贺兰山地区青海云杉林等边坡的稳定性及影响因素研究未见报道，因此尚不能对其稳定边坡能力是不是与人们预想和期待的一致等问题给出科学的解释。

随着计算机运算能力的提高和岩土有限元理论的发展，采用有限元理论及软件对降雨条件下边坡的稳定性进行数值模拟分析，逐渐成为这一领域主要的研究方式^[4-8]。其中以达索系统(Dassault Systèmes)开发的大型通用有限元模拟软件ABAQUS，在解决复杂条件下的边坡非线性问题表现最为出色，被越来越多的科研人员用以降雨边坡的研究工作^[9-12]。为此，笔者在通过室内土工试验所获得的参数的基础上，采用有限元软件ABAQUS建立降雨条件下的贺兰山青海云杉林边坡和无林边坡(对照)稳定性计算模型，研究降雨强度和历时对青海云杉林边坡安全系数和破坏时间的影响规律。研究结果对于评价植被对降雨边坡的稳定作用和采用生物措施防治贺兰山浅层滑坡灾害具有重要的参考意义。

1 研究区概况

贺兰山位于宁夏和内蒙古交界处，是半荒漠草原与荒漠之间的分界线，具有典型的大陆性气候特征。年均气温-0.9 ℃，年均降水量287.2~429.8 mm，降水的年内分配极不均匀，主要集中在7—9月。土壤类型从上而下依次是山地草甸土、山地灰褐土、山地灰钙土、粗骨土和荒漠土。植被类型垂直分布依次为荒漠化草原、山地疏林草原、山地针叶林、亚高山灌丛草甸或高山草甸^[13]。本文研究地点位于贺兰山苏峪口国家森林公园兔儿坑护林点(E 105°54′39.10″，N 38°44′07.43″；海拔2 313 m)，以贺兰山主要的水土保持树种青海云杉林及林下根土复合体和素土(不含根的土)为研究对象。兔儿坑护林点为青海云杉纯林，郁闭度75%，平均树龄52 a。

2 材料与方法 2.1 模型中的土壤参数

模型中土壤的各参数(表 1)由室内三轴试验、饱和渗透试验获得；根土复合体的土水特征曲线(SWCC)采用GEOSTUDIO^Ⓡ软件中的土水特征曲线预测模型来估算^[14]。三轴仪采用南京土壤仪器厂生产的TSZ10-1.0型应变控制式三轴仪，采用不固结不排水三轴试验；土壤饱和渗透系数由TST-70常水头土壤渗透仪获得(北京泰达骏业)。经现场调查，兔儿坑青海云杉林土层厚度约为1.5 m，基岩为砂岩，砂岩力学特性参数参考谢仁海等^[15]编著的《构造地质学》。模型参数的详细确定方法可参见文献[16]。

表 1 有限元模型中的土壤参数 Tab. 1 Soil parameters in finite element model

2.2 边坡稳定性有限元计算模型的建立

参考贺兰山2016年8月21日18时至22日10时发生的强暴雨(降雨量239.5 mm降雨历时16 h，相当于平均15 mm/h)，因此本文设置了4个持续降雨强度，分别为25、20、15、10 mm/h。降雨条件下的边坡稳定性计算共分为4个步骤：第1步(初始步)设置土壤参数和边界条件。第2步(稳态渗流)加载重力(采用Gravity类型的分布荷载施加重力，即分析基于总孔压进行)，软件自动计算孔压、饱和度分布，同时为下一步计算提供初始条件。第3步(瞬态渗流)模拟降雨历时和降雨强度，模型中每荷载步最大孔压变化值(Max. pore pressure change per increment)设置为10 kPa，最大增量步步长设置为1 h，这2个值决定了孔压对时间积分的精确度。此外为了保证时间积分的正确性，还应该选择合适的初始时间增量步长，文中根据下式^[20]计算：

$ \Delta t > \frac{{{\rho _{\rm{w}}}g}}{{6Ek}}{(\Delta l)^2}。$

(1)

式中：Δt为初始时间增量步长，h；ρ_w为水的密度，kg/m³；g为重力加速度，m/s²；E为土壤的弹性模量，kPa；k为土壤的饱和渗透系数，mm/h；Δl为渗流部位的单元尺寸，m。经计算本文的边坡降雨入渗模型的Δt取0.1 h。第4步(强度折减步)对降雨后的边坡进行土壤强度折减，计算边坡安全系数F_s。

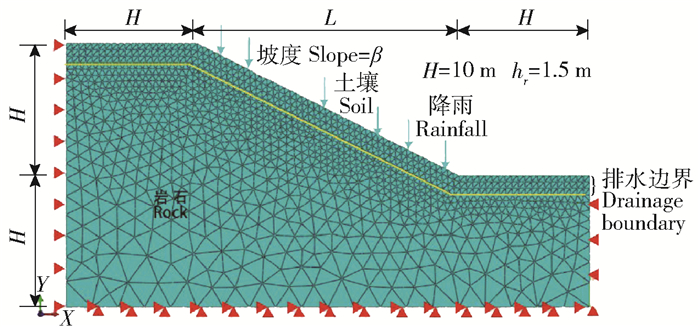
模型的几何尺寸和边界条件如图 1所示，边坡高2H(H=10 m)，坡顶与坡脚长H，坡面长L(变量)，含根土壤层厚度h_r=1.5 m，含根土层以下为基岩(砂岩)。由于有渗流还需要设置孔隙水压力边界，本模型的排水边界在右侧坡脚，此边界上孔隙水压力u=0。整个模型都采用平面应变三角形单元划分(CPE6MP)，在竖向施加水平约束，在底部施加水平和竖向约束。文中采用强度折减法计算边坡的安全系数F_s，折减后的抗剪强度参数可以分别表示为：

边坡高为2H(H=10 m)；L为坡面的长度(变量)，h_r为含根土壤层厚度，m。土壤网格单元类型为CPE6MP；岩石网格单元类型为CPE6M。 Height of slope is 2H (H=10 m). L is length of slope (variable). h_r is thickness of root-soil layer, m. Grid cell type of soil and rock is CPE6MP and CPE6M respectively. 图 1 贺兰山青海云杉林边坡稳定性计算有限元模型 Fig. 1 Finite element model for stability calculation of Picea crassifolia slope in Helan mountain

$ {c^\prime } = \frac{1}{{{F_{{\rm{trial }}}}}}c。$

(2)

$ {\varphi ^\prime } = \arctan \left( {\frac{1}{{{F_{{\rm{trial }}}}}}\tan \varphi } \right)。$

(3)

不断降低土壤的c、φ值，直到边坡破坏，破坏时的c、tanφ降低倍数F_trial就是安全系数F_s。

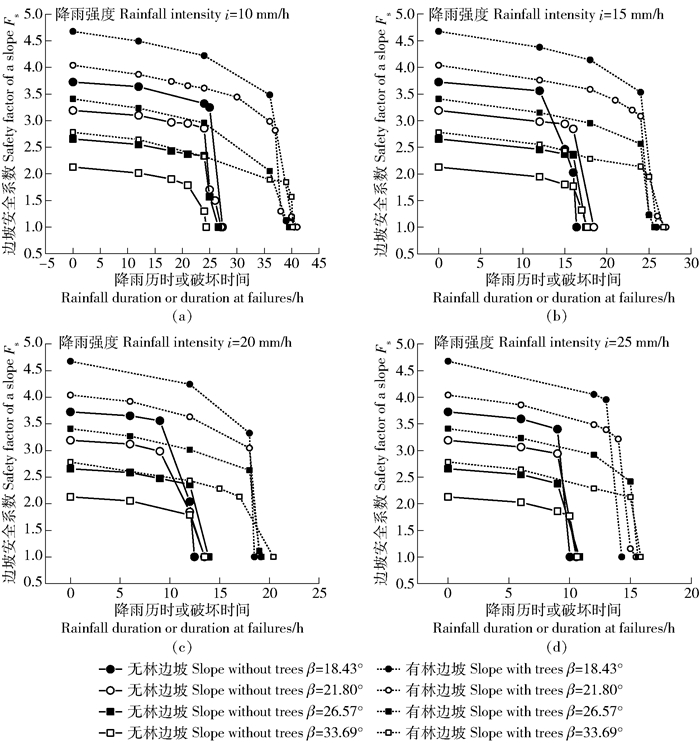
3 结果与分析 3.1 不同降雨强度和坡度条件下边坡安全系数随降雨历时的变化规律

图 2是在不同降雨强度条件(10、15、20和25 mm/h)和不同坡度条件(18.43°、21.80°、26.57°和33.69°)下，青海云杉林与无林边坡安全系数F_s随降雨历时的变化规律。由图 2可知青海云杉林与无林边坡的安全系数随着降雨历时的增加都逐渐减小，相同降雨历时下无林边坡安全系数明显小于有林边坡。在同样的降雨强度条件下，有林边坡的破坏时间(即F_s=1.0时的降雨历时)高于无林边坡。

图 2 不同降雨强度i与坡度β下边坡安全系数与降雨历时的关系 Fig. 2 Relationship between safety factor of a slope and rainfall duration under different rainfall intensity (i) and slope angle (β)

图 2还反映出坡度因素对边坡安全系数F_s的影响。在图 2(a)~(d)4个降雨强度下都可以看到在相同的降雨历时下边坡坡度越陡，安全系数越小，且青海云杉林边坡安全系数高于无林边坡。

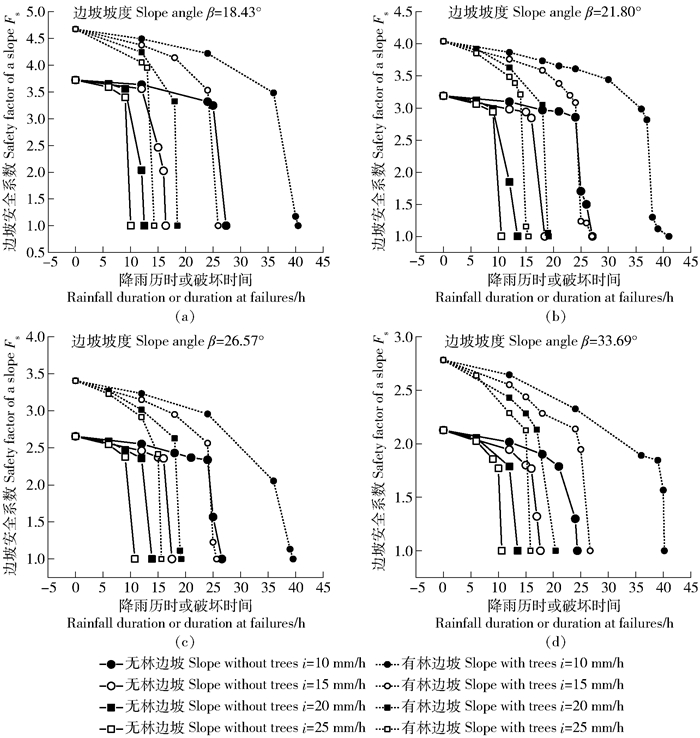
图 3示出在不同坡度下边坡安全系数随降雨历时的变化规律，可以看出：在不同坡度和降雨强度下，青海云杉林边坡的安全系数和破坏时间均高于无林边坡；在同一坡度下，青海云杉林和无林边坡的安全系数和破坏时间都随着降雨强度的增加而减小。

图 3 不同边坡坡度下边坡安全系数与降雨历时的关系 Fig. 3 Relationship between safety factor of a slope and rainfall duration under different slope angle

3.2 降雨强度i与边坡破坏时间t_f的回归关系

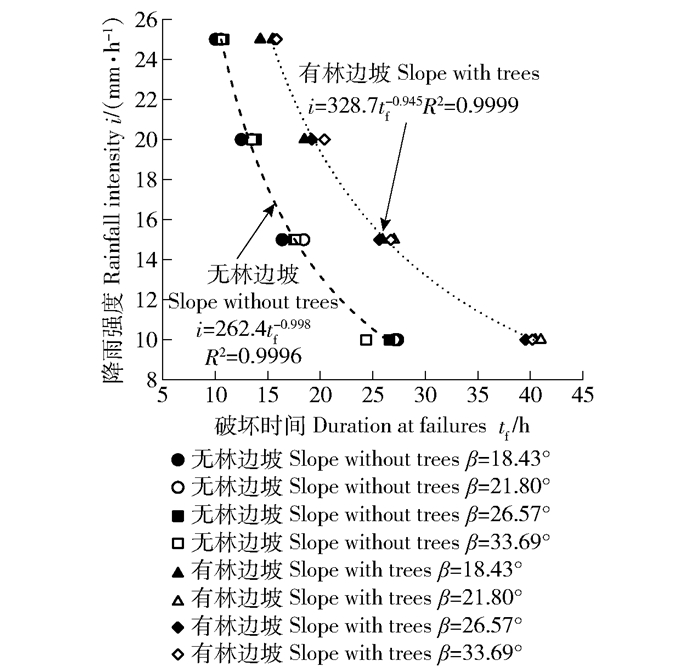
通过模拟32次不同坡度和降雨条件下的边坡破坏，建立了贺兰山无林边坡和青海云杉林边坡的ID(intensity and duration at failures regression)回归模型(图 4)：i=262.4t_f^-0.998，R²=0.999 6(无林边坡)；i=328.7t_f^-0.945，R²=0.999(有林边坡)，其拟合度R²都均能达到0.999以上。从图 4也可以明显看出，降雨条件下青海云杉林边坡的破坏时间要明显高于无林边坡。另外，通过对图 4中的数据进行方差分析，发现坡度因素(β)对边坡破坏时间(t_f)的影响不显著(F=0.991 0，P=0.440 0＞0.1)，但是降雨强度因素(i)对边坡破坏时间t_f的影响是极显著的(F=252.493，P=0.000 1＜0.01)。

图 4 边坡破坏时间与降雨强度的关系 Fig. 4 Relationship between duration at failures and rainfall intensity

3.3 贺兰山青海云杉林提高边坡稳定性的影响程度分析

表 2是青海云杉林在不同降雨强度下增加边坡破坏时间的具体分析，可以看出在4个设定的降雨强度下，青海云杉林边坡的破坏时间相对无林边坡有明显增长。其中i=10 mm/h时增长了53.20%，i=15 mm/h时增长了50.57%，i=20 mm/h时增长了44.96%，i=25 mm/h时增长了45.70%，平均值达到48.61%。但是，从表 2中可以看到随着降雨强度的增大，青海云杉林边坡相对于无林边坡的破坏时间的增长率有逐渐减小的趋势。

表 2 不同坡度和降雨强度条件下青海云杉林与无林边坡的破坏时间 Tab. 2 Duration at failures between slopes without and with trees (Picea crassifolia) under different slope and rainfall intensity

表 3示出青海云杉林和无林边坡在不同降雨强度和坡度下破坏时的最大位移U_max和最大塑性应变PEMAG_max及其增长率的变化。可以看到无林边坡破坏时的最大位移U_max平均值为(0.20±0.04)m，青海云杉林边坡破坏时的最大位移U_max平均值为(0.62±0.13)m，青海云杉林边坡比无林边坡提高了(224.42±80.29)%。表 3还示出不同降雨强度和坡度条件下青海云杉林和无林边坡破坏时的最大塑性应变PEMAG_max及其增长率的变化。其规律与最大位移类似，无林边坡破坏时的最大塑性应变PEMAG_max平均值为(0.44±0.05)，有林边坡破坏时的最大塑性应变PEMAG_max平均值为(0.86±0.13)，青海云杉林边坡比无林边坡提高(95.28±33.74)%。

表 3 不同坡度和降雨强度条件下青海云杉林与无林边坡破坏时的最大位移和最大塑性应变及增长率 Tab. 3 U_max and PEMAG_max and their growth rate between slopes without and with trees (Picea crassifolia) under different slope and rainfall intensity

边坡坡度 Slope/(°)	降雨强度 Rainfall Intensity i/mm	最大位移(无林) Maximum displacement(slope without trees) U_max/m	最大位移(有林) Maximum displacement(slope with trees) U_max/m	最大位移增长率 Maximum displacement growth rate W_u/%	最大塑性应变(无林) Maximum plastic strain(slope without trees) PEMAG_max	最大塑性应变(有林) Maximum plastic strain(slope with trees) PEMAG_max	最大塑性应变增长率 Maximum plastic strain growth rate W_PEMAG/%
18.43	10	0.17	0.65	285.27	0.47	0.78	66.15
	15	0.12	0.67	457.84	0.35	0.89	157.45
	20	0.16	0.44	183.51	0.41	0.70	69.23
	25	0.19	0.41	115.86	0.48	0.68	42.86
21.80	10	0.17	0.57	229.40	0.43	0.74	72.30
	15	0.21	0.64	207.11	0.46	0.88	92.38
	20	0.16	0.51	222.39	0.38	0.88	129.82
	25	0.17	0.50	198.92	0.43	0.70	63.16
26.57	10	0.24	0.57	138.14	0.53	0.80	50.72
	15	0.18	0.56	205.09	0.38	0.76	101.25
	20	0.26	0.60	130.94	0.50	0.96	92.57
	25	0.20	0.60	196.47	0.44	0.89	101.15
33.69	10	0.24	0.82	248.34	0.47	0.98	109.75
	15	0.24	0.78	219.79	0.48	0.95	97.95
	20	0.23	0.83	254.99	0.47	1.17	145.83
	25	0.19	0.75	296.61	0.41	0.95	131.94
平均值Mean±SD		0.20±0.04	0.62±0.13	224.42±80.29	0.44±0.05	0.86±0.13	95.28±33.74

4 结论与讨论

降雨入渗过程较为复杂，一般采用3个参数描述降雨入渗的过程，即：降雨强度i、土壤入渗率f、土壤饱和渗透系数k。1)当i＜k时，不会产生地表径流，降雨全部入渗，土壤入渗率与i保持一致；2)当k＜i＜f时，降雨也全部入渗，地表径流不会发生，但土壤入渗率f在减小；3)当k＜f＜i时，部分降雨不能入渗，形成地表径流^[21]。本文模拟降雨入渗过程是第2种情况(k＜i＜f)，不产生地表径流。这是由于目前ABAQUS还不能直接模拟有坡面径流的降雨情况，如要模拟必须通过复杂的二次开发。为了克服ABAQUS在进行降雨入渗模拟方面的局限性，李宁等^[21]和许建聪等^[22]做了大量工作，如采用Python语言将降雨边界作为不定边界，并利用迭代算法对降雨入渗边界进行处理，但其可靠性还有待于进一步的验证。虽然本文对降雨的模拟不考虑地表径流，但是不影响青海云杉林显著提高边坡稳定性结论的得出，因为，本文的研究结果是采用青海云杉林与无林边坡的比值，而非绝对值。文中随着降雨强度的增大，青海云杉林相对于无林边坡破坏时间的增长率有逐渐减小的趋势。由于植被的护坡作用是有限的，当降雨强度增加到一定值时，植被对边坡的稳定作用相对于降雨对边坡的破坏作用就会减弱，这就是造成边坡破坏时间增长率逐渐降低的主要原因。通过本文的研究可以得出以下结论：

1) 在贺兰山，青海云杉林与无林边坡的安全系数随降雨历时、降雨强度、边坡坡度的增加而减小。降雨条件下青海云杉林边坡的破坏时间要显著高于无林边坡(平均高出48.61%)；降雨强度与破坏时间的回归关系满足幂函数，降雨强度增大，破坏时间减小。

2) 降雨条件下，青海云杉林的固土护坡作用是有限的，随着降雨强度的增加(从10 mm/h增加到25 mm/h)，固土护坡作用在减弱(从53.20%降低到45.70%)；青海云杉林可以明显提高边坡破坏时的最大位移(提高224.42%)和最大塑性应变(提高95.28%)。青海云杉林显著增强了降雨边坡的稳定性。

5 参考文献

[1]	宁贵财, 尚可政, 王式功, 等. 贺兰山对银川一次致灾暴雨过程影响的数值模拟[J]. 中国沙漠, 2015, 35(2): 464. NING Guicai, SHANG Kezheng, WANG Shigong, et al. Numerical simulation of terrain effects of the Helan Mountain on a rainstorm process in Yinchuan, Ningxia, China[J]. Journal of Desert Research, 2015, 35(2): 464.
[2]	杨淑萍, 孙银川, 尤志宇, 等. 宁夏地质灾害气象条件的初步研究[J]. 新疆气象, 2005, 28(6): 7. YANG Shuping, SUN Yinchuan, YOU Zhiyu, et al. A preliminary study of Ningxia on meteorological conditions geological disasters[J]. Bimonthly of Xinjiang Meteorology, 2005, 28(6): 7.
[3]	魏晓, 孙峰华. 宁夏水土保持及区划研究[J]. 水土保持研究, 2005, 12(6): 119. WEI Xiao, SUN Fenghua. Study on soil and water conservation of Ningxia and its division[J]. Research of Soil and Water Conservation, 2005, 12(6): 119.
[4]	LIN Derguey, HUANG Borshun, LIN Shinhwei. 3-D numerical investigations into the shear strength of the soil-root system of Makino bamboo and its effect on slope stability[J]. Ecological Engineering, 2010, 36(8): 992. DOI:10.1016/j.ecoleng.2010.04.005
[5]	CHOK Y H, JAKSA M B, KAGGWA W S, et al. Assessing the influence of root reinforcement on slope stability by finite elements[J]. Geo-Engineering, 2015, 6(12): 13.
[6]	KOKUTSE N K, TEMGOUA A G, KAVAZOVIC Z. Slope stability and vegetation: Conceptual and numerical investigation of mechanical effects[J]. Ecological Engineering, 2016, 86(1): 146.
[7]	MICKOVSKI S B, STOKES A, van BEEK R, et al. Simulation of direct shear tests on rooted and non-rooted soil using finite element analysis[J]. Ecological Engineering, 2011, 37(10): 1523. DOI:10.1016/j.ecoleng.2011.06.001
[8]	MAO Zhun, YANG Ming, BOURRIER F, et al. Evaluation of root reinforcement models using numerical modelling approaches[J]. Plant and Soil, 2014, 381(1/2): 249.
[9]	易绍基.基于ABAQUS的边坡稳定敏感性分析及模型验证[D].昆明: 昆明理工大学, 2011: 20. YI Shaoji. Sensitivity analysis and model verification of slope stability based on ABAQUS[D]. Kunming: Kunming University of Science and Technology, 2011: 20. http://cdmd.cnki.com.cn/Article/CDMD-10674-1012263754.htm
[10]	RAHARDJO H, ONG T H, REZAUR R B, et al. Response parameters for characterization of infiltration[J]. Environmental Earth Sciences, 2010, 60(7): 1369. DOI:10.1007/s12665-009-0273-4
[11]	YUBONCHIT S, CHINKULKIJNIWAT A, HORPIBULSUK S, et al. Influence factors involving rainfall-induced shallow slope failure: numerical study[J]. International Journal of Geomechanics, 2017, 17(7): 387.
[12]	CHINKULKIJNIWAT A, YUBONCHIT S, HORPIBULSUK S, et al. Hydrological responses and stability analysis of shallow slopes with cohesionless soil subjected to continuous rainfall[J]. Canadian Geotechnical Journal, 2016, 53(12): 2001. DOI:10.1139/cgj-2016-0143
[13]	赵晓春, 刘建军, 任军辉, 等. 贺兰山4种典型森林类型凋落物持水性能研究[J]. 水土保持研究, 2011, 18(2): 107. ZHAO Xiaochun, LIU Jianjun, REN Junhui, et al. Study on water-holding capacity of litter in four forest types of Helan Mountain[J]. Research of Soil and Water Conservation, 2011, 18(2): 107.
[14]	胡欣.湿陷性黄土路基水分场及其变形特性数值分析[D].重庆: 重庆交通大学, 2016: 10. HU Xin. The numerical analysis on moisture field and deformation characteristics of collapsible loess subgrade[D]. Chongqing: Chongqing Jiaotong University, 2016: 10. http://cdmd.cnki.com.cn/Article/CDMD-10618-1016163285.htm
[15]	谢仁海, 渠天祥, 钱光谟. 构造地质学[M]. 徐州: 中国矿业大学出版社, 2007: 25. XIE Renhai, QU Tianxiang, QIAN Guangmu. Tectonic geology[M]. Xuzhou: China University of Mining and Technology Press, 2007: 25.
[16]	田佳, 及金楠, 钟琦, 等. 贺兰山云杉林根土复合体提高边坡稳定性分析[J]. 农业工程学报, 2017, 33(20): 144. TIAN Jia, JI Jinnan, ZHONG Qi, et al. Analysis on improvement of slope stability in root-soil composite of Picea crassifolia forest in Helan Mountain[J]. Transactions of the CSAE, 2017, 33(20): 144. DOI:10.11975/j.issn.1002-6819.2017.20.018
[17]	及金楠, 张志强, 郭军庭, 等. 黄土高原刺槐和侧柏根系固坡的有限元数值模拟[J]. 农业工程学报, 2014, 30(19): 146. JI Jinnan, ZHANG Zhiqiang, GUO Junting, et al. Finite element numerical simulation of Black Locust (Robinia pseudoacacia) and Arborvitae (Platycladus orientalis) roots on slope stability on Loess Plateau of China[J]. Transactions of the CSAE, 2014, 30(19): 146. DOI:10.3969/j.issn.1002-6819.2014.19.018
[18]	田佳, 曹兵, 及金楠, 等. 花棒根-土复合体直剪试验的有限元数值模拟与验证[J]. 农业工程学报, 2015, 31(16): 152. TIAN Jia, CAO Bing, JI Jinnan, et al. Numerical simulation of direct shear test for root-soil composite of Hedysarum scoparium using a finite element method[J]. Transactions of the CSAE, 2015, 31(16): 152. DOI:10.11975/j.issn.1002-6819.2015.16.021
[19]	JI Jinnan, KOKUTSE N, GENET M, et al. Effect of spatial variation of tree root characteristics on slope stability. A case study on Black Locust (Robinia pseudoacacia) and Arborvitae (Platycladus orientalis) stands on the Loess Plateau, China[J]. Catena, 2012, 92: 139. DOI:10.1016/j.catena.2011.12.008
[20]	费康, 张建伟. ABAQUS在岩土工程中的应用[M]. 北京: 中国水利水电出版社, 2013: 223. FEI Kang, ZHANG Jianwei. Application of ABAQUS in geotechnical engineering[M]. Beijing: China Water Conservancy Press, 2013: 223.
[21]	李宁, 许建聪. 基于ABAQUS的三维边坡降雨入渗模块的开发及其应用[J]. 岩土工程学报, 2015, 37(4): 668. LI Ning, XU Jiancong. Development and application of three-dimensional rainfall infiltration module based on ABAQUS[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(4): 668.
[22]	李宁, 刘冠麟, 许建聪, 等. 降雨条件下边坡有限元强度折减法计算平台开发及其应用[J]. 水文地质工程地质, 2018, 45(3): 63. LI Ning, LIU Guanlin, XU Jiancong, et al. Development of shear strength reduction analysis under rainfall conditions method and its for slope stability application[J]. Hydrogeology and Engineering Geology, 2018, 45(3): 63.