2. 国家测绘地理信息局第三航测遥感院, 610100, 成都
-
项目名称
- 四川省科技计划项目"基于多源多尺度遥感影像的自然资源资产信息提取技术研究"(2017SZ0027)
-
第一作者简介
- 王枭轩(1992-), 男, 硕士生。主要研究方向:定量遥感, 农业遥感。E-mail:1244377865@qq.com
-
通信作者简介
- 左小清(1972-), 男, 博士, 教授。主要研究方向:农业与生态环境遥感。E-mail:514012196@qq.com
-
文章历史
-
收稿日期:2018-10-23
修回日期:2018-12-24
2. 国家测绘地理信息局第三航测遥感院, 610100, 成都
2. The Third Institute of Photogrammetry and Remote Sensing of National Bureau of Surveying, Mapping and Geographic Information, 610100, Chengdu, China
国际政府间气候变化专门委员会(IPCC)研究指出,以气候变暖为主要特征的全球气候变化已成事实[1],与此同时降水的过程机制、时空分布模式也将发生变化。作为水循环过程中的重要环节,降水联系着大气、植被、土壤等系统间的能量流动,其过程变化将产生深刻的环境扰动[2-3]。以“天府之国”闻名的成都市近半世纪以来气候变化显著,特别是以西南与东亚季风异常导致极端降水增加,这不仅影响着植被的物候节律与健康演替,还造成水土流失等环境问题。降水的时空不确定性带来降水强度、侵蚀力的分布无序性,这对区域水土流失空间结构稳定性与水土保持来说均是不利的;因此,研究成都市降水时空变化特性,对水土流失监测预报、区域资源环境规划管理具有重要意义。
在气候系统耗散过程、地表环境梯度以及人为干扰等影响下,降水呈现非线性和随机性特点[4]。此前的相关研究,主要侧重于采取时域统计[5]、地统计[6]、分形[7]等方法,探讨其时间倾向斜率、周期、空间分布等特点,而关于其不确定性的定量研究较少[8]。近年来信息熵方法在该领域的应用得到国内外学者们广泛认可。Pascale等[9]应用信息熵结合Hurst指数分析了美国大陆日降水量熵场分布格局,指出了降水变化趋势不确定性分布与多尺度周期;Adera等[10]提出了应用传递熵分析巴西雨林地区降水时空相关、连续性,并试图解释其对雨林斑块分布的影响;Brunsell[11]提出解析熵无序指数(AEDI)的方法来捕捉加拿大安大略地区月降水量的时空变化,并成功应用于水文预测模型中。降水量时空信息熵是降水变化的状态函数,其熵值大小指示了水循环过程在环境梯度制约下呈现有序性特征,能够有效检测外部非规整因素影响下极端降水的发生概率。就国内而言,目前该方案仅在新疆[12]、江淮[13]、湖北[14]等地得到应用,而在降水集中性强且侵蚀力较大的西南地区和其他地区研究报道尚不多见。鉴于此,笔者以成都市14个气象站点气象资料为基础,采用Mann-Kendall非参数检验法提取区域降水趋势特征,并基于信息熵理论定量分析降水的空间不确定性,以期从时空双维的角度揭示气候变化背景下成都市近37年来降水时空变化规律,从而为水土保持规划、气象灾害防御提供科学依据。
1 研究区概况成都地处我国西南腹地、四川盆地西部,地理坐标为E102°54′~104°54′、N30°05′~31°26′,区域面积1万4 605 km2(含简阳市)。地势自东向西升高,高程介于387~5 364 m,形成以平原、丘陵、山地为主的地貌。区域大部分属亚热带季风气候,温暖湿润、雨热同期,年平均气温为16 ℃,年降水量为900~1 300 mm,无霜期为278 d,西北局部受地势影响形成高寒气候, 旱涝、冰雹、大风等气象灾害频现。长江干流横穿过境,有岷江、沱江等较大支流,河网密度、水资源丰沛。
2 资料与方法 2.1 Mann-Kendall检验对于降水等时间序列自然事件的趋势性分析,Mann-Kendall(以下简称M-K)检验法具有不受样本值、分布类型等的影响,并被世界气象组织推荐而广泛应用[15]。对于时间序列变量(x1,x2,…,xt),t为时间序列长度,M-K法定义了统计量
| $ S = \sum\limits_{k = 1}^{n - 1} {\sum\limits_{j = k + 1}^n {{\mathop{\rm sgn}} } } \left( {{x_j} - {x_k}} \right)。$ | (1) |
式中:n为样本总量,j、k=1, 2,…,n;xj、xk分别为第j、k时刻的样本值。sgn()为符号函数,规则如下:
| $ {\mathop{\rm sgn}} \left( {{x_j} - {x_k}} \right) = \left\{ {\begin{array}{*{20}{l}} {1, }&{{x_j} - {x_k} > 0}\\ {0, }&{{x_j} - {x_k} = 0}\\ { - 1, }&{{x_j} - {x_k} < 0} \end{array}} \right\}。$ | (2) |
S为正态分布,其均值为0,方差var(S)=n(n-1)(2n+5)/18,当n>10时,正态分布统计量计算如下:
| $ Z = \left\{ {\begin{array}{*{20}{c}} {\frac{{S - 1}}{{\sqrt {{\mathop{\rm var}} (S)} }}, }&{S > 0}\\ {0, }&{S = 0}\\ {\frac{{S + 1}}{{\sqrt {{\mathop{\rm var}} (S)} }}, }&{S < 0} \end{array}} \right\}。$ | (3) |
若Z>0,则表明降水在该时间序列呈增加趋势,否则为降低趋势,并且绝对值越大,则趋势越明显[2, 14]。
2.2 信息熵原理对于自然时间序列变量内部不确定性信息的测试,Shannon[16]提出信息熵计算公式
| $ H(x) = \sum\limits_{k = 1}^n p \left( {{x_k}} \right){\log _2}p\left( {{x_k}} \right)。$ | (4) |
式中:H(x)为信息熵,是以概率分布函数表征的不确定性,其值越大,表明自然事件不确定性越大、系统无序性强、信息越丰富,反之系统平稳有序、信息量少;n为间隔数;xk为k处对应事件的状态值;p(xk)为事件概率。信息熵作为状态函数,是系统信息存量或混沌特征的度量,Singh等[17]将其应用于水科学研究中,用以刻画水文过程中的不确定性,对于区域降水这一时间序列自然变量,其稳定性为水循环过程在环境梯度制约下呈现有序性特征,其熵值信息则较小、水循环系统稳定、降水变率平稳;反之水循环过程受外部非规整因素或随机干扰影响,其信息熵较大、降水变率大、极端降水概率增加。
2.3 研究数据研究数据为中国气象局国家气候中心网站(http://data.cma.cn/)提供的成都市逐日降水观测资料(1980—2016年),共14个气象基准站(图 1),为满足空间插值需要,另选取成都周边地区4个站点做辅助。研究尺度分为年、季2种时间尺度,其中季节尺度划分为:3—5月为春季、6—8月为夏季、9—11月为秋季、12—翌年2月为冬季。采用Excel 2016软件汇总逐日降水量数据,并绘制其变化趋势图;于DPS软件平台上对降水变化特征进行M-K检验分析。应用Matlab2017b编程实现降水时间序列M-K检验和信息熵计算,在Surfer13.0上绘制降水量变化趋势空间分布图。
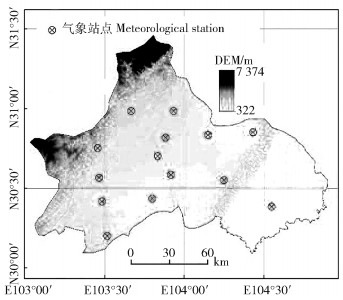
|
图 1 成都市位置和气象站点分布 Fig. 1 Location of the Chengdu city and distribution of meteorological stations |
1) 降水量时间变化趋势。1980—2016年成都市年降水量逐年变化趋势如图 2所示,年降水量最大值为2013年的1 274.77 mm,最低值为1997年的768.6 mm,平均值为950.10 mm全市平均降水量呈减少趋势,其气候倾向斜率为-2.049 mm/a,但未达到显著水平(P>0.05),表明变化趋势不显著。从季节来看,除了秋季降水呈微弱增加趋势外(倾向斜率为0.042 0 mm/a,P>0.05),其他季节降水变化总趋势均为减少,其中夏季降水变化最大,其倾向斜率为-2.164 mm/a,春冬季节较小,依次为-0.189 3、-0.117 2 mm/a,但这种趋势均不显著。
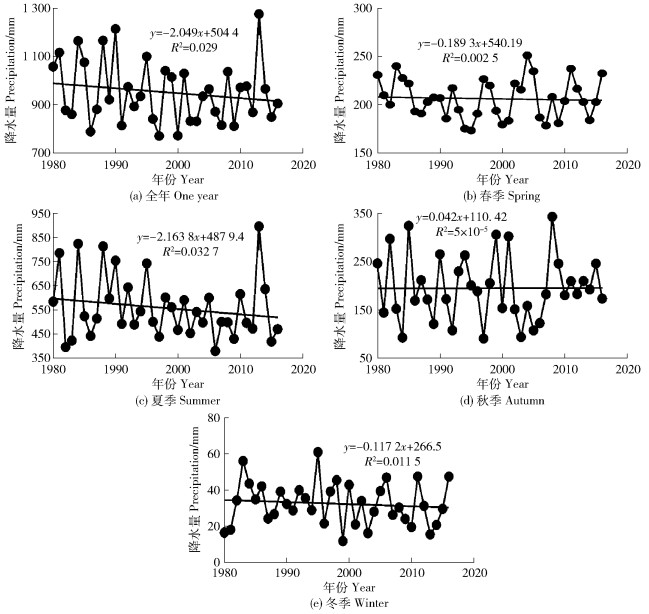
|
图 2 1980—2016年成都市降水量的时间变化 Fig. 2 Temporal changes of annual and seasonal precipitation in the Chengdu city during 1980-2016 |
为进一步了解降水量变化局部信息,采用M-K非参数检验绘制成都市年季降水量变化过程与离差平方和曲线,如图 3所示,图中设定显著性水平为0.05,阈值线为±1.96。成都市降水量的UF-UB统计量在1981年相交,考虑到交点起初时刻不确定性大和变化趋势线延续性,故而确定该年并非突变点,并且UF值均小于0,表明年降水量呈减少态势,这与图 2(a)的结论相符。春秋季节降水的UF、UB值在研究时域内并为交点,表明降水变化不存在突变。夏季降水的UF、UB值存在多个交点,表明其变化趋势较复杂,结合Pettitt检验,确定1993年为突变点,但未通过5%水平信度检验;其中冬季降水于1996年由前期的弱增加趋势发展为之后的减少趋势,但该突变并不显著(P>0.05)。
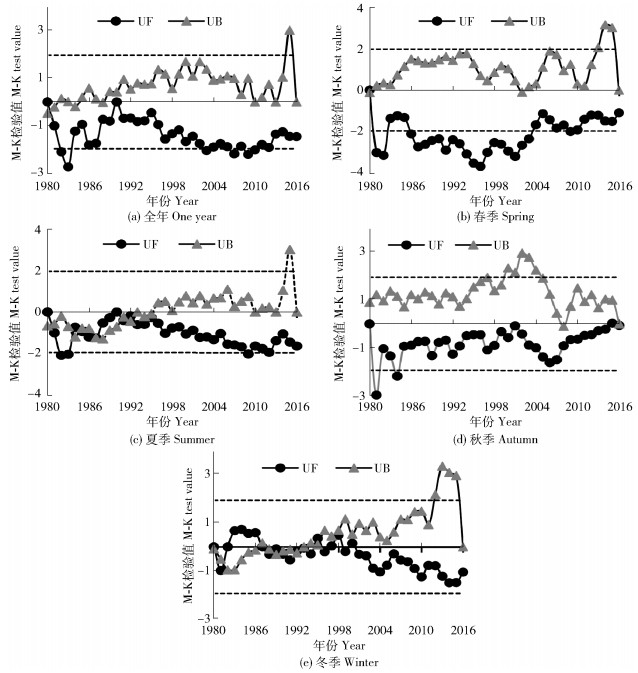
|
图 3 1980—2016年成都市年季降水M-K检验 Fig. 3 M-K test of annual and seasonal precipitation in the Chengdu city during 1980-2016 |
2) 年降水量空间变化趋势。以各站点年序列降水量数据为基础,经M-K非参数检验得到成都市1980—2016年间降水量Z值,其空间可视化如图 4所示。统计表明,14个站点中年降水量呈增加趋势的站点仅有双流、简阳,其增量分别为0.563、1.191 mm/a。年降水量呈减少趋势的有12个,其中成都中部的温江、郫县、新都、新津、金堂等5个站点的年降水量减少量较小,介于-0.170~0.852 mm/a之间,成都西部的都江堰、彭州、大邑、崇州、蒲江等站点降水量减少量较大,介于-1.242~1.884 mm/a之间;龙泉驿、邛崃的年降水量Z值达到-1.974、-2.210,并通过0.05水平检验,表明其减少趋势明显。
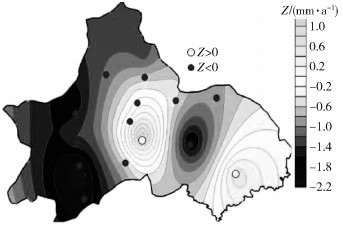
|
图 4 1980—2016年成都年降水量的空间变化 Fig. 4 Spatial changes of annual precipitation across Chengdu city during 1980-2016 |
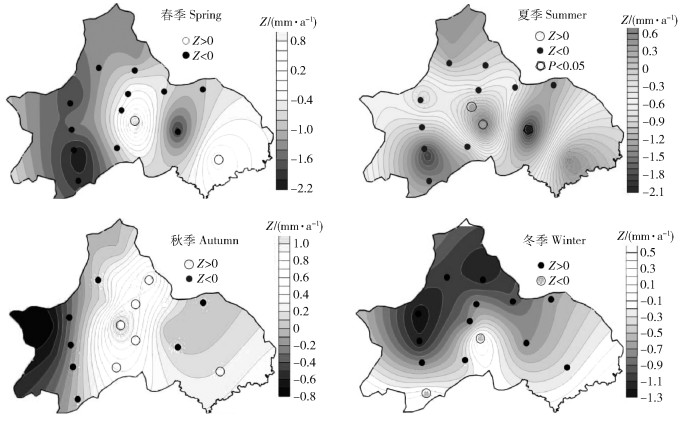
3) 季节降水量变化趋势空间分布。图 5为成都市季节性降水量变化趋势空间分布。依图可知,1980—2016年间成都市大部分地区春季降水量呈减少趋势,以邛崃站变化最大,达-1.949 mm/a,双流、简阳站春季降水量有所增加,增量分别为0.829、0.563 mm/a。夏季降水量空间变化特征与春季基本一致,其中温江站降水量变化为增加趋势,龙泉驿站夏季降水量Z值达-2.079,在0.05水平上呈显著性。秋季除了成都中部和东部简阳站共7个站点的降水量呈增加趋势,西部和东部丘陵区的7个站点降水量呈减少趋势。冬季降水量仅有浦江、双流站有所增加,增量分别为0.183、0.236,其他各站降水量均为减少趋势,Z值介于-0.052~-1.268 mm/a之间。综合来看,成都市各季节降水量空间变化特征基本一致,降水增加地区集中于中部和简阳,其他大部分地区降水量略有减少。
|
图 5 成都地区季节降水量趋势变化 Fig. 5 Trend coefficient of seasonal precipitation across Chengdu city |
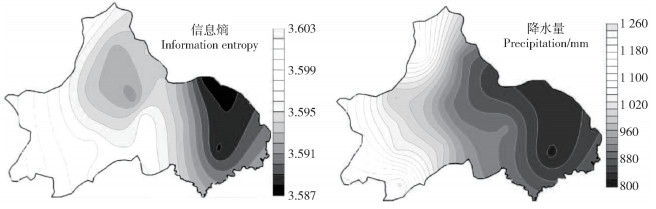
1) 年降水量信息熵空间分布。将单站时间序列降水量数据视为一组随机变量,进而求得信息熵,在此基础上采用Kriging法进行空间插值,得到成都年降水量信息熵空间分布。如图 6所示,虽然信息熵值相差较小,但其依然呈现明显的自西向东递减分布趋势,高值区位于西南的浦江站和西北部的都江堰站,低值区为东部金堂、简阳站。将成都近37年各站点的年降水量平均值进行插值(图 6),可知成都年降水量空间分布与其信息熵分布格局一致,西部深丘山地区降水量高于东部平原区。表明地形因素年降水空间分异的原因之一,东西部海拔悬殊造成降水分布不均,西部地势较高、起伏大,容易形成地形雨。信息熵分布表明:成都西部地区年降水量不确定性较强,更易受到水循环过程或气候异常影响,极端天气的发生概率相对较高;东部地区年降水量相对平稳,这对局域降水预测预报有利。
|
图 6 成都市年信息熵降水量空间分布 Fig. 6 Spatial distribution of information entropy and annual precipitation across Chengdu city |
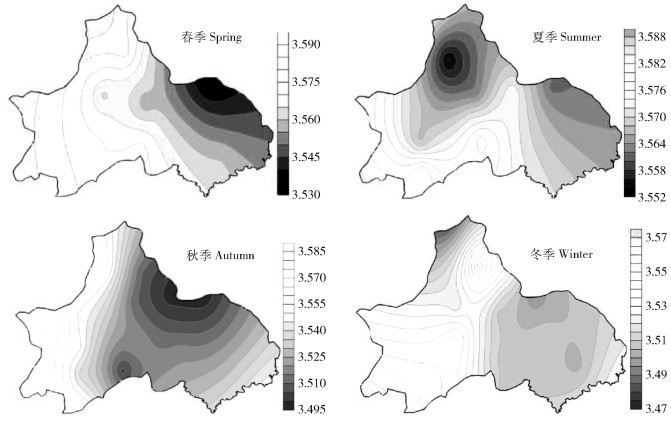
2) 季节性降水量信息熵空间分布。图 7为成都地区各季节降水量的信息熵空间分布,依图可知春季降水量信息熵由西南向东北递减,以都江堰—崇州—大邑—邛崃—浦江一线为界,西部地区高于东部,信息熵低值向东北部的金堂站集中。夏季信息熵以西南边缘地区较高,其他大部分地区信息降水量,以西北部都江堰站信息熵最小。秋季降水量信息熵由成都中部向东西两侧增加,其中,西部地区信息熵略高于东部,低值区聚集于新都站附近;冬季信息熵低值区扩展至成都平原东部大部分地区,并且北缘高山地区信息熵也较小,信息熵高值区集中于彭州站及其西南地区。综合来看,成都西南部和东部地区降水量信息熵随季节变化较小,北部和中南部随季节变化相对明显。由于海陆位置差异,印度洋季风对成都西南部降水的影响更敏感,局域降水不确定性较大。
|
图 7 成都市各季节降水量信息熵空间分布 Fig. 7 Spatial distribution of information entropy of seasonal precipitation changes across Chengdu city |
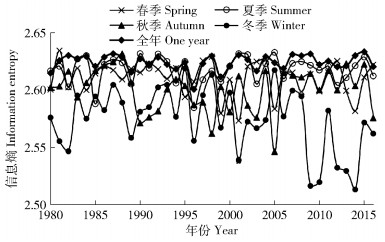
3) 年季降水量信息熵变化。以成都市14个气象站点在历年(季)尺度上的降水数据为一组变量,计算信息熵。如图 8所示,1980—2016年间,成都市降水量信息熵无明显变化趋势,但仍能反映信息熵在年季尺度上的大小。可知,大部分年份年尺度的降水量信息熵高于季节尺度,而各季节尺度上信息熵以夏季最大,春秋季次之,冬季最小,表明时间尺度上成都市降水量不确定性的大小不尽相同。总的来说,年降水量的不确定性大于各季节的降水量,而降水量最为集中的夏季降水量不确定性较大,春秋季降水量的不确定性较小,降水量年分配相对较少的冬季,其降水不确定性最小。
|
图 8 成都年季降水量信息熵逐年变化 Fig. 8 Information entropy of annual and seasonal precipitation changes across Chengdu city |
1) 1980—2016年成都市年平均降水量为950.10 mm,气象倾向斜率为-2.049 mm/a,春、夏、冬呈减少趋势,秋季呈微弱增加,其倾向斜率依次为1.893、-21.638、0.42、-1.172,但变化趋势均不显著(P>0.05)。
2) 除了夏冬季节降水分别在1993、1996年发生弱的突变,年降水与春秋季节降水均不存在显著突变。
3) 成都市年季降水量变化趋势呈现明显的空间分布差异,年季降水量增加地区集中于中部双流和东部简阳地区,其他大部分地区降水量略有减少。
4) 成都市降水量信息熵在不同时间尺度存在差异,表现出全年>夏季>春季、秋季>冬季,时间尺度上降水量越丰富的,其信息熵越大。另外,年季降水量信息熵在空间上呈现明显的经向分布特征,与降水量分布特征基本一致,呈自西向东呈减小趋势,空间上降水量越多,其信息熵越大。
| [1] |
SOLOMON S. IPCC (2007): Climate change the physical science basis[C]//AGU Fall Meeting, 2007.
|
| [2] |
LAL R. Soil Carbon sequestration impacts on global climate change and food security[J]. Science, 2004, 304(5677): 1623. DOI:10.1126/science.1097396 |
| [3] |
KOVATS S, AKHTAR R. Climate, climate change and human health in Asian cities[J]. Environment & Urbanization, 2008, 20(1): 165. |
| [4] |
CHERNOGOR L F, ROZUMENKO V T. Earth-atmosphere-geospace as an open nonlinear dynamical system[J]. Radio Physics and Radio Astronomy, 2012, 13(2): 120. |
| [5] |
SIEPIELSKI A M, MORRISSEY M B, BUORO M, et al. Response to Comment on "Precipitation drives global variation in natural selection"[J]. Science, 2018, 359(6374): eaan5760. DOI:10.1126/science.aan5760 |
| [6] |
HEVESI J A, ISTOK J D, FLINT A L. Precipitation Estimation in Mountainous Terrain Using Multivariate Geostatistics. Part I:Structural Analysis[J]. Journal of Applied Meteorology, 1992, 31(7): 661. DOI:10.1175/1520-0450(1992)031<0661:PEIMTU>2.0.CO;2 |
| [7] |
SAIEDI N, BESALATPOUR A A, SHIRANI H, et al. Aggregation and fractal dimension of aggregates formed in sand dunes stabilized by PistachioPAM and PistachioPVAC mulches[J]. European Journal of Soil Science, 2017, 68(5): 783. DOI:10.1111/ejss.12458 |
| [8] |
HAWKINS E, SUTTON R. The potential to narrow uncertainty in projections of regional precipitation change[J]. Climate Dynamics, 2011, 37(1/2): 407. |
| [9] |
PASCALE S, LUCARINI V, XUE F, et al. Analysis of observed and modeled rainfall seasonality with new indicators based on information entropy[C]//EGU General Assembly Conference. EGU General Assembly Conference Abstracts, 2014.
|
| [10] |
ADERA S, LARSEN L, LEVY M C, et al. Functional connectivity of precipitation networks in the Brazilian Rainforest-Savanna Transition Zone[C]//AGU Fall Meeting. AGU Fall Meeting Abstracts, 2016.
|
| [11] |
BRUNSELL N A. A multiscale information theory approach to assess spatial-temporal variability of daily precipitation[J]. Journal of Hydrology, 2010, 385(1): 165. |
| [12] |
黄家俊, 张强, 张生, 陈晓宏. 基于信息熵的新疆降水时空变异特征研究[J]. 生态学报, 2017, 37(13): 4444. HUANG J J, ZHANG Q, ZHANG S, CHEN X H. Information entropy-based analysis of spatial and temporal variation in precipitation in Xinjiang[J]. Acta Ecologica Sinica, 2017, 37(13): 4444. |
| [13] |
郑泳杰, 张强, 张生, 陈永勤.基于信息熵的淮河流域降水时空变异特征研究[J].水电能源科学, 2016, 34(1): 1. ZHENG Y J, ZHANG Q, CHEN Y Q. Information entropy investigation on variability of precipitation in Huai river[J].Water Resource and Power, 2016, 34(1): 1. http://www.cnki.com.cn/Article/CJFDTotal-SDNY201601001.htm |
| [14] |
余冲, 刘冀, 董晓华. 基于信息熵的湖北省降雨时空变化规律研究[J]. 水电能源科学, 2011, 29(1): 6. YU C, LIU J, DONG X H. Information entropy-based spatial and temporal variation rule of rainfall in Hubei Province[J]. Water Resourse and Power, 2011, 29(1): 6. DOI:10.3969/j.issn.1000-7709.2011.01.002 |
| [15] |
HAMED K H. Trend detection in hydrologic data:the Mann-Kendall trend test under the scaling hypothesis[J]. Journal of Hydrology, 2008, 349(3/4): 350. |
| [16] |
SHANNON C E. Communication theory of secrecy systems[J]. Bell Labs Technical Journal, 1949, 28(4): 656. DOI:10.1002/j.1538-7305.1949.tb00928.x |
| [17] |
SINGH R N, MANGLIK A. Entropy-information perspective to radiogenic heat distribution in continental crust[J]. Nonlinear Processes in Geophysics, 2013, 20(3): 423. DOI:10.5194/npg-20-423-2013 |
 2019, Vol. 17
2019, Vol. 17 
