鲁中南低山丘陵区是华北土石山区水土流失非常严重的地区，降雨径流是引起该区水土流失的重要因素^[1]。近些年来随着水文监测站网的建设和发展，该区域内的径流观测已有初步成效，但不同土地利用方式下的径流与土壤侵蚀规律的研究仍然不够深入^[2]。为了更好地在鲁中南低山丘陵区开展水土流失预报、合理布设水土保持措施以及满足该区在山东省水土保持区划中的定位和要求，建立原理明晰、应用便利的地表产流模型从而定量计算不同下垫面条件下的径流量，有着重要意义。

由美国农业部土壤保持局(USDA SCS)于20世纪50年代开发用于估算地表径流量的数学模型——径流系数法(SCS-CN，soil conservation service curve number method)，因其计算过程简单，所需参数较少，被广泛应用于无径流资料地区地表径流估算等方面。影响SCS-CN模型预测结果的参数有2个：一个是径流曲线数CN，在0~100之间取值；另一个是初损率λ，在0~0.3之间变化^[3]。该模型自引进国内以来，在我国一些地方得到初步应用和发展。例如：王英等^[4-5]、王红艳等^[6-7]将SCS模型应用于黄土高原地区，并通过引入降雨强度、前期降雨量等参数的方法对SCS模型进行优化；吴志宜等^[8]在浙江省宁绍平原建立适用于平原水网地区的SCS扩展模型，采用逐步拟合的方法对不同土地利用类型中的CN值和λ值；符素华等^[9-10]将SCS模型应用于北京地区，并依据实测径流资料，采用5种方法反推CN值，对SCS模型进行了优化。大多数国内外学者对模型优化的方法为优化参数λ或CN使模型适用于应用地区^{[4-5, 11-12]}，或引入参数改进SCS模型^{[7, 13-14]}，从应用结果来看，优化方法均有一定参考价值。但在山地丘陵坡度大、沟谷众多、冲蚀切割严重、降雨分布极不均匀的鲁中南低山丘陵区，SCS模型尚未得到研究及应用。

笔者以鲁中南低山丘陵地区的典型流域山东药乡小流域自2011年建立以来观测到的2012—2016年降雨和径流实测资料为基础，以4个不同土地利用方式(坡耕地、梯田、裸地和草地)的径流小区作为研究对象，应用1stOpt软件中的粒子群算法(PSO)对标准SCS-CN模型及MS模型(即在标准SCS模型基础上增加前期土壤含水量参数)进行优化，分别形成SCS-CN_Les模型和MS_Les模型，运用标准SCS-CN模型、SCS-CN_Les模型和MS_Les模型进行径流预测，探讨3种模型对于不同土地利用方式小区的适用性，同时为解决单一指标评价片面的缺陷，首次采用TOPSIS综合评价了几种模型的应用效果，以期对鲁中南低山丘陵区不同土地利用方式的径流预报和水文模型评价选择等方面提供便利的方式和方法。

泰安药乡小流域(E 117°05′39″~117°09′26″，N 36°17′58″~36°20′30″)位于山东省泰安市城市水源地黄前流域，行政上属山东省泰安市大津口乡，地处北方土石山区鲁中南山丘区西北部，所属一级流域为黄河流域。该流域属暖温带大陆性亚湿润季风气候，多年平均降水量758mm，实测最大年降水量1303mm(1964年)，最小年降水量334.4mm(1989年)，75%的降水集中在6—9月，由于降雨集中，常出现冬干、春旱、初夏旱、盛夏暴雨等自然灾害。土壤类型主要是棕壤。

本研究的基础研究数据选自药乡小流域径流小区2012—2016年降雨和径流资料，其中2012—2015年数据用作模型参数率定，2016年数据用作模型验证，而对于标准SCS-CN模型则将2012—2016年数据用于验证。以坡耕地、梯田、裸地和草地共4个小区作为研究对象，分别代表 4种不同土地利用方式，于2017年8月环刀取各小区土壤，以定水头法依次测定各小区内的土壤最小下渗率，依此得到4个小区的CN值。小区基本资料等如表 1所示。

表 1(Tab. 1)

表 1 药乡小流域试验小区基本资料 Tab. 1 Basic data of experimental plots in Yaoxiang small watershed 土地利用方式 Land use types 坡度 Slope/(°) 土壤类型 Soil types 观测年限 Observation period 径流事件数/次 Number of runoff events/PCS SCS水文土壤组 SCS hydrologic soil groups CN 参数率定期Calibration period 模型验证期Validation period 参数率定期Calibrationperiod 模型验证期Validationperiod 坡耕地Sloping farmland 10 2012—2015 2016 38 11 D 89.0 水平梯田Level terrace 15 棕壤Brown soil 2012—2015 2016 37 7 D 88.0 裸地Bare land 15 2012—2015 2016 37 9 D 94.0 草地Grassland 25 2012—2015 2016 38 9 B 83.0 注：4个小区均为长20m，宽5m，面积100m2。Note: The four residential areas are 20 meters long, 5 meters wide, an area of 100 square meters.

表 1 药乡小流域试验小区基本资料 Tab. 1 Basic data of experimental plots in Yaoxiang small watershed

产流公式为：

式中: Q为实际径流深，mm；P为单次降雨总量，mm；S为土壤可能最大保持量，mm；λ为初损率。当λ=0.2时，由式(1)可得标准SCS-CN模型经典公式：

式中，S可由径流曲线数CN表示(式3)，且CN值由前期土壤湿度(AMC)、坡度、土地利用方式、土壤类型等因素决定：

对于CN值的确定，需根据土壤的最小下渗率确定其所属的SCS水文土壤组，结合产流前5d的降雨量和SCS手册得到不同土地利用方式下、不同土壤类型下的标准CN值。

是Mishra等为提高径流预测精度，在标准SCS-CN模型基础上加入前期土壤含水量参数M从而建立的，其最终公式^[7]为

式中，M≥0，当初损率λ变化时，M可表示为

本研究中模型参数优化均采用七维高科有限公司独立开发的1stOpt软件5.0版本中的粒子群优化算法(PSO)，该软件被广泛用于水文水资源及其他工程模型优化计算。粒子群优化算法的基本思想是用随机解初始化一群随机粒子，然后通过迭代找到最优解，该算法优势在于具有记忆性，没有交叉和变异运算，依靠粒子速度完成搜索，并且在迭代进化中只有最优的粒子把信息传递给其他粒子，搜索速度快。本研究中，将1stOpt软件中粒子群优化算法的各项参数设置如下：种群数为20，邻近种群数为2，学习因子C₁和C₂均为2.05，算法模式为CFPSO。

将模型合格率^[10]、Nash-Sutcliffe效率系数、均方根误差RMSE值以及线性拟合方程的决定系数R²作为评价指标，基于TOPSIS原理构建综合评价体系^[15]，对比分析各土地利用方式在不同模型中的应用效果。

常被用来作为水文模型的效率评价指标，变化范围从-∞到1。E越接近于1值，说明预测值和实测值的越匹配。其计算公式如下：

式中：Q_oⁱ为第i次降雨的实测径流深，mm；Q_mⁱ为第i次降雨的预测径流深，mm；$ {\bar Q_o}$为实测径流深的平均值，mm。

是GB/T 22482—2008《水文情报预报规范》中检验水文模型的常用指标，运算步骤如下：

式中：QS为合格预测；E_AOⁱ为第i次降雨的许可误差；MQR为模型合格率。

可以较好地反映出预测值同实测值之间的偏差，其值越小，说明预测值相对于实测值偏差越小，其计算公式如下：

是一种对多项指标、多个方案分别构造正、负理想解，使方案尽可能远离负理想解的同时接近正理想解，据此比较选择出最优方案的分析方法^[16]，具体计算步骤见文献[16]。

根据式(1)~(3)及查表得到的CN值(表 1所示)，运用标准SCS-CN模型分别计算4个小区2012—2016年每次降雨事件的预测值，并与实际值进行比较，结果如图 1(a)所示。实测值与预测值所对应的点(Q_oⁱ, Q_mⁱ)较多的分布在1:1直线上方，每个小区所对应的线性拟合线均在1:1直线上方。表 2为各模型参数值及评价指标，可见，4个小区的线性拟合方程截距分别为6.13、7.95、13.88、2.00，均＞0，斜率分别为1.44、2.18、1.10、6.17，均＞1。以上说明在运用标准SCS-CN模型预测径流时，预测值大于实测值，这与王英等^[4]在黄土高原地区径流小区应用标准SCS-CN模型的结果相反，可能的原因是黄土地区的径流小区坡度较药乡小流域的径流小区要大，且2地的土壤类型有所不同，从而影响λ及CN值，导致预测结果相反。在标准SCS-CN模型中4个小区的NSE值分别为-1.49、-15.76、-2.83、-98.01，均＜0，同时RMSE较大，模型合格率较低。以上结果表明利用标准SCS-CN模型无法实现对4个小区径流的准确预测，因此需要对模型进行优化。

图 1(Fig. 1)

图 1 3种模型实测径流深与预测径流深对照 Fig. 1 Comparison of measured runoff depth with predicted runoff depth by three models

表 2(Tab. 2)

表 2 率定期3种预测模型参数值及各项评价指标 Tab. 2 Parameter values and evaluation indexes of three forecasting models during calibration period 模型 土地利用方式 Land use types λ CN 线性拟合线Linear 模型合格率 Model qualification rate/% NSE RMSE 方程式Equation R2 坡耕地Sloping farmland 0.200 89.0 y=1.4429x+6.1289 0.6454 25.49 -1.49 12.48 标准SCS-CN模型 水平梯田Level terrace 88.0 y=2.1821x+7.9490 0.4225 23.40 -15.76 14.48 Standard SCS-CN model 裸地Bare land 94.0 y=1.0949x+13.882 0.4313 14.00 -2.83 18.82 草地Grassland 83.0 y=6.1744x+2.0093 0.5781 42.86 -98.01 11.17 坡耕地Sloping farmland 0.250 74.8 y=0.7599x+0.7313 0.7804 55.26 0.78 3.83 SCS-CNLes模型 水平梯田Level terrace 0.131 60.6 y=0.5712x+0.8276 0.5615 89.19 0.56 2.58 SCS-CNLes model 裸地Bare land 0.267 77.6 y=0.4851x+2.3714 0.5083 56.76 0.51 7.32 草地Grassland 0.074 40.0 y=0.8628x+0.1021 0.6579 100.00 0.53 0.60 坡耕地Sloping farmland 0.160 71.2 y=0.8683x-0.0729 0.8467 71.05 0.84 3.26 MSLes模型 水平梯田Level terrace 0.022 30.1 y=0.6001x+0.6280 0.5628 80.56 0.55 2.60 MSLes model 裸地Bare land 0.214 72.7 y=0.5171x+2.2775 0.5453 59.46 0.54 7.04 草地Grassland 0.030 20.1 y=1.0997x-0.1192 0.7548 100.00 0.59 0.52

表 2 率定期3种预测模型参数值及各项评价指标 Tab. 2 Parameter values and evaluation indexes of three forecasting models during calibration period

运用1stOpt软件中粒子群优化算法，对标准SCS-CN模型参数λ、CN同时进行优化，形成SCS-CN_Les模型。应用该模型对4个小区2012—2015年降雨事件进行径流预测，点(Q_oⁱ, Q_mⁱ)分布图如图 1(b)所示，模型各项参数值如表 2所示。

4个小区的实测值和预测值所对应的点(Q_oⁱ, Q_mⁱ)杂乱的分布于1:1直线两侧，所对应的线性拟合线分布于1:1直线下方，草地小区的线性拟合线就偏离程度而言较，其他3个小区更接近于1:1直线。4个小区的初损率λ由0.2分别变为0.250、0.131、0.267、0.074，CN值变为75.8、60.6、77.6、40.0。相对于标准SCS-CN模型，4个小区的模型合格率显著提高，水平梯田小区的增加量最多(65.79%)，坡耕地小区增加量最少(29.77%)，但数值也达到55.26%；NSE均变为正值且较接近于1，坡耕地小区的NSE值最接近于1(0.78)，裸地小区提升较为明显，数值量上增加98.54，达到0.51；RMSE显著变小，水平梯田小区减少量最大(11.9)，坡耕地小区减少量最少(8.65)；线性拟合方程决定系数R²显著增加，水平梯田小区相对提升32.90%为最多，草地小区相对提升13.82%为最少。综上，优化后形成的SCS-CN_Les模型相较于标准SCS-CN模型，对于4个径流小区径流预测效果均更好。

根据式(4)~(5)及软件处理，对模型进行优化后形成MS_Les模型，实测径流深和预测径流深所对应点(Q_oⁱ, Q_mⁱ)的分布情况如图 1(c)所示，模型各项参数值如表 2所示。

MS_Les模型中4个小区的实测值和预测值所对应的点(Q_oⁱ, Q_mⁱ)同样较杂乱的分布于1:1直线两侧，4个小区的初损率λ由0.2分别变为0.160、0.022、0.214、0.030，CN值变为71.2、30.1、72.7、20.1。除草地小区线性拟合线位于1:1直线上方外，其他3个小区线性拟合线均位于1:1直线下方，说明总体预测效果上，草地小区的预测值要大于实测值，而其他3个小区则预测值小于实测值。相对于标准SCS-CN模型，4个小区的模型合格率均变大，NSE均提高且接近于1，RMSE值均变小，线性拟合方程决定系数R²均显著增加；相对于SCS-CN_Les模型，水平梯田小区的模型合格率和NSE值降低、RMSE值增加，坡耕地、裸地和草地小区的模型合格率和NSE值增加、RMSE值降低，同时4个小区的线性拟合方程决定系数R²均增加。综上而论，率定期内MS_Les模型相对于标准SCS-CN模型，4个小区预测效果都更好，而相对于SCS-CN_Les模型，坡耕地、裸地和草地小区预测效果相对提升，但水平梯田小区预测效果相对降低。

为进一步验证经过参数率定后的各模型是否适用，同时分析对比得出不同土地利用方式小区的适用模型，将2016年降雨等数据分别带入SCS-CN_Les模型和MS_Les模型得到预测径流值，与实测值进行对比(图 2)，并求出各项模型评价指标(表 3)。

图 2(Fig. 2)

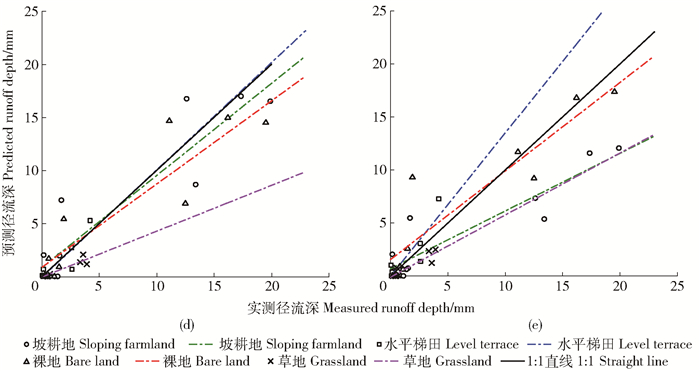
图 2 验证期SCS-CNLes模型(d)和MSLes模型(e)实测径流深与预测径流深对照 Fig. 2 Comparison of measured runoff depth with predicted runoff depth by SCS-CNLes model (d) and MSLes model (e) during validation period

表 3(Tab. 3)

表 3 SCS-CNLes模型和MSLes模型验证期各项评价指标 Tab. 3 Evaluation indicators during validation period by SCS-CNLes model and MSLes model 模型Model 土地利用方式 Land use types 线性拟合方程Equation of linear 模型合格率 Model qualification rate/% NSE RMSE 方程式Equation R2 与1:1直线相交点 Intersection point with 1:1 straight line 坡耕地Sloping farmland y=0.5432x+0.6986 0.8574 (1.53, 1.53) 54.55 0.65 4.35 SCS-CNLes模型 水平梯田Level terrace y=1.3500x-0.0190 0.7951 (0.05, 0.05) 85.71 0.32 1.31 SCS-CNLes model 裸地Bare land y=0.8342x+1.5593 0.8445 (9.40, 9.40) 77.78 0.84 2.84 草地Grassland y=0.5846x-0.0947 0.8331 (-0.23, -0.23) 100.00 0.53 1.03 坡耕地Sloping farmland y=0.8678x+0.8385 0.8529 (6.34, 6.34) 72.73 0.85 2.84 MSLes模型 水平梯田Level terrace y=1.0111x-0.0702 0.7725 (6.32, 6.32) 100.00 0.70 0.87 MSLes model 裸地Bare land y=0.7836x+0.8759 0.8227 (4.05, 4.05) 55.56 0.81 3.10 草地Grassland y=0.4319x-0.04970 0.8623 (-0.09, -0.09) 100.00 0.29 1.27

表 3 SCS-CNLes模型和MSLes模型验证期各项评价指标 Tab. 3 Evaluation indicators during validation period by SCS-CNLes model and MSLes model

在SCS-CN_Les模型验证期内，坡耕地和草地小区线性拟合线则位于1:1直线下方，实测值和预测值所对应的点(Q_oⁱ, Q_mⁱ)也较多的分布于1:1直线下方，表明在总体上两个小区径流预测值要小于实测值；水平梯田小区线性拟合线位于1:1直线上方，表明在总体预测效果上预测值要大于实测值，模型合格率为85.72%，NSE=0.32，RMSE=1.31；裸地小区线性拟合线与1:1直线相交于点(9.40, 9.40)处，线性方程斜率为0.87＜1，截距为1.56＞1，表明对于实测径流深在0~9.4mm的径流事件，SCS-CN_Les模型在裸地小区中的预测值要大于实测值，而当实测径流深大于9.4mm时，预测值小于实测值。

在MS_Les模型验证期内，坡耕地小区线性拟合线与1:1直线较为接近，相对于在SCS-CN_Les模型验证期中的应用结果，模型合格率、NSE值和决定系数R²均有增加，RMSE值显著降低，表明MS_Les模型在坡耕地小区中应用结果较好；水平梯田小区线性拟合线与1:1直线相交于(6.32, 6.32)，线性拟合线基本与1:1直线重合，模型合格率较高，NSE值较接近于1，表明在总体预测效果上预测值与实测值基本吻合，预测效果较好，但对于实测径流深＜6.3mm左右的降雨事件，预测值要大于实测值，而当降雨事件的实际径流深＞6.3mm时，预测值要小于实测值。

由表 3可见，若仅根据某一指标评价模型在不同土地利用方式中的径流预测效果，必然造成评价结果不全面的情况，因此建立综合评价体系是非常必要的。笔者基于TOPSIS法建立综合评价指标体系，以模型合格率、模型效率系数E值(NSE)、均方根误差(RMSE)和线性拟合方程R²作为评价指标。据文献[16]中介绍的计算步骤，首先对表 2、表 3中3种模型的各项评价指标数据进行同趋化处理，其中R²、模型合格率和效率系数作为正向指标不作处理，而RMSE作为逆向指标，采用“取倒数”方法进行处理。将同趋化处理后的数据进行规范化处理，利用熵权法求得4项评价指标的具体权重，并求得TOPSIS法的最终结果如表 5所示。4种土地利用方式在SCS-CN_Les模型和MS_Les模型中应用结果均比在标准SCS-CN模型中的应用结果较好。梯田在MS_Les模型中的应用效果最佳，坡耕地和梯田在MS_Les模型中应用结果相对较好，草地和裸地在SCS-CN_Les模型中应用结果较好。综合评价排序先后顺序与图 1、2和表 2、3基本一致，但仍存在差异，这是因为图 1和图 2较为直观地反映了实测值与模型预测值之间总体线性关系，而对于模型拟合效率及个体误差等的表达较为有限，是片面的。

表 4(Tab. 4)

表 4 各土地利用方式小区在不同模型中的Ci值及最终排序结果 Tab. 4 Ci values of different land use types in different models and final ranking results 模型Model 土地利用方式 Land use type Di+ Di- Ci 排序结果 Ranking results 坡耕地Sloping farmland 0.1813 0.0553 0.2337 9 标准SCS-CN模型 水平梯田Level terrace 0.2080 0.0142 0.0638 11 Standard SCS-CN model 裸地Bare land 0.2011 0.0340 0.1446 10 草地Grassland 0.2000 0.0386 0.1618 12 坡耕地Sloping farmland 0.1151 0.1498 0.5655 8 SCS-CNLes模型 水平梯田Level terrace 0.0819 0.1553 0.6548 4 SCS-CNLes model 裸地Bare land 0.1320 0.1290 0.4943 5 草地Grassland 0.0237 0.2072 0.8975 2 坡耕地Sloping farmland 0.1387 0.1254 0.4748 6 MSLes模型 水平梯田Level terrace 0.0930 0.1412 0.6028 1 MSLes model 裸地Bare land 0.1477 0.1170 0.4420 7 草地Grassland 0.0668 0.1641 0.7106 3

表 4 各土地利用方式小区在不同模型中的Ci值及最终排序结果 Tab. 4 Ci values of different land use types in different models and final ranking results

模型经过优化后，初损率λ存在裸地>坡耕地>水平梯田>草地的关系，这是因为坡耕地和裸地小区土壤较为松散、植物截留作用较小或没有，下渗率大，λ值也大，而水平梯田和草地小区的植物截留作用较大，下渗率小，λ值小，这与郭晓军等^[17]在干热河谷区应用SCS模型时修正初损率λ值的结果一致；4个小区的CN值均变小但仍保持裸地>坡耕地>水平梯田>草地的关系，这与张鹏等^[18]在甘肃南部小流域应用SCS模型时得到的CN值越高，越易产生径流的结果相一致，也与实际情况相符。以上体现了SCS-CN_Les模型和MS_Les模型的参数合理性。

经过优化后模型在预测径流精度上仍存在不足的问题，张兴奇等^[19]通过在贵州石桥小流域应用SCS模型发现，降雨雨型、径流小区的坡长和坡度会对SCS模型中的参数造成一定影响，从而导致径流预测结果，王英等^[4]将降雨强度引入SCS模型并应用于黄土高原地区，发现径流预测准确度显著提高，而对于鲁中南低山丘陵区药乡小流域而言，有研究表明该地区产流的主控因子是降雨量、降雨历时、最大30min降雨强度^[20]；因此将以上因素引入SCS模型进行优化可能是下一步研究如何提高模型预测精度的有效方法。

单目标拟合优化的实质是以某一目标函数为约束条件，优化模型使其在该约束条件下，目标函数达到收敛，但模型参数、类型及输入数据都会影响模型的拟合效果，因此有学者为弥补单目标拟合的缺点，采用多目标拟合的方法^[21-22]，即将绝大部分可影响模型结果的因素作为目标函数，进行拟合。本研究则采用TOPSIS综合评价法弥补单目标拟合方法的不足，相对于多目标拟合更为简便，且TOPSIS法是系统工程中一种常用的评价方法，具有对样本资料要求少、方法简便等特点，适用范围广泛，尤其多见于卫生医疗、经济管理和工业机械等专业文献，从应用结果来看很好。

1) 标准SCS-CN模型在选取的4种土地利用方式中径流模拟效果较差，线性拟合方程决定系数R²较小、模型合格率较低、NSE＜0且RMSE值较大。

2) 使用1spOt软件中的粒子群优化算法，对标准SCS模型和MS模型进行了优化，形成SCS-CN_Les模型和MS_Les模型，二者参数值均具有一定的有效性，分别将优化后的模型在4种土地利用方式中进行应用，在率定期和验证期SCS-CN_Les模型及MS_Les模型应用结果都较好，各项模型评价指标均高于标准SCS-CN模型。

3) 通过TOPSIS综合评价分析，梯田中MS_Les模型的应用效果最佳，坡耕地和梯田中MS_Les模型的应用结果相对较好，草地和裸地中SCS-CN_Les模型的应用结果较好。