文章快速检索     高级检索
  中国水土保持科学   2018, Vol. 16 Issue (6): 48-55.  DOI: 10.16843/j.sswc.2018.06.007
0

引用本文 

杨维, 张学霞, 赵静瑶. 基于Geosail模型和SVR算法的叶面积指数遥感反演[J]. 中国水土保持科学, 2018, 16(6): 48-55. DOI: 10.16843/j.sswc.2018.06.007.
YANG Wei, ZHANG Xuexia, ZHAO Jingyao. Remote sensing inversion of leaf area index based on Geosail model and SVR algorithm[J]. Science of Soil and Water Conservation, 2018, 16(6): 48-55. DOI: 10.16843/j.sswc.2018.06.007.

项目名称

国家科技支撑计划项目子课题"华北土石山区防护林体系景观格局调控与空间配置技术研究"（2015BAD07B030201）

第一作者简介

杨维(1993-), 女, 硕士研究生。主要研究方向:3S技术集成开发与应用。Email:819034870@qq.com

通信作者简介

张学霞(1975-), 女, 副教授, 硕士生导师。主要研究方向:生态环境遥感。Email:xuexiazh@yeah.net

文章历史

收稿日期：2018-02-08
修回日期：2018-10-24
Contents              Abstract              Full text              Figures/Tables              PDF
基于Geosail模型和SVR算法的叶面积指数遥感反演
杨维, 张学霞, 赵静瑶     
北京林业大学水土保持学院, 100083, 北京
收稿日期：2018-02-08; 修回日期：2018-10-24
项目名称：国家科技支撑计划项目子课题"华北土石山区防护林体系景观格局调控与空间配置技术研究"（2015BAD07B030201）
第一作者简介：杨维(1993-), 女, 硕士研究生。主要研究方向:3S技术集成开发与应用。Email:819034870@qq.com
通信作者简介：张学霞(1975-), 女, 副教授, 硕士生导师。主要研究方向:生态环境遥感。Email:xuexiazh@yeah.net
摘要：叶面积指数（LAI）控制着植物冠层的多种生理和生态过程，是陆地生态、水文模型中不可或缺的植被参数，因此准确反演区域LAI对研究植被与土壤侵蚀具有重要意义。本文以北京地区阔叶林为研究对象，利用Geosail模型模拟LAI和7种植被指数：比值植被指数（RVI）、归一化植被指数（NDVI）、绿波段植被指数（GNDVI）、重归一化植被指数（RDVI）、土壤调整植被指数（SAVI）、调整土壤亮度植被指数（OSAVI）和修正的土壤调整植被指数（MSAVI），并采用支持向量机回归（SVR）算法和4种统计回归方法（线性函数、二次函数、指数函数和对数函数）建立LAI反演模型，同时通过Landsat 8 OLI遥感数据和实测数据验证模型精度。研究表明：1）SVR算法相比其他统计回归方法可以提高LAI反演的模型精度和预测精度；2）OSAVI指数在LAI反演方面的表现要优于NDVI等指数；3）NDVI指数的建模精度很高，但预测精度较低；4）OSAVI和SVR算法构建的模型精度和稳定性更好，是LAI反演的优选模型，其预测结果最为精确。因此，基于Geosail模型和SVR算法的反演方法可提高LAI反演精度，为大区域LAI反演的应用提供了新的思路，扩展了Geosail模型、SVR算法和Landsat 8 OLI遥感数据在LAI反演方面的应用潜力。
关键词：SVR算法    Geosail模型    叶面积指数    Landsat 8 OLI    阔叶林    
Remote sensing inversion of leaf area index based on Geosail model and SVR algorithm
YANG Wei, ZHANG Xuexia, ZHAO Jingyao     
College of Soil and Water Conservation, Beijing Forestry University, 100083, Beijing, China
Abstract: [Background] As an indispensable vegetation parameter in land ecosystem and hydrological models, Leaf area index controls many physiological and ecological processes of plant canopies. Therefore, real-time and accurate acquisition of regional LAI is very important for studying vegetation and soil erosion. Combining the physical model and the statistical model to estimate physiological parameters of the plant is non-destructive, simple, and highly efficient, which is one of the major approaches to quantitative remote sensing. [Methods] In the paper, leaf area index of broad-leaved forest was studied in Beijing. Geosail model, a combination of a geometric model and a mixed medium model, was used to simulate the broad band reflectance of canopy. Prospect model, a kind of leaf optical physical model, was used to simulate the leaf hyperspectral reflectance of broad-leaved forest. The leaf hyperspectral reflectance was converted into leaf broad band reflectance by the spectral response function, and then Geosail model used leaf broad band reflectance to simulate reflectance of canopy of broad-leaved forest. LAI and 7 kinds of remote sensing vegetation indexes were generated by simulated canopy reflectance, including RVI, NDVI, GNDVI, RDVI, SAVI, OSAVI, and MSAVI. Then 4 types of statistical regression methods (Linear function, quadratic function, exponential function, logarithmic function) and SVR algorithm were used to establish LAI inversion models. The accuracy of LAI inversion models was verified by Landsat 8 OLI remote sensing data and measured data. [Results] The analysis showed:1) SVR algorithm could improve accuracy and prediction accuracy of LAI inversion models than other statistical regression methods. 2) The prediction results of LAI inversion models showed that the performance of OSAVI was better than that of NDVI and other vegetation indices in the field of LAI inversion. This indicated that OSAVI could eliminate the most influence of atmospheric condition and soil background by using the correction factor of canopy background in computing formula, and had better anti-interference ability. 3)The LAI inversion modeling and models prediction showed that the modeling accuracy of NDVI index was very high, but in reality, the prediction accuracy of NDVI index was relatively low. 4) The accuracy and stability of the model constructed by the OSAVI and SVR algorithm were better, and it was the preference model for LAI inversion. Its prediction results were the most accurate, its value of coefficient of determination (R2) was 0.852 8, its value of root mean square error (RMSE) was 0.204 6, and its value of Slope was 0.988 1. [Conclusions] Therefore, the inversion method based on Geosail model and SVR algorithm was feasible, which could improve the accuracy of LAI inversion and provide new ideas and methods for the application of LAI inversion in large area. Through the LAI inversion model, the ground measured data could be converted to the remote sensing image data scale, which expanded the application potential of Geosail model, SVR algorithm and Landsat 8 OLI remote sensing data in LAI inversion.
Key words: support vector regression algorithm    Geosail model    leaf area index    Landsat 8 OLI    broad-leaved forest    

叶面积指数(Leaf Area Index, LAI)是指单位面积上植物叶片的垂直投影面积的总和，是估计植物冠层功能的重要参数，也是陆地生态、水文模型中不可或缺的植被参数[1]。LAI能反映植被水平与垂直结构特征，可计算土壤流失方程中的生物因子，是水土保持定量估算与评价的重要参数[2]；因此，实时、准确获取LAI对研究植被与土壤侵蚀具有重要意义。传统LAI获取的是点状或线状数据，难以应用于大区域、大尺度的研究中，遥感技术具有覆盖范围广、时间和空间分辨率高的优点，为准确反演区域LAI提供了有效途径[3]。

遥感反演LAI的方法主要有3种——统计模型、物理模型以及统计模型与物理模型相结合的方法。统计模型方法主要是在植被指数和LAI之间建立线性或非线性模型，简单灵活且计算方便；但对研究的地区、植被类型具有较大的依赖性，普适性较低[4]。相比传统植被指数的方法，运用支持向量机回归(Support Vector Regression, SVR)算法、BP神经网络方法反演植被LAI，反演精度有所提高，说明通过改进数学算法可以提高精度[5-6]。物理模型方法考虑植物结构参数、光学参数和光照参数，不依赖具体植被类型和背景环境，具有较高的普适性；但模型比较复杂，存在模型解的非唯一性等问题[7]。杨贵军等[8]利用PROSAIL模型和PROBA/CHRIS遥感数据反演春小麦LAI，反演精度R2为0.854；李海洋等[9]利用Geosail模型结合TM遥感数据反演森林LAI，实测精度达83.7%。其中Geosail模型是一个几何模型和一个混合介质模型的结合，物理意义明确，用于描述不连续冠层反射率[7]，适合反演森林植被参数。

根据统计模型和物理模型的优点，将二者结合起来定量反演植被冠层参数的方法受到国内外学者的青睐，这种方法既借鉴了植被指数方法简单实用的优点，又利用物理模型的理论基础，可快速、准确地进行冠层参数的反演[4, 10]。Santis等[11]使用Geosail模型和查找表的反演方法，对森林火灾严重程度及灾后恢复进行评估。同时，Surya等[12]和Tan等[13]利用SVR算法反演植物冠层参数，使反演值逼近真实值。其中，SVR算法通过非线性映射，将样本空间映射到一个高维的特征空间，通过在特征空间中应用线性学习机方法解决样本空间中高度非线性问题，具有全局最优、泛化能力强、算法简单、易于实现等优点[5, 14]。

笔者以北京市阔叶林为研究对象，采用Geosail模型模拟LAI和光谱指数，结合统计回归方法和SVR算法建立反演模型，并利用Landsat 8 OLI遥感数据计算的预测值与实测数据进行验证，得到LAI反演的优选模型，为准确反演区域LAI提供方法。

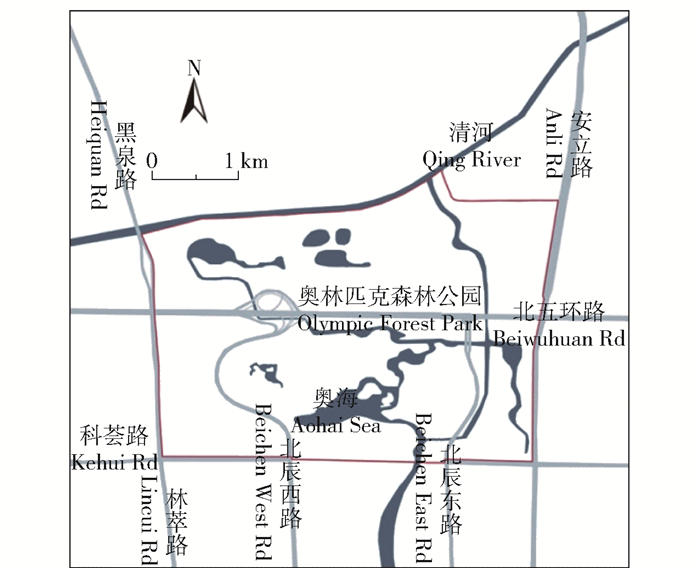
1 研究区概况

北京市位于华北平原的西北部(N 39°28′~41°25′，E 115°25′~117°30′)隶属暖温带半湿润气候区，植被类型以暖温带落叶阔叶林和温带针叶林为主。奥林匹克森林公园位于北京市朝阳区北五环林萃路，森林资源丰富。笔者实测样地LAI在奥林匹克森林公园进行测量，研究区地理位置如图 1。

图 1 研究区地理位置图 Fig. 1 Geographical location map of the study area
2 材料与方法 2.1 数据获取

LAI实测数据使用LAI-2000植物冠层分析仪进行获取, 测量原理参考文献[15]。其中，为消除冠层高度过高引起的测量值不真的误差，LAI-2000测量的树木的冠层高度、冠幅面积、镜盖应满足方程

$ A = f{\rm{ \mathit{ π} }}{H^2}。$ (1)

式中：A为被测树木的冠幅面积, m2；f为视窗范围(以0.75、0.5、0.25和0.125代表 270°、180°、90°和45°的镜盖)，当不加镜盖时，f=1，冠幅值与冠高值接近；H是冠层高度，m。当冠层高度值偏高时，根据式(1)选择合适镜盖。

在测量样地LAI时，每组LAI测量值的标准误差在0.03~0.08之间，以保证试验数据的精度。共测量研究区内18个阔叶林样地的LAI，阔叶林的优势树种分别是毛白杨(Populus tomentosa Carrière)、刺槐(Robinia pseudoacacia Linn)、洋白蜡(Fraxinus pennsylvanica Marshall)。选择天气晴朗、微风、大气能见度好的午后进行测量，测量日期为2016年8月8日，实测样地平均高程为47m，样地概况见表 1。

表 1 样地概况 Tab. 1 Samples general situation

遥感数据使用Landsat 8 OLI影像，条带号为123/32，成像日期为2016年8月8日，其多光谱波段的地面分辨率为30m，研究区无云覆盖。Landsat 8 OLI遥感数据来自于地理空间数据云网站，产品类型为Level1T地形矫正影像。影像预处理在ENVI 5.1进行，包括辐射定标和大气校正[16]。在ArcGIS 10.1中，对预处理后的Landsat 8 OLI影像进行裁剪得到研究区的影像，匹配实测样地的位置获取样地的反射率数据。

2.2 Geosail模型

Geosail模型是2000年由Huemmrich提出，用于描述不连续冠层反射率的模型。该模型结合SAIL模型和几何模型，SAIL模型计算树木内的辐射传输，几何模型利用SAIL模型的结果生成场景反射率[7, 17]。Geosail模型的主要输入参数包括叶片反射率/透射率、LAI和树冠高与宽的比(Canopy Height and Width, CHW)。其中叶片反射率/透射率使用Prospect模型生成。

Prospect模型是目前应用较为广泛的叶片光学物理模型，它表达了植株从波长400~2500nm的光学特性[7]。笔者通过在Prospect模型中输入叶片结构参数、叶绿素含量、水含量和干物质含量值，对应输出400~1000nm波段范围内光谱分辨率为1nm的叶片高光谱反射率和透射率。

由于Prospect模型获取的叶片反射率数据的光谱分辨率为1nm，而Geosail模型模拟的Landsat 8 OLI影像反射率数据是宽波段反射率数据；因此需要通过波谱等效计算将高光谱数据等效成宽波段数据。其等效计算公式为

$ {\rho _{{\rm{multi}}}}({\lambda _i}) = \frac{{\sum \rho \left( \lambda \right)f({\lambda _i})}}{{f({\lambda _i})}}。$ (2)

式中：ρmulti(λi)为多光谱数据中心波长为λi的通道的反射率；ρ(λ)为高光谱反射率；f(λi)为多光谱数据中心波长为λi的通道的光谱响应函数[18]。

基于上述原理，结合Landsat 8 OLI影像的4个波段(Blue、Green、Red、NIR波段)的波长范围，对波段>1000nm并对反射率产生影响的参数可以不予以考虑，水含量在1000nm以后对叶片反射率影响较大，可以取固定值[9]。根据研究区阔叶树种的实测优势树木特征(表 1)并参考李海洋等[9]的参数值，取CHW=2，本文中Prospect模型和Geosail模型参数变化范围及步长如表 2所示。

表 2 Prospect模型和Geosail模型参数 Tab. 2 Parameters of Prospect model and Geosail model
1.4 选取植被指数与回归模型

笔者选取7种常用植被指数参与LAI遥感反演建模，分别是比值植被指数(RVI)、归一化植被指数(NDVI)、绿波段植被指数(GNDVI)、重归一化植被指数(RDVI)、土壤调整植被指数(SAVI)、调整土壤亮度植被指数(OSAVI)和修正的土壤调整植被指数(MSAVI)，计算公式详见文献[19]。根据Geosail模型模拟生成1600组LAI值和宽波段数据，对宽波段数据进行波段计算，生成上述植被指数，并对LAI和7种植被指数进行显著性双侧检验(显著性水平都为P < 0.01)。

反演模型的建立在MATLAB软件中进行。利用1600组LAI与7种植被指数，首先采用统计回归方法建模，统计回归建模函数的类型包括4种：线性函数、二次函数、指数函数和对数函数。其次采用基于结构风险最小化原理的支持向量机回归(SVR)算法建模，核函数类型为RBF(Radial Basis Function)。对基于RBF的SVR，其性能是由惩罚系数(C)和核函数参数(g)决定的，C的作用是调节学习机器置信区间范围，g决定线性分类达到的最小误差，选取最优的惩罚系数和RBF参数组合可以提高SVR的回归精度[20-21]。对比分析统计回归建模和SVR算法在LAI反演方面的表现情况，同时挖掘各植被指数在LAI反演方面的潜力。

2 结果与分析 2.1 LAI反演模型的建立 2.1.1 统计回归反演模型

笔者利用Geosail模型模拟的LAI和7种植被指数，采用4种统计回归方法建立LAI反演模型，得到回归模型的方程，以模型决定系数(R2)和均方根误差(Root mean square error, RMSE)为指标对各植被指数的建模估测结果进行比较，各植被指数统计回归建模结果见表 3。

表 3 统计回归模型及评价指标 Tab. 3 Statistical regression models and evaluation indicators

在7种植被指数中，RVI建模精度较低，线性函数建模的R2最低，为0.6495；对数函数建模的R2最高，为0.8723，说明选择合适的统计回归模型有利于提高RVI建模精度。RDVI、SAVI、OSAVI、MSAVI统计回归建模的精度R2都大于0.80，RMSE均 < 1，其中OSAVI的二次函数模型和指数的R2=0.8781且RMSE=0.7054，说明考虑土壤背景影响的植被指数在估算LAI方面有较好的优势。NDVI二次函数建模的精度最高，R2=0.8898，RMSE=0.6707，线性函数、指数函数和对数函数的建模R2分别为0.8641、0.8890、0.7813，说明NDVI与植被LAI有较好的关系，其建模精度受统计回归模型影响。GNDVI的4种统计回归模型建模精度相比其他植被指数较低，R2介于0.701~0.722之间，RMSE>1，统计回归模型的选择对建模精度的变化不大，说明GNDVI在估算植被LAI方面的表现不如RDVI、SAVI、OSAVI、MSAVI、NDVI。

2.1.2 支持向量机回归(SVR)反演模型

笔者以Geosail模型模拟的LAI和各植被指数建立SVR模型，分别以RVI、NDVI、GNDVI、RDVI、SAVI、OSAVI、MSAVI为自变量在MATLAB R 2013a软件中生成7个对应的SVR模型，各模型的SVR参数寻优结果和评价指标见表 4。对比表 3和表 4的结果，采用SVR建模的R2较高且RMSE较小，其中RVI、RDVI、SAVI、OSAVI为自变量的SVR建模精度都高于统计回归的建模精度，NDVI、GNDVI、MSAVI为自变量的SVR建模精度都高于对数函数的建模精度。说明基于SVR的建模方法可以提高LAI反演的建模精度。

表 4 SVR模型及评价指标 Tab. 4 SVR models and evaluation indicators
2.2 LAI反演模型预测能力与验证分析

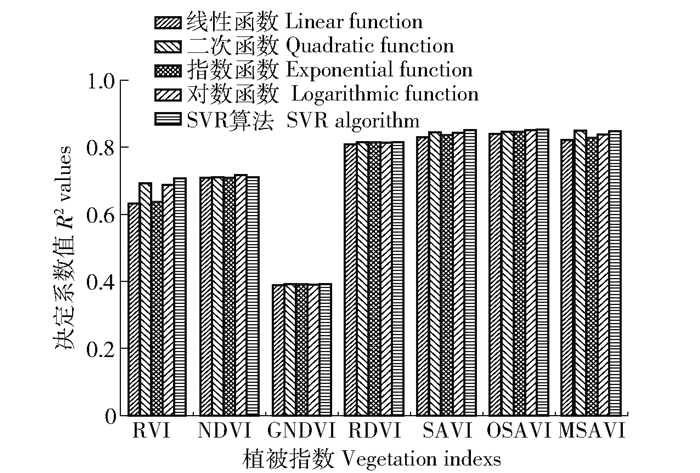
为对比上述LAI反演模型的预测能力，本文使用Landsat 8 OLI影像数据生成LAI预测值，并与研究区18个样地的LAI实测值进行回归拟合，对模型的预测结果进行验证。以线性回归决定系数(R2)、均方根误差(RMSE)和斜率(Slope)3个统计量评估LAI反演模型的预测精度和稳定性，得到预测能力评价结果如图 2、图 3和图 4。

图 2 模型预测结果的决定系数 Fig. 2 R2 values of prediction results of models
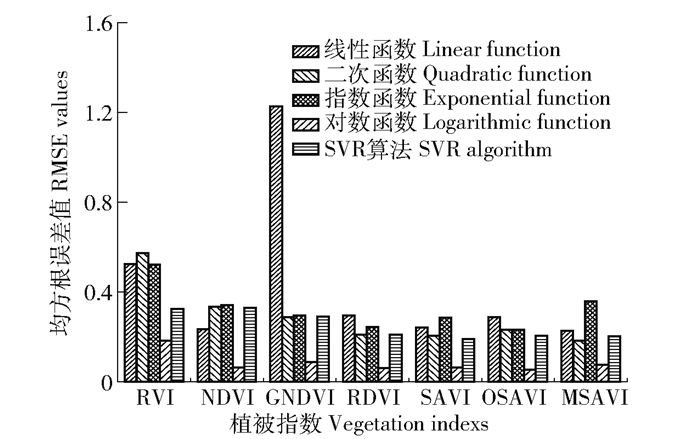
图 3 模型预测结果的均方根误差 Fig. 3 RMSE values of prediction results of models
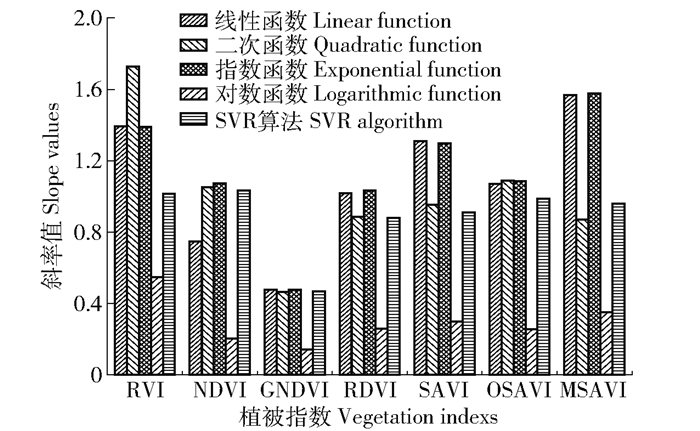
图 4 模型预测结果的斜率 Fig. 4 Slope values of prediction results of models

由图 2可知，RDVI、SAVI、OSAVI、MSAVI这4种植被指数反演模型的预测精度较高，最高R2分别为0.8143、0.8502、0.8528和0.8492，其中OSAVI-SVR的R2最大。NDVI、RVI模型预测结果R2在0.63~0.72之间，GNDVI的R2最低且 < 0.40。

由图 3可知，GNDVI线性函数模型的RMSE相比其他模型异常高，其线性函数模型预测的误差最大；RDVI、SAVI、OSAVI模型的RMSE都很低且 < 0.3；NDVI、MSAVI模型的RMSE较低且 < 0.4；RVI模型的RMSE相对较高。对比可知RDVI、SAVI、OSAVI模型的预测误差RMSE较小。

由图 4可知，各模型预测结果中实测值与预测值的回归斜率(Slope)差异很大。总体上，相比统计回归方法，采用SVR算法的模型，回归斜率接近于1。RDVI-SVR、SAVI-SVR、OSAVI-SVR、MSAVI-SVR模型的斜率分别为0.8810、0.9089、0.9881、0.9595，其中OSAVI-SVR的斜率最接近于1，说明OSAVI-SVR模型预测的LAI值与实测值的变化幅度基本相同。综上，通过对比不同LAI反演模型的预测能力，得到OSAVI-SVR模型的预测结果精度更高。

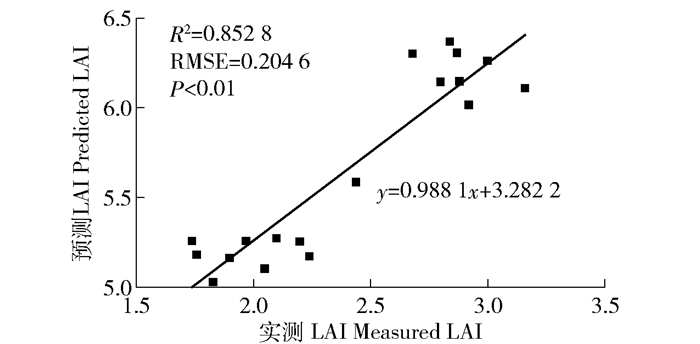
OSAVI-SVR模型的预测值与实测值的验证分析结果如图 5。OSAVI-SVR模型的预测值与实测值在0.01水平上显著相关，R2=0.8528，RMSE=0.2046，Slope=0.9881。图 5中反演值高于实测值，原因是本文实测的LAI为有效LAI，因聚集效应的存在，有效LAI相比真实LAI的值偏低[22]。

图 5 OSAVI-SVR模型验证分析 Fig. 5 Verification and analysis of OSAVI-SVR model
3 结论

1) SVR算法相比其他统计回归方法能提高LAI反演的建模精度和预测精度，SVR算法建模的R2较高且RMSE较低，预测结果的R2较高、RMSE较低且Slope接近1。

2) LAI反演模型预测结果表明OSAVI指数在LAI反演方面的表现要优于NDVI等指数。在统计回归模型中，OSAVI的建模精度高于RVI、GNDVI；在SVR模型中，OSAVI的建模精度高于RDVI、SAVI、MSAVI；在预测能力分析中，OSAVI的预测精度高于其他6种植被指数。

3) LAI反演建模和模型预测表明NDVI指数的建模精度虽然很高，但在实际中NDVI模型的预测精度不是很高。

4) LAI反演模型预测结果表明，基于OSAVI和SVR算法构建的模型精度和稳定性更好，表征LAI的变化情况更为真实，是LAI反演的优选模型。

4 讨论

结合物理模型和优化算法反演植被物理化学参数是定量遥感在生态上应用的必然需求。本文利用Geosail模型和SVR算法相结合的方法构建阔叶林LAI的反演模型，得到较高的精度，对大区域LAI反演具有一定的借鉴意义。

在LAI反演建模过程中，统计回归函数的选择与建模精度有关，不同植被指数的最优统计回归模型的函数类型也不同。其中OSAVI利用计算式中的冠层背景校正因子项消除了大气条件与土壤背景的大部分影响[23]，具有更好的抗干扰能力，相比其他植被指数更适合LAI的反演[5]。NDVI的预测精度不是很高，可能与NDVI对高植被覆盖区的饱和特性有关。有研究表明NDVI在高植被覆盖区对LAI的敏感性较低，具有饱和特性[24]。

相比统计回归模型，采用SVR算法能提高LAI反演的精度。同时，梁栋等[25]研究得到基于植被指数的SVR算法比经验模型的预测精度更高，说明SVR算法适用于LAI遥感反演。与林卉等[5]运用实测数据，采用OSAVI指数和SVR算法反演的LAI相比，本文的预测结果R2更高，RMSE更小，说明运用Geosal模型反演LAI具有可行性。

笔者基于Geosail模型和SVR算法反演LAI，方法快速高效，且具有普适性和稳定性，但其反演精度受Geosail模型模拟精度、SVR算法精度等因素的影响[26]。在未来的研究中，可根据研究区森林特征优化模型参数提高模拟精度，或结合其他算法反演LAI，提高计算效率和精度。在实际应用中，可以进一步探讨林分结构和LAI的关系，同时由于不同地理环境的差异性，也可综合考虑更多地理因素进行研究。

参考文献
[1]
王志慧, 姚文艺, 汤秋鸿, 等. 2000-2014年黄土高原植被叶面积指数时空变化特征[J]. 中国水土保持科学, 2017, 15(1): 72.
WANG Zhihui, YAO Wenyi, TANG Qiuhong, et al. Spatio-temporal change analysis of leaf area index in the Loess Plateau during 2000-2014[J]. Science of Soil and Water Conservation, 2017, 15(1): 72.
[2]
林杰, 张金池, 顾哲衍, 等. 基于叶面积指数的植被覆盖管理措施因子C的遥感定量估算[J]. 林业科学, 2013, 49(2): 87.
LIN Jie, ZHANG Jinchi, GU Zheyan, et al. Quantitative assessment of Vegetation cover and management factor based on leaf area index and remote sensing[J]. Scientia Silvae Sinicae, 2013, 49(2): 87.
[3]
刘晓臣, 范闻捷, 田庆久, 等. 不同叶面积指数反演方法比较研究[J]. 北京大学学报(自然科学版), 2008(2): 57.
LIU Xiaochen, FAN Wenjie, TIAN Qingjiu, et al. Comparative analysis among different methods of leaf area index inversion[J]. Acta Scientiarum Naturalium Universitatis Pekinensis, 2008(2): 57.
[4]
谷成燕, 杜华强, 周国模, 等. 基于PROSAIL辐射传输模型的毛竹林叶面积指数遥感反演[J]. 应用生态学报, 2013, 24(8): 2248.
GU Chengyan, DU Huaqiang, ZHOU Guomo, et al. Retrieval of leaf area index of Moso bamboo forest with Landsat Thematic Mapper image based on PROSAIL canopy radiative transfer moedel[J]. Chinese Journal of Applied Ecology, 2013, 24(8): 2248.
[5]
林卉, 梁亮, 张连蓬, 等. 基于支持向量机回归算法的小麦叶面积指数高光谱遥感反演[J]. 农业工程学报, 2013, 29(11): 139.
LIN Hui, LIANG Liang, ZHANG Lianpeng, et al. Wheat leaf area index inversion with hyperspectral remote sensing based on support vector regression algorithm[J]. Transactions of the CSAE, 2013, 29(11): 139.
[6]
杨敏, 林杰, 顾哲衍, 等. 基于Landsat 8 OLI多光谱影像数据和BP神经网络的叶面积指数反演[J]. 中国水土保持科学, 2015, 13(4): 86.
YANG Min, LIN Jie, GU Zheyan, et al. Leaf area index retrieval based on Landsat 8 OLI multi-spectral image data and BP neural network[J]. Science of Soil and Water Conservation, 2015, 13(4): 86. DOI: 10.3969/j.issn.1672-3007.2015.04.013.
[7]
薛云, 陈水森, 夏丽华, 等. 几个典型的叶片/冠层模型[J]. 西部林业科学, 2005, 34(1): 70.
XUE Yun, CHEN Shuisen, XIA Lihua, et al. A brief introduction to several typical leaf/canopy models[J]. Journal of West China Forestry Science, 2005, 34(1): 70. DOI: 10.3969/j.issn.1672-8246.2005.01.018.
[8]
杨贵军, 赵春江, 邢著荣, 等. 基于PROBA/CHRIS遥感数据和PROSAIL模型的春小麦LAI反演[J]. 农业工程学报, 2011, 27(10): 88.
YANG Guijun, ZHAO Chunjiang, XING Zhurong, et al. LAI inversion of spring wheat based on PROBA/CHRIS hyperspectral multi-angular data and PROSAIL model[J]. Transactions of the Chinese Society of Agricultural Engineering, 2011, 27(10): 88. DOI: 10.3969/j.issn.1002-6819.2011.10.016.
[9]
李海洋, 范文义, 于颖, 等. 基于Prospect, Liberty和Geosail模型的森林叶面积指数的反演[J]. 林业科学, 2011, 47(9): 75.
LI Haiyang, FAN Wenyi, YU Ying, et al. Leaf area index retrieval based on prospect, liberty and Geosail models[J]. Scientia Silvae Sinicae, 2011, 47(9): 75.
[10]
QI J, KERR Y H, MORAN M S, et al. Leaf area index estimates using remotely sensed data and BRDF models in a semiarid region[J]. Remote Sensing of Environment, 2000, 73: 18. DOI: 10.1016/S0034-4257(99)00113-3.
[11]
SANTIS A D, CHUVIECO E, VAUGHAN P J. Short-term assessment of burn severity using the inversion of PROSPECT and GeoSail models[J]. Remote Sensing of Environment, 2009, 113(1): 126. DOI: 10.1016/j.rse.2008.08.008.
[12]
SURYA S D, ROGER L K, NICOLAS H Y. Support vector machines regression for retrieval of leaf area index from multiangle imaging spectroradiometer[J]. Remote Sensing of Environment, 2007, 107(1): 348.
[13]
TAN K, WANG S, LIU Y, et al. Estimating nitrogen status of rice canopy using hyperspectral reflectance combined with BPSO-SVR in cold region[J]. Chemometrics & Intelligent Laboratory Systems, 2017, 172.
[14]
张强, 黄生志, 陈晓宏. 基于支持向量机的土壤湿度模拟及预测研究[J]. 土壤学报, 2013, 50(1): 60.
ZHANG Qiang, HUANG Shengzhi, CHEN Xiaohong. Simulation and prediction of soil moisture based on support vector machine technique[J]. Acta Pedologica Sinica, 2013, 50(1): 60.
[15]
康峰峰.北京西南山森林绿量遥感反演的研究[D].北京: 北京林业大学, 2011: 25.
KANG Fengfeng. Study on remote sensing retrieval of forest vegetation quantity in mountainous area South-western Beijing China[D]. Beijing: Beijing Forestry University, 2011: 25. http://cdmd.cnki.com.cn/article/cdmd-10022-1011132788.htm
[16]
蒲莉莉, 刘斌. 结合光谱响应函数的Landsat-8影像大气校正研究[J]. 遥感信息, 2015(2): 117.
PU Lili, LIU Bin. Atmospheric correction of Landsat-8 imagery based on spectral response function[J]. Remote Sensing Information, 2015(2): 117.
[17]
HALL F G, HUEMMRICH K F. BOREAS TE-18 GeoSail Canopy Reflectance Model[M]. NASA Goddard Space Flight Center, 2000: 3.
[18]
莫云华, 张文娟, 张连蓬. 基于PROSAIL模型的高光谱遥感图像模拟研究[J]. 红外, 2016, 37(9): 7.
MO Yunhua, ZHANG Wenjuan, ZHANG Lianpeng. Simulation of hyperspectral remote sensing image based on PROSAIL model[J]. Infrared, 2016, 37(9): 7.
[19]
罗桑扎西.基于SPOT5影像的植被类型识别及叶面积指数定量估算研究[D].南京: 南京农业大学, 2013: 54.
LUOSANGZHAXI. Study on forest classification and estimation of LAI based on SPOT-5 image[D]. Nanjing: Nanjing Agricultural University, 2013: 54. http://cdmd.cnki.com.cn/Article/CDMD-10307-1014216357.htm
[20]
林升梁, 刘志.基于RBF核函数的支持向量机参数选择[J].浙江工业大学学报, 2007, 35(2): 164.
LIN Shengliang, LIU Zhi.[J]. Journal of Zhejiang University of Technology, 2007, 35(2): 164.
[21]
CHANG C C, LIN C J. 2001. LIBSVM: A library for support vector machines[EB/OL]. Software available at http://www.csie.ntu.edu.tw/~cjlin/libsvm.
[22]
杜育璋, 姜小光, 张雨泽, 等. 基于Landsat-8遥感数据和PROSAIL辐射传输模型反演叶面积指数[J]. 干旱区地理, 2016(5): 1101.
DU Yuzhang, JIANG Xiaoguang, ZHANG Yuze, et al. Retrieving leaf area index using PROSAIL radiative transfer model based on Landsat 8 image[J]. Arid Land Geography, 2016(5): 1101.
[23]
邢丽玮, 李小娟, 李昂晟, 等. 基于高光谱与多光谱植被指数的洪河沼泽植被叶面积指数估算模型对比研究[J]. 湿地科学, 2013, 11(3): 316.
XING Liwei, LI Xiaojuan, LI Aangsheng, et al. A Comparative on estimation model for leaf area index of vegetation in marshes in Honghe National Nature Reserve based on hyperspectral and multispectral vegetation indices[J]. Wetland Science, 2013, 11(3): 316.
[24]
吴朝阳, 牛铮. 基于辐射传输模型的高光谱植被指数与叶绿素浓度及叶面积指数的线性关系改进[J]. 植物学报, 2008, 25(6): 714.
WU Chaoyang, NIU Zheng. Improvement in linearity between hyperspectral vegetation indices and chlorophyll content, leaf area index based on radiative transfer models[J]. Chinese Bulletin of Botany, 2008, 25(6): 714. DOI: 10.3969/j.issn.1674-3466.2008.06.012.
[25]
梁栋, 管青松, 黄文江, 等. 基于支持向量机回归的冬小麦叶面积指数遥感反演[J]. 农业工程学报, 2013(7): 117.
LIANG Dong, GUAN Qingsong, HUANG Wenjiang, et al. Remote sensing inversion of leaf area index based on support vector machine regression in winter wheat[J]. Transactions of the CSAE, 2013(7): 117.
[26]
刘轲, 周清波, 吴文斌, 等. 基于多光谱与高光谱遥感数据的冬小麦叶面积指数反演比较[J]. 农业工程学报, 2016, 32(3): 160.
LIU Ke, ZHOU Qingbo, WU Wenbin, et al. Comparison between multispectral and hyperspectral remote senseing for LAI estimation[J]. Transactions of the CSAE, 2016, 32(3): 160.