2. 北京林业大学 北京市水土保持工程技术研究中心, 100083, 北京
-
项目名称
- 国家自然科学基金面上项目"基于数值模拟的植物根系对人工土质边坡稳定性效应"(31570707)
-
第一作者简介
- 丁雪坤 (1994-), 女, 硕士研究生。主要研究方向:水土保持工程。E-mail:dxk_0225@126.com
-
通信作者简介
- 张守红 (1985-), 男, 博士, 副教授。主要研究方向:城市雨洪管理。E-mail:zhangs@bjfu.edu.cn
-
文章历史
-
收稿日期:2016-11-10
修回日期:2016-12-08
2. 北京林业大学 北京市水土保持工程技术研究中心, 100083, 北京
2. Beijing Engineering Research Center of Soil and Water Conservation, 100083, Beijing, China
植物护坡技术不仅能够恢复或重建坡面原有生态系统,也可强化农业生产和景观生态的基础,具有固土护坡、改善生境、涵养水土、造价低廉等优势[1];但在实际应用中,不同类型、种类的植被及其生长发育的阶段和状态 (林龄、林冠、四季生长规律等),都可能会影响表层坡面的受力情况和土壤理化性质,进而对坡体的稳定产生影响。有研究表明植被生长要素如自重、弯曲生长等会破坏土层结构导致边坡失稳[2]。另有研究通过对比分析有利与不利因素发现植被对坡体稳定性的影响非常复杂,需根据具体植被和坡体特征而定[3]。植被对坡体稳定性的影响随植物生长过程复杂多变且不可控制,更难以对其稳固能力进行测定[4]。目前相关研究大都是只考虑坡体自然形态的稳定性,而未充分考虑植物对坡体稳定的贡献,更忽略了植物护坡效果的年际变化规律。
本文通过构建单株植物模型,综合考虑植被自重、风荷载和根系的影响,定量地研究不同种类的植物在生长变化过程中对浅层坡体稳定的影响机制,分析含有不同类型植被的浅层均质土坡安全系数的年际变化规律,初步探寻典型植物固土护坡效果最优的生长时期。
1 材料与方法 1.1 植物生长模型本文根据植物的形态学和生理学特点,提出以下几个关键形态学特征,分别研究对应的生长规律及模型。
1.1.1 自重植物地上部分的枝干、茎和叶片,所产生的自重荷载会对浅层土壤产生力学作用,其自身拉伸也会改变土壤剪应力,从而影响土壤的抗剪强度。本文通过树高、胸径 (DBH)、树形和树龄几个生长特性来研究植物的自重荷载。通过树高曲线[5]来表明树高和胸径之间的关系,茎干的曲线方程[5]和圆锥模型计算树干体积Vd(定义n≤7)。假定存在密度常量ρ,则地上部分自重可定义为
| $\begin{align} & {{W}_{\text{b}}}=\frac{\rho \left( l\sum\limits_{i=1}^{n}{\text{ }\!\!\pi\!\!\text{ }r_{\text{c}}^{2}}+\frac{1}{3}\text{ }\!\!\pi\!\!\text{ }r_{\text{c}}^{2}l' \right)}{\frac{2}{3}}\left( 1-\frac{1}{6} \right)g= \\ & \frac{5}{4}\rho g\left( l\sum\limits_{i=1}^{n}{\text{ }\!\!\pi\!\!\text{ }r_{\text{c}}^{2}}+\frac{1}{3}\text{ }\!\!\pi\!\!\text{ }r_{\text{c}}^{2}l' \right) \\ \end{align}$ | (1) |
式中:Wb为自重,N;ρ为植物密度,kg/m3;l为顶端树干长度,m;n为主干数量;rc为茎干横截面半径,cm;l′为主干长度,m;g=9.8 N/kg。
1.1.2 根系根系形态结构复杂,对于植物的生长有很重要的作用。为便于研究,本文将其简单地解释成一个主根和侧根的联合体。植物整个生长过程中,主根数量基本可以确定,在高含水量的土壤 (田间持水量高于60%) 里增加,在低含水量的土壤里减少。侧根的数量则可以描述为一个随着时间增长的类型“s”,可定义为:
| $\begin{gathered} {N_l} = \left( {{k_1}t - {c_1}} \right)w。\;\;\;\;\;\;\;\left( {t \leqslant {t_0}} \right) \hfill \\ {N_l} = \left( { - {k_2}{t^2} + {c_2}t - {c_3}} \right)w。\;\;\;\;\;\;\;\left( {t \leqslant {t_0}} \right) \hfill \\ \end{gathered} $ | (2) |
式中:Nl为侧根的数量;k1,k2,c1,c2,c3为植物种类不同的系数;t为生长时间;t0为增长曲线的断点;ω为田间持水量,%。
根系的最大埋深长度受到发育条件和周围环境的影响,在快速增长期后逐渐停止生长,并在植物发育后期保持不变;因此,主根和侧根的最大埋深可定义为:
| ${L_{\max }} = \frac{k}{{\left( {1 + a{e^{ - bt}}} \right)}},$ | (3) |
| ${L_e}\left( {S,t} \right) = \frac{{{L_{\max }}\left( t \right)}}{{\left( {a + bS + c{S^2}} \right)}},\left( {t > 0} \right)。$ | (4) |
式中:Lmax为主根系最大埋深,m;a, b, c, k为植物种类系数;Le为水平侧根最大埋深,m;S为最大根系直径出现的深度,m。
1.2 坡体稳定性影响因素分析 1.2.1 冠层冠层对于坡体稳定性的影响可划分为2个部分:自重和风荷载。为便于统计,将冠层的重量计入到树干重量重。根据Brown、Sheu和Ancelin[6-7]涉及风速局部压力的研究,植物受到的局部风压力可以通过土壤传递到坡面上形成荷载。在Guan等[8]研究的基础上对CD进行修正,则传入坡体土壤的风荷载可定义为 (笔者限定风速为14 m/s)
| $D = \sum\limits_{i = {h_1}}^{i = {h_2}} {\left( {P{{\cos }^2}\beta e} \right)i = } \sum\limits_{i = {h_1}}^{i = {h_2}} {\left( {0.5{\rho _{\text{a}}}{\mu ^2}{C_D}{{\cos }^2}\beta e} \right)i} 。$ | (5) |
式中:D为传递进坡体的风压力,kg;h1为冠层底部距离地面的高度,m;h2为冠层顶部距离地面的高度,m;P为风压力,kPa;β为坡度,(°);e为冠层横断面宽度增加量,m;ρa为根密度,kg/m3;μ为风速,m/s;CD为冠层阻力系数。
1.2.2 根系1) 根的分支类型。根系结构在很大程度上决定着力传播的方式及大小[9],笔者着重讨论根系密度、根的倾向、分支点以及分支结构等特征,进而评价垂直根和侧根的对于土壤抗剪强度的增强作用。笔者参考Coutts[10]的研究,采用已经应用于实际的2D模型,下文中主要应用混合分支结构类型。
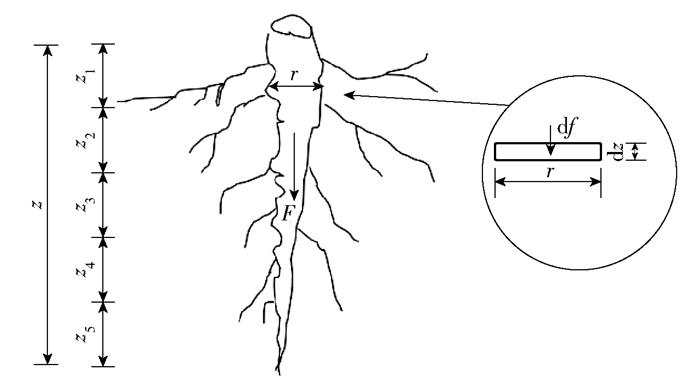
2) 垂直根的锚固作用。垂直根对土壤根系复合体来说具有锚固作用。垂直根一般都具有较大的根系直径,因此被认为是刚性材料[11],且对于整个垂直根来说,假设埋深与根的平均直径存在关系式,则类似地也存在埋深与根的数量的关系式。那么垂直根的最大静摩擦力可定义为
| $F=\int_{0}^{\infty }{\sum{{{d}_{f}}=\int_{0}^{\infty }{N2\text{ }\!\!\pi\!\!\text{ }\overline{r}{{K}_{0}}v\gamma z{{d}_{z}}}}}。$ | (6) |
式中:F为总最大静摩擦力,N;df为最大静摩擦力,N;N为根的数量;r为根节的直径,mm;K0为横向力系数;ν为摩擦系数;γ为土壤容重,kg/m3;z为土壤深度,m;dz为长度,m。摩擦系数ν与横向力系数K0是通过野外根系拔出实验和参考Gray和Barker[12]的论文得到的,其值的大小会受到植物种类以及土壤类型的变化而变化,在本文中滑动摩擦力取值0.8,而侧向压力系数取值0.2。
|
z:土壤深度Soil depth,m;r:直径Root diameter, mm;F:锚固力Anchorage force, N;df:最大静摩擦力The maximum static friction force, N;dz:长度Length, m 图 1 垂直根的锚固作用 Figure 1 Anchorage of vertical roots |
3) 侧根的加筋作用。为了评估侧根对抗剪强度的影响,笔者将根的刚性和柔性作为上下限定值,定义水平根对土壤的加筋作用取这2种性质的平均。假设土壤和根一起发生移动,则刚性根引起的抗剪强度增量为:
| $\begin{align} & {{\tau }_{r1}}=\frac{\sum\limits_{j=1}^{m}{{{T}_{j}}\sin {{\theta }_{j}}}}{A}+\frac{\sum\limits_{j=1}^{m}{{{T}_{j}}\cos {{\theta }_{j}}\tan \phi }}{A}+ \\ & \frac{\sum\limits_{j=m+1}^{n}{{{T}_{j}}\sin \left( {{90}^{{}^\circ }}-{{\psi }_{j}} \right)}}{A}+\frac{\sum\limits_{j=m+1}^{n}{{{T}_{j}}\cos \left( {{90}^{{}^\circ }}-{{\psi }_{j}} \right)\tan \phi }}{A} \\ & {{\psi }_{j}}={{\tan }^{-1}}\left[ \frac{1}{{{k}_{j}}+{{\left( {{\tan }^{-1}}i \right)}_{j}}} \right]\left( j=m+1,m+2,\cdots ,n \right)。 \\ \end{align}$ | (7) |

|
z:土壤深度Soil depth, m;θ:剪切角Shear deformation angle, (°);lr:水平根长度Length of lateral roots;σx:水平作用力Horizontal force, kPa;τr1:刚性水平根引起的抗剪强度增量Increment shear strength caused by stiffness lateral roots, kPa;τr2:弹性水平根引起的抗剪强度增量Increment shear strength caused by flexible lateral roots, kPa;δ:侧根与土壤水平线夹角Angle of lateral roots and horizontal force, (°) 图 2 侧根的加筋作用 Figure 2 Reinforcement of lateral roots |
式中:τr1为刚性侧根引起的抗剪强度的增量,kPa;m为与土壤垂直相交的根的数量;T为单一根的拉力,N;θ为剪切变形角,(°);A为根土复合区域的面积,m2;ψ为侧根水平倾角,(°);φ为侧根竖直方向倾角,(°);i为根系扩展方向和剪切断面的初始角度,(°);kj为剪切变形的比率;nr为根的数量。
考虑弹性侧根时,需要把水平作用力列入计算中,根据Oden等[13]的研究结果,水平作用力在根土复合区可以被定义为
| ${\sigma _x} = {K_0}{\sigma _z} = {K_0}\gamma z。$ | (8) |
式中:σx为水平作用力,kPa;σz为侧根在土壤中所受作用力,kPa。
当有n个根时,方程式则变成
| ${\tau _{r2}} = \frac{{\sum\limits_{n = 1}^n {{T_n}\cos {\delta _n}} }}{A} + \frac{{\sum\limits_{n = 1}^n {{T_n}sin{\delta _n}T\tan \phi } }}{A}。$ | (9) |
式中:τr2为弹性水平侧根引起的抗剪强度增量,kPa;δn为侧根与土壤水平线夹角,(°)。
综上所述,根据Waldron[14]的关系式,水平侧根引起的抗剪强度增量可以定义为
| $\tau = d + \frac{{{\tau _{r1}} + {\tau _{r2}}}}{2}。$ | (10) |
式中:τ为水平侧根引起的抗剪强度增加量,kPa;d为调整系数。
1.3 边坡稳定性计算本文采用极限平衡法计算坡体稳定性[15],通过比较沿滑动面的下滑力和抗滑力,来评估最危险滑动面的稳定性[16],并分为2种情况讨论。
1.3.1 裸露坡面当坡面上没有植被覆盖时,使用条分法分析坡面稳定性[15, 17]。应用Mohr-Coulomb的强度关系,可计算得到滑动面的总稳定性
| ${F_b} = \frac{{\sum {\left( {c'{l_s} + N'\tan \phi '} \right)} }}{{\sum {W\sin \alpha } }}。$ | (11) |
式中:c′为有效黏聚力,kPa;ls为滑动面的长度, m;N′为滑动面的有效正交力, N;φ′为滑动面的有效内摩擦角, (°);α为基础条块的角度,(°);W为条块的重量, N。
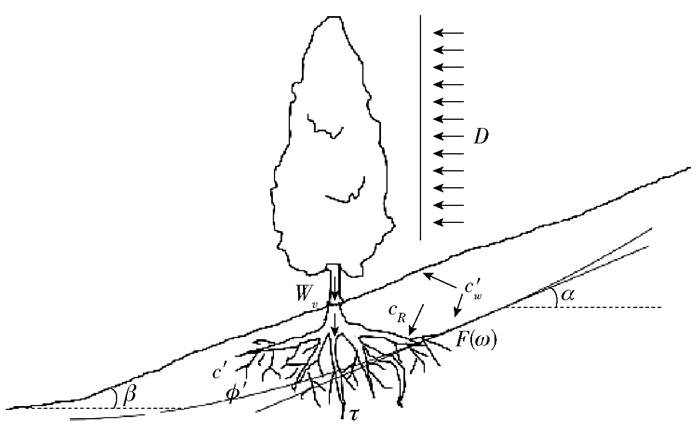
1.3.2 有植被覆盖的坡面笔者选择Greenwood General法[17-18]对基础稳定方程 (式11) 进行修改,简化由地面加固、季节变化或是植物根系引起的附加载荷 (图 3)。假设U1和U2相等,且斜坡中存在水压力,那么方程式可变为
| $\begin{gathered} {F_b} = \hfill \\ \frac{{\sum {\left\{ {\left( {c' - c{'_w}} \right){l_r} + \left[ {\left( {W + {W_v} + F} \right)\cos \alpha - D\sin \left( {\alpha - \beta } \right)} \right]\tan \phi + {\tau _r}} \right\}} }}{{\sum {\left[ {\left( {W + {W_v}} \right)\sin \alpha - D\cos \left( {\alpha - \beta } \right)} \right]} }} \hfill \\ \end{gathered} $ | (12) |
|
β:坡度Gradient of slope;Wv:植物荷载Loading of vegetation;τ:剪切力Available shear stress;α:基础块角度Angle of base of slice;c′:有效黏聚力Effective cohesion;cR:根系增加的黏聚力Enhanced cohesion by roots;c′w:根系生长产生的水分降低的内黏聚Removed cohesion by water in soil due to root growth;φ′:内摩擦角Effective angle of friction at the slip surface;D:风压力Wind force transmitted into the slope 图 3 含植被坡面稳定性分析 Figure 3 Stability analysis of vegetated slope |
式中:c′w为土壤中由于根系生长产生的水分降低的内凝聚力,N;lr为根系长度,m;Wv为植被荷载,N;β为坡角,(°)。理论上,当Fb>1.0时,坡体趋于稳定;当Fb为1.0时,坡体处于极限平衡状态;当Fb < 1.0时,边坡发生破坏的可能性较大 (在一般工程实践情况下Fb为1.1~1.3)。
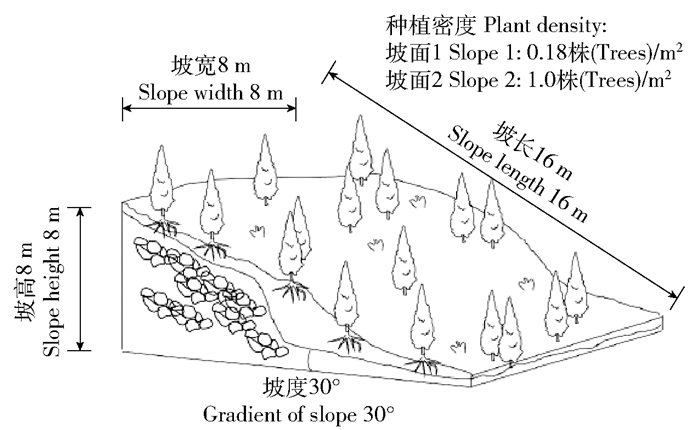
1.4 坡体条件与植被参数笔者模拟设定2个均值等厚土坡坡面,设置相关坡体参数 (坡高、坡长、坡度、坡宽) 如表 1,使得坡体条件基本保持一致。
| 表 1 坡体基本条件参数 Table 1 Parameters of basic conditions of the slope |
| 表 2 侧柏、荆条生长特性年际特征值 Table 2 Annual eigenvalues of characteristic of Platycladus orientalis and Vitex negundo |
|
图 4 坡面示意图 Figure 4 Schematic diagram of vegetated slope |
坡面植被分别选择北京山区分布广泛的2种植物:侧柏 (Platycladus orientalis (L.) Franco) 与荆条 (Vitex negundo var. heterophylla)。其耐干旱、耐严寒,抗性和适应性极强,是北方地区重要的水土保持树种。收集侧柏和荆条的林木调查信息[19-22],包括株高、胸径 (1.3 m高处的树干直径)、地径 (地面20 cm以上的茎干直径)、冠幅高、根系数量等参数。建立侧柏、荆条的植物生长模型,通过公式 (1)~(10),计算得植物体自重、风荷载、最大根系埋深、垂直根的平均直径等要素的多年特征值。最终得到两种植物在生长过程中自重、根系的垂直锚固力、水平加筋力以及风荷载的数值变化情况。
2 结果与分析综合前文所述的植物固土护坡机理的理论,将模拟设置的坡面基本条件参数、土壤参数、植物生长要素参数,带入到所构建的含植被坡体模型中,利用式 (11) 和式 (12) 计算2个坡面的坡体安全系数值,得到2种坡面在3种情况下,安全系数值的年际变化曲线。
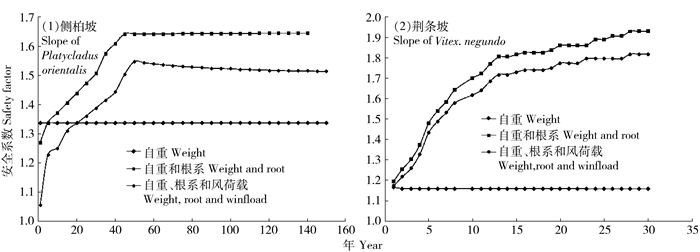
从图 5中可以看出,坡面1和坡面2的安全系数值总体上是先逐年增加,后基本保持不变。只考虑自重时,种植侧柏的坡面1的安全系数值由1.338下降为1.336,变化率为0.1%;种植荆条的坡面2的安全系数值由1.166下降为1.158,下降0.7%。在同时考虑自重、根系时,坡面1的安全系数值的初始值低于只考虑自重的情况,并在1~7年间快速增大,到60年左右达到最大值1.646,增幅为55.9%,60~70年后保持不变;坡面2的安全系数值在1~30年间逐渐增大,到30年左右达到最大值1.93,增幅为61.4%,30年之后基本不变。同时考虑自重、根系和风荷载时,坡面1的安全系数值在1~7年间快速增大,而后到50年左右达到最大值1.549,增幅为46.8%,其数值和增幅均小于同时考虑自重、根系的情况,50~60年后逐渐稳定保持不变;坡面2的安全系数值在1~30年间逐年增大,到30年左右达到最大值1.817,增幅为54.9%,其数值和增幅均小于同时考虑自重和根系的情况,30年之后趋于稳定。
|
图 5 含植被坡面安全系数年际变化情况 Figure 5 Inter-annual variability of safety values of plants |
在已知边坡条件及坡面植被条件的情况下,本文所构建的含植被坡体模型可用于覆盖不同种类植被的乔木林坡、灌木林坡和草坡的边坡稳定性计算以及安全系数年际变化规律的研究。通过模拟2个分别种有侧柏、荆条的含植被均质土坡,发现随着植被的生长发育,自重变化对坡面土壤稳定性产生的影响较小;但根系生长和风荷载对坡面土壤稳定性产生的影响较大,其作用都是在生长前期不断增加,后期稳定不变。在一定条件下,根系的锚固和加筋作用能使安全系数值增大,有效增强坡面表层土壤的稳定性;而冠层风荷载会导致安全系数值降低,削弱坡面稳定性,且会抵消一定的根系产生的固坡作用。本文通过分析2种类型植被的浅层均质土坡安全系数的变化规律,初步探寻到植被护坡是一个长期复杂的动态变化过程,植被的生长规律会对其护坡能力的可持续性产生影响;因此,在评价植被边坡稳定性的时候不能忽略植物自重、根系和风荷载的作用,且在生长中期时,植物固土护坡的效果能达到最优。
| [1] |
陈丽华, 余新晓, 宋维峰, 等.
林木根系固土力学机制[M]. 北京: 科学出版社, 2008: 15.
CHEN Lihua, YU Xinxiao, SONG Weifeng, et al. Root reinforcement of soil[M]. Beijing: Science Press, 2008: 15. |
| [2] |
张超波, 蒋静, 陈丽华. 植物根系固土力学机制模型[J].
中国农学通报, 2012, 31: 1.
ZHANG Chaobo, JIANG Jing, CHEN Lihua. Review on the models of mechanical mechanism of soil reinforcement by plant roots[J]. Chinese Agricultural Science Bulletin, 2012, 31: 1. DOI: 10.3969/j.issn.1007-7774.2012.10.001. |
| [3] |
周云艳, 陈建平, 王晓梅. 植物根系固土护坡机理的研究进展及展望[J].
生态环境学报, 2012, 21(6): 1171.
ZHOU Yunyan, CHEN Jianping, WANG Xiaomei. Progress of study on soil reinforcement mechanisms by root and its expectation[J]. Ecology and Environmental Sciences, 2012, 21(6): 1171. |
| [4] |
周云艳. 植物根系固土机理与护坡技术研究[D]. 中国地质大学, 2010: 40.
ZHOU Yunyan. Study on mechanism of soil reinforcement by roots and slope protection technology [D]. China University of Geosciences, 2010:40. |
| [5] | STOFFELS A, VAN S J. The main problems in sample plots[J]. Ned Boschb Tijdschr, 1953, 25: 190. |
| [6] | BROWN C B, SHEU M S. Effects of deforestation of slopes[J]. Journal of the Soil Mechanics and Foundations Division, 1975, 101(2): 147. |
| [7] | ANSELIN L. Exploring spatial data with GeoDaTM: a workbook[J]. Urbana, 2004, 51: 61801. |
| [8] | HSI G, NATH J H. Wind drag within simulated forest canopies[J]. Journal of Applied Meteorology, 1970, 9(4): 592. DOI: 10.1175/1520-0450(1970)009<0592:WDWSFC>2.0.CO;2. |
| [9] | COUTTS M P. Root architecture and tree stability[J]. Plant and soil, 1983, 71(1/2/3): 171. |
| [10] | COUTTS M P, NIELSEN C C N, NICOLL B C. The development of symmetry, rigidity and anchorage in the structural root system of conifers[J]. Plant and Soil, 1999, 217(1/2): 1. DOI: 10.1023/A:1004578032481. |
| [11] | KHUDER H, STOKES A, DANJON F, et al. Is it possible to manipulate root anchorage in young trees?[J]. Plant and Soil, 2007, 294(1/2): 87. |
| [12] | GRAY D H, BARKER D. Root-soil mechanics and interactions[J]. Riparian Vegetation and Fluvial Geomorphology, 2004: 113. |
| [13] | ODEN J T, RIPPERGER E A. Mechanics of elastic structures[M]. Hemisphere Pub. Corp., 1981. |
| [14] | WALDRON L J. The shear resistance of root-permeated homogeneous and stratified soil[J]. Soil Science Society of America Journal, 1977, 41(5): 843. DOI: 10.2136/sssaj1977.03615995004100050005x. |
| [15] | WRIGHT S G, DUNCAN J M. Soil strength and slope stability[M]. John Wiley & Sons, 2005. |
| [16] | BISHOP A W. The use of the slip circle in the stability analysis of slopes[J]. Geotechnique, 1955, 5(1): 7. DOI: 10.1680/geot.1955.5.1.7. |
| [17] | GREENWOOD J R. SLIP4EX–A program for routine slope stability analysis to include the effects of vegetation, reinforcement and hydrological changes[J]. Geotechnical & Geological Engineering, 2006, 24(3): 449. |
| [18] | GREENWOOD J R. Design approach for slope repairs and embankment widening [C]. Reinforced Embankments Symposium. 1989: 51. |
| [19] |
陈英, 杨华, 李伟, 等. 北京地区侧柏人工林标准木生长过程研究[J].
西北林学院学报, 2012, 27(5): 153.
CHEN Ying, YANG Hua, LI Wei, et al. Standard tree growth of Platycluadus orientalis plantation in Beijing[J]. Journal of Northwest Forestry University, 2012, 27(5): 153. |
| [20] |
陈英. 北京山区侧柏人工林生长模型及合理密度研究[D]. 北京林业大学, 2013: 31.
CHEN Ying. Research on growth model and stand reasonable density of Platycladus orientalis plantation in Beijing mountain area [D]. Beijing Forestry University, 2013:31. http://cdmd.cnki.com.cn/Article/CDMD-10022-1013213533.htm |
| [21] |
张春霞. 水土保持灌木——荆条的生物生态学特性初步研究[D]. 北京林业大学, 2007: 32.
ZHANG Chunxia. Study on bioecological characteristics of soil and water conservation shurb-Vitex negundo [D]. Beijing Forestry University, 2007:32. http://cdmd.cnki.com.cn/Article/CDMD-10022-2007076731.htm |
| [22] |
包昱峰, 高甲荣, 何明月, 等. 密云水库集水区荆条灌丛年龄结构研究[J].
林业资源管理, 2008(6): 67.
BAO Yufeng, GAO Jiarong, HE Mingyue, et al. Study on age structure of Vitex negundo community in Miyun reservoir watershed[J]. Forest Resources Management, 2008(6): 67. |
 2017, Vol. 15
2017, Vol. 15 
