大量的社会学量化研究是基于特定的统计模型展开的(Raftery,2001)。通过这些统计模型,研究者能够确认变量之间的概率关系,并依据统计推论(statistical inference)的基本原则将此关系由随机样本推广至研究总体。这一量化研究范式随着近十几年来各种因果推论模型(causal model)的开发与推广,展现出越来越强的影响力(Morgan,2014)。在这些因果推论模型中,“倾向值方法”(propensity score method)因其方便、易操作得到国内外很多社会学研究者的青睐(Rosenbaum and Rubin,1983;Rubin,1997;胡安宁,2012;Imbens and Rubin,2015)。
从本质上讲,基于统计模型估计出的变量间关系代表的是一种概率关系而非决定性关系,对于这一点,目前社会学量化研究还没有给予足够的重视。在诠释量化模型结果的时候,很多学者倾向于采用一种“决定论”(deterministic)式的态度。比如,对于线性模型E(Y)=βX,一般会将其诠释为:X变动一个单位会带来Y的期望值E(Y)变动β个单位。这种诠释虽不错误,却片面的关注点估计(point estimate)结果,忽视了系数β本身也是存在变异(variation)的情况。换句话说,β的“不确定性”(uncertainties)没有被考虑到。
按照统计学家德雷珀(Draper,1995)的定义,一个统计模型至少存在两种“不确定性”。第一种被称为“参数(parametric)的不确定性”。意指我们在利用样本数据估计整体(population)模型系数的时候,由于样本本身的随机抽样,最后研究者得到的只能是一个关于某系数的变动区间,而不可能是一个百分之百确定的数值。1第二种“不确定性”是“模型形式(model form)的不确定性”。这种“不确定性”是指在分析特定研究问题的时候,研究者通常会面临很多备选模型,从而带来模型拟合形式上的不确定。2这两种统计模型的“不确定性”在当下逐渐兴起的倾向值方法中尤为突出。通常而言,倾向值分析要求研究者通过一个广义线性模型(例如逻辑斯蒂回归)计算出每个被研究个体的倾向值得分(此模型被称为“倾向值模型”),然后再将此倾向值得分通过细分(sub-classification)、加权(weighting)、回归调整(regression adjustment)等方式纳入结果模型(outcome model)。3在这样一个分析过程中,一方面,我们基于样本得到的广义线性回归模型系数会随着不同的抽样样本而变化,这就决定了我们基于此模型计算出的每个个体的倾向值得分也必然是一个随机变量,从而间接体现系数的不确定性。另一方面,预测倾向值得分的时候,我们会考虑很多的混淆变量(confounding variables)。4但是,社会学研究者在通常情况下需要自主决定应当采用哪些混淆变量来预测倾向值(Western,1996)。所以,在大多数情况下,混淆变量的纳入依据颇具主观性。此时,不同的混淆变量组合就会就产生多个备选模型,从而带来模型形式的不确定性。在倾向值方法中,这两种不确定性同时存在。也即,每一个备选模型都会存在一个倾向值的变动区间。很明显,这两类模型不确定性的共同作用使得倾向值方法最终的分析结果存在不容忽视的不确定性问题。
1. 例如,当用样本收入均值估算总体收入均值时,我们无法知道总体收入均值的具体值,而只能估算出其可能取值的区间。这一区间的大小和我们希望达到的统计效率(efficiency)有关。
2. 一般而言,所有的备选模型构成了一个模型空间(model space)。
3. 结果模型是指因变量为我们需要解释的变量的模型。与结果模型相比,倾向值方法中还涉及估算倾向值的广义线性模型,后者的因变量为处理变量(treatment)。
4. 混淆变量是指同时与因变量和自变量相关的变量。由于混淆变量的存在,自变量和因变量之间的关系有可能是虚假的。
在此背景下,本研究的目标有三:第一,通过系统梳理目前统计学、经济学、政治学、社会学、心理学等不同学科对于统计模型不确定性问题的讨论,帮助量化社会学研究者对于模型不确定性问题有一个系统和清晰的了解与把握。第二,目前对于统计模型不确定性问题的探讨往往片面关注上述两种不确定中的一种。本文通过“蒙特卡洛模拟”与经验实例,展示这两类不确定性如何共同作用,以影响倾向值分析的结果。此外,通过综合运用“贝叶斯模型平均法”与“似然函数联合估计法”,本研究提供了一种同时处理两种不确定性问题的实践策略(有关这一部分的讨论下面有专门展开)。第三,基于对模型不确定性的理论探讨和经验分析,本文进一步论述了统计模型不确定性问题对如何提高社会科学量化结果的可信度和接受度,如何建立可复制的社会学量化研究,以及如何避免“统计至上主义”(statisticism)等重要议题所具有的启示。
二、 什么是统计模型的“不确定性”由于社会学量化研究中普遍使用线性模型,这部分对于统计模型不确定性的讨论主要依据线性模型展开。具体而言,一个线性模型可以表示为以下形式:
| $Y=f(X)+\varepsilon $ | (1) |
其中,Y是我们希望解释的因变量向量,X是用以解释Y的自变量与控制变量构成的矩阵,f(X)是衡量X与Y关系的一个函数,ε代表了一种随机扰动向量。在这个表达式中,我们关心的是f(X)。例如,在一般线性模型中,f(X)采用了一个最简单的线性组合的方式,即X与其系数向量β的乘积βX。而在其他广义线性模型中,f(X)可以是某种函数变换(例如逻辑斯蒂变换)。模型(1)很好地展示了上文所谈到的两种不确定性。其中,参数的不确定性取决于ε。我们通过假设随机扰动ε的分布来确定因变量Y的分布,由此,我们便可以建立估计系数的变异区间,即置信区间。模型的不确定性则来自f(·)。比如,在线性模型中通过引入变量的二次方、三次方等项,Y与X的关系可以呈现线形、抛物线形、波浪形等多种模型形式。
在模型(1)中,参数的不确定性一般通过标准误来表示。然而,对标准误的使用方式却因研究目的不同而有所差异。对大多数社会学经验研究而言,标准误主要起到假设检验的作用。通过观察0值是否在置信区间之内,研究者能够近似判断回归系数在总体层面的统计显著性。诚然,如果研究者仅仅关注某一特定变量的处理效果在总体中是否成立(即显著不为零),这样操作就是妥当的。但如果研究者的目的不是检验假设,而是希望通过统计模型来预测因变量的取值,标准误能够告诉研究者的就不再仅仅是统计上是否显著,而是基于此模型预测得到的因变量取值所可能体现出的变动区间。比如,假设我们估计一个简单线性回归模型E(y)=βx,其中回归系数β的点估计值为0.5,95%的置信区间为0.3—0.6。此时,如果用x去预测y的时候,在总体层面,我们基本可以认为y的期望值在0.3x和0.6x之间。换句话说,当我们用统计模型来做预测的时候,y的预测值由于参数β本身的不确定性而存在变化。这一点在倾向值方法中尤为明显,因为倾向值方法的第一步恰恰要求研究者通过统计模型来预测每一个研究对象的倾向值得分(Mc Candless et al.,2009;An,2010;Kaplan and Chen,2012,2014)。
与参数不确定性相比,模型形式的不确定性不再关注模型系数和预测值的变动,而是强调模型本身所具有的多种形式。模型形式的多样性在社会科学的不同学科中都很常见,因为很多研究者在分析数据的过程中往往会拟合多个统计模型。比如,在分析教育的经济回报时,研究者可能尝试放入不同的控制变量,从而得到不同的统计模型(例如,一个模型控制了居住地,而另一个模型没有考虑居住地)。尽管此类实践非常普遍,但最终报告统计分析结果的时候,读者能够看到的只是诸多备选模型中的一个,也即研究者在众多模型中有意和无意所选取的一个最优模型。此时,其他备选模型都被忽略了。这种对模型形式不确定的忽视会带来经济学家利摩尔(Leamer,1983)所谈到的“视界问题”(the horizon problem)。所谓视界,是指研究者在分析经验数据时所可能持有的潜在假设、倾向和偏好等。利摩尔认为,社会科学研究者应保证极宽的视界以承认和展示统计模型拟合过程中的复杂性和不确定性。否则,量化研究不可避免地会基于数据人为“定做”一个最希望得到的模型,结果便是,社会科学的研究者成为“数据的按摩师”,其量化研究结论也同时丧失了可信度。哈佛大学社会学系的威斯顿(Western,1996)也有过类似的呼吁。他指出,社会学的宏大理论对具体的量化研究而言是非常“模糊”(vague)的。这是因为社会学理论无法具体告诉经验研究者在一个特定的统计模型中应当放入哪些变量,需要采用何种模型形式,以及如何设定随机扰动项的分布状态。在这种情况下,社会学的经验研究必然面临模型形式的不确定性问题,而不同研究者有可能因为拟合了不同形式的模型而得到截然相反的结论。现有文献提供了很多例证来支持威斯顿的观点。例如,扬(Young,2009)重新分析了巴罗(Robert Barro)和麦克莱里(Rachel M. Mc Cleary)所做的宗教与经济关系的研究后发现,他们的模型拟合过程只要有细微的变动,其结论便不再成立。经济学领域内也有过类似的研究。马格纳斯与摩尔根(Magnus and Morgan,1999)曾邀请不同学者同时利用统计模型估算客户对某一产品的需求度。结果,不同学者之间因为模型的差异而得到不同的结论。这些研究都表明,社会科学量化研究的确存在比较普遍的模型形式不确定性问题。
正因为这一问题如此普遍,如何明确地展示研究者的多种备选模型,以及如何在备选模型中进行选择便成为社会科学量化研究的重要任务之一。在这方面,目前使用最广泛的方法是“贝叶斯模型平均法”(Bayesian Averaging Method)。这一方法发轫于统计学领域(Drake,1993;Raftery,1995;Hoeting et al.,1999;Zigler and Dominici,2014),并被经济学5(Sala-i-Martin,1997;Sala-i-Martin et al.,2004;Cohen-Cole et al.,2009;Durlauf et al.,2012;Moral-Benito,2015)、政治学(Bartels,1997;Ho et al.,2007;Montgomery and Nyhan,2010)和社会学(Western,1996)等学科逐渐接纳。下文对于模型形式不确定性的处理也以“贝叶斯模型平均法”为基础展开。
5. 在经济学领域中,被广泛使用的模型平均方法是萨拉伊马丁等(Sala-i-Martin,1997;Sala-i-Martin et al.,2004)的“经典估计贝叶斯平均法”(Bayesian Averaging of Classic Estimates)。在政治学领域中,“贝叶斯平均方法”最早被巴特尔斯(Bartels,1997)引入政治学量化分析。
三、 倾向值方法中的“不确定性”问题在这一部分,笔者着重讨论倾向值方法中的系数不确定性与模型形式不确定性问题。常规的倾向值方法一般关注的是一个二分处理变量X对于因变量Y的影响。由于存在混淆变量U,我们需要首先利用U去预测X=1的概率,也即倾向值得分。然后,通过某种数据处理手段(例如匹配),研究者可以近似地保证被研究个体的倾向值得分彼此接近,之后便可以采用一般的线性模型来分析X与Y的关系。这一分析思路可以用式(2)表示:
| $\left\{ \begin{matrix} p\left( X=1 \right)=\frac{exp\left( \gamma U \right)}{1+exp\left( \gamma U \right)} \\ Y=\beta X+\varepsilon ,基于匹配样本 \\ \end{matrix} \right.$ | (2) |
在式(2)中,我们用逻辑斯蒂回归计算倾向值得分p(X=1),其中混淆变量U的系数表示为γ。之后,假设这里采用了倾向值匹配的策略,我们可以基于匹配样本(matched sample)来拟合Y与X的简单线性回归模型。此时,X的系数β便是我们所关注的因果效应。在式(2)中,模型形式的不确定性主要发生在预测倾向值的逻辑斯蒂模型中。6这里我们假设备选模型有k个,分别表示为M1、M2、...、Mk,其中,每个备选模型的先验概率设为π(Mk)。在每个备选模型下,我们进一步设定,混淆变量的系数的先验概率为π(γ|Mk)。基于这些设定,我们便可以进行“贝叶斯模型平均法”的计算。这些设定的基本信息参见式(3):
| $\left\{ \begin{matrix} {{M}_{k}}\tilde{\ }\pi \left( {{M}_{k}} \right) \\ \gamma |{{M}_{k}}\tilde{\ }\pi (\gamma |{{M}_{k}}) \\ X|\gamma ,{{M}_{k}}\tilde{\ }逻辑斯蒂分布(\gamma U) \\ \end{matrix} \right.$ | (3) |
6. 理论上讲,如果结果模型中也纳入其他控制变量的话,结果模型中也会存在模型不确定性问题。为了计算方便,本文的结果模型设定为一个简单线性模型。由于简单线性模型只有一个自变量,因此,结果模型便不存在模型不确定性问题。
“贝叶斯模型平均法”的基本思路在于,通过上述的参数设定来计算特定的观测数据下每个备选模型的后验概率p(Mk|X)。这一后验概率可以近似的理解为特定备选模型就某一观测数据所具有的“解释力”。解释力高的模型对于数据的拟合效果更好,也就更应当保留。按照“贝叶斯定理”,模型k的后验概率可以表示为:
| $p({{M}_{k}}|X)=\frac{p(X|{{M}_{k}})\pi ({{M}_{k}})}{{{\sum }_{k}}p(X|{{M}_{k}})\pi ({{M}_{k}})}$ | (4) |
很明显,在式(4)中,我们需要计算的是p(X|Mk)。这一统计量可以从式(3)推导出来,即:
| $p(X|{{M}_{k}})=\int \int p(X|\gamma ,{{M}_{k}})\pi (\gamma |{{M}_{k}})d\gamma $ | (5) |
在得到每个备选模型的后验概率之后,我们可以按照后验概率的大小对这些备选模型进行排序。在实际操作中,备选模型的数量有很多。例如,如果混淆变量有n个,那么我们会有2n个备选模型。针对这一问题,统计学家马迪根和拉夫特瑞(Madigan and Raftery,1994)提出了“奥卡姆窗口”(Occam’s Window)原则进行备选模型数量的删减。这一原则可以表述为:与最有可能出现的模型相比,后验概率要小很多(例如小n倍,其中n由研究者确定)的模型被剔除;如果简化模型的后验概率更大,则复杂模型被剔除。基于这两个原则,研究者实际需要考察的备选模型数量会大大减少。例如,在拉夫特瑞(Raftery,1995)的一个研究中,按照“奥卡姆窗口”原则,备选模型数量从一开始的32 768个降到了14个。
综上所述,基于“贝叶斯模型平均法”,我们能够明确地展示研究者的多个备选模型及其后验概率。换句话说,研究过程中的模型形式的不确定性被直接量化出来了。研究者此时可以依据不同模型的后验概率决定选择哪个模型。
需要说明的是,已有的“贝叶斯平均方法”的使用最后会将多个备选模型的系数估计值综合起来得到一个最终的估计值δ。例如,假设每个备选模型都有一个我们关心的系数δMk,那么,最后综合起来的系数就是不同备选模型的加权平均数,其中权重便是不同备选模型的后验概率p(Mk|X),亦即δ=∑p(Mk|X)×δMk。在本研究中,我们不采用这种加权平均的综合,而是利用“贝叶斯模型平均法”的分析过程产生最优的几个备选模型,然后针对每个备选模型进行分析。换句话说,我们没有对备选模型进行“平均”。
另外一点需要说明的是,模型的不确定性问题本质上关心的是应当纳入哪些变量来估计倾向值。对于这一问题,一个可能的质疑是,倾向值估计本身就代表了一种降维操作。无论有多少混淆变量,最后都“总结”成为一个数值,即倾向值。那么,又何必对这些混淆变量进行“挑选”呢?这一问题的答案在于,如果混淆变量过多,其彼此之间会产生虚假关联(Fan et al.,2014),此时,未经挑选的模型所估计出来的倾向值可能会有很高的均方误(mean square error),从而带来倾向值估计上的问题。正因为如此,一般而言,对于存在大量混淆变量的情形,我们仍需要采用某种手段确定哪些混淆变量值得放进倾向值模型,这也是模型选择的题中之意。
在考察了模型形式的不确定性之后,我们接下来讨论如何处理系数的不确定性。在倾向值方法中,系数不确定性涉及两个模型:预测倾向值得分的倾向值模型与计算处理效应的结果模型。这是因为在表达式(2)中,我们估计的γ和β都有各自的置信区间,因此,参数的不确定性需要将这两个系数的置信区间同时考虑在内。这一分析过程主要是通过对倾向值模型和结果模型的似然方程进行联合估计(joint estimation)实现的。顾名思义,联合估计要求我们同时估计γ和β。这就要求我们写出包含γ和β的似然方程,并将其合并起来。假设决定处理效应的过程与决定结果变量的过程独立,预测倾向值的逻辑斯蒂回归模型的似然方程就可以表示为:
| ${{L}_{X}}={{\prod }^{n}}_{i=1}{{\left[ \frac{exp(\gamma U)}{1+exp(\gamma U)} \right]}^{{{X}_{i}}}}{{\left[ 1-\frac{exp(\gamma U)}{1+exp(\gamma U)} \right]}^{1-{{X}_{i}}}}$ | (6) |
其中,X是一个二分的处理变量,其他参数的含义参见上文。同理,我们也能够写出计算处理效应的结果模型的似然方程。如果Y是一个连续型变量,我们可以假设其服从正态分布。如果其为二分型变量,我们假设Y服从“伯努利分布”。此时,似然方程可以写成:
| ${{L}_{Y}}\left\{ \begin{matrix} {{\prod }^{n}}_{i=1}\frac{1}{\sigma \sqrt{2\pi }}{{e}^{-\frac{{{({{Y}_{i}}-\beta {{X}_{i}})}^{2}}}{2{{\sigma }^{2}}}}},如果Y\tilde{\ }N\left( \beta X,{{\sigma }^{2}} \right) \\ {{\prod }^{n}}_{i=1}{{\left[ \frac{exp(\gamma U)}{1+exp(\gamma U)} \right]}^{{{Y}_{i}}}}1-{{\left[ \frac{exp(\gamma U)}{1+exp(\gamma U)} \right]}^{1-{{Y}_{i}}}}, \\ 如果Y\tilde{\ }Bernoulli\left( \frac{exp(\beta X)}{1+exp(\beta X)} \right) \\ \end{matrix} \right.$ | (7) |
由于我们之前已经假设了两个似然方程彼此独立,因此,联合似然方程二者的乘积为:
| $L={{L}_{X}}\times {{L}_{Y}}$ | (8) |
联合估计之所以能够处理系数估计的不确定性,是因为在联合估计过程中,γ是作为一个待估计的“变量”进入结果模型的似然方程的。反之,在结果模型中,我们关心的系数β对于倾向值模型而言也是一个待估计的变动参数。此外,联合估计的另外一个优势在于,研究者在写出公式(8)的表达式之后,可以很轻易地利用“贝叶斯估计”的手段,通过设定不同参数的先验概率来计算后验概率。相比于联合估计的方法,常规的独立估计只能单独考虑单一模型中的参数不确定性,而无法关照其他模型中的参数不确定性。例如,在传统的独立估计过程中,研究者首先单独估计公式(6),从而计算出γ的估计值。然后利用来计算每个个体的倾向值得分。之后,将估计出的倾向值得分代入结果模型,再单独估计公式(7)。但问题在于,在单独估计公式(7)时,已经不被看做“变量”,而是一个确定的数据点,也就是说,其在公式(6)估计过程中所产生的不确定性在单独估计公式(7)时被忽视了。反之,如果我们利用公式(8)来计算β的置信区间,γ的不确定性就已经被考虑在内,反之亦然。也就是说,两个模型的系数不确定性同时被考虑。此时,我们计算得到的处理效果β除了自身的系数不确定性之外,也综合了γ的系数不确定性。
需要指出的一点是,我们通常会认为,当同时考虑了两个统计量(β和γ)的变动时,最后的因果效果的标准误会出现膨胀。这个理解实际上并不准确。当采用如式(8)所示的方法去联合估计倾向值模型与结果模型的时候,我们最后得到的标准误有可能会变小。这一点在最近的很多研究中都得到了支持。例如,安卫华(2010)考察了联合似然方程,并通过倾向值方程和倾向值匹配的方法估计了平均因果效果。与常规方法(即将倾向值看做固定的值而非随机变量)相比,同时估计Lx和Ly得到的结果展现出更小的标准误。这一点在教育学的研究中也得到了支持(Kaplan and Chen,2012)。此外,从“频率学派”的角度出发,经济学家阿巴迪与伊姆本斯(Abadie and Imbens,2016)也通过公式推导指出,考虑倾向值估计中γ的不确定性后,平均因果效果β的方差应当向下调整。也就是说,我们会得到更小的标准误。7
7. 但是阿巴迪和伊姆本斯的方法有可能产生负值的标准误,因此在实际应用中有一定的局限性。
四、 已有研究及本文的贡献倾向值方法中的不确定性问题长期以来并没有得到学界的重视,直到近几年“贝叶斯方法”与倾向值分析过程的结合才逐渐使这一研究议题进入方法论研究者的视野。在这一领域,比较早的探索是麦坎德勒斯及其同事(Mc Candless et al.,2009)的一篇研究,他们明确提出,在倾向值分析过程中,所估计的倾向值本身的不确定性被忽视了。为了解决这一问题,他们采用了贝叶斯联合估计的方法。与之相关的另外一篇研究来自安卫华(An,2010),他同样通过引入贝叶斯联合估计来解决倾向值估计值的不确定性问题。与麦坎德勒斯等(其偏重于分析倾向值细分)不同,安卫华的研究偏重于分析倾向值不确定性对倾向值回归以及倾向值匹配的影响。此外,这个研究还与阿巴迪和伊姆本斯(Abadie and Imbens,2016)对话,试图解决后者在使用估计的倾向值进行结果模型方差调整时出现的负方差问题。最后,教育心理学家卡普兰与其同事(Kaplan and Chen,2012)也有专文讨论如何通过贝叶斯联合估计的手段处理倾向值细分、加权和最优全匹配(optimal full matching)时出现的不确定性问题。
虽然上述的这些探索极大地推动了学界对倾向值不确定性的研究,但依照上文所做的分类,这些研究所关注的不确定性属于系数的不确定性。相比较而言,模型的不确定性并没有得到足够重视。在综合处理系数的不确定性和模型的不确定性方面,现有的研究还很少。比较有代表性的有两个研究。一个是卡普兰及其合作者(Kaplan and Chen,2014)利用“贝叶斯模型平均方法”,基于每一个备选模型计算其对应的倾向值的后验分布,按照每个模型的后验分布对多个倾向值的后验分布进行加权平均,以此计算最终的倾向值分布。8依据此倾向值分布,卡普兰等利用倾向值分组、加权等手段计算因果效果。另外一个研究来自齐格勒和多米尼茨(Zigler and Dominici,2014),他们将模型选择过程与系数估计的不确定性问题统一整合进贝叶斯分析框架。具体而言,他们在倾向值模型和结果模型的相关系数前都加上一个新的二分系数α。9由于α在0和1之间的变动决定了哪些变量需要纳入模型,α的分布本身代表了模型的不确定性。基于这种设计,齐格勒和多米尼茨利用联合估计过程处理了模型形式不确定性问题。
8. 例如,假设有k个模型,每个模型的后验分布为p(Mk|X)。对应于每个模型,倾向值的后验分布为pk。那么,最终的倾向值分布为p=∑p(Mk|X)×pk。
9. 例如,一个模型中某变量X的系数表示为αβX。其中,β代表X的实质效果,α则表明是否需要将变量X纳入模型。
相比于仅关注参数不确定性的研究,本文的突破点在于同时考虑到参数的不确定性与模型的不确定性。在这一点上,本文的基本取向是和卡普兰、齐格勒等人的研究一致的。然而,和卡普兰等(Kaplan and Chen,2014)的研究不同,我们没有对倾向值的后验分布进行加权平均,而是针对每个可能的模型,分别利用联合似然函数做因果关系估计,这样会更加直接展现基于模型差异所体现出的异质性。齐格勒和多米尼茨的分析策略中的一个局限在于要求对α与因果效果的联合后验概率分布进行估计。如果用Δ来指代因果关系的话,这个联合后验概率分布就表示为p(α,Δ|经验数据)。不难看出,这一联合后验分布的估计是很困难的。为此,研究者不得不采用更为复杂的“马尔科夫链-蒙特卡洛算法”(Markov Chain Monte Carlo,MCMC)(例如,齐格勒和多米尼茨所采用的MC3以及SSVS算法)。本文绕开了复杂的算法设计,首先采用“贝叶斯模型平均法”列举研究者所可能获得的候选模型(模型的不确定性问题)。由于这种候选模型数量很多,我们仅列出最优的五个模型。之后,基于每个备选模型,我们通过联合估计倾向值模型与结果模型来估计因果关系(系数的不确定性问题)。换句话说,我们没有直接估计α与Δ的联合后验分布p(α,Δ|经验数据),而是将其分解为:p(α,Δ|经验数据)= p(Δ|α,经验数据)×p(α|经验数据),继而分别考察p(Δ|α,经验数据)和p(α|经验数据)。
五、 基于“蒙特卡洛模拟”的示例在这一部分,笔者利用“蒙特卡洛模拟”(Monte Carlo Simulation)方法,具体展示了在进行倾向值分析的时候所存在的不同类型的模型不确定性问题。需要说明的是,在联合估计过程中,我们很难通过常规数学方法直接计算出估计值及其置信区间,因此,依照前人研究,笔者采用了“马尔科夫链-蒙特卡洛算法”以迭代计算出因果效果的边际后验分布(marginal posterior distribution)。为了最大限度地模拟现实研究环境中的变量类型,我们在设置模拟数据的时候建立了18个服从不同分布类型的自变量,分别命名为x1 到x18。其中x1 到x6服从正态分布,x7到x12服从“伯努利分布”,x13到x18服从“泊松分布”。其具体的参数值如下:
x1~N(0,1)
x2~N(0,2)
x3~N(2,1)
x4~N(2,2)
x5~N(1,0.8)
x6~N(-1,3)
x7,…,x12~Bo(κ),其中κ是一个介于0.1 到0.9之间的随机数。
x13~Poisson(λ=0.1)
x14~Poisson(λ=0.5)
x15~Poisson(λ=1)
x16~Poisson(λ=3)
x17~Poisson(λ=5)
x18~Poisson(λ=10)
基于以上设定,我们产生了一个样本量为2 000的模拟数据。由于x1到x18都是用来估算倾向值的混淆变量,我们需要进一步设定倾向值与处理变量的值。这里的倾向值通过逻辑斯蒂函数生成,其中每个混淆变量的系数都服从介于-0.1 到0.1 之间的均匀分布。假设所有混淆变量构成了一个2 000×8 的矩阵X,而系数β则是一个18×1的向量,则倾向值等于$\frac{exp(\beta X)}{1+exp(\beta X)}$。由于倾向值代表了个体接受处理变量影响的概率,且处理变量是二分变量,因此,处理变量向量T服从以$\frac{exp(\beta X)}{1+exp(\beta X)}$为发生概率的“伯努利分布”。基于这些信息,T也可以被模拟出来。最后,我们生成因变量Y(这里的Y是2 000×1的向量)。严格来讲,所有混淆变量X和处理变量T都会对Y产生影响,所以我们在这里将Y写成X和T的线性函数。将T与X合并,得到一个2 000×19的矩阵Z。设这一矩阵的19×1系数向量为γ,则Y=γZ。在不失一般性的前提下,可以假设γ服从均匀分布,且取值范围在-1到1之间。在模拟出γ之后,我们就能够得到Y的取值。至此,我们的模拟数据已经完成,其中包括因变量Y、自变量T、倾向值得分和18个混淆变量。
基于上述的模拟数据,我们首先利用“贝叶斯模型平均法”考察模型形式的不确定性。通过“贝叶斯模型平均法”和“奥卡姆窗口”原则,我们得到12个候选模型。在这些模型中,按照贝叶斯因子(Bayes Factor)的数值排序,最后留下排在前五位的模型。10这些模型的累计后验概率达到了78%,说明通过这5个模型基本能够涵盖大部分的数据信息。这5个模型的具体信息参见表 1。
| 表 1 基于贝叶斯平均法的模型选择(模拟数据) |
10. 贝叶斯模型选择过程通常依据贝叶斯因子进行备选模型的排序。具体而言,参见公式(4),我们针对两个备选模型k和t,有$\frac{p({{M}_{k}}|X)}{p({{M}_{t}}\left| \left. X \right) \right.}=\frac{p(\left. X \right|{{M}_{k}})}{p(X|{{M}_{t}})}\times \frac{p({{M}_{k}})}{p({{M}_{t}})}$,其中,贝叶斯因子=$\frac{p(\left. X \right|{{M}_{k}})}{p(X|{{M}_{t}})}$,而$\frac{p(\left. X \right|{{M}_{k}})}{p(X|{{M}_{t}})}$代表不同模型的先验概率比。通常而言,我们在先验概率上不会偏向于特定模型,因此$\frac{p(\left. X \right|{{M}_{k}})}{p(X|{{M}_{t}})}$=1。此时,贝叶斯因子也就是$\frac{p({{M}_{k}}|X)}{p({{M}_{t}}\left| \left. X \right) \right.}$,即模型后验概率比。很明显,基于特定的基准模型,贝叶斯因子值越大的模型对于数据的拟合效果越好。故而我们可以采用贝叶斯因子对备选模型排序。在实际操作用,贝叶斯因子近似等于BIC。
表 1的第一列是我们设定的18个混淆变量和截距项。这些混淆变量被用来估计倾向值得分。第二列的信息是在所有备选模型中,每一个变量(包括截距)被纳入某一模型进行倾向值估算的概率。如果概率为0,说明这个变量在所有备选模型中都不会被考虑到。同理,如果概率为1,则说明这个混淆变量非常重要,故而所有的备选模型都会考虑到它。例如,x2的不为0概率是1,说明所有的候选模型都会纳入x2。与之相比,x3几乎不会被任何模型考虑,而x1只被纳入不到6个候选模型(一共12个备选模型,120×0.46=5.52)。从某种意义上说,表 1第二列告诉我们的是,不同的混淆变量在预测倾向值得分的时候具有不同程度的“重要性”或者“相关性”。从第三列开始,表 1列举了不同的备选模型。如上所述,这里我们只保留了5个备选模型。其中,模型1是基于现有数据最好的模型,其后验概率为0.18。在模型1中,并非所有的混淆变量都被考虑进来。恰恰相反,除了截距之外,模型1仅仅纳入3个混淆变量(x2、x6和x15)。同理,模型2纳入4个变量(x1、x2、x6和x15),其后验概率为0.16,以此类推。按照表 1所示的结果,我们实际上有5种不同的备选模型来预测倾向值得分,这就是所谓的模型形式的不确定性问题。
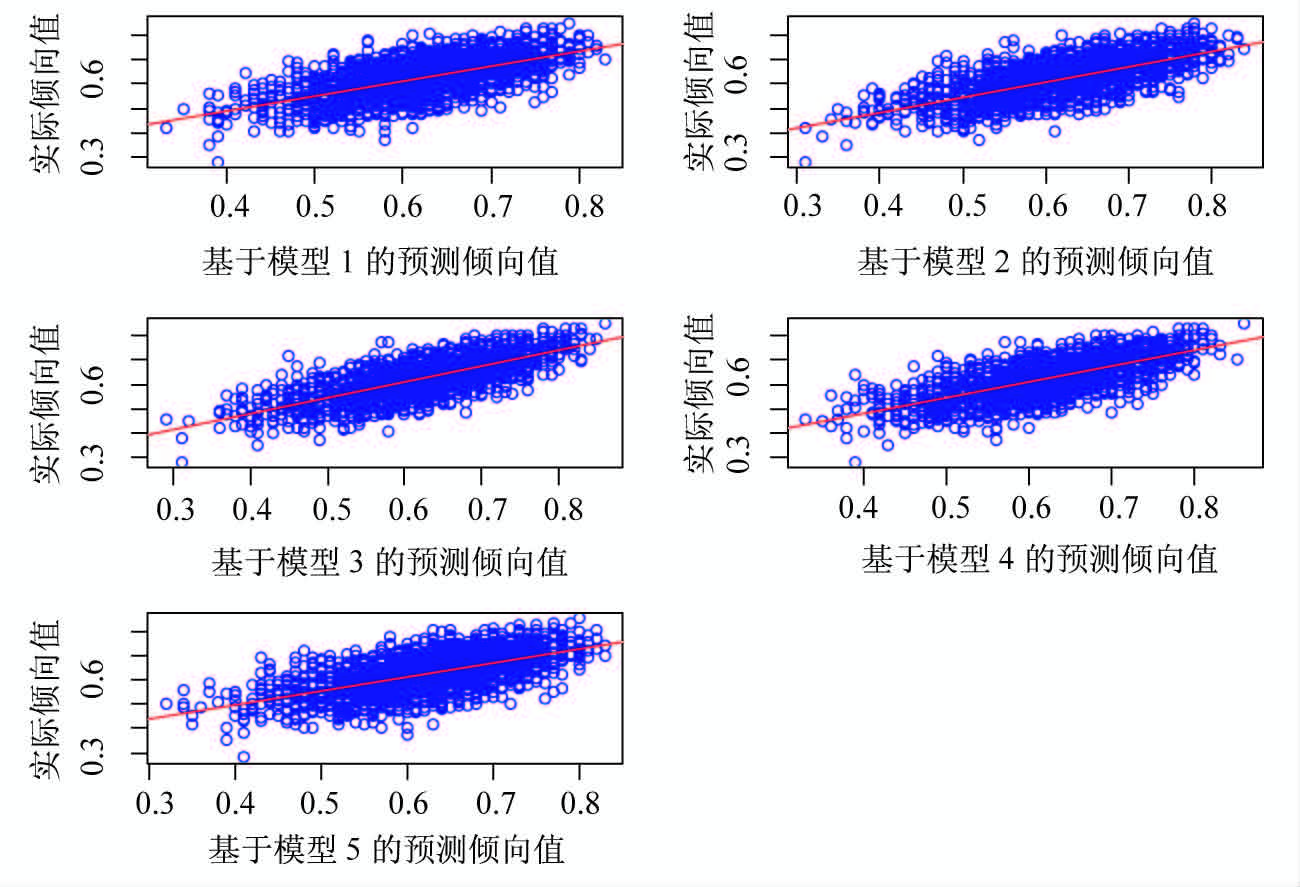
“蒙特卡洛模拟”的一个好处是,我们能够预先知道真正的倾向值是多少,并用它来和不同的模型所预测的倾向值比较(这方面的信息参见表 2)。在表 2中,我们计算了实际倾向值得分与基于不同模型所估计出的倾向值得分之间的相关系数矩阵。可以发现,虽然基于不同的模型所估计出的倾向值得分总是和实际的倾向值得分正相关,但这种相关性并不是非常强。例如,我们用最好的模型估计的倾向值得分与实际倾向值得分之间的相关系数为0.64。最高的相关系数来自模型3估计出的倾向值得分(相关系数=0.74)。因此,无论我们采用什么模型,最后得到的只能是实际倾向值得分的一个趋近值。此外,不同模型得出的倾向值得分和实际倾向值得分之间的相关性也各有高低,这再一次凸显了模型形式不确定性对于实质研究结论的可能影响。为了更好地展现这一点,我们进一步绘制了实际倾向值得分和模型预测的倾向值得分之间的散点图(见图 1)。通过图 1可以发现,无论采用何种模型,估计出的倾向值得分和实际的倾向值得分相比都表现出一定程度的变异性(variation),也即不确定性(并非所有的点都分布在45度斜率的直线上)。
| 表 2 不同模型估计的倾向值的相关系数矩阵 |
|
图 1 不同模型估计的倾向值与实际倾向值的相关分析 |
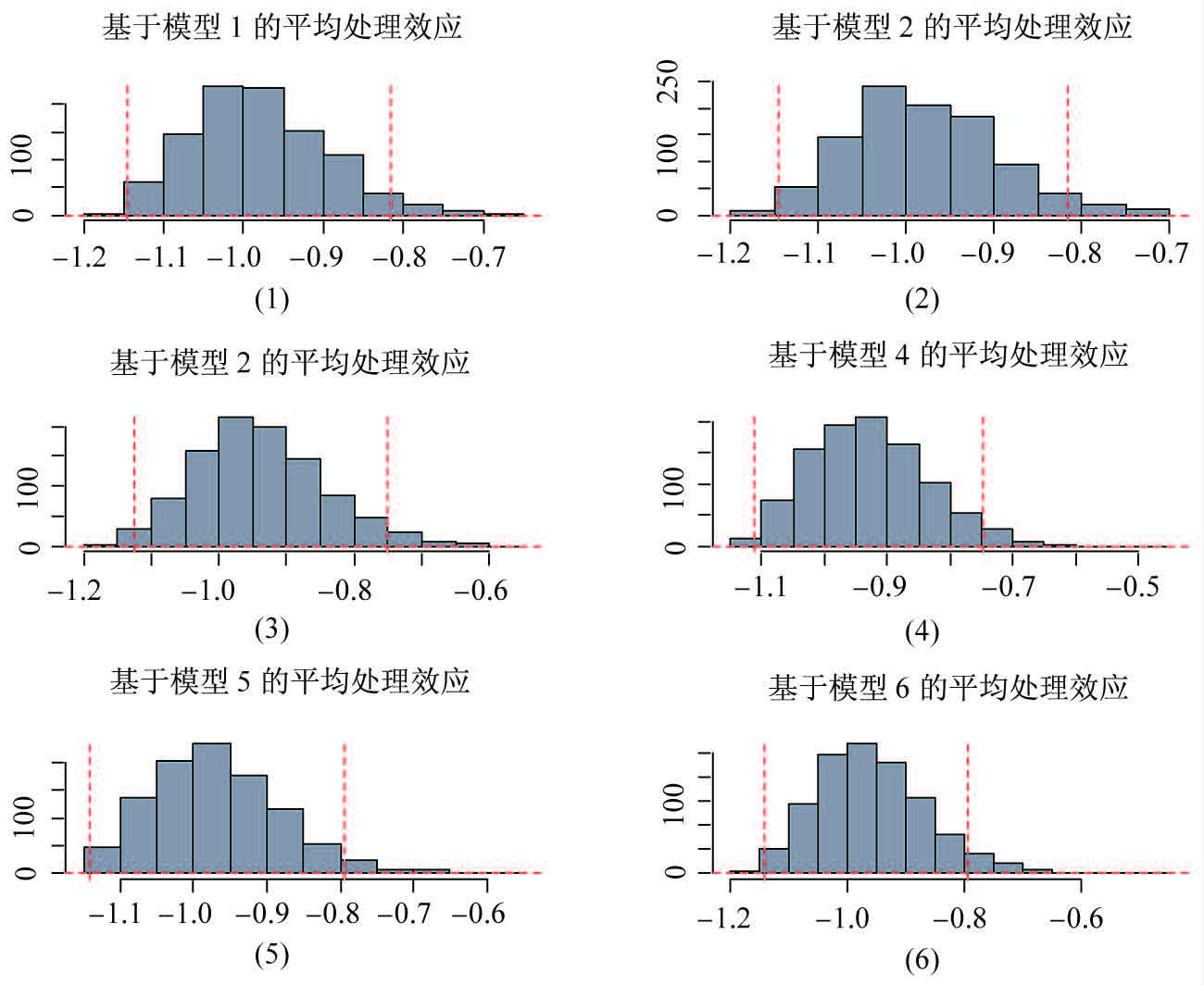
在展示了模型形式的不确定性之后,我们进一步考察参数的不确定性问题。针对上文所展示的5个备选模型,我们通过MCMC的方法联合估计了倾向值模型和结果模型,由此将倾向值得分估计过程中的不确定性整合进因果效应的估计。11针对每个备选模型的因果效应分布如图 2所示。在每一个子图中,95%的置信区间用虚线标识出来。同时,综合5个模型的信息,我们在图 2的(6)中报告了综合考虑所有备选模型后估算出的因果效果。为了更加直观地展现MCMC模型和常规模型的区别,我们将5个候选模型估计的因果效果与相应的常规模型估计得因果效果进行了对比(图 3)。如上文所述,这里的常规模型是指将倾向值作为固定值而非随机变量处理的模型。
|
图 2 不同模型的平均处理效应估计以及综合所有模型的平均处理效应估计 |
|
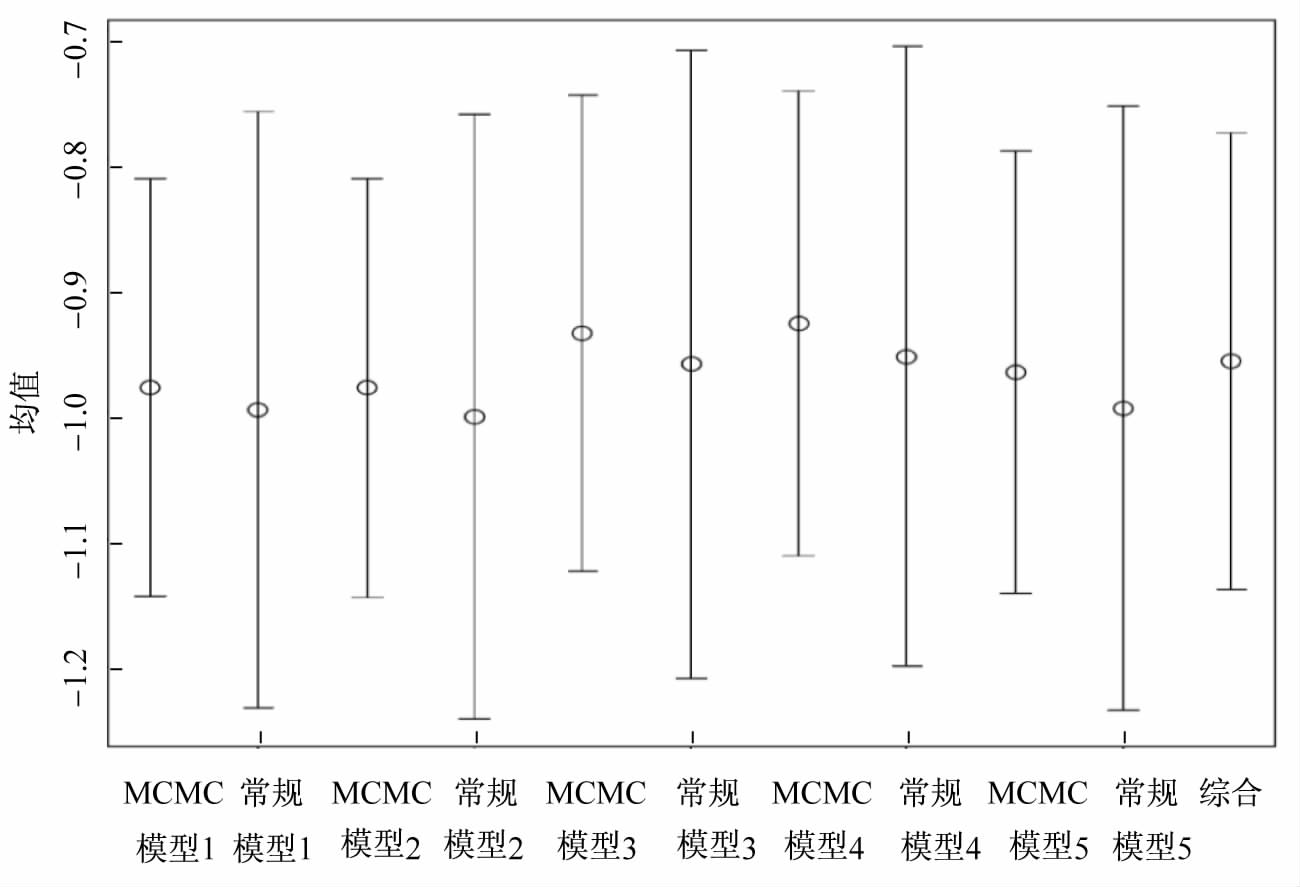
图 3 基于MCMC的模型与常规模型的处理效应比较 |
11. 如上文所述,由于联合似然函数[公式(8)]中的多个参数通常而言难以通过常规的数学方法进行估计,一般而言,研究者会对这些参数设定先验分布,然后通过MCMC来计算其后验概率分布。虽然MCMC也可以看作是一种贝叶斯估计方法,但MCMC与贝叶斯(转下页)(接上页)平均的分析过程是不一样的。在这里,MCMC是一种参数估计的手段,主要用于估计联合似然函数中特定变量系数的后验分布。但是“贝叶斯平均法”是将不同的模型作为变量进行估计,其目的是为了获得模型的后验分布。正因为如此,“贝叶斯平均法”被用来处理模型的不确定性问题,而通过MCMC来对联合似然函数进行估计则被用来处理系数的不确定性。从某种意义上说,齐格勒与多米尼茨将贝叶斯模型平均与MCMC方法进行系数估计整合进了一套MCMC的估计过程,他们的方法或可称之为“完全MCMC”(full MCMC)。但正如文中所述,其估计过程更为复杂。
通过图 3我们可以发现,几乎所有的MCMC模型的置信区间都要小于常规模型的置信区间。也就是说,当同时考虑到倾向值估计的不确定性和因果效果估计的不确定性时,我们得到的结果更加具有统计效率(efficiency),也更加精确。12这一特点对于经验社会科学研究而言无疑是非常重要的。把所有5个备选模型的置信区间综合起来,我们能够得到了一个如图 3最右边线段所示的置信区间,13可以发现,即使是综合多个模型后得到的置信区间也要比所有的常规模型置信区间小。这些发现再一次证明了安卫华、阿巴迪和伊姆本斯等人之前的研究结论。
12. 需要说明的是,这里MCMC模型仅涉及处理系数的不确定性。因为针对每个备选模型都进行了MCMC估计,因此模型的不确定性尚未被控制。
13. 这里的综合过程是以每个模型的后验概率为权重进行的加权平均。
通过“蒙特卡洛模拟”的方法,我们展示了研究者在拟合统计模型时所可能面对的多个备选模型。针对特定的数据,这些备选模型具有不同的拟合优度。针对每一个备选模型,我们所估计的倾向值得分具有一定的变动性。之后,通过MCMC的计算过程,我们进一步发现,当我们将倾向值估计过程的不确定性考虑进来以后,平均因果效果的置信区间反而相比于常规的估计过程更小。那么,这一特点在实际的经验数据中是否也能够成立呢?下面的分析将对这一问题进行探索。
六、 基于经验数据的示例这里的经验分析利用“中国综合社会调查”2010年的数据,讨论的问题是高等教育是否对个人的自评健康产生积极的促进效果(胡安宁,2014;Hu,2014)。由于高等教育的接受过程本身涉及样本的选择性,因此,在分析教育和健康关系的时候,需要通过特定的统计手段对个体接受高等教育的概率差异进行控制。但是,究竟哪些因素会影响个体进入大学的概率呢?这一问题很难通过现有理论进行回答。经济学家通常会将父母的教育水平作为工具变量来分析子女教育成就的社会效果(Heckman and Li,2004)。除了父母的教育成就之外,父母还会体现出其他的社会特征,例如职业、政治身份和单位性质。那么,我们在估计子女进大学概率的时候有没有必要在考虑父母教育水平之外还考虑这些社会特征呢?这一问题并没有固定的答案。通常,研究者可能根据自身的研究习惯和理论取向对混淆变量进行取舍,从而引起模型形式的不确定性问题。
在这里,我们首先拟合一个模型,利用性别、民族和父母的教育水平来计算倾向值得分。之后,我们采用“贝叶斯平均法”来考察模型形式的不确定性(参见表 3)。通过表 3可以发现,除了父母的教育水平之外,父母的很多其他社会特征也会对子女的教育成就产生影响,例如,父母的单位性质和父亲的政治身份,这些变量的不为零概率都达到了1。相比较而言,母亲的政治身份对于子女教育成就的影响不是很大,民族变量亦如此。基于这些变量,贝叶斯平均过程返回了3个备选模型,其中备选模型1具有极高的后验概率(0.81)。与模型1相比,模型2的后验概率为0.14,而模型3的后验概率仅为0.05。综合这些信息,我们应当采用模型1所指示的混淆变量来估计倾向值得分。
| 表 3 基于贝叶斯平均的模型选择(经验数据) |
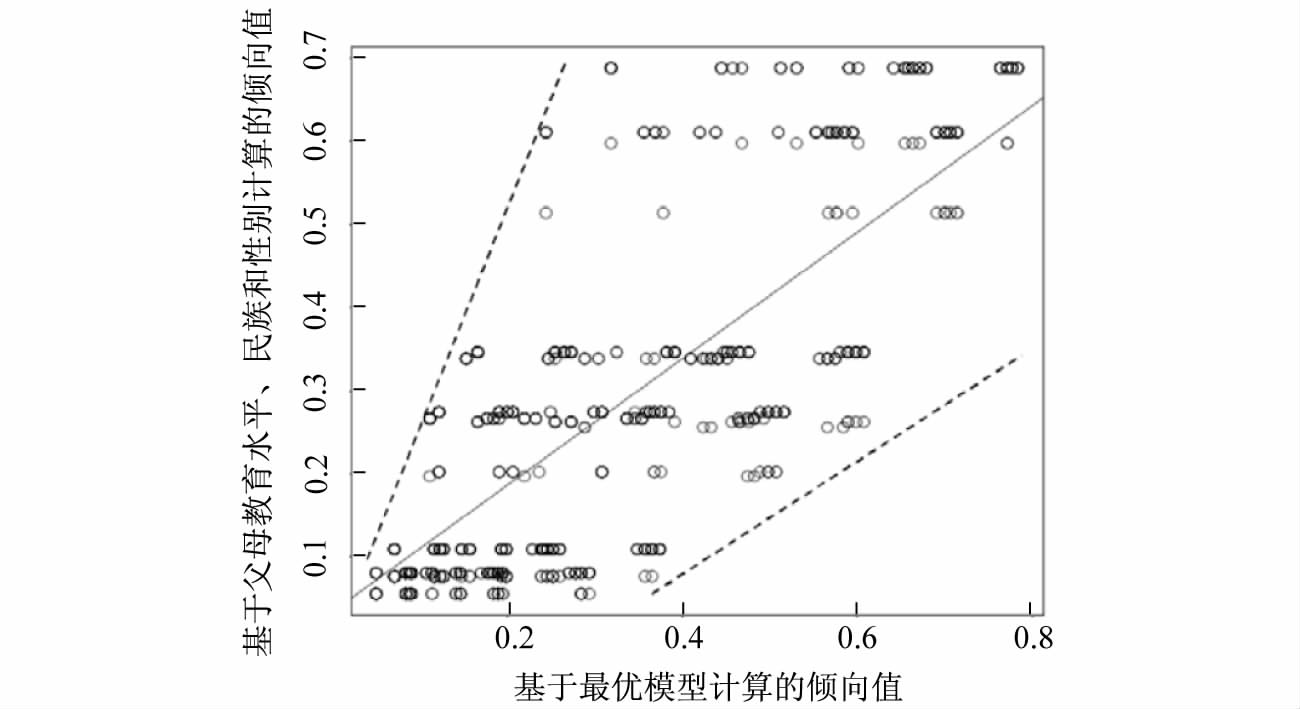
当我们按照模型1中所指示的混淆变量来计算倾向值得分的时候,所得到的结果和上述基于性别、民族和父母教育水平的模型所得到的倾向值得分有何差异呢?为了回答这一问题,我们描绘了二者之间的散点图(见图 4),可以发现,基本上二者之间还是呈现正向关系的。但这两个模型估计出的倾向值并不是完全一致(没有均匀分布于45度线上)。相反,我们可以看到,数据点的分布状况具有比较大的离散性(其变动范围如虚线所示)。这在一定程度上说明,这两种模型的估算所得到的倾向值具有一定程度的差异性。
|
图 4 基于最优模型和实践模型计算出的倾向值得分的散点图 |
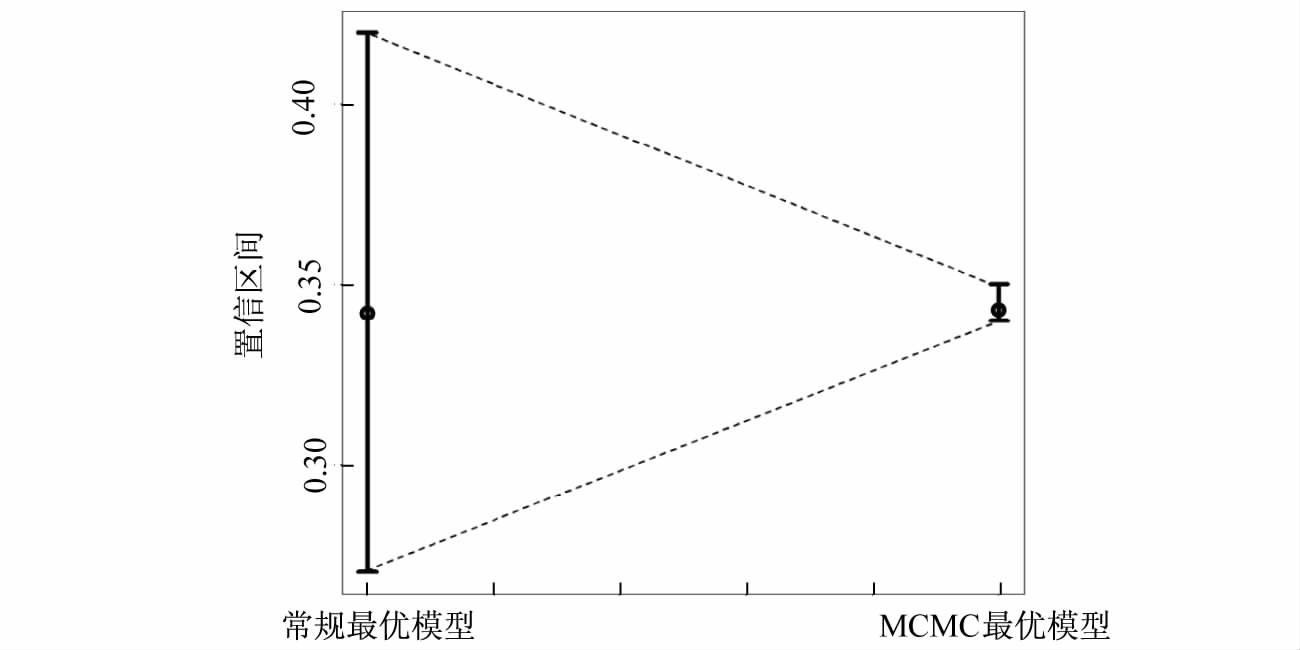
下面,我们按照“贝叶斯平均法”所指示的最优模型(模型1)重新估计倾向值得分。和上面一样,我们拟合了两个模型,一个模型是将倾向值看做固定的值(称为常规最优模型),另一个是采用MCMC的方法进行联合估计以考虑倾向值估计过程中的不确定性(称为“MCMC最优模型”)。这里的目的是希望比较两个模型的置信区间。相关的结果参见图 5。
|
图 5 因果效果的置信区间比较 |
如图 5所示,我们在考虑了倾向值估计的不确定性之后,所估计得到的平均因果效应的置信区间被极大地缩小了。也就是说,我们估计的高等教育对于个人自评健康的影响效应更加精确。此外,需要说明是,无论是常规的最优模型,还是MCMC的最优模型,点估计的值是一致的(在一条水平线上)。
我们通过以上一个具体的经验实例,展示了如何利用“贝叶斯平均法”进行模型的选择。基于最优模型,我们再一次证实,在综合考虑倾向值估计过程中的不确定性之后,平均因果效果的估计展示出更小的置信区间。也就是说,通过MCMC过程估计得到的因果效果具有更高的统计效率。
七、 结论与讨论当代社会学经验研究越来越多地依赖统计模型。在针对特定数据拟合统计模型的时候,研究者会遇到模型形式的不确定性与模型系数的不确定性问题。这些不确定性问题在已有的社会学方法论研究中并没有被足够重视。本文系统梳理和讨论了这两类不确定性问题在倾向值方法中的表现及其处理方法。之后,通过“蒙特卡洛模拟”与经验调查数据分析,展示了量化研究过程中研究者所可能面对的多个备选模型,以及如何通过“贝叶斯平均法”进行备选模型的展示与选择。之后,在利用似然方程联合估计来分析系数不确定性的时候,本文的研究亦表明,在考虑倾向值估计过程的不确定性之后,结果模型中对于因果关系的估计呈现出更小的置信区间和更高的统计效率。
统计模型的不确定性问题对于当下社会学的量化研究具有重要的启示价值。首先,正视统计模型的不确定性对于提高社会学量化研究的可信度具有积极的作用。社会学家瓦茨(Watts,2015)最近撰文指出,长期以来,社会学经验研究结果总是服从于“可理解性”(understandability)原则。也就是说,社会学家总是试图让自己的研究结果服从于人们的常识判断,让人们能够“理解”,觉得“有道理”。如果一项研究的结果和大家的常识相左(例如,发现读书越多,收入越低),那么研究者往往就会怀疑并修正自己的模型设定(例如增加或者减少控制变量、增加交互项等等),直至最终满足“可理解性”原则(例如,修正后的结论变成了读书越多,收入越多)。不难发现,如果社会学者总是遵从瓦茨所批评的“可理解性”原则,那么量化研究便会成为利摩尔眼中的“数据按摩”,其结论便会成为常识的复制。而常识本身的个体性与不稳定性则进一步决定了量化研究结论具有很低的可信度或者很小的适用范围。因此,为了提高社会学经验研究的可信度与影响力,我们需要做的是避免屈从于常识判断来选择统计模型,而应付诸于正式的模型选择过程。此时,最后所报告的模型不再是研究者所主观认可的“最优模型”,而是数据所反映的“最优模型”,其模型系数无论和常识一致与否,都是最能反映当下数据信息的真正“最优”结果。
其次,统计模型的不确定性也对正在兴起的“可复制性研究”具有启示作用(陈云松、吴晓刚,2012)。所谓“可复制性研究”,是指某个研究者的分析能够为其他研究者所重复以交叉验证其分析结果。到目前为止,可复制性研究一般要求研究者向学界同行提供分析代码,以便于其他研究者可以基于这一代码进行重复分析。但是,从统计模型的不确定性角度出发,仅仅是提供研究者所使用的代码或许并不能够完全涵盖可复制研究的全部内涵,这是因为,研究者所提供的代码本身已经是研究者的假设、偏好等“视界”(Leamer,1983)的产品。因此,一个更为全面的可复制研究不仅需要研究者提供某个模型的复制过程和分析代码,还要要求研究者报告自己研究过程中的基本“视界”和模型选择机制。只有这样,其他研究同行才能够完全了解一项研究的全部过程。从这个意义上讲,本文所介绍的分析统计模型形式与系数不确定性的方法为经验研究者提供了一种报告研究“视界”的手段。
最后,统计模型的不确定性问题再一次提醒社会学经验研究者,应当避免对统计模型的过度依赖和统计结果的过分解读。这在谢宇和吴晓刚(Xie and Wu,2005)那里被称为“统计主义”。从本质上讲,任何统计模型都是研究者设定的,因此,统计模型的拟合过程本质上反映的是统计模型对于社会模式的简化与纷繁复杂的现实经验数据之间的契合程度。严格来讲,任何统计模型都不可避免地具有主观性。从这个角度出发,本文所介绍的统计模型不确定性问题及其处理方式代表了一种正式的、量化的手段来将这种统计分析中的主观性和统计模型的潜在变异展现出来。对于社会学研究者来讲,无论是解读别人的统计分析,还是自己从事量化研究,都不应当将统计模型“预设”成为对现实世界的“真实”描述。更为恰当的做法或许应当是采取一种相对保守的态度,敢于承认统计模型的不确定性,并尽量通过正式的研究手段告诉其他研究者自己在面对模型不确定性时所做的选择。
当然,这里需要说明的是,统计模型虽然存在不确定性问题,但这并不构成为对量化研究范式的质疑。从某种意义上,我们恰恰可以说,量化研究之所以在社会科学不同学科中都具有旺盛的生命力,正是因为其有能力采用一种形式化的手段自我检视,并向其他同行详尽地展现其自身的不确定性。
| [] | 陈云松, 吴晓刚. 2012. 走向开源的社会学——定量分析中的复制性研究. 社会, 32 (3) : 1-23. |
| [] | 胡安宁. 2012. 倾向值匹配与因果推论:方法论述评. 社会学研究 (1) : 221-242. |
| [] | 胡安宁. 2014. 教育能否让我们更健康——基于,2010 年中国综合社会调查的城乡比较分析. 中国社会科学 (5) : 116-130. |
| [] | Abadie, Alberto and Imbens Guido. 2016. Matching on the Estimated Propensity Score. Econometrica, 84 (2) : 781-807. DOI:10.3982/ECTA11293 |
| [] | A n, Weihua. 2010. Bayesian Propensity Score Estimators:Incorporating Uncertainties in Propensity Scores into Causal Inference. Sociological Methodology, 40 (1) : 151-189. DOI:10.1111/j.1467-9531.2010.01226.x |
| [] | Bartels, Larry M. 1997. Specification Uncertainty and Model Averaging. American Journal of Political Science, 41 (2) : 641-674. DOI:10.2307/2111781 |
| [] | B ox, George E. P. and Norman R. Draper. 1987. Empirical Model Building and Response Surfaces. New York: Wiley . |
| [] | Cohen-Cole, Ethan, Steven Durlauf, Jeffrey Fagan, and Daniel Nagin. 2009. Model Uncertainty and the Deterrent Effect of Capital Punishment. American Law and Economics Review, 11 (2) : 335-369. DOI:10.1093/aler/ahn001 |
| [] | Drake, Christiana. 1993. Effects of Misspecification of the Propensity Score on Estimators of Treatment Effect. Biometrics, 49 (4) : 1231-1236. DOI:10.2307/2532266 |
| [] | Draper, David. 1995. Assessment and Propagation of Model Uncertainty. Journal of the Royal Statistical Society:Series B, 57 (1) : 45-97. |
| [] | Durlauf, Steven, Chao Fu, and Salvador Navarro. 2012. Assumptions Matter:Model Uncertainty and the Deterrent Effect of Capital Punishment. American Economic Review, 102 (3) : 487-492. DOI:10.1257/aer.102.3.487 |
| [] | F an, Jianqing, Fang Han, and Han Liu. 2014. Challenges of Big Data Analysis. National Science Review, 1 (2) : 293-314. DOI:10.1093/nsr/nwt032 |
| [] | Heckman, James and Xuesong Li. 2004. Selection Bias,Comparative Advantage and Heterogeneous Returns to Education:Evidence from China in, 2000. Pacific Economic Review, 9 (3) : 155-171. DOI:10.1111/per.2004.9.issue-3 |
| [] | H o, Daniel, Kosuke Imai, Gary King, and Elizabeth Stuart. 2007. Matching as Nonparametric Preprocessing for Reducing Model Dependence in Parametric Causal Inference. Political Analysis, 15 (3) : 199-236. |
| [] | Hoeting, Jennifer, David Madigan, Adrian Raftery, and Chris Volinsky. 1999. Bayesian Model Averaging:A Tutorial. Statistical Science, 14 (4) : 382-417. DOI:10.1214/ss/1009212519 |
| [] | H u, Anning. 2014. The Health Benefits of College Education in Urban China:Selection Bias and Heterogeneity. Social Indicators Research, 115 (3) : 1101-1121. DOI:10.1007/s11205-013-0266-2 |
| [] | Imbens, Guido and Donald Rubin. 2015. Causal Inference for Statistics,Social,and Biomedical Sciences:An Introduction. New York: Cambridge University Press . |
| [] | Kaplan, David and Jianshen Chen. 2012. A Two-Step Bayesian Approach for Propensity Score Analysis:Simulations and Case Study. Psychometrika, 77 (3) : 581-609. DOI:10.1007/s11336-012-9262-8 |
| [] | Kaplan, David and Jianshen Chen. 2014. Bayesian Model Averaging for Propensity Score Analysis. Multivariate Behavioral Research, 49 (6) : 505-517. DOI:10.1080/00273171.2014.928492 |
| [] | Leamer, Edward. 1983. Let's Take the Con Out of Econometrics. American Economic Review, 73 (1) : 31-43. |
| [] | Madigan, David and Adrian Raftery. 1994. Model Selection and Accounting for Model Uncertainty in Graphical Models Using Occam's Window. Journal of the American Statistical Association, 89 (428) : 1535-1546. DOI:10.1080/01621459.1994.10476894 |
| [] | Magnus, Jan and Mary Morgan. 1999. Methodology and Tacit Knowledge:Two Experiments in Econometrics. New York: Wiley . |
| [] | McCandless, Lawrence C. 2009. Paul Gustafson,and Peter C. Austin, 2009."Bayesian Propensity Score Analysis for Observational Data. Statistics in Medicine, 28 (1) : 94-112. DOI:10.1002/sim.v28:1 |
| [] | Montgomery, Jacob M. and Brendan Nyhan. 2010. Bayesian Model Averaging:Theoretical Development and Practical Applications. Political Analysis, 18 (2) : 245-270. DOI:10.1093/pan/mpq001 |
| [] | Moral-Benito, Enrique. 2015. Model Averaging in Economics:An Overview. Journal of Economic Surveys, 29 (1) : 46-75. DOI:10.1111/joes.2015.29.issue-1 |
| [] | Morgan,Stephen L. 2014. Handbook of Causal Analysis for Social Research. Springer. |
| [] | Raftery, Adrian E. 1995. Bayesian Model Selection in Social Research. Sociological Methodology (25) : 111-163. |
| [] | Raftery, Adrian E. 2001. Statistics in Sociology,1950-2000:A Selective Review. Sociological Methodology, 31 (1) : 1-45. DOI:10.1111/some.2001.31.issue-1 |
| [] | Rosenbaum, Paul R.and Donald B. Rubin. 1983. The Central Role of the Propensity Score in Observational Studies for Causal Effects. Biometrika, 70 (1) : 41-55. DOI:10.1093/biomet/70.1.41 |
| [] | Rubin, Donald B. 1997. Estimating Causal Effects from Large Data Sets Using Propensity Scores. Annals of Internal Medicine, 127 (8) : 757-763. |
| [] | Sala-i-Martin, Xavier X. 1997. I Just Ran Two Million Regressions. American Economic Review, 87 (2) : 178-183. |
| [] | Sala-i-Martin, Xavier X., G.Doppelhofer, and R. I.Miller. 2004. Determinants of Longterm Growth:A Bayesian Averaging of Classical Estimates (BACE) Approach. American Economic Review, 94 (4) : 813-835. DOI:10.1257/0002828042002570 |
| [] | Watts, Duncan. 2015. Common Sense and Sociological Explanations. American Journal of Sociology, 102 (2) : 313-351. |
| [] | Western, Bruce. 1996. Vague Theory and Model Uncertainty in Macrosociology. Sociological Methodology (26) : 165-192. |
| [] | X ie, Yu and Xiaogang Wu. 2005. Reply:Market Premium,Social Process,and Statisticism. American Sociological Review, 70 (5) : 865-870. DOI:10.1177/000312240507000508 |
| [] | Young, Christobal. 2009. Model Uncertainty in Sociological Research:An Application to Religion and Economic Growth. American Sociological Review, 74 (3) : 380-397. DOI:10.1177/000312240907400303 |
| [] | Zigler, Corwin Matthew and Francesca Dominici. 2014. Uncertainty in Propensity Score Estimation:Bayesian Methods for Variable Selection and Model-Averaged Causal Effect. Journal of the American Statistical Association, 109 (505) : 95-107. DOI:10.1080/01621459.2013.869498 |
 2016, Vol. 37
2016, Vol. 37
