空间点格局分析源于植物生态学,用于分析一定距离尺度下植物的空间分布情况。上个世纪50年代末至60年代初,这种方法被推广到其他研究领域(Gatrell et al., 1996:256274)。上个世纪70年代以来,经过一些学者的发展,这一方法日臻完善。它的基本思路是:划分一定面积的研究区域,在平面图中标出在此研究区域内的所有点事件,通过一定的计算方法,分析点事件在一定距离尺度下是否存在空间聚集的现象。在环境流行病学中,空间点格局分析还被用来探索疾病风险的空间变异情况。由于点事件是对研究对象的一种抽象概括,点事件既可以代表植物、疾病,也可以代表一些社会研究命题,如越轨事件、贫民窟问题,对于充足社会学定量化研究是十分有意义的。“时间和空间是社会生活‘环境’,这一观点在某些方面帮助加强了学科的划分,因而时间可能受到历史学家们的极大关注,空间可能受到地理学家们的关注,而社会科学的其他部分则极大地忽略了这些方面。我认为时间和空间对于社会科学是极为基本的问题。”(吉登斯,[2000]2003:155)本文旨在对空间点格局分析中的一些具有代表性的方法作一介绍,为社会学的学者提供一种可供选择的研究方法。
一、基本定义和基本定理11 此部分内容主要参阅了Diggle,P.2000年兰开斯特大学的内部讲稿Spatial Statistics for Environmental Epidemiology。
定义1:一个空间点过程的一阶强度函数
| $ \lambda \left(x \right) = \mathop {{\rm{lim}}}\limits_{\left| {dx} \right| \to 0} \left\{ {\frac{{E\left[ {N\left({dx} \right)} \right]}}{{\left| {dx} \right|}}} \right\} $ |
其中,x表示平面上任意一点;dx表示包含点x的一个小区域。
定义2:一个空间点过程的二阶强度函数
| $ {\lambda _2}\left( {x,y} \right) = \mathop {{\rm{lim}}}\limits_{\begin{array}{*{20}{c}} {\left| {dx} \right| \to 0}\\ {\left| {dy} \right| \to 0} \end{array}} \left\{ {\frac{{E\left[ {N\left( {dx} \right)N\left( {dy} \right)} \right]}}{{\left| {dx} \right|\;\left| {dy} \right|}}} \right\} $ |
定义3:一个空间点过程的协方差密度
| $ y\left({x, y} \right) = {\lambda _2}\left({x, y} \right) - \lambda \left(x \right)\lambda \left(y \right) $ |
如果在整个研究区域A内,一阶强度函数是常数λ(x)=λ=E[N(A)/|A|],则称这个点过程是稳定的;如果二阶强度函数λ2(x,y)=λ2(‖x-y‖)=λ2(u),说明其只依赖于事件的方向和距离,而不依赖于事件的绝对位置。如果进一步假设u仅仅表示距离,则称这个点过程是同向性的。对于一个具有稳定性和同向性的空间点过程而言,则有:
| $ \gamma \left(u \right) = {\lambda _2}\left(u \right) - {\lambda ^2} $ |
定义4:一个稳定的、同向性的空间点过程,其减少的二阶矩函数为:
| $ K\left(s \right) = 2\pi {\lambda ^{ - 2}}\int_0^S {{\lambda _2}\left(u \right)udu} $ |
定理1:对一个稳定的、同向性的空间点过程而言,有
K(s)=λ-1E(距离任意一事件的长度小于s的若干事件的数量)
其中,s是距离尺度;E(·)表示在整个研究区域内距离任意一点的长度小于s的其他点数量的数学期望(也可以理解为均值)。
定理2:对于一个同质性的平面泊松过程而言,则有:
| $ K\left(s \right) = \pi {s^2} $ |
同质性的假设很重要,它表示事件的发生是一个完全的随机过程,K(s)可直观地理解为以一点为圆心,半径为s的圆中所有点的集合。在空间点格局分析中,事件究竟是不是完全随机的,就要看它等不等于πs2。于是需要对事件的K(s)进行估计。现在,我们以被研究区域内所有事件的数量为n,则有:
| $ \hat \lambda = n/\left| A \right| $ |
| $ \hat E\left(s \right) = {n^{ - 1}}\sum\limits_{i = 1}^n {\sum\limits_{j \ne i} {{w_{ij}}I\left({{d_{ij}} \le s} \right)} } $ |
其中,字母上的帽子表示估计,I(·)是指示器函数,如果研究区域内其他点j距离一点i的距离dij大于指定的距离尺度s,则I(·)=0;反之,则有I(·)=1;wij,是边缘校正权重,它等于整个圆周长与以i点为圆心、dij为半径的圆落在研究区域内的弧长的比值。它表示校正圆以外还可能存在未被考虑的点,于是假设校正圆上点发生的概率和所在弧长成比例。因为对于不规则的研究区域求出边缘校正的数学表达式较难,于是在传统研究中,一般把研究区域选为矩形,这样边缘校正权重精确的数学表达式能够得到(Diggle,1983:72;汤孟平等,2003:15331538)。Rowlingson和Diggle(1993:627655)、时培建等(《生态学报》待刊稿)提出了对研究区域为任意多边形边缘校正权重的计算机解法。
根据上式,则有:
| $ \hat K\left(s \right) = \frac{{\left| A \right|}}{{{n^2}}}\sum\limits_{i = 1}^n {\sum\limits_{j \ne i} {{w_{ij}}I\left({{d_{ij}} \le s} \right)} } $ | (1) |
完全空间随机化方法是建立在空间同质性的假设基础之上的,在一定距离尺度s上,事件的

|
图 1 俄克拉何马城白人和黑人所进行财产偷窃的案发地点1 |
1 数据来源于Splancs软件包自带的数据表okwhite和数据表okblack,原始数据区域横坐标范围,纵坐标范围。为了分析方便,本文将它们都转化在区间。这些数据可进一步追溯到Bailey和Gatrell(1995:122125)的文献。
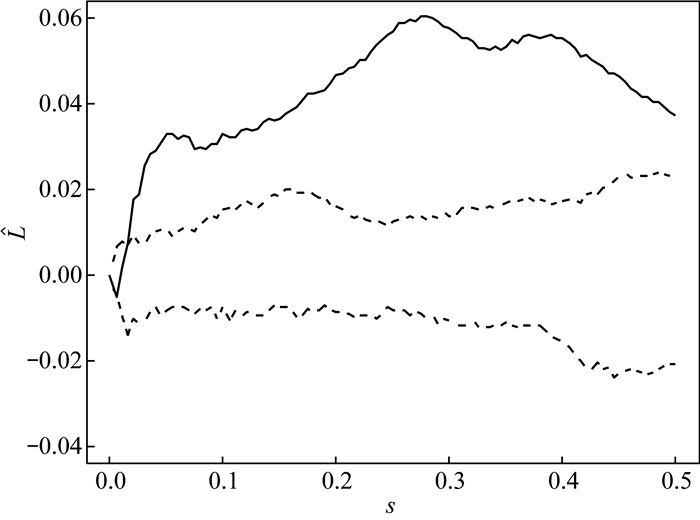
|
注:在完全空间随机化假设条件下仅对白人偷窃的案发地点的分析;s表示距离尺度,从0到0.5,步长选取为0.005;Monte-Carlo模拟的次数为99次,虚线部分为包迹线,即由随机标定模拟99次得到L(s)估计值的上下限;实线部分为观测组L(s)的估计值。按照完全空间随机化方法,其结论是白人偷窃的案发地点呈聚集分布。 图 2 完全空间随机化方法 |
在环境流行病学、社会学等与人口密切相关的空间点格局研究中,事件的发生与人口的空间分布密切相关,然而人口分布并不是均质的,而是呈空间异质性的。显然,完全空间随机化方法对于这些研究是不可行的,于是Cuzick和Edwards(1990:73104)、Diggle和Chetwynd(1991:11551163)分别设计了基于case-control数据的二阶分析方法。他们的方法大致分如下几个步骤。
第一步:划定研究区域,把研究区域内被研究对象点集通称为观测组(cases),同时根据研究区域内分布的人口随机抽取一定的点集作为控制组(controls)。为了保证选取的随机性,选取控制组的方法一般分两种:一是使用研究区域内人口出生登记簿随机抽取他们的居住地,标出位置,即控制组;二是使用研究区域的邮政编码,随机选定邮政编码,因为英国一个邮政编码代表了1到20投递地址(Prince et al., 2001:10831088),划分较细,对于大尺度的研究区域,这种选取方法在英国具有可行性。
第二步:分别计算观测组和控制组的K(s)之差,即D(s)=K11(s)-K22(s)。根据零假设,如果观测组的空间分布也是随机的,则由观测组和控制组来自同一总体,它们不过都是这一总体中的样本,那么两组的K(s)应该是相同的,并且它们和两组混合构成的点集的K(s)也应该是相同的。
| $ \begin{array}{l} {K_{ij}}\left(s \right) = \lambda _j^{ - 1}E\left({{\rm{距离来自}}\mathit{i}{\rm{组中任意一事件的}}} \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\left. {{\rm{长度小于}}\mathit{s}{\rm{的}}\mathit{j}{\rm{组中若干事件的数量}}} \right) \end{array} $ |
其中,j=1,2(分别表示观测组和控制组的点);K11(s)表示观测组的K(s);K22(s)表示控制组的K(s);K12(s)表示混合组的K(s)。如果零假设成立,则有:
| $ {K_{11}}\left(s \right) = {K_{22}}\left(s \right){K_{12}}\left(s \right) $ |
它们的估计值分别为:
| $ {{\hat K}_{11}} = \frac{{\left| A \right|}}{{{n_1}\left( {{n_2} - 1} \right)}}\sum\limits_{i = 1}^{{n_1}} {\sum\limits_{j = 1}^{{n_1}} {{w_{ij}}I\left( {{d_{ij}} \le s} \right)} } $ | (2) |
| $ {{\hat K}_{22}} = \frac{{\left| A \right|}}{{{n_2}\left({{n_2} - 1} \right)}}\sum\limits_{i = {n_1} + 1}^n {\sum\limits_{j = {n_1} + 1}^n {{w_{ij}}I\left({{d_{ij}} \le s} \right)} } $ | (3) |
| $ {{\hat K}_{12}} = \frac{{\left| A \right|}}{{n\left({{n_1} - 1} \right)\left({{n_2} - 1} \right)}}\sum\limits_{i = 1}^{{n_1}} {\sum\limits_{j = {n_1} + 1}^n {\left({{n_2}{w_{ij}} + {n_1}{w_{ji}}} \right)I\left({{d_{ij}} \le s} \right)} } $ | (4) |
其中,n1表示在研究区域内观测组中点的数量;n2表示在研究区域内控制组中点的数量;n=n1+n2。
对于给定的距离尺度s和u,如果令
| $ \begin{array}{l} Cov\left\{ {\hat D\left(s \right), \hat D\left(u \right)} \right\} = \frac{{{{\left| A \right|}^2}}}{{{{\left({n_1^{\left(2 \right)}n_2^{\left(2 \right)}} \right)}^2}}}\left\{ {{{\left({n_2^{\left(2 \right)}} \right)}^2}{\mu _1} - 2\left({n_1^{\left(2 \right)}n_2^{\left(2 \right)}} \right){\mu _2}} \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. { + {{\left({n_1^{\left(2 \right)}} \right)}^2}{\mu _3}} \right\} \end{array} $ | (5) |
其中,
| $ \begin{array}{l} {\mu _1} = \left({n_1^{\left(4 \right)}/{n^{\left(4 \right)}}} \right)\left({WV - 4Z + 2X} \right) + 4\left({n_1^{\left(3 \right)}/{n^{\left(3 \right)}}} \right)\left({Z - X} \right)\\ \;\;\;\;\;\;\; + 2\left({n_1^{\left(2 \right)}/{n^{\left(2 \right)}}} \right)X \end{array} $ |
| $ {\mu _2} = \left({n_1^{\left(2 \right)}\mathit{n}_2^{\left(2 \right)}/{n^{\left(4 \right)}}} \right)\left({WV - 4Z + 2X} \right) $ |
| $ \begin{array}{l} {\mu _3} = \left({n_2^{\left(4 \right)}/{n^{\left(4 \right)}}} \right)\left({WV - 4Z + 2X} \right) + 4\left({n_2^{\left(3 \right)}/{n^{\left(3 \right)}}} \right)\left({Z - X} \right)\\ \;\;\;\;\;\;\; + 2\left({n_2^{\left(2 \right)}/{n^{\left(2 \right)}}} \right)X \end{array} $ |
第三步:随机标定观测组和控制组,即在由观测组和控制组共同构成的点集中随机抽取n1个点作为新的观测组,剩余的n2个点作为新的控制组,分别计算它们的
另外,Diggle和Chetwynd还提供了一种对观测组是否存在空间聚集的总体检验方法,即:
| $ D = \sum\limits_{k = 1}^m {\frac{{\hat D\left({{s_k}} \right)}}{{\sqrt {Var\left\{ {\hat D\left({{s_k}} \right)} \right\}} }}} $ |
其中,Var{
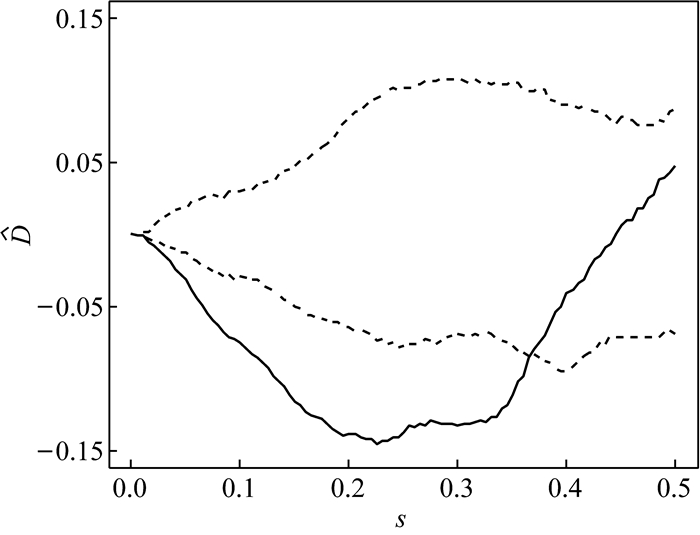
|
注:以白人偷窃的案发地点为观测组,以黑人偷窃的案发地点为控制组;s表示距离尺度,从0到0.5,步长选取为0.005;Monte-Carlo模拟的次数为99次,虚线部分为包迹线,即由随机标定模拟99次得到D(s)估计值的上下限;实线部分为观测组D(s)的估计值。从图中可以看出在s < 0.37的距离尺度下,白人偷窃案发地点呈均匀分布,位于包迹线之下;而在s≥0.37的距离尺度上,白人偷窃的案发地点呈随机分布,位于包迹线之内。这个结论和完全空间随机化方法得到的结论显然是不同的,产生的原因在于完全空间随机化方法没有使用控制组。 图 3 基于case-control数据的二阶分析方法 |
在空间点格局研究中,除了建立在距离尺度上的方法之外,建立在面积上事件发生的风险分析也同样备受关注(Gatrell et al., 1996:256274),因为通过这种方法,事件发生风险趋势面(risk surface)可以直观地反映这种风险。假设观测组和控制组在研究区域内的强度函数分别为λ1(x)和λ2(x),1用对数风险函数来衡量事件发生风险在研究区域内的空间变异,规定其为:
| $ \rho \left(x \right) = {\rm{log}}\left\{ {{\lambda _1}\left(x \right)/{\lambda _2}\left(x \right)} \right\} $ |
1 此处λ2(x)不再表示二阶强度函数,而是指控制组的一阶强度函数。
这个公式中ρ(x)很难通过λ1(x)和λ2(x)直接求出,因为后者都是不知道的。需要估算ρ(x)的方法很多(参见Kelsall & Diggle,1998:559573)。本文主要介绍二项回归(binary regression)的方法。
使用标签y1,y2,Λ,yn对由观测组和控制组构成的点集x1,x2,Λ,xn,规定:
| $ y = \left\{ \begin{array}{l} 1\;\;\;i \in \left[ {1, {n_1}} \right], \\ 0\;\;i \in \left[ {{n_1} + 1, n} \right] \end{array} \right. $ |
依赖于点xi,则yi实际上是相互独立的伯努力随机变量Yi的结果,而P(Yi=1|Xi=x)=p(x),此处
| $ p\left(x \right) = \frac{{{q_1}{\lambda _1}\left(x \right)}}{{{q_1}{\lambda _1}\left(x \right) + {q_2}{\lambda _2}\left(x \right)}} $ |
那么,继而能够得到:
| $ {\rm{ln}}\left\{ {p\left(x \right)/1 - p\left(x \right)} \right\} = \rho \left(x \right) + {\rm{ln}}\left({{q_1}/{q_2}} \right) $ |
可以看出,除了常数项ln(q1/q2),logit{p(x)}近似等于ρ(x),而p(x)可以通过核方法进行估计(Hastie et al., 2003:115-134),选用Nadaraya-Watson核回归估计值,则有:
| $ {{\hat p}_h}\left(x \right) = \sum\limits_{i = 1}^n {\left[ {{\kappa _h}\left({x - {x_i}} \right){y_i}} \right]/\sum\limits_{i = 1}^n {{\kappa _h}\left({x - {x_i}} \right)} } $ |
此处,核估计函数κh(u)=
| $ L\left\{ {p\left(\cdot \right)} \right\} = \prod\limits_{i = 1}^n {p{{\left({{x_i}} \right)}^{{y_i}}}{{\left\{ {1 - p\left({{x_i}} \right)} \right\}}^{1 - {y_i}}}} $ |
通过极大似然就可得到最优带宽h。但当出现p(·)=1或p(·)=0,这种方法难以达到满意的效果。为了解决这个问题,Kelsall和Diggle(1998:559573)提出用交叉验证来改进最大似然。
| $ C{V_2}\left(h \right) = {\left[ {\prod\limits_{i = 1}^n {\hat p_h^{ - i}{{\left({{x_i}} \right)}^{{y_i}}}{{\left\{ {1 - \hat p_h^{ - i}\left({{x_i}} \right)} \right\}}^{1 - {y_i}}}} } \right]^{ - 1/n}} $ |
其中,
| $ \hat p_h^{ - i}\left({{x_i}} \right) = \sum\limits_{j = 1, j \ne i}^n {\left[ {{\kappa _h}\left({{x_i} - {x_j}} \right){y_i}} \right]/} \sum\limits_{j = 1, j \ne i}^n {{\kappa _h}\left({{x_i} - {x_j}} \right)} $ |
当h→+∞时,由上式明显可以得到:
| $ \hat p_h^{ - i}\left({{x_i}} \right) = \left\{ \begin{array}{l} \left({{n_1} - 1} \right)/n\;\;\;\;i \in \left[ {1, {n_1}} \right]\\ {n_1}/\left({n - 1} \right)\;\;\;\;i \in \left[ {{n_1} + 1, n} \right] \end{array} \right. $ |
于是,当h→+∞时:
| $ CV\left({ + \infty } \right) = \left({n - 1} \right){\left({{n_1} - 1} \right)^{ - {n_1}/n}}{\left({{n_2} - 1} \right)^{ - {n_2}/n}} $ |
如果规定:
| $ CV\left(h \right) = C{V_2}\left(h \right)/CV\left({ + \infty } \right) $ | (6) |
显然如果h增大时,CV(h)最终会等于1。而如果存在较小的h使得CV(h) < 1,那么存在一个h使得CV(h)最小,此时即为最优带宽。
根据上述结论,使用核二项回归的方式,可以用logit{h(x)}代替(x),形成风险趋势面。为了更清晰地反映风险的空间变异,令
| $ \hat s\left(x \right) = \hat \rho \left(x \right) - {n^{ - 1}}\sum\limits_{i = 1}^n {\hat \rho \left({{x_i}} \right)} $ |
这样,
同样对观测组和控制组进r次随机标定,零假设认为H0:ρ(x)=c。将上面求出的最优带宽h代入,求出
除此而外,还需要执行Monte-Carlo检验来衡量风险总体上偏离零假设的显著性程度,根据下式:
| $ {t_j} = {n^{ - 1}}\sum\limits_{i = 1}^n {{{\hat s}_j}{{\left({{x_i}} \right)}^2}} $ |
使用p=r0/(r+1)来求p值,其中r0表示t0在由其自身和tj(j=1,2,Λ,r)构成的降序数列中的位置。
五、含有位置隐含变量的空间点格局分析在以上几种分析方法中都忽略了点事件在一定位置受到其他因素的影响,影响事件发生的变量未被充分利用,而观测事件的空间变异性极有可能受到这些变量的影响。例如把某一城市作为研究区域,把一定时间内在该城市发生的自杀行为作为事件,上述介绍的方法仅仅利用了自杀事件发生的空间地理位置,并没有考虑在自杀地点存在的位置隐含变量,例如自杀者的家庭收入、职业声望、家庭组成等因素。因此,如果在空间点格局分析中能把这些位置隐含变量考虑进去,似乎更为合理。对于许多社会学学者而言,他们可以根据自己的职业判断,分析这些事件发生的潜在影响因素,发掘位置隐含变量,使分析的结果更具解释力。幸运的是,近年来空间点格局分析方法进一步发展,通过在分析中引入广义线性模型或广义相加模型,这些可能影响事件发生的位置隐含变量得到了重视。
Baddeley等人(2000:329-350)假设观测组的一阶强度函数已知,减少的二阶矩函数的估计值为:
| $ {{\hat K}_l}\left({s, \lambda } \right) = \frac{1}{{\left| A \right|}}\sum\limits_{i = 1}^n {\sum\limits_{j \ne i}^{} {\frac{{{w_{ij}}I\left({{d_{ij}} \le s} \right)}}{{\lambda \left({{x_i}} \right)\lambda \left({{x_j}} \right)}}} } $ | (7) |
其中,λ(x)的估计式如下:
| $ {\hat \lambda _h}\left( x \right) = \sum\limits_i^n {{\kappa _h}\left( {x - {x_i}} \right)/{C_h}\left( x \right)} $ |
κh(·)和上边提到的κh(u)函数形式相同;
| $ {{\hat \lambda }_h}\left({{x_i}} \right) = \sum\limits_{i \ne j} {{\kappa _h}\left({{x_j} - {x_i}} \right)/{C_h}\left({{x_j}} \right)} $ |
Diggle等人(2007:550557)扩展了Baddeley等人的研究,建立起一种既包含对控制组一阶强度函数核估计(非参数估计),又包含对位置隐含变量的参数(如果使用广义线性模型来估计)或非参数估计(如果使用广义相加模型来估计)的分析方法。
假设λ1代表观测组的一阶强度函数,λ2代表控制组的一阶强度函数。首先根据控制组的数据使用核方法估计λ2,但是λ1并不使用观测组的数据直接估计,而是寻找λ1和λ2之间的关系,通过λ2间接估计出λ1。一个最简单的假设是两者呈比例模型,即:
| $ {\lambda _1} = b{\lambda _2} $ |
b反映了观测组和控制组点数量之间的比例。这个简单的假设可以进一步扩展,使其能够包含对位置隐含变量的讨论。把比例常数换成含有位置隐含变量的函数。广义线性模型(Nelder & Wedderburn,1972:370-384)和广义相加模型(Hastie & Tibshirani,1986:297-318)被建议采用。如果使用广义线性模型,则有:
| $ {\lambda _1} = {\lambda _2}{\rm{exp}}\left\{ {\alpha + z\left(x \right)\beta } \right\} $ | (8) |
其中z(x)代表位置隐含变量的诸个变量构成的变量数组(z1,z2,Λ,zr),相应的β=(β1,β2,Λ,β4)。如果只考虑一个位置隐含变量z1(x),则有z(x)=z1(x),β=β1。可以看出,使用广义线性模型来估计λ1,所有位置隐含变量的解释性较好,因为它是一种参数估计,参数α和β都可以拟合得到。但是一般而言,广义线性模型的拟合效果较广义相加模型差。如果使用广义相加模型,则有:
| $ {\lambda _1} = {\lambda _2}f\left({z\left(x \right);\beta } \right) $ | (9) |
其中,f(·)是未指定的光滑函数,此处必须是非负的。由于广义相加模型是一种非参数估计,虽然拟合效果较好,但是模型的解释性不强。比较广义线性模型和广义相加模型来说,各有长短。它们对于拟合logit函数都十分有效。现在将观测组和控制组合为一个点集,根据此点集中的点是否属于观测组,设定标志变量Yi等于1或0。假设这个点集取自异质性的泊松过程,Yi彼此独立且有:
| $ P\left({{Y_i} = 1\left| {{z_i}} \right.} \right) = \frac{{{\rm{exp}}\left({\alpha + z'{\;_{i\beta }}} \right)}}{{1 + {\rm{exp}}\left({\alpha + z'{\;_{i\beta }}} \right)}} $ | (10) |
P(Yi=1|zi)表示某点隶属观测组的概率。此处使用的是广义线性模型。把求得的参数α和β代入(8)式,再根据(7)式求得K函数。如果使用的是广义相加模型,P(Yi=1|zi)=f(zi)/{1+f(zi)},则把估计的f(·)代入(9)式,再根据(7)式求得K函数。
当我们要判断观测组在研究区域内一定距离尺度下是否存在聚集,同样需要建立零假设,此处零假设认为观测组是一个异质性的泊松过程。如果观测组较零假设而言具有更强的聚集性,直接使用观测组数据进行核估计则可能仅仅把这种聚集性归咎于在强度函数上表现出的空间变异,而忽略了位置隐含变量导致的聚集性。因此,间接估计λ1(x)较为合理。为了分析观测组在异质性空间的聚集性,我们同样需要对零假设进行多次Monte-Carlo模拟。在由观测组和控制组合并的点集中,按照公式(10)求出的概率任选n1个点作为新的观测组,其余n2个点作为新的控制组。再根据公式(8)和已经得到的相关参数,求出若干次模拟得到的K函数。现在我们设这若干次模拟求得的K函数的均值和方差分别为E(s)和V(s),则检验观测组聚集显著程度的公式如下:
| $ {T_q} = \sum\limits_{k = 1}^m {\frac{{\hat K_I^q\left({{s_k};{{\hat \lambda }_2}} \right) - E\left({{s_k}} \right)}}{{\sqrt {V\left({{s_k}} \right)} }}} $ |
其中,q=1,2,Λ,r;
上述方法均假定研究区域内的事件是在一定时间中发生,在这段时间中不存在时间效应,即事件发生的时间先后对事件聚集的空间构成不产生影响,在合适的时间段内,这种假定是没有问题的,但是如果事件发生的时间先后差异很大,需要在空间点格局分析中考虑时间因素的影响。Diggle等人(1995:124136)定义了“时空”K函数:
| $ \begin{array}{l} K\left({s, t} \right) = {\lambda ^{ - 1}}E\left({{\rm{距离任意一事件长计小于}}\mathit{s}、} \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {{\rm{时间小于}}\mathit{t}{\rm{的若干事件的数量}}} \right) \end{array} $ |
其中,强度λ被定义为在单位空间、单位时间上预期事件的数量。在有限的时空A×(0,T)中,如果时间和空间是相互独立的,则有:
| $ K\left({s, t} \right) = {K_1}\left(s \right){K_2}\left(t \right) $ | (11) |
此处,K1(·)和K2(·)分别指空间过程的K函数和时间过程的K函数。它们分别为:
| $ \begin{array}{l} {K_1}\left(s \right) = \lambda _1^{ - 1}E\left({{\rm{距离任意一事件长度小于}}\mathit{s}{\rm{的若干事件的数量}}} \right)\\ {K_2}\left(s \right) = \lambda _2^{ - 1}E\left({{\rm{距离任意一事件长度小于}}\mathit{s}{\rm{的若干事件的数量}}} \right) \end{array} $ |
λ1和λ2分别是空间强度和时间强度,λ1=λT,λ2=λ|A|。这三个K函数相应的估计式为:
| $ \begin{array}{l} \hat K\left({s, t} \right) = \frac{{\left| A \right|\;T}}{{n\left({n - 1} \right)}}\sum\limits_i^n {\sum\limits_{j \ne i}^{} {{w_{ij}}I\left({{d_{ij}} \le s} \right){v_{ij}}I\left({{u_{ij}} \le t} \right)} } \\ \hat K\left(s \right) = \frac{{\left| A \right|}}{{n\left({n - 1} \right)}}\sum\limits_i^n {\sum\limits_{j \ne i}^{} {{w_{ij}}I\left({{d_{ij}} \le s} \right)} } \\ \hat K\left({s, t} \right) = \frac{T}{{n\left({n - 1} \right)}}\sum\limits_i^n {\sum\limits_{j \ne i}^{} {{v_{ij}}I\left({{u_{ij}} \le t} \right)} } \end{array} $ | (12) |
这里,wij是用以估计空间二阶属性的边缘校正权重,与上文规定的相同,计算中十分重要;vij是用以估计空间二阶属性的边缘校正权重,它等于2uij除以以i为中点长度为2uij的线段落在(0,T)中的长度。因为后者在实际计算中不太重要,所以可以近似计算,只要以i为中点长度为2uij的线段完全落在(0,T)中,规定vij=1,否则,vij=2。
现在面临的问题是如何诊断时间和空间是否存在着依赖关系。为了解决这个问题,Diggle等人首先定义了下边的两个重要函数:
| $ \begin{array}{l} \hat D\left({s, t} \right) = \hat K\left({s, t} \right) - {{\hat K}_1}\left(s \right){{\hat K}_2}\left(t \right)\\ {{\hat D}_0}\left({s, t} \right) = \hat D\left({s, t} \right)/\left\{ {{{\hat K}_1}\left(s \right){{\hat K}_2}\left(t \right)} \right\} \end{array} $ | (13) |
显然,
现在设
| $ \begin{array}{l} E\left\{ {\hat D\left({s, t} \right)} \right\} = 0\\ Cov\left\{ {\hat D\left({s, t} \right), \hat D\left({s', t'} \right)} \right\} = \frac{{{{\left| A \right|}^2}{T^2}}}{{n_2^2}}\\ \;\;\;\;\left\{ {\frac{{\left({{W_1}{{W'}_1} - 4{W_2} + 2{W_3}} \right)\left({{V_1}{{V'}_1} - 4{V_2} + 2{V_3}} \right)}}{{{n_4}}}} \right.\\ \;\;\;\;\left. {{\rm{ + }}\frac{4}{{{n_3}}}\left({{W_2} - {W_3}} \right)\left({{V_2} - {V_3}} \right) + \frac{{2{W_3}{V_3}}}{{{n_2}}} - \frac{{{W_1}{V_1}{{W'}_1}{{V'}_1}}}{{n_2^2}}} \right\} \end{array} $ | (14) |
既然
利用R(s,t),还可以从总体上判断时空互动的影响为正还是为负。现在我们设:
| $ U = \sum\limits_s^{} {\sum\limits_t^{} {R\left({s, t} \right)} } $ | (15) |
其中,s表示规定的空间距离尺度,t表示规定的时间尺度,U的正负就代表时空互动的正负。基于上述公式(15),我们同样可以通过Monte-Carlo模拟来检验零假设(即不存在时空互动)。具体方法是,通过对时间点观测值的随机排列,假设共进行了r次排列,根据公式(14)和公式(15),计算出这r次排列得到的U值,让其构成降序数列Ui(i=1,2,3,…,r),再令使用观测值(包含观测的空间数据和时间数据)计算的U值为U0。现在看U0在降序数列中的位置,如果排在第r0位,则p值就为r0/(r+1),进而就可以根据p值来判断零假设是否成立了。
七、讨论谢宇(2006:9-28)认为,社会科学研究存在着三个基本原理:变异性原理,社会分组原理和社会情境原理。而在空间点格局分析中,对变异的研究,可以说是研究的主线,而社会分组和社会情境也得到了体现。在简单的完全空间随机化方法中,通过空间完全随机化假设,假定观测数据在一定距离尺度下是随机分布的,通过Monte-Carlo方法设定了完全随机分布的上下包迹线(即模拟结果的上下限),落在包迹线之内与假设不背离,符合空间完全随机化的假设,然而如果落在包迹线的上方则是对零假设的背离,聚集分布对随机分布而言,显然是一种变异,变异通过曲线之间的位置关系得到证实,最后对事件聚集进行判断。值得注意的是,空间点格局分析中对聚集的判断,并不是直接设定判断聚集的指标,即零假设不直接认为事件呈空间聚集状态,而是假定事件是随机分布,聚集只是对随机的一种变异。其他几种分析方法也都体现了通过研究变异而间接研究聚集的这种思想,在对事件发生风险的空间变异分析中,变异思想得到了更为直接的体现,设计了非常精巧的检验方法就是去消除随机波动对分析的影响。
社会分组的原理在空间点格局分析中也得到了体现。由于在一定面积的研究区域内人口分布往往不是均匀的,即人口密度分布不均,单纯使用空间完全随机化假设就显得不太合理,因为这种假设忽略了事件与人口分布的联系。诸如在社会学研究中,社会事实的分析离不开对人的分析,一定的社会学命题(尤其是在城市社会学研究中)显然需要考虑人口分布的特点。于是巧妙地安排零假设成为决定这种分析方法能否适用于分析与人口分布相关联的事件空间聚集状况的关键。根据现有的人口分布,随机在其中抽出一定的位置作为控制组,零假设认为观测组和控制组来自同一总体,于是如果观测组在考虑了人口分布的因素以后还存在空间聚集,则结果一定会超出根据随机标定方法计算了
“群体变异性的模式会随社会情境的变化而变化,这种社会情境常常是由时间和空间来界定的。”(同上)在空间点格局分析中,根据研究对象的特点,需要划分好研究区域。聚集是在一定距离尺度上而言的,离开了对空间情境的界定,这种研究方法的基础将不复存在。如果说对变异的研究是空间点格局分析方法的主线、灵魂的话,对空间情境的界定则是这种分析方法的基础。在上述介绍的方法中,也都暗含对时间情境的界定,所有事件都是在一定时间内产生的,除最后介绍的方法外,其余方法都假设事件在界定的时间内不存在受时间因素影响的变异。在使用这些方法时,需要从事社会科学研究的学者对时间段进行理性的划分,这将使分析渗透着研究者的职业判断,这也很正常,因为在社会科学研究中,没有纯粹的、脱离人为价值判断的机械性研究。
需要指出,本文介绍的几种空间点格局分析方法,只是为了起到丰富社会科学研究方法的目的,它们并不是万能的,它们很可能只是对于研究发生在较大空间尺度上的一些社会学命题有效,对于发生在微观组织内的社会学命题可能会显得苍白无力。然而由于这种方法考虑了时空情境和事件的空间性变异,在分析许多社会问题时无疑会起到重要的作用。由于空间点格局在环境流行病学上已经成熟,因此毫无疑问,这种分析模式至少应该在医学社会学研究中得到重视。Prince等人(2001:1083-1088)和Diggle等人(2007)的研究都显示,原发性胆汁性肝硬化(primary biliary cirrhosis)在一定距离尺度上的聚集性反映了这种流行性的起因很可能来自一种未被觉察到的“社会经济”风险因子。
另外在空间点格局分析中还有其他一些重要的方法,例如个体相搭配观测组控制组(individually matched case-control)的空间聚集研究方法(Chetwynd et al., 2001:277-293)、使用相搭配观测组控制组数据的点—源模型方法(Diggle et al., 2000:89-105),有兴趣的读者可以参见相应的文献,学习、使用这些方法,以期繁荣空间点格局分析在社会学研究中的普及。
此外,实现上述方法一般都有相应的软件包,绝大多数可以在网上免费获取。本文介绍的大部分方法可以使用软件包Splancs1或软件包Spatstat2来实现,它们是在R软件3中使用的,但事件发生风险的空间变异之衡量方法目前需要下载专门的软件包epiS4,但这个软件包是在S-plus中使用的。不过S-plus和R都是基于S语言开发的优秀统计软件,稍作调整,许多函数命令就可以互用。有关这些软件包的使用方法,可以在下载这些软件包的网络地址上同时获得,还可以参考Rowlingson和Diggle(1993:627-655)的论文以及Jarner和Diggle(2002)的技术报告。
1 http://cran.r-project.org/web/packages/splancs/index.html。
2 http://cran.r-project.org/web/packages/spatstat/index.html。
3 可在 http://www.r-project.org/ 免费下载R软件。
4 http://www.maths.lancs.ac.uk/Software/epiS/。
黑斯蒂等. 2003.统计学习基础—数据挖掘、推理与预测.范明、柴玉梅、昝红英, 等, 译.北京: 电子工业出版社.
|
吉登斯, 安东尼. 2003.社会理论与现代社会学.文军、赵勇, 译.北京: 社会科学文献出版社.
|
时培建、戈峰、杨清培, 等.点格局分析中边缘校正的一种新算法及其应用.生态学报(待刊稿).
|
汤东孟平, 唐守正, 雷相东, 等. 2003. Ripley's K(d)函数分析种群空间分布格局的边缘校正[J]. 生态学报(23). |
谢宇. 2006. 社会学方法与定量研究[M]. 北京: 社会科学文献出版社.
|
薛毅, 陈立萍. 2007. 统计建模与R软件[M]. 北京: 清华大学出版社.
|
张金屯. 1998. 植物种群空间分布的点格局分析[J]. 植物生态学报(22). |
Baddeley A., Moller J., Waagepetersen R. 2000. Non- and Semi-parametric Estimation of Interaction in Inhomogeneous Point Patterns[J]. Statistica Neerlandica(54). |
Bailey T. C., Gatrell A. C. 1995. Interactive Spatial Data Analysis[M]. Harlow: Longman.
|
Barnard G. A. 1963. Contribution to the Discussion of Professor Bartlett's Paper[J]. Journal of the Royal Statistical Society. Series B(25). |
Berman M., Diggle P.J. 1989. Estimating Weighted Integrals of the Second-order Intensity of a Spatial Point Process[J]. Journal of the Royal Statistical Society. Series B(51). |
Besag J., Diggle P.J. 1977. Simple Monte Carlo Tests for Spatial Patterns[J]. Applied Statistics(26). |
Chetwynd A. G., Diggle P. J., Marshall A., Parslow R. 2001. Investigation of Spatial Clustering from Individually Matched Case-control Studies[J]. Biostatistics(2). |
Diggle P. J. 1983. Statistical Analysis of Spatial Point Patterns[M]. London: Academic Press.
|
Diggle P. J., Chetwynd A.G. 1991. Second-order Analysis of Spatial Clustering for Inhomogeneous Populations[J]. Biometrics(47). |
Diggle P. J., Chetwynd A., Haggkvist R., Morris S. 1995. Second-order Analysis of Space-time Clustering[J]. Statistical Methods in Medical Research(4). |
Diggle P. J., Morris S. E., Wakefield J. C. 2000. Point Source Modeling Using Matched Case-control Data[J]. Biostatistics(1). |
Diggle P. J., Gomez-Rubio V., Brown P.E., Chetwynd A.G., Gooding S. 2007. Second-order Analysis of Inhomogeneous Spatial Point Process Using Case-control Data[J]. Biometrics(63). |
Jarner, M.F. and P.J.Diggle. 2002. "An S+ Library on Risk Estimation and Cluster Detection in Case-control Studies.".
|
Gatrell A. C., Bailey T.C., Diggle P.J., Rowlingson B.S. 1996. Spatial Point Pattern Analysis and Its Application in Geographical Epidemiology[J]. Transactions of the Institute of British Geographers. New Series(21). |
Hastie T., Tibshirani R. 1986. Generalized Additive Models[J]. Statistical Science(1). |
Kelsall J. E., Diggle P.J. 1998. Spatial Variation in Risk of Disease: a Nonparametric Binary Regression Approach[J]. Applied Statistics(47). |
Nelder J. A., Wedderburn R.W.M. 1972. Generalized linear Models[J]. Journal of the Royal Statistical Society. Series A (General)(135). |
Prince M. I., Chetwynd A., Diggle P.J., Jarner M., Metcalf J., James O.F.W. 2001. The Geographical Distribution of Primary Biliary Cirrhosis in a Well-defined Cohort[J]. Hepatology(34). |
Rowlingson B. S., Diggle P.J. 1993. Splancs: Spatial Point Pattern Analysis Code in S-plus[J]. Computers in Geosciences(51). |
 2009, Vol. 29
2009, Vol. 29