在常规的统计分析如多元回归分析中,前提条件之一是要求自变量之间相互独立,否则会出现“共线性”,它会引起一些问题。例如,在完全共线性的条件下,将得不到参数的估计量;在近似共线性情况下OLS估计量非有效。多重共线性使参数估计值的方差和标准差增大,变量的显著性检验失去意义;模型的预测功能失效。在研究“亲属关系”是否提供借款,即“亲属关系”和“资金关系”之间是否有关系的时候,假设通过常规统计分析发现二者之间确实有关。实际上,此时的相关是虚假的,一方面可能因为村民之间在地理位置上的相近;另一方面,这种研究本身就具有重大缺陷:“亲属关系”和“资金关系”本身就有相关性。如何检验这种虚假相关?对于这个问题,学者们利用一种随机化检验(randomization test)方法来检验,QAP即属于此。QAP是一种以重新抽样为基础的方法,已经在社会网络研究中得到了广泛的应用,其研究对象都是“关系”数据。
一、QAP的含义社会关系是社会学研究的核心内容之一。如何研究“关系”?视角多种多样。从量化角度讲,由于“关系”数据本身就是关于“联系”的数据,因而直接违背避免“共线性”的原则。这意味着,很多常规的统计技术(如OLS)是不能简单地应用于对关系数据的统计分析之中的,特别是在研究“关系”之间的关系,如“亲属”是否更容易提供借款,即“亲属关系”与“资金关系”是否有关的时候,就需要特定的方法,QAP就是其方法之一。
QAP(Quadratic Assignment Procedure,二次指派程序)是一种对两个(或多个)方阵中对应的各个元素值进行比较的方法,它通过比较各个方阵对应的格值,给出两个矩阵之间的相关系数,同时对系数进行非参数检验,它以对矩阵数据的置换为基础。其原理如下(参见Everett,2002)。
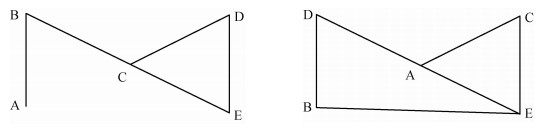
假设用两个矩阵分别表示5个人(A、B、C、D、E)之间的“朋友关系”和“建议关系”(假设这两种关系都是对称的),如表 1所示(1代表朋友,0表示不是朋友)。每两个人之间的关系都对应着关系矩阵中的格值,矩阵中的各行和各列对应着5个人。一般情况下,矩阵的格值只有两个:1和0。从矩阵(1)中可见,A和B是朋友,B和D不是朋友,C和E是朋友,其他情况可从中分析出来;从矩阵(2)中可见,A和B之间无建议关系,B和D相互提供建议,其他情况也可从图 1中分析出来。也可以用矩阵式(参见表 1)分别表示这两种关系的具体内涵。
|
图 1 朋友关系和建议关系的网络图 |
| 表 1 朋友关系矩阵和建议关系矩阵 |
上述两个矩阵分别表达了5个人之间的两类关系。就上述两个矩阵来说,二者之间在多大程度上相似,或者说相关性如何?对这个问题来说,不能用一些常规的统计程序来进行统计推断,因为观察项之间不独立,否则会计算出错误的标准差。此时可利用QAP法,它要求进行如下所示的随机化操作步骤。
具体地说,为了比较两个矩阵之间的相关性,首先把每个矩阵中的所有取值看成是一个长向量,每个向量包含n(n-1)个数字(对角线上的数字忽略不计)。例如,就“朋友关系”矩阵来说,该长向量是1,0,0,0,1,1,0,0,0,1,1,1,0,0,1,1,0,0,1,1,即把“朋友关系矩阵”的第二、第三、第四和第五行的值(对角线上的值除外)分别依次并置在第一行后面得到的向量,同理根据“建议关系矩阵”得到第二个向量。然后计算这两个向量之间的相关系数,得到的值为-0.8165,这表明两者之间是负相关的。也就是说,越是“朋友”,越不提供“建议”。
问题是,这个实际的相关系数值是否具有统计显著性?实际上,在这种情况下,我们不能利用标准的统计方式来推断,因为其前提性假设被违背。此时可以利用一种重排法(permutation approach)。从本质上讲,我们要追问的问题是,相对于在各个关系的取值是随机的情况下计算得到的相关系数来说,观察到的相关系数是大还是小?
我们可以随机地对矩阵的标签(A、B、C、D、E)进行置换,然后再计算相关系数。就上述“朋友关系”和“建议关系”例子来说,可以对其中的一个矩阵(如建议关系矩阵)中的“标签”进行置换。对于包含5个元素的矩阵来说,其最多有5!=120种置换方式(Krackhardt,1987:176),针对每种置换重新计算相关系数,得到的分布如表 2所示。
| 表 2 全体120种置换的分布 |
由表 2可知,在“建议关系矩阵”的全部120个置换矩阵中,有4个(占总数的3.3%)与“朋友关系”是强相关的(相关系数为0.8165);有32个(占总数的26.7%)与“朋友关系”是中等程度相关的(相关系数为0.4082);有48个(占总数的40%)与“朋友关系”是无关的,相关系数为0.0;其余的30%是负相关的。由这一分析可以得出如下结论:如果图 1代表实际数据,那么计算结果表明这种置换只有3.3%的概率是随机造成的,也就是说,如果原假设为“建议数据是随机指派的”,那么在原假设成立的情况下,即在已知“‘朋友关系’与‘建议关系’无关”的情况下,我们实际观察到的数据在3.3%的水平上是显著的。该值小于常见的0.05这个显著性水平,因此可以认为,原假设是不成立的,即朋友关系与建议关系之间不是无关的,而是存在如上所述的负相关关系。
该例子比较简单。如果网络规模较大,那么需要置换的次数将急剧增加。然而一个矩阵和另外一个矩阵的全部可能的转置矩阵之间的相关系数的均值和标准差恰恰是这两个矩阵中元素的函数。因此,观察到的相关系数可表示为一个标准化的Z-值。假设在进行全部置换的情形下,置换的矩阵和原矩阵之间的相关系数服从标准正态分布的话,那么观察到的相关系数的显著性水平就仅取决于在标准正态曲线下超出Z-值之外的区域的面积(同上:178)。
上述案例针对的是数据的标签进行重排。在具体的计算中,QAP是针对一个矩阵的行和列同时进行置换。具体做法是有三步。
首先,计算已知的两个矩阵之间的相关系数,即把矩阵转换为长向量,计算二者之间的相关系数。
其次,对其中的一个矩阵的行和相应的列同时进行随机的置换(而不是仅仅置换行或者列,否则破环原始数据),然后计算置换后的矩阵与另一个矩阵之间的相关系数1,保存计算的结果;重复这种计算过程几百次甚至几千次,将得到一个相关系数的分布,从中可以看到这种随机置换后计算出来的几百或几千个相关系数大于或等于在第一步中计算出来的观察到的相关系数的比例。
最后,比较在第一步中计算出来的观察到的相关系数与根据随机重排计算出来的相关系数的分布,看观察到的相关系数是落入拒绝域还是接受域,进而作出判断。也就说,如果上述比例低于0.05(假设研究者确定的显著性水平为0.05),就在统计意义上表明所研究的两个矩阵之间存在强关系,或者说二者之间出现在相关系数不太可能是随机带来的。
另外,既然QAP只对某个矩阵的行和列同时进行置换,然后计算置换后的矩阵与另一个矩阵(即模式矩阵)之间的相关系数,这就保证了自变量矩阵和因变量矩阵在行和列上都相互依赖。最后计算出显著性以及相关系数大于或者小于实际系数的概率。
二、QAP例示QAP分析又可以分为QAP相关分析和QAP回归分析,下面分别加以例示。
(一) QAP相关分析QAP相关分析既可以研究两种“关系”矩阵之间是否相关,还可以研究一个属性(如性别)与一种关系(如朋友关系)之间是否有关。下面分别加以展示。
1. 两种“关系”之间关系的QAP检验在UCINET中有一套数据名为PADGETT,它记载了14世纪意大利佛罗伦萨地区多个家族中间的“婚姻关系”和“商业关系”等数据,研究的是通过婚姻建立的商业联盟关系。为了展示QAP的操作步骤,下面利用UCINET中的QAP命令计算“婚姻关系”和“商业关系”之间的相关性,从而对该假设进行检验。如果在统计意义上显著,则研究假设“‘婚姻关系’和‘商业关系’之间有关”成立。
在UCINET 6.143中,沿着Tools→Testing Hypotheses→Dyadic(QAP)→QAP correlation这条路径,选择“PADGM”(婚姻关系)和“PADGB”(商业关系)作为输入矩阵2,然后提交运算。运算结果给出的是这两种关系之间的相关关系检验。在计算结果中,如果相关系数在统计意义上显著,则认为“婚姻关系”和“商业关系”是存在联系的。计算结果参见表 3:
| 表 3 PADGM(婚姻关系)和PADGB(商业关系)之间的相关关系检验 |
这里的“Obs Value”是这两个矩阵实际的相关系数;“Significa”是显著性水平;“Average”是根据5000次随机置换计算出来的相关系数的均值;“SD”是标准差;Minimum和Maximum分别代表随机计算的相关系数中出现的最小值和最大值;Prop >= 0和Prop < = 0分别代表这些随机计算出来的相关系数大于或等于以及小于或等于实际相关系数的概率。实际上,“显著性水平”是关注的重点。
由表 3可知,上述两个矩阵之间是正相关的,相关系数为0.372,并且在统计意义上显著。因此,“婚姻关系”与“商业关系”在统计意义上是相关联的。这说明,多个家族之间确实通过建立婚姻关系建立商业联盟。
2. 属性变量与关系矩阵之间关系的QAP检验性别相同的人是否容易相互提供建议?也就是说,对于一个二元邻接矩阵来说,它与一个单一变量(代表每个行动者的属性的变量)之间是否相关?例如,“朋友关系”矩阵与“性别”是否有关?QAP程序会计算出朋友关系是否根据性别来分组,也就是说是否男孩倾向于与男孩建立朋友关系,女孩与女孩是朋友关系?可采用两种办法。
(1) 利用UCINET中的“自相关”(AUTOCORRELATION)分析法。在UCINET中,沿着TOOLS→STATISTICS→AUTOCORRELATION→CATEGORICAL→JOIN COUNT这样的路径即可进行自相关分析。具体地说,该程序对一个对称矩阵和分为两组的向量之间进行自相关分析的随机检验(randomization test of autocorrelation)。需要注意,该程序只能针对分为两组(如男孩和女孩)的数据进行检验,检验的基础是计算组内和组间的关系数量,并且与一种随机的模型进行比较。
假设上述5人图中每个人的性别分别是男,女,男,男,女,即性别向量是(1,0,1,1,0),在UCINET中输入该向量,并令其为sex。然后计算该向量与“建议关系”矩阵之间的关系。在UCINET 6.143中,沿着Tools→Testing Hypotheses→Mixed Dyadic/Nodal→Categorical attributes→Join-Count这条路径,点击之后,出现对话框,键入(或选出)输入数据“advice”和分区向量sex,点击“OK”后即计算出如表 4所示。
| 表 4 “建议关系”和“性别向量”之间关系的QAP |
可见,计算的结果给出了实际的关系数量和期望的数量。第一行给出的是群体1的内部关系数量,第二行给出的是群体1和群体2之间的关系数量,第三行给出的是群体2的内部关系数量。其中,期望值指的是,如果各个1是随机地在群体内部和群体之间分布的话,出现1的数量。观察值就是实际出现的关系数量。“差量”(difference)就是把前者减去后者得到的数,即观察值减去期望值。P>=Diff和P < =Diff这两项给出的是根据随机重排的矩阵计算出来的差量大于(小于)或等于观察值的相对频次概率(relative frequency)。这些列的值可用来检验观察值的显著性。
从上述计算结果来看,无论是群体1的内部关系数量,群体1和群体2之间的关系数量,还是群体2的内部关系数量,都不显著。
(2) 也可以利用QAP,但是需要构建“性别关系矩阵”。“建议关系矩阵”已经在前文中构建出来,问题在于如何构建“性别关系矩阵”?方法如下:如果A和B的性别相同,则在矩阵的A,B交叉处的值赋予1,否则为0。
假设A=男,B=女,C=男,D=男,E=女,那么根据上述思想构建的矩阵如表 5所示。
| 表 5 性别关系和建议关系的矩阵 |
然后就可以利用QAP计算二者之间的相关关系了,具体计算步骤与上述例子相同,此处不再赘述,下面只展示计算的结果如下。
| 表 6 “建议关系”和“性别关系矩阵”之间关系的QAP检验 |
可见,“性别关系”与“建议关系”之间存在负相关关系,尽管这种关系在统计意义上不是显著的。读者完全可以根据自己的课题研究与本例相似的相关关系问题。
(二) QAP回归分析QAP回归的目的是研究多个矩阵和一个矩阵之间的回归关系,并且对r平方的显著性进行评价。在具体计算的时候要经过两步。首先,针对自变量矩阵和因变量矩阵的对应元素进行标准的多元回归分析;其次,对因变量矩阵的各行和各列进行(同时)随机置换,然后重新计算回归,保存所有的系数值以及判定系数r2值。重复这种步骤几百次,以便估计统计量的标准误(standard errors)。对于每个系数来说,该程序将计算出在全部随机置换的次数中,产生的系数大于或等于第一步计算时得到的系数的随机置换所占的比例。在进行多元回归的QAP分析的时候,最主要要求是回归中的所有变量(即所有矩阵)必须是1-模矩阵,即必须是N×N的方阵。如果给出的是“个人-事件”关系网络等隶属关系数据,可以利用UCINET中的算法(Data→Affiliations)转换为N×N矩阵,这里仅举一例加以说明(有关QAP回归的具体细节,参见Krackhardt,1988)。
在UCINET中有一个数据库Trade,它记录的是24个国家之间的外交关系和四种贸易关系。现在我们可利用QAP来对四种贸易关系与外交关系之间是什么关系加以检验。沿着Tools→Testing Hypotheses→Dyadic(QAP)→QAP Regression这条路径,点击后出现对话框,键入作为因变量的矩阵DIPLOMATIC_EXCHANGE,分别输入作为自变量的四个矩阵的名称CRUDE_MATERIALS、FOODS、MANUFACTURED_GOODS和MINERALS。点击OK后得到的结果为:
| 表 7 QAP回归分析结果 |
分析结果包含两个部分:第一部分简单介绍模型的拟合情况。从结果可见,判定系数(R-square)和调整的判定系数(Adj R-Sqr)基本相同,都比较大。前者达到0.317,后者达到0.314。这说明,当知道“原材料”(CRUDE_MATERIALS)、“食品”(FOODS)、“制造品”(MANUFACTURED_GOODS)和“矿物质”(MINERALS)与“全面外交关系”之间存在线性关系的时候,可以用上述四个矩阵数据解释“全面外交关系”的31.7%的方差,因为该判定系数是从数据当中计算出来的“观察到的判定系数”。
判定系数右侧的一项是概率。要注意,这个概率是满足如下条件的随机置换的次数占总随机置换次数的比例(也是一种概率),即该次随机置换产生的回归系数不小于观察到的判定系数,它是单尾检验(one-tailed probability)的概率。
第二部分给出了截距、每个自变量的非标准化回归系数、标准化回归系数和统计显著性检验的结果等。与上表不同的是,这里给出了两个概率(proportion as large和proportion as small)。这两个概率是满足如下条件的随机置换的次数占总随机置换次数的比例,“proportion as large”和“proportion as small”分别代表随机置换产生的回归系数的绝对值不小于和不大于观察到的回归系数的随机置换占总置换次数的比例。此处进行的是双尾检验(two-tailed probability)。
在本例中,CRUDE_MATERIALS、MANUFACTURED_GOODS和MINERALS)的回归系数在统计的意义上是“显著”的(其显著性水平分别是0.011、0.000和0.005),中间者最显著。“FOODS”不显著,表明“食品”对“全面外交关系”的贡献在统计意义上不显著。
三、小结及讨论置换检验与常规统计检验之间存在一定的关系,二者之间的关系可表示如下(参见表 8)。
| 表 8 常规统计检验与置换检验之间的关系 |
QAP研究的范围很广,如可用它来研究拥有共同董事的公司在股票市场上的行为是否类似,或年龄相仿的人是否容易成为朋友等。需要注意,QAP是一种非参数检验(non-parametric test),进行这种检验需要多次随机地对各个输入的矩阵数据进行重新标签,不断地计算检验统计量(test statistic),然后评价大于(小于)或等于观察值的比例。
QAP的前提假设是,在多个图或矩阵基础上观察到的图论层次上的统计量来源于在对全部重新作标签的图集合进行评价后得到的统计量的分布。在解释QAP检验结果的时候,需要注意不要把结果解释为是评价其背后的结构差异。确实,QAP可以被精确地理解为检验在控制已知的矩阵结构的基础上,通过引入一个特定的点的标签的变化引起的结构差异。实际上在所研究的矩阵之间常常存在着实质性的同构。一般情况下,利用QAP来检验两个变量的图统计量的时候不能获得一个单尾显著性水平。反之,QAP下的显著性并不一定意味着观察到的结构关系涉及到从诸如图的规模、密度等典型结构中期望得到的结构关系。当然,如果调查者关注的问题不是“关系”之间的关系,那么就不用QAP进行检验了。
注释:
1 但要注意的是,这里所说的相关是指两个矩阵(作为两个变量)之间的相关,给出的Pearson系数是两个矩阵之间的相关系数。还要指出的是,矩阵中的值是1或者0,而在统计分析的时候通常不用Pearson系数来分析分类变量之间的相关性。但是,考虑到虚拟变量的平均值和方差都是有意义的,因此可以把两个矩阵看成是两个"虚拟变量",视之为"连续变量",在这个意义上也可以进行两个矩阵之间的相关分析。上述Pearson系数就是这样计算出来的。
2 PADGM(婚姻关系)和“PADGB”(商业关系)这两个矩阵并不单独存在于UCINET的数据库中,而是共同存在于PADGETT这个文件之中。因此,在计算之前,需要用“unpack”程序先把这两个矩阵打开,然后才能提交运算,否则是不能计算出二者之间的相关系数的。
刘军.2006.法村社会支持网络[M].北京: 社会科学文献出版社.
|
Borgatti, S.P., M.G.Everett and L.C.Freeman. 2007. Ucinet for Windows: Software for Social Network Analysis. Harvard, MA: Analytic Technologies.
|
Krackhardt, D. 1987. "QAP Partialling as a Test of Spuriousness." Social Networks.
|
——. 1988. "Predicting with Networks: Non-Parametric Multiple Regression Analysis of Dyadic Data." Social Networks.
|
Simpson, W. QAP. http://fmwww.bc.edu/RePEc/nasug2001/simpson.pdf.
|
 2007, Vol. 27
2007, Vol. 27