一、导言

本文基于资源有限和“报”的概念提出一个模型，用以解释中国组织内形成派系的原因，并以计算机仿真方法将此理论描述的派系形成过程建构成正式模型(formal model)。

P.布劳(Blau，1964)的社会交换理论指出，社会交换不同于经济交换，它的回报不能是实时，也不能明确计量，所以不能像经济交易一般银货两讫互不相欠；相反地，一个帮助可能要在很长的时间以后以另一种形式的帮助加以回报，施恩者必须对受惠者心存信心，相信对方的善意，当这个信心获得证实时，信任感也会逐渐建立。你来我往的社会交换，使双方都累积了对方会善意回报的经验，因此信任关系得以建立。这种信任感会使相熟的双方每次在寻找交换的对象时倾向找信任感较强的人，于是一个人会与信任的对象建立紧密联系的交换关系，而排除了大多数一般关系与之交换的机会。

社会交换的概念十分类似于中国人的“报”，该概念是在熟人连带中进行人情交换时最重要的规范(Hwang，1987)。在工具性交换的弱连带中，中国人的社会交换仍然可以明言回报，讨价还价。但是在熟人连带中，这种行为就不被认可，因为熟人间的交换是掩饰在情感关系下的(黄光国，1988；Luo，2005：437-458)，所有得到的好处，都是欠了人情，施惠的一方不好明言，受惠的一方也不能忘记，必须记入“人情帐”中，以待他日偿还。所以当施惠方需要帮忙时，会优先想到向受惠方要求帮忙，受惠方也会“回报”，以展现其感恩图报的诚意，而且回报可能更多，使对方又欠了人情，务必使双方的人情账不能结清，这样，双方的交换关系才会持续很久。熟人连带在这种往复多次施惠、受惠与回报的过程中建立起来，所以双方追求的都是长期的关系，而且“人情账”不能结清，也因此受惠的一方在需要更多帮忙时，除了想到自已曾施惠的对象外，也会想到曾施惠于己的人，欠更多的人情没有关系，只要在长时间中有欠有还，保持“报”的规范，则熟人关系反而能得到增强。

这个理论应用在中国组织内，工作求助是一种组织内非常重要的资源，但却不必然要有情感关系才能传递这种资源，组织内乐于受人求助的员工往往可以得到他人的善意回报，因此求助关系甚至超越情感关系成为员工间产生信任最主要的关系。除此之外，学习曲线理论称长时间且频繁的社会交换能够提高交际的效率，因此过往的合作经验使得此后的交往更加顺利。因此为了降低“交易成本”，个人更倾向于与具有长期关系的人合作(Williamson，1996；Granovetter，1992)。

本文的理论陈述如下，当资源有限时，有人资源多，有人资源少，故前者可以施惠于后者，因分配的不稳定，所以这人另一时间又会变成资源不足者，而须向外求取帮助。根据“报”的理论(罗家德，2006)，参与交换的各方心中都有一笔“人情账”，双边的互助行为使个人间关系越趋紧密，“熟人”间因为有回报的义务而使得个人在向他人提供帮助时，优先考虑那些曾对他施惠的人；而在需要帮助时，也会优先找那些曾经欠他恩惠的人。其次，基于多次交往建立起来的信任，他也会找施惠者再提供帮助，因为施惠者相信他将累积恩惠在“人情账”中，他日偿还。在这种“报”的关系中，人们倾向找旧有的关系施惠、受惠，于是，这些关系不断加强，而减少与其他关系的互动，终至一个人只剩少数互助关系。一群人都只有少数互助关系，且相互重叠，渐渐形成一个内部有互助关系，却很少向外人求助或施惠的团体，派系也由此形成了。

下面本文就以计算机仿真模型来仿真这个理论所描述的派系形成过程。本文假设某组织内有20名员工，均从事类似的工作，可以互相给予工作支持。根据上述资源有限假设与“报”的理论，本文对其行为作如下基本预设：

(1) 当工作量超过个人资源量时，个人向其他人寻求帮助。初始时随机向他人询问；当具备了交往的经验与记忆后，他根据经验与记忆向合适的人寻求帮助。当被询问人有余力时，同样会根据经验与记忆选择优先帮助的对象。

(2) 假设N次的相互帮助在两个人之间建立“熟人”连带——也就是双向求助连带；同样，向同一个人的求助连续被拒绝N次则永远不向这个人求助，也拒绝其求助。

(3) 求助时选择的优先级如下：首先，欠我人情的；其次，我欠人情的；最后为其他人。提供帮助时的优先级如下：首先，我欠人情的；其次，欠我人情的；最后为其他人。

本文选择与工作环境相关的两个变量：一为平均的工作量与资源量的差值，这个差值越大，就表示组织资源相对于工作量而言越显不足；二为工作量分配的方差，方差值越大表示组织外在环境越不稳定，工作量忽多忽少。另外与“报”相关的一个变量N——本文称为“忆阈值”，也就是在一定的组织气氛与文化下个人记恩与记恨的程度，N越大，以此表示人们越不容易记恩与记恨。这些为外生变量，以此可以考察派系形成的数量与时间趋势。

二、方法

行动者的模型(agent-based model)提供了一个很好的考察复杂自我适应系统(complex adaptive system)的理论入门模型。这是一种自下而上的模型，从获取系统中核心行动者的基本行为模式并将其抽象成简单算法开始，生成行动者互动的整体模型。该行动者的模型特别适用于分析由结构相异又可以自我适应的行动者构成的动态系统。这类系统用传统的建模方法通常难以考察(Macy & Willer，2002：58-437)。同时该类模型致力于提供一种理论上的平衡：集体的构型(configuration)大于个体属性的集合；但集体构型又产生个体的关系以及关系的动态变化(同上)。

本文的模型用面向对象的程序语言Java完成。组织中的每一雇员均为模型中的一个独立行动者，当程序运行以后，每一个行动者根据前文所述的行为预设进行互动，在任何时间点均可获得它们的互动信息与集体的网络形态。

(一) 假设、参数与变量

在这种理论模型中，本文探讨前述三个变量如何影响组织中派系的形成。这里首先说明一些环境参数及其背后的模型假设。

(1) 为了控制资源的作用，首先假设每个雇员的资源相同。这里不考虑雇员们能干什么类型的工作。换言之，对于资源没有什么特别的说明，而且任何人在本文的模型里都能从事任何工作。

(2) 第二个假设是每个雇员具有相同的资源量。控制了资源以及其他的个体特征，本文认为所有雇员的资源量是相等的，并且被看成是一个整数。在本文的模型之中，每个雇员的资源量是每天完成十项工作，因此将资源量设为整数10。

(3) 第三种假设是中等规模的小组。组织中的雇员数量在以下所有的模拟实验中被设定为20。

对于模型中的几个外生变量，通过控制它们的值来理解它们在派系形成中的影响。其外生变量的规定如下：

(1) 工作日的数量模型中的“一天”实际上是行动者互动的一个独立时间单位。在“一天”开始就把工作量分给每一个雇员，且不管雇员能否胜任，这项工作不会留到下一天。如果一个人被分给了一份超过了他资源量的工作量时，他将寻求帮助或在下班以后的时间里完成它。而当新的一天到来时，雇员的工作量资源量又重新开始，因而，一天只是一个能被理解为在社会中相互求助的完整过程的抽象时间段。

(2) 记忆的阈值n次互助行为之后，本文认为两人之间建立了双向的求助连带，同时，如果一个人寻求帮助的要求被另外一个人拒绝了n次后，那么他就会把那个人列入他的“拒绝往来户”中，而且今后将会拒绝后者提出的任何要求。换句话说，如果一边的要求被另外一边拒绝了n+1次，一个可能的双向求助连带就会被打断。在本文的试验中，n取值3、5、7或9。

(3) 工作量每一天利用gamma分布¹来为每一个个体设置工作量。Γ(α，λ)分布的均值是α / λ，方差是α / λ²。因此在模型里选择α和λ的值来产生合适的工作量的均值和方差。因为将资源量定为一个常数10，所以工作量的变化代表着资源的有限性。在下列实验里，取α / λ值在7~12之间，它们代表工作量在一个特定运行的模拟实验中的均值。

本文考察的被解释变量是组织中的派系的数量，使用具有超过三个节点的递归连带(recursive ties)的组件(component)²来定义派系。正如社会网络分析里的普通定义一样，如果员工A认为B是其优先求助的伙伴，同时，B也认为A是他的伙伴，这样的话他们就是递归连接。派系即是整体图中的一个递归连接的子图。

(二) 模型结构(规则与步骤)

模型由三部分组成，为前文最初的行为预设提供了详细的规则。

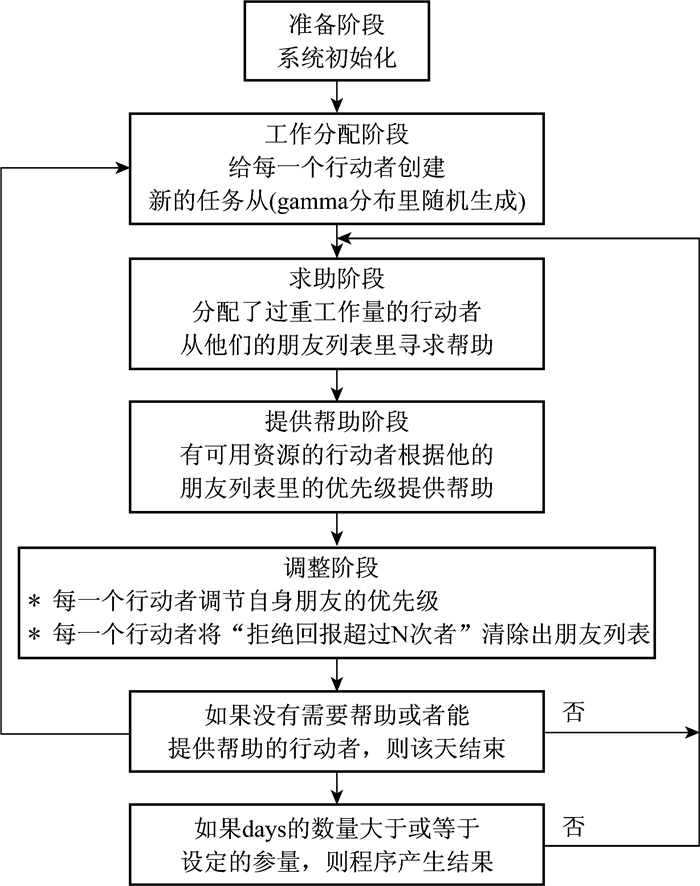
实验模拟的内容是雇员的日常工作生活。在本文的模型中，每个雇员对应一个行动者(agent)。他们首先被分配一定的工作量，然后他们会重复两件事情：如果需要，他们会求助，或者对他人的求助作出响应。据此，我们进行模型结构设计(见图 1)。

(1) 分配工作量在该模型中，每一个行动者有三种属性：资源量、工作量以及可使用的价值(简称可用值，available-value)。资源量值保持为10，而工作量每日根据伽马函数随机为每一个人生成；可用值由资源量值减去工作量得到。如果一个行动者的可用值是负的，那么就将其纳入需要帮助者的名单；反之，则将其列入提供帮助的名单。

(2) 要求与响应在分配任务之后，被设定为需要帮助的行动者开始寻求别人的帮助。他们不会在同一时间向所有人发出求助的信息——这在现实中也是不可能的——他们依次向他人寻求帮助。系统会让所有需要帮助的人向他们的首选者发出求助信号。然后，那些能够提供帮助的人就会处理收到的求助信号，并作出响应。如果自身是需要帮助者收到求助信号，就会拒绝他。经过响应过程，需要帮助却没有得到帮助，或者没有得到足够帮助的人会再一次提出求助。系统会不断重复，直到需要帮助者或提供帮助者人数的一方为零。

上述过程需澄清一些细节。首先，向谁发出求助。规则如下：第一，根据谁欠他(人情)的情况——从多到少来决定；第二，根据他欠谁(人情)的情况——从多到少来决定；最后是那些与他有过平等交往的人或是未交往过的人，随机抽取。每个行动者都会有一个表格用来记录他的朋友。表格中的记录有两部分组成：谁是他的朋友以及与其相关一个数值——朋友帮他的次数减去朋友欠他的次数。对于每一次实验，初始化表格为每一个行动者对所有人一视同仁，即相关值为0。在每次实验最初阶段，求助者随机地选定对象。如果该对象提供了帮助，那么他就给其相关值加1。因此，当一个行动者做出求助时，他首先选择那些相关值为负的，从最小值到最大值，然后选择那些相关值为正的了，从最大值到最小值；最后随机从那些相关值为零的人中选择。

第二，向谁提供帮助。虽然一个行动者在一轮里只被允许发出一个要求，但那些能提供帮助的人在同一时间会收到很多求助。一个行动者按照以下优先级提供帮助：首先，是相关值为正的人们(他亏欠的人)从最大到最小排序；第二，是为负的人们(亏欠他的人)，根据优先权的顺序要求，检查它的有效可用值是否不低于要求的数量，如果不是的话，他发送回馈信息以按要求提供相应数量，从要求者在他的表格里的数值中减1，同时减少自己的可用值。如果可用值仍然不为零，他选择下一个要求者重复以上步骤。如果他的可用值低于所要求的数量，则他只提供与他的可用值相等的数量，然后拒绝剩余的要求者。

求助者会记住所有他提出过求助的人。如果他得到响应，他就会给帮助者的相关值加1，如果没有响应，他就会检查其相关值是否为负。若果为负，则再减1。

要求与响应的过程中有一个很重要的规则：一旦行动者降低了某人的相关值，那么他就会检查其相关值是否低于N。如果是，他就会将其剔除出朋友列表，并不再对其任何要求作出响应。系统还存在多张表格以记录所有发生过的互动信息。

(3) 模拟实验及结果计算。对于每一个实验，根据记录的互动信息与每个行动者的朋友列表，可以生成所有行动者间的关系矩阵。在这个矩阵中，元素α_ij被定义为：

$ {\alpha _{ij}} = \left\{ \begin{array}{l} 1\;\;\;\;\;\;\;\;{\rm{如果行动者}}i{\rm{和}}j{\rm{之间有双向连带}}\\ 0\;\;\;\;\;\;\;\;{\rm{如果}}i{\rm{和}}j{\rm{之间没有双向连带}} \end{array} \right. $

本文通过编写java语言程序由该关系矩阵计算派系数目，然后，运行同一个实验100次，得到100个结果，求取它们的平均值，是为一组外生变量作用下的派系数量的结果。

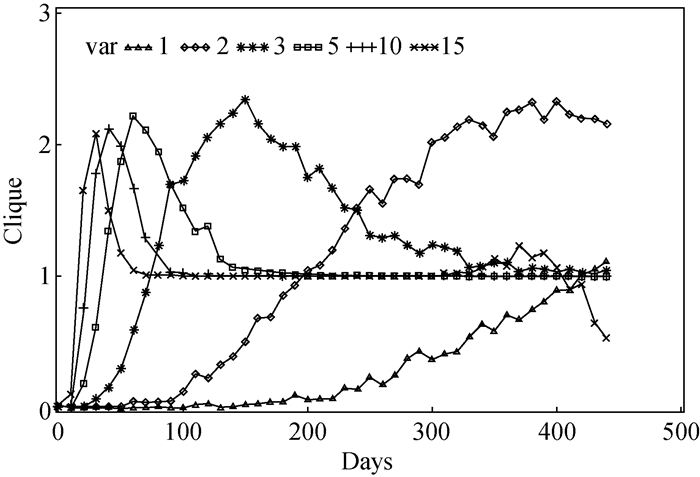
三、实验结果与分析 (一) 工作分配方差对结果的影响作用

图 2显示的是当工作量均值为8，记忆阈值设为3，分配方差分别为1、2、3、5、10、15时，在0－450天内的派系形成过程。在第0天时，由于行动者间相互不熟识，因此派系数目为0。随着时间的推移，派系数目上升。从图 2可以看出，当方差较小，例如为1或2时，派系数目增加得很缓慢，行动者间“熟识”的过程很长，较长时间内行动者处于陌生与孤立状态。当方差居中，例如取3、5、10，这时在短时间内行动者的双向互动大大增加，派系数目很快上升到一个峰值，接下来由于跨团体间的互动，使得派系之间又联合在一起，因此最后形成全部人的团结(或可能是多数人的团结与极个别人的孤立)，实际不再存在派系。如方差为5和10时，分别在100与150天后进入仅存在一个团体的稳定期。当方差取15时，可以看到在稳定期之后出现了第二个峰值，而随后派系数目又快速下降。第二个峰值的出现主要是“记恨”产生的效果，当工作分配的差异性太大，每一天中的求助不能满足的次数增加，使得相互记恨的可能性增加，因此团结的行动者又开始出现分裂。在分裂的派系里的持续互动，由于可用的资源进一步减少，致使派系持续不断地分裂，直至一盘散沙(派系数为0)。

基本上每一个方差值都表现出上述的发展模式，唯一不同的是方差值越大，越早出现派系，也越早团结成一体，更越早因记恨而使互助关系瓦解，成为一盘散沙。方差代表了工作分配环境的不稳定性，其结果表示，工作分配稳定性与时间成反比，越不稳定的环境会越快走完上述的发展历程。原因是，在不稳定的环境中，人们求助的需求较大，一个人一时段内“闲”下来而能施惠的机会也较多，所以互动频繁，因记恩而结盟，因记恨而背盟的情况较多，发展历程走得较快。

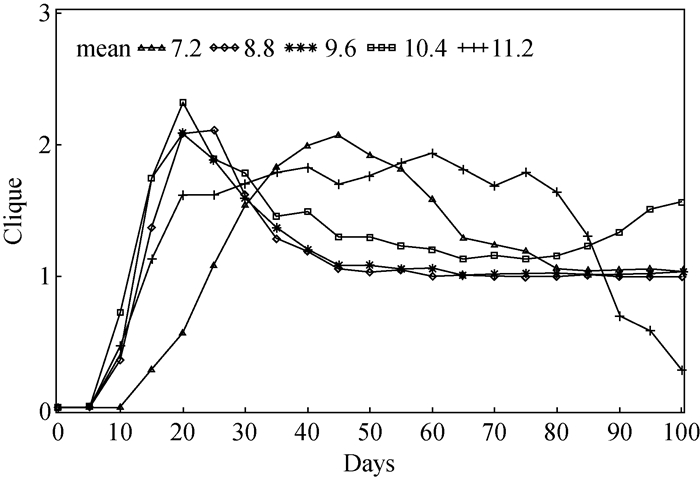
(二) 工作量均值对结果的影响作用

图 3显示当工作分配的方差设为15，记忆阈值设为3，工作量均值分别为8.8、9.6、10.4与11.2时，0－100天内派系形成的过程。可知，当平均工作量小于资源量10时，即取8.8与9.6时，图形与图 2中方差为5与10的情况类似，即行动者先通过互动熟识，再团结成最大的团体；当取较小的均值7.2时，其趋势明显趋缓。而当均值为10.4时，在第一个峰值后，派系数目一直大于1，即没有出现所有人团结的情况，随后出现第二个峰值。当均值更大，例如取11.2时，趋势完全改变，派系数目在较长一段时间内保持较高的值，随后直接进入分裂与孤立阶段。

工作量均值大，表示提供给员工的资源相对不足，代表了资源缺少的程度，均值很大则资源不足以应付工作；相反，均值小代表资源相对于工作量十分充足。从仿真中可以看到，在资源充足时，一开始会形成派系，但很快地就因为大家都有多余资源支持别人，而团结成一体。当均值接近10，如达到9.6时，派系存在的时间相对变长，而如果达到10.4时，则派系一直存在。然而资源变得不太充足时，固然也会有一段派系存在的时间，却最终会迅速解体，变成散沙一片。

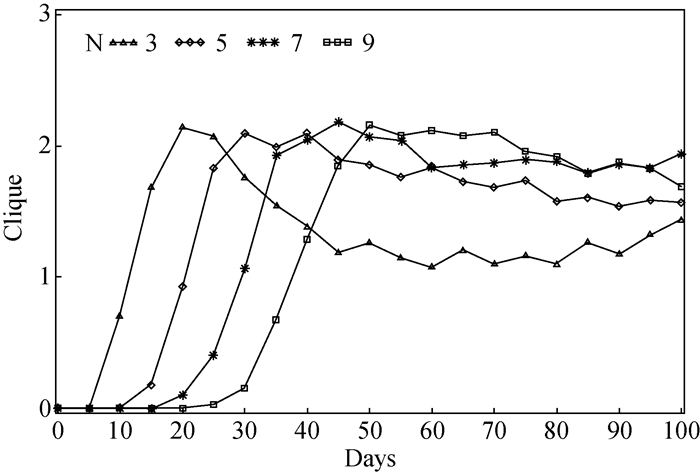
(三) 记忆阈值对结果的影响作用

图 4显示的是当工作量均值为9.8，分配方差为15，N值分别取3、5、7、9时的0－100内的派系形成过程。当记忆阈值N值是3时，很快形成派系，但随即派系数下降，在有派系与团结一片之间来回振荡。当记忆阈值N值增大，由于建立连带的门槛提升，因此从图 4可看出图形不断向右位移。N值越大，行动者对于交往者拒绝的忍耐度提高，而对于团体接受新成员的门槛也随之提高，因此N值比较大时，派系数目几乎在峰值上维持较长一段时期，从而形成一个组织中稳定存在派系的局面。记忆阈值表示一个团体报恩与报仇的倾向，记忆阈值低，则表示团体成员很快会结盟，但也很不宽容别人的“忘恩负义”；相反，记忆阈值高，则表示该团体成员结盟比较谨慎，但也比较宽容。

四、讨论 (一) 结论

从模拟模型的结果可以看出，组织内倾向与“熟人”交换的行为方式在一定条件下会造成“排他性”，从而使得组织内出现派系，而派系的出现、数目、时间趋势，与工作环境因素及组织中“报”的气氛均有关，并且可以看出该互动系统具备一定的复杂性(Macy & Willer，2002：58-437)。当设置的外生变量值在一定范围内变化时，系统的改变呈线性状态；但当外生变量值超过一定的阈，则系统发生根本性转变。

本文的仿真模型在理论上描述了在一个资源不足的环境中，人们因相互间施惠、受惠与回报而形成关系，最终会因一些外在因素而使得派系产生，仿真结果至少提供了三个理论推导出的命题。这些命题如下：(1)工作分配的稳定性与时间成反比，在工作分配不稳定的环境中，派系生成的速度明显加快。(2)在其他同等条件下，当工作量接近或略超过平均资源量时，派系存在的时间很长，系统更可能处于不稳定状态。工作量低，会很快形成团结，工作量太高，则很快趋向松散，派系存在的时间都相对较少。(3)由记忆阈值的影响作用可以看出，在谨慎宽容倾向比较高的组织气氛里，成员之间虽然形成派系较慢，但派系也不易瓦解，所以派系存在的时间反而较长。

因此，本文推论一个组织在资源有限却又不会太稀缺时，及组织气氛表现得谨慎结盟却又不易闹翻时，在组织生命周期里，派系存在的时间较长。

(二) 理论模型限制

这一个理论模型指出了中国人形成派系的原因是资源有限下资源交换时，施惠、受惠与报恩报仇的结果。然而这与我们对中国人的派系的了解仍有一些距离。首先，中国人的派系其实都是起源于扈从体系，一个有权力分配资源的人在资源有限时，会成为很多人依附的对象，所以一群人形成派系往往不只是为了求助与受惠，更是为了取得资源分配者对其工作量作有利的分配，也就是为了取得更多的资源。本模型中，资源分配过程采取随机分配，并无资源分配者的扈从体系，此一解释模型的后续发展应纳入一个与扈从体系相关的资源分配过程。

其二，派系总留给我们一个印象即“只问立场，不问是非”。派系集结既然是为了依附资源分配者以争取到更多的资源分配，所以派系成员会竭力争取派系利益，以扩大可分配的资源，不惜牺牲非派系成员的利益，甚至破坏法制与规范，变成不问是非地维护派系利益。这种行为自然会引发别人也集结成派系，依附在其他资源分配者身边以相对抗。这种排挤非派系成员的资源争夺，以及在不同派系间可能有的资源争夺，在本文的模型中也未展现。

其三，如果一旦有了派系之间的对抗或形成对非派系人员的排挤，则报仇的行为会被激化，因此报恩与报仇行为不再适合仅以记忆阈值来表现某一组织“报”的文化，而可能报恩记忆阈值与报仇记忆阈值会有所不同，而且对派系成员与派系外人员的记忆阈值也会不同。这样的模型会更接近现实，但也会使模型更复杂，有待未来加以改进，将上述的现象都纳入考虑之中，使之更接近现实。

然而本文仍然提供了一个基础的模型，表现了在资源有限的情况下，“报”的行为所造成的派系形成的过程，可以作为未来类似模型的一个发展基础。计算机仿真模型是使理论正式化(formalization)的有效工具，但是正如理论的建构需一步一步发展完善那样，模型建构也需要一步一步复杂化，使之更贴近现实，这有待于未来的研究加以改善，也需要实证工作者将这样的理论转化为假设，并在组织中收集资料，以实证资料证实这个理论的准确性。

注释：

1 Gamma分布：Γ(α，λ)定义为：如果一个随机变量X拥有一个这样的一个密度函数：$f\left(x \right) = f\left({x;\alpha, \lambda } \right) = \frac{{{\lambda ^\alpha }}}{{\mathit{\Gamma }\left(\alpha \right)}}{x^{\alpha - 1}}g{e^{ - \lambda t}}\;\;\;\;\;0 \le x \le \infty ;\alpha, \lambda > 0$则$\mathit{\Gamma }\left(\alpha \right) = \int_0^\infty {{x^{\alpha - 1}}{e^{ - x}}} dx$称为gamma函数。

2 相关的定义来自于《社会网分析：方法与应用》(Stanley Wasserman & Katherine Faust，1994)一对点n_i，n_j为：(1)强连接。如果n_i到n_j有一条路径，并且n_j到n_i也有一条路径。n_i到n_j的路径可能包含着从n_j到n_i不同的节点。(2)递归连接。如果它们是强连接，并且从n_i到n_j的路径与n_j到n_i的路径经过同样的节点。一个有向图(A directed graph)为：(1)强连接。如果所有节点间连接都是强连接。(2)递归连接。如果所有节点间都是递归连接。