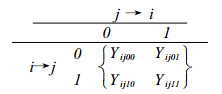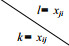社会科学的定量研究中都涉及到“分析单位”的问题。分析单位是什么?对这个问题的回答,一方面要看研究的对象是什么;另一方面又要结合社会研究中的资料类型来分析。总的来说,社会科学研究中的数据有多种,因而对应着不同的分析单位。
一、三种数据类型J·斯考特(J·Scott,1992:3)认为,社会科学数据可以分为“属性数据”(attribute data)、“关系数据”(relational data)和观念数据(ideational data)三类。属性数据指的是社会行动者1(social actor)自身拥有的态度、观点以及行为等方面的数据,它们一般被视为社会行动者内在的性质、特点,如一个人的收入、教育程度,或一个国家的GDP等。与属性数据对应的变量可称为属性变量(attribute variable)。对属性数据进行定量分析的方法主要是一些传统的“变量分析”(variable analysis)技术,确切地说是“属性变量”分析技术。这要用到许多常见的统计方法,如多元回归、方差分析、鉴别分析和路径分析等。
社会行动者不是孤立存在,而是处于各种关系之中的。关系数据是关于行动者之间的联系的数据。由于这类数据至少要涉及到两个行动者,因此,此类数据不能还原为单个社会行动者的属性。
属性数据是我们熟悉的,不管它表现为定类数据、定序数据,还是定距数据,分析它的方法都是比较完善的。对于中国人来说,我们似乎很熟悉“关系”,但是,对关系数据的量化研究在国内才刚刚起步(贺寨平,2004;刘军, 2004a, 2004b;罗家德,2005)。国内学界对关系数据的分析主要是定性的分析(丘海雄等,1998)和“个体网络”意义上的统计描述和统计推断分析(张文宏、阮丹青,1999),在整体网络研究方面是比较薄弱的。
J·斯考特认为,第三类数据是观念数据(ideational data),它描述的是意义、动机和定义等。虽然此类数据在社会科学研究中也占据重要地位,但是,分析它的方法更为欠缺。
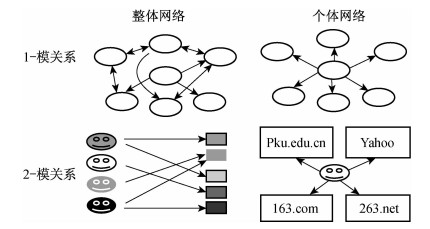
本文主要针对前两种数据进行分析,重点放在“关系数据”。根据不同的标准,“关系数据”可以分为多种类型,比如根据关系的“方向”,可分为有向关系(如借款关系)和无向关系(朋友关系);根据关系的“紧密程度”,可分为二值关系(关系“有”和“无”)和多值关系(关系“很好”,“较好”、“普通”、“无关系”);根据关系的“种类”,两个社会行动者之间可能存在单种关系(朋友关系)和多种关系(例如同时存在“朋友关系”、“借款关系”和“邻居关系”);根据关系的“构成”,可分为1-模(1-mode)关系(同一个行动者群体内部成员两两之间的关系)数据和2-模(2-mode)关系(两个行动者群体之间的关系)数据,后者的特例是隶属(affiliation)关系(即一个群体的成员“隶属于”某些团体的数据);根据关注的“角度”,亦可分为个体网络(以个体为中心的关系网络——以下简称个体网)数据和整体网络(一个群体内部所有成员之间关系网——以下简称整体网)数据。将后两种分类的角度结合起来,可以得到交互分类图式,如图 1所示:
|
图 1 网络数据的交互分类 |
与关系有关的变量可以称为“网络变量”(network variables)。用来分析这些关系数据的方法就是发端于20世纪30年代、并且从20世纪80年代以来有重要突破的社会网络分析(social network analysis)(刘军,2003;2004a)。
在个体网研究中涉及到一些网络变量。例如可以把个体网的密度、规模、同质性等看成是网络变量。在整体网研究,特别是P模型研究2中,网络变量至少可以包括如下5类。
(1) 个体层次网络变量,它又包括两类,可以分别称为“扩张性变量”和“聚敛性变量”。举一个例子,在朋友关系网中,假设有一个人有很强的向外发出关系的趋势,即有很强的主动选择他人作为朋友的趋势,我们就说此人有很大的“扩张性”(expansiveness),与之对应的变量就是扩张性变量;假设有一个人有很强的向内回收关系的趋势(例如他声望很高,很多人选择他为朋友),就称此人有“聚敛性”(attractiveness),与之对应的变量就是“聚敛性变量”。
(2) 双边关系网络变量(dyadic network variables)。假设两人之间存在相互选择对方作为朋友的趋势,并且在实际中互选对方为朋友,也就是说二人之间存在互惠性变量。
(3) 三边关系网络变量。三个行动者之间所有可能存在的二值有向关系,包括16个同构类(Wasserman & Faust,1994:566)。其中具有明确的理论解释意义的占一小部分,如关系的“传递性”(transitivity)、“出-2-星”(2-out-star)等(见图 2所示)。具体地说,如果A选择B作为朋友,B选择C作为朋友,并且A认为朋友的朋友就是自己的朋友,于是也选择C作为朋友,那么这就是一种传递关系,与这三个人之间的这种传递关系对应的变量叫做“传递性变量”。要注意的是,该变量是由3个行动者构成的,三者缺一不可。又如,假设A有很强的扩张关系网络的动力,于是在选择B作为朋友之后,又选择C作为朋友,可见,A有两个向外发出的朋友关系,与这种关系类型对应的变量叫作“出-2-星变量”。

|
图 2 |
(4) 块网络变量,在一个网络中可能有很多子群体,与子群有关的一些变量叫做“块”(block)层次网络变量,例如块内的互惠度、块内“出-2-星”变量等。
(5) 整体网络变量,整体网络中存在的总体的结构趋势,例如总的关系数目。3
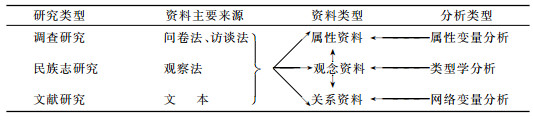
虽然数据类型可以有多种,每种数据又有其独特的分析方法,但是,各种数据的收集方法并不见得有什么独特之处。例如,问卷法、访谈法、参与观察或者文献分析法等都可用于收集多种数据。上述论述可以总结如表 1所示(Scott,2000:3,引用时稍加修改)。
| 表 1 社会研究资料类型及分析方法 |
数据类型不同,与之相应的分析单位也各异。纵观社会学方法方面的文献,可以梳理出两种关于“分析单位”的观点,笔者分别称之为“点”分析单位观和“关系”分析单位观。前者把分析单位看成是一个“点”,不管该“点”表现为独立的个人、群体、组织、社区,乃至民族国家。这种视角把“点”看成是独立存在的,只描述“点”的各种属性,而不关注各个点之间的“关系”。后者的着眼点恰恰是各个点之间的“关系”,研究“关系”的特点或者结构。笔者以为,这种“关系式的”分析单位视角可以在一定程度上补充“点分析单位观”的不足,更能推进我们对“分析单位”的认识。用来分析关系数据的社会研究范式就是当代社会学的一个重要分支学科——社会网络分析。以下在简单分析“点”单位观之后,重点考察“关系”单位观,最后对二者之间的关系进行比较分析。
(一) “点”分析单位观“单位”大体上指的是“单个人或者对象”、“一群人或者对象的集合”。而“分析单位是研究者所要调查和描述的对象,它是研究的基本单位,研究的最终目的是将这些分析单位的基本特征汇集起来以描述由它们组成的较大集合体或解释某种社会现象”(袁方,1997:150-151)。“分析单位是研究者所要了解的一些个案,它在很大程度上决定了研究方案的制定”(袁方,1997:153)。
问题在于,什么是“对象”或“个案”?什么是“基本单位”?对此的理解见仁见智。从字面上看,“基本单位”指的是相对独立的“基本”的对象。在社会学中存在多种对分析单位的分类学意义上的看法。但是,这些分类或者可能出于对研究兴趣的考虑,或者出于对研究重点的关照,因而基本上都把“分析单位”看成一个个孤立“点”,分析“点”的各种“属性”特征,不关注“关系”。例如,“社会学的分析单位至少有7类:个体、群体、组织、制度、空间、文化以及社会单位等都是分析单位”(Rosenberg,1968:242-247);“社会研究中的分析单位包括:个人、群体、组织、社区以及社会产物等”(袁方,1997:151-153);“社会研究的分析单位包括:个体、群体、组织、社会产物等”(巴比,2000:119-123)。
我们称上述观点为“点”分析单位观。在这种观点看来,分析单位是具有明确边界的作为一个整体而独立存在的实体,因而可以抽象地看成是一个“点”。不管该“点”表现为个人、群体或是正式的组织,它都是作为一个整体而独立存在的,因而可以描述性或者解释性地研究它的各种属性特征。很多关于社会研究方法和统计分析方面的著述也基本上是从这个角度来理解分析单位的。
(二) “关系”分析单位观“点”分析单位观不研究各个“分析单位”之间的联系。而如果研究社会网络,关注的焦点则是各个“点”之间的“关系”(tie)。关系是“网络分析的基石”(Knoke and Kuklinski, 1982:11)。因此,本文坚持一种“广义”的分析单位观,把“关系”也看成是分析单位。4
1.分析关系数据的技艺——社会网络分析
社会网络分析把关系作为研究的核心,发展出一整套系统地收集、整理、分析关系数据的技术和方法,这也是它的独特之处。但我们认为,社会网络分析不单纯是一套对关系数据进行量化分析的技术和方法,它还是一种含义更广的研究范式,因为社会网络分析在本体论、认识论以及方法论上都有自己的独特之处(刘军,2004:12-26;Wellman and Berkowitz, 1988),尽管这些独特之处没有引起网络学者的充分关注。例如,网络的结构在一定程度上影响“点”的行为和态度;世界是由网络构成的,而不是由群体构成的;网络研究可以沟通“宏观”和“微观”之间的连接,提供很多“中层理论”(罗家德,2005:第一章)。因此,社会网络分析在社会科学的诸多领域已经得到了广泛的应用。
在“关系单位观”看来,社会分析的单位主要是双边关系(dyads),在此基础上可以考察三边关系(triads)、“块模型”(blockmodel)关系以及整个关系网络。不管怎样,在处理关系数据的时候,都是以两个行动者之间实际发生的关系为基础的。而社会关系研究的“内容”主要是“关系”的各种属性特征和结构特征。关系的“属性特征”指的是关系的“类别属性”,如“收入”、“声望”等;关系的“结构属性”指的是前述5个“网络变量”,例如“扩张性”、双边关系(dyads)的3个同构类、三边关系(triads)的16个同构类以及“块”的各种属性等。各个网络统计量的含义参见瓦瑟曼和帕梯逊(Wasserman,S. & Pattison,P.E.,1996)的相关著作和论述。因此,此类研究需要特殊的方法,这恰恰是“社会网络分析”的任务。
2.分析“关系数据”的具体步骤(以P1模型为例)
对关系数据的分析在哪些方面不同于对“属性数据”的分析?下面简要探讨这个问题。实际上,“关系资料”类型的不同,表达关系资料的方式以及分析资料的方法也不甚一致。针对“个体网络资料”,如个体网的“规模”、“同质性”、“构成”等特点,可以利用常规的SPSS软件进行分析;针对整体网络资料,应该利用“关系矩阵”表达数据,利用专有的软件(如UCINET、STRUCTURE等)和特定的分析程序进行分析。以下结合P1模型,用一例子展示整体网络数据的表示方法和处理过程。
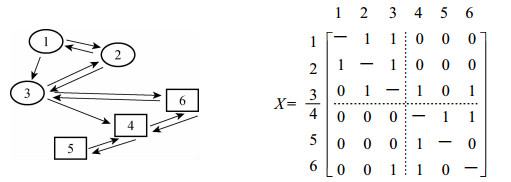
(1) 构建数据矩阵,构建P1模型。假设我们有一个由6个村民家庭构成的“整体”。图 3表达的是这6个家庭之间的“帮工关系”及与之对应的“帮工关系矩阵”。我们假设“1、2、3、4、5、6”分别代表着两个家族中的6个家庭,其中,“1、2、3”属于B家族,“4、5、6”属于C家族。箭头指向谁,意味着给谁帮工。例如,“1”指向了“3”,这意味着“1”向“3”帮工,相应地,在矩阵中的第1行第3列的值就是“1”。反过来,“3”没有指向“1”,这意味着“3”没有反过来帮助“1”,相应地,在矩阵中的第3行第1列的值就是“0”。由图可见,很多村民之间的帮工关系是相互的,如“2”和“3”,“4”和“6”等。该数据矩阵代表的就是整体网数据。
|
图 3 6户村民之间的帮工关系及帮工关系矩阵 |
问题是,该关系网络中的各种结构在多大程度上影响着帮工行为?例如,同一家族的三个家庭之间是否更容易相互帮工?尽管我们可以从多个角度研究这种趋势是否存在,但是,社会网络分析中的P1模型可以在统计的意义上检验上述假设是否成立(参见Anderson,Wasserman & Crouch,1999;Robin,Pattison & Wasserman,1999)。
P1模型最早是由霍兰德和雷因哈泽(Holland,P.W. & Leinhardt,S.,1981)及费恩伯格和瓦瑟曼(Fienberg,S.E. & Wasserman,1981)提出来的。该模型考察的是有哪些因素(即扩张性α、聚敛性β以及互惠性ρ等三个参数)使得某个“二方组”处于3种同构类中的一种。然后,我们把这些因素结合在一个概率对数模型当中。P1模型利用二方组概率的自然对数作为基本的模型单位,给出的是当行动者j以某种强度选择i的时候,i选择j的概率的自然对数形式。以下就是针对二值有向关系的P1模型:
log P(Yij00=1) = λij
log P(Yij10=1) = λij+θ+αi+βj
log P(Yij01=1) = λij+θ+αj+βi
log P(Yij11=1) = λij+2θ+αi+αj+βi+βj+ρ
该模型中各个参数的含义为:参数λij是数学上的必要条件,它保证上述4个概率对于每一个二人组来说总和为1;密度(density)参数θ代表关系在网络中存在的可能性,反映总选择趋势,它相当于在对数线性模型中的主效应,即总平均值;ni和nj的“扩张性”(expansiveness)参数αi和αj,反映每个行动者扩展自己关系网络的趋势;ni和nj的“聚敛性” (attractiveness)参数和βi和βj,反映每个行动者被网络成员选择的趋势;二者之间存在“互惠效应”(reciprocal effects)参数ρ,则反映整个网络的互惠趋势(Wasserman & Faust,1994:614)。对这些参数进行估计的技术是对数线性模型技术。总之,i有一个指向j或者来自j之关系的概率的对数形式就变为包含i和j的扩张性参数α、聚敛性参数β和二者之间的互惠性参数ρ等的加法函数。
值得指出的是,密度参数θ在第一个方程中不存在,因为在该方程中不存在“关系”。互惠性参数ρ仅在第4个方程中存在,这也不难理解,因为只有此方程才包含两个行动者之间互选的情况。另外,还要给出上述方程的限制性条件,即Σiαi = 0,并且Σj βj = 0。
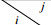
(2) 构造Y阵列。在对P1模型进行拟合检验的过程中,不是直接针对“关系”来进行分析,而是要经过各种数据转换过程的。首先要把上述的关系矩阵转换为Y阵列(Y-array),然后再利用对数线性模型(参见郭志刚,1999:215-256)进行拟合检验(参见Wasserman & Faust,1994),这可以用网络分析软件UNINET轻易地完成。在上述模型中存在Yijkl(k,l = 0,1)这一项,它实际上就是为了拟合检验上的方便而由费恩伯格和瓦瑟曼(1981)给出的一种新的记法,即在与整体网数据对应的G×G矩阵的基础上,构造一个新的G×G×C×C维度的交互表Y = (Yijkl),称之为Y阵列。5建构Y阵列的目的是为了把网络数据转换成交互表中的“频次”数据,从而可以利用对数线性模型进行拟合检验,其中的i和j是两个行动者,而k和l指的是i和j之间关系的几种状态。具体地说,Y阵列的定义是,从矩阵X中引出一个满足如下条件的新矩阵Y:
| $ {{\rm{Y}}_{{\rm{ijkl}}}}{\rm{ = }}\left\{ \begin{array}{l} 1\;\;\;\;{\rm{如果}}{{\rm{D}}_{{\rm{ij}}}}{\rm{的取值:(}}{{\rm{X}}_{{\rm{ij}}}}{\rm{ = k, }}{{\rm{X}}_{{\rm{ji}}}}{\rm{ = 1)}}\;\;{\rm{0}} \le {\rm{k, 1}} \le {\rm{C}} - 1\\ 0\;\;\;\;其他 \end{array} \right. $ |
可见,Y阵列是一个含有4个变量的交叉分类列联表(Wasserman and Faust, 1994:608-610),其取值Yijkl有4个下标:作为发出者的行动者(i),作为接受者的行动者(j),以及两个关系网络变量Xij (用第三个下标k标记)和Xji(用第四个下标l标记)。因此,Y的结构与社群矩阵类似,其“行”代表发送者,“列”代表接受者。在一个社群矩阵X中,其第i,j项的取值为xij,但是在Y阵列中,其取值就不是单个值,而是C×C子矩阵,该子矩阵中只有一个1,其余C2-1项都是0(见表 2)。例如,如果Dij是一个互惠对,那么Yij11 = 1(此时的C=2,因为此时我们研究的是“二值关系数据”)。
| 表 2 Y阵列中子矩阵的取值规则(2×2矩阵) |
下面以前文介绍的“6位村民之间的帮工关系”为例,6说明Y阵列到底是如何构造的,该例可以使我们对Y阵列有更清晰的认识。假设这6位村民的代号分别是1、2、3、4、5、6,他们之间的帮工关系矩阵如图 3所示。令n1=1,n2=2,n3=3,n4=4,n5=5,n6=6。由此矩阵可见,村民3向村民4提供帮工,即x34=1;反之,3却没有得到4的帮工,即x43=0。可见,二方组D34=(x34,x43)=(1,0),因此,y3410 = 1,在n3和n4交叉处的子矩阵的其余三个值都是0。其他子矩阵中yijkl的取值依此类推。按照上述Y阵列的定义,我们就可以构造出这6个村民家庭之间的帮工关系的Y阵列,这是一个对称矩阵,如表 3所示:
| 表 3 6位村民家庭之间帮工关系的Y阵列 |
这是一个6×6×2×2维的表格,因为行动者是6个村民家庭(i,j = 1,2,3,4,5,6),发出关系的“强度”和接受的“强度”都是二值的(即C = 2)。在Y阵列中包含6×6 = 36个2×2子矩阵,在每一个子矩阵中,都包含一个1,其余3个都是0。另外,在对角线上的子矩阵都用小横线(-)来代替,因为我们认为自己不“帮助”自己。
Y阵列有几种边际值(margins)。这些边际值是Y的各个元素之和,并且用包含(+)的小下标表示。例如,y++k+表达的意思是,对每一个k来说,y取遍所有的i,j,l后的值的总和。这样,{y++k+}这个边际值给出的就是与各种关系强度k = 0,1,…,C-1对应的关系的数量。例如,在上表中,{y++k+}的边际值是:y++0+=18;y++1+ =12。这些数字告诉我们,强度是k=0的关系有18个,强度是k=1的关系有12个,这两个值分别对应的是上述“6位村民之间的帮工关系矩阵”中“0”的数目和“1”的数目。
(3) 提交给对数线性模型程序进行拟合检验。我们还可以看看yi+k+这个边际值。下面给出的边际值是每个村民的“关系存在”(k=1)和“关系不存在” (k=0)的数目:
| 表 4 6位村民家庭之间帮工关系的Y阵列的边际值 |
最后一步是把这个2行6列的数据提交给对数线性模型进行检验,本文利用UCINET软件(Borgatti,Everett,and Freeman,2004)中的P1模型程序进行拟合检验,计算出来的主要结果经过整理如下所示:
G2(df:33)=25.80,θ=2.8377,ρ =5.0698
每个点的扩张性参数和聚敛性参数如下:
| 表 |
层次聚类分析的结果为:

|
对于有向关系来说,我们关注的是行动者的“扩张性”、“聚敛性”和关系的“互惠性”这三个效应在多大程度上影响关系的发生。在计算结果中给出了每个点的扩张性参数α和聚敛性参数β。例如,村民1的扩张性参数最大,达到1.239,这说明该村民拥有最大的帮助他人的趋势;其次是村民3。村民4的聚敛性参数最大,达到1.896,说明他拥有最大的得到帮工的趋势;其次也是村民3。
互惠性参数ρ等于5.0698。由于它测量的是整个网络的互惠趋势,该参数既然是比较大的正数,说明在帮工关系中存在很大的互惠性。整个网络的密度参数θ等于2.8377。这个参数反映的是网络密度趋势,相当于对数线性模型中的常数项。
需要注意的是,对上述参数的解释不同于常规的解释(参见郭志刚,1999;Wasserman and Faust, 1994)。如果某个参数为正数,其作用是使该参数对应的频数增加。但是,由于这些参数是对数形式的,因此,这种“增加”也不是线性的。具体地说,如果参数α增加一个单位,例如从1增加到2,那么一个“关系”发生的概率的对数也增加一个单位,或者说,实际的概率增加了e1 = 2.718个单位。例如,村民1的扩张性参数值为1.239,其含义为:如果参数α1增加一个单位,比如从1增加到2,那么第一个村民发出“关系”的实际概率将增加e1.239个单位。对其它参数的解释也类似。
另外,从层次聚类分析的结果可以看到,村民1,2,3可以归为一类,村民4,5,6可以归为另外一类。这个分析结果可使我们对村民们的分派情况有大致的了解。
最后有一点需要指出,P1模型由一个重要的前提性假设——“二方组独立性假设”,即两个二方组之间要求是独立的,否则不能进行P1模型分析。后续模型(P*模型)正是由于不需要这种假定,因而推进了P1模型(参见Anderson,Wasserman & Crouch,1999;Robin,Pattison & Wasserman,1999)。
(三) 两种分析单位的比较“属性数据”和“关系数据”可能同时出现在一项研究之中,二者是互补的。与之类似,“点”和“关系”也是相互补充的。对“关系”的研究离不开对“点”的分析,但又不等于对“点”的分析。对社会行动者既可以从属性的角度进行研究,也可以从关系的角度进行探讨,二者各具特色,相互之间无优劣之分。在笔者看来,通过对各种“网络变量”的研究,我们可以更深入地揭示社会行动者之间的社会结构。7
例如,在研究大尺度社会空间中的社会分层状况的时候,我们完全可以从“收入”、“声望”、“职业”等属性变量的角度加以分析,这是当下学者所熟知并可行的研究方式;而如果研究一个社区中的社会分层的具体细节,我们就可以从“关系”的角度进行分析,这种研究可能得到更细致的结论。例如,笔者根据“贷款关系”,利用社会网络方法研究了黑龙江省一个拥有103户家庭的自然村落在2002年末的社会分层的整体情况,得到如下结论:该村村民分为三个阶层:(1)由4户组成的“富有阶层”团体,他们相互之间具有亲属关系,共同向外发放高息民间贷款;(2)60多户“中等户”,他们基本上没有欠债,或许有少量存款;(3)其余都是“贫困户”,他们每年都要举债度日。显然,这种研究更细致一些。当然,如果研究一个拥有十万人的社区中的分层情况,我们只能利用“收入”、“声望”等变量,而不能利用网络方法。
总之,无论是“属性研究”,还是“关系分析”,二者各具特色,可视之为两类研究。二者之间的关系可总结如表 5所示:
| 表 5 两类分析单位及其研究内容对照表 |
本文探讨了作为整体网研究对象的“关系”,认为对“关系”的分析往往不同于对“点”的分析,并结合P1模型分析了关系数据的具体处理过程。需要补充说明的是,个体网研究可以进行随机抽样,因而可以做“统计推断”;整体网研究往往不能通过随机抽样的方式获得资料,因此,严格地说,其研究结论不具有“统计推断”的价值。尽管如此,我们认为整体网研究具有自己的适用范围,即它适用于研究一个群体内部网络的整体结构,或者说适用于研究小群体。尽管随着电脑技术的发展,我们越来越有能力分析更大的整体网,但是随之而来的问题是,在调查大的整体网络的时候,数据的收集、整理和测量和拟合检验等都变得很困难,罗家德(2005)已经指出这一点。然而,如果研究者的目的是为了获得对“整体”的充分认知,那么“整体网”研究无疑是可行的,并且这种研究是对“个体网研究”和“属性数据研究”的有效补充;另外,如果承认“麻雀虽小,五脏俱全”,那么通过对“典型案例”进行整体网研究,我们或许能得到某种“共识性”的、具有局部“普遍意义”的关系模式,因而在“一定意义上”获得对其它类似现象的认识。
注释
1在社会网络分析者看来,社会行动者既可以指个人、群体,也可以指社区、城市,乃至国家等。
2整体网研究的内容很多,在下文表 5中给出的五类网络变量(参见表 5“研究内容”一列中关系[单位]一栏)只是针对其中的一种模型,即所谓的P模型研究(该模型从量化的角度研究双边关系、三边关系、子群关系等网络结构属性与行动者的行为之间有何相互影响)来说的。其它类型的整体网研究(如子群研究、三边关系研究、核心边缘结构研究)一般不涉及这些变量。
3至于如何利用这些变量及相关模型对关系数据进行拟合检验,则是另外一篇文章的工作,对这些变量的具体解释,参见Wasserman & Pattison,1996;Robin,Pattison & Wasserman,1999;Robin & Pattison,2002。
4尽管有学者(Rosenberg,1968:246)已经指出,可以把各种“关系”(如人际关系、婚姻关系、区域关系、国际关系等)作为分析单位,也可以把不同层次的分析单位之间的关系作为分析单位,但是,本文之所以明确提出“关系”分析单位观,一方面是考虑到对“关系”分析的重要性,而上述对各种“关系”的研究多数只是“质的研究”或者描述性的统计分析,并且在笔者看来,这种观点背后所坚持的分析方法仍然是对各种“属性变量”的分析,而不是社会网络意义上的对“关系”的分析;另一方面是由于进入20世纪90年代以来,西方社会学领域对“关系数据”的量化研究已经大大地突破了“统计描述”的局限,达到根据“网络变量”进行“统计推断”、对“多种关系”、“多值关系”和“隶属关系”进行统计推断的程度。
5其中“array”可以译作“数字排列”、“数组”、“阵列”等。考虑到这里要构造一个新的矩阵排列,因而权且译为“Y阵列”。这里的G指的是整体网络的“规模”,C指关系的“强度”。例如,如果研究的关系有“好”、“一般”、“无关系”这三类,那么C=3。
6该例参考了瓦瑟曼和佛斯特在1994年出版的《社会网络分析》一书中的举例(Wasserman & Faust,1994:610-612)。
7社会网络分析意义上的“社会结构”指的是“社会行动者之间实存或者潜在的关系模式。”
8此处所说的社会网络的研究内容主要指的是“整体网络”的研究内容。“个体网络”研究主要关注的是个体的各种网络属性特征,如个体网络的规模、个体网络的构成等。
巴比, 2000, 《社会研究方法》, 邱泽奇译, 北京: 华夏出版社.
|
郭志刚, 1999, 《社会统计分析方法——SPSS应用》, 北京: 中国人民大学出版社.
|
贺寨平, 2004, 《社会网络与生存状态》, 北京: 中国社会科学出版社.
|
刘军, 2003, 《法村社会支持网络——一个整体研究的视角》, 北京大学社会学系博士论文.
|
——, 2004a, "社会网络模型研究论析", 《社会学研究》第1期.
|
——, 2004b, 《社会网络分析导论》, 北京: 社会科学文献出版社.
|
罗家德, 2005, 《社会网分析讲义》, 北京: 社会科学文献出版社.
|
丘海雄等, 1998, "社会支持结构的转变: 从一元到多元", 《社会学研究》第4期.
|
袁方, 1997, 《社会研究方法教程》, 北京大学出版社.
|
张文宏、阮丹青, 1999, "城乡居民的社会支持网", 《社会学研究》第3期.
|
Anderson, C. J., Wasserman, S. and Crouch, B. 1999. "A p* primer: Logit Models for Social Networks. " Social Networks. 21, 37-66.
|
Borgatti, S. P., Everett, M. G. and Freeman, L. C. 2004. Ucinet 6 for Windows. Harvard: Analytic Technologies.
|
Fienberg, S. E., & Wasserman, S. 1981. "Categorical Data Analysis of Single Sociometric Relations. " In Leinhardt, S. (ed. ) Sociological Methodology. 156-192. San Francisco: Jossey-Bass.
|
Holland, P. W. and Leinhardt, S. 1981. "An Exponential Family of Probability Distribution for Directed Graph. " American Journal of statistical Association. 76, 33-50.
|
Knoke, D. and Kuklinski, J. H., 1982. Network Analysis. Beverly Hills, Calif. : Sage.
|
Robin, G., & Pattison, P. 2002. "A Workshop on Exponential Random Graph (p*) Models for Social Networks. " University of Melbourne. 18 April. 下载自Robin的个人主页.
|
Robin, G., Pattison, P. E. and Wasserman, S. 1999. "Logic Models and Logistic Regression for Social Networks, Ⅲ, Valued relations. " Psychometrika. 64, 371-394.
|
Rosenberg, M. 1968. The Logic of Survey Analysis. New York: Basic Book, Inc., Publishers.
|
Scott, J. 2000. Social Network Analysis. London: Sage Publications.
|
Wasserman, S. and Faust, K. 1994. Social Networks Analysis: Methods and Applications. Cambridge, England: Cambridge University Press.
|
Wasserman, S. and Pattison, P. E. 1996. "Logic Models and Logistic Regressions for Social Networks: Ⅰ. An Introduction to Markov Graphs and p*. " Psychometrika. 60, 406-426.
|
Wellman, B. and Berkowitz, S. D. (eds. ). 1988. Social Structures: A Network Approach. Cambridge, England: Cambridge University Press.
|
 2005, Vol. 25
2005, Vol. 25