社会统计分析是社会研究方法中十分重要的一部分,因为定量研究所得的原始资料在经过审核、整理与汇总之后,需要进行科学系统的统计分析,才能揭示出研究资料所包含的众多信息,从而得出研究的结论。在多元统计分析方法中,研究者用得比较多的是多元线性回归分析、方差分析、log线性模型、probit模型及logistic回归分析,这些分析方法能够帮助我们对数据进行简化、对变量之间的相互依赖关系进行分析,以及根据模型进行预测。但上述方法也存在着一定的使用局限性,比如,方差分析法要假定进行均值比较的总体具有相同的方差和服从正态分布,如果不符合这两个条件,方差分析的结果将不是很稳健(柯惠新,1992:184);而多元线性回归分析、log线性模型、probit模型和logistic回归分析等方法,均采用线性的函数关系来替代现实生活中未知的函数关系,但现实生活的社会和政治关系通常都是十分复杂的、非线性的关系。因此,用这几种统计分析方法对资料进行处理之后得出的结论的准确性依赖于模型可否分段线性化,而要进行分段线性化是比较困难的。
人工神经网络的内在特性为弥补以上这些缺陷提供了可能性。本文试图将人工神经网络引入社会统计分析方法中,以期提供一种新的研究方法和思路。
一、人工神经网络简介人脑是宇宙中已知的最复杂、最完善和最有效的信息处理系统,是生物进化的最高产物,是人类智能、思维和情绪等高级精神活动的物质基础,也是人类认识较少的领域之一。长期以来,人们不断地通过神经学、生物学、心理学、认知学、数学、电子学和计算机科学等一系列学科对神经网络进行分析和研究,企图揭示人脑的工作机理,了解神经系统进行信息处理的本质,并通过对人脑结构及其信息处理方式的研究,利用大脑神经网络的一些特性,设计出具有类似大脑某些功能的智能系统来处理信息和解决问题。
人工神经网络(Artificial Neural Network,简称ANN)正是人类在对大脑神经网络认识理解的基础上人为构造的能够实现某种功能的神经网络。它是理论化的人脑神经网络的数学模型,是基于对大脑神经网络的结构和功能的模仿而建立起来的一种信息处理系统。它实际上是由大量简单元件相互连接而成的复杂网络,具有高度的非线性,能够进行复杂的逻辑操作和实现非线性关系的系统。人工神经网络吸取了生物神经网络的许多优点,如高度的并行性、高度的非线性全局作用、良好的容错性与联想记忆功能以及强大的自适应、自学习功能。
人工神经网络的神经元模型和结构描述了一个网络如何将它的输入矢量转化为输出矢量的过程。这个转化过程从数学角度来看就是一个计算的过程,也就是说,人工神经网络的实质体现了网络输入和输出之间的一种函数关系。通过选取不同的模型结构和激活函数,可以形成各种不同的人工神经网络,得到不同的输入/输出关系式,并达到不同的设计目的,完成不同的任务。人工神经网络是对生物神经网络进行仿真研究的结果,它根据现已掌握的生物神经网络机理的基本知识,按照控制工程的思路和数学描述的方法,建立相应的数学模型,并采用适当的算法,有针对性地确定数学模型的参数(如联接权值、阈值等),以便获得某个特定问题的解。神经元之间相互联接的方式称为联接模式,相互之间的联接度由联接权值体现。在人工神经网络中,改变信息处理过程及其能力就是修改网络权值的过程。所以在利用人工神经网络解决实际应用问题之前,必须首先掌握人工神经网络的模型结构、特性及其对输出矢量的计算。下面我们简要地介绍一下人工神经网络的基本内容。
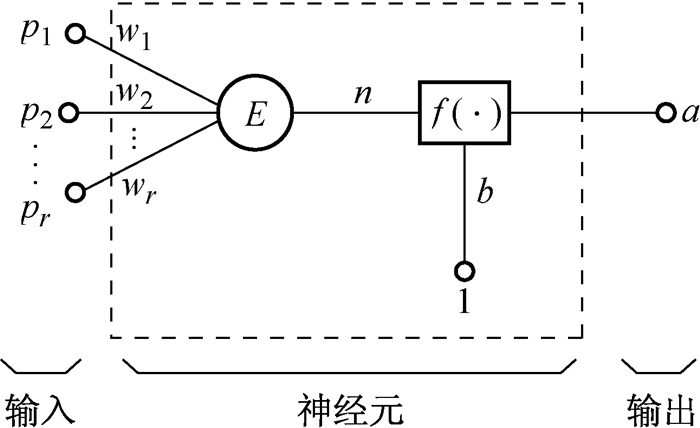
(一) 人工神经元神经元是人工神经网络的基本处理单元,它一般是一个多输入/单输出的非线性元件。神经元输出除受输入信号的影响外,同时也受到神经元内部其它因素的影响,所以在人工神经元的建模中,常常还加有一个额外输入信号,称为偏差(bais),有时也称为阈值或门限值。一个具有r个输入分量的神经元如图 1所示。
|
图 1 神经元示例 |
其中,输入分量pj(j=1,2,…r)通过与同它相乘的权值分量wj(j=1, 2, …r)相连,以
权值wj和输入pj的矩阵形式可以由W的行矢量以及P的列矢量来表示:
| $ \begin{gathered} W = [{w_\mathit{1}}\;{w_\mathit{2}}K\;\;{w_r}] \hfill \\ P = {[{p_\mathit{1}}\;{p_\mathit{2}}K\;{p_r}]^{\text{T}}} \hfill \\ \end{gathered} $ |
神经元模型的输出矢量可表示为:
| $ A = f\left({W*P + b} \right) = f(\sum\limits_{j = 1}^r {{w_j}{p_j} + b}) $ |
可以看出偏差被简单地加在W*P上作为激活函数的另一个输入分量。实际上偏差也是一个权值,只是它具有固定常数为1的输入。在网络的设计中,偏差起着重要的作用,它使得激活函数的图形可以左右移动从而增加了解决问题的可能性。
(二) 激活函数激活函数(Activation Function)是人工神经网络的核心。网络解决问题的能力与功效在很大程度上取决于网络所采用的激活函数。激活函数的基本作用有:控制输入对输出的激活作用;对输入、输出进行函数转换;将可能无限域的输入变换成指定的有限范围内的输出。
常用的激活函数包括以下几种:
1. 阈值型(硬限制型)这种激活函数将任意输入转化为0或1的输出,函数f(·)为单位阶跃函数。
| $ A = f\left({W*P + b} \right) = \left\{ {\begin{array}{*{20}{l}} 1&{W*P + b \ge 0}\\ 0&{W*P + b < 0} \end{array}} \right. $ |
线性激活函数使网络的输出等于加权输入之和加上偏差。
| $ A = f\left({W*P + b} \right) = W*P + b $ |
S型激活函数将任意输入值压缩到(0,1)的范围内。对数S型激活函数关系为:
| $ f = \frac{1}{{1 + \exp \left[ { - \left({n + b} \right)} \right]}} $ |
而双曲正切S型曲线的输入/输出函数关系为:
| $ f = \frac{{1 - \exp \left[ { - 2\left({n + b} \right)} \right]}}{{1 + \exp \left[ { - 2\left({n + b} \right)} \right]}} $ |
在人工神经网络中,学习规则是修正联接权值的一个算法,现有的学习规则大体上可分为以下几类:
1、相关规则。仅根据联接之间的激活水平来改变权值;
2、纠错规则。依赖关于输出结点的外部反馈来改变权值,使实际结点的输出与外部的期望输出相一致;
3、无导师规则。表现为自适应于输入空间的检测规则。
(四) 人工神经网络的特点 1. 分布存储和容错性在人工神经网络中,一个信息并不只存储在一个地方,而是按内容分布在整个网络上,同时网络中的某一处不只存储一个信息,而是每个神经元均存储多种信息的部分内容。在神经网络中,要获得存储的知识可采用“联想”的办法,即当一个神经网络输入一个激励时,它可在已存的知识中寻找与该输入匹配最好的存储知识。当然在信息输出时,也还要经过一种处理,而不是直接从记忆中取出。这种存储方式的优点在于若部分信息不完全,它仍能恢复出原来正确的完整的信息,系统仍能运行。这就是人工神经网络所具有的容错和联想记忆的功能。
2. 高度的非线性全局作用人工神经网络中的每个神经元都接受大量其它神经元的输入,并通过并行网络产生输出,影响其它神经元。网络之间的这种互相制约和互相影响,实现了从输入状态到输出状态空间的非线性映射。从全局的观点来看,网络整体性能不是网络局部性能的简单叠加,而是某种集体性的行为。
3. 十分强的自学习、自组织和自适应性学习和适应要求随着时间的变化,系统内部的结构和联系方式也作出相应改变。神经元网络是一种变结构系统,恰好能完成对环境的适应和对外界事物的学习。神经元之间的连接多种多样,各元之间的连接强度也具有一定的可塑性,因此,网络可以通过学习和训练进行自组织,以适应不同的信息处理要求。
4. 大规模并行处理的能力人工神经网络是由许多相同的处理单元并联而成的,虽然每个单元的功能均很简单,但大量简单处理单元的并行活动使其对信息的总的处理能力非常强大。
二、一个运用人工神经网络分析的实例由于人工神经网络所具有的非线性全局作用及其自学习、自组织、自适应性等特点,将其运用于函数关系复杂的社会科学领域中的统计分析应该是具有广泛前景的。人工神经网络模型在分析之前不需要事先假定生成数据的效用函数或噪声的特殊函数形式,而是从抽样数据中“学习”输入变量与输出变量之间的关系,并且能够最大限度地逼近真实的函数关系,这就能避免了简单地用线性函数关系来替代非线性函数关系,从而获得尽可能真实的分析结果。
此处以笔者曾经做过的武汉市大学生考试作弊行为调查为例试说明其运用。该研究运用判断抽样方法选取了华中理工大学(现华中科技大学)、武汉水利电力大学、湖北大学和湖北工学院(现湖北工业大学)4所高校进行问卷调查。通过整群抽样的方法,从以上各校教务部门提供的本科生班级名单中各抽取两到三个班级,发放自填式问卷330份,通过集中填答法来收集资料。最后共回收有效问卷301份,有效回收率为91.2%。在统计中,将学生在“考试中有否作弊”视作一个因变量,对它可能有影响的自变量包括“本人对作弊的态度”、“同辈群体对考试作弊的态度”、“同班同学考试作弊的情况”、“监考老师对考场的管理情况”、“所在学校对考试作弊的管理”、“性别”、“所在年级”、“文理科”、“平均成绩”、“是否中国共产党党员或学生干部”和“所在学校”等。为了便于检验模型的泛化能力及与常规社会统计方法的分析结果相比较,研究者将301个观测数据随机分为两组:第一组包括281个观测数据,作为训练组来估计模型;第二组为检验组,含有20个数据,用来检测模型的泛化能力。
(一) 模型结构我们选择人工神经网络中的反向传播网络(Back-Propagation Network,简称BP网络)对数据进行分析。BP网络主要可用于函数逼近(即用输入矢量和相应的输出矢量训练一个网络来逼近一个函数)、模式识别、分类及数据压缩等方面,这里所采用的BP网络分为三层:
1、输入层
包含上述11个自变量;
2、隐层
包含72个隐藏神经元;
3、输出层
输出层为1个神经元,对应于因变量——“考试有否作弊”。
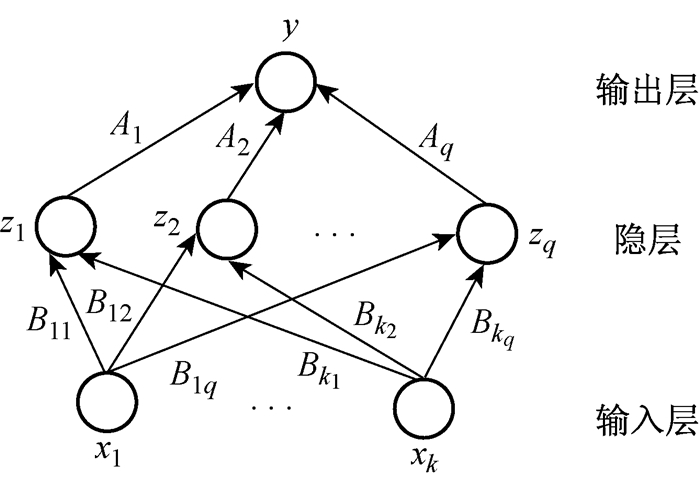
其网络结构如图 2所示:
|
图 2 网络结构图 |
其中:k(=11)为输入变量的个数;q(=72)为隐藏神经元的个数;A和B为连接权值。
输出和隐层的激活函数均采用对数S型激活函数关系。
(二) BP算法我们采用反向传播算法(即BP算法)对281个训练组样本进行训练。BP算法属于δ算法,是一种监督式的学习算法。其主要思想为:对于q个输入学习样本:P1,P2,…,Pq,已知与其对应的输出样本为:T1,T2,…,Tq。学习的目的是用网络的实际输出A1,A2,…,Aq与目标矢量T1,T2,…,Tq之间的误差来修改其权值,使Al(l=1,2,…q)与期望的Tl尽可能地接近,即使网络输出层的误差平方和达到最小。它是通过连续不断地在相对于误差函数斜率下降的方向上计算网络权值和偏差的变化而逐渐逼近目标的。每一次权值和偏差的变化都与网络误差的影响成正比,并以反向传播的方式传递到每一层。
BP算法由两部分组成:信息的正向传递与误差的反向传播。在正向传递过程中,输入信息从输入经隐含层逐层计算传向输出层,每一层神经元的状态只影响下一层神经元的状态。如果在输出层没有得到期望的输出,则计算输出层的误差变化值,然后转向反向传播,通过网络将误差信号沿原来的连接通路反传回来以修改各层神经元的权值直到达到期望目标。在本次研究中BP算法用Matlab来实现。
(三) 训练过程为了训练一个BP网络,需要计算网络加权输入矢量以及网络输出和误差矢量,然后求得误差平方和。当所训练矢量的误差平方和小于误差目标,训练则停止,否则便在输出层计算误差变化,且采用反向传播学习规则来调整权值,并重复此过程。当网络完成训练后,对网络输入一个不是训练集合中的矢量,网络将以泛化方式给出输出结果。具体过程如下:
1、用小的随机数对每一层的权值W和偏差B初始化,以保证网络不被大的加权输入饱和,并进行以下参数的设定或初始化——
* 期望误差最小值err-goal,
* 最大循环次数max-epoch,
* 修正权值的学习速率lr(一般情况下lr=0.01~0.7),
* 从1开始的循环训练:for epoch=1:max-epoch;
2、计算网络各层输出矢量以及网络误差;
3、计算各层反传的误差变化并计算各层权值的修正值以及新权值;
4、再次计算权值修正后的误差平方和;
5、检查误差平方和(SSE)是否小于err-goal,若是则训练结束;否则继续。
本研究设定各参数值如下:
初始权值W为[0.005,0.05]的随机数,B为[0.005,0.05]的随机数,期望误差最小值err-goal=10,最大循环次数max-epoch=281,修正权值的学习速率lr=0.01。针对不充分的样本,采用以预激励为基础的不完全训练方法进行训练。
(四) 灵敏度分析运用神经网络模型分析数据得出的结果不会象常规社会统计方法分析得出的结果那样直接,而且在神经网络模型中对某个参数进行显著性检验比较困难且意义不大。但是,我们可以运用诸如数值灵敏度分析之类的方法来估计输入变量对输出变量的影响并比较输入变量的相对重要性。
灵敏度分析操作规则是这样的:对某一个案,将一个自变量加上一个小的扰动(0.1),其它的自变量保持不变,计算因变量的变化;对所有个案都这样计算因变量的变化,然后取平均值,即得该自变量的灵敏度。灵敏度分析结果如表 1所示。
| 表 1 数据的灵敏度分析结果 |
由灵敏度分析结果可以看到,在11个自变量中,对“考试有否作弊”有较大影响的因素依次是“本人对作弊的态度”、“同辈群体对作弊的态度”、“同班同学作弊情况”、“平均成绩”、“监考教师对考场的管理”和“学校对作弊的管理”等。本人和其周围的同辈群体对作弊越是持否定态度,考试时越不可能作弊;同班同学作弊情况越严重,考试时越可能作弊;平均成绩越好,考试时越不可能作弊;监考老师和学校对作弊的管理越严,越不可能作弊。
三、logistic模型对实例的分析以下试用常规统计方法处理本例数据。
本例的11个自变量之间存在较强的自相关关系,如果将它们不加处理就直接引入统计分析模型,是难以取得理想结果的。在这种情况下,可以考虑运用因子分析法(Factor Analysis)对变量进行分类,将自相关性较高的变量分在一组中,并用一个本质因子来作为代表,这样就可以较好地达到简化变量和减少变量间的自相关的目的(柯惠新,1992:485)。因此,笔者对解释考试作弊行为的5个变量进行了因子分析,第一步分析结果参见表 2。
| 表 2 自变量的因子分析资料 |
由表 2中可以看出:用主成份法提取了两个公共因子,大约可以解释全部变量方差的66%,这个比率还算高。从共同度(Communality)一栏看,各变量的共同度在0.5~0.8之间,说明各变量对两个公共因子的贡献率比较高。从这些指标看,因子分析比较成功。
第二步是对因子负荷矩阵进行旋转,以便确定各个公共因子的意义,对原矩阵进行“方差最大正交旋转”后,得到已旋因子矩阵如表 3所示。
| 表 3 旋转后的因子分析解 |
从表 3的已旋因子负荷矩阵可以看出,两个因子的含义是很明确的:因子一与“同班同学作弊情况”、“监考老师对考场的管理”和“学校对考试作弊的管理”3个能反映对考试作弊的管理情况的变量相对应;因子二对应于“本人对作弊的态度”和“同辈对作弊的态度”2个与对待考试作弊的态度有关的变量,因此,我们分别将这两个公共因子命名为“作弊管理因子”和“作弊态度因子”,并计算相应的因子得分,以之作为新的可能影响考试作弊行为的自变量。这样,可以将自变量简化为以下8个自变量:作弊管理和作弊态度2个解释变量,性别、所在年级、文理科、平均成绩、是否中国共产党党员或学生干部和所在学校等6个控制变量。
由于因变量“考试有否作弊”是一个二分变量,因此采取logistic模型多元回归方法来进行分析。为了便于检验模型的泛化能力并与人工神经网络模型的分析结果相比较,我们同样将301个观测数据随机地分为两组:第一组包括281个观测数据,作为训练组来估计模型;第二组为检验组,共20个数据,用来检测模型的泛化能力,分析结果见表 4。
| 表 4 以大学生考试有否作弊为因变量建立的Logistic模型 |
从统计结果可以得出下列结论:
据各变量的回归系数及其显著性水平判断,“作弊管理因子”与“作弊态度因子”对“考试有否作弊”起着相当显著的影响,老师及学校对考试及考试作弊的管理越严,学生越不可能作弊;同辈群体及学生自身对考试作弊越持否定态度,则学生越不可能作弊。
控制变量中,“平均成绩”是唯一对“考试有否作弊”起显著作用的因素,学生的平均成绩越差,考试作弊行为发生的可能性越大。
根据各变量的EXP(B)系数来判断,上面提到的这些有显著影响的变量中,依影响大小依次为:作弊管理因子、平均成绩和作弊态度因子。除此之外,其它因素的影响均不显著。
该方法的不足之处在于,由于考虑到各变量之间可能存在自相关关系且自变量较多,笔者采用因子分析方法进行了数据分析前的处理。但因子分析的前提是假定各个变量都是定距变量,而且存在直线性关系(李沛良,1993:335)。本研究中的各自变量虽然可以被当作定距变量来处理,但实际上并不是定距变量,各自变量之间也不一定存在着线性关系,因此,本研究中因子分析的可行性和准确性还有待商榷。
具体到因子分析过程,从共同度一栏看,两个因子对各变量方差的解释不算很高(最高也不超过0.8),另外两个因子总共解释了约66%的方差,因子的效力也不是很强。可见,用“作弊管理因子”和“作弊态度因子”来代替部分的自变量进入到回归分析中,虽然大大地减少了自变量的数目和自变量之间的相关关系,但同时也丢失了样本中的不少有用信息,从而降低了分析的准确度。
当自变量为定类变量、定序变量或定距变量,因变量为二分的定类变量时,运用logistic模型进行回归分析是社会学中常常采用的方法之一,不过,logistic模型与logit模型一样也具有天然缺陷,即事先假定产生分类数据的效用函数(Utility Function)为输入变量的线性函数,误差服从极值分布。具体来说,在本研究中,logistic模型假定某大学生衡量考试作弊行为与考试不作弊行为之间效用大小的效用函数是线性的,此线性函数可以运用最小二乘法从样本数据中求出:U=b0+b1X1+b2X2+…+bnXn,其中X为研究中的自变量,n为自变量的个数,在本研究中n=8。根据考试作弊行为的效用大于考试不作弊行为的效用的条件,可以推导出该学生考试作弊的概率表达式为:
为了更精确地比较人工神经网络与Logistic模型在本案例上的差异,本文再分别对训练组和检验组进行正确预测率及平均绝对误差的比较。
正确预测率是指通过模型正确预测到的分类结果的比率。操作规则是:如果模型计算出某个案的考试作弊的概率大于0.5,则因变量“考试有否作弊”的值计为1,反之则计为0。将此结果与调查所得的数据进行比较可得正确预测率。
在计算平均绝对误差时,将因变量“考试有否作弊”观测到的值当作概率来看待。例如,因变量取1时,认为考试作弊的概率为1,如果模型计算得到考试作弊的概率为0.85,则此观测值的绝对误差为0.15,将全部数据取平均即得平均绝对误差。比较结果见表 5:
| 表 5 正确预测率及平均绝对误差比较 |
从上述正确预测率和平均绝对误差的比较结果来看,人工神经网络模型比logistic模型能取得更高预测率及更小的平均绝对误差,因此能更真实地逼近现实存在的函数关系。可见,人工神经网络在描述和预测逼近现实的输入/输出的非线性关系时具有相当高的准确性。不过应该指出的是,如果实际的函数关系不是非线性时,或者噪声特别大时,人工神经网络与常规社会统计方法就没有什么明显的差异了。
在自然科学中有许多已经发展得比较成功的研究方法,比如人工神经网络理论、遗传算法、人工智能、模糊数学等等,如果能够将其恰当地运用于社会科学领域,无疑将有助于社会科学的发展。本文依据一个实例探讨了人工神经网络应用于社会学研究中的可能性及优越性,但真正要将人工神经网络大量地、恰当地运用于社会统计分析中,尚有诸多问题有待深入研究,如:第一,人工神经网络模型一般要求样本的容量较大,在研究的人力、物力和财力有限的前提下,如何选取合适的样本及变量,以使人工神经网络模型得到充分激励、获得较好的泛化能力的问题;第二,如何设计客观的调查问卷,减少主观因素的影响,从而令用来训练神经网络的样本较少地受到有色噪声干扰的问题;第三,如何选取适合所研究问题的神经网络结构、激活函数、训练算法和初始权值,以使其收敛性得到保证的问题;第四,运用神经网络模型分析数据得出的结果不会像常规社会统计分析方法分析得出的结果那样直接,如何寻找除灵敏度分析之外的更多更好的结果分析方法的问题等。
从爽. 1998. 面向MATLAB工具箱的神经网络理论与应用[M]. 合肥: 中国科学技术大学出版社.
|
风笑天. 1996. 现代社会调查方法[M]. 武汉: 华中理工大学出版社.
|
柯惠新, 1992, 《调查研究中的统计分析法》, 北京广播学院出版社。 |
李沛良. 2001. 社会研究的统计应用[M]. 北京: 社会科学文献出版社.
|
刘瑛, 2000, 《大学生考试作弊行为研究——运用人工神经网络理论所作的分析》, 华中理工大学硕士毕业论文。 |
袁曾任. 1999. 人工神经元网络及其应用[M]. 北京: 清华大学出版社.
|
Diekhoff, George M, Emily E. LaBeff, Robert E. Clark, Larry E. Williams, Billy Francis, Valerie J. Haines. 1996. "College Cheating: Ten Years Later." Research in Higher Education, 37(4): 487-502. DOI:10.1007/BF01730111 |
Macy Michael. 1996. "Natural Selection and Social Learning in Prisoner's Dilemma Co-adaptation with Genetic Algorithms and Artificial Neural Networks." Sociological Methods and Research, 25(1): 103-137. DOI:10.1177/0049124196025001004 |
Pulvers Klm, George M. Diekhoff. 1999. "The Relationship between Academic Dishonesty and College Classroom Environment." Research in Higher Education, 40(4): 487-497. DOI:10.1023/A:1018792210076 |
Zeng Langche. 1999. "Prediction and Classification with Neural Network Models." Sociological Methods and Research, 27(4): 499-524. DOI:10.1177/0049124199027004002 |
 2005, Vol. 25
2005, Vol. 25