文章信息
- 李福明, 冯泳翰, 赵怡, 朱景康, 魏曦, 梁文俊
- LI Fuming, FENG Yonghan, ZHAO Yi, ZHU Jingkang, WEI Xi, LIANG Wenjun
- 蔡家川流域人工刺槐生物量模型的构建与比较
- Construction and comparison of artificial Robinia pseudoacacia biomass model in Caijiachuan Watershed
- 森林与环境学报,2024, 44(1): 62-70.
- Journal of Forest and Environment,2024, 44(1): 62-70.
- http://dx.doi.org/10.13324/j.cnki.jfcf.2024.01.008
-
文章历史
- 收稿日期: 2023-08-10
- 修回日期: 2023-09-23
森林生物量是森林植物在一定时空范围内产生的干物质累积量,是森林生态系统的重要数据之一[1],研究森林生物量对评价森林生态系统的结构和功能,分析森林生态系统的物质交换和能量流动具有重要意义[2]。森林是陆地生态系统中最大的碳库[3],对森林生物量准确预测是研究森林碳汇,实现“双碳”目标的必要过程。20世纪70年代末,冯宗炜等[4]、李文华等[5]开始研究我国森林生物量,至今成果丰硕。常见的生物量测定方法有全收获法和模型估计法,其中,全收获法可获得最准确的数据,但耗时长、工作量大、对林地的破坏也较大[6],相比之下,模型估计法较为准确且简便、效率高。我国目前已有的生物量模型有5 000多种[2],但森林生物量受地理地形、气候、林分结构、人为等因素的影响,造成单一生物量模型无法适用于所有的区域[7],因此,构建特定区域内生物量模型十分必要。目前基于林木形态因子所构建的生物量模型主要有生物量异速生长模型、多元线性模型、相容性生物量模型等。王霞等[8]通过建立生物量异速生长模型,对麻栎林地下生物量进行研究,建立的幂函数相对生长模型预测效果较好;而欧建德等[9]的研究表明,导入树冠形态因子后,立木多元线性模型的预测精度与水平有了明显提高;为解决总生物量与各器官生物量的相容性,学者们又引入联立方程组模型解决生物量相容性问题,其中,较多的学者选择使用代数和控制法建立生物量模型[10-11]。PARRESO[12]提出的似乎不相关回归方法很好地解决了生物量相容问题。目前生物量模型构建的3种方法均有使用,但大多数只采用单一建模方法进行模型的建立与验证,而对3种建模方法的比较研究较少。
刺槐(Robinia pseudoacacia)属豆科,原产于北美洲的亚热带和温带地区,具有耐贫瘠、生长速度快、易繁殖、适应能力强等特点。刺槐的根系浅而发达,具有良好的保土保肥性能,是黄土高原人工林建设的主要树种[13]。蔡家川流域位于黄土高原的西南部,面积达40 km2,人工林覆盖率达70%,碳汇潜力巨大。本研究基于该流域内的生物量实测数据,采用不同的方法构建3种生物量模型,并进行比较,从中选取适合该流域的刺槐生物量预测模型,为蔡家川流域刺槐人工林碳汇研究提供科学依据。
1 研究区概况与研究方法 1.1 研究区概况研究区位于山西省吉县蔡家川流域(36°14′27″~36°18′23″N,110°39′45″~110°47′45″E),地处黄土高原西南部,吕梁山脉南部,海拔900~1 513 m。该区气候属温带大陆性气候,年平均降雨量575.9 mm,年平均气温10 ℃,年平均日照时间2 563.8 h。土壤类型主要为褐土,黄土母质,呈碱性。流域内植被主要有刺槐、辽东栎(Quercus wutaishansea)、山杨(Populus davidiana)、侧柏(Platycladus orientalis)、胡枝子(Lespedeza bicolor)等;人工植被主要有油松(Pinus tabuliformis)、苹果(Malus domestica )、山杏(Armeniaca vulgaris)、梨(Pyrus spp)等;农作物以玉米(Zea mays)、小麦(Triticum aestivum )、谷子(Setaria italica)为主。
1.2 数据采集2022年6—7月,在研究区采用典型的样地调查法选取24块大小为20 m×20 m人工刺槐林样地。对样地内的林木进行每木检尺,根据每木检尺的数据,在每个样地内选取1~3株标准木进行生物量测定,共计48株。将标准木从根颈处伐倒,并挖掘其全部根系,将地上部分摘除枝、叶后,每隔1 m截断,分别称取树干、树枝、树叶、根系的鲜重。根系在称量鲜重时应去除残带的泥土,树干截取10 cm厚的树盘样本,其余器官各采集500 g样本。将采集样品带回实验室后在85 ℃下烘48 h,称量其干重,根据干重与鲜重之比,计算各器官的总干重。由于在生物量采集时期,刺槐无花和果实,故忽略不计。标准木的基本情况见表 1。
| 统计特征 Statistical characteristics |
树龄 Tree age/a |
胸径 Diameter at breast height/cm |
树高 Tree height/m |
冠长 Crown length/m |
冠幅 Crown breadth/m |
树干生物量 Trunk biomass/kg |
树枝生物量 Branch biomass/kg |
树叶生物量 Leaf biomass/kg |
根系生物量 Root biomass/kg |
总生物量 Total biomass/kg |
| 平均值Mean | 20.60 | 12.29 | 10.24 | 6.71 | 5.69 | 39.87 | 14.02 | 6.08 | 19.10 | 79.06 |
| 最小值Minimum value | 9.00 | 5.60 | 4.20 | 1.60 | 1.00 | 4.57 | 2.11 | 1.40 | 1.23 | 11.20 |
| 最大值Maximum value | 38.00 | 18.50 | 14.10 | 12.80 | 7.50 | 72.60 | 27.12 | 10.98 | 45.77 | 153.20 |
| 标准偏差Standard deviation | 6.35 | 3.14 | 2.26 | 2.59 | 1.22 | 19.07 | 6.79 | 2.20 | 11.51 | 38.31 |
树冠特征的计算公式如下:
| $ L_{\mathrm{C}}=h-h_{\mathrm{C}} $ | (1) |
| $ W_{\mathrm{C}}=\left(W_{\mathrm{C}, \mathrm{wE}}+W_{\mathrm{C}, \mathrm{NS}}\right) / 2 $ | (2) |
式中:LC为冠长(m);h为树高(m);hC为枝下高(m);WC为冠幅(m);WC, WE为东西冠幅(m);WC, NS为南北冠幅(m)。
生物量的计算公式如下:
| $ m_{\mathrm{D}}=m_{\mathrm{F}} R $ | (3) |
| $ B_{\mathrm{T}}=B_{\mathrm{S}}+B_{\mathrm{B}}+B_{\mathrm{L}}+B_{\mathrm{R}} $ | (4) |
式中:mD为各器官的干重(kg);mF为各器官的鲜重(kg);R为干重比(%);BT为总生物量(kg);BS为树干生物量(kg);BB为树枝生物量(kg);BL为树叶生物量(kg);BR为根系生物量(kg)。
1.3 模型建立首先对各器官生物量、总生物量、立木形态因子及胸径、树高的复合因子[胸径的平方(DBH2)、胸径与树高的乘积(DBHh)、胸径的平方与树高的乘积(DBH2h)]进行Pearson相关性分析,筛选合适的因子进行生物量模型构建。所选取的标准木胸径、树高、树冠数据分布均匀,根据典型抽样方法选取32株标准木生物量的数据进行模型构建,剩余16株标准木数据则作为检验数据进行模型精确度的检验。
1.3.1 生物量异速生长模型与多元线性模型的构建以胸径、树高、冠长、冠幅及胸径、树高的复合因子为自变量,选用常见的对数函数、逆函数、二次多项式、三次多项式、复合函数和幂函数进行生物量异速生长模型的拟合;以胸径、树高及其复合因子构建的生物量线性模型为基础,导入冠长、冠幅因子构建多元线性模型的拟合。
1.3.2 相容性生物量模型的构建研究表明,B1=aDBHb+ε、B2=a(DBH2h)b+ε、B3=aDBHbhc+ε(式中:B为各器官生物量或总生物量;a、b、c为待拟合参数;ε为误差项)常作为独立模型进行相容性生物量模型拟合。本研究采用这3种独立模型进行相容性模型的拟合。联立方程组如下:
| $ \left\{\begin{array}{l} B_{\mathrm{S}}=f_{\mathrm{S}}(x)+\varepsilon_1 \\ B_{\mathrm{B}}=f_{\mathrm{B}}(x)+\varepsilon_2 \\ B_{\mathrm{L}}=f_{\mathrm{L}}(x)+\varepsilon_3 \\ B_{\mathrm{R}}=f_{\mathrm{R}}(x)+\varepsilon_4 \\ B_{\mathrm{T}}=f_{\mathrm{S}}(x)+f_{\mathrm{B}}(x)+f_{\mathrm{L}}(x)+f_{\mathrm{R}}(x)+\varepsilon_5 \end{array}\right. $ | (5) |
式中:BS、BB、BL、BR、BT分别为树干、树枝、树叶、根系和总生物量;fS(x)、fB(x)、fL(x)、fR(x)分别为树干、树枝、树叶、根系生物量模型;ε为误差项。
在进行独立模型和方程组的参数拟合时需要消除异方差,本研究采用加权回归法[9]消除异方差。方程组通过非线性似乎不相关回归进行参数估计。
1.4 模型检验首先用决定系数(R2,R2的取值越接近1,模型的拟合度越高)和预测值的均方根误差(root mean square error, RMSE或ERMS,ERMS值越小,模型的拟合度越高,预测效果越好)进行模型的初步筛选,然后用估计标准误差(standard error of estimate,SEE或ESE)、总相对误差(total relative error,TRE或ETR)、平均相对误差(average relative error,ARE或EAR)和平均百分比误差(mean percentage error,MPE或EMP, ETR、EAR、EMP值越接近0,模型的预测效果越好)对筛选的模型进行精确度的检验。计算公式为:
| $ R^2=1-\sum\left(y_i-\hat{y}_i\right)^2 / \sum\left(y_i-\bar{y}_i\right)^2 $ | (6) |
| $ E_{\mathrm{RMS}}=\sqrt{\sum\left(y_i-\hat{y}_i\right)^2 / N} $ | (7) |
| $ E_{\mathrm{SE}}=\sqrt{\sum\left(y_i-\hat{y}_i\right)^2 / N-T} $ | (8) |
| $ E_{\mathrm{TR}} / \%=\sum\left(y_i-\hat{y}_i\right) / \sum \hat{y}_i \times 100 $ | (9) |
| $ E_{\mathrm{AR}} / \%=\frac{1}{N} \sum\left(y_i-\hat{y}_i\right) / \hat{y}_i \times 100 $ | (10) |
| $ E_{\mathrm{MP}} / \%=t_\alpha\left(E_{\mathrm{SE}} / \bar{y}_i\right) / n \times 100 $ | (11) |
式中:yi为实测值;
通过对刺槐生物量与建模因子进行Pearson相关性分析(表 2), 可知各器官生物量、总生物量与胸径、树高、冠长、冠幅及胸径、树高的复合因子均呈显著正相关,生物量与建模因子的相关性系数大于0.669,其中与胸径的相关性系数均大于0.910。因此,胸径是生物量预测最重要的解释变量,其余依次是树高、冠长、冠幅。各器官生物量和总生物量与胸径、树高的复合因子的相关性系数也极高,均大于0.900。因此,胸径、树高的复合因子也可以用于各器官生物量和总生物量模型的构建。鉴于较多的建模因子,本研究将采用逐步筛选法选取合适的建模因子进行各器官生物量和总生物量模型的构建。
| 建模因子 Model factor |
树干生物量 Trunk biomass |
树枝生物量 Branch biomass |
树叶生物量 Leaf biomass |
根系生物量 Root biomass |
总生物量 Total biomass |
| DBH | 0.959** | 0.913** | 0.929** | 0.918** | 0.971** |
| h | 0.902** | 0.902** | 0.843** | 0.876** | 0.914** |
| LC | 0.900** | 0.874** | 0.817** | 0.879** | 0.908** |
| WC | 0.805** | 0.749** | 0.728** | 0.669** | 0.773** |
| DBH2 | 0.946** | 0.905** | 0.937** | 0.933** | 0.968** |
| DBHh | 0.963** | 0.917** | 0.932** | 0.926** | 0.963** |
| DBH2h | 0.960** | 0.912** | 0.935** | 0.911** | 0.978** |
| 注:**表示0.01水平极显著相关。Note: ** indicates a very significant correlation at 0.01 level. | |||||
根据各器官生物量和总生物量与各建模因子的相关性分析结果,以胸径、树高、冠长、冠幅及胸径、树高的复合因子为自变量分别进行对数函数、逆函数、二次多项式、三次多项式、复合函数和幂函数形式的生物量模型拟合。各器官生物量和总生物量模型共拟合35个,根据模型的R2和RMSE,每部分选取3个拟合度较高的生物量模型(表 3),所选的生物量模型R2均在0.860以上,最大达到0.965,其中4种器官生物量模型的RMSE均位于合理的范围内,这证明所选的模型拟合度很高。在所选的15个模型中,幂函数模型明显优于其他模型,其余依次为二次多项式、三次多项式和复合函数形式。以胸径、树高的复合因子为自变量构建的生物量模型居多,并且采用冠长、冠幅的较少,这说明将树冠因子单独作为预估因子用于生物量的预测效果并不理想。在树干和总生物量模型中,以DBH2h为自变量的幂函数模型拟合效果最好;树枝、根系生物量模型是以DBHh为自变量的幂函数模型拟合效果最好;树叶生物量模型以DBH2为自变量的幂函数模型拟合效果最好。
| 器官 Organ |
模型 Model |
自变量 Independent variable |
模型 Model |
决定系数 R2 |
均方根误差 RMSE |
| 三次多项式Cubic | DBH | BS=17.618-8.186DBH+1.248DBH2-0.035DBH3 | 0.926 | 3.697 | |
| 树干Trunk | 幂函数Power function | DBHh | BS =0.074(DBHh)1.282 | 0.915 | 3.208 |
| 幂函数Power function | DBH2h | BS =0.08(DBH2h)0.834 | 0.927 | 3.197 | |
| 复合函数Composition | H | BB =1.158×1.258h | 0.878 | 0.195 | |
| 树枝Branch | 幂函数Power function | DBHh | BB =0.11(DBHh)0.993 | 0.927 | 1.150 |
| 幂函数Power function | DBH2h | BB =0.124(DBH2h)0.64 | 0.918 | 1.160 | |
| 三次多项式Cubic | DBH | BL =-6.415+2.265DBH-0.17DBH2+0.005DBH3 | 0.871 | 0.784 | |
| 树叶Leaf | 幂函数Power function | DBH2 | BL =0.192(DBH2)0.681 | 0.879 | 0.152 |
| 二次多项式Quadratic | DBHh | BL =1.587+0.027(DBH2h)+3.542(DBH2h)2 | 0.863 | 0.837 | |
| 幂函数Power function | DBH | BR =0.022DBH2.646 | 0.924 | 0.228 | |
| 根系Root | 三次多项式Cubic | DBH2 | BR =-0.518+0.085(DBH2)+0.000 3(DBH2)2-5.184(DBH2)3 | 0.922 | 3.100 |
| 幂函数Power function | DBHh | BR =0.012(DBHh)1.495 | 0.936 | 0.151 | |
| 二次多项式Quadratic | DBH | BT=-35.44+6.924DBH+0.193DBH2 | 0.946 | 8.222 | |
| 总生物 Total biomass |
幂函数Power function | DBHh | BT =0.215(DBHh)1.204 | 0.960 | 9.131 |
| 幂函数Power function | DBH2h | BT =0.237(DBH2h)0.781 | 0.965 | 7.126 |
根据相关性分析结果, 以胸径、树高及胸径、树高的复合因子为自变量进行生物量线性模型的构建,共构建20个模型,每部分根据R2和RMSE筛选出两个拟合度最高的模型,然后将冠长、冠幅因子导入所筛选出的两个模型中,完成多元线性模型的拟合,结果见表 4。所构建的多元线性模型R2的取值范围为0.827~0.960,各模型的RMSE无较大差异,模型的拟合效果较好。树干、根系、总生物量的简单线性模型均以DBH、h、DBH2h为自变量;树枝模型以DBHh、DBH2h为自变量;树叶模型以DBH2、DBH2h为自变量。将冠长、冠幅因子导入后,R2提高了0.007~0.057,并且降低了RMSE,冠长、冠幅的导入提高了模型的拟合度。
| 器官 Organ |
建模因子 Model factor |
模型 Model |
决定系数 R2 |
均方根误差 RMSE |
| DBH、h | BS=-36.994+4.612DBH+2.043h | 0.925 | 5.524 | |
| 树干Trunk | DBH2h | BS=11.329+0.016DBH2h | 0.880 | 6.865 |
| DBH、h、LC、WC | BS=-36.508+3.923DBH+0.779h+1.376LC+2.391WC | 0.933 | 5.187 | |
| DBH2h、LC、WC | BS=-12.213+0.01DBH2h+1.694LC+4.594WC | 0.937 | 5.248 | |
| DBHh | BB=0.563+0.103DBHh | 0.875 | 2.236 | |
| 树枝Branch | DBH2h | BB=5.336+0.005DBH2h | 0.827 | 2.625 |
| DBHh、LC、WC | BB=-2.402+0.088DBHh+0.174LC+0.641WC | 0.885 | 2.251 | |
| DBH2h、LC、WC | BB=-1.976+0.003DBH2h+0.637LC+0.989WC | 0.856 | 2.398 | |
| DBH2 | BL=1.656+0.027DBH2 | 0.875 | 0.801 | |
| 树叶Leaf | DBH2h | BL=2.623+0.002DBH2h | 0.875 | 0.814 |
| DBH2、LC、WC | BL=0.737+0.02DBH2-0.004LC+0.22WC | 0.884 | 0.800 | |
| DBH2h、LC、WC | BL=1.283+0.002DBH2h-0.09LC+0.372WC | 0.888 | 0.796 | |
| DBH、h | BR=-22.842+2.783DBH+0.741h | 0.896 | 3.574 | |
| 根系Root | DBH2h | BR=1.959+0.009DBH2h | 0.942 | 2.672 |
| DBH、h、LC、WC | BR=-16.488+2.873DBH+0.514h+0.879LC+2.016WC | 0.921 | 3.341 | |
| DBH2h、LC、WC | BR=1.213+0.008DBH2h+0.746LC-0.528WC | 0.949 | 2.638 | |
| DBH、h | BT=-72.818+9.033DBH+4.058h | 0.951 | 8.573 | |
| 总生物量 Total biomass |
DBH2h | BT=21.247+0.032DBH2h | 0.936 | 9.781 |
| DBH、h、LC、WC | BT=-69.229+8.348DBH+2.406h+2.438LC+0.656WC | 0.957 | 8.563 | |
| DBH2h、LC、WC | BT=-16.692+0.024DBH2h+2.987LC+5.427WC | 0.960 | 7.735 |
根据表 4中的模型评价指标,优选出各部分的生物量模型:树干为BS=-12.213+0.01DBH2h+1.694LC+4.594WC;树枝为BB=-2.402+0.088DBHh+0.174LC+0.641WC;树叶为BL=1.283+ 0.002DBH2h-0.09LC+0.372WC;根系为BR=1.213+0.008DBH2h+0.746LC-0.528WC;总生物量为BT=-16.692+0.024DBH2h+2.987LC+5.427WC。
2.4 相容性生物量模型用代数和控制法进行相容性生物量模型的构建,使用加权回归法消除异方差后模型的参数估计值见表 5。所拟合的3组生物量模型组中各器官和总生物量R2为0.699~0.946,RMSE较小,3组生物量模型的拟合度在可接受范围。以DBH2h为自变量构建的相容性生物量模型比以DBH及DBH、h为自变量构建的拟合度高。其中,以DBH及DBH、h为自变量的模型中,树干、总生物量的拟合度较高,其余依次是树枝、树叶、根系;而以DBH2h为自变量的模型中,总生物量、树干的拟合度较高,根系、树叶、树枝次之。相容性生物量模型依旧遵循多个建模因子比单一建模因子拟合效果好,以单因子DBH及DBH、h为例,只采用DBH时,树干、树枝、树叶、根系和总生物量模型的R2分别为0.859、0.784、0.728、0.699和0.872,加入h变量后,R2分别上升至0.896、0.801、0.780、0.701和0.880。
| 建模因子 Model type |
器官 Organ |
参数估计值Parameter estimates | 决定系数 R2 |
均方根误差 RMSE |
||
| a | b | c | ||||
| DBH | 树干Trunk | 4.288 | 1.092 | 0.859 | 3.550 | |
| 树枝Branch | 0.838 | 1.224 | 0.784 | 2.521 | ||
| 树叶Leaf | 0.083 | 1.632 | 0.728 | 1.874 | ||
| 根系Root | 0.133 | 2.006 | 0.699 | 1.590 | ||
| 总生物量Total biomass | 0.872 | 10.625 | ||||
| DBH2h | 树干Trunk | 1.645 | 0.480 | 0.934 | 2.993 | |
| 树枝Branch | 0.372 | 0.513 | 0.871 | 2.230 | ||
| 树叶Leaf | 0.037 | 0.654 | 0.881 | 0.766 | ||
| 根系Root | 0.051 | 0.805 | 0.901 | 1.516 | ||
| 总生物量Total biomass | 0.946 | 8.707 | ||||
| DBH、h | 树干Trunk | 1.274 | 1.012 | 0.557 | 0.896 | 3.120 |
| 树枝Branch | 0.135 | 0.961 | 1.082 | 0.801 | 2.391 | |
| 树叶Leaf | 0.047 | 1.499 | 0.658 | 0.780 | 1.791 | |
| 根系Root | 0.629 | 1.062 | 0.258 | 0.701 | 1.531 | |
| 总生物量Total biomass | 0.880 | 9.800 | ||||
从以上3种不同建模方法中分别选取拟合度最优的模型,用剩余的16株样木数据进行模型精确度的检验,采用估计的SEE、TRE、ARE、MPE等4个指标来检验,检验结果见表 6。3种建模方法构建的生物量模型的SEE在0.221~3.170 kg之间;TRE在-12.88%~10.80%之间;ARE在-7.96%~13.75%之间;MPE均小于1.35%。所选的3种模型预测结果较好,均可用于蔡家川流域人工刺槐生物量的预测。
| 建模方法 Modeling method |
器官 Organ |
检验结果Test result | |||
| 估计标准误差 SEE/kg |
总相对误差 TRE/% |
平均相对误差 ASE/% |
平均百分比误差 MPE/% |
||
| 生物量异速生长模型Biomass allometric growth model |
树干Trunk | 2.169 | 4.71 | 4.18 | 0.78 |
| 树枝Branch | 0.772 | 4.96 | 11.09 | 0.79 | |
| 树叶Leaf | 0.630 | 9.01 | 8.94 | 1.35 | |
| 根系Root | 0.887 | 1.97 | 4.84 | 0.62 | |
| 总生物量Total biomass | 3.170 | -2.31 | -5.49 | 0.56 | |
| 多元线性模型 Multiple linear model |
树干Trunk | 2.498 | -8.95 | -7.78 | 0.89 |
| 树枝Branch | 0.754 | -2.83 | -4.11 | 0.78 | |
| 树叶Leaf | 0.229 | 2.75 | 5.17 | 0.49 | |
| 根系Root | 1.096 | 10.80 | 5.15 | 0.77 | |
| 总生物量Total biomass | 2.323 | 1.27 | 13.75 | 0.41 | |
| 相容性生物量模型 Compatible biomass model |
树干Trunk | 2.591 | -12.88 | 0.21 | 0.93 |
| 树枝Branch | 0.770 | -2.90 | -7.96 | 0.79 | |
| 树叶Leaf | 0.231 | 5.58 | 5.38 | 0.49 | |
| 根系Root | 0.837 | 7.47 | 10.29 | 0.59 | |
| 总生物量Total biomass | 2.406 | -0.90 | -1.02 | 0.43 | |
对各种模型的检验结果比较发现,相容性生物量模型的SEE在0.231~2.591 kg之间,其中,树叶的最小,树干的最大;多元线性模型的SEE在0.229~2.498 kg之间,其中,树叶的最小,树干的最大;生物量异速生长模型的SEE在0.630~3.170 kg之间,其中,树枝的最小,总生物量的最大。生物量异速生长模型的SEE、MPE总体上大于其他模型,结合TRE、ARE进行比较,相容性生物量模型的估测效果最好。在进行生物量异速生长模型的构建中造成了过拟合现象,而对各部分生物量检验结果分析发现,相容性生物模型在树枝、树叶的SEE、TRE、ARE、MPE大于多元线性模型,这说明相容性生物量模型对树枝、树叶的预测效果低于多元线性模型。
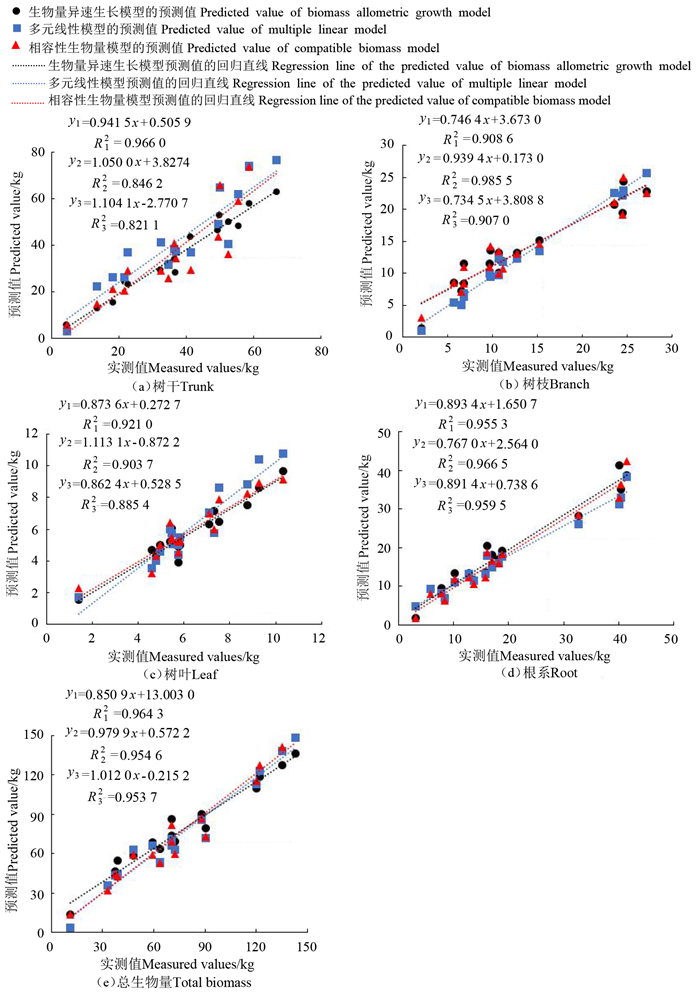
为进一步探究3种模型的预测值与实测值的关系,对不同模型各器官和总生物量的预测值、实测值作散点图(图 1),进行直线回归方程(y=bx+a)的拟合,并比较斜率b值。结果表明,回归方程的R2在0.821 1~0.985 5之间,拟合效果较好。回归直线的斜率b值在0.734 5~1.113 1之间,接近于1,3种模型的预测值均接近于实测值。其中,相容性生物量模型的回归直线b值除树枝、树叶外,更接近于1,而多元线性模型树枝、树叶的b值比其他两个模型更接近于1。综上所述,所构建3种模型的预测效果依次为相容性生物量模型、多元线性模型、生物量异速生长模型。
|
注:y1为生物量异速生长模型预测值的回归方程;y2为多元线性模型预测值的回归方程;y3为相容性生物量模型预测值的回归方程。 Note: y1 is the regression equation of predicted value of biomass allometric growth model; y2 is the regression equation of the predicted value of multiple linear model; y3 is the regression equation of the predicted value of compatible biomass model. 图 1 3种模型预测值与实测值的关系 Fig. 1 Relationship between the predicted values and the measured values of the three models |
本研究以蔡家川流域不同立地条件的48株刺槐立木测量数据为基础,采用不同建模方法构建了生物量异速生长模型、多元线性模型、相容性生物量模型,通过对模型拟合效果、预测结果分析发现,在模型构建中,立木形态因子中对生物量的估计贡献最大的是胸径(DBH),其余依次为树高(h)、冠长(LC)、冠幅(WC)。ZHOU et al[16]、黄光灿等[17]的研究结果均证明了DBH对生物量估计的重要性。同时,本研究中,以DBH、h的复合因子建立的生物量模型拟合度更高,这与李燕等[18]对人工杉木林的研究结果一致。本研究的3种模型中均以DBH2h为自变量的拟合效果最优,MENSAH et al[19]的研究表明,以DBH2h为复合变量有助于避免共线性的问题,能够提高模型的预测准确度。本研究在相容性生物量模型自变量的选择与CUI et al[11]、郑雪婷等[15]的相容性生物量模型研究结果不同,这可能是由于研究区域和树种不同造成的。本研究在生物量异速生长模型的拟合结果中,幂函数、多项式函数、复合函数形式的拟合结果较优且预测精度较好,其中,幂函数最优,这与尹惠妍等[20]对中国主要乔木树种生物量方程的研究结果相同,彭健健等[21]对人工杨梅林进行生物量模型的构建中也发现幂函数的拟合度较高。本研究在多元线性模型构建中发现,随着建模因子的增加,模型的拟合度和估测精度也随之提高,这与欧建德等[22]对云南红豆杉单木生物量模型,菊花等[23]对人工油松单木生物量模型的研究结果相同,这一结果也与立木生物量由DBH、h、WC等多种立木形态因子决定相呼应。本研究通过对3种模型的检验结果显示,相容性生物量模型对生物量的预估效果整体上优于生物量异速生长模型和多元线性模型,这两个模型无法保证各器官生物量与总生物量的相容性问题[11, 15, 24],且对树枝、树叶生物量估测效果不佳,这与许多学者的研究[11, 15, 26]结果相似,而多元线性模型对树枝、树叶的预测精度要优于相容性生物量模型,这可能是由于树冠因子对枝叶生物量的影响[25],有研究[23]表明,导入树冠因子可以提高模型估计精度。从模型的拟合上分析,相容性生物量模型的构建以每株样木的数据为单个单元进行方程组参数的拟合,为了兼顾相容性问题,使得在各器官生物量模型参数估计时有所妥协,而在建立生物量异速生长模型和多元线性模型时,则以每个器官对应的生物量数据为1组单元进行模型的拟合,从而使得部分器官生物量模型的拟合度和预测精度优于相容性生物量模型。
使用模型进行生物量的估测是一个复杂问题,立木生物量受到多种因素的影响,如树种、生长环境、林龄及立木形态等。众所周知,DBH对生物量估测的贡献最大,但只用DBH进行生物量模型构建时,所构建的模型无法解释DBH相同而生物量不同的现象,而过于复杂的模型又会造成过拟合现象,导致估测效果不好,并且当模型中有较多的测量因子时,一方面会增加数据采集的工作量,另一方面数据采集产生的误差又会降低生物量估测的精确度。本研究中,3种生物量模型均可用于蔡家川流域人工刺槐立木生物量的估测,其中,相容性生物量模型整体的估测效果最好,该模型对总生物量、树干、根系、树枝、树叶的预测精度高达93.90%、91.38%、90.83%、87.87%、88.79%,并且解决了各器官生物量与总生物量的相容性问题。而多元线性模型对树枝、树叶的预测精度为90.11%、89.72%,略高于相容性生物量模型。在实际应用中,应根据研究对象选取合适的生物量模型。模型的建立为评估蔡家川流域内人工刺槐碳汇能力提供了依据,为探究流域内刺槐人工林固碳能力的影响因子奠定基础,进而为刺槐人工林的抚育管理提供科学指导。
| [1] |
WEST P W. Tree and forest measurement[M]. Berlin: Springer-Verlag, 2015: 53.
|
| [2] |
LUO Y, WANG X, OUYANG Z, et al. A review of biomass equations for China's tree species[J]. Earth System Science Data, 2020, 12(1): 21-40. DOI:10.5194/essd-12-21-2020 |
| [3] |
徐耀粘, 江明喜. 森林碳库特征及驱动因子分析研究进展[J]. 生态学报, 2015, 35(3): 926-933. |
| [4] |
冯宗炜, 张家武, 邓仕坚. 杉木人工林生物产量的研究[M]. 郑州: 河南科学技术出版社, 1980.
|
| [5] |
李文华, 邓坤枚, 李飞. 长白山主要生态系统生物量研究[J]. 森林生态系统研究, 1981(2): 34-50. |
| [6] |
欧光龙, 胥辉. 森林生物量模型研究综述[J]. 西南林业大学学报(自然科学), 2020, 40(1): 1-11. |
| [7] |
DIMOBE K, GOETZE D, OUÉDRAOGO A, et al. Aboveground biomass allometric equations and carbon content of the shea butter tree(Vitellaria paradoxa C.F. Gaertn., Sapotaceae) components in Sudanian savannas(West Africa)[J]. Agroforestry Systems, 2018, 93: 1 119-1 132. |
| [8] |
王霞, 胡海波, 张世豪, 等. 不同林龄麻栎林地下部分生物量与碳储量研究[J]. 生态学报, 2019, 39(22): 8 556-8 564. |
| [9] |
欧建德, 欧家琳, 吴昊宇, 等. 云南红豆杉单木生物量模型选择与树冠调控[J]. 西北林学院学报, 2022, 37(5): 194-201. |
| [10] |
马克西, 曾伟生, 李智华. 新疆云杉一体化立木生物量模型系统研建[J]. 林业科学研究, 2018, 31(6): 105-113. |
| [11] |
CUI Y H, BI H X, LIU S Q, et al. Developing additive systems of biomass equations for Robinia pseudoacacia L. in the region of loess plateau of western Shanxi Province, China[J]. Forests, 2020, 11(12): 1332. DOI:10.3390/f11121332 |
| [12] |
PARRESO I B R. Additivity of nonlinear biomass equations[J]. Canadian Journal of Forest Research, 2001, 31(5): 865-878. DOI:10.1139/x00-202 |
| [13] |
李敏敏, 魏天兴, 李信良, 等. 黄土区蔡家川流域刺槐人工林林下物种多样性[J]. 浙江农林大学学报, 2018, 35(2): 227-234. |
| [14] |
BASKERVILLE G L. Use of logarithmic regression in the estimation of plant biomass[J]. Canadian Journal of Forest Research, 1972, 2(1): 49-53. DOI:10.1139/x72-009 |
| [15] |
郑雪婷, 仪律北, 李强峰, 等. 青藏高原典型人工林幼树生物量模型构建[J]. 应用生态学报, 2022, 33(11): 2 923-2 935. |
| [16] |
ZHOU X, BRANDLE J R, SCHOENEBERGER M M, et al. Developing above-ground woody biomass equations for open grown, multlple-stemmed tree species: shelterbelt-grown Russian olive[J]. Ecological Modelling, 2007, 202(3): 311-323. |
| [17] |
黄光灿, 吴宏炜, 赖建明, 等. 福建木荷多元生物量模型及2种权函数的比较[J]. 西部林业科学, 2020, 49(2): 137-146. |
| [18] |
李燕, 张建国, 段爱国, 等. 杉木人工林生物量估算模型的选择[J]. 应用生态学报, 2010, 21(12): 3 036-3 046. |
| [19] |
MENSAH S, VELDTMAN R, SEIFERT T. Allometric models for height and aboveground biomass of dominant tree species in South African mistbelt forests[J]. Southern Forests: A Journal of Forest Science, 2017, 79(1): 19-30. DOI:10.2989/20702620.2016.1225187 |
| [20] |
尹惠妍, 张志伟, 李海奎. 中国主要乔木树种生物量方程[J]. 中南林业科技大学学报, 2019, 39(5): 63-69. |
| [21] |
彭健健, 王增, 张勇, 等. 杨梅人工林相容性单株生物量模型构建[J]. 浙江农林大学学报, 2022, 39(2): 272-279. |
| [22] |
欧建德, 欧家琳, 康永武. 基于树冠形态特征因子的云南红豆杉单木生物量模型拟合[J]. 西南林业大学学报(自然科学), 2022, 42(4): 117-124. |
| [23] |
菊花, 张明铁, 张秋良. 大青山人工油松单木生物量模型的研究[J]. 内蒙古农业大学学报(自然科学版), 2010, 31(3): 60-65. |
| [24] |
符利勇, 雷渊才, 曾伟生. 几种相容性生物量模型及估计方法的比较[J]. 林业科学, 2014, 50(6): 42-54. |
| [25] |
欧建德, 吴志庄. 峦大杉人工林树冠、根系生长和林木分级的早期密度效应[J]. 东北林业大学学报, 2018, 46(12): 15-19. |
| [26] |
刘秀红, 姜春前, 徐睿, 等. 相容性单木生物量模型估计方法的比较: 以青冈栎为例[J]. 林业科学, 2020, 56(9): 164-173. |
 2024, Vol. 44
2024, Vol. 44


