文章信息
- 陈浩, 罗扬
- CHEN Hao, LUO Yang
- 马尾松树高-胸径非线性混合效应模型构建
- Construction of nonlinear mixed effect height-diameter model for Pinus massoniana
- 森林与环境学报,2021, 41(4): 439-448.
- Journal of Forest and Environment,2021, 41(4): 439-448.
- http://dx.doi.org/10.13324/j.cnki.jfcf.2021.04.015
-
文章历史
- 收稿日期: 2021-05-07
- 修回日期: 2021-06-07
2. 贵州省林业科技推广总站, 贵州 贵阳 550001
2. Forestry Science and Technology Extension Station of Guizhou Province, Guiyang, Guizhou 550001, China
胸径和树高作为衡量林分结构特征,调查森林资源的两个重要指标[1],在估算蓄积量、确定立地指数、预测生产力、描述林分生长等方面起着不可或缺的作用[2]。在调查中,胸径的测量简单且准确,而树高的测量不仅繁琐、耗时费力,还很难获得精确值。因此,建立树高-胸径模型估算未观测林木树高,具有实践应用意义[3]。对于树高-胸径模型的研究,早期仅以胸径为自变量构建,但并不能很好地描述两者关系[4]。随后,为了避免以胸径为单一自变量对树高预测产生较大的误差,研究学者们采取逐步回归方法,增加立地条件、林分状况、竞争关系等相关因子作为预测变量,构建含林分变量的广义模型[5-6]。广义模型虽然提升了模型的预测精度,但都是基于最小二乘法模拟参数,只能反映模型平均变化趋势,并不能体现林木个体之间的差异性和样地之间树高-胸径曲线变化,而非线性混合效应模型能有效弥补上述不足[7]。利用非线性关系在固定效应的基础上,考虑不同随机效应组合形式建立非线性混合效应模型,不仅能丰富方差、协方差信息,也可以促进模型的灵活性[8-9]。近年来,以此方法构建树高-胸径模型是热点,大多数研究表明混合模型对树高值预测精度优于固定效应模型。如李春明等[10]通过非线性混合效应模拟陕西省10个不同区域栓皮栎(Quercus variabilis Bl.)树高与胸径关系,对基于最小二乘法建立的6个常用方程进行拟合,比较决定系数(R2)、均方根误差(root mean square error,RMSE)等,确定基础模型,并以区域和样地作为随机效应构建非线性混合模型,结果显示,混合效应模型考虑了不同区域、样地的随机影响,使固定参数值发生变化,模型精度得到提升。CALAMA et al[11]以西班牙455个样地8 614株石松(Pinus pinea L.)为研究对象,采用传统回归方法和混合方法构建树高-胸径模型,比较不同模型精度,结果表明,将随机效应引入树高-胸径模型后,含随机参数的混合效应模型对树高预测效果优于传统回归模型。HUANG et al [12]采取同样的方法对黑云杉[(Picea mariana (Mill.) B.S.P.]研究发现,混合效应模型拟合能力较好,残差值相对较小。在非线性混合效应模型中,关于基础混合效应模型和广义混合效应模型拟合能力比较,存在不同的研究结果。如SHARMA et al [13]对毛桦(Betula pubescens Ehrh.)研究表明,与基础混合效应模型相比,优势木平均高等变量降低了样地间树高-胸径关系的差异性,使广义混合效应模型具有更好的预测能力,而周晏平等[14]在前人研究基础上,构建樟子松(Pinus sylvestris var. mongolica Litv.)树高-胸径混合模型,发现两者预测精度差异不大。李婉婷等[15]对落叶松(Larix gmelinii Rupr.)、樊伟等[16]对杉木[Cunninghamia lanceolata (Lamb.) Hook.]、MEHTÄTALO et al [17]对火炬松(Pinus taeda L.)研究得到相同结论。
马尾松(Pinus massoniana Lamb.)作为贵州省主要用材树种之一,具有材质好、用途广、耐干旱等特点,不仅提供了高质量木材产品,还发挥着重要的生态效益,但传统的经营理念、管理措施制约了马尾松人工林林木资源的发展和林分质量的提升[18]。为了准确监测林木生产和估计产量,并为生态服务功能和林分质量提升制定合理规划设计,有必要建立马尾松树高-胸径模型。目前,已有后向传输(back propagation,BP)神经网络等方法拟合马尾松树高曲线[19-20],但利用非线性混合效应模型研究马尾松树高与胸径关系还鲜见报道。为此, 本研究基于11个常用树高-胸径模型筛选基础模型,构建广义模型与非线性混合效应模型,比较各模型性能,探讨非线性混合效应对马尾松树高值预测的准确度和稳定性,以期为马尾松人工林生长收获预估和质量提升提供理论依据和科学指导。
1 材料与方法 1.1 研究区概况研究区位于贵州省东北部石阡县及印江土家族苗族自治县地区(27°17′~28°28′N,107°44′~108°48′E),均属亚热带季风气候区,地貌复杂多样,以喀斯特地貌为主,并含溶蚀、侵蚀等类型。石阡县地处黔东北斜坡地带,地势由东南部向西北部逐渐降低,海拔为388.3~1 869.3 m,年平均温度为17.1 ℃,年平均降雨量为1 073.2 mm;印江土家族苗族自治县位于梵净山西部,地势呈现东部高于西部,海拔为378~ 2 494 m,年平均温度为16.8 ℃,年均降雨量为1 100 mm。研究区主要代表性植物有马尾松、杉木、柏木(Cupressus funebris Endl.)、楠木[Phoebe bournei (Hemsl.) Yang]、榉木(Zelkova schneideriana Hand-Mazz)、光皮桦(Betula luminifera Winkl)、麻栎(Quercus acutissima Carruth.)和化香(Platycarya strobilacea Sieb.)等。
1.2 数据采集与预处理2020年8—11月, 在石阡、印江两县设立马尾松人工林标准地,标准地形状为圆形,大小为0.067 hm2,共254块。采用每木检尺法调查标准地内胸径大于5 cm的林木,记录树高、胸径、坡向、坡度等林分因子,剔除异常值后,共获得15 275株马尾松数据。根据调查数据,按比例计算各马尾松标准地的林分密度、胸高断面积,并基于6株优势木确定林分优势木平均高,随机选取203块标准地, 计12 300(80%)株马尾松构成建模数据,剩余51块标准地, 计2 975(20%)株马尾松构成检验数据。样地调查因子信息见表 1。
| 指标 Index |
建模数据Fitting data (n=12 300) | ||||
| 胸径Diameter at breast height /cm |
树高 Tree height /m |
林分密度 Stand density /(tree·hm-2) |
优势木平均高 Dominant height /m |
胸高断面积 Stand basal area /(m2·hm-2) |
|
| 最小值Minimum | 5.00 | 3.50 | 360 | 11.66 | 7.60 |
| 最大值Maximum | 48.70 | 26.30 | 2 280 | 25.85 | 48.64 |
| 均值Mean | 17.10 | 13.96 | 912 | 18.20 | 24.82 |
| 标准差Standard deviation | 7.43 | 4.10 | 403 | 2.87 | 7.43 |
| 变异系数Coefficient of variation | 0.43 | 0.29 | 0.44 | 0.16 | 0.30 |
| 指标 Index |
检验数据Validation data (n=2 975) | ||||
| 胸径Diameter at breast height /cm |
树高 Tree height /m |
林分密度 Stand density /(tree·hm-2) |
优势木平均高 Dominant height /m |
胸高断面积 Stand basal area /(m2·hm-2) |
|
| 最小值Minimum | 5.00 | 3.00 | 390 | 11.68 | 11.81 |
| 最大值Maximum | 46.80 | 24.10 | 1 740 | 22.17 | 36.73 |
| 均值Mean | 17.12 | 13.79 | 881 | 18.02 | 23.86 |
| 标准差Standard deviation | 7.36 | 3.90 | 337 | 2.38 | 6.47 |
| 变异系数Coefficient of variation | 0.43 | 0.28 | 0.38 | 0.13 | 0.27 |
为了更好地拟合非线性混合效应模型,结合已往研究成果,选择生物学意义较好的11个非线性树高-胸径模型(表 2,H为树高值、D为胸径值、a1、a2、a3为模型待估参数)[21],筛选预测精度最高的作为马尾松树高-胸径关系的基础模型。
| 模型名称 Function name |
参数类型 Function type |
函数形式 Equation |
| Curtis | 二参数2-parameter | H=1.3+a1D/(1+D)a2 |
| Meyer | 二参数2-parameter | H=1.3+a11-exp-a2D |
| Power | 二参数2-parameter | H=1.3+a1Da2 |
| Michaelis-Menten | 二参数2-parameter | H=1.3+a1D/a2+D |
| Wykoff | 二参数2-parameter | H=1.3+expa1-a2D+1-1 |
| Prodan | 三参数3-parameter | H=1.3+D2/a1D2+a2D+a3 |
| Logistic | 三参数3-parameter | H=1.3+a1/1+a2exp-a3D |
| Chapman-Richards | 三参数3-parameter | H=1.3+a11-exp-a2Da3 |
| Weibull | 三参数3-parameter | H=1.3+a11-exp-a2Da3 |
| Gomperz | 三参数3-parameter | H=1.3+a1exp-a2exp-a3D |
| Hossfeld IV | 三参数3-parameter | H=1.3+a1/1+1/a2Da3 |
传统的基础模型并不能很好地描述树高-胸径之间的关系,尤其在地形地貌复杂、立地类型多样的地区。为了提高模型预测精度,将树高、胸径与林分密度、优势木平均高、胸高断面积变量因子进行相关性分析,并在1.3.1确定的最佳树高-胸径基础模型上,增加不同组合形式的预测变量(1~3个)构建广义模型,以检验不同因子对树高-胸径关系的影响,选择最优树高-胸径广义模型。
1.3.3 非线性混合效应模型基本形式。在树高-胸径基础模型和广义模型上,增加随机效应部分,构建马尾松树高-胸径的非线性混合效应模型,其一般形式为:
| $ \left\{ {\begin{array}{*{20}{l}} {{H_{ij}} = f\left( {\beta , {\mu _i}, {D_{ij}}} \right) + {\varepsilon _{ij}}}\\ {{\mu _i} \sim N(0, \mathit{\boldsymbol{D}}){\varepsilon _{ij}}\sim N\left( {0, {\mathit{\boldsymbol{R}}_{ij}}} \right)} \end{array}} \right. $ | (1) |
式中:Hij为第i个样地第j株树的树高测量值(m);Dij为第i个样地第j株树的胸径测量值(cm);f(β,μi,Dij)描述的是Hij与Dij的关系,即胸径与树高之间的函数关系; μi为标准地随机效应参数估计值; D为随机效应方差-协方差矩阵;Rij为样地内方差-协方差矩阵;μi~N(0,D)表示随机参数服从期望为0、方差为D的正态分布;εij为误差项,服从期望为0、方差为Rij的正态分布,εij与μi相独立。
随机参数及方差协方差结构。拟合模型时,随机参数的确定一般取决于研究数据,如果没有关于参数选定的先验信息使模型收敛,PINHEIRO et al[22]建议将模型中所有参数视为随机参数。以赤池信息准则(AIC)、贝叶斯信息准则(BIC)为标准,比较不同参数下模型的收敛情况和拟合精度,确定最优混合模型。所选方差协方差结构矩阵因含随机参数个数的不同分为4种类型(1×1、2×2、3×3、4×4),现以包括两个随机参数的为例,其结构为:
| $ \boldsymbol{D}=\left[\begin{array}{cc} \sigma_{\mu_{1}}^{2} & \sigma_{\mu_{1} \mu_{3}} \\ \sigma_{\mu_{1} \mu_{3}} & \sigma_{\mu_{3}}^{2} \end{array}\right] $ | (2) |
式中:μ1、μ3为随机参数;
样地内方差-协方差结构矩阵,具体表达式为:
| $\boldsymbol{R}_{i j}=\sigma^{2} \boldsymbol{I}_{n} $ | (3) |
式中:σ2为模型误差方差;In为描述样地内误差的n×n维方差矩阵。
1.4 模型的评价与检验 1.4.1 模型评价通过R2、RMSE、平均相对误差绝对值(relative mean absolute error,RMA)、平均绝对误差(mean absolute error,MAE)4个统计指标比较模型的拟合性能[23]。R2用于确定实际数据与估计数据间的相关性,指标值越大, 表明模型拟合能力越优;RMSE、RMA、MAE用于评估模型的拟合准确性,指标值越小,则表明模型性能越好。统计指标表达式如下:
| $ R^{2}=1-\frac{\sum\limits_{i=1}^{m} \sum\limits_{j=1}^{n_{i}}\left(H_{i j}-\widehat{H}_{i j}\right)^{2}}{\sum\limits_{i=1}^{m} \sum\limits_{j=1}^{n_{i}}\left(H_{i j}-\bar{H}\right)^{2}} $ | (4) |
| $ E_{\mathrm{RMA}} / \%=\frac{\sum\limits_{i=1}^{m} \sum\limits_{j=1}^{n_{i}}\left|\frac{H_{i j}-\widehat{H}_{i j}}{\widehat{H}_{i j}}\right|}{n} \times 100 $ | (5) |
| $E_{\mathrm{RMS}}=\sqrt{\frac{\sum\limits_{i=1}^{m} \sum\limits_{j=1}^{n_{i}}\left(H_{i j}-\widehat{H}_{i j}\right)^{2}}{n}} $ | (6) |
| $ E_{\mathrm{MA}}=\frac{\sum\limits_{i=1}^{m} \sum\limits_{j=1}^{n_{i}}\left|H_{i j}-\widehat{H}_{i j}\right|}{n} $ | (7) |
式中:Hij为第i个样地第j株树的实测树高值(m);
固定效应模型的检验,直接将检验数据及各参数值代入模型,对于混合效应模型检验,固定效应部分与前者相同,随机效应部分需重新抽取样本计算各检验样地随机参数值。有研究表明,各样地随机抽取6株林木能较好检验混合模型预测精度[16],采取该方法计算,其公式为[24]:
| $ \widehat{\mu}_{i} \cong \widehat{\boldsymbol{D}} \widehat{\boldsymbol{Z}}_{i}^{\mathrm{T}}\left(\widehat{\boldsymbol{Z}}_{i} \widehat{\boldsymbol{D}} \widehat{\boldsymbol{Z}}_{i}^{\mathrm{T}}+\widehat{\boldsymbol{R}}_{i}\right)^{-1} \widehat{\boldsymbol{\varepsilon}}_{i} $ | (8) |
式中:
数据整理、计算在Excel、R语言软件中完成,其中非线性混合效应模型选用nlme程序包拟合,制图选用Origin软件。
2 结果与分析 2.1 基础模型拟合基于建模数据,对以往报道的11个树高-胸径方程进行拟合,比较R2、RMSE、RMA、MAE四个指标值,筛选马尾松树高-胸径基础模型。结果表明,对于树高-胸径关系函数的拟合,11个模型均有较好的适应性(表 3),R2介于0.550~0.636之间,RMA介于14.597%~16.858%之间,RMSE介于2.472~2.750 m之间,MAE则在1.917~2.223 m之间。以Chapman-Richards模型拟合结果最优,R2、RMA、RMSE、MAE分别为0.636、14.597%、2.472 m、1.917 m。采取同样的方法对检验数据进行拟合,得到相同结果。选取Chapman-Richards作为基础模型,其一般表达式为:
| $ H_{i j}=1.3+a_{1}\left[1-\exp \left(-a_{2} D_{i j}\right)\right]^{a_{3}}+\varepsilon_{i j} $ | (9) |
| 模型名称 Function name |
决定系数 R2 |
平均相对误差 绝对值RMA/% |
均方根误差 RMSE/m |
平均绝对误差 MAE/m |
排名 Rank |
| Curtis | 0.570 | 14.893 | 2.687 | 2.149 | 9 |
| Meyer | 0.581 | 16.344 | 2.654 | 2.069 | 8 |
| Power | 0.616 | 14.975 | 2.540 | 1.977 | 5 |
| Michaelis-Menten | 0.623 | 15.120 | 2.515 | 1.944 | 4 |
| Wykoff | 0.555 | 16.858 | 2.735 | 2.122 | 10 |
| Prodan | 0.629 | 15.095 | 2.498 | 1.927 | 3 |
| Logistic | 0.583 | 15.631 | 2.647 | 2.083 | 7 |
| Chapman-Richards | 0.636 | 14.597 | 2.472 | 1.917 | 1 |
| Weibull | 0.632 | 14.600 | 2.485 | 1.932 | 2 |
| Gomperz | 0.607 | 15.079 | 2.570 | 2.024 | 6 |
| Hossfeld IV | 0.550 | 15.176 | 2.750 | 2.223 | 11 |
式中:a1、a2、a3为模型待估参数。
2.2 广义模型拟合将树高、胸径与林分变量进行相关性分析,探讨各变量间逻辑关系,结果如表 4所示。树高、胸径与优势木平均高、胸高断面积呈极显著正相关关系(P<0.01),与林分密度呈极显著负相关关系(P<0.01),3个变量均对树高有显著性影响,具有统计学意义。因此,以Chapman-Richards为基础模型[公式(9)],引入3个变量构建广义模型,并比较不同组合形式模型拟合能力(表 5),筛选最优广义模型。结果表明:增加变量后,广义模型R2值明显增大,RMSE、RMA、MAE值均减小,说明考虑立地、林分条件能提升树高-胸径模型的拟合能力。当增加1个变量时,以含优势木平均高的模型[公式(10)]最好,较基础模型[公式(9)]的R2提高了0.140, RMSE、RMA、MAE分别降低了0.534 m、2.916%、0.443 m;增加两个变量时,以含优势木平均高、林分密度的模型拟合优度最佳,F检验结果显示,与公式(10)差异显著(F=883.3,P<0.001),说明在优势木平均高基础上,考虑林木之间竞争关系,进一步促进模型的拟合效果;增加3个变量时,拟合效果最佳的为公式(12),F检验与公式(11)差异显著(F=364.49,P<0.001),说明增加胸高断面积因子,可显著提升模型预测精度。因此,本研究以公式(13)为最优广义模型,一般表达式如下:
| $ H_{i j}=1.3+a_{1} H_{\mathrm{D}, i}^{a_{2}} A_{\mathrm{B}, i}^{a_{3}}\left[1-\exp \left(-a_{4} \rho_{i}^{a_{5}} D_{i j}\right)\right]^{a_{6}}+\varepsilon_{i j} $ | (13) |
| 变量Variable | 树高 Tree height |
胸径 Diameter at breast height |
林分密度 Stand density |
优势木平均高 Dominant height |
胸高断面积 Stand basal area |
| 树高Tree height | 1.000 | ||||
| 胸径Diameter at breast height | 0.775** | 1.000 | |||
| 林分密度Stand density | -0.331** | -0.411** | 1.000 | ||
| 优势木平均高Dominant height | 0.596** | 0.352** | -0.457** | 1.000 | |
| 胸高断面积Stand basal area | 0.311** | 0.262** | 0.140** | 0.414** | 1.000 |
| 注:**表示在0.01水平上显著相关。Note: **indicates statistically significant correlation at P < 0.01. | |||||
| 公式 Equation |
函数形式 Function form |
决定系数 R2 |
平均相对误差绝对值 RMA/% |
均方根误差 RMSE/m |
平均绝对误差 MAE/m |
| (10) | 0.776 | 11.681 | 1.938 | 1.474 | |
| (11) | 0.791 | 11.113 | 1.872 | 1.414 | |
| (12) | 0.797 | 10.913 | 1.845 | 1.383 |
式中:HD, i为i个样地优势木平均高(m);AB, i为第i个样地胸高断面积(m2·hm-2);ρi为第i个样地密度(株·hm-2);a1、a2、a3、a4、a5、a6为模型待估参数。
2.3 非线性混合效应模型拟合 2.3.1 基础混合效应模型在基础模型[公式(9)]上增加随机效应,通过R语言nlme包构建基础混合效应模型。结果显示,共3种情况收敛(表 6),其中基础模型未考虑随机参数时,AIC、BIC值最大,分别为57 173.29、57 143.56;当引入1个随机参数拟合基础混合效应模型,仅随机参数为μ1的混合模型收敛(AIC=49 050.55、BIC=49 087.64),经似然比检验,发现该模型拟合结果显著优于基础模型(LRT=8 090.7,P<0.000 1);引入两个随机参数拟合基础混合效应模型,混合模型AIC、BIC值降低,通过似然比检验,发现与随机效应作用于μ1的混合模型差异显著(P<0.000 1)。说明在随机参数为μ1的基础上,考虑μ2、μ3参数能促进模型预测效果。以随机效应作用于μ1、μ3时,AIC值为46 890.87、BIC值最小,为46 942.79,模型拟合能力最优。然而,在基础模型上考虑其它随机参数组合,模型均不收敛。故选取随机效应作用于μ1、μ3的拟合模型作为最优基础混合效应模型,其一般表达式为:
| $ H_{i j}=1.3+\left(a_{1}+\mu_{1 i}\right)\left[1-\exp \left(-a_{2} D_{i j}\right)\right]^{a_{3}+\mu_{3 i}}+\varepsilon_{i j} $ | (14) |
| 模型Model | 随机参数 Random parameter |
参数个数 Number of parameters |
赤池信息 准则AIC |
贝叶斯信息 准则BIC |
对数似然值 log-likelihood |
似然比检 验值LRT |
P值 P-value |
| 基础模型Basic model | 3 | 57 173.29 | 57 143.56 | -28 565.65 | |||
| 基础混合效应模型 | μ1 | 4 | 49 050.55 | 49 087.64 | -24 520.27 | 8 090.7 | < 0.000 1 |
| Basic fixed model | μ1+μ2 | 5 | 47 017.82 | 47 069.74 | -23 501.91 | ||
| μ1+μ3 | 5 | 46 890.87 | 46 942.79 | -23 438.43 | 2 163.7 | < 0.000 1 |
式中:μ1i、μ3i为样地水平的随机参数。
2.3.2 广义混合效应模型与2.3.1的方法相同,在广义模型基础上,将随机效应以不同组合形式作为自变量构建广义混合效应模型,共15种组合形式收敛(表 7)。比较模型拟合结果,所有混合模型AIC、BIC值均小于含林分变量的广义模型[公式(13)],表明以样地水平效应增加随机参数,能促进模型预测精度的提升。当引入1个随机参数拟合广义混合效应模型,仅随机参数为μ2、μ3、μ5、μ6四种情况时模型收敛,其余均不收敛,以随机效应作用于μ6时拟合能力最佳,经LRT检验,发现该模型拟合结果显著优于广义模型(LRT=3 180.2、P<0.000 1);当引入两个随机参数拟合广义混合效应模型,有7种组合形式收敛,以随机效应作用于μ2、μ6时模型预测精度最优,AIC、BIC值分别为46 421.44、46 495.61,并与含随机参数μ6的混合模型进行似然比检验,结果表明,含μ2、μ6的混合模型拟合能力得到显著提升(LRT=384.7、P<0.000 1);当引入3个或更多的随机参数拟合模型,AIC、BIC值增大,模型精度反而降低,说明增加过多的随机参数,不仅不能提高模型拟合能力,也会造成模型出现过参数化问题。故选取随机效应作用于μ2、μ6的拟合模型作为最优广义混合效应模型,一般表达式为:
| $ H_{i j}=1.3+a_{1} H_{\mathrm{D}, i}^{a_{2}+\mu_{2 i}} A_{\mathrm{B}, i}^{a_{3}}\left[1-\exp \left(-a_{4} \rho_{i}^{a_{5}} D_{i j}\right)\right]^{a_{6}+\mu_{6 i}}+\varepsilon_{i j} $ | (15) |
| 模型Model | 随机参数 Random parameter |
参数个数 Number of parameters |
赤池信息 准则AIC |
贝叶斯信息 准则BIC |
对数似然值 log-likelihood |
似然比检 验值LRT |
P值 P-value |
| 广义模型Generalized model | 6 | 49 980.36 | 50 032.29 | -24 983.18 | |||
| 广义混合效应模型 | μ2 | 7 | 48 255.73 | 48 315.07 | -24 119.87 | ||
| Generalized fixed model | μ3 | 7 | 48 262.41 | 48 321.75 | -24 123.23 | ||
| μ5 | 7 | 46 942.54 | 47 001.86 | -23 463.26 | |||
| μ6 | 7 | 46 802.11 | 46 861.45 | -23 393.06 | 3 180.2 | < 0.000 1 | |
| μ1+μ6 | 8 | 46 806.14 | 46 880.31 | -23 393.07 | |||
| μ2+μ3 | 8 | 48 259.73 | 48 333.90 | -24 111.87 | |||
| μ2+μ5 | 8 | 46 942.77 | 46 556.94 | -23 236.38 | |||
| μ2+μ6 | 8 | 46 421.44 | 46 495.61 | -23 200.72 | 384.7 | < 0.000 1 | |
| μ3+μ5 | 8 | 46 509.40 | 46 583.57 | -23 244.70 | |||
| μ3+μ6 | 8 | 46 431.49 | 46 505.67 | -23 205.75 | |||
| μ4+μ5 | 8 | 46 946.52 | 47 020.70 | -23 463.26 | |||
| μ2+μ3+μ5 | 9 | 46 498.84 | 46 595.26 | -23 236.42 | |||
| μ2+μ3+μ6 | 9 | 46 416.51 | 46 512.94 | -23 193.50 | 10.9 | 0.012 1 | |
| μ3+μ4+μ5 | 9 | 46 515.46 | 46 611.88 | -23 244.73 | |||
| μ2+μ3+μ4+μ5 | 10 | 46 506.83 | 46 632.93 | -23 236.42 |
式中:μ2i、μ6i为样地水平的随机参数。
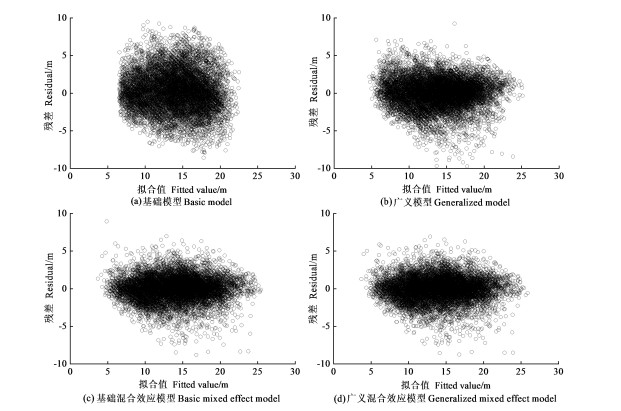
2.4 模型评价基础模型、广义模型、基础混合效应模型及广义混合效应模型残差分布见图 1。广义模型残差分布较基础模型紧密,离散程度较小,对树高值预测更为准确。混合模型不存在明显的异方差现象,不考虑对模型做异方差处理。此外,混合模型的残差分布较均匀、没有出现明显的不规则形状,优于固定效应模型,说明混合效应模型具有较强的稳定性和预测能力。
|
图 1 基础模型、广义模型、基础混合效应模型、广义混合效应模型残差分布图 Fig. 1 Residual distribution of the basic model, generalized model, basic mixed model, and the generalized mixed model |
表 8给出了基础模型、广义模型、基础混合效应模型、广义混合效应模型的固定参数值、方差组成值以及拟合统计量。结果表明:广义模型比基础模型的拟合精度高,其R2提高了0.161,RMSE、RMA、MAE分别降低了0.627 m、3.684%、0.534 m。混合模型估计精度较固定模型得到明显提升,其中与基础模型相比[公式(9)],基础混合效应模型[公式(14)]R2提高了0.228,RMSE、RMA、MAE分别降低了0.960 m、5.970%、0.810 m;与广义模型[公式(13)]相比,广义混合效应模型[公式(15)]R2提升了0.066,RMSE、RMA、MAE分别降低了0.329 m、2.256%、0.270 m。虽然基础混合效应模型拟合能力略优于广义混合效应模型,但两者并未有显著差异,R2仅提升0.001。表明在混合效应中林分密度、优势木平均高、胸高断面积对树高-胸径关系的影响被样地水平所掩盖。
| 参数 Parameter |
基础模型 Basic model |
基础混合效应模型 Basic mixed model |
广义模型 Generalized model |
广义混合效应模型 Generalized mixed model |
|
| 固定参数 | a1 | 24.344 0 | 17.937 4 | 1.569 7 | 1.076 0 |
| Fixed parameter | a2 | 0.040 0 | 0.102 9 | 0.954 6 | 1.089 3 |
| a3 | 0.896 0 | 1.500 6 | -0.103 8 | -0.107 4 | |
| a4 | 0.015 3 | 0.019 9 | |||
| a5 | 0.279 5 | 0.237 5 | |||
| a6 | 1.423 4 | 1.413 3 | |||
| 方差组成 | σ2 | 6.050 3 | 2.359 3 | 3.504 5 | 2.363 3 |
| Composition of | σμ12 | 9.855 2 | |||
| variance | σμ22 | 0.000 3 | |||
| σμ32 | 0.231 4 | ||||
| σμ62 | 0.189 6 | ||||
| σμ1μ3 | 0.931 7 | ||||
| σμ2μ6 | 0.005 6 | ||||
| 拟合统计量 | 决定系数R2 | 0.636 | 0.864 | 0.797 | 0.863 |
| Fitting statistics | 平均相对误差绝对值RMA/% | 14.597 | 8.627 | 10.913 | 8.657 |
| 均方根误差RMSE/m | 2.472 | 1.512 | 1.845 | 1.516 | |
| 平均绝对误差MAE/m | 1.917 | 1.107 | 1.383 | 1.113 | |
基于2 975组马尾松树高-胸径独立数据对两个固定效应模型、两个混合效应模型进行检验,各模型RMA、RMSE、MAE值见表 9。可以看出4个模型的预测精度从小到大依次为基础模型、广义模型、广义混合效应模型、基础混合效应模型,说明增加林分变量和样地水平随机参数均能提升模型拟合能力,与建模数据研究一致。
| 模型Model | 检验指标Validation indicators | |||
| 平均相对误差绝对 值RMA/% |
均方根误差 RMSE/m |
平均绝对误差 MAE/m |
||
| 固定效应模型Fixed effect model | 基础模型Basic model | 13.643 | 2.284 | 1.799 |
| 广义模型Generalized model | 10.319 | 1.692 | 1.295 | |
| 混合效应模型Mixed effect model | 基础模型Basic model | 8.465 | 1.417 | 1.067 |
| 广义模型Generalized model | 8.507 | 1.420 | 1.071 | |
准确的树高预测对于估算单木材积、评价立地质量、描述林分生长至关重要。本研究在11个常用树高-胸径模型中,确定Chapman-Richards为马尾松树高-胸径基础模型。该模型的3个参数,决定着树高的上渐近值和模型曲线形状[25],反映了随着胸径生长,树高逐渐增大后变缓的趋势,使模型具有较好的预测功能和生物学意义[26]。先前有研究报道,树高-胸径关系受环境状况、林分特征的影响与制约[27]。为了更好地描述不同林分之间树高-胸径关系,本研究采用逐步回归法将优势木平均高、林分密度、胸高断面积作为协变量构建广义模型,发现广义模型的估计精度和稳定性优于基础模型。当基础模型引入1个变量时,以含优势木平均高的模型对树高-胸径关系影响最大,R2变化幅度达14%,而优势木平均高是反映林分立地条件的重要指标[28],说明考虑立地条件因素较好地促进了模型拟合效果。王冬至等[29]在构建白桦(Betula platyphylla Suk.)树高-胸径模型时,发现与本研究类似结论。此外,密度、胸高断面积具备表达林分稳定性和竞争关系的特性[30],继续引入林分密度、胸高断面积变量至模型,发现模型拟合能力得到提升,以增加3个变量的模型[公式(13)]为最优广义模型。说明林分条件的变化对树高-胸径模型具有不同程度的影响,综合考虑立地质量、林木竞争等情况,能更好地预测树高值。赵俊卉等[31]在构建长白山云杉(Picea koraiensis Nakai)、冷杉(Abies holophylla Maxim.)树高曲线时表示,将林分变量作为因变量参与建模,提高了模型精度,MISIR[32]的研究也与本研究结论相同。
基于两个最优固定效应模型,对应构建两个非线性混合效应模型,比较不同随机参数下模型AIC、BIC值,筛选最佳混合模型。研究发现,基础混合效应模型在a1、a3位置上增加随机参数μ1、μ3,预测精度最优;广义混合效应模型则是将μ2、μ6同时作为随机参数,拟合效果最佳。两个混合模型均在曲线拐点位置处加入随机效应参数,以解释不同样地间树高曲线的变化。此外,通过比较各模型R2、RMSE、MAE、RMA值,显示非线性混合效应模型对树高值的预测效果优于传统回归模型,表明考虑样地效应的随机影响能更好地描述树高生长趋势。董云飞等[33]在构建杉木不同树高-胸径模型时指出,非线性混合效应模型较固定效应模型具有更好的拟合能力,与本研究结果一致。同样,CRECENTE-CAMPO et al[34]对蓝桉(Eucalyptus globulus L.)研究也得到相同结论。XU et al[35]认为由于随机效应参数的引入,使样地之间的差异逐渐减小,混合效应模型更真实地描述了树高-胸径关系。为了得到最佳树高-胸径模型,本研究对非线性混合效应模型评价发现,基础混合效应模型拟合能力略优于广义混合效应模型,但差异不大。说明样地水平效应代表了林分密度、优势木平均高、胸高断面积对树高-胸径关系的影响,导致增加随机效应参数后,再加入林分变量等因子对混合模型影响较弱。臧颢等[36]对红松(Pinus koraiensis sieb. et Zucc.)、周晏平等[14]对樟子松、李婉婷等[15]对落叶松研究均发现,基于混合效应构建的基础模型与广义模型拟合效果未有显著差异,与本研究结果一致,类似的情况也出现韩艳刚等[37]对冠幅的研究当中。虽然非线性混合模型提高了模型拟合精度,但利用该方法预测树木高度时,需抽取样本重新估计随机效应。本研究在每个标准地内随机抽取6株树,计算各标准地随机参数值,通过比较评价指标值发现,模型预测能力能得到较好的保证,樊伟等[16]对杉木研究也发现类似结论。综上所述,由于森林环境复杂,林分因子调查难度大,在实践应用中选择基础非线性混合效应模型预测马尾松人工林树高值,不仅具有较高的预测精度,还能降低调查成本,提高工作效率。
本研究构建并比较了不同马尾松树高-胸径模型,在固定效应模型中,确定Chapman-Richards为基础模型,广义模型对树高值的预测效果比基础模型更具有优越性。由于非线性混合效应模型考虑了样地水平的随机影响,与固定效应模型相比,模型拟合能力得到显著提高,而基础混合效应模型与广义混合效应模型对树高的预测精度差异不大。在森林资源调查中,若不考虑随机效应,则选择广义模型预测马尾松树高值;若考虑随机效应,由于基础混合效应模型自变量较少,具有较好的预测趋势,可选取该模型预测马尾松树高值。贵州地区生态环境多样及复杂,树高-胸径模型又受海拔、气候、降水、立地等环境因素影响,而本研究区域仅限于贵州东北部,地理上具有局限性,后续还需进一步扩大研究范围,充实标准地数据,保证非线性混合效应模型拟合效果,为马尾松人工林可持续发展及经营管理提供参考依据。
| [1] |
PENG C H, ZHANG L J, LIU J X. Developing and validating nonlinear height-diameter models for major tree species of Ontario's boreal forests[J]. Northern Journal of Applied Forestry, 2001, 18(3): 87-94. DOI:10.1093/njaf/18.3.87 |
| [2] |
马武, 雷相东, 徐光, 等. 蒙古栎天然林单木生长模型的研究Ⅱ.树高-胸径模型[J]. 西北农林科技大学学报(自然科学版), 2015, 43(3): 83-90. |
| [3] |
曾翀, 雷相东, 刘宪钊, 等. 落叶松云冷杉林单木树高曲线的研究[J]. 林业科学研究, 2009, 22(2): 182-189. DOI:10.3321/j.issn:1001-1498.2009.02.006 |
| [4] |
SHARMA M. Comparing height-diameter relationships of boreal tree species grown in plantations and natural stands[J]. Forest Science, 2016, 62(1): 70-77. DOI:10.5849/forsci.14-232 |
| [5] |
LEI X D, PENG C H, WANG H Y, et al. Individual height-diameter models for young black spruce (Picea mariana) and jack pine (Pinus banksiana) plantations in New Brunswick, Canada[J]. The Forestry Chronicle, 2009, 85(1): 43-56. DOI:10.5558/tfc85043-1 |
| [6] |
郭嘉, 孙帅超, 田相林, 等. 引入优势木树高建立的秦岭林区松栎林树高-胸径模型[J]. 东北林业大学学报, 2019, 47(11): 66-72. DOI:10.3969/j.issn.1000-5382.2019.11.013 |
| [7] |
李春明. 混合效应模型在森林生长模拟研究中的应用[D]. 北京: 中国林业科学研究院, 2010.
|
| [8] |
符利勇. 非线性混合效应模型及其在林业上应用[D]. 北京: 中国林业科学研究院, 2012.
|
| [9] |
TRINCADO G, VANDERSCHAAF C L, BURKHART H E. Regional mixed-effects height-diameter models for loblolly pine (Pinus taeda L.) plantations[J]. European Journal of Forest Research, 2007, 126(2): 253-262. DOI:10.1007/s10342-006-0141-7 |
| [10] |
李春明, 李利学. 基于非线性混合模型的栓皮栎树高与胸径关系研究[J]. 北京林业大学学报, 2009, 31(4): 7-12. DOI:10.3321/j.issn:1000-1522.2009.04.002 |
| [11] |
CALAMA R, MONTERO G. Interregional nonlinear height-diameter model with random coefficients for stone pine in Spain[J]. Canadian Journal of Forest Research, 2004, 34(1): 150-163. DOI:10.1139/x03-199 |
| [12] |
HUANG S M, MENG S X, YANG Y Q. Using nonlinear mixed model technique to determine the optimal tree height prediction model for black spruce[J]. Modern Applied Science, 2009, 3(4): 3-18. |
| [13] |
SHARMA R P, BREIDENBACH J. Modeling height-diameter relationships for Norway spruce, Scots pine, and downy birch using Norwegian national forest inventory data[J]. Forest Science and Technology, 2015, 11(1): 44-53. DOI:10.1080/21580103.2014.957354 |
| [14] |
周晏平, 雷泽勇, 赵国军, 等. 沙地樟子松不同树高-胸径模型比较分析[J]. 华南农业大学学报, 2019, 40(3): 75-81. |
| [15] |
李婉婷, 姜立春, 万道印. 基于混合效应的兴安落叶松树高与胸径关系模拟[J]. 植物研究, 2014, 34(3): 343-348. |
| [16] |
樊伟, 许崇华, 崔珺, 等. 基于混合效应的大别山地区杉木树高-胸径模型比较[J]. 应用生态学报, 2017, 28(9): 2 831-2 839. |
| [17] |
MEHTÄTALO L, DE-MIGUEL S, GREGOIRE T G. Modeling height-diameter curves for prediction[J]. Canadian Journal of Forest Research, 2015, 45(7): 826-837. DOI:10.1139/cjfr-2015-0054 |
| [18] |
刘建忠, 余娜. 贵州省马尾松林地质量空间评价与低效林防控措施研究[J]. 湖北农业科学, 2016, 55(20): 5 202-5 206. |
| [19] |
张鹏, 王新杰, 许昊. 将乐地区马尾松标准树高曲线的研究[J]. 中南林业科技大学学报, 2015, 35(3): 69-73. |
| [20] |
卯光宪, 谭伟, 柴宗政, 等. 基于BP神经网络的马尾松人工林胸径-树高模型预测[J]. 浙江农林大学学报, 2020, 37(4): 752-760. |
| [21] |
CHAI Z Z, TAN W, LI Y Y, et al. Generalized nonlinear height-diameter models for a Cryptomeria fortunei plantation in the Pingba region of Guizhou Province, China[J]. Web Ecology, 2018, 18(1): 29-35. DOI:10.5194/we-18-29-2018 |
| [22] |
PINHEIRO J C, BATES D M. Mixed effects models in S and S-PLUS[M]. New York: Springer, 2000.
|
| [23] |
姚丹丹, 徐奇刚, 闫晓旺, 等. 基于贝叶斯方法的蒙古栎林单木树高-胸径模型[J]. 南京林业大学学报(自然科学版), 2020, 44(1): 131-137. |
| [24] |
VARGAS-LARRETA B, CASTEDO-DORADO F, ÁLVAREZ-GONZALEZ J G, et al. A generalized height-diameter model with random coefficients for uneven-aged stands in El Salto, Durango (Mexico)[J]. Forestry: an International Journal of Forest Research, 2009, 82(4): 445-462. DOI:10.1093/forestry/cpp016 |
| [25] |
付晗, 魏亚伟, 殷有, 等. 基于小班和树高生长方程比较不同立地条件对树木生长的差异[J]. 林业资源管理, 2017(2): 46-52. |
| [26] |
张冬燕, 王冬至, 李晓, 等. 基于分位数回归的针阔混交林树高与胸径的关系[J]. 浙江农林大学学报, 2020, 37(3): 424-431. |
| [27] |
SANTIAGO-GARCÍA W, JACINTO-SALINAS A H, RODRÍGUEZ-ORTIZ G, et al. Generalized height-diameter models for five pine species at Southern Mexico[J]. Forest Science and Technology, 2020, 16(2): 49-55. DOI:10.1080/21580103.2020.1746696 |
| [28] |
李春明, 张会儒. 利用非线性混合模型模拟杉木林优势木平均高[J]. 林业科学, 2010, 46(3): 89-95. DOI:10.3969/j.issn.1672-8246.2010.03.020 |
| [29] |
王冬至, 张冬燕, 张志东, 等. 基于非线性混合模型的针阔混交林树高与胸径关系[J]. 林业科学, 2016, 52(1): 30-36. DOI:10.3969/j.issn.1006-1126.2016.01.006 |
| [30] |
杜志, 陈振雄, 孟京辉, 等. 基于混合效应的马尾松单木断面积预估模型[J]. 中南林业科技大学学报, 2020, 40(9): 33-40. |
| [31] |
赵俊卉, 亢新刚, 张慧东, 等. 长白山3个主要针叶树种的标准树高曲线[J]. 林业科学, 2010, 46(10): 191-194. DOI:10.11707/j.1001-7488.20101032 |
| [32] |
MISIR N. Generalized height-diameter models for Populus tremula L. stands[J]. African Journal of Biotechnology, 2010, 9(28): 4 348-4 355. |
| [33] |
董云飞, 孙玉军, 许昊, 等. 基于非线性混合模型的杉木标准树高曲线[J]. 东北林业大学学报, 2014, 42(11): 72-76, 81. DOI:10.3969/j.issn.1000-5382.2014.11.017 |
| [34] |
CRECENTE-CAMPO F, TOMÉ M, SOARES P, et al. A generalized nonlinear mixed-effects height-diameter model for Eucalyptus globulus L. in northwestern Spain[J]. Forest Ecology and Management, 2010, 259(5): 943-952. DOI:10.1016/j.foreco.2009.11.036 |
| [35] |
XU H, SUN Y J, WANG X J, et al. Height-diameter models of Chinese fir (Cunninghamia lanceolata) based on nonlinear mixed effects models in southeast China[J]. Advance Journal of Food Science and Technology, 2014, 6(4): 445-452. DOI:10.19026/ajfst.6.53 |
| [36] |
臧颢, 雷相东, 张会儒, 等. 红松树高-胸径的非线性混合效应模型研究[J]. 北京林业大学学报, 2016, 38(6): 8-16. |
| [37] |
韩艳刚, 雷泽勇, 赵国军, 等. 樟子松人工固沙林冠幅-胸径模型[J]. 干旱区研究, 2018, 35(5): 1 129-1 137. |

 2021, Vol. 41
2021, Vol. 41


