文章信息
- 杨士凯, 周运超, 黄磊, 王港
- YANG Shikai, ZHOU Yunchao, HUANG Lei, WANG Gang
- 杉木成熟林土壤容重空间变异特征
- Spatial variation characteristics of soil bulk density in mature forest of Cunninghamia lanceolata
- 森林与环境学报,2020, 40(1): 30-38.
- Journal of Forest and Environment,2020, 40(1): 30-38.
- http://dx.doi.org/10.13324/j.cnki.jfcf.2020.01.005
-
文章历史
- 收稿日期: 2019-11-03
- 修回日期: 2019-12-11
2. 贵州大学林学院, 贵州 贵阳 550025;
3. 贵州省林业科学研究院, 贵州 贵阳 550005
2. College of Forestry, Guizhou University, Guiyang, Guizhou 550025, China;
3. Guizhou Academy of Forest, Guiyang, Guizhou 550005, China
土壤容重指自然状态下单位体积土壤的干重[1],是反映土壤质量的重要因素[2],用于土壤质量评价、土地利用管理[3],评估土壤养分储量、有机碳[4],调节土壤水肥气热[5],影响土壤透水性、持水性、抗侵蚀能力[6]。在野外,由于试验时间、劳动强度、成本等限制,如何通过测定的辅助变量精确估算土壤容重是很有必要的[7]。成土母质、地形、生物、植被和人为活动等因素造成土壤养分空间分布差异[8],进而土壤容重高度变异[9],不同时间、不同空间位置导致土壤容重数值变化[10-11],加大了土壤容重空间变异研究难度。研究土壤容重空间变异、制作土壤容重预测模型,能更加简便、快捷地获取土壤容重数值,减少由土壤容重传统环刀法取样所导致的大量人力、物力的消耗[12]。
目前,国内外学者们对土壤容重空间变异的研究,主要采用地统计学方法,该方法与地理信息系统结合可成功用于土壤性质空间预测[13]。Kriging插值法可用于空间插值,克服土壤容重数据缺乏问题,最大限度降低调查成本,量化与减少估计误差的方差[14]。半方差函数可用于考虑土壤容重的相对重要性,估计其结构因素或随机因素[15]。学者们采用地统计学揭示了土壤容重空间变异的影响因素,如坡位[16]、植被[17]、海拔[18]、土地利用[19-22]和气候[23],但土地利用、坡度和植被盖度等土壤容重主要影响因素,只能解释58.15%左右的土壤容重变异[24]。通过地统计学分析,土壤容重具有明显的空间自相关性[25],局部土壤容重会出现偏大或偏小的斑块[26],西北干旱区土壤容重在空间上呈西向东减小的条带分布[27],进一步表明不同区域土壤容重空间变异情况。即便如此,仍鲜有关于如何减少土壤容重采样数的研究。
此外,实际进行林地调查时,取样间距为100 m会产生巨大工作量,因此,本研究通过经典统计学与地统计学相结合,以杉木成熟林内土壤容重空间分布为例,试图通过小尺度(100 m×100 m)土壤容重空间变异特征,进一步对不同土层采样间距“再采样”分析,确立土壤容重适宜采样间距与采样数,旨在为土壤容重采样节省人力、物力,为土壤管理提供科学依据,为土壤调控优化提供理论参考。
1 材料与方法 1.1 研究区概况石井山国有林场位于贵州省黎平县,北纬25°41′~26°08′,东经108°31′~109°31′,涉及德凤镇、中潮镇。该地属亚热带湿润季风气候,雨量充沛,湿度较大,林场内基岩主要为变质岩,土壤以黄壤或红黄壤为主,pH值4.5~5.5,自然环境优越,为杉木生长提供了适宜环境[28]。研究区杉木为1992年种植,属成熟林,林下植被包括红豆杉[Taxus chinensis (Pilger) Rehd.]、菝契(Smilax china L.)、细齿叶柃(Eurya nitida Korthals)、飞蛾槭(Acer oblongum Wall. ex DC.)、润楠(Machilus pingii Cheng ex Yang)、刺楸[Kalopanax septemlobus (Thunb.) Koidz.]、构树[Broussonetia papyrifera (Linn.) L′Hér. ex Vent.]、草珊瑚[Sarcandra glabra (Thunb.) Nakai]、穗序鹅掌柴[Schefflera delavayi(Franch.) Harms ex Diels.]、悬钩子(Rubus corchorifolius L.f.)、蛇葡萄[Ampelopsis sinica (Mig.) W.T.Wang.]、寒莓(Rubus buergeri Miq.)、鳞毛蕨(Dryopteris filix-mas)、假福王[Paraprenanthes sororia (Miq.) Shih]草等。
1.2 数据获取在研究区的杉木成熟林中布设100 m×100 m样地,并于2019年3月采用网格法(10 m×10 m)布设样方共计100个,用容积200 cm3的环刀对样方中心杉木成熟林进行林下土壤取样。为排除气候因子对试验的影响,依据采样进度,1 d内采集0~20、20~40 cm土层深度的土样,共计200份土样,并利用全球定位系统(global positioning system,GPS)记录样点空间位置。用精度0.01 g、量程500 g的便携式天平在野外及时对鲜土进行称重,带回试验室测定土壤容重。
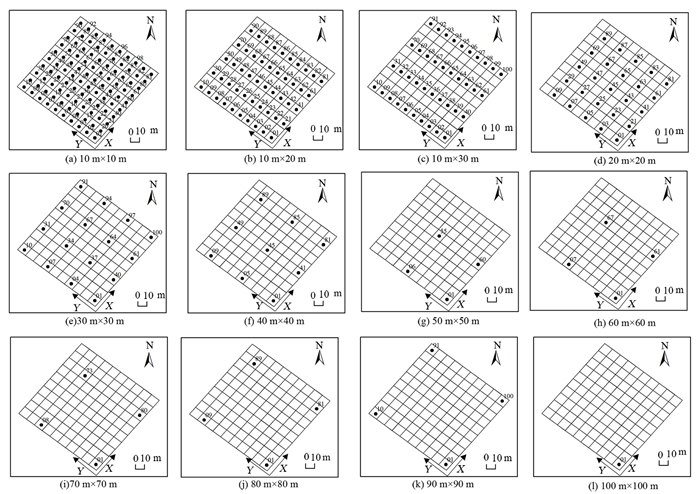
1.3 再采样设置对实际采样范围(100 m×100 m)数据进行“再采样”模拟,既能减少实际取样所导致人力、物力消耗,也能排除土壤本身空间变异特征对土壤容重的影响。因此,以“01”样地为基础样地进行“再采样”,如图 1所示,新增模式为“Y×X”的11种采样间距,分别为10 m×20 m、10 m×30 m,20 m×20 m、30 m×30 m,40 m×40 m、50 m×50 m,60 m×60 m、70 m×70 m,80 m×80 m、90 m×90 m,100 m×100 m。
|
图 1 “再采样”土壤容重样点布设图 Fig. 1 "Resampling" layout of soil bulk density sampling points |
主要利用SPSS 22.0与Excel 2019软件完成。其中,变异系数(coefficient of variation,VC)指标准差与平均值之比,是经典统计学用于确定变异程度的重要指标,若VC < 10%,表明数据呈弱变异,10%≤VC < 100%呈中等变异,VC≥100%表示为强变异。
1.4.2 地统计学分析地统计学与地理信息系统(geographic information system, GIS)技术相结合方面则利用ArcGIS 10.2软件地统计学模块,采用趋势面分析、半方差函数分析,确立最佳拟合模型,依据最佳模型采用Kriging插值分析,按掩膜提取建立土壤容重空间分布图,分析土壤容重空间变异特征。以此为基础,对土壤容重空间分布进行“再采样”,分析不同采样间距半方差函数参数及其变异程度。
地统计学分析工具主要采用变异函数[30],依据空间变异分析原理,用块金效应表示空间相关性强弱。块金效应为块金值与基台值的比值,若块金效应小于25%,则说明空间强相关;块金效应为25%~75%,表示空间中等相关,大于75%表示空间相关程度较弱,若值无限接近1,则表明土壤性质在该研究尺度上属于恒定变异[31]。此外,通过采用标准化均方根误差(root mean square standardized error, RMSSE)与标准化平均误差(mean square error, MSE)筛选模型拟合精度,若RMSSE接近于1,MSE接近于0,则说明模型拟合精度较高[32]。
2 结果与分析 2.1 土壤容重的基本统计特征杉木成熟林经典统计学的处理结果显示,0~20 cm土层的土壤容重均值为1.13 g·cm-3,变幅0.70~1.52 g·cm-3,标准差为0.19;20~40 cm土层土壤容重均值1.15 g·cm-3,变幅0.75~1.56 g·cm-3,标准差为0.19。以上结果表明,土壤容重随土层深度增加而增大。0~20、20~40 cm土层土壤容重变异系数分别为16.47%、17.00%,均在10%~100%间,属中等变异。
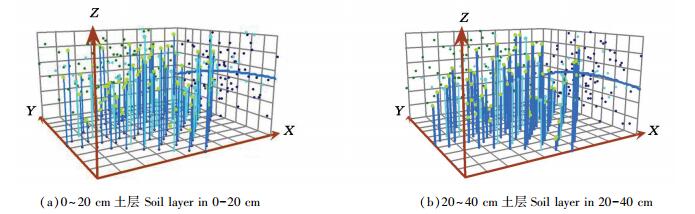
2.2 土壤容重的空间分布特征在ArcGIS 10.2软件中采用地统计分析模块中的趋势面分析,对试验区域内进行趋势面分析,图 2为0~20与20~40 cm土层土壤容重趋势面分布情况。其中,X轴表示方向为西向东,Y轴表示方向为南向北,Z轴为土壤容重。XYZ轴所组成的XY面上的点表示采样点在空间上的分布情况,XY面上的蓝色竖线表示每个样点处土壤容重数值,该数据值在YZ面与XZ面进行投影。从图 2可以看出,不同土层土壤容重从西至东方向无趋势变化,由南至北方向则呈逐渐减小的趋势,土壤容重变化趋势0~20 cm弧度较20~40 cm大。
|
图 2 杉木成熟林土壤容重趋势面分布 Fig. 2 Distribution of the trend of soil bulk density in the mature forest of C. lanceolata |
采用半方差函数对线性、球状、指数、高斯4种模型进行拟合分析,获取最佳函数模型及其相关参数(表 1)。结果表明,0~20 cm比较符合指数模型,而20~40 cm则比较符合球状模型。表 1中0~20、20~40 cm土壤容重块金效应分别为29.25%、56.37%,属空间中等相关。
| 土层Layer/cm | 模型Model | 块金值Nugget | 基台值Sill | 块金效应Nugget effect/% | 变程Range/m |
| 0~20 | 指数Exponential | 0.298 4 | 1.02 | 29.25 | 1.76 |
| 20~40 | 球状Spherality | 0.662 1 | 1.17 | 56.37 | 3.90 |
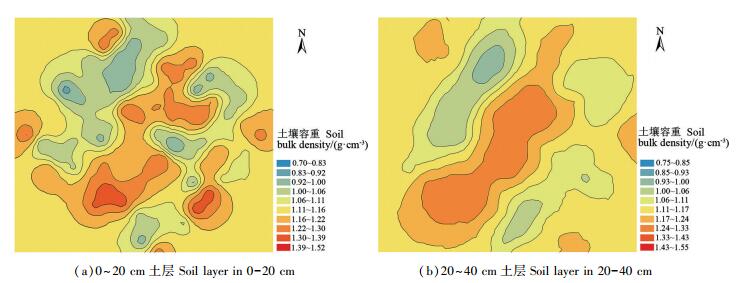
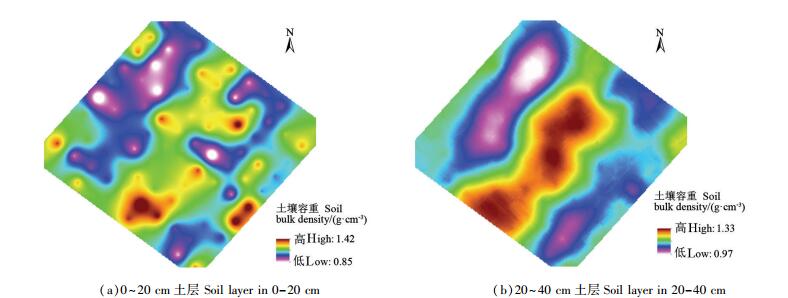
利用Kriging插值法进行土壤容重空间插值分析,0~20 cm土层选择指数模型,20~40 cm土层选择球面模型,得到不同层次土壤容重空间分布等值线图(图 3),但由于Kriging插值法所得区域与实际样地区域有出入,进一步利用等值线图进行掩膜提取获取空间分布图(图 4)。图 3、图 4说明,土壤容重在不同土层的空间分布上呈现出斑块状分布,高容重主要出现在中部偏西南区域,0~20 cm土层在偏东南区域有小部分高容重;低容重主要分布在西北偏中区域。此外,0~20 cm土层土壤容重相对变化较大,部分区域出现与周边较明显的差异值,而20~40 cm土层土壤容重变化较为稳定。
|
图 3 不同土层土壤容重空间分布等值线图 Fig. 3 Contour map of spatial distribution of soil bulk density at different soil layer |
|
图 4 不同层次土壤容重空间分布图 Fig. 4 Spatial distribution map of soil bulk density at different soil layer |
在原有采样范围(100 m×100 m)内进行“再采样”,对不同采样间距的土壤容重数值进行描述性统计(表 2)。从表 2可以看出,在一定区域内,随间距的增大,采样数逐渐减少,当采样间距达到某一程度时,采样数随采样间距的增大而保持不变,当采样间距与采样范围一致时,采样数达到最小值。采样数≥9时,0~20 cm土层土壤容重均值主要表现为随采样间距的增大而减小(在10 m×30 m处略有减少),20~40 cm土层均值表现为随采样间距的增大而增大;采样数均为4时,土壤容重在0~20 cm处均值同样随采样间距的增大而减小,而20~40 cm处则随采样间距增大而出现增大-减小-增大变化,采样间距100 m×100 m时采样数有且仅有1个,此时采样数过少,无法进行描述性统计。
| 间距Spacing | 采样数Number | 均值Mean/(g·cm-3) | 标准差Standard deviation | 变异系数Coefficient of variation/% | ||||||||
| 0~20 cm | 20~40 cm | 0~20 cm | 20~40 cm | 0~20 cm | 20~40 cm | 0~20 cm | 20~40 cm | |||||
| 10 m×10 m | 100 | 100 | 1.13 | 1.15 | 0.19 | 0.19 | 16.47 | 17.00 | ||||
| 10 m×20 m | 50 | 50 | 1.14 | 1.16 | 0.18 | 0.20 | 16.01 | 17.59 | ||||
| 10 m×30 m | 40 | 40 | 1.13 | 1.16 | 0.16 | 0.19 | 14.61 | 16.48 | ||||
| 20 m×20 m | 25 | 25 | 1.14 | 1.20 | 0.18 | 0.22 | 15.56 | 18.06 | ||||
| 30 m×30 m | 16 | 16 | 1.15 | 1.24 | 0.16 | 0.17 | 14.34 | 13.42 | ||||
| 40 m×40 m | 9 | 9 | 1.16 | 1.21 | 0.25 | 0.27 | 21.72 | 22.36 | ||||
| 50 m×50 m | 4 | 4 | 1.21 | 1.23 | 0.14 | 0.32 | 11.22 | 26.35 | ||||
| 60 m×60 m | 4 | 4 | 1.20 | 1.36 | 0.13 | 0.10 | 10.46 | 7.00 | ||||
| 70 m×70 m | 4 | 4 | 1.19 | 1.01 | 0.18 | 0.26 | 15.58 | 25.50 | ||||
| 80 m×80 m | 4 | 4 | 1.16 | 1.23 | 0.23 | 0.24 | 20.22 | 19.23 | ||||
| 90 m×90 m | 4 | 4 | 1.19 | 1.21 | 0.18 | 0.15 | 14.84 | 12.72 | ||||
| 100 m×100 m | 1 | 1 | 1.36 | 1.40 | ||||||||
土壤容重变异系数在采样数≥9时,表现为0~20 cm土层随采样间距的增大呈减小-增大交替出现的变化趋势,在20~40 cm土层随采样间距增大呈增大-减小交替出现的变化趋势;同一采样间距下,不同土层的土壤容重变异系数表现为0~20 cm < 20~40 cm(除30 m×30 m采样间距外);在采样数为4时,不同土层土壤容重变异系数均表现为随采样间距增大呈减小-增大-减小的变化趋势,采样间距相同,土壤容重在不同土层间变异系数变化较为复杂,时而0~20 cm>20~40 cm,时而0~20 cm < 20~40 cm。此外,随采样间距的增大,不同土层土壤容重变异系数变化范围分别为10.46%~21.72%、7.00%~26.35%,土壤容重变异系数除60 m×60 m间距下20~40 cm土层为7.00%外,其余间距均属中等变异。
表 3为不同采样间距下,土壤容重半方差函数最佳拟合模型及参数。结果表明,相对于实际采样,各“再采样”间距下,土壤容重在不同层次间最佳模型表现为3种形式:单一指数模型;线性与高斯模组合;线性、球状、高斯、指数4种模型组合。块金值在采样间距40 m×40 m时为0.001 8,已趋近于0,大于50 m×50 m时出现块金值为0的情况。块金效应变化较复杂,采样间距20 m×20 m、10 m×10 m均为中等空间相关;采样间距10 m×20 m、10 m×30 m为弱空间相关;采样间距超过30 m×30 m(包括30 m×30 m)时,块金效应表现为:块金效应为100%时,块金值与基台值相等时;块金效应为0时,块金值为0,基台值不为0;当0<块金效应<100%时,块金值与基台值均不为0。
| 间距Spacing | 土层Layer/cm | 模型Model | 块金值Nugget | 基台值Sill | 块金效应Nugget effect/% | 变程Range/m | |
| 10 m×10 m | |||||||
| 0~20 | 指数Exponential | 0.298 4 | 1.020 3 | 29.25 | 1.76 | ||
| 20~40 | 球状Spherality | 0.662 1 | 1.174 4 | 56.37 | 3.90 | ||
| 10 m×20 m | |||||||
| 0~20 | 线性、高斯Linear, Gauss | 0.861 1 | 1.136 4 | 75.78 | 6.10 | ||
| 20~40 | 线性、高斯Linear, Gauss | 0.916 9 | 1.178 1 | 77.83 | 5.29 | ||
| 10 m×30 m | |||||||
| 0~20 | 高斯Gauss | 0.862 8 | 1.031 7 | 83.63 | 6.07 | ||
| 20~40 | 线性、高斯Linear, Gauss | 0.929 4 | 1.095 9 | 84.81 | 1.84 | ||
| 20 m×20 m | |||||||
| 0~20 | 线性、高斯Linear, Gauss | 0.849 6 | 1.489 8 | 57.02 | 15.11 | ||
| 20~40 | 线性、高斯Linear, Gauss | 0.510 7 | 1.027 7 | 49.69 | 3.59 | ||
| 30 m×30 m | |||||||
| 0~20 | 线性、高斯Linear, Gauss | 0.866 4 | 1.114 1 | 77.77 | 9.02 | ||
| 20~40 | 线性、球状、高斯、指数Linear, Spherality, Gauss, Exponential | 1.066 7 | 1.066 7 | 100.00 | 17.02 | ||
| 40 m×40 m | |||||||
| 0~20 | 线性Linear | 0.001 8 | 1.822 2 | 0.10 | 10.24 | ||
| 20~40 | 指数Exponential | 0.747 3 | 1.216 4 | 61.44 | 10.24 | ||
| 50 m×50 m | |||||||
| 0~20 | 线性、球状、高斯、指数Linear, Spherality, Gauss, Exponential | 1.333 3 | 1.333 3 | 100.00 | 28.18 | ||
| 20~40 | 指数Exponential | 0.000 0 | 2.991 2 | 0.00 | 28.18 | ||
| 60 m×60 m | |||||||
| 0~20 | 线性、球状、高斯、指数Linear, Spherality, Gauss, Exponential | 1.332 7 | 1.332 7 | 100.00 | 33.76 | ||
| 20~40 | 指数Exponential | 0.000 0 | 2.961 9 | 0.00 | 33.76 | ||
| 70 m×70 m | |||||||
| 0~20 | 指数Exponential | 0.000 0 | 3.025 2 | 0.00 | 39.46 | ||
| 20~40 | 线性Linear | 0.157 0 | 1.354 6 | 11.59 | 13.63 | ||
| 80 m×80 m | |||||||
| 0~20 | 指数Exponential | 0.000 0 | 3.035 5 | 0.00 | 45.09 | ||
| 20~40 | 指数Exponential | 0.000 0 | 2.659 7 | 0.00 | 37.01 | ||
| 90m×90m | |||||||
| 0~20 | 指数Exponential | 0.000 0 | 3.060 3 | 0.00 | 50.84 | ||
| 20~40 | 线性、高斯Linear, Gauss | 0.002 5 | 2.462 3 | 0.10 | 18.98 | ||
| 100 m×100 m | |||||||
| 0~20 | 数值不足,无法计算Insufficient value to calculate | ||||||
| 20~40 | 数值不足,无法计算Insufficient value to calculate | ||||||
研究表明,杉木成熟林内土壤容重及其变异系数随土壤深度增加而增加,结合于冬雪等[33]对黄土区不同土层、不同土地利用方式的土壤容重研究结果,进一步验证土壤容重随土层深度的增加而增大。0~20、20~40 cm土层最佳模型分别为指数模型、球状模型,块金效应值表现为中等空间相关,与于冬雪等对林地、农田、草地等不同土地利用研究一致。一般而言,土壤异质性主要由成土母质、地形、土壤类型等结构因素与施肥等人为活动导致的随机因素共同决定,杉木成熟林内土壤容重属中等空间相关,说明该林地土壤容重空间变异受结构因素与随机因素共同作用。地统计学趋势面分析中,土壤容重空间变异趋势表现出从南向北逐渐减小,从西向东无变化,与孙国军等[34]的研究结果相似;在空间分布上呈斑块状镶嵌分布,与姚荣江等[35]对黄河三角洲地区土壤容重研究结果相似,而本试验区位于云贵高原,与黄土区气候、地形、海拔、植被类型等有所差异,所得结果相似,说明土壤容重在不同区域间既有整体相似性,又有局部差异性。
3.2 土壤容重采样尺度效应土壤容重作为土壤属性较为重要的因子之一,其研究难点在于传统环刀法会导致大量人力、物力的消耗,而采样尺度及样点空间分布是决定样点数据的两个关键因素,且能直接影响下一步采样设计结果。通过“再采样”分析表明,采样数随着采样间距的增大呈“减小-稳定-极限”变化趋势,这是由于在一定区域内,早期随采样间距的增大,各个采样点所控制的区域面积随之增大,进而导致采样点数目减少;采样间距大于100 m×100 m时,无论采样点所控制面积如何变化,试验区域均能提供且仅能提供该采样数目,即本研究采样间距50 m×50 m至90 m×90 m;当采样点所控制的可采样面积等同于试验区时,有且仅有1个采样点,该情况对于土壤容重采样最省时、省力,但却无法用于任何统计计算与插值估算,因此在空间变异方面研究最少需要4个点。采样数≥9时,0~20 cm土层土壤容重均值表现为随采样间距的增大而减小(在10 m×30 m处略有减少),20~40 cm土层土壤容重均值表现为随采样间距的增大而增大;采样数均为4时,土壤容重在0~20 cm土层随采样间距的增大而减小,20~40 cm土层土壤容重随采样间距的增大而出现增—减—增的复杂变化,这是由于土壤容重在空间上分布不同,导致土壤容重数值差异,同时采样数不同,进一步造成0~20 cm土层土壤容重随采样间距的增大而减小,20~40 cm土层土壤容重随采样间距的增大而增大;同一采样间距下,采样间距大于50 m×50 m时采样数为4,采样数过少,不具备统计学意义。
随采样间距增大,采样数减少,变异系数均为中等变异系数,主体上表现为0~20 cm < 20~40 cm;采样数相同时,变异系数属于中等变异,但变化趋势较为复杂,这是由于在一定采样范围内,采样间距的增加虽不能使变异系数发生较大偏差,却能获得土壤容重更为真实的变异系数。南方农田土壤容重变异系数随采样间距的增大呈先减后增趋势[36],而本研究变异系数与之不同,两者虽同为南方土壤,结果却有所差异,这是由于农田土壤与森林土壤结构性因素与随机性因素的不同,导致两者存在差异性,而采样深度、采样尺度不同也会造成土壤容重差异性,因此,对于不同采样尺度下土壤容重空间变异特征的研究是很有必要的。
采样点数量与采样点设置需要进一步研究[37],一般而言,地统计插值最少需30个样地[38],但这并不是绝对的,而是由土壤本身及样点空间分布共同作用,采样尺度仅仅是通过样点影响布局而改变空间分析结果,估测精度虽随采样尺度减小而增加,却将提高土壤采样成本[39],如何确定最佳采样尺度与样点数之间的关系,是估测精度所需进行的必要研究。此外,每一尺度都有其约束体系和临界值,本研究通过“再采样”模拟,以小尺度(地块)为空间变异研究区域[40],借助杉木成熟林不同土层土壤容重研究最佳采样间距及采样数。研究表明,采样间距的增大,导致土壤容重半方差函数最佳模型变化复杂,采样间距增至一定程度时,块金值、偏基台值会出现0,导致空间插值精度过低,该种情况下的采样间距与采样数并不适合用于空间变异研究。因此,综合考虑下,小尺度(100 m×100 m)采样间距在20 m×20 m时最佳。
本研究选择尺度为100 m×100 m,主要是由于尺度过大,会导致林业用地间坡度差异,进而导致温度、水分等不同,影响土壤容重空间变异特征,在100 m范围内,海拔变化较小,导致温度上下之间差距不大,尽量减少由于环境因子所导致的综合性变化,同时,为避免土壤容重在时间上的变异,本研究所有样品均于同一日进行采样,然而,土壤内部砾石含量、根系等不同也会影响土壤容重数值。因此,在今后研究中,可进一步结合土壤内部石砾含量、根系等因子综合分析,估算更为准确的土壤容重,将有助于土壤容重空间变异更深入的研究。
4 结论杉木成熟林内土壤容重随土壤加深而增大,变异系数呈中等变异。小尺度下(100 m×100 m),0~20、20~40 cm土壤容重最佳拟合效果分别为指数模型、球状模型,块金效应均在25%~75%间,属中等空间自相关性,土壤容重空间上呈斑块镶嵌状。随采样间距增大,采样数呈“减小-稳定-极限”的变化趋势,变异系数受采样间距增大的影响较小。采样间距过大(大于50 m×50 m),样点仅为1~4个,不具备统计学意义,该情况导致块金值为0,块金效应变化也较复杂,因此,小尺度(100 m×100 m)采样间距在20 m×20 m时最佳,此时仅需采集25份土样,便能满足空间估算精度的最低要求,节省大量人力、物力的消耗。
| [1] |
黄昌勇, 徐建明. 土壤学[M]. 北京: 中国农业出版社, 2010: 111.
|
| [2] |
李渊, 刘子琦. 石漠化区不同土地类型土壤侵蚀与理化性质特征[J]. 森林与环境学报, 2019, 39(5): 515-523. |
| [3] |
LI S, LI Q Q, WANG C Q, et al. Spatial variability of soil bulk density and its controlling factors in an agricultural intensive area of Chengdu Plain, Southwest China[J]. Journal of Integrative Agriculture, 2019, 18(2): 290-300. |
| [4] |
黄一敏, 李心清, 杨放, 等. 中国西南喀斯特森林土壤有机碳空间变化及影响因素[J]. 地球与环境, 2016, 44(1): 1-10. |
| [5] |
王小云. 不同水土保持植物种类对土壤物理性质的影响[J]. 安徽农业科学, 2018, 46(26): 113-115. |
| [6] |
柴华, 何念鹏. 中国土壤容重特征及其对区域碳贮量估算的意义[J]. 生态学报, 2016, 36(13): 3903-3910. |
| [7] |
SUUSTER E, RITZ C, ROOSTALU H, et al. Soil bulk density pedotransfer functions of the humus horizon in arable soils[J]. Geoderma, 2011, 163(1/2): 74-82. |
| [8] |
宋贤冲, 项东云, 郭丽梅, 等. 猫儿山森林土壤养分的空间变化特征[J]. 森林与环境学报, 2016, 36(3): 349-354. |
| [9] |
LARK R M, RAWLINS B G, ROBINSON D A, et al. Implications of short-range spatial variation of soil bulk density for adequate field-sampling protocols:methodology and results from two contrasting soils[J]. European Journal of Soil Science, 2014, 65(6): 803-814. |
| [10] |
ALLETTO L, COQUET Y. Temporal and spatial variability of soil bulk density and near-saturated hydraulic conductivity under two contrasted tillage management systems[J]. Geoderma, 2009, 152(1/2): 85-94. |
| [11] |
WANG S L, MA C. The spatial heterogeneity of the soil bulk density under different management types of Pinus koraiensis forests[J]. Advanced Materials Research, 2013, 726-731: 4315-4318. |
| [12] |
HAN G Z, ZHANG G L, GONG Z T, et al. Pedotransfer functions for estimating soil bulk density in China[J]. Soil Science, 2012, 177(3): 158-164. |
| [13] |
MARCHANT B P, SABY N P, LARK R M, et al. Robust analysis of soil properties at the national scale:cadmium content of French soils[J]. European Journal of Soil Science, 2010, 61(1): 144-152. |
| [14] |
YANG Q Y, LUO W Q, JIANG Z C, et al. Improve the prediction of soil bulk density by cokriging with predicted soil water content as auxiliary variable[J]. Journal of Soils and Sediments, 2016, 16(1): 77-84. |
| [15] |
WANG Y Q, SHAO M A, LIU Z P, et al. Prediction of bulk density of soils in the loess plateau region of China[J]. Surveys in Geophysics, 2014, 35(2): 395-413. |
| [16] |
张湘潭, 曾辰, 张凡, 等. 藏东南典型小流域土壤饱和导水率和土壤容重空间分布[J]. 水土保持学报, 2014, 28(1): 69-72. |
| [17] |
周李磊, 朱华忠, 钟华平, 等. 新疆伊犁地区草地土壤容重空间格局分析[J]. 草业学报, 2016, 25(1): 64-75. |
| [18] |
厉方桢, 朱华忠, 李愈哲, 等. 阿勒泰地区草地表层土壤容重的空间格局分析[J]. 草业科学, 2018, 35(12): 2801-2811. |
| [19] |
邱倩倩, 张卓栋, 孙传龙, 等. 锡林郭勒草地景观系统土壤容重空间变异及其与风蚀的关系[J]. 水土保持通报, 2016, 36(6): 58-62. |
| [20] |
伍星, 李辉霞, 傅伯杰, 等. 三江源地区高寒草地不同退化程度土壤特征研究[J]. 中国草地学报, 2013, 35(3): 77-84. |
| [21] |
乔宇鑫, 朱华忠, 钟华平, 等. 内蒙古地区草地表层土壤容重空间格局分析[J]. 草地学报, 2016, 24(4): 793-801. |
| [22] |
潘宗涛, 陈志强, 陈志彪. 朱溪流域土壤容重空间分异与地形和土地利用的关系[J]. 水土保持通报, 2018, 38(3): 263-268. |
| [23] |
易小波, 邵明安, 赵春雷, 等. 黄土高原南北样带不同土层土壤容重变异分析与模拟[J]. 农业机械学报, 2017, 48(4): 198-205. |
| [24] |
冯强, 段宝玲, 姜硕. 小流域尺度土壤容重及其影响因素的空间变异[J]. 山西农业大学学报(自然科学版), 2016, 36(1): 39-45. |
| [25] |
张川, 陈洪松, 张伟, 等. 喀斯特坡面表层土壤含水量、容重和饱和导水率的空间变异特征[J]. 应用生态学报, 2014, 25(6): 1585-1591. |
| [26] |
耿韧, 张光辉, 李振炜, 等. 黄土丘陵区浅沟表层土壤容重的空间变异特征[J]. 水土保持学报, 2014, 28(4): 257-262. |
| [27] |
李晓晓, 刘京, 赵世伟, 等. 西北干旱区县域农田表层土壤容重空间变异性特征[J]. 水土保持学报, 2013, 27(4): 148-151. |
| [28] |
廖海坤, 杨承荣, 王朝霞. 石井山林场杉木采伐迹地更新及效果分析[J]. 现代农业科技, 2016(24): 170-171. |
| [29] |
王军, 傅伯杰, 邱扬, 等. 黄土丘陵小流域土壤水分的时空变异特征:半变异函数[J]. 地理学报, 2000, 55(4): 428-438. |
| [30] |
郭军玲, 吴士文, 金辉, 等. 农田土壤微量元素含量的空间变异特征和影响因素[J]. 水土保持学报, 2010, 24(1): 145-149. |
| [31] |
ZHANG S R, SUN B, ZHAO Q G, et al. Temporal-spatial variability of soil organic carbon stocks in a rehabilitating ecosystem[J]. Pedosphere, 2004, 14(4): 501-508. |
| [32] |
李强, 闫晨兵, 刘勇军, 等. 郴州植烟土壤pH空间分布及影响因素初探[J]. 中国烟草学报, 2019, 25(4): 50-58. |
| [33] |
于冬雪, 贾小旭, 黄来明, 等. 黄土区不同土层土壤容重空间变异与模拟[J]. 土壤学报, 2019, 56(1): 55-64. |
| [34] |
孙国军, 李卫红, 朱成刚, 等. 新疆伊犁河谷表层土壤容重的空间变异性分析[J]. 资源科学, 2016, 38(7): 1222-1228. |
| [35] |
姚荣江, 杨劲松, 刘广明. 黄河三角洲地区土壤容重空间变异性分析[J]. 灌溉排水学报, 2006, 25(4): 11-15. |
| [36] |
徐翠兰, 侯淑楠, 姚紫东, 等. 南方农田土壤容重空间变异性及其尺度效应[J]. 排灌机械工程学报, 2017, 35(5): 424-429. |
| [37] |
谭艳, 吴承祯, 洪伟, 等. 邓恩桉林地土壤pH空间变异分析[J]. 植物资源与环境学报, 2012, 21(1): 14-19. |
| [38] |
张仁铎. 空间变异理论及应用[M]. 北京: 科学出版社, 2005: 20.
|
| [39] |
潘瑜春, 刘巧芹, 阎波杰, 等. 采样尺度对土壤养分空间变异分析的影响[J]. 土壤通报, 2010, 41(2): 257-262. |
| [40] |
冯晓, 乔淑, 胡峰, 等. 土壤养分空间变异研究进展[J]. 湖北农业科学, 2010, 49(7): 1738-1741. |

 2020, Vol. 40
2020, Vol. 40


