文章信息
- 刘洵, 曾思齐, 贺东北, 龙时胜, 向博文
- LIU Xun, ZENG Siqi, HE Dongbei, LONG Shisheng, XIANG Bowen
- 基于混合效应的湖南省栎林生长收获模型
- Growth and yield model of oak forest based on mixed effect
- 森林与环境学报,2019, 39(5): 475-482.
- Journal of Forest and Environment,2019, 39(5): 475-482.
- http://dx.doi.org/10.13324/j.cnki.jfcf.2019.05.005
-
文章历史
- 收稿日期: 2019-04-18
- 修回日期: 2019-05-14
2. 国家林业和草原局中南林业调查规划设计院, 湖南 长沙 410014
2. Central South Forest Inventory and Planning Institute, National Forestry and Grassland Administration, Changsha, Hunan 410014, China
林分生长和收获模型是指一个或者一组描述林木生长和林分状态及立地条件的关系的数学函数[1],经历了从传统的回归建模到根据林分生长规律演绎出来的理论模型,由单因子的简单模型到多因子的综合模型的发展过程[2]。近年来,一些学者对过去应用模型进行改进以及在过去模型的基础上应用其他学科新方法等方式,提出大量先进实用的模型,包括联立方程组以及混合效应模型等近代模型技术[3-4]。生长量模型与收获量模型之间存在相容性,以及在估计模型参数时一些变量在某一方程中以自变量的形式出现而在另一个方程组则又以因变量的形式出现,即多个模型相互之间存在着连续相关的问题[5],因此,在构建林分生长与收获模型时,经常要用到联立方程组模型[6-7]。在进行参数估计时,为了避免联立方程组中各方程间随机误差的相关性,很多学者采用二步最小二乘法和三步最小二乘法等方法[8-9],但这些方法都没有很好地解决模型偏差的问题,模型的估计精度也没有很大地提高。混合效应模型包含固定效应参数和随机效应参数两个部分,又有线性[10]和非线性[11]之分,其既可以通过加入随机参数, 同时反映样本总体平均变化和个体之间的差异,又可以通过不同的方差协方差结构来描述数据间的异方差和自相关性,在提高模型预估精度方面有着很大的优势,主要应用于分组数据,如重复测量数据、纵向数据和多变量多层数据等[12]。在林分生长与收获混合效应模型的研究方面,FANG et al[5]基于混合效应模型方法构建了美国乔治亚州和佛罗里达州湿地松(Pinus elliottii)林分优势木平均高、林分断面积以及林分蓄积量作为内生变量的联立方程组,并考虑了样地层次的随机效应及重复观测相关性,预测了经过不同经营措施处理的蓄积量生长趋势,结果显示与传统方法相比,基于混合效应模型的误差大幅度下降。HALL et al[13]利用一个三元的多元多层次的非线性混合效应模型方法来模拟美国乔治亚州和佛罗里达州湿地松的优势木高、断面积和株数,然后利用这几个变量的预测值输入到蓄积量模型中,最后对林分未来的生长和收获进行预测。李春明[14]基于非线性混合效应方法建立了江西杉木[Cunninghamia lanceolata (Lamb.)Hook.]人工林林分优势木平均高、断面积模型以及基于对数形式线性蓄积量模型的联立方程组,并利用验证数据与传统模型回归方法的模拟结果进行比较分析,结果显示基于混合效应模型方法的模拟结果明显好于传统回归估计方法。李春明[14]和FANG et al[5]构建林分优势木平均高、林分断面积及林分蓄积量的联立方程组模型,其研究对象都是人工林,并且没有考虑林分生长量与收获量一致的问题。因此,本研究基于湖南省国家森林资源连续清查中以栎类为优势树种的样地复测数据,构建反映林分生长模型和收获模型相一致的相容性林分生长和收获预测模型,然后在建立的相容性林分模型的基础上,加入样地层次的混合效应,并选择验证数据对传统的相容性林分模型和加入混合效应的相容性林分模型方法进行验证与预测,以期为准确预估未来栎类林分生长提供方法支撑。
1 研究区概况湖南省简称“湘”,因全省大部分地处洞庭湖以南而得名,地处中国东南部,长江中游,属于华中地区,省会长沙,位于东经108°47′~114°15′,北纬24°39′~30°08′,全省地貌以山地、丘陵为主,三面环山,形成从东南西三面向北倾斜开口的马蹄形状。湖南为大陆性亚热带季风湿润气候,气候温暖,四季分明,光热充足,降水丰沛,雨热同期,气候条件优越。湖南位于中国东部中亚热带常绿阔叶林地带,植被类型多种多样,植物资源异常丰富,是中国植物资源丰富的省份之一。根据第八次国家森林资源连续清查结果,湖南栎(Quercus acutissima)类资源丰富,全省范围内均有分布,栎类总面积达86 400 hm2,总蓄积量达5.098 8×106 m3,较常见的有石栎属(Lithocarpus)和青冈属(Cyclobalanopsis)等,不过大多处于自然生长状态,并且存在林分过密、老桩萌生、细长杆材等质量低下问题。
2 材料与方法 2.1 数据来源以湖南省国家森林资源连续清查的栎类次生林为研究对象,选择数据完整, 以栎类为优势树种且林分类型为天然次生林的176个固定样地(1989—2014年, 共6期)的复测数据作为研究数据。固定样地面积0.066 7 hm2,调查间隔时间5 a,起测胸径5 cm,主要样地调查包括林木胸径、树种、树高、郁闭度、相对位置、样地的地形因子(包括地貌、海拔、坡向、坡位和坡度)、土层因子(包括土层厚度、枯枝落叶层厚度和腐殖质层厚度)等。由于部分样地在不同调查期间受到不同程度的人为干扰,株数变动较大,对林分断面积和蓄积量有很大的影响,因此,选择相邻两期调查株数变动在10%以内并且林分断面积和蓄积量有增长的样地,剔除其中有数据缺失、异常的样地,最后选择了符合条件的96块样地(共204个样本)。从96块样地中随机选取70块样地(150个样本)数据作为建模数据,其余的26块样地(共54个样本)数据作为检验数据。最后计算和统计每个样地的平均胸径、平均年龄、断面积、蓄积量以及株数(表 1)。
| 样本数据 Sample data |
平均胸径 Mean DBH/cm |
平均年龄 Mean age/a |
断面积 Basal area /(m2·hm-2) |
蓄积量 Stock volume /(m3·hm-2) |
株数 Number of trees /(tree·hm-2) |
|
| 建模数据 Fitting data |
最小值Minimum | 6.8 | 17 | 3.94 | 12.35 | 540 |
| 最大值Maximum | 18.5 | 69 | 46.06 | 185.23 | 2 685 | |
| 平均值Mean | 11.9 | 40 | 15.83 | 75.81 | 1 470 | |
| 检验数据 Validation data |
最小值Minimum | 7.6 | 21 | 4.23 | 12.43 | 525 |
| 最大值Maximum | 17.2 | 66 | 43.76 | 166.73 | 2 640 | |
| 平均值Mean | 11.5 | 40 | 15.32 | 72.18 | 1 455 | |
林分生长的主要影响因子包括立地质量、林分平均年龄、林分密度、林分类型以及林分结构。根据一类连续清查数据,可以得到两期样地的观测因子:期初的平均年龄、平均直径、株数、断面积、蓄积量等;相应期末的因子有期末的平均年龄、平均直径、株数、断面积、蓄积量等。一般来讲,林分蓄积量是林分地位指数、林分平均年龄和林分密度的函数。林分地位指数的确定见刘洵等[15]的研究,根据Schumacher曲线方程,林分密度用林分断面积表示,形成期初林分蓄积量的方程
| $ \ln {{M}_{1}}={{b}_{1}}+{{b}_{2}}{{I}_{\text{S}}}+{{b}_{3}}{{t}_{1}}^{-1}+{{b}_{4}}\ln {{G}_{1}} $ | (1) |
式中:M1为期初林分蓄积量(m3);IS为样地地位指数;t1为期初林分年龄(a);G1为期初林分断面积(m2);b1、b2、b3、b4为模型参数。
由于期末断面积是在期初断面积的基础上生长的,因此, 使用林分断面积方程对年龄求导可得到林分断面积生长方程,然后对林分断面积生长方程积分可得到期末断面积的预测方程,其表达式为
| $ \ln {{G}_{2}}=\frac{{{t}_{1}}}{{{t}_{2}}}\ln {{G}_{1}}+{{a}_{1}}(1-\frac{{{t}_{1}}}{{{t}_{2}}})+{{a}_{2}}{{I}_{\text{S}}}\left( 1-\frac{{{t}_{1}}}{{{t}_{2}}} \right) $ | (2) |
式中:G2为期末林分断面积(m2);t2为期末林分年龄(a);a1、a2为模型参数。
期末蓄积量是在期初蓄积量上生长的,且它是年龄和断面积增量的函数,由此构造出期末每公顷蓄积量预测方程为
| $ \ln {{M}_{2}}=\ln {{M}_{1}}+{{b}_{3}}\left( {{t}_{2}}^{-1}-{{t}_{1}}^{-1} \right)+{{b}_{4}}(\ln {{G}_{2}}-\ln {{G}_{1}}) $ | (3) |
式中:M2为期末林分蓄积量(m3)。
在以往的回归模型中,一般认为自变量的观测值不含误差而因变量的观测值含有误差,当自变量和因变量二者都含有度量误差时,无论哪个方程用通常的最小二乘估计的参数既不是无偏的,也不是相合的估计量[16],为解决这个问题,引入度量误差模型[17],当自变量和因变量的观测值中都含有度量误差时,称为度量误差模型。多元非线性误差变量联立方程组也叫非线性度量误差模型[18],联立方程组中一些因变量在另一个方程中以自变量的形式出现,即有些变量既是因变量又是自变量,因此,联立方程组中无法使用常规的方法来划分自变量和因变量。为了明确起见,采用内生变量和外生变量来代替通常使用的因变量和自变量,其中内生变量是含随机误差的变量,外生变量是不含随机误差的变量。将模型(1)、(2)、(3)组合成联立方程组模型(4),模型(4)中,lnM1、lnG2和lnM2为内生变量,而lnG1、IS、t1和t2为外生变量。由于联立方程组中各方程间随机误差的相关性,其参数估计不能采用普通的最小二乘法,而应采用二步最小二乘法或三步最小二乘法。
| $ \left\{ \begin{align} & \ln {{M}_{1}}={{b}_{1}}+{{b}_{2}}{{I}_{\text{S}}}+{{b}_{3}}{{t}_{1}}^{-1}+{{b}_{4}}\ln {{G}_{1}} \\ & \ln {{G}_{2}}=\frac{{{t}_{1}}}{{{t}_{2}}}\ln {{G}_{1}}+{{a}_{1}}(1-\frac{{{t}_{1}}}{{{t}_{2}}})+{{a}_{2}}{{I}_{\text{S}}}(1-\frac{{{t}_{1}}}{{{t}_{2}}}~) \\ & \ln {{M}_{2}}=\ln {{M}_{1}}+{{b}_{3}}\left( {{t}_{2}}^{-1}-{{t}_{1}}^{-1} \right)+{{b}_{4}}(\ln {{G}_{2}}-\ln {{G}_{1}}) \\ \end{align} \right. $ | (4) |
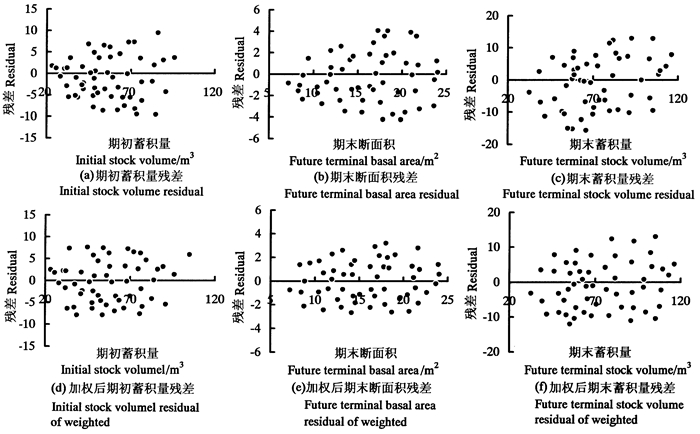
分别使用二步最小二乘法和三步最小二乘法对联立方程组模型(4)进行参数估计,利用平均误差、平均绝对相对误差、均方根误差(root ean quared rror,RMSE)、预测精度和决定系数对两种方法得到的参数值进行检验,最终选择误差较小,精度较高的二步最小乘法对模型(4)进行参数估计。模型中异方差的问题,采用原函数的倒数作为权函数的加权二步最小二乘法对模型的异方差进行修正。联立方程组的残差分布见图 1,其中图 1(a)、(b)、(c)为二步最小二乘法拟合的联立方程组的残差分布,图 1(d)、(e)、(f)为加权的二步最小二乘法拟合的联立方程组的残差分布。修正后的模型残差分布较均匀,异方差问题得到较好的解决,但是,模型预测的残差值仍然较大,没有得到很好的解决,因此,使用混合效应模型方法对模型进行模拟。
|
图 1 联立方程组残差分布 Fig. 1 Residual distribution diagram model of simultaneous equations |
当样地随机效应时,利用S-PLUS软件的NLMIXED模块对模型进行参数估计,首先将模型中的全部参数都当作混合参数,然后再逐次减少混合参数的个数并将其随机组合进行模拟,最后选择拟合精度最高的方程作为估计方程。对模型(1)和模型(2)分别进行混合效应模拟,利用赤池信息量准则(AIC)、贝叶斯信息准则(BIC)和-2倍的对数似然值(-2LL)作为模型的效果评价指标,3个评价指标值越小说明模型的拟合效果越好,最后选择b2、b3作为模型(1)的混合效应参数, a2作为模型(2)的混合效应参数时模型的拟合精度最高。对联立方程组模型(4)进行拟合,结果显示,b2、b3、a2同时作为混合参数时模型不能收敛,b2和b3作为混合参数时模型也不能收敛,对b2、a2和b3、a2作为混合效应参数的两种情况进行拟合,结果见表 2。b3、a2作为混合效应参数时的AIC、BIC和-2LL值均小于没有考虑混合效应参数和b2、a2作为混合效应参数时模型的检验值,同时,如果只有1个参数作为混合效应参数,发现模型的拟合效果明显降低。因此,最终选择b3、a2作为联立方程组模型(4)的混合效应参数。
| 混合参数Mixed parameters | AIC | BIC | -2LL |
| 无None | -93.65 | -75.59 | -105.65 |
| b2a2 | -114.40 | -90.32 | -130.40 |
| b3a2 | -137.57 | -119.50 | -149.57 |
利用混合效应模型方法模拟林分生长和收获模型时,不可避免的两个问题就是模型的异方差和拟合数据的时间序列自相关性问题。
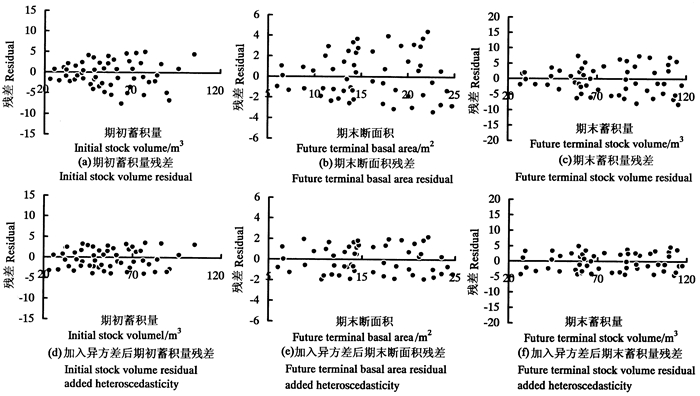
3.3.1 异方差模型是否存在异方差问题,通常最直观的判断方法就是利用模型的残差分布。图 2(a)、(b)、(c)为未加入异方差结构的联立方程组混合效应模型的残差分布,可以明显地看出基于混合效应模型的联立方程组模型具有异方差问题。因此,采用指数函数和幂函数这两种异方差结构来修正基于混合效应模型的联立方程组产生的异方差问题,结果见表 3。似然比检验值(LRT)和P值可以说明加入异方差结构和未加入异方差结构的混合效应模型具有显著差异,即加入异方差结构可以修正模型产生的异方差。比较两种异方差结构模型模拟结果的AIC、BIC和-2LL值,幂函数作为异方差结构的AIC、BIC和-2LL值均小于指数函数作为异方差结构的模型模拟结果。因此,最终选择幂函数来描述联立方程组混合效应模型的异方差结构。
|
图 2 联立方程组混合效应模型的残差分布 Fig. 2 Residual distribution diagram of mixed effect model of simultaneous equations |
| 异方差方程 Heteroscedasticity equation |
AIC | BIC | -2LL | LRT | P |
| 无None | -137.57 | -119.50 | -149.57 | ||
| 幂函数Power function | -160.39 | -132.44 | -178.39 | 26.53 | < 0.000 1 |
| 指数函数Exponential function | -152.63 | -124.68 | -170.63 | 19.32 | < 0.000 1 |
图 2(d)、(e)、(f)为加入幂函数作为异方差结构的联立方程组混合效应模型的残差分布。从图 1(d)、(e)、(f)和图 2(a)、(b)、(c)可以看出,未加入异方差结构的联立方程组混合效应模型的残差值分布范围[M1、G2和M2的残差范围分别为(-6)~6 m3、(-4)~4 m2和(-8)~8 m3]虽然小于加权二步最小二乘法拟合联立方程组的残差值分布范围[M1、G2和M2的残差范围分别为(-10)~10 m3、(-4)~4 m2和(-15)~15 m3],但仍存在随着预测值的增大而逐渐增大的趋势,说明未加入异方差结构的联立方程组混合效应模型仍然存在异方差问题。对比图 2(a)、(b)、(c)和图 2(d)、(e)、(f)修正异方差前后的残差分布,加入幂函数作为异方差结构的联立方程组混合效应模型的残差分布不仅在残差值的分布范围明显减少[M1、G2和M2的残差范围分别为(-4)~4m3、(-2)~2 m2和(-5)~5 m3],而且其分布大致均匀,明显优于未加入异方差结构的联立方程组混合效应模型结果,可以说明选择幂函数作为异方差结构能较好地解决了联立方程组混合效应模型的异方差问题。
3.3.2 时间序列的相关性联立方程组中林分期初蓄积量、期末断面积和期末蓄积量三者间存在一定的序列自相关性,且本研究数据来源于一类清查数据,是连续的6次测量数据,因此, 数据间存在着时间序列自相关性。本研究中使用常用且能显著提高模型精度的AR(1)、ARMA(1, 1)、CS三个自相关结构矩阵来表示联立方程组混合效应模型之间的时间序列自相关性,结果见表 4。加入AR(1)、ARMA(1, 1)和CS三个时间序列自相关结构矩阵的模型拟合效果均优于不加入时间序列自相关结构矩阵的模型拟合效果,且根据LRT值与P值的分析表明差异显著。3个结构矩阵中,加入AR(1)结构矩阵的模型模拟的AIC、BIC和-2LL均小于其余2个结构矩阵模型模拟结果,因此, 本研究选择AR(1)结构矩阵来描述联立方程组混合效应模型的时间序列自相关性。
| 自相关结构 Autocorrelation structure |
AIC | BIC | -2LL | LRT | P |
| 无None | -160.39 | -132.44 | -178.39 | ||
| AR(1) | -211.70 | -190.64 | -225.71 | 58.35 | < 0.000 1 |
| ARMA(1, 1) | -187.52 | -163.45 | -203.54 | 33.56 | < 0.000 1 |
| CS | -168.83 | -147.77 | -182.84 | 15.63 | < 0.000 1 |
对不同异方差模型和不同时间序列自相关结构矩阵进行模拟比较后,最终确定b3和a2作为联立方程组模型的混合效应参数,幂函数作为异方差模型、AR(1)作为时间序列自相关结构矩阵时,联立方程组混合效应模型的拟合精度最高。综合以上结果,最后形成的联立方程组混合效应模型见公式(5)。
| $ \left\{ \begin{array}{l} \ln {M_1} = {b_1} + {b_2}{I_{\rm{S}}} + ({b_3} + {u_{3i}}){t_1}^{ - 1} + {b_4}\ln {G_1} + {\varepsilon _1}\\ \ln {G_2} = \frac{{{t_1}}}{{{t_2}}}\ln {G_1} + {a_1}(1 - \frac{{{t_1}}}{{{t_2}}}) + \left( {{a_2} + {u_{6i}}} \right){I_{\rm{S}}}(1 - \frac{{{t_1}}}{{{t_2}}}) + {\varepsilon _2}\\ \ln {M_2} = \ln {M_1} + \left( {{b_3} + {u_{3i}}} \right)\left( {{t_2}^{ - 1} - {t_1}^{ - 1}} \right) + {b_4}(\ln {G_2} - \ln {G_1}) + {\varepsilon _3}\\ {({u_{3i}},{u_{6i}})^T} \sim N(0,\mathit{\boldsymbol{D}}{\rm{ }})\\ {({\varepsilon _1},{\rm{ }}{\varepsilon _2},{\rm{ }}{\varepsilon _3})^T} \sim N(0,{\rm{ }}{R_i})\\ {\mathit{\boldsymbol{R}}_\mathit{\boldsymbol{i}}} = {\sigma _i}^2{\mathit{\boldsymbol{K}}_\mathit{\boldsymbol{i}}}^{\mathit{\boldsymbol{0}}\mathit{\boldsymbol{.5}}}{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_\mathit{\boldsymbol{i}}}(\mathit{\boldsymbol{\theta }}){\mathit{\boldsymbol{K}}_\mathit{\boldsymbol{i}}}^{\mathit{\boldsymbol{0}}\mathit{\boldsymbol{.5}}}\\ {\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_\mathit{\boldsymbol{i}}}(\mathit{\boldsymbol{\theta }}) = {\rm{AR}}\left( 1 \right)\\ {\mathit{\boldsymbol{K}}_\mathit{\boldsymbol{i}}}^{\mathit{\boldsymbol{0}}\mathit{\boldsymbol{.5}}} = {Y_i}^{\alpha /2} \end{array} \right. $ | (5) |
式中:D为样地间随机效应方差协方差矩阵; Ri为样地内误差效应方差协方差矩阵; Κi0.5为异方差矩阵; Γi(θ)为时间序列自相关矩阵; Y为联立方程组因变量;i为样地数;u为混合参数;ε为误差项。
通过S-PLUS软件的NLMIXED模块对模型(5)进行模拟,并将其模拟结果与加权二步最小二乘法的模拟结果进行比较, 结果见表 5。
| 参数 Parameter |
加权二步最小二乘法 Weighted two-step least squares method |
混合效应模型方法 Mixed effect model |
|||||||
| 估计值 Estimation |
标准差 Standard deviation |
t | P | 估计值 Estimation |
标准差 Standard deviation |
t | P | ||
| b1 | 1.750 4 | 0.133 8 | 13.080 0 | < .0.000 1 | 1.748 | 0.140 5 | 12.442 | < .0.000 1 | |
| b2 | 0.029 7 | 0.010 5 | 2.834 6 | 0.005 2 | 0.032 9 | 0.010 2 | 3.246 4 | 0.001 7 | |
| b3 | -18.358 0 | 1.997 9 | -9.188 6 | < .0.000 1 | -19.747 9 | 2.129 7 | -9.272 8 | < .0.000 1 | |
| b4 | 0.989 4 | 0.039 4 | 25.085 0 | < .0.000 1 | 0.993 8 | 0.040 4 | 24.620 | < .0.000 1 | |
| a1 | 3.990 5 | 0.707 7 | 5.638 9 | < .0.000 1 | 3.824 7 | 0.718 9 | 5.319 9 | < .0.000 1 | |
| a2 | -0.003 0 | 0.065 5 | -0.045 6 | 0.008 3 | 0.026 3 | 0.066 | 0.398 2 | 0.003 5 | |
| AIC | -93.65 | -211.703 5 | |||||||
| BIC | -75.59 | -190.639 2 | |||||||
| -2LL | -105.65 | -225.713 6 | |||||||
| 样地间方差协方差矩阵 Vari-ance covariance matrix of plot-plot |
\ | |
|||||||
| 时间序列自相关性 Time series autocorrelation |
\ | ρ=-0.092 5 | |||||||
| 异方差Heteroscedasticity | \ | α=0.247 7 | |||||||
| 方差Variance | σ2=0.16 | σ2=0.024 | |||||||
混合效应模型的验证最重要的是计算每个样地的随机效应参数值bk,其具体的计算表达式如下
| $ {{\hat b}_k} \approx \mathit{\boldsymbol{\hat D}}{{\mathit{\boldsymbol{\hat Z}}}_\mathit{\boldsymbol{k}}}^\mathit{\boldsymbol{T}}{\left( {{{\mathit{\boldsymbol{\hat Z}}}_\mathit{\boldsymbol{k}}}\mathit{\boldsymbol{\hat D}}{{\mathit{\boldsymbol{\hat Z}}}_\mathit{\boldsymbol{k}}}^\mathit{\boldsymbol{T}} + {{\hat R}_k}} \right)^{ - 1}}{{\hat e}_k} $ | (6) |
式中:
采用未参与建模的26块固定样地(共54个样本)对混合效应模型的拟合结果进行检验,并选择平均误差、平均绝对相对误差、均方根误差(RMSE)以及预测精度4个评价指标对模型的拟合效果进行评价,然后将混合效应模型方法与加权二步最小二乘法的检验结果进行比较,模型的检验结果见表 6。联立方程组的3个模型中加入异方差结构和自相关结构的混合效应模型方法的平均误差、平均绝对相对误差、均方根误差都小于使用加权二步最小二乘法的模型拟合结果;预测精度都高于使用加权二步最小二乘法的模型拟合结果。说明加入异方差结构和自相关结构的混合效应模型方法的预测精度要高于加权二步最小二乘法。
| 方法Method | 模型Model | 平均误差 Average error |
平均绝对相对误差 Mean absolute relative error |
均方根误差 RMSE |
预测精度 Prediction accuracy/% |
| 混合效应模型方法 Mixed effect model |
模型(1)Model(1) | -0.319 1 | 0.033 2 | 2.317 0 | 98.90 |
| 模型(2)Model(2) | 0.073 4 | 0.060 7 | 1.094 9 | 98.11 | |
| 模型(3)Model(3) | -0.177 7 | 0.033 0 | 2.931 9 | 98.95 | |
| 加权二步最小二乘法 Weighted two-step least squares method |
模型(1)Model(1) | 0.904 3 | 0.101 6 | 6.938 2 | 95.34 |
| 模型(2)Model(2) | 0.423 8 | 0.119 4 | 2.049 1 | 94.95 | |
| 模型(3)Model(3) | 0.310 3 | 0.094 1 | 8.039 3 | 95.82 |
研究构建了林分生长量与收获量一致的相容性林分生长收获模型,并且在此模型的基础上考虑样地层次的混合效应。确定单个模型混合效应参数时,首先将模型中的全部参数都当作混合参数,然后逐次减少混合参数的个数并将其随机组合进行拟合,利用AIC、BIC和-2LL值对不同混合参数模型进行评价,最终选择b2、b3作为期初林分蓄积量模型的混合效应参数,a2作为期末林分断面积作为模型的混合效应参数。对联立方程组模型进行拟合时,模拟结果表明,联立方程组模型中b3作为期初林分蓄积量模型的混合效应参数,a2作为期末林分断面积模型的混合效应参数时的模型拟合效果最好。经过对比分析,选择幂函数作为异方差结构、AR(1)结构矩阵作为自相关结构可以较好地描述联立方程组异方差问题和时间序列自相关性。分析联立方程组模型残差分布图可知,混合效应模型方法的残差分布图不仅分布均匀,而且残差分布范围也大大减少。利用检验数据计算两种方法的平均误差、平均绝对相对误差、均方根误差以及预测精度4个检验评价指标并对比分析,发现混合效应模型方法的4个评价指标值均优于加权二步最小二乘法的评价指标值。综合以上两点,说明混合效应模型方法的拟合效果要优于加权二步最小二乘法的拟合效果。
为提高模型的预测精度,将混合效应模型方法应用到林分生长和收获联立方程组模型中,随机效应参数是基于样地效应的混合模型确定的,本研究因研究数据不足,并未考虑区域水平以及区域与样地两层次水平效应,因此,随机效应参数的确定是基于样地水平或区域水平的单水平混合效应模型,还是基于样地水平和区域水平的双水平混合效应模型,还需进一步研究。在研究林分生长与收获模型基础模型时,并未考虑林分树种组成、林分密度以及海拔、坡度等地形因子的影响,因此在下一步研究中一方面可以在加入树种组成、林分密度和地形因子等补充完善基础模型,另一方面可以考虑样地水平、区域水平以及区域与样地两层次水平效应的混合效应模型来做对比分析,并最终选择出拟合效果最好的模型。
| [1] |
孟宪宇. 测树学[M]. 3版. 北京: 中国林业出版社, 2006.
|
| [2] |
唐伟东. 落叶松人工林林分生长与收获模型的研究[J]. 林业勘查设计, 2016(2): 41-42. DOI:10.3969/j.issn.1673-4505.2016.02.020 |
| [3] |
王少杰, 邓华锋, 向玮, 等. 基于混合模型的油松林分蓄积量预测模型的建立[J]. 西北农林科技大学学报(自然科学版), 2018, 46(2): 29-38, 46. |
| [4] |
郎璞玫. 建立在固定样地上的林分生长线性联立方程组模型研究[J]. 北京林业大学学报, 2007, 29(1): 37-41. DOI:10.3321/j.issn:1000-1522.2007.01.007 |
| [5] |
FANG Z X, BAILEY R L, SHIVER B D. A multivariate simultaneous prediction system for stand growth and yield with fixed and random effects[J]. Forest Science, 2001, 47(4): 550-562. |
| [6] |
HASENAUER H, MONSERUD R A, GREGOIRE T G. Using simultaneous regression techniques with individual-tree growth models[J]. Forest Science, 1998, 44(1): 87-95. |
| [7] |
李春明. 基于混合效应模型的杉木人工林蓄积联立方程系统[J]. 林业科学, 2012, 48(6): 80-88. |
| [8] |
BORDERS B E, BAILEY R L. A compatible system of growth and yield equations for slash pine fitted with restricted three-stage least squares[J]. Forest Science, 1986, 32(1): 185-201. |
| [9] |
BORDERS B E. Systems of equations in forest stand modeling[J]. Forest Science, 1989, 35(2): 548-556. |
| [10] |
陈兴彬, 肖复明, 余林, 等. 基于混合线性模型估算杉木生长性状遗传参数[J]. 森林与环境学报, 2018, 38(4): 419-424. |
| [11] |
符利勇, 唐守正, 张会儒, 等. 基于多水平非线性混合效应蒙古栎林单木断面积模型[J]. 林业科学研究, 2015, 28(1): 23-31. |
| [12] |
王永刚, 舒清态, 李圣娇, 等. 香格里拉高山松天然林林分蓄积混合效应模型构建[J]. 西南林业大学学报, 2016, 36(3): 121-125. |
| [13] |
HALL D B, CLUTTER M. Multivariate multilevel nonlinear mixed effects models for timber yield predictions[J]. Biometrics, 2004, 60(1): 16-24. DOI:10.1111/j.0006-341X.2004.00163.x |
| [14] |
李春明.混合效应模型在森林生长模拟研究中的应用[D]].北京: 中国林业科学研究院, 2010. http://cdmd.cnki.com.cn/Article/CDMD-82201-2010264671.htm
|
| [15] |
刘洵, 曾思齐, 龙时胜, 等. 湖南省栎类天然次生林胸径地位指数表研制[J]. 森林与环境学报, 2019, 39(3): 265-272. |
| [16] |
张树森, 王蒙, 董利虎. 黑龙江省小黑杨人工林分生长收获模型研究[J]. 防护林科技, 2017(8): 39-41. |
| [17] |
李永慈, 唐守正. 度量误差对全林整体模型的影响研究[J]. 林业科学, 2005, 41(6): 166-169. DOI:10.3321/j.issn:1001-7488.2005.06.029 |
| [18] |
刘薇祎, 邓华锋, 冉啟香, 等. 湖南省杉木林分相容性树高曲线方程组研究[J]. 浙江农林大学学报, 2017, 34(6): 1051-1058. |

 2019, Vol. 39
2019, Vol. 39


