文章信息
- 刘洵, 曾思齐, 龙时胜, 向博文, 甘世书
- LIU Xun, ZENG Siqi, LONG Shisheng, XIANG Bowen, GAN Shishu
- 湖南省栎类天然次生林胸径地位指数表研制
- Establishment of a diameter at breast height site index table for natural secondary oak forest in Hunan Province
- 森林与环境学报,2019, 39(3): 265-272.
- Journal of Forest and Environment,2019, 39(3): 265-272.
- http://dx.doi.org/10.13324/j.cnki.jfcf.2019.03.006
-
文章历史
- 收稿日期: 2018-10-23
- 修回日期: 2019-01-07
2. 国家林业和草原局中南林业调查规划设计院, 湖南 长沙 410014
2. Central South Forest Inventory and Planning Institute, National Forestry and Grassland Administration, Changsha, Hunan 410014, China
栎(Quercus acutissima Carruth.)林在我国分布广泛,面积广阔,是最重要的森林类型之一[1]。湖南省是我国栎类重要的分布地区,栎类资源丰富,种类多,面积大,分布广[2]。由于历史原因,我国大多数栎林是经历破坏后形成的次生林,绝大多数处于自生自灭状态,利用率低,产业链不完整[3]。同时,栎类作为优良的经济树种和造林绿化树种,具有极高的经济和生态价值。因此,为了改变栎类次生林的现状,提高生产力,确定森林经营方向,对现有栎类次生林林分的立地质量进行评价,为进一步提高林分生产力的经营以及天然林的保护奠定基础。
立地质量是指某一立地条件下,既定的森林或树种的生产潜力[4]。在造林规划设计、森林抚育经营和森林经营规划等林业生产实践中,立地质量评价是基础,科学的立地质量评价方法对提高林分生长收获预估准确性、优化抚育经营设计、实现森林可持续经营具有极其重要的意义[5]。国内外形成了多种立地质量评价方法,有林分因子直接评价法、环境因子间接评价法和两者综合评价方法等[6]。地位级和立地指数是常用且行之有效的立地质量评价方法,地位级简单易行,但其精度和准确性低于地位指数。地位指数表是森林经营工作的基础数表,用地位指数表对立地质量进行评价在我国使用十分广泛[9-12]。一般地位指数表依据基准年龄时的林分优势木平均高编制[13]。树高和胸径是森林资源调查中2个重要的测树因子,相比较而言,树高受林分状况以及测量方法等因素的影响,测量困难且精度不高,而胸径在立木条件下容易测定[14-15]。在国家森林资源连续清查数据中只有部分样地的平均树高,且准确性不高,科研价值较低,而对胸径的测量每5 a进行1次,精度高,信息量大,科研价值较高。因此,本研究采用多期的胸径-年龄数据编制胸径地位指数表。
1 研究区概况湖南省地处东经108°47′~114°15′,北纬24°39′~30°08′,位于长江中游、洞庭湖以南,是我国东南腹地。湖南省省会长沙,地貌以山地、丘陵为主,东西宽667 km,南北长774 km,三面环山,形成从东南西三面向北倾斜开口的马蹄形状。湖南为大陆性亚热带季风湿润气候,四季分明,光热充足,降水丰沛,雨热同期,气候条件比较优越,全省年平均气温16~19 ℃,年平均日照时间1 300~1 800 h,无霜期253~311 d,年平均降水量1 200~1 700 mm。土壤以红壤和黄壤为主,红壤面积约占全省土地总面积的36.3%,主要分布于武陵雪峰山以东的丘陵山麓及湘、资两水流域;黄壤面积占全省土地总面积的15.4%,主要分布于雪峰山、南岭山区。湖南省位于中国东部中亚热带常绿阔叶林地带,植被类型多样,植物资源丰富,主要树种有马尾松(Pinus massoniana Lamb.)、杉(Taxodiaceae)、樟[Cinnamomum camphora (L.) presl]、檫[Sassafras tzumu (Hemsl.) Hemsl]、栲(Castanopsis fargesii Franch)、青冈栎[Cyclobalanopsis glauca (Thunb.) Oerst.]、枫香(Liquidambar formosana Hance)以及竹类(Bambusoideae),此外还有银杏(Ginkgo biloba L.)、红豆杉[Taxus wallichiana var. chinensis (Pilg.) Florin]、水杉(Metasequoia glyptostroboides)、珙桐(Davidia involucrata Baill)、杜仲(Eucommia ulmoides)、伯乐树(Bretschneidera sinensis Hemsl)等60多种珍贵树种。湖南省栎类资源丰富,据统计有6属77种,呈现出分布不均匀、偏远、经纬度地带性差异和垂直地带性差异显著等特点[16]。
2 研究方法 2.1 数据来源研究数据来源于湖南省国家森林资源连续清查(1989—2014年,共6期)的复查数据,筛选其中以栎类为优势树种且林分类型为天然次生林的146个样地数据作为建模样本,30个未参与建模的样地数据作为检验样本。连续清查样地的抽样设计间距按4 km×8 km进行抽取,面积为666.7 m2,调查间隔时间为5 a,调查时采用GPS定位与复位,对样地内的林木进行每木检尺,起测胸径为5 cm,达到起测胸径的林木采用铁牌编号。样地调查内容包括林木胸径、树种、平均树高、郁闭度、相对位置;样地地形因子包括地貌、海拔、坡向、坡位和坡度;土层因子包括土层厚度、枯枝落叶层厚度和腐殖质层厚度。
2.2 数据分析处理与异常数据剔除编表前使用Excel 2007、SPSS 22软件对调查数据进行统计分析。首先对146个样地的每期数据进行统计、分析以及处理计算,得到样地每期的加权平均胸径和加权平均年龄[17]。然后将获得的胸径-年龄数据组按照5 a一个龄阶,将20~60 a划分为9个龄阶,剔除郁闭度小于0.4的胸径-年龄数据组后,计算各龄阶的平均胸径和标准差,再以每龄阶的平均胸径为基准,按3倍标准差法对各龄阶内异常的胸径-年龄数据组进行剔除,以最终得到399组胸径-年龄数据作为建模样本,进而统计出各龄阶的样本数量、平均胸径、标准差、平均断面积和平均材积(表 1)。
| 龄阶 Age class/a |
样本数 Number of samples |
平均胸径 Mean diameterat breastheight/cm |
株数 Number /(tree·hm-2) |
平均断面积 Mean sectional area/(m2·hm-2) |
平均材积 Mean volume /(m3·hm-2) |
胸径范围 Range of DBH/cm |
胸径3倍 标准差下限 DBH lower limit of the 3 times SD/cm |
胸径3倍 标准差上限 DBH upper limit of the 3 times SD/cm |
| 20 | 19 | 7.9 | 24 870 | 7.19 | 22.96 | 6.6~9.3 | 5.1 | 10.6 |
| 25 | 72 | 8.3 | 112 935 | 9.70 | 37.65 | 6.6~10.2 | 5.7 | 10.9 |
| 30 | 83 | 9.3 | 141 150 | 13.22 | 55.69 | 6.7~12.0 | 5.7 | 12.9 |
| 35 | 70 | 10.3 | 119 355 | 16.94 | 79.50 | 7.5~14.1 | 6.2 | 14.4 |
| 40 | 67 | 10.8 | 102 525 | 16.65 | 82.37 | 8.1~15.1 | 6.3 | 15.3 |
| 45 | 41 | 11.2 | 66 150 | 18.71 | 94.07 | 8.0~15.4 | 6.4 | 15.9 |
| 50 | 23 | 11.7 | 38 745 | 22.17 | 120.04 | 8.7~14.3 | 6.5 | 16.9 |
| 55 | 17 | 12.8 | 18 660 | 19.96 | 119.88 | 9.7~15.7 | 7.5 | 18.2 |
| 60 | 7 | 12.8 | 9 345 | 20.86 | 124.05 | 10.5~17.4 | 4.6 | 21.0 |
本研究选择理查德式、单分子式、逻辑斯蒂式、坎派兹式、对数曲线式、韦布尔式和双曲线式7个常用的生长曲线方程对胸径生长曲线进行拟合。拟合使用SPSS 22统计软件,参数估计使用最小二乘法,各方程的表达式及拟合结果见表 2。比较表 2中7个胸径曲线方程表达式及其结果,综合考虑决定系数(R2)、残差平方和(sum of squares for error,SSE)以及均方根误差(root mean squared error,RMSE)后,选择R2最大,SSE和RMSE最小的逻辑斯蒂式方程为最优导向曲线的拟合方程,其R2=0.985 7,SSE=0.365 8,RMSE=0.201 6,表达方程为:
| $ D = 15.4084/\left( {1 + 2.2099{{\rm{e}}^{ - 0.04064}}} \right) $ | (1) |
| 方程名称Equation | 表达式 Expression |
a | b | c | 决定系数 R2 |
残差平方 和SSE |
均方根 误差RMSE |
| 理查德式Richards | D=a(1-e-bA)c | 53.378 6 | 0.000 9 | 0.477 9 | 0.984 9 | 0.387 1 | 0.207 4 |
| 单分子式Mitscherlich | D=a(1-e-bA) | 14.344 5 | 0.035 9 | 0.971 6 | 0.755 8 | 0.289 8 | |
| 逻辑斯蒂式Logistic | D=a/(1+be-cA) | 15.408 4 | 2.209 9 | 0.040 6 | 0.985 7 | 0.365 8 | 0.201 6 |
| 坎派兹式Gompertz | D=ae-be-cA | 16.650 5 | 1.324 9 | 0.027 6 | 0.985 6 | 0.368 7 | 0.202 4 |
| 对数曲线式Logarithmic curve | D=a+blgA | -6.767 0 | 10.991 9 | 0.978 9 | 0.539 8 | 0.244 9 | |
| 韦布尔式Weibull | D=a(1-e-bAc) | 398.362 1 | 0.004 7 | 0.476 1 | 0.984 9 | 0.387 2 | 0.207 4 |
| 双曲线式Hyperboliccurve | D=a+b/A | 14.951 2 | -155.371 0 | 0.929 8 | 1.800 0 | 0.447 2 | |
| 注:a、b、c为模型参数。Note: a、b、c are model parameters。 | |||||||
式中:D为样地平均胸径(cm);A为样地平均年龄(a)。
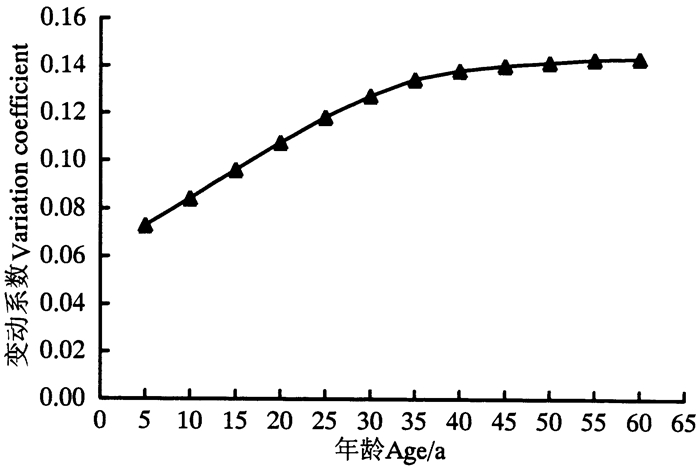
3.2 基准年龄和地位指数级距的计算基准年龄的确定一般需要综合考虑采伐年龄、自然成熟龄的一半左右的年数以及林分生长过程中平均生长量最大或生长趋于稳定后的年龄[18]。本研究以经过整理最终得到的399组胸径-年龄建模样本为对象,计算各龄阶的胸径标准差(SA)以及胸径变动系数(CA),根据各龄阶的胸径变动系数(CA)绘制折线图(图 1)。从图 1可以看出,前30 a胸径变动系数(CA)的变化幅度较大,40 a后趋于平稳,综合考虑栎林生长较平缓时的年龄以及其成熟林年龄较大的特点,确定其基准年龄为40 a。指数级距的确定取决于编表树种在基准年龄时胸径的绝对变动幅度。在本研究中,栎林在基准年龄40 a时的胸径变化范围为8.1~15.1 cm,因此确定指数级距为3 cm,指数级为6、9、12、15、18、21。
|
图 1 胸径变动系数变化趋势 Fig. 1 Trend of DBH coefficient of variation |
以年龄-优势木高编制地位指数表时形成地位曲线簇常用的方法有标准差调整法[19]、变动系数调整法[20]和相对优势高法[21]。以往研究表明,相对优势高法导出各指数曲线的不同龄阶树高值精度相对较低[22],变动系数法多用于针叶树种,标准差调整法多用于阔叶树种[20],但都是针对优势木平均高而言,对于平均胸径是否也存在相同或类似的情况,还有待商榷。因此,本研究根据树高编制地位指数表的3种方法进行胸径地位指数表的编制,并对其检验结果进行比较分析。
3.3.1 标准差调整法首先,利用各龄阶年龄(A)和导向曲线方程(1),得到各龄阶导向曲线胸径值。然后根据各龄阶胸径标准差与年龄之间的相关关系,选择理查德式、逻辑斯蒂式、对数曲线式和双曲线式4个常用数学方程进行曲线拟合,得到各方程的表达式及拟合结果。比较4个标准差曲线方程表达式及其结果,综合考虑决定系数(R2)、残差平方和(SSE)以及均方根误差(RMSE),最终确定逻辑斯蒂方程为标准差方程,其R2=0.976 3,SSE=0.019 8,RMSE=0.049 8。表达式为:
| $ {S_{{\rm{A}}, i}} = 2.0061/\left( {1 + 5.6914{{\rm{e}}^{ - 0.0702A}}} \right) $ | (2) |
式中:SA, i为第i龄阶胸径标准差(cm)。
将各龄阶代入标准差曲线方程(2)中,可以得到各龄阶胸径标准差理论值。根据导向曲线上各龄阶的胸径(DK)、基准年龄时各指数级的胸径(DO)、基准年龄时导向曲线胸径(DOK)、基准年龄时所在龄阶胸径标准差理论值(SAO)以及各龄阶胸径标准差理论值,可以直接导算出各地位指数曲线各龄阶胸径值,具体可采用公式(3)进行导算:
| $ {D_{ij}} = {D_{{\rm{K}}, i}} + \frac{{{D_{0, j}} - {D_{{\rm{ok}}}}}}{{{S_{{\rm{AO}}}}}}{S_{A, i}} $ | (3) |
式中:Dij为第i龄阶第j指数级调整后的胸径(cm);DK,i为第i龄阶的导向曲线胸径(cm);DO,j为基准年龄时第j指数级的胸径(cm);DOK为基准年龄时导向曲线胸径(cm);SAO为基准年龄时所在龄阶胸径标准差理论值(cm);SA, i为第i龄阶胸径标准差理论值(cm)。
3.3.2 变动系数调整法标准差调整法与变动系数法的原理基本相同,根据胸径变动系数与年龄的相关关系选择理查德式、逻辑斯蒂式、对数曲线式和双曲线式4个常用数学方程进行曲线拟合,得到各方程的表达式及拟合结果。综合考虑决定系数(R2)、残差平方和(SSE)以及均方根误差(RMSE),最终确定逻辑斯蒂方程为变动系数的拟合方程,其R2=0.938 4,SSE=0.000 3,RMSE=0.005 8。表达式为:
| $ {C_{{\rm{A}}, i}} = 0.1482/\left( {1 + 4.031{{\rm{e}}^{ - 0.0993A}}} \right) $ | (4) |
式中:CA, i为第i龄阶胸径变动系数理论值。
根据方程(4)计算各龄阶变动系数理论值,然后根据导向曲线上各龄阶的胸径值、基准年龄时各指数级的胸径值、基准年龄时导向曲线胸径、基准年龄时所在龄阶胸径变动系数理论值(CAO)以及各龄阶胸径变动系数理论值,可以直接导算出各地位指数曲线各龄阶胸径值,具体可采用公式(5)进行导算:
| $ {D_{ij}} = {D_{{\rm{K}}, i}}\left( {1 + \frac{{{D_{{\rm{O}}, j}} - {D_{{\rm{OK}}}}}}{{{D_{{\rm{OK}}}}}} \times \frac{{{C_{{\rm{A}}, i}}}}{{{S_{{\rm{AO}}}}}}} \right) $ | (5) |
相对胸径法是依据相对优势高法的原理,按照一定比例将导向曲线平移的一种方法。根据导向曲线上各龄阶的胸径值、基准年龄时各指数级的胸径值、基准年龄时导向曲线胸径值,可以直接导算出各地位指数曲线各龄阶胸径值,具体可采用公式(6)进行导算:
| $ {D_{ij}} = {D_{{\rm{K}}, i}}\frac{{{D_{0, j}}}}{{{D_{{\rm{OK}}}}}} $ | (6) |
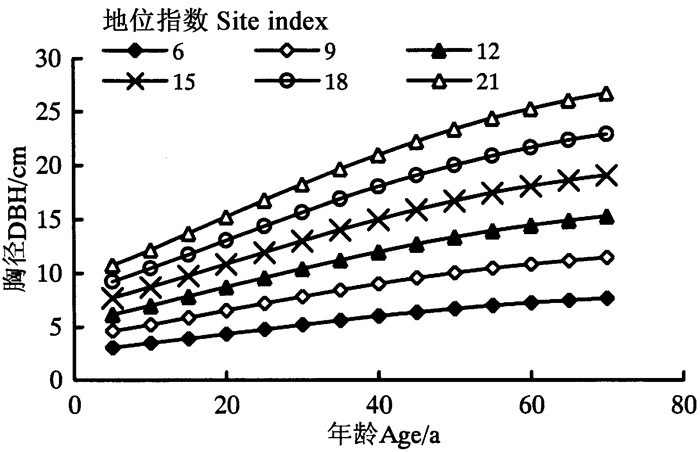
以相对树高法为例,根据公式(6)导算出各地位指数曲线各龄阶胸径值(基准年龄40 a;级距3 cm),形成地位指数曲线簇(图 2)。根据各地位指数曲线各龄阶胸径计算值,将各地位指数曲线各龄阶的胸径值加减其所对应的每差一级调整值的一半,即可得到各地位指数各龄阶胸径的取值范围,将其整理可得到湖南省栎类天然次生林胸径地位指数表(表 3)。
|
图 2 地位指数曲线簇 Fig. 2 Curve cluster of the site index |
| 龄阶 Age class/a |
地位指数 Site index |
|||||
| 6 | 9 | 12 | 15 | 18 | 21 | |
| 5 | 2.3~3.8 | 3.8~5.4 | 5.4~6.9 | 6.9~8.5 | 8.5~10.0 | 10.0~11.5 |
| 10 | 2.6~4.4 | 4.4~6.1 | 6.1~7.8 | 7.8~9.6 | 9.6~11.3 | 11.3~13.1 |
| 15 | 2.9~4.9 | 4.9~6.8 | 6.8~8.8 | 8.8~10.8 | 10.8~12.8 | 12.8~14.8 |
| 20 | 3.3~5.4 | 5.4~7.6 | 7.6~9.8 | 9.8~12.0 | 12.0~14.1 | 14.1~16.3 |
| 25 | 3.6~6.0 | 6.0~8.4 | 8.4~10.8 | 10.8~13.2 | 13.2~15.6 | 15.6~17.9 |
| 30 | 3.9~6.5 | 6.5~9.1 | 9.1~11.7 | 11.7~14.3 | 14.3~16.9 | 16.9~19.5 |
| 35 | 4.2~7.0 | 7.0~9.8 | 9.8~12.6 | 12.6~15.5 | 15.5~18.3 | 18.3~21.1 |
| 40 | 4.5~7.5 | 7.5~10.5 | 10.5~13.5 | 13.5~16.5 | 16.5~19.5 | 19.5~22.5 |
| 45 | 4.8~7.9 | 7.9~11.1 | 11.1~14.3 | 14.3~17.5 | 17.5~20.7 | 20.7~23.8 |
| 50 | 5.0~8.3 | 8.3~11.7 | 11.7~15.0 | 15.0~18.4 | 18.4~21.7 | 21.7~25.0 |
| 55 | 5.2~8.7 | 8.7~12.2 | 12.2~15.7 | 15.7~19.2 | 19.2~22.6 | 22.6~26.1 |
| 60 | 5.4~9.0 | 9.0~12.6 | 12.6~16.2 | 16.2~19.9 | 19.9~23.5 | 23.5~27.1 |
在30个检验样地中随机抽取100组胸径-年龄样本进行卡方检验。卡方检验是根据检验样本的年龄和胸径值查出对应的立地指数,得到各样本的胸径理论值,然后与实际胸径值进行卡方检验,检验公式为:
| $ {\chi ^2} = \sum {\left[ {{{\left( {D - {D_理}} \right)}^2}/{D_理}} \right]} $ | (7) |
式中:χ2为卡方检验值;D为样本测量胸径值(cm);D理为样本的胸径理论值(cm)。
卡方检验是根据卡方检验值与临界值判断模型精度是否符合要求,卡方检验值均低于临界值时,卡方检验值越小,表明胸径理论值与实际值之间的偏离程度越小,模型的精度越高。本研究对选取的100对胸径-年龄样本进行卡方检验,最终得到的结果:标准差调整法的卡方检验值31.60,变动系数调整法的为34.17,相对胸径法的为30.02,均小于卡方检验临界值χ0.052(100-1)=123.225, 符合精度要求,相对胸径法的卡方检验值最小。
4.2 胸径地位指数表适用性检验根据国家森林资源连续清查固定样地多期连续测定的特点,同一样地每期调查数据在胸径地位指数表上所对应的地位指数级应该是相同的,因此可以根据同一样地6期的调查数据所得到地位指数是否相同来对胸径地位指数表的适用性进行检验。根据以上3种方法编制的胸径地位指数表分别查得29个检验样地共165对胸径-年龄样本所对应的地位指数,然后选择各样地6期数据对应的地位指数出现次数最多的作为该样地的地位指数,其余的数据当做发生跳级现象。从最后的统计结果来看,标准差调整法检验结果中有跳级现象的样本占总样本的25.4%,并且大多发生跳级现象的也只是上下各一级,跳2级以上的样本只占总样本的1.2%。变动系数调整法检验结果中有跳级现象的样本占总样本的27.3%,并且大多发生跳级现象的也只是上下各一级,跳2级以上的样本只占总样本的1.2%。相对胸径法检验结果中有跳级现象的样本占总样本的23.6%,并且发生跳级现象的都只是上下各一级,没有跳2级的现象发生。因此,结合卡方检验以及跳级检验的结果,表明3种方法所编制的胸径地位指数表都具有较高的精度,可以适用于栎类天然次生林立地质量评价以及后期生长模型的构建和经营管理,但3种方法比较而言,相对胸径法的精度略高于其他两种方法,所以本研究最终选用相对胸径法编制湖南栎类天然次生林胸径地位指数表,检验结果见表 4。
| 样地号 Sample number |
地位指数Site index | |||||
| 1989年 Year 1989 |
1994年 Year 1994 |
1999年 Year 1999 |
2004年 Year 2004 |
2009年 Year 2009 |
2014年 Year 2014 |
|
| 51 | 9 | 9 | 12 | 9 | 12 | 9 |
| 85 | 9 | 12 | 12 | 12 | 12 | 12 |
| 155 | 12 | 12 | 15 | 12 | 12 | 12 |
| 430 | 12 | 12 | 12 | 12 | 12 | 12 |
| 657 | 9 | 9 | 9 | 9 | 9 | 9 |
| 1152 | 12 | 12 | 12 | 12 | 12 | 15 |
| 1449 | 15 | 12 | 15 | 15 | 12 | 12 |
| 1616 | 9 | 12 | 12 | 9 | 9 | 9 |
| 1706 | 9 | 12 | 12 | 12 | 12 | 9 |
| 1797 | 9 | 12 | 9 | 12 | 12 | 12 |
| 2186 | 9 | 12 | 12 | 9 | 9 | 9 |
| 2253 | 9 | 12 | 12 | 12 | 12 | 9 |
| 2413 | 12 | 12 | 12 | 12 | 12 | 12 |
| 2547 | 9 | 12 | 12 | 9 | 9 | 9 |
| 2819 | 9 | 12 | 12 | 9 | 12 | 12 |
| 2991 | 9 | 9 | 9 | |||
| 3248 | 9 | 9 | 12 | 9 | 12 | 9 |
| 3356 | 9 | 12 | 12 | 12 | 9 | 9 |
| 3499 | 12 | 12 | 15 | 12 | 15 | 12 |
| 4217 | 12 | 12 | 15 | 12 | 9 | 9 |
| 5106 | 12 | 12 | 12 | 12 | 12 | 12 |
| 5190 | 9 | 9 | 9 | 9 | 9 | 9 |
| 5300 | 9 | 12 | 9 | |||
| 5465 | 12 | 15 | 12 | 12 | 12 | 12 |
| 5490 | 9 | 9 | 9 | |||
| 5555 | 9 | 9 | 9 | 9 | 9 | 9 |
| 5698 | 15 | 15 | 12 | 15 | 15 | 12 |
| 6294 | 12 | 15 | 12 | 12 | 12 | 12 |
| 6514 | 12 | 9 | 9 | 12 | 12 | 12 |
固定标准地数据是建模的最理想数据[5],但大量固定标准地的数据获取工作量大,在实际工作中由于各种原因较难获取,同时,典型固定标准地数据具有典型性却缺少随机性[23],而用国家森林资源连续清查固定样地的数据进行建模,数据具有范围广,分布均匀,随机性强等特点。本研究使用胸径数据代替树高数据编制胸径地位指数表,原因在于:立地质量是指某一立地上既定森林或者其他植被类型的生产潜力[18],所以树高、胸径、断面积以及蓄积等表示林分生产潜力的指标都可以对立地质量进行评定,只是相对来说树高受林分密度和间伐等的影响较小,所以现实中一般采用树高来评定立地质量;国家森林资源连续清查固定样地的数据中只有部分样地的平均树高,且其数据的测定准确性较差,精度不高,而胸径数据测定准确性较高,且为多期连续测定,具有较高的科研价值;随着大量人工林和天然林树高-胸径模型的建立以及在林业生产和实践中广泛应用[24-27],说明林分树高和胸径是存在相关关系的,因此直接将胸径作为评价立地质量的指标也是可行的[28]。此外,本研究在数据处理过程中还曾将断面积作为立地质量评价的指标,编制断面积地位指数表,并使用样地是否发生跳级的方法对地位指数表进行适用性检验,从结果来看,使用断面积作为立地质量评价指标时,样地的地位指数发生跳级现象的比率达39.8%,远远大于使用胸径作为立地质量评价指标时的23.6%,因此,最终选择胸径作为立地质量评价指标,并运用胸径理论值与实际值进行卡方检验和同一样地不同期数据所查得地位指数是否发生跳级现象的方法对3种方法所编制的胸径地位指数表进行适用性检验。结果表明,3种方法所编胸径地位指数表都具有较高的精度,其中相对胸径法的精度最高,适用性最强,能为栎类天然次生林的立地质量评价提供科学依据和评价方法。但本次研究使用的栎类天然次生林数据大多处于20~50 a,50~60 a的较少,20 a以下和60 a以上的很少甚至没有,这会影响到低龄林分和高龄林分立地质量的评价。为此,如有条件需加入20 a以下和60 a以上的林分数据, 完善栎类天然次生林胸径地位指数表。此外,林分胸径除受立地质量的影响外,可能还受其他因素如密度、地形、海拔等的影响,在国外的研究中已有加入气象的相关因素[29-30],因此,可在后期的研究中可以适当加入相关因素,进一步完善胸径地位指数表。
| [1] | 祝维, 张西, 贾黎明. 伏牛山地区栓皮栎天然次生林地位指数表的编制[J]. 东北林业大学学报, 2017, 45(12): 32–37. DOI:10.3969/j.issn.1000-5382.2017.12.007 |
| [2] | 胡芳名, 李建安. 湖南省栎类资源开发利用研究[J]. 经济林研究, 1999, 17(2): 1–5. |
| [3] | 王敬贤. 我国栎类资源利用技术研究现状与发展趋势[J]. 防护林科技, 2017(4): 72–74. |
| [4] | EVERETT C J, THORP J H. Site quality evaluation of loblolly pine on the South Carolina Lower Coastal Plain, USA[J]. Journal of Forestry Research, 2008, 19(3): 187–192. DOI:10.1007/s11676-008-0033-4 |
| [5] | 吴恒, 党坤良, 田相林, 等. 秦岭林区天然次生林与人工林立地质量评价[J]. 林业科学, 2015, 51(4): 78–88. |
| [6] | 黄国胜, 马炜, 王雪军, 等. 基于一类清查数据的福建省立地质量评价技术[J]. 北京林业大学学报, 2014, 36(3): 1–8. |
| [7] | 孟宪宇, 陈东来. 山杨次生林地位指数表编制方法的研究[J]. 北京林业大学学报, 2001, 23(3): 47–51. DOI:10.3321/j.issn:1000-1522.2001.03.011 |
| [8] | 张瑜, 贾黎明, 郑聪慧, 等. 秦岭地区栓皮栎天然次生林地位指数表的编制[J]. 林业科学, 2014, 50(4): 47–54. |
| [9] | 翟文元, 许玉婷, 夏泰英, 等. 山东省107-杨树地位指数表的编制[J]. 山东农业大学学报(自然科学版), 2012, 43(2): 227–231. DOI:10.3969/j.issn.1000-2324.2012.02.014 |
| [10] | 杨传强, 李士美, 孔雨光, 等. 山东省松类人工林立地指数表的编制与应用[J]. 林业资源管理, 2018(2): 43–47, 118. |
| [11] | 郭小阳.秦岭中段南坡松栎混交林立地分类及评价[D].咸阳: 西北农林科技大学, 2017. http://cdmd.cnki.com.cn/Article/CDMD-10712-1017100056.htm |
| [12] | 吴恒.秦岭林区松栎混交林立地质量评价[D].咸阳: 西北农林科技大学, 2016. http://cdmd.cnki.com.cn/Article/CDMD-10712-1016158903.htm |
| [13] | 王艳辉, 曾思齐, 王伟, 等. 马尾松次生林地位指数表的编制[J]. 内蒙古林业科技, 2007, 33(3): 17–20. DOI:10.3969/j.issn.1007-4066.2007.03.006 |
| [14] | LEI X D, PENG C H, WANG H Y, et al. Individual height-diameter models for young black spruce (Picea mariana) and jack pine (Pinus banksiana) plantations in New Brunswick, Canada[J]. The Forestry Chronicle, 2009, 85(1): 43–56. DOI:10.5558/tfc85043-1 |
| [15] | SHARMA M, PARTON J. Height-diameter equations for boreal tree species in Ontario using a mixed-effects modeling approach[J]. Forest Ecology and Management, 2007, 249(3): 187–198. DOI:10.1016/j.foreco.2007.05.006 |
| [16] | 胡芳名, 李建安, 李若婷. 湖南省主要橡子资源综合开发利用的研究[J]. 中南林学院学报, 2000, 20(4): 41–45, 95. DOI:10.3969/j.issn.1673-923X.2000.04.005 |
| [17] | 龙时胜, 曾思齐, 甘世书, 等. 基于林木多期直径测定数据的异龄林年龄估计方法[J]. 中南林业科技大学学报, 2018, 38(9): 1–8. |
| [18] | 孟宪宇. 测树学[M]. 3版. 北京: 中国林业出版社, 2006. |
| [19] | 张咏祀. 标准差法在森林立地质量评价中的应用:用标准差法编制恩施州马尾松人工林地位指数表[J]. 西华师范大学学报(自然科学版), 2008, 29(4): 348–351. |
| [20] | 陶吉兴, 唐明荣. 常规立地指数表的误差来源与分析[J]. 浙江林学院学报, 1990, 7(4): 391–395. |
| [21] | 段劼, 马履一, 贾黎明, 等. 北京低山地区油松人工林立地指数表的编制及应用[J]. 林业科学, 2009, 45(3): 7–12. DOI:10.3321/j.issn:1001-7488.2009.03.002 |
| [22] | 郑聪慧, 贾黎明, 段劼, 等. 华北地区栓皮栎天然次生林地位指数表的编制[J]. 林业科学, 2013, 49(2): 79–85. |
| [23] | 施灵栋. 规划设计调查数据在林分生长模型中的应用初探[J]. 华东森林经理, 2006, 20(2): 14–16. DOI:10.3969/j.issn.1004-7743.2006.02.004 |
| [24] | 李海奎, 法蕾. 基于分级的全国主要树种树高-胸径曲线模型[J]. 林业科学, 2011, 47(10): 83–90. DOI:10.11707/j.1001-7488.20111013 |
| [25] | 赵俊卉, 刘燕, 张慧东, 等. 长白山天然林不同树种树高曲线对比研究[J]. 浙江林学院学报, 2009, 26(6): 865–869. DOI:10.3969/j.issn.2095-0756.2009.06.017 |
| [26] | 袁晓红, 李际平. 杉木人工林南北坡向树高-胸径生长曲线研究[J]. 西北林学院学报, 2012, 27(2): 180–183. DOI:10.3969/j.issn.1001-7461.2012.02.36 |
| [27] | 朱光玉, 罗小浪. 湖南栎类天然混交林优势木树高曲线哑变量模型研究[J]. 林业资源管理, 2017(4): 22–29. |
| [28] | 马炜, 孙玉军. 长白落叶松人工林立地指数表和胸径地位级表的编制[J]. 东北林业大学学报, 2013, 41(12): 21–25, 38. DOI:10.3969/j.issn.1000-5382.2013.12.006 |
| [29] | SABATIA C O, BURKHART H E. Predicting site index of plantation loblolly pine from biophysical variables[J]. Forest Ecology and Management, 2014, 326: 142–156. DOI:10.1016/j.foreco.2014.04.019 |
| [30] | YUE C F, MÄKINEN H, KLÄDTKE J, et al. An approach to assessing site index changes of Norway spruce based on spatially and temporally disjunct measurement series[J]. Forest Ecology and Management, 2014, 323: 10–19. |

 2019, Vol. 39
2019, Vol. 39


