文章信息
- 潘辉, 江振蓝, 张宝玉
- PAN Hui, JIANG Zhenlan, ZHANG Baoyu
- 土地利用与地表温度的空间关系
- Geographically weighted regression-based research on the spatial relationship of the influence of urban land use on land surface temperature
- 森林与环境学报,2019, 39(2): 165-173.
- Journal of Forest and Environment,2019, 39(2): 165-173.
- http://dx.doi.org/10.13324/j.cnki.jfcf.2019.02.008
-
文章历史
- 收稿日期: 2018-08-01
- 修回日期: 2018-11-21
2. 闽江学院海洋学院, 福建 福州 350108
2. College of Ocean, Minjiang University, Fuzhou, Fujian 350108, China
近年来,由于城市化的快速发展,植被、农田等被建筑物、道路和其它不透水地表取代,影响了近地面水和热的自然交换,使城市地区通常有更高的太阳辐射吸收率、热容量和传导率,加剧了城市的热岛效应。国内外学者针对城市土地利用对地表温度(land surface temperature, LST)的影响进行了大量研究,取得了许多代表性成果[1-8]。研究普遍认为,建设用地对地表具有较强的增温作用,而绿地和水体则具有显著的降温作用,如李文亮等[9]利用Landsat影像进行哈尔滨市城市扩展对地表热环境的影响研究认为建设用地的扩张对地表热效应的贡献是最大的。孙俊等[10]研究认为林地比农田和草地的调节温度效果好,在城市中增加林地的面积,对缓解城市热岛效应的作用最大。赵梓淇等[11],梁保平等[12]研究则认为水体和林地在缓解城市热岛效应方面作用十分显著,两者比较,水体的降温效果优于林地。前人的这些研究无疑为解决城市热岛问题、土地合理布局提供详实的数据和可靠的依据。但这些研究大多从全局的角度出发探讨土地利用变化对城市地表温度的影响,将研究区域内地表温度受各土地利用类型的影响程度设定为常数,忽视土地利用影响的空间非平稳性,然而,城市地表温度的变化规律和过程十分复杂,其自身及其影响因子是与特定的空间位置相关联,具有强烈的空间非平稳性,随着空间位置变化,其主导因素及其影响程度可能发生变化[13-15]。
地理权重回归(geographically weighted regression, GWR)模型是对普通最小二乘法回归(ordinary least squares regression, OLS)进行空间扩展而建立的局部空间回归分析方法,自1996年FORTHERINGHAM et al[16]提出后,已被广泛应用于空间非平稳性关系探讨[17-20],但目前鲜少将该模型应用到土地利用与地表温度二者关系的研究中。本研究选择福建省福州市为研究对象,在360 m×360 m格网尺度下(栅格总数为6 210),以地表温度为因变量,各土地利用比例为自变量,构建揭示土地利用与地表温度空间关系的GWR模型,从格网尺度上探讨城市土地利用变化对地表温度影响的空间非平稳性,为模型推广提供理论和技术支持。
1 研究区域与数据 1.1 研究区概况福州是福建省的省会城市,地处我国东南沿海(东经118°24′~ 120°30′,北纬25°16′~ 26°39′),属于亚热带海洋性季风气候,境内多山,濒临海洋,地势自东向西倾斜,地形起伏大。随着城镇化水平的不断提高,福州城市范围急剧扩大,从而导致了土地利用发生了显著变化,使得城市热岛效应日益严重,已成为福州可持续发展迫切需要解决的生态问题[21],本文研究区选择面积为795 km2的福州建成区及其周边区域。
1.2 数据来源及预处理遥感数据主要包括Landsat 5 TM影像,获取时间为1996年8月21日和2006年8月17日; Landsat 8影像, 获取时间为2016年7月27日,行列号均为119/42。3期影像的成像时间均为10:30左右,研究区上空无云覆盖,数据质量良好,地物识别度较高。其它数据主要有用于辅助土地利用分类和精度检验的福州市第2次土地调查数据。遥感数据预处理包括辐射定标、大气校正、几何校正及影像裁剪等。
1.3 土地利用信息提取参照中国土地资源分类系统的土地分类标准[22],并结合研究区的土地利用特征和遥感影像的可分辨程度,将研究区土地利用类型划分为耕地(水田和旱地)、林草地(有林地、灌木林地、疏林地、草地和其它林地)、建设用地(城镇用地、农村居民地用地、工矿交通用地)、水体(湖泊、河流、水库、池塘)和裸地(裸土地和沙滩) 5类。并采用人机交互式方式对分类数据进行校正和修改。
1.4 地表温度反演目前Landsat 8第11波段(TIRS 11)值仍不稳定,故本文利用Landsat 8的第10波段和Landsat TM数据的第6波段进行地表温度反演,具体反演步骤如下[21, 23]。
首先,通过公式T=K2/ln(K1/L+1)计算亮温。其中,T为地表亮温(K);L为热红外波段辐射校正后的光谱辐射值(W · m-2 · sr-1 · μm-1);K1和K2为热红外波段的定标常数,TM6的K1和K2分别为607.76 W · m-2 · sr-1 · μm-1和1 260.56 K,TIRS10的K1和K2分别为774.89 W · m-2 · sr-1 · μm-1和1 321.08 K。
其次,采用覃志豪等[24]提出的经验公式法进行地表比辐射率ε的估算,将地类分为水面、城镇和自然表面3类,计算各地类的植被覆盖度,进而计算各地类的地表比辐射率。
最后,根据公式
GWR模型是在OLS模型[公式(1)]的基础上,假定其回归系数为变量空间位置的函数而建立的一种空间变参数模型[公式(2)][16]。
| $ {y_i} = {\beta _0} + \sum\limits_{i = 1}^k {{\beta _k}{x_{ik}} + {\varepsilon _i}} $ | (1) |
| $ {y_i} = {\beta _0}\left( {{\mu _i}, {\nu _i}} \right) + \sum\limits_{i = 1}^k {{\beta _k}\left( {{\mu _i}, {\nu _i}} \right){x_{ik}} + {\varepsilon _i}} $ | (2) |
式中:yi为样本点i的因变量,β0为回归的常数项,βk为变量k的回归参数,xik为样本点i的第k个变量观测值,εi为误差项,(μi, νi)为样本点i的地理坐标,β0 (μi, νi)为样本点i的回归常数项,βk (μi, νi)为xk在样本点处i的回归参数。
可采用加权最小二乘法实现GWR模型中βk (μi, νi)的估算,矩阵形式表示如公式(3):
| $ {{\hat \beta }_k}\left( {{\mu _i}, {\nu _i}} \right) = {[{\mathit{\boldsymbol{X}}^{\rm{T}}}\mathit{\boldsymbol{W}}\left( {{\mu _i}, {\nu _i}} \right)\mathit{\boldsymbol{X}}]^{ - 1}}{\mathit{\boldsymbol{X}}^{\rm{T}}}\mathit{\boldsymbol{W}}\left( {{\mu _i}, {\nu _i}} \right)\mathit{\boldsymbol{Y}} $ | (3) |
式中:X为自变量矩阵,XT为矩阵X的转置,Y为因变量矩阵,W (μi, νi)为空间权重矩阵,由回归点与其周围样本点之间地理距离的衰减函数,假设距离回归点i越近的样本点对局部回归参数的影响越大。空间权重矩阵是估算βk (μi, νi)的关键,本文采用高斯函数来实现[公式(4)]。
| $ {W_{ij}} = {\rm{ex}}{{\rm{p}}^{ - \frac{1}{2}\left( {\frac{{{d_{ij}}}}{h}} \right)2}} $ |
式中:Wij为利用空间样点j估计待测点i时的权重,dij为样点j与待估测点i间的欧氏距离,h为带宽,利用最小赤池信息准则(Akaike information criterion,AIC)进行确定。
由于ArcGIS 10.2 GWR模型建立的门槛限制,如采用热红外波段的空间分辨率进行模型拟合时,格网内土地类型单一,土地利用比例出现较多的0值和1值,导致模型无法建立,故本文以120 m为间隔重采样,采用局部方差法[25],即平均局部方差最大时所对应的空间分辨率为研究的最佳格网尺度,最终选择的研究格网尺度为360 m×360 m。在ArcGIS 10.2软件支持下,统计360 m×360 m格网的平均地表温度和各土地利用比例,以地表温度为因变量,土地利用比例为自变量,分别建立OLS模型和GWR模型,定量揭示土地利用与地表温度的关系。并采用AIC、决定系数(R2)、残差及残差的空间自相关性等指标,将GWR模型拟合结果与OLS结果进行比较分析,探讨GWR模型在土地利用与地表温度空间关系的非平稳性研究中的有效性。
3 结果与分析 3.1 福州市的土地利用变化特征分别在1996、2006、2016年的土地利用分类图上,每个地类各随机选取50个点(共250个),以相应年份遥感影像的目视解译结果为参照数据,运用混淆矩阵进行精度检验。1996、2006、2016年土地利用分类图的总体分类精度分别为86.39%、91.44%和92.11%,Kappa系数分别为0.80、0.89和0.90,满足分类精度要求。对土地利用图进行统计,福州市土地利用及其变化特征如表 1所示。
| 土地利用类型Type of land use | 1996 | 2006 | 2016 | 1996—2006 | 2006—2016 | |||||||||
| 面积Area /km2 | 比例Percentage /% | 面积Area /km2 | 比例Percentage /% | 面积Area /km2 | 比例Percentage /% | 变化量Quantity of change/km2 | 变化率Rate of change/% | 变化量Quantity of change/km2 | 变化率Rate of change/% | |||||
| 建设用地Construction land | 99.99 | 12.59 | 188.12 | 23.69 | 288.37 | 36.32 | 88.13 | 88.14 | 100.25 | 53.29 | ||||
| 林草地Forest-grass land | 437.73 | 55.13 | 384.69 | 48.45 | 366.03 | 46.10 | -53.04 | -12.12 | -18.66 | -4.85 | ||||
| 水体Water | 98.77 | 12.44 | 90.88 | 11.45 | 77.67 | 9.78 | -7.89 | -7.99 | -13.21 | -14.54 | ||||
| 耕地Cultivated land | 137.59 | 17.33 | 96.94 | 12.21 | 47.31 | 5.96 | -40.65 | -29.54 | -49.63 | -51.20 | ||||
| 裸地Bare land | 19.94 | 2.51 | 33.41 | 4.21 | 14.64 | 1.84 | 13.47 | 67.55 | -18.77 | -56.18 | ||||
由表 1可知,福州市土地利用以林草地、建设用地、耕地和水体为主,但随着时间推移,建设用地在研究期间呈现快速增长趋势,占全区比重由1996年的12.59%增加到2016年的36.32%,成为面积仅次于林草地的土地利用类型;而林草地和耕地面积则快速缩减,其中,耕地面积降幅最大,占全区比重由1996年的17.33%减少到2016年的5.96%;林草地面积占全区比重也从1996年的55.13%减少至2016年的46.10%。而水体的面积在研究期间略有下降,变化相对较小。
3.2 福州市不同土地利用类型的地表温度差异图 1为福州市不同土地利用类型的地表温度统计特征。其中,2006年反演的地表温度总体偏低主要是由于影像获取时间是2006年8月17日,受8月中上旬(8月5日—8月11日)超强台风桑美的持续影响,相较于其它年份相同月份气温偏低,相应地地表温度总体偏低。1996、2006、2016年各土地利用类型的地表温度差异明显,并表现出较为一致的规律,平均地表温度最高的为裸地,其次为建设用地,接着依次为耕地、林草地和水体。其中,裸地和建设用地的平均温度较为接近,明显高于全区平均温度,耕地的平均温度略高于全区均温,而水体和林草地的平均温度则明显低于全区平均温度。
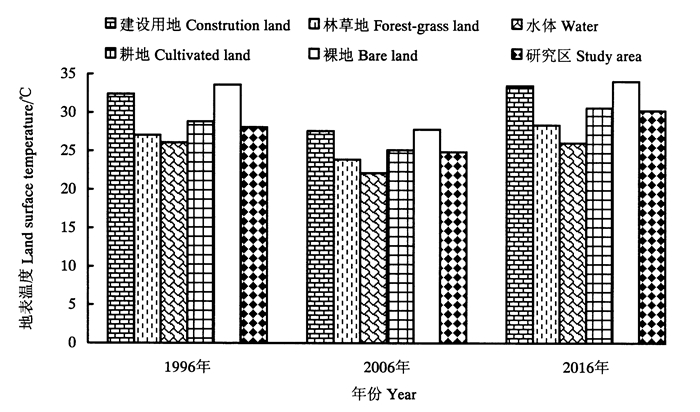
|
图 1 福州市不同土地利用类型的地表温度统计特征 Fig. 1 Land surface temperature values of different types of land use in Fuzhou |
土地利用比例与地表温度的普通最小二乘法回归拟合结果如表 2所示,所有方程均通过P=0.00水平的显著性检验,说明各土地利用类型对地表温度均有显著影响。其中,增加林草地和水体的比例能对研究区的地表温度起到很好的降温作用(方程拟合系数为负数),随时间推移,林草地和水体的回归系数均呈现下降趋势,说明该两种地类的降温作用逐渐增强,尤其是水体,到了2006和2016年,其降温作用已超过了林草地,每增加10%的水体,温度分别降低0.33和0.49 ℃,超过了林草地的0.24和0.44 ℃;而增加建设用地、裸地和耕地的比例则对研究区地表温度有明显的增温作用(方程拟合系数为正数),其中,以裸地的增温作用最为突出,每增加10%的裸地面积,地表温度可增加0.61~0.96 ℃ (1996、2006、2016年拟合回归系数分别为0.091、0.061和0.096)。建设用地的增温作用仅次于裸地,每增加10%的建设用地,地表温度可增加0.52~0.76 ℃。而耕地相较于建设用地与裸地,其增温作用较小,每增加10%的建设用地,地表温度可增加0.06~0.24 ℃,而且这种增温作用随着时间的推移呈现逐渐递减趋势,3a的回归系数分别为0.024、0.015和0.006。
| 年份Year | 土地利用类型Type of land use | 普通最小二乘法回归模型Ordinary least squares regression model | R2 | F | P |
| 建设用地Construction land | Y=0.076x+27.122 | 0.514 | 6 554.065 | 0.00 | |
| 林草地Forest-grass land | Y=-0.037x+29.876 | 0.286 | 2 489.057 | 0.00 | |
| 1996 | 水体Water | Y=-0.025x+28.377 | 0.066 | 437.936 | 0.00 |
| 耕地Cultivated land | Y=0.024x+27.661 | 0.056 | 372.721 | 0.00 | |
| 裸地Bare land | Y=0.091x+27.849 | 0.141 | 1 016.974 | 0.00 | |
| 建设用地Construction land | Y=0.052x+23.669 | 0.730 | 16 745.409 | 0.00 | |
| 林草地Forest-grass land | Y=-0.024x+24.071 | 0.293 | 2 571.476 | 0.00 | |
| 2006 | 水体Water | Y=-0.033x+25.253 | 0.178 | 1 348.409 | 0.00 |
| 耕地Cultivated land | Y=0.015x+24.706 | 0.019 | 122.371 | 0.00 | |
| 裸地Bare land | Y=0.061x+24.627 | 0.127 | 906.282 | 0.00 | |
| 建设用地Construction land | Y=0.072x+27.642 | 0.832 | 31 914.084 | 0.00 | |
| 林草地Forest-grass land | Y=-0.044x+32.295 | 0.413 | 4 363.722 | 0.00 | |
| 2016 | 水体Water | Y=-0.049x+30.719 | 0.178 | 1 343.261 | 0.00 |
| 耕地Cultivated land | Y=0.006x+29.887 | 0.042 | 269.829 | 0.00 | |
| 裸地Bare land | Y=0.097x+29.694 | 0.112 | 1 476.939 | 0.00 |
从解释能力来看,建设用地对研究区地表温度的解释能力最强,1996、2006和2016年的R2均为同期所有地类中的最大值,其次为林草地和水体,而耕地对研究区的地表温度的解释能力则最小。随着时间推移,建设用地、林草地和水体的R2呈现持续增大趋势,尤以建设用地最为显著,其R2从1996年的0.513 5提高至2006年的0.725 9至2016年的0.832 1,而耕地和裸地的R2则呈波动式下降趋势。这说明了在研究期间,建设用地、林草地和水体对研究区地表温度的影响越来越大,越来越成为影响研究区地表温度的关键因素。故本文重点探讨建设用地、林草地和水体3种地类与地表温度关系的空间非平稳性。
3.3.2 土地利用对地表温度影响的空间非平稳性建设用地、林草地和水体与地表温度空间关系的GWR拟合结果见表 3和图 2~图 4。
| 年份Year | 土地利用类型Type of land use | 回归系数Regression coefficient | R2 | |||
| 最小值 Minimum value |
最大值 Maximum value |
平均值 Mean value |
标准差 Standard deviation |
|||
| 建设用地Construction land | -1.027 | 1.707 | 0.098 | 0.171 | 0.791 | |
| 1996 | 林草地Forest-grass land | -0.108 | 0.070 | -0.024 | 0.029 | 0.542 |
| 水体Water | -0.255 | -0.457 | -0.015 | 0.069 | 0.740 | |
| 建设用地Construction land | -0.599 | 0.539 | 0.071 | 0.060 | 0.876 | |
| 2006 | 林草地Forest-grass land | -0.047 | 0.010 | -0.026 | 0.012 | 0.635 |
| 水体Water | -0.331 | 0.608 | -0.027 | 0.056 | 0.839 | |
| 建设用地Construction land | -0.269 | 0.146 | 0.068 | 0.028 | 0.918 | |
| 2016 | 林草地Forest-grass land | -0.074 | 0.038 | -0.034 | 0.024 | 0.705 |
| 水体Water | -1.640 | 4.425 | -0.013 | 0.172 | 0.904 | |
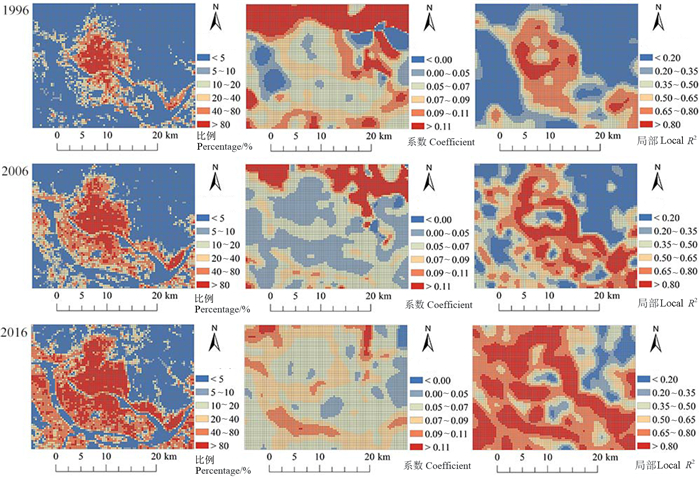
|
图 2 建设用地比例与地表温度空间关系的GWR拟合 Fig. 2 GWR regression of spatial correlation between built-up ratio and LST |
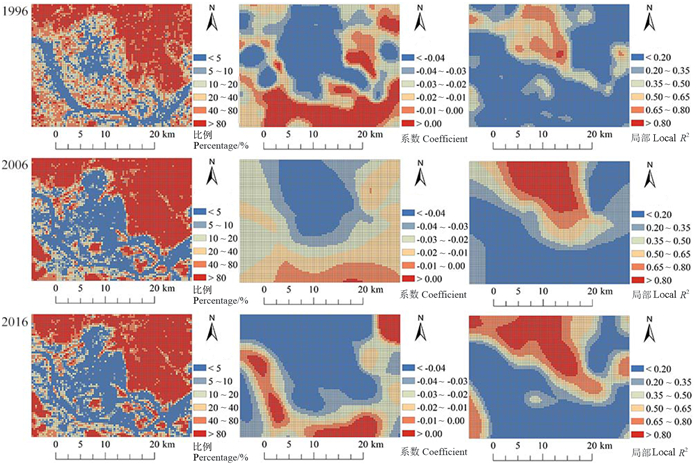
|
图 3 林草地比例与地表温度空间关系的GWR拟合 Fig. 3 GWR regression of spatial correlation between forest-grassland ratio and LST |
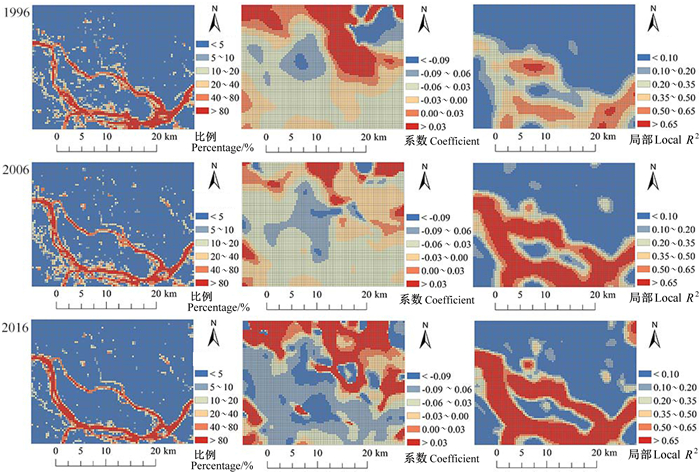
|
图 4 水体比例与地表温度空间关系的GWR拟合 Fig. 4 GWR regression of spatial correlation between water body ratio and LST |
从表 3和图 2~图 4可知,GWR拟合结果总体上与OLS模型一致,建设用地与地表温度的拟合系数平均值大于0,且以大于0的区域为主,其对研究区以增温作用为主。而林草地和水体与地表温度的拟合系数平均值均小于0,且以小于0区域为主,该两种地类对研究区以降温作用为主,但该3种地类对地表温度的影响均存在显著的空间非平稳性。
建设用地比例的增加在北部林区的增温作用远大于中部建成区及耕地分布较为集中区域(表 3和图 2),这种差异在1996年表现得尤为显著,建设用地比例每增加10%,在北部区域的地表温度将上升1.1 ℃以上,而在中部区域的地表温度上升则小于0.7 ℃。但随着时间的推移,回归系数平均值(1996、2006、2016年分别为0.098、0.071、0.068)和标准差(分别为0.171、0.060和0.028)均呈现持续下降的趋势,说明单位建设用地比例的增加对研究区地表温度的影响及其空间非平稳性均有所下降。
增加单位面积林草地的降温效果以建成区及其周边林区效果最好(表 3和图 3),该区域回归系数小于-0.04,即每增加10%的林草地,可使地表温度下降0.4 ℃以上。以这些区域为中心向外,回归系数逐渐递增,降温作用逐渐减弱,到南部的闽江流域,回归系数甚至大于0,对水域则起增温作用;水体降温作用以福州城市中心区域效果最好(表 3和图 4),该区域回归系数小于-0.06,每增加10%的水体表面可以使地表温度下降0.6 ℃以上,由市中心区域向外,水体的降温作用逐渐降低,并逐渐过渡到林区的增温作用。研究期间,林草地回归系数标准差呈波动式略有下降,其对研究区地表温度的影响空间非平稳性略有下降,而水体对地表温度的影响却随着时间推移其空间分异越来越明显,水体显著降温区(系数 < -0.06)的范围越来越大,到2016年已包含建成区及闽江流域的大范围区域,成为比重最大的区域,而增温区域(系数>0)集中分布于北部山区及南部的部分山区,比重仅次于显著降温区。
3.4 OLS和GWR模型对比分析OLS模型和GWR模型均能有效地模拟不同土地利用与地表温度的关系,GWR模型是对土地利用与地表温度间关系的局部拟合,可以体现不同土地利用类型对地表温度作用的空间非平稳性。而OLS模型是对土地利用与地表温度间关系的全局拟合,揭示的仅是研究区土地利用与地表温度间关系的平均状态,在一定程度上存在高估或低估各类土地利用对地表温度的影响程度。在中部建成区,OLS模型高估了建设用地的增温作用(GWR模型系数以大于OLS模型系数区域为主),却低估了林草地和水体的降温作用(GWR模型系数以小于OLS模型系数区域为主);在北部林区,OLS模型低估了建设用地的增温作用和林草地的降温作用,但高估了水体对地表的降温作用;在水域,OLS模型低估了建设用地的增温作用和水体的降温作用,但高估了林草地的降温作用;而在部分林区和水域,OLS模型的拟合结果甚至与GWR模型揭示的在水域增加林草地或在林区增加水体会使地表温度升高的结果截然相反。
为了更好地评估GWR对土地利用和地表温度空间关系的预测能力,利用R2、AIC值、残差和残差的空间自相关性等指标对GWR和OLS的结果进行比较分析(表 4)。
| 年份Year | 土地利用类型Type of land use | 调整R2 Adjusted R2 |
赤池信息准则 Akaike information criterion |
残差 Residual error |
残差的Moran's I指数 Moran's I index of residual error |
|||||||
| OLS | GWR | OLS | GWR | OLS | GWR | OLS | GWR | |||||
| 建设用地Construction land | 0.514 | 0.780 | 24 886.66 | 20 080.39 | 1.794 | 1.206 | 0.765 | 0.492 | ||||
| 1996 | 林草地Forest-grass land | 0.286 | 0.540 | 27 268.14 | 22 169.34 | 2.173 | 1.430 | 0.771 | 0.511 | |||
| 水体Water | 0.066 | 0.733 | 28 938.50 | 21 210.08 | 2.486 | 1.328 | 0.869 | 0.594 | ||||
| 建设用地Construction land | 0.729 | 0.863 | 17 662.61 | 13 696.61 | 1.003 | 0.714 | 0.631 | 0.317 | ||||
| 2006 | 林草地Forest-grass land | 0.293 | 0.630 | 23 630.73 | 20 569.98 | 1.622 | 1.308 | 0.771 | 0.660 | |||
| 水体Water | 0.178 | 0.831 | 24 562.36 | 14 857.17 | 1.748 | 0.793 | 0.886 | 0.538 | ||||
| 建设用地Construction land | 0.837 | 0.913 | 19 641.83 | 15 917.50 | 1.172 | 0.862 | 0.636 | 0.374 | ||||
| 2016 | 林草地Forest-grass land | 0.413 | 0.691 | 27 606.84 | 24 774.99 | 2.233 | 1.773 | 0.771 | 0.694 | |||
| 水体Water | 0.178 | 0.894 | 29 696.31 | 17 196.65 | 2.643 | 0.947 | 0.913 | 0.412 | ||||
从表 4可知,各地类GWR模型的AIC值远小于OLS模型(不同模型中的AIC值若能减少3个单位,认为模型有显著改善[20, 26]),拟合残差较OLS模型也有显著下降,而调整R2则较OLS模型有显著提高,说明相较于OLS模型,各地类与地表温度的GWR模型均有显著改善,能更好地揭示建设用地、林草地以及水体与地表温度之间的关系。其中,水体的GWR模型较OLS模型提升效果尤为显著:GWR模型的解释度较OLS模型提高了65.3%以上,而1996、2006、2016年GWR模型的拟合残差较OLS模型则分别下降了1.158、0.916、1.696,为3种地类中的最大值。从模型拟合残差的Morans′I指数看,各地类的GWR模型较OLS模型均有较为明显的下降,但值仍较大,说明GWR模型能够消除OLS模型中出现的部分空间自相性,但存在一定的局限性,在今后的研究中,还需对模型进一步完善。
4 讨论与结论本研究在360 m×360 m格网尺度下,以地表温度为因变量,各土地利用比例为自变量,运用GWR模型揭示土地利用与地表温度的空间关系,研究结果表明:福州市不同土地利用的地表温度差异明显,其中,裸地和建设用地的平均温度明显高于全区平均温度,耕地的平均温度略高于全区均温,而水体和林草地的平均温度则明显低于全区平均温度,这与戚鹏程等[5],青松等[6],王敏等[8],孙俊等[10]研究结论基本一致。这主要是由于研究区不同土地利用类型的下垫面性质不同造成:裸地主要由沙滩、裸土、裸石以及待建的开发用地构成,其表明粗糙吸热快且热容量小,同时植被覆盖度低造成植被蒸腾作用弱,一旦吸收太阳辐射后地表温度上升较快,成为地表平均温度最高的土地利用类型;而水体则由于其比热容性质较大,在吸收同样的太阳辐射之后,温度升高较慢,成为地表平均温度最低的土地利用类型;建设用地的下垫面几乎为不透水面,且人为释放热量、绿色植被较少,其地表温度较高,平均温度仅略低于裸地;林草地的植被覆盖率较高,由于植被生理活动的作用,对太阳辐射有很强的吸收作用,植被的蒸腾作用较强,有利于地表和大气的热量交换,平均地表温度明显低于研究区;而耕地一方面由于表面较为粗糙,对太阳辐射有着较强的吸收作用,另一方面由于夏季植被覆盖较高,植被的蒸腾作用较强,使得其平均地表温度3 a分别为28.83、25.12和30.64 ℃,略高于同期研究区的平均地表温度。
从全局看,增加林草地和水体比例可明显降低研究区地表温度,而增加建设用地、裸地和耕地比例则会使研究区地表温度升高。其中,建设用地、林草地和水体是影响研究区地表温度变化的主要土地利用类型。该3种地类对地表温度的影响存在显著的空间非平稳性:增加建设用地比例使得北部林区地表温度的增加幅度远大于中部建成区及耕地分布集中区域;林草地的降温能力以建成区及其周边林区最强,以这些区域为中心向外降温作用逐渐减弱,到南部水域,林草地比例增加将使地表温度升高;水体的降温能力以建设用地密集分布的市中心最强,向外逐渐降低,过渡到林区的增温作用。
以上研究结果说明了地表温度与土地利用变化作为典型的生态过程,具有强烈的空间异质性,二者关系的变化规律和过程十分复杂,是与特定的空间位置相关联。如仅从全局的角度出发,忽视土地利用/覆盖作用的空间差异来探讨土地利用/覆盖对城市地表温度的影响,即将研究区域内城市热岛受各土地利用/覆盖类型的影响程度设定为常数,这与实际情况不相吻合,研究结果的通用性势必将受到影响。如孙俊等[10]利用环境一号卫星的红外波段反演地表温度,揭示地表温度与地表类型的关系,研究认为林地比农田和草地的调节温度效果好,在城市中增加林地的面积,对缓解城市热岛效应的作用最大。而赵梓淇等[11],梁保平和李晓宁[12]在城市LUCC时空格局对地表温度的影响研究中发现,水体和林地在缓解城市热岛效应方面作用十分显著,两者比较,水体的降温效果要优于林地。这些研究由于忽视土地利用/覆盖作用的空间异质性,揭示的是不同土地利用对地表温度作用的平均状态,有可能高估或低估某一地类的增温或降温作用,使得不同研究区域研究得出的结论可能是不同的。
GWR模型的应用前提是空间非平稳性,是对传统回归模型的扩展,将数据的地理位置嵌入到回归参数中,其结果是局部性的并非全局性的,从而能够探测到空间数据的空间非平稳性。本文运用GWR模型揭示土地利用与地表温度二者的空间关系,允许在不同的位置有不同空间关系的存在,充分体现了二者关系的空间非平稳性,使得GWR模型的调整R2较OLS模型提高显著,而AIC值和拟合残差则下降显著,GWR模型较OLS模型能更好地揭示建设用地、林草地以及水体与地表温度之间的空间关系,可为土地利用和地表温度的关系研究提供参考。
| [1] | ZHOU W Q, QIAN Y G, LI X M, et al. Relationships between land cover and the surface urban heat island:seasonal variability and effects of spatial and thematic resolution of land cover data on predicting land surface temperatures[J]. Landscape Ecology, 2014, 29(1): 153–167. DOI:10.1007/s10980-013-9950-5 |
| [2] | ASGARIAN A, AMIRI B J, SAKIEH Y. Assessing the effect of green cover spatial patterns on urban land surface temperature using landscape metrics approach[J]. Urban Ecosystems, 2015, 18(1): 209–222. DOI:10.1007/s11252-014-0387-7 |
| [3] | 刘宇, 匡耀求, 吴志峰, 等. 不同土地利用类型对城市地表温度的影响:以广东东莞为例[J]. 地理科学, 2006, 26(5): 597–602. DOI:10.3969/j.issn.1000-0690.2006.05.014 |
| [4] | 彭征, 廖和平, 郭月婷, 等. 山地城市土地覆盖变化对地表温度的影响[J]. 地理研究, 2009, 28(3): 673–684. DOI:10.3321/j.issn:1000-0585.2009.03.012 |
| [5] | 戚鹏程, 赵传燕, 冯兆东, 等. 干旱荒漠区土地利用变化对地表温度的影响[J]. 农业工程学报, 2010, 26(11): 310–316. DOI:10.3969/j.issn.1002-6819.2010.11.053 |
| [6] | 青松, 包玉海, 阿如娜. 呼和浩特区域地表温度反演及其对土地利用/覆盖类型的响应[J]. 红外, 2017, 38(1): 36–42, 48. DOI:10.3969/j.issn.1672-8785.2017.01.007 |
| [7] | 蒋晶, 乔治. 北京市土地利用变化对地表温度的影响分析[J]. 遥感信息, 2012, 27(3): 105–111. DOI:10.3969/j.issn.1000-3177.2012.03.018 |
| [8] | 王敏, 孟浩, 白杨, 等. 上海市土地利用空间格局与地表温度关系研究[J]. 生态环境学报, 2013, 22(2): 343–350. DOI:10.3969/j.issn.1674-5906.2013.02.028 |
| [9] | 李文亮, 张丽娟, 陈红, 等. 哈尔滨市城市扩展与地表热环境变化关系研究[J]. 地域研究与开发, 2010, 29(2): 49–52, 58. DOI:10.3969/j.issn.1003-2363.2010.02.010 |
| [10] | 孙俊, 张慧, 王桥, 等. 基于环境一号卫星的太湖流域地表温度与地表类型的关系分析[J]. 环境科学研究, 2011, 24(11): 1291–1296. |
| [11] | 赵梓淇, 李丽光, 王宏博, 等. 沈阳市区土地利用类型与地表温度关系研究[J]. 气象与环境学报, 2016, 32(6): 102–108. DOI:10.3969/j.issn.1673-503X.2016.06.013 |
| [12] | 梁保平, 李晓宁. 城市LUCC时空格局对地表温度的影响效应研究:以广西柳州市为例[J]. 中国土地科学, 2016, 30(11): 41–49. |
| [13] | 王佳, 钱雨果, 韩立建, 等. 基于GWR模型的土地覆盖与地表温度的关系:以京津唐城市群为例[J]. 应用生态学报, 2016, 27(7): 2128–2136. |
| [14] | BUYANTUYEV A, WU J. Urban heat islands and landscape heterogeneity:linking spatiotemporal variations in surface temperatures to land-cover and socioeconomic patterns[J]. Landscape Ecology, 2010, 25(1): 17–33. DOI:10.1007/s10980-009-9402-4 |
| [15] | LI S, ZHAO Z, XIE M, et al. Investigating spatial non-stationary and scale-dependent relationships between urban surface temperature and environmental factors using geographically weighted regression[J]. Environmental Modelling & Software, 2010, 25(12): 1789–1800. |
| [16] | FORTHERINGHAM A, CHANRLTON M, BRUNSDON C. The geographically of parameter space:an investigation of spatial nonstationarity[J]. International Journal of Geographical Information Systems, 1996, 10: 605–627. DOI:10.1080/02693799608902100 |
| [17] | SHENG J C, HAN X, ZHOU H. Spatially varying patterns of afforestation/reforestation and socio-economic factors in China:a geographically weighted regression approach[J]. Journal of Cleaner Production, 2017, 153(1): 362–371. |
| [18] | CHEN Q, MEI K, DAHLGREN R A, et al. Impacts of land use and population density on seasonal surface water quality using a modified geographically weighted regression[J]. Science of the Total Environment, 2016, 572(1): 450–466. |
| [19] | DUAN S B, LI Z L. Spatial downscaling of MODIS land surface temperatures using geographically weighted regression:case study in northern China[J]. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(11): 6458–6469. DOI:10.1109/TGRS.2016.2585198 |
| [20] | 江振蓝, 杨玉盛, 沙晋明. GWR模型在土壤重金属高光谱预测中的应用[J]. 地理学报, 2017, 72(3): 533–544. |
| [21] | 江振蓝, 潘辉, 张宝玉, 等. 基于空间自相关的城市热岛时空格局变化[J]. 安徽农业科学, 2016, 44(30): 41–45, 135. DOI:10.3969/j.issn.0517-6611.2016.30.017 |
| [22] | 张景华, 封志明, 姜鲁光. 土地利用/土地覆被分类系统研究进展[J]. 资源科学, 2011, 33(6): 1195–1203. |
| [23] | NASA. Landsat 7 science data users handbook[EB/OL]. (2011-03-11)[2012-12-28]. http://landsathandbook.gsfc.nasa.gov. |
| [24] | 覃志豪, 李文娟, 徐斌, 等. 陆地卫星TM6波段范围内地表比辐射率的估计[J]. 国土资源遥感, 2004, 61(3): 28–36, 41. DOI:10.3969/j.issn.1001-070X.2004.03.007 |
| [25] | 赵金, 陈曦, 包安明. 土地利用监测适宜尺度选择方法研究:以塔里木河流域为例[J]. 地理学报, 2007, 62(6): 659–668. DOI:10.3321/j.issn:0375-5444.2007.06.011 |
| [26] | 王库. 基于地理权重回归模型的土壤有机质空间预测[J]. 土壤通报, 2013, 44(1): 21–28. |

 2019, Vol. 39
2019, Vol. 39


