文章信息
- 任向辉, 余昊, 杨萌, 吕栋标, 刘俊杰, 李鹏
- REN Xianghui, YU Hao, YANG Meng, LÜ Dongbiao, LIU Junjie, LI Peng
- 基于随机森林模型的紫薇绒蚧微环境因子排序
- Microenvironment factor permutation of Eriococcus lagerostroemiae based on random forest model
- 森林与环境学报,2018, 38(4): 506-512.
- Journal of Forest and Environment,2018, 38(4): 506-512.
- http://dx.doi.org/10.13324/j.cnki.jfcf.2018.04.019
-
文章历史
- 收稿日期: 2018-01-29
- 修回日期: 2018-02-27
2. 新乡市农作物重大有害生物防控重点实验室, 河南 新乡 453003
2. Key Laboratory for Crops Pest Management of Xinxiang, Xinxiang, Henan 453003, China
紫薇(Lagerstroemia indica L.)花期长且品种多样, 兼具观赏与药用价值, 广布于我国南北各省。紫薇绒蚧(Eriococcus legerstroemiae Kuwana)是寄生于该植物最重要的寡食性害虫, 近年来在全国各地危害严重, 可引起煤污病并造成紫薇植株枯死。该虫雌成虫为刺吸式口器且体披蜡质层, 因此防治难度大[1-3]。
紫薇绒蚧在紫薇枝条上的分布受环境因子的影响, 这些因子包括上一代密度、本年度气候条件、害虫生长的小气候条件、寄主生长指标特别是植株冠层结构、天敌[1-3]。随机森林(random forest, RF)模型是一种基于分类树结构的分析模型, 可用于多个自变量对一种因变量的分类与非线性回归分析, 是各种机器学习理论中一种较新的算法。在昆虫测报领域RF算法有对支持向量机与神经网络等算法取而代之的趋势, 但是应用该算法对影响紫薇绒蚧发生的环境因子进行随机森林模型排序的文献还没有见到[4-8]。因此, 可在对紫薇枝条小气候信息、冠层信息等该害虫发生的宿主微环境因素进行初步的灰色关联度分析(grey relational analysis, GRA)与主成分分析(principal component analysis, PCA)基础上, 对有关生态因子进行RF建模分析, 以期探明该害虫的发生规律, 为其科学防治提理论依据[4-8]。
1 材料与方法 1.1 调查地点与样方设计本次调查的地点位于河南省新乡市东郊的河南科技学院东校区, 调查时间是2017年9月27日, 此时为紫薇绒蚧一年中雌成虫的为害盛期。紫薇绒蚧寄主植株选择绕东操场与东人工湖边弧形的景观路两旁的紫薇。该处栽种的紫薇有1 000余株, 品种全是株高120 cm以下的“粉花矮紫薇”。由于景观路的走向与路旁法国梧桐(Platanus orientalis Linn.)对紫薇的光照条件影响很大, 因此紫薇植株的枝条走向、植株高低、各枝条叶片数与紫薇绒蚧发生量差异很大, 最后选择有代表性的120枝一级分枝枝条进行调查。2017年度冬季1月份平均最低气温2 ℃, 较常年湿冷; 8月份无暴雨记录且气候较常年湿热, 因此该年度新乡市紫薇绒蚧密度较低, 适宜计数。调查时天气已连续3 d晴天, 考虑到冠层仪每天不同时段的使用可能导致同一样本的调查结果出现一些差异, 为消去这个系统误差, 所有被测枝条的调查与测定时间集中在光照条件最好的上午10:00—12:00。为减小人为因素的影响, 调查时选择位置靠近、枝条角度和叶片数相近的3枝条为1个调查样方, 将组成各样方的3枝条调查数据取平均数作为1个样方的紫薇绒蚧发生量和环境因子数据进行处理[6-10]。
1.2 数据采集与处理方法调查地点紫薇的品种、水肥条件、四周植物相、杂草与害虫天敌条件单一, 因此每株紫薇的气候与土壤因子、周围的杂草与树木因素可看作一致, 选择紫薇枝条长度、枝条相对正南方向的角度、枝条叶片数、枝条小气候信息(叶丛温湿度)与植株冠层信息等指标作为数据建模分析的12个自变量, 每个样方3枝条各个自变量均值为该编号样方各自变量赋值; 每样方3枝条紫薇绒蚧雌成虫发生量均值四舍五入得每枝条平均发生虫口数为因变量赋值。
紫薇冠层信息的采集利用LAI-2000植物冠层分析仪(美国LI-COR公司)。根据操作说明将植物冠层仪传感器放在被测枝条30 cm高处对准天空读取仪器分析所需的A值。然后鱼眼探头移至每一要取样的紫薇枝条基部之下30 cm处, 将探头鱼眼对准被测枝条中心位置读取B值。重复测定次数设定为该仪器默认值。记录冠层仪显示的叶面积指数(leaf area index, LAI)、叶面积指数标准误(standard error of LAI, SEL)、无截取散射(diffuse non-interceptance, DIFN)、平均叶倾角(mean tilt angle, MTA)、平均倾角标准误(standard error of MTA, SEM)、使用样本对数(number of samples pairs used, SMP)与转换LAI计算指数(S+1), SI]等7个变量数据。利用探头式电子温湿度计在被测植株枝条叶丛中心处测定温度(temperature, T)与相对湿度(relative humidity, RH)作为小气候变量数据, 同时记录枝条长度(L)、枝条叶片数(foliage number, FN)还有枝条相对正南方向的角度(direction from south, DI)作为植株长势指标, 被测枝条的紫薇绒蚧的雌成虫数目(Eriococcus lagerostroemiae, El)为因变量赋值。每条一级分枝枝条从分枝基部到顶芽尖端的距离为L测量值, 而从分枝基部到顶芽尖端的所有叶片数为FN的取值; 测量时将每枝条分枝基部与顶芽两点在地面的垂直投影连线与正南方射线夹角一并记录于绘图纸上, 用量角器测量各个夹角度数则为DI的值。目测40~50 cm的紫薇枝条一般紫薇绒蚧雌成虫15头以上就会严重影响紫薇小树的观感, 发生量大于20头叶片形状与枝条颜色有很大改变, 每枝条10头虫以下由于虫口密度低可以考虑不防治, 因此将紫薇绒蚧发生量15头虫以下的发生级别赋值为A, 15头或15头以上则定为B。
上述12个自变量和1个因变量构成了一个数据模糊性关联的灰色系统, 所以数据处理时可先利用DPS 9.5平台进行数据均值化变换, 然后进行各变量的灰色关联度分析, 以初步确定各自变量对因变量灰色关联度。此外利用DPS的PCA分析模块可以确定各自变量的影响权重, 利用生态学软件CONOCO可以绘制出PCA结果二维图。RF分析采用的是R软件的随机森林工具包randomForest_4.6-12。
2 结果与分析 2.1 紫薇绒蚧发生量及相关微环境因子的调查结果所调查的120条枝条来自40个样方。发现有2个样方部分枝条有修剪痕迹, 所以数据可能有不同于其它组的数据特点, 因此样方编号时将这两个样方编为最后的sa39与sa40号。40个样方所有自变量与因变量调查的数据见表 1。各自变量由于量纲影响不便直接比较, PCA与RF建模前要先进行无量纲化处理。处理方法是在DPS 9.5平台对12列自变量的每个数据减去各列的平均值并除以各列的方差, 表中因变量只有一个且数据直接显示该样方3枝条的平均害虫密度, 因此不用无量纲化处理。
| 样方 编号 No. | 叶片数 FN |
枝条长 L/cm |
枝方向 DI/(°) |
温度 T/(℃) |
湿度 RH/% |
叶面积 指数 LAI |
SEL | 无截 散射 DIFN |
平均 倾角 MTA |
平均倾角 标准误 SEM |
SMP | SI | El | 发生级别 Occurringe level |
| sa1 | 25 | 46 | 30 | 28.2 | 52.1 | 2.14 | 0.07 | 0.174 | 0 | 39 | 14 | 2.070 | 0 | A |
| sa2 | 0 | 120 | 180 | 29.0 | 43.5 | 2.20 | 0.02 | 0.153 | 30 | 25 | 15 | 2.170 | 73 | B |
| sa3 | 50 | 97 | 90 | 30.8 | 41.5 | 2.01 | 0.07 | 0.211 | 0 | 0 | 15 | 1.720 | 88 | B |
| sa4 | 81 | 100 | 180 | 27.8 | 43.0 | 2.21 | 0.04 | 0.173 | 0 | 7 | 15 | 2.030 | 0 | A |
| sa5 | 15 | 69 | 70 | 26.6 | 41.7 | 2.10 | 0.03 | 0.193 | 32 | 20 | 15 | 2.170 | 2 | A |
| sa6 | 30 | 50 | 80 | 29.3 | 41.8 | 2.29 | 0.15 | 0.141 | 40 | 9 | 15 | 2.170 | 2 | A |
| sa7 | 25 | 78 | 60 | 29.3 | 40.2 | 2.86 | 0.07 | 0.092 | 50 | 11 | 15 | 3.000 | 0 | A |
| sa8 | 22 | 82 | 0 | 28.9 | 39.2 | 2.11 | 0.05 | 0.160 | 44 | 12 | 9 | 2.200 | 5 | A |
| sa9 | 20 | 109 | 55 | 30.5 | 39.8 | 0.99 | 0.08 | 0.464 | 12 | 46 | 5 | 0.980 | 0 | A |
| sa10 | 55 | 75 | 60 | 30.0 | 38.0 | 0.60 | 0.06 | 0.600 | 0 | 7 | 13 | 0.500 | 0 | A |
| sa11 | 45 | 77 | 0 | 28.9 | 36.7 | 0.53 | 0.05 | 0.636 | 23 | 18 | 8 | 0.480 | 2 | A |
| sa12 | 30 | 56 | 30 | 34.8 | 35.1 | 0.47 | 0.06 | 0.699 | 41 | 20 | 1 | 0.410 | 3 | A |
| sa13 | 15 | 36 | 45 | 19.2 | 39.5 | 0.42 | 0.07 | 0.690 | 0 | 0 | 6 | 0.350 | 1 | A |
| sa14 | 19 | 66 | 0 | 29.8 | 42.1 | 0.68 | 0.08 | 0.548 | 0 | 26 | 10 | 0.630 | 0 | A |
| sa15 | 15 | 35 | 15 | 32.0 | 43.2 | 0.25 | 0.02 | 0.809 | 0 | 0 | 3 | 0.180 | 2 | A |
| sa16 | 30 | 85 | 30 | 28.5 | 39.0 | 0.46 | 0.03 | 0.678 | 37 | 11 | 5 | 0.430 | 35 | B |
| sa17 | 29 | 57 | 60 | 31.0 | 36.7 | 1.09 | 0.06 | 0.384 | 42 | 8 | 5 | 1.100 | 55 | B |
| sa18 | 30 | 66 | 60 | 29.0 | 36.0 | 0.49 | 0.03 | 0.649 | 40 | 5 | 6 | 0.490 | 75 | B |
| sa19 | 25 | 60 | 90 | 29.3 | 36.5 | 0.23 | 0.02 | 0.837 | 63 | 13 | 1 | 0.230 | 15 | B |
| sa20 | 35 | 64 | 30 | 29.3 | 34.5 | 0.00 | 0.00 | 0.000 | 1 | 57 | 0 | 0.000 | 8 | A |
| sa21 | 28 | 84 | 60 | 30.2 | 34.0 | 0.48 | 0.07 | 0.650 | 2 | 21 | 5 | 0.480 | 57 | B |
| sa22 | 35 | 95 | 0 | 34.0 | 32.0 | 0.32 | 0.03 | 0.770 | 0 | 0 | 11 | 0.090 | 2 | A |
| sa23 | 7 | 35 | 15 | 33.2 | 31.9 | 0.52 | 0.02 | 0.482 | 0 | 0 | 12 | 0.350 | 9 | A |
| sa24 | 22 | 72 | 45 | 32.8 | 34.5 | 0.71 | 0.05 | 0.544 | 0 | 0 | 12 | 0.570 | 0 | A |
| sa25 | 9 | 75 | 90 | 31.8 | 36.9 | 0.56 | 0.03 | 0.672 | 0 | 0 | 11 | 0.670 | 25 | B |
| sa26 | 23 | 83 | 60 | 31.0 | 39.8 | 0.84 | 0.05 | 0.480 | 0 | 0 | 0 | 0.670 | 0 | A |
| sa27 | 10 | 45 | 15 | 32.8 | 37.3 | 0.56 | 0.01 | 0.501 | 39 | 0 | 3 | 0.215 | 29 | B |
| sa28 | 8 | 51 | 90 | 30.2 | 34.9 | 0.91 | 0.03 | 0.357 | 0 | 0 | 1 | 0.459 | 65 | B |
| sa29 | 19 | 35 | 60 | 31.9 | 32.8 | 0.78 | 0.15 | 0.247 | 1 | 0 | 2 | 0.218 | 28 | B |
| sa30 | 21 | 45 | 45 | 31.3 | 32.8 | 0.82 | 0.36 | 0.530 | 21 | 0 | 13 | 0.129 | 75 | B |
| sa31 | 45 | 70 | 60 | 29.9 | 30.3 | 0.73 | 0.25 | 0.010 | 11 | 0 | 0 | 0.058 | 9 | A |
| sa32 | 30 | 58 | 45 | 30.1 | 29.8 | 0.01 | 0.21 | 0.150 | 13 | 0 | 0 | 0.012 | 18 | B |
| sa33 | 38 | 65 | 60 | 28.9 | 30.2 | 0.12 | 0.20 | 0.350 | 12 | 0 | 1 | 0.350 | 0 | A |
| sa34 | 25 | 37 | 90 | 29.9 | 30.0 | 0.02 | 0.23 | 0.121 | 11 | 0 | 0 | 0.120 | 1 | A |
| sa35 | 19 | 49 | 60 | 30.1 | 31.8 | 0.05 | 0.07 | 0.360 | 9 | 0 | 0 | 0.139 | 35 | B |
| sa36 | 11 | 43 | 30 | 29.8 | 30.9 | 1.01 | 0.05 | 0.390 | 9 | 0 | 1 | 0.201 | 18 | B |
| sa37 | 35 | 46 | 60 | 29.3 | 30.1 | 0.01 | 0.10 | 0.300 | 5 | 1 | 3 | 0.312 | 0 | A |
| sa38 | 18 | 39 | 45 | 28.7 | 29.9 | 0.11 | 0.15 | 0.050 | 10 | 0 | 11 | 0.270 | 5 | A |
| sa39 | 35 | 65 | 60 | 29.0 | 30.3 | 0.05 | 0.03 | 0.120 | 10 | 1 | 12 | 0.356 | 75 | B |
| sa40 | 38 | 65 | 60 | 29.9 | 30.2 | 0.12 | 0.05 | 0.670 | 21 | 0 | 12 | 0.291 | 95 | B |
利用DPS灰色关联度模块对表 1数据进行灰色关联度分析以初步判断环境因子对该虫分布的数量关联程度, 分析时以因变量的原始值为母序列、12个自变量的无量纲化转换数据为12个子序列, 数据转换设定为DPS默认的均值化变换[5]。最后得到的12个环境因子对紫薇绒蚧发生量的关联系数具体数值见表 2。由表 2看出, 紫薇绒蚧的数目与小气候条件叶丛温度(T)的关联性最强, 另外11个自变量的关联系数很接近, 都是0.55左右。关联系数相近的结果说明, 利用灰色系统模型进行环境因子排序分析结果不算太理想, 只是对影响紫薇绒蚧的环境因子进行了初步的估计。
| 环境因子 Environmental factor | 关联系数 Correlation coefficient |
| 叶片数 FN | 0.578 76 |
| 枝条长度 L | 0.636 34 |
| 枝条方向 DI | 0.622 63 |
| 温度 T | 0.837 55 |
| 湿度 RH | 0.534 18 |
| 叶面积指数 LAI | 0.428 77 |
| 叶面积指数标准误 SEL | 0.449 16 |
| 无截取散射 DIFN | 0.503 33 |
| 平均叶倾角 MTA | 0.766 81 |
| 平均倾角标准误 SEM | 0.562 40 |
| 使用样本对数 SMP | 0.570 77 |
| 转换LAI指数 SI | 0.547 05 |
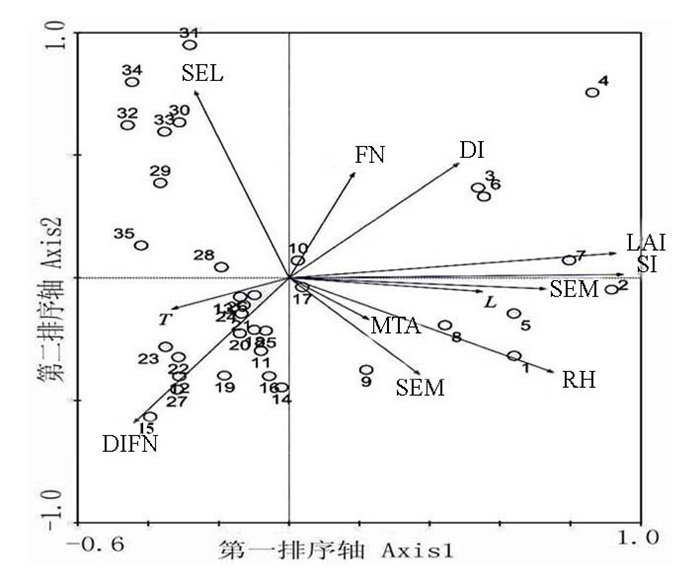
在DPS 9.5平台对12个无量纲化变换后的自变量数据进行PCA分析, 所有计算有效数字的设定都取DPS软件的默认值。最后得到12个变量的特征值与累计百分率见表 3。由表 3可知, 前6个主分量特征值累计百分率达82.035 14%, 即前6个自变量的信息量占变量总信息量的绝大部分。将12个无量纲变换数据的Excel文件粘贴板按要求输入CONOCO 5.0再进行算法相同的PCA分析, CONOCO所建PCA模型的3个主分量特征值与表 2头三行变量的特征值完全一致[3-5]。运行CONOCO软件的绘图程序绘制样方与环境因子二维散点图(图 1)。
| 自变量 Independent variable | 特征值 Characteristic value | 百分率 Percentage/% | 累计百分率 Accumulative percentage/% |
| 叶片数 FN | 3.885 72 | 32.381 02 | 32.381 02 |
| 枝条长度 L | 1.707 99 | 14.233 29 | 46.614 31 |
| 枝条方向 DI | 1.304 86 | 10.873 86 | 57.488 18 |
| 温度 T | 1.079 76 | 8.997 97 | 66.486 14 |
| 湿度 RH | 0.963 86 | 8.032 18 | 74.518 32 |
| 叶面积指数 LAI | 0.902 02 | 7.516 82 | 82.035 14 |
| 叶面积指数标准误 SEL | 0.768 66 | 6.405 53 | 88.440 67 |
| 无截取散射 DIFN | 0.497 25 | 4.143 73 | 92.584 40 |
| 平均叶倾角 MTA | 0.444 78 | 3.706 47 | 96.290 87 |
| 平均倾角标准误 SEM | 0.316 83 | 2.640 22 | 98.931 09 |
| 使用样本对数 SMP | 0.091 67 | 0.763 95 | 99.695 04 |
| 转换LAI计算指数 SI | 0.036 60 | 0.304 96 | 100.000 00 |
由图 1可知, 40个样方散点分布较分散, 说明针对这12个环境因子本次调查样方的差异性较好, 所取样方有很好的代表性。每个环境因子图中对应的向量在其它变量向量射线上的垂直投影长短定量反映了二者的相关性, 因此可以看出冠层仪所测数据除DIFN和SEL外, 其它几个植物冠层指标有很强的关联性。图中DIFN与DI是典型的负相关关系, 说明枝条角度越偏离正南则叶片越稀疏且枝条遮蔽度越低。此外害虫生活的小气候指标T与RH也是负相关的, 即叶丛温度高的、接近大气温度的枝条其叶片较稀疏, 而昆虫此处生活环境的湿度较低。
|
图 1 样方与环境因子的PCA分析二维散点图 Fig. 1 2-D spot diagram of environmental factors and samples for PCA |
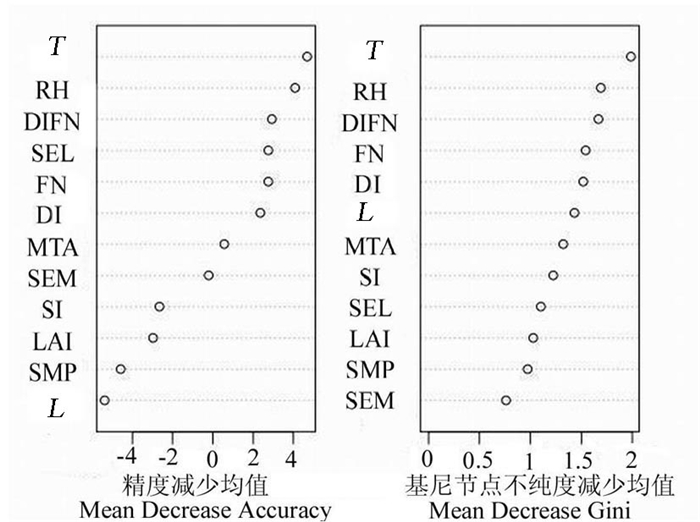
将表 1数据无量纲变换后样方sa1到sa35的数据(包括紫薇绒蚧发生级别信息)做成Excel分隔符文件(CSV格式), 命名为zwrj.csv。此Excel的前35样方作为RF模型的训练样本用于建模; RF分类模型建好后, 将sa36到sa38三个样方的数据作为预测样本以验证模型的准确性, 含修剪过枝条的sa39与sa40两样方作为试错的样本也进行模型预测。R平台加载并打开随机森林工具包后, 运行R软件“zhmc < -read.csv ("F:/lzwrj.csv", header=TRUE) ”命令, 将此分隔符文件以文件名zwrj的名称输入R软件。然后运行“ RF1 < -randomForest(zwrj, zwrj, importance=TRUE, ntree=1 000) ”命令, 建立1个分支树1 000的紫薇绒蚧发生级别为因变量且12个环境因子为自变量的随机森林分类模型RF1。运行varImpPlot (RF1)命令可绘制各环境因子排序图(图 2)。从图 2可看出, 环境因子对紫薇绒蚧发生级别影响的重要性排序, 重要性前三的变量为T、RH与DIFN, 此结论与GRA与PCA分析的结论是一致的, 因为三者灰色关联系数与PCA二维图向量的模也较大。图 2中左右两列圆点依次表示随着一个变量取随机数则分类分析时精度减少的平均值与基尼节点不纯度的平均值, 两类平均值越高说明对因变量影响越大。
|
图 2 环境因子对紫薇绒蚧发生级别的重要性排序图 Fig. 2 Importance ordination diagram of environment factors to E. lagerostroemiae occurring levels |
如果运行“round[importance(RF1), 2] ”命令则可以看出这些影响值的具体数值。将5个预测样方的环境因子数据作为newdata分别录入R软件, 运行predict (RF, new.data, type=′prob′)命令可预测各个预测样方的预测级别, 预测样方紫薇绒蚧发生级别的预测结果与实际调查结果如表 4所示。由表 4可知, RF1分类模型的预测结果准确度较高, 3个预测样方发生级别全部预测正确, 准确率100%, 而试错样方sa39与sa40的预测结果说明修剪会给本次调查带来误差。此预测结果说明图 2随机森林建模对紫薇绒蚧各个环境因子重要性排序的分析结果是可靠的。将40个样方的数据因变量实际值及自变量无量纲转换数据全录入R软件, 再运行randomForest命令建立一个RF回归模型RF2。运行命令“RF2”发现RF2的回归残差平方均值(mean of squared residuals)为994.598 9, 说明回归效果不错。
| 样方编号 No.of sample |
样本类型 Style of sample |
预测为A的概率 Probability of A |
预测为B的概率 Probability of B |
预测发生级别 Forecast level |
实际发生级别 Actual level |
| sa36 | 预测样本 Predicted sample | 0.426 | 0.574 | B | B |
| sa37 | 预测样本 Predicted sample | 0.602 | 0.398 | A | A |
| sa38 | 预测样本 Predicted sample | 0.669 | 0.331 | A | A |
| sa39 | 试错样本 Wrong sample | 0.746 | 0.254 | A | B |
| sa40 | 试错样本 Wrong sample | 0.604 | 0.396 | A | B |
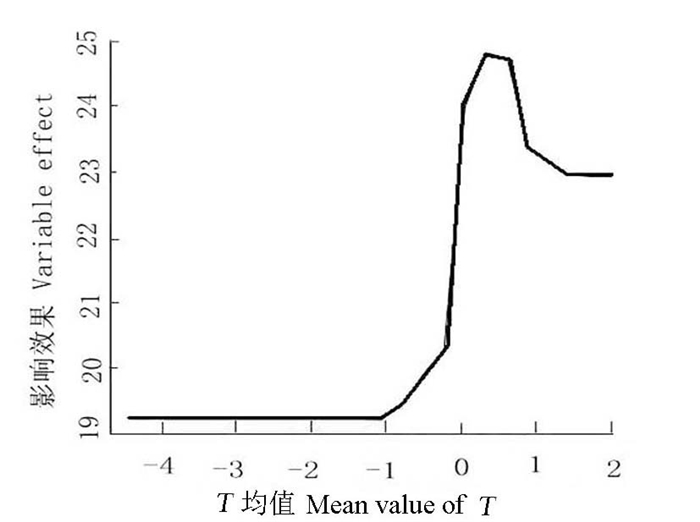
运行partialPlot (RF2, zwrj2, T, "0", mian=′′, xlab=′T(m)′, ylab="Variable effect")命令可得到关于不同水平的温度变量对紫薇绒蚧发生的影响效果图。温度变量对因变量影响效果图(图 3)。图 3纵轴为T变量对因变量的影响大小, 横轴表示T变量无量纲化变换值大小, 横轴0位点为T变量均值(Mean of T)位点。由图 3可知, T无量纲变换值即横轴坐标小于等于0时, 害虫发生量很低, 也就是说枝条叶片较密、温湿度计探头插入叶丛显示温度明显低于大气气温的健康枝条害虫密度较低; 相反枝条生长不良且叶片稀疏的样方害虫则密度较高。但是T变换值大于1时害虫密度反而下降, 说明枝条长势特别差营养不好的枝条害虫也不喜欢聚集。
|
图 3 T变量对紫薇绒蚧发生量的影响曲线 Fig. 3 Influence curve of T value on occurrence amount of E. lagerostroemiae |
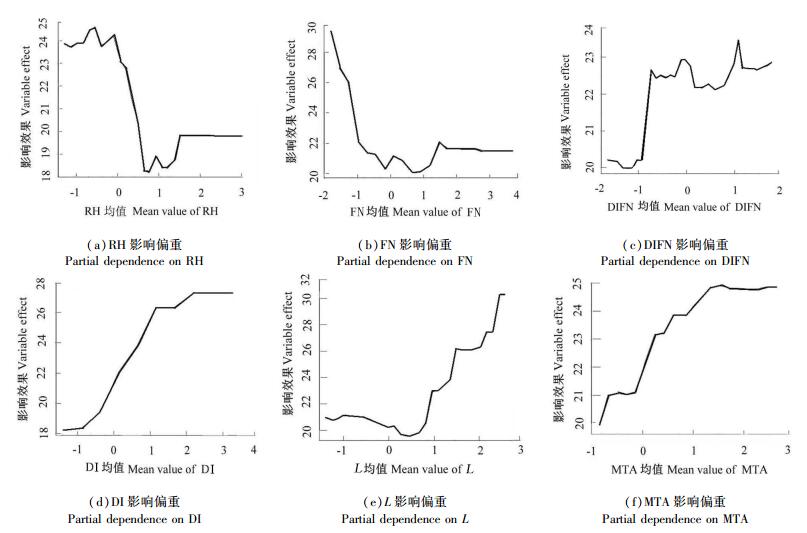
同样运行L、RH、DI、DIFN、MTA及FN对应的partialPlot命令可得到这6个自变量对紫薇绒蚧发生的影响效果图(图 4)。由图 4可知RH与FN变量的取值越大紫薇绒蚧密度一般越小, 而DIFN、DI、L、MTA取值越大紫薇绒蚧密度也越大, 因此这些效果图也可看出叶片数少、叶丛间湿度低且枝条遮蔽度低等具长势较弱的宿主微环境因子特征的枝条紫薇绒蚧发生密度较高。RH值小、FN小的枝条叶片稀疏透风, 虫子不爱聚集, 所以图 4 (a)、(b)曲线呈减函数样式, 但这两个变量在无量纲变换值1左右紫薇绒蚧密度特别低, 说明叶片稀疏略度高于平均情况的健康枝条虫子特别不爱滋生, 但春季害虫发生量大导致煤污病严重叶片特别稀疏的枝条RH值FN值特别小, 此类枝条夏季滞留的雌成虫也不算少。DIFN、DI、L、MTA值越大的枝条虫子越多, 说明紫薇绒蚧春夏季若虫及会飞雄成虫喜欢在生长密集遮蔽度高的枝条、荫处偏北向生长的枝条、徒长的不健康枝条以及叶片生长不健康叶片较小较翘的枝条等四类枝条处聚集。这些长势弱且生长密集的枝条招引害虫的醇类植物挥发物较浓, 容易把害虫吸引过来, 因为徒长其颜色浓郁也容易吸引害虫。L变量在平均值附近紫薇绒蚧密度特别低说明了比一般枝条略长的一级分枝枝条长势最健康且害虫不喜欢聚集, 因为此类枝条抗虫害能力最强[10-15]。
|
图 4 L、RH、DI、DIFN、MTA及FN对紫薇绒蚧发生的影响曲线 Fig. 4 Influence curves of L, RH, DI, DIFN, MTA and FN on the E. lagerostroemiae occurrence |
紫薇绒蚧是一种适应性强、虫害发展迅速且防治难度较大的林木害虫, 长势弱的、徒长的枝条有虫率较高, 此外温度是影响虫害进程的重要因素, 因此该虫在不同地域有不同的季节发生特点, 在高温的8、9月份各地紫薇绒蚧密度都是顶峰[1-3, 11-15]。通过RF建模分析可以进一步看出叶丛间的小气候条件对该虫分布影响巨大, 平均叶倾角(MTA)、无截取散射(DIFN)与叶面积指数(LAI)这些宿主微环境因子指标与紫薇绒蚧分布密切相关。植物叶面颜色与植物对天空遮蔽度对能够迁徙害虫虫态的虫体有吸引作用的原因, 此外还有可能是虫害改变了叶片大小与平均倾斜度以及对天空遮蔽度所导致的。未来针对紫薇绒蚧主流的防治措施是生物防治与化学防治的相结合, 这就需要通过一定栽培措施对紫薇植株进行多层次立体配置, 通过空间的立体利用来改变害虫生长的小气候条件与食物条件、天敌条件, 充分利用各种环境因素控制害虫发生。因此, 通过R语言随机森林建模分析对紫薇绒蚧的综合防治有一定的参考意义, 但对紫薇绒蚧与紫薇环境要素对应关系的进一步深入研究仍有很多工作可作[16-18]。
| [1] | 秦绪兵, 李东军, 赵洋民, 等.紫薇绒蚧生物学特性研究[C]//李典谟.走向21世纪的中国昆虫学: 中国昆虫学会2000年学术年会论文集.北京: 中国科学技术出版社, 2000: 916-918. |
| [2] | 罗庆怀, 谢祥林, 周莉, 等. 紫薇毡蚧种群生物学特性研究[J]. 昆虫学报, 2000, 43(1): 35–42. |
| [3] | 李雪艳, 梁耀琦. 紫薇毡蚧发生规律与防治简报[J]. 陕西林业科技, 1992(2): 95–96. |
| [4] | 张金屯. 数量生态学[M]. 2版. 北京: 科学出版社, 2011: 131-192. |
| [5] | 唐启义, 冯明光. 实用统计分析及其DPS数据处理系统[M]. 北京: 科学出版社, 2002: 221-326. |
| [6] | 方匡南, 吴见彬, 朱建平, 等. 随机森林方法研究综述[J]. 统计与信息论坛, 2011, 26(3): 32–38. DOI:10.3969/j.issn.1007-3116.2011.03.006 |
| [7] | BREIMAN L. Random forests[J]. Machine Learning, 2001, 45(1): 5–32. DOI:10.1023/A:1010933404324 |
| [8] | BREIMAN L. Statistical modeling: the two cultures[J]. Statistical Science, 2001, 16(3): 199–231. |
| [9] | 李欣海. 随机森林模型在分类与回归分析中的应用[J]. 应用昆虫学报, 2013, 50(4): 1 190–1197. |
| [10] | 刘震, 闫淑君, 田高飞, 等. 小果紫薇林近自然种群结构及动态特征[J]. 森林与环境学报, 2017, 37(3): 342–347. |
| [11] | 刘博, 刘旭, 谭军, 等. 苏北地区紫薇绒蚧生活史及防治方法[J]. 江苏农业学报, 2017, 33(5): 1 022–1027. |
| [12] | 姜年俊, 许惠. 紫薇绒蚧的观察研究[J]. 安徽农业大学学报, 1998, 25(2): 142–144. |
| [13] | 秦绪兵, 李东军, 赵洋民, 等. 紫薇绒蚧防治研究[J]. 植保技术与推广, 1999, 19(6): 26–27. DOI:10.3969/j.issn.1672-6820.1999.06.019 |
| [14] | 赵玲. 紫薇绒蚧的发生规律及防治技术[J]. 现代农业科技, 2015(15): 145–146. DOI:10.3969/j.issn.1007-5739.2015.15.088 |
| [15] | 魏筱.四种毡蚧的形态学研究(同翅目: 蚧总科)[D].北京: 北京林业大学, 2004: 1-34. |
| [16] | 张雷, 王琳琳, 张旭东, 等. 随机森林算法基本思想及其在生态学中的应用:以云南松分布模拟为例[J]. 生态学报, 2014, 34(3): 651–659. |
| [17] | 张璐, 敬小丽, 苏志尧, 等. 亚热带常绿阔叶林枯立木与冠层结构的关系[J]. 森林与环境学报, 2018, 38(1): 64–70. |
| [18] | 姚雄, 曾琪, 刘健, 等. 毛竹林分冠层叶面积指数高光谱估测[J]. 森林与环境学报, 2018, 38(1): 44–49. |

 2018, Vol. 38
2018, Vol. 38

