2. 大洋渔业资源可持续开发教育部重点实验室, 上海 201306;
3. 国家远洋渔业工程技术研究中心, 上海 201306;
4. 农业农村部大洋渔业开发重点实验室, 上海 201306
渔业资源评估是渔业资源管理的基础,其中声学评估技术优势明显,具有广泛的应用前景[1-2]。声波在水中的穿透性强,衰减程度相对较低,基于水体中被探测生物的声波反射强弱,利用声学评估技术可有效估算其资源量。对于栖息在中上层水体,且具有集群现象、资源结构较简单的优势种类来说,其资源量的估算相对准确。利用声学评估资源量主要分为两部分内容,一是声学调查方案的设计,包括走航方式[3]、声学仪器校正[4]、生物样本的采集等;二是声学调查数据的处理、包括鱼探仪回波数据的处理[5],目标强度计算和资源量估算等[6]。其中,准确计算评估对象的目标强度(Target strength,TS)是其核心问题,利用声散射模型计算目标强度是解决该问题的方法之一。
目标强度代表物体对入射声波反射能力的强弱,是声学资源评估研究中的研究热点和重要参数之一。目标强度的研究,除模型法之外还有测定法,测定法是对目标强度的直接测量,又分为实验室测定和野外实测两种。模型法是通过将鱼体外形构建为近似的几何形状,根据其对声波的散射特征预测(评估/分析)鱼类的目标强度[7-8]。测定法相较于模型法,强调现场测量的真实性、准确性,但现场测量的场地要求高,需要花费一定的试验成本,模型法则相对灵活,易于开展[9]。采用模型法研究目标强度,既可得到有效的数值,也是对目标强度现场测量和实验室测定研究的有效补充和侧面验证[10]。同时,通过建立鱼体声散射模型可简化复杂的鱼体结构,利于分析鱼体的声散射机理和特征值,实现鱼类的种类识别研究。为此,本文将常见声散射模型研究的理论基础和适用范围进行了梳理,分析这些模型在鱼类目标强度研究中的应用和不足之处,并对宽频技术在声散射模型中的应用进行展望。
1 声散射模型构建原理及其类型将声散射体近似看作空间中简单规则的几何模型,基于声波的散射原理,利用模型估算出不同频率声波下的散射强度值,即为声散射模型研究[11]。鱼体是一种复杂的声散射体,一是鱼体形态复杂,不同鱼种的外形各异,如球体,扁椭球体等,且不同生长阶段体型会发生改变;二是鱼体解剖结构复杂,鱼体组织、器官的状态,有无鱼鳔、鳔体的大小以及充满程度,鱼肉、鱼骨等的变化,都会引起鱼体的散射特征的变化[12]。因此,对鱼体的简单测量往往会对其目标强度的计算产生较大误差[13]。长期以来,国内外学者围绕鱼体声散射模型的建立开展了大量工作,分析鱼体声散射特征,以期准确估计鱼体目标强度,同时基于声学数据反演鱼体的大小,实现对不同鱼种的分类识别[13-14]。根据其模拟的核心对象不同,鱼类声散射模型分为鱼体近似模型和鱼鳔近似模型。对于有鳔鱼类而言,鱼鳔是有鳔鱼声散射的主要贡献组织,约占单体鱼声散射信号能量的90%以上,因此有鳔鱼的声散射模型主要是对鱼鳔和鱼体分别进行形态学建模,然后对二者进行叠加[13-14]。经过近30 a的发展,鱼类声散射模型对其目标强度预测的精度越来越高,有力地促进了渔业资源声学评估的发展。
声散射模型根据其是否以规则的几何形状为建模基础,可分为基准模型和非基准模型两大类[15]。基准模型中的几何形状包括:球体、球形壳体、长椭球体及有限圆柱体。非基准模型则以数值计算方法为基础进行模型模拟分析。
1.1 基准模型 1.1.1 球体模型(Sphere model)球体模型[15-16]一般基于分离变量来计算声散射,其方程为
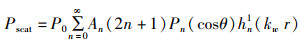 (1)
(1)
式中:P0为入射声波声压;An为参考系数;Pn(cosθ)为n次勒让德多项式;hn1为n阶的第一类球形汉克尔函数;kw为入射声波的声波数,k=2π/λ,λ为波长,m;r为声场到目标的距离,m。
当散射角θ=π时,勒让德多项式为Pn(-1)=(-1)n,在远场散射中,当kw r≫1时,其散射振幅的表达式为
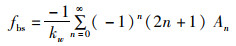 (2)
(2)
其目标强度为
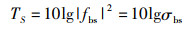 (3)
(3)
在长椭球模型法的研究中,一般将鱼肉抽象为黏性流体,所以目标强度研究中多为流体型的椭球模型[17]。长椭球模型根据边界限制条件的不同,分为固定刚性型、释压型和流体型3种基准模型。基于长椭球模型的远场散射振幅波动方程为
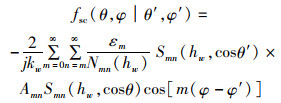 (4)
(4)
目标强度计算公式为
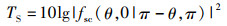 (5)
(5)
式中:(θ, φ)和(θ′, φ′)分别为入射声波和散射声波的球型角坐标;j为已知参数;εm为诺伊曼因子;hw约等于kwq,kw为声波数,q为该长椭球体模型的半焦距长;Smn为m阶n次幂的第一类角球面波函数;Nmn为Smn的标准化因子;Amn为系数,取决于不同的边界条件;θ为入射波与模型长轴的倾角。
1.1.3 有限圆柱体模型(Finite cylinder model, FCM)有限圆柱体模型法中几何形状的边界难以界定,不能对其进行测定[18]。因此目前主流的使用方法是基于该模型的形变圆柱体模型。
1.2 非基准模型 1.2.1 形变圆柱体模型(Deformed cylinder model, DCM)形变圆柱体模型[19]为近似分析模型的一种,在有限圆柱体模型的基础上忽略边界影响。该模型基于微元法,将研究目标抽象为一系列单位长度的圆柱体微元,然后通过积分计算圆柱体微元的散射声压,即为散射体目标的后向散射振幅:
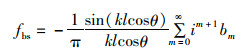 (6)
(6)
式中:k为入射声波的声波数,k=2π/λ,λ为波长,m;l为圆柱体的长轴长度,m;θ为入射声波与圆柱体长轴间的夹角;bm为散射体的远场散射系数。
f(Ω)为声散射振幅,微分散射截面σ(Ω)=|f(Ω)|2,其目标强度为
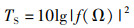 (7)
(7)
边界元模型[20]利用赫姆霍兹波动方程的积分形式计算散射声场中任意点的散射声压,即在该方程中通过计算每个节点的积分值得到后向散射振幅f(r)。
其中节点为i,位置为ri赫姆霍兹积分方程为
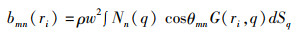 (8)
(8)
式中:m为微元;n为节点;ρ为流体密度;q为微元面各积分点位置向量;G为格林函数;N(q)为微元形态函数;cosθmn为在n节点的微元m处平均法线导数。
任一点位置的散射声压:
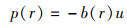 (9)
(9)
则距离为r处的后向散射振幅为
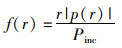 (10)
(10)
式中:u为散射面的法向位移;Pinc为入射平面波振幅。目标强度由f(r)计算得到。
1.2.3 有限元模型(Finite element model, FEM)有限元模型适用于模拟复杂的类流体的非均质目标[21]。该方法通常将完整的连续几何体处理成若干有限离散单元,基于拉格朗日算法,用网格的密度代表声波,并利用非齐次赫姆霍兹波动方程计算散射声场中的散射声压[22]。其中:
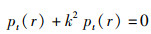 (11)
(11)
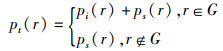 (12)
(12)
公式(11)为各向同性赫姆霍兹波动方程,r为空间任意点位置矢量; k=2πf/c, f为频率,c为声速;pt(r)为总声压;pi (r)为入射声压;ps (r)为散射声压;G为散射体。
结合公式(11)和(12)可计算目标强度值:
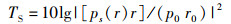 (13)
(13)
网格的设置中,需满足每个波长至少十个节点,该模型目前可通过商业物理仿真软件COMSOL中提供的声学模块实现。
1.2.4 傅里叶匹配模型(Fourier matching model, FMM)傅里叶匹配模型主要适用于呈轴对称几何形状的目标声散射问题。该模型利用牛顿拉普拉斯算法实现二维坐标系的保角变换,而从保证合理表征两个不同坐标系中散射体的声散射特征[23]。牛顿拉普拉斯算法的保角映射函数为
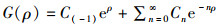 (14)
(14)
基于该函数的散射体散射振幅为
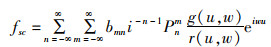 (15)
(15)
式中:Cn为映射系数;ρ为转换坐标系后的极坐标参数;m和n根据散射体的不同而不同,但任一散射体中均需满足其值大于ka+3,k为声浪波长,a为散射体单位;bmn为不同散射体的远场散射系数;Pnm为连带勒让德函数;r(u, w)与g(u, w)是转换坐标系后的新坐标函数。
1.2.5 基尔霍夫近似模型(Kirchhoff approximation model, KAM)基尔霍夫近似模型属于近似分析模型的一种,是一个忽略衍射的高频模型。该模型的计算方法类似边界元模型,即利用赫姆霍兹波动方程的积分形式计算散射声场中任意点的散射声压,但其积分算法不同,基尔霍夫近似模型采用曲线面元的高斯积分法[24]。
该模型的散射振幅表达式为
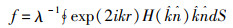 (16)
(16)
式中:λ和k分别为入射声波的波长和散射方向;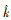
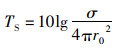 (17)
(17)
式中:r0为参考距离,取值1 m。
1.2.6 基尔霍夫射线模型(Kirchhoff ray-mode model, KRM)基尔霍夫射线模型是将研究目标近似为多个连续不同半径的小圆柱体,根据外部媒介以及其间距的不同,计算其反射系数和透射系数[25]。入射声波穿透散射目标,离目标距离为R的散射声压可表示为
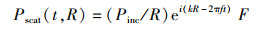 (18)
(18)
式中:Pinc为入射声波的散射振幅;Pinc为入射平面波振幅;R为离目标的距离;F为散射体的散射长度。该模型中散射横截面计算方式为σbs =|F|2,结合公式(18)可得基尔霍夫射线模型目标强度值:
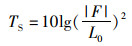 (19)
(19)
式中:L0为参考距离,取值1 m。
1.2.7 畸变波玻恩近似模型(Distorted wave born approximation model, DWBA)畸变波玻恩近似模型适用于属于声波的弱散射体的研究目标,即目标的材料特性约为周围水体的5%,且声波散射过程中不会产生剪切波[26]。DWBA模型对弱散射体目标强度的计算具有良好的适用性,该模型不受目标材料性质,规格尺寸的限制,普遍应用到各种弱散射体的研究中。目前,在原模型的基础上发展出应用于不同实验条件的模型,包括相位跟踪的畸变波玻恩近似模型(PT-DWBA)和随机畸变波玻恩近似模型(SDWBA)[27]。
其中,随机畸变波玻恩近似模型将散射目标视为沿中心轴线排列的连续圆柱体微元,其目标强度值等于多个连续微元相叠加,该模型的散射振幅表达式为
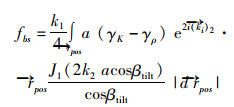 (20)
(20)
式中:k1和k2分别为入射声波的波数;a为圆柱体微元的半径;βtilt为入射声波与各圆柱体微元轴线之间的夹角,为0°到90°;J1为一阶贝塞尔函数;γK=(k2-k1)/k1,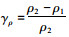
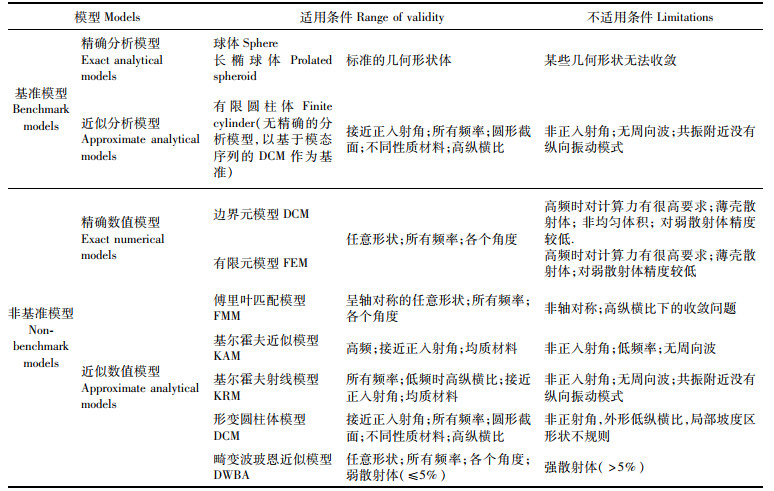
以上所提及的模型各有其适用的范围和不适用的条件(表 1),因此如何合理选择声散射模型,对渔业生物资源量评估是极为重要的。实际应用过程中,应针对调查物种的特点,结合调查仪器的不同,选择和开发适合的声散射模型,以有效提高声学资源评估的准确性。
|
表 1 声散射模型的分类与适用性 Tab.1 Classification and applicability of acoustic scattering models |
鱼体的目标强度是渔业资源声学评估中的核心参数之一,是表征鱼体反射声波能力的物理参数,目标强度的定义为
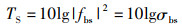 (21)
(21)
式中:TS为鱼类目标强度,dB;σbs为鱼类的后向声散射截面,m2[28]。
σbs在鱼体目标强度研究中代表声波的有效散射截面面积,其无法通过直接测量得到,但σbs散射面积和鱼体的长度密切相关,因此可以建立鱼体可度量的生物学特征量与不可度量的物理截面的物理量的关系,即目标强度-体长经验公式:
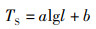 (22)
(22)
式中:l为鱼体体长,cm;a,b为回归系数,由目标强度测定实验确定。通过目标强度-体长经验公式关系,对于鱼种类型已知,且体长可通过测量得到,则可根据两式对其声学散射截面或目标强度进行换算[28]。该经验公式通过一定的现场调查数据的累积,在某些鱼种方面已经得到了广泛的应用,但对于一些了解不充分,采样较为困难的鱼种,以及某个鱼群而言,仍难以满足实际应用需求。随着水声学技术的快速发展,计算机数值模拟技术的成熟,以模拟鱼群回波为主要技术手段的模型法研究开始被利用到鱼体目标强度的研究中。
2.2 单体鱼目标强度模型研究对于有鳔鱼类, 鱼鳔贡献了主要的声散射强度,球体模型在建模时需考虑到鳔体与鱼体之间的位置关系,如LOVE等[29]采用球体模型将有鳔鱼建模成一个球形壳体,验证了渔业声学数据和体积混响的声学测量的关联性。相较于有鳔鱼,无鳔鱼的鱼体是主要散射源,FURUSAWA等[30]基于两种鱼体的特性区别,采用PSM分别构建了软体材料椭球体的有鳔鱼,以及液体稀球体的无鳔鱼模型,研究证明了声波的传播速度、鱼体密度与海水密度之间的差异对目标强度的影响,同时计算了利用鱼体实际物理参数的椭球体模型后向散射频率,其目标强度的模型计算结果与沙丁鱼(Sardina pilch-ardus)、鲭鱼(Pneumatophorus japonicus)、磷虾(Euphausia)等目标强度实验观测结果较为一致。
在国内,于海圆等[10]利用PSM计算了鳀鱼(Engraulis japonicus)的目标强度,尚晓明[31]则对大黄鱼(Pesudosciaena crocea)、小黄鱼(P. polyactis)以及银鲳(Pampus argenteus)的目标强度,通过模型法与实验室测量的方法进行了比较研究。DCM通过将鱼体建模为一系列轴对称圆柱,被广泛应用于橘棘鲷(Hoplostethus atlanticus)、杖鱼(Thyrsites atun)、红鳕鱼(Pseudophysic bachus)、南蓝鳕鱼(Micromesistius poutassou)[32]和狭鳕(Gadus chalcogrammus)[33]的目标强度研究中。其中李佩杰等[34]采用椭圆柱体模型(MB-DCM),计算出不同声波频率下尾明角灯鱼(Ceratoscopehus warmingii)的目标强度变化情况。基尔霍夫近似模型(KRM)和基尔霍夫射线模型(KAM)通过直接对鱼鳔的精确形状进行建模,近似计算目标强度[35]。KRM的计算相对简单,但当波束照射角较大时会出现模拟精度下降,计算不准确的情况,不适用于大角度范围鱼体目标强度的计算。李斌等[9]采用KRM模型,分别计算出不同体长下多鳞
边界元模型(BEM)和傅立叶匹配模型(FMM)可以实现较宽的入射声波频率范围内,任意方向角的鱼体目标强度的计算。其中BEM模型的基本原理是将鱼体抽象为一系列散射微元,再通过波动方程转换为亥姆霍兹积分最后进行计算。FOOTE等[37]同时采用基尔霍夫射线模型(KAM)和边界元模型(BEM)进行对比研究,研究结果表明,在计算鳕鱼目标强度时,BEM精度高于KAM,但其计算更加复杂。傅里叶匹配模型(FMM)对呈轴对称形状的鱼体可实现较为精确的声散射建模,尤其在其他模型不能满足的大的声波照射角度的散射问题时,傅里叶匹配模型表现优秀。REEDER等[33]通过对鲱鱼(Clupea pallasi)目标强度的计算,验证了FMM模型在鱼体声散射模型研究中的适用性。波恩近似模型适用于弱散射体目标强度的研究,DEMER等[38]将其应用于南极磷虾目标强度的研究中。
2.3 鱼群目标强度模型研究多数鱼类都具有集群行为,以鱼群整体为声散射建模研究目标,可以合理估算鱼类的资源丰度,有助于鱼种分类识别研究。自然状态下的鱼群的移动方向一致,由不同数量的单体鱼决定了鱼群整体的集群形状,密度与声散射的强弱,所以鱼群声散射模型通常基于单体鱼的声散射特性进行建模[12]。
在鱼群的声散射模型研究中,入射声波的频率和鱼鳔的有无是较为重要的影响因素。对于频率低于10 kHz的入射声波,鱼群的鱼鳔对声波会产生明显的共振现象,许多学者对该频率附近的鱼群散射模型开展了一些研究。FEUILLADE等[39]考虑到中小鱼群中每条鱼的散射特征,以及声波在每条鱼之间二次甚至多次散射的特征,提出了一种基于耦合微分方程组的低频散射模型,该模型通过相干求和计算鱼群整体的散射场,进而求解其目标强度,对中小鱼群具有良好的适用性。NERO[40]以黄鳍金枪鱼(Thunnus albacares)鱼群为研究对象,在较宽的频率范围内模拟了不同规格鱼群的目标强度,研究结果表明鱼群的大小、深度不同,其鱼群整体的目标强度不同。WEBER等[41]对比分析了现场观测和模型法研究对小种群大西洋蓝鳍金枪鱼(Thunnus thynnus)鱼群的声散射特征的影响。对于自由鱼群,由于组成该鱼群的鱼种不同,其声散射特征不同,且一般鱼群较为分散,难以通过相同鱼种的声散射叠加进行研究。HAHN[42]将自由鱼群抽象为理想鱼群,将有效介质理论引入该鱼群的声散射建模研究中,实现了对不同大小和密度的鱼群目标强度计算。NERO等[43]考虑到鱼体不同的物理性质,通过在聚乙烯包装材料中切割三维气泡阵列来模拟来自鱼群的散射。
实际上,在渔业资源的声学研究中,数据来源主要依靠各种类型的鱼探仪,目前主流鱼探仪的工作频率多在38 kHz及以上的高频,高频利于鱼类资源丰度估算,鱼种识别等研究,部分学者研究建立了基于常用鱼探仪需求的不同鱼群声散射模型。HORNE等[44]采用基尔霍夫近似模型(KRM)计算单体鱼的声散射强度作为参考,再结合建模和测量后的反向散射值,计算每个群体的反向散射并估计生物丰度。BOSWELL等[45]考虑了鱼体的不同体长分布对鱼群目标强度的影响,模拟分析3个体长组的鱼群声散射变化,同时研究证明不同的声波入射角度对鱼群生物量估计的影响不同。HOLMIN等[46]通过对比模拟生成鱼群回波图与实际回波,验证了多波束以及多频率声呐的工作性能,其所采用的模型对模拟特定形状的鱼群声散射特征具有一定参考意义。FURUSAWA等[47]通过相干叠加单体鱼的散射特征计算鱼群目标强度,研究结果表明鱼群分布密度与体积后向散射强度之间具有显著的线性关系。
3 声散射模型在鱼种识别中的应用利用声学方法对不同鱼种的分类识别研究,一直是渔业资源声学评估技术中的难点问题。尤其在多鱼种混合的研究中,区分不同种类鱼群是准确计算生物量的关键。鱼种识别的基础是鱼类目标强度的差异,而鱼类目标强度的这种差异主要是通过声散射模型计算的或预测的。目标强度的差异就像鱼种识别的窗口。目前基于声学数据获取方式的不同,可分为被动声学识别和主动声学识别。
被动声学识别方法主要通过捕获水下鱼类发出的声信号,其中不同物种,其发声信号的频谱特征不同,基于此可区分出不同鱼种[48];但现实水体中,波浪、水中砂石等都会产生环境噪声,导致被动水声信号信噪比较低,在数据分析时难以提取有用信息,鱼类的识别难度较大。
主动声学识别是通过发射声波,再收集物体反射回来的声信号进行判别,该方法作用范围广,声波探测范围从几十米到上千米不等,且声波在水中穿透性强,不受能见度限制,可有效采集回波信号,信噪比较高,是目前鱼类物种识别的常用方法。对于不同鱼类的主动声学识别,根据数据分析方法的不同,又分为两种方式:第一种是基于声呐图像的特征提取与分类方法,该方法以鱼群目标为研究对象,通过标记鱼探仪回波信号中鱼群大小和栖息深度等进行分类;第二种是基于声散射信号的特征提取与分类方法,通过分析提取鱼体的声散射信号特征对鱼种进行分类。
基于声散射信号的特征提取与分类方法:主要包括基于频域特性的分类、基于波形特征的分类及基于相位特性的分类[13]。其中,基于频域特性的分类方法应用广泛。
(1) 基于频域特性的分类。根据频谱应用的不同,又可细分为基于多频的分类和基于宽频的分类。基于多频的分类通常应用主流鱼探仪的声学数据,通过提取不同频率下的声散射特征量对鱼种进行识别和分类[49]。该方法目前应用广泛,在多个鱼种的分类识别试验中得到了很好的验证,如KANG等[50]基于不同物种在不同频率下的体积散射强度不同,通过测量38和120 kHz下鳕鱼群和磷虾群的体积散射强度均值,成功对两者实现区分,取得了良好的分类效果。KORNELIUSSEN等[51]通过计算鲭鱼鱼群在38和120 kHz不同频率下体积散射强度的差值,实现了对鲭鱼鱼群的判别。SUNARDI等[52]通过现场测量和实验室测定,分别得到38 kHz和120 kHz两个频率下竹
与多频探测所获取的回波相比,基于宽频信号(通常为100~200 kHz)的鱼体声散射特征信息更加丰富。BO等[53]和JECH等[54]采用宽频信号和窄带信号,通过模型模拟的对比分析,最终实现了对鳕鱼幼鱼的分类研究。利用宽频信号,BRUNDAGE等[55]基于神经网络分类器对短鼻鲟鱼(Acipenser brevirostrum)实现了鉴别;ROGERS等[56]实现了对鲱鱼、胡瓜鱼(Osmerus mordax)和白鲑鱼(Coregonus clupeaformis)的分类识别;JUNG等[57]成功对两种不同的大马哈鱼(Oncorhynchus keta)进行了分类。在通过宽频信号获取声散射数据的研究中,CONTI等[58]发现,沙丁鱼和凤尾鱼(Anchovy)在不同频率下的目标强度存在明显的差异。ROBERTS[59]采取了不同的声散射数据特征提取方法,基于小波变换分析了带宽及换能器基阵孔径对分类性能的影响。
(2) 基于波形特性的分类主要利用声散射信号的包络特征对鱼种进行分类。KULINCHENKO等[60]采用宽频和窄带信号分别对大比目鱼(Hippoglossus)和石鱼(Synanceia verrucosa)进行探测,通过提取频谱特征和声散射信号包络特征,利用神经网络对二者进行了判别。研究对比发现,窄带信号的包络特征具有更好的鉴别能力。
(3) 基于相位特性的分类,BARR等[61]研究发现,不同鱼体的声散射回波相位信息存在差异,因此存在利用相位特征差异进行鱼类分类与识别研究的可行性。
4 总结与展望利用声散射模型计算鱼体目标强度,不受调查条件的限制,方便快捷,是研究鱼体目标强度的有效方法之一。通过与现场实验测量的目标强度值进行对比研究,可不断完善声散射模型的不足之处。影响鱼类目标强度的因素有很多,主要为两个方面:一是内部因素,包括鱼体结构差异,不同鱼种体型不同,相同鱼种的不同生活史阶段其体长大小不同;同时鱼体的不同组织和不同器官等对鱼体声散射强弱也会产生重要影响[62],比如鱼类在不同的摄食阶段、不同生长阶段的肌肉发育程度等,以及有无鱼鳔及不同的鳔室结构等,其声学特性可能都不一样。二是外部因素,包括不同探测频率,鱼类活动状态以及栖息水层等。为此,如何结合鱼群的理化特性和运动状态,建立一个更为有效、高精度的鱼体声散射模型,是今后的一个重要研究方向。
同时随着声呐技术的发展,宽频技术已经逐步应用到声学评估技术中。窄带信号一直以来都存在一个技术问题,即难以同时保证声波在较深探测距离下的高探测分辨率。而宽频信号在拥有高时间分辨率的同时,通过宽频带内的连续覆盖,增加了信号内的信息量。同时,鱼类所表现出的声散射特性与其对入射声波的频率响应特征密切相关,宽频带信号意味着更宽的频率覆盖范围,因此收集到的鱼体声散射信号更加丰富,所提取的声散射特征能更充分地表征不同鱼类声学特性的基本差异,可一定程度上解决单频信号探测时鱼群信息模糊不清等问题[13]。因此,宽频探鱼声呐在鱼群探测中有较好的优势,具有很好的应用前景。
在今后的研究中,通过鱼群声散射建模、理论分析、计算机仿真、实测数据验证相结合的研究方式,可在宽频探鱼声呐获取鱼群信息的基础上,构建更加精确、完善的声学评估技术,为合理利用开发渔业资源提供可靠的科学研究手段。
| [1] |
赵宪勇, 陈毓桢, 李显森, 等. 多种类海洋渔业资源声学评估技术与方法[C]//我国专属经济区和大陆架勘测研究专项学术交流会论文集. 北京: 海洋出版社, 2002: 341-353. ZHAO X Y, CHEN Y Z, LI X S, et al. Acoustic estimation of multi-species marine fishery resources[C]//Proceedings of China's Exclusive Economic Zone and Continental Shelf Investigation and Research Special Academic Exchange Conference. Beijing: China Ocean Press, 2002: 341-353. |
| [2] |
ELLIOTT J M, FLETCHERJ M. A comparison of three methods for assessing the abundance of Arcticcharr, Salvelinus alpinus, in Windermere(Northwest England)[J]. FisheriesResearch, 2001, 53(1): 39-46. |
| [3] |
李哲, 朱文斌, 陈峰, 等. 近年我国渔业资源声学评估研究进展[J]. 浙江海洋大学学报(自然科学版), 2021, 40(1): 80-85, 92. LI Z, ZHU W B, CHEN F, et al. Recent advances in acoustic assessment of fishery resources in China[J]. Journal of Zhejiang Ocean University (Natural Science), 2021, 40(1): 80-85, 92. DOI:10.3969/j.issn.1008-830X.2021.01.012 |
| [4] |
赵宪勇, 陈毓桢. 狭鳕(Theragra chalcogramma Pallas)目标强度的现场测定[J]. 中国水产科学, 1996, 3(4): 19-27. ZHAO X Y, CHEN Y Z. In-situ target strength measurements on walleye pollock (Theragra chalcogramma Pallas)[J]. Journal of Fishery Sciences of China, 1996, 3(4): 19-27. |
| [5] |
屈泰春, 黄洪亮, 汤勇, 等. 渔业声学数据后处理中噪声剔除的研究进展[J]. 渔业信息与战略, 2013, 28(3): 208-213. QU T C, HUANG H L, TANG Y, et al. Research progress on post-processing technique to remove noises in fishery acoustic data[J]. Fishery Information & Strategy, 2013, 28(3): 208-213. DOI:10.3969/j.issn.1004-8340.2013.03.006 |
| [6] |
杨洋, 朱国平. 海洋渔业资源声学评估技术及在南极磷虾资源声学评估中的应用[J]. 海洋渔业, 2018, 40(3): 368-376. YANG Y, ZHU G P. Assessment on marine living resources based on acoustic technology and its application in Antarctic krill abundance estimation[J]. Marine Fisheries, 2018, 40(3): 368-376. DOI:10.3969/j.issn.1004-2490.2018.03.013 |
| [7] |
MACLENNAN D N. Acoustical measurement of fish abundance[J]. The Journal of the Acoustical Society of America, 1990, 87(1): 1-15. DOI:10.1121/1.399285 |
| [8] |
陈刚, 陈卫忠. 渔业资源评估中声学方法的应用[J]. 上海水产大学学报, 2003, 12(1): 40-44. CHEN G, CHEN W Z. The application of acoustic method in fishery resources survey[J]. Journal of Shanghai Fisheries University, 2003, 12(1): 40-44. |
| [9] |
李斌. 基于基尔霍夫近似模型的多鳞 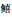 (Sillago sihama)和红牙 (Sillago sihama)和红牙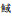 (Otolithes ruber)目标强度测量研究[D]. 大连: 大连海洋大学, 2017. (Otolithes ruber)目标强度测量研究[D]. 大连: 大连海洋大学, 2017. LI B. Target strength measurement of Sillago sihama and Otolithes ruber based on Kirchoff ray-mode approximation[D]. Dalian: Dalian Ocean University, 2017. |
| [10] |
于海圆, 赵宪勇. 鳀鱼(Engraulis japonicus)目标强度的模型法研究[J]. 应用声学, 2007, 26(5): 267-276. YU H Y, ZHAO X Y. Modeling study on the target strength of anchovy (Engraulis japonicus)[J]. Applied Acoustics, 2007, 26(5): 267-276. DOI:10.3969/j.issn.1000-310X.2007.05.003 |
| [11] |
蔡志宇. 长江7种鱼类声学目标强度研究[D]. 武汉: 华中农业大学, 2019. CAI Z Y. Acoustic target strength of seven fish speciesin the Yangtze River[D]. Wuhan: Huazhong Agricultural University, 2019. |
| [12] |
尚悦. 鱼种回波信号特征提取及分类方法研究[D]. 杭州: 浙江大学, 2019. SHANG Y. Study on feature extraction and classification methods of fish species echoes[D]. Hangzhou: Zhejiang University, 2019. |
| [13] |
杜伟东. 多波束探鱼声纳关键技术研究[D]. 哈尔滨: 哈尔滨工程大学, 2015. DU W D. Research on key techniques of multibeam fish-finding sonar[D]. Harbin: Harbin Engineering University, 2015. |
| [14] |
SWADA K, TAKAO Y, MIYANOHANA Y, et al. Introduction of the precise TS measurement for fisheries acoustics[J]. Turkish Journal of Veterinary and Animal Science, 2002, 26(2): 209-214. |
| [15] |
JECH J M, HORNE J K, CHU D Z, et al. Comparisons among ten models of acoustic backscattering used in aquatic ecosystem research[J]. The Journal of the Acoustical Society of America, 2015, 138(6): 3742-3764. DOI:10.1121/1.4937607 |
| [16] |
ANDERSON V C. Sound scattering from a fluid sphere[J]. The Journal of the Acoustical Society of America, 1950, 22(4): 426-431. DOI:10.1121/1.1906621 |
| [17] |
STRATTON J A, MORSE P M, CHU L J, et al. Spheroidal wave functions[J]. Physics Today, 1956, 9(6): 30-31. DOI:10.1063/1.3060000 |
| [18] |
STANTON T K. Sound scattering by cylinders of finite length. Ⅰ. Fluid cylinders[J]. TheJournal of the Acoustical Society of America, 1988, 83(1): 55-63. DOI:10.1121/1.396184 |
| [19] |
STANTON T K. Sound scattering by cylinders of finite length. Ⅲ. Deformed cylinders[J]. The Journal of the Acoustical Society of America, 1989, 86(2): 691-705. DOI:10.1121/1.398193 |
| [20] |
CHEN L H, SCHWEIKERT D G. Sound radiation from an arbitrary body[J]. The Journal of the Acoustical Society of America, 1963, 35(10): 1626-1632. DOI:10.1121/1.1918770 |
| [21] |
PIERCE A D, SMITHP W. Acoustics: an introduction to its physical principles and applications[J]. Physics Today, 1981, 34(12): 56-57. |
| [22] |
CHAI Y B, LI W, LI T Y, et al. Analysis of underwater acoustic scattering problems using stable node-based smoothed finite element method[J]. Engineering Analysis with Boundary Elements, 2016, 72: 27-41. DOI:10.1016/j.enganabound.2016.08.005 |
| [23] |
REEDER D B, STANTON T K. Acoustic scattering by axisym-metric finite-length bodies: An extension of a two-dimensional conformal mapping method[J]. The Journal of the Acoustical Society of America, 2004, 116(2): 729-746. DOI:10.1121/1.1648681 |
| [24] |
FOOTE K G. Rather‐high‐frequency sound scattering by swimbladderedfish[J]. The Journal of the Acoustical Society of America, 1985, 78(2): 688-700. DOI:10.1121/1.392438 |
| [25] |
STANTON T K. Sound scattering by rough elongated elastic objects. Ⅰ: means of scattered field[J]. The Journal of the Acoustical Society of America, 1992, 92(3): 1641-1664. DOI:10.1121/1.403905 |
| [26] |
CHU D Z, FOOTE K G, STANTON T K. Further analysis of target strength measurements of Antarctic krill at 38 and 120 kHz: Comparison with deformed cylinder model and inference of orientation distribution[J]. The Journal of the Acoustical Society of America, 1993, 93(5): 2985-2988. DOI:10.1121/1.405818 |
| [27] |
GARCIA N. Normalized distorted-wave Born approximation for soft potentials in atom-surface scattering[J]. Physical Review B, 1982, 25(8): 4994-4996. DOI:10.1103/PhysRevB.25.4994 |
| [28] |
SIMMONDS J, MACLENNAN D N. Fisheries acoustics: theory and practice[M]. 2nd ed. Oxford: Blackwell Science, 2005.
|
| [29] |
LOVE R H. A comparison of volume scattering strength data with model calculations based on quasisynoptically collected fishery data[J]. The Journal of the Acoustical Society of America, 1993, 94(4): 2255-2268. DOI:10.1121/1.407497 |
| [30] |
FURUSAWA M. Prolate spheroidal models for predicting general trends of fish target strength[J]. Journal of the Acoustical Society of Japan, 1988, 9(1): 13-24. |
| [31] |
尚晓明. 大黄鱼、小黄鱼和银鲳声学目标强度的研究[D]. 舟山: 浙江海洋学院, 2015. SHANG X M. The research on acoustical target strength of yellow croaker, Pseudosciaena polyactis and pomfret[D]. Zhoushan: Zhejiang Ocean University, 2015. |
| [32] |
MCCLATCHIE S, YE Z. Target strength of an oily deep-water fish, orange roughy (Hoplostethus atlanticus) Ⅱ. Modeling[J]. The Journal of the Acoustical Society of America, 2000, 107(3): 1280-1285. DOI:10.1121/1.428416 |
| [33] |
REEDER D B, JECH J M, STANTON T K. Broadband acoustic backscatter and high-resolution morphology of fish: measurement and modeling[J]. The Journal of the Acoustical Society of America, 2004, 116(2): 747-761. DOI:10.1121/1.1648318 |
| [34] |
李佩杰. 尾明角灯鱼目标强度的模型法研究[D]. 大连: 大连海洋大学, 2016. LI P J. Modeling study on the target strength of Ceratoscopelus warmingii[D]. Dalian: Dalian Ocean University, 2016. |
| [35] |
DIPERNA D T, STANTONT K. Sound scattering by cylinders of noncircular cross section: a conformal mapping approach[J]. The Journal of the Acoustical Society of America, 1994, 96(5): 3064-3079. DOI:10.1121/1.411243 |
| [36] |
孙扬, 汤勇, 邢彬彬, 等. 基于基尔霍夫射线模型法的高白鲑目标强度研究[J]. 大连海洋大学学报, 2021, 36(2): 310-316. SUN Y, TANG Y, XING B B, et al. Target strength of northern whitefish Coregonus peled by using Kirchhoff ray mode methods[J]. Journal of Dalian Ocean University, 2021, 36(2): 310-316. DOI:10.16535/j.cnki.dlhyxb.2020-082 |
| [37] |
FOOTE K G, FRANCIS D T I. Comparing Kirchhoff- approximation and boundary-element models for computing gadoid target strengths[J]. The Journal of the Acoustical Society of America, 2002, 111(4): 1644-1654. DOI:10.1121/1.1458939 |
| [38] |
DEMER D A, CONTI S G. Reconciling theoretical versus empirical target strengths of krill: effects of phase variability on the distorted-wave Born approximation[J]. ICES Journal of Marine Science, 2003, 60(2): 429-434. DOI:10.1016/S1054-3139(03)00002-X |
| [39] |
FEUILLADE C, NERO R W, LOVE R H. A low-frequency acoustic scattering model for small schools of fish[J]. The Journal of the Acoustical Society of America, 1996, 99(1): 196-208. DOI:10.1121/1.414503 |
| [40] |
NERO R W. Model estimates of acoustic scattering from schools of large yellowfin tuna[EB/OL]. Naval Research Laboratory, Stennis Space Center, Mississippi, USA, 1996, Report NRL/MR/774-95-7708. https://www.zhangqiaokeyan.com/ntis-science-report_ad_thesis/02071970068.html
|
| [41] |
WEBER T C, LUTCAVAGE M E, SCHROTH-MILLER M L. Near resonance acoustic scattering from organized schools of juvenile Atlantic bluefin tuna (Thunnus thynnus)[J]. TheJournal of the Acoustical Society of America, 2013, 133(6): 3802-3812. DOI:10.1121/1.4802646 |
| [42] |
HAHN T R. Low frequency sound scattering from spherical assemblages of bubbles using effective medium theory[J]. The Journal of the Acoustical Society of America, 2007, 122(6): 3252-3267. DOI:10.1121/1.2793610 |
| [43] |
NERO R W, FEUILLADE C, THOMPSON C H, et al. Near-resonance scattering from arrays of artificial fish swimbladders[J]. TheJournal of the Acoustical Society of America, 2007, 121(1): 132-143. DOI:10.1121/1.2382277 |
| [44] |
HORNE J K, JECH J M. Multi-frequency estimates of fish abundance: constraints of rather high frequencies[J]. ICES Journal of Marine Science, 1999, 56(2): 184-199. DOI:10.1006/jmsc.1998.0432 |
| [45] |
BOSWELL K M, ROTH B M, COWANJR J H. Simulating the effects of side-aspect fish orientation on acoustic biomass estimates[J]. ICESJournal of Marine Science, 2009, 66(6): 1398-1403. |
| [46] |
HOLMIN A J, HANDEGARD N O, KORNELIUSSEN R, et al. Simulations of multibeam sonar echoes from schooling individual fish[J]. The Journal of the Acoustical Society of America, 2011, 129(4): 2632-2642. |
| [47] |
FURUSAWA M, AMAKASU K. Exact simulation of fish school echoes and its applications[C]//OCEANS 2008 - MTS/IEEE Kobe Techno-Ocean. Kobe: IEEE, 2008.
|
| [48] |
MALFANTE M, MURA M D, MARS J I, et al. Automatic fish sounds classification[J]. The Journal of the Acoustical Society of America, 2016, 139(4): 2115-2116. |
| [49] |
ANDERSON C I H, HORNE J K, BOYLE J. Classifying multi-frequency fisheries acoustic data using a robust probabilistic classification technique[J]. TheJournal of the Acoustical Society of America, 2007, 121(6): EL230-EL237. |
| [50] |
KANG M, FURUSAWA M, MIYASHITAK. Effective and accurate use of difference in mean volume backscattering strength to identify fish and plankton[J]. ICES Journal of Marine Science, 2002, 59(4): 794-804. DOI:10.1006/jmsc.2002.1229 |
| [51] |
KORNELIUSSEN R J, DINERN, ONAE, et al. Proposals for the collection of multifrequency acoustic data[J]. ICES Journal of Marine Science, 2008, 65(6): 982-994. DOI:10.1093/icesjms/fsn052 |
| [52] |
SUNARDI S, DINJ, YUDHANAA, et al. Target strength for fish identification using echo sounder[J]. Applied Physics Research, 2009, 1(2): 92-101. |
| [53] |
BO L, NIELSEN J R. A method for the possible species discrimination of juvenile gadoids by broad-bandwidth backscattering spectra vs. angle of incidence[J]. ICES Journal of Marine Science, 2008, 65(4): 581-593. DOI:10.1093/icesjms/fsn031 |
| [54] |
JECH J M, HORNE J K. Three-dimensional visualization of fish morphometry and acoustic backscatter[J]. Acoustics Research Letters Online, 2002, 3(1): 35-40. DOI:10.1121/1.1430676 |
| [55] |
BRUNDAGE H, JUNG J B. Experiments with broadband sonar for the detection and identification of endangered shortnosesturgeon[J]. Marine Technology Society Journal, 2009, 43(3): 78-82. DOI:10.4031/MTSJ.43.3.8 |
| [56] |
ROGERS E O, FLEISCHER G W, SIMPSON P K, et al. Broadband fish identification of Laurentian Great Lakes fishes[C]//2004 IEEE International Geoscience and Remote Sensing Symposium. Anchorage: IEEE, 2004.
|
| [57] |
JUNG J B, JACOBS J H, DOWDING G A, et al. Initial species discrimination experiments with riverine salmonids[C]//Proceedings of the International Joint Conference on Neural Networks. Portland: IEEE, 2003.
|
| [58] |
CONTI S G, DEMER D A. Wide-bandwidth acoustical characterization of anchovy and sardine from reverberation measurements in an echoic tank[J]. ICES Journal of Marine Science, 2003, 60(3): 617-624. DOI:10.1016/S1054-3139(03)00056-0 |
| [59] |
ROBERTS P L D. Multi-view, broadband, acoustic classification of marine animals[D]. San Diego: University of California, 2009.
|
| [60] |
KULINCHENKO A B, SIMPSON P K, DENNY G F. Tethered fish data collection and species classification: Prince William Sound bottomfish[C]//IGARSS 2004.2004 IEEE International Geoscience and Remote Sensing Symposium. Anchorage: IEEE, 2004.
|
| [61] |
BARR R, COOMBS R F. Target phase: an extra dimension for fish and plankton target identification[J]. The Journal of the Acoustical Society of America, 2005, 118(3): 1358-1371. DOI:10.1121/1.1979503 |
| [62] |
MUN J H, LEE D J, SHIN H I, et al. Fish length dependence of target strength for black rockfish, goldeye rockfish at 70 kHz and 120 kHz[J]. Journal of the Korean Society of Fisheries and Ocean Technology, 2006, 42(1): 30-37. DOI:10.3796/KSFT.2006.42.1.030 |
2. Key Laboratory of Sustainable Exploitation of Oceanic Fisheries Resources, Ministry of Education, Shanghai 201306, China;
3. National Engineering Research Center for Oceanic Fisheries, Shanghai 201306, China;
4. Key Laboratory of Ocean Fisheries Exploitation, Ministry of Agriculture and Rural Affairs, Shanghai 201306, China
 2023,
Vol. 32
2023,
Vol. 32


