2. 国家远洋渔业工程技术研究中心, 上海 201306;
3. 大洋渔业资源可持续开发教育部重点实验室 上海 201306;
4. 浙江海洋大学 水产学院, 浙江 舟山 316000
鱼类经过长期的进化,已具备了低能耗、高效快速前进的能力。具有鱼类外形及运动能力的新型水下航行器因其在运动形态控制方面具备优势,对探索和开发海洋有重要意义,近年来受到了国内外学者[1-3]的广泛关注。
海洋中约有85%的鱼类是采用身体/尾鳍推进(body and/or caudal fin propulsion,BCF)推进模式[4],该模式具有快速与高效的优势。早期对于鱼类游动的研究工作主要是通过理论分析与实验测量方法开展。LIGHTHILL[5]根据鱼体体型特点,提出了细长体理论,为BCF推进模式的数值研究奠定了重要基础。近年来计算流体力学(computational fluid dynamics,CFD)方法的迅速发展为研究这类涉及非定常流体力学、软体运动学和游泳控制等问题提供了一种新的工具[6]。在鱼类游动数值模拟的早期阶段,学者们主要关注推力产生机制和涡流的相互作用,SCHULTZ等[7]提出鱼尾往复摆动在尾迹中形成的反卡门涡街诱导出向后的纵向射流会对鱼体产生推力,这一论断在WOLFGANG等[8]的实验中得到了证实。然而鱼类游动时尾流场中涡的形态与分布不是简单的反卡门涡街,而是需要对各种运动学模型下的尾流模式进行研究,以揭示更深层次的机制[9]。此外,尾鳍对鱼类游泳能力至关重要,相关学者已经广泛研究了尾鳍形状对推进性能的影响[10-12]。随着仿生技术的日益发展,部分学者开始对鱼体体型、行为特性开展相关研究[13-15],以期更为深入地探究鱼类的游动机制。
前人对于鱼类游泳行为数值模拟往往侧重于从流体力学角度对运动模型及推进原理开展研究,并未结合鱼类自身的生物学特性与行为特性进行深入分析与探讨。为此,研究通过数值模拟与实验研究相结合的方法,在建立有效的鱼体游动数值模型基础上,结合鱼类生物学特性系统地探究鱼体运动学参数(摆动频率、摆动幅度和体波波长)及体型对鱼类游泳能力的影响规律,旨在为仿生型水下航行器的设计与制作提供参考。
1 材料与方法 1.1 数值方法 1.1.1 数值模型本研究采用无量纲计算,分别以鱼体长度L和来流速度U为特征长度和特征速度进行无量纲化。
流体运动控制方程采用二维不可压缩Navier-Stokes方程组:
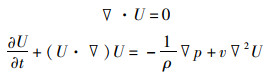 (1)
(1)
式中:▽·U为速度矢量U的散度;U为来流速度;ρ为流体密度;p为流体压力;v为流体的动力学黏性系数;t为时间。
VIDELER等[16]以实验观测为基础,利用傅立叶数列提出的鱼体波状摆动方程:
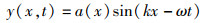 (2)
(2)
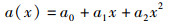 (3)
(3)
式中:y(x,t)为t时刻横向坐标位置;x为沿鱼体方向位置坐标;k为波数,k=2π/λ,其中λ为体波波长;ω为鱼体摆动的角频率ω=2πf,f为尾拍频率;a(x)为波幅包络线函数[17],在研究的基本计算模型中,a0=0.02、a1=-0.08、a2=0.16,即鱼尾摆幅最大值a(x)max=0.1,ymax=0.1 L,尾拍频率f=1 Hz。
设沿鱼体体干方向为X方向,垂直体干方向为Y方向,对模型参数及相关物理量进行无量纲化处理。鱼体X方向、Y方向的水动力系数如下:
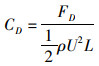 (4)
(4)
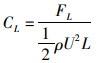 (5)
(5)
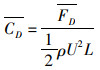 (6)
(6)
式中:ρ为流体密度;L为鱼体特征长度;U为来流速度;CD为X方向作用力系数;CL为Y方向作用力系数;CD为平均阻力系数;FD、FL、FD分别为X、Y方向的作用力及X方向的作用力的平均值。
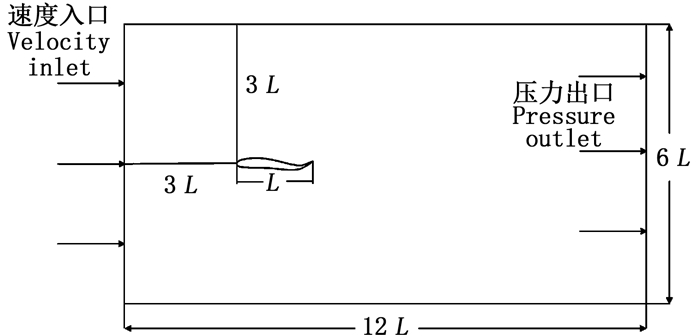
1.1.2 数值模型参数设置多数针对鱼类游动的数值模拟结果显示,采用美国国家航空咨询委员会(national advisory committee for aeronautics,NACA)翼型作为鱼体的简化模型可以较为有效地模拟出鱼体外形及水动力特性[13-15],因此基于NACA翼型建立鱼体在均匀来流中运动的二维数值模型,如图 1所示。为避免流场壁面边界及流出边界对鱼体水动力性能计算分析的影响,同时给鱼体的游动及其尾涡的发展留足空间[18],计算域尺寸设定为6 L×12 L,入口条件设置为速度入口,出口为压力出口,计算域顶部和底部设置为无滑移壁面条件。鱼体头部距流场入口距离为3 L。
|
图 1 鱼体在均匀来流中运动的水动力特性流场示意图 Fig. 1 Sketch for the fluid domain of fish-like swimming |
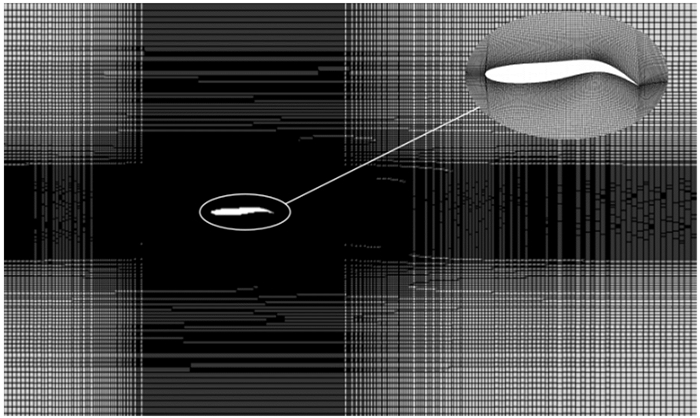
对整体流场用分块方式生成结构网格,主流场区网格尺寸为0.02 L。在距离鱼身0.5 L范围内,设置增长率为1.03实现对鱼身周围的网格加密,加密后最小网格尺寸为0.003 L。同时为得到更为细致准确的鱼体尾流场分布,将鱼体四周水平与垂直方向的流场网格也进行加密。为保证鱼体运动过程中动网格的质量,采用弹簧光顺法和局部重构法对网格质量进行控制,对变形较大的网格进行扩散光顺法处理。基于公式(2)和公式(3),编写用户自定义函数(user-defined functions,UDF)对鱼体运动进行控制,从而实现鱼体做波状摆动过程中相应网格的动态变化,流场全局网格及形变后的网格如图 2所示。计算采用SST k-ω湍流模型,压力速度耦合方式为SIMPLE法,动量、湍流动能和湍流耗散率均采用二阶迎风格式。
|
图 2 流场全局网格及鱼体形变后的局部网格 Fig. 2 Global grid of the flow field and local mesh after the fish body is deformed |
为深入探索鱼类游泳机理,并在此基础上系统研究来流速度、尾拍频率、摆动幅值、体波波长和鱼体体型对鱼类游泳能力的影响,在上述计算模型的基础上,设置为以下几种计算工况:
(1) 不同鱼种的游泳速度在前人的研究中已有初步结论[19],基于上述数值模型,设置来流速度U分别为0.5、1.0和5.0 L/s,以此代表几种典型鱼种的游泳速度,进而开展规律性的研究;
(2) 为探讨尾拍频率对鱼类游泳能力的影响,据真实鱼类的游动情况[8],将尾拍频率分别设置为1、2、3、4和5 Hz,计算其在不同的游泳速度、相同摆动幅值[a(x)max=0.1)]及相同体波波长(λ=L)下的游动情况;
(3) 为分析尾鳍摆动幅度对鱼类游泳能力的影响,将a(x)max依次设置为0.050、0.075、0.100、0.125、0.150,此时得到不同尾鳍摆动幅值的拟合公式如公式(6)~(10)所示,计算其在固定尾拍频率(f=1 Hz)、固定来流速度(U =0.5 L/s)、固定体波波长(λ=L)下的游动情况。
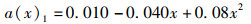 (6)
(6)
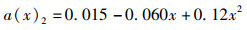 (7)
(7)
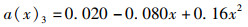 (8)
(8)
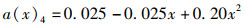 (9)
(9)
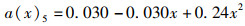 (10)
(10)
需要说明的是,在采用本研究的数值模型改变鱼体摆动幅值时,鱼体体长会随之发生微小的变化,但这种微小变化对鱼体摆动的水动力性能计算结果影响较小[20-21],故计算时忽略数值模型体长的变化。
(4) 体波波长的改变将在一定程度上影响鱼类的游泳方式,为探讨体波波长对鱼类游泳能力的影响,将鱼体体波波长分别设置为0.50 L、0.75 L及1.00 L,计算其在固定来流速度(U=0.5 L/s)、固定尾拍频率(f=1 Hz)及固定摆动幅度[a(x)max=0.1)]下的游动情况;
(5) 为研究鱼体体型对游泳能力的影响,据真实鱼类的厚度系数[22],基于NACA翼型模型将鱼体厚度系数(D/L)分别设为6%、12%、18%、27%、31%、35%,计算其在固定来流速度(U=0.5 L/s)、固定尾拍频率(f=1 Hz)、固定摆动幅度[a(x)max=0.1)]及固定体波波长(λ=L)下的游动情况。
1.2 实验方法为验证本研究计算结果的有效性,选取尾鳍摆动推进类型的生物鱼类(鲫鱼)为研究对象,进行实验研究。
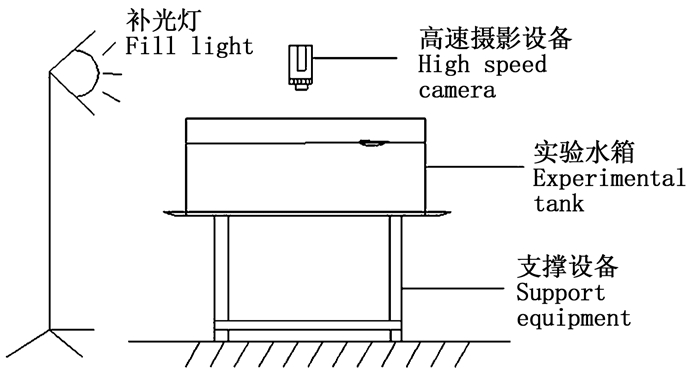
在市场上选择5条活性好,体长(不含尾鳍)、体质量相当的鲫鱼幼鱼作为实验对象,在实验前将样本鱼放在水中静养48 h来适应水中环境。实验装置如图 3所示,其中实验水箱为有机玻璃材质,长1.2 m,宽0.4 m,在水箱左侧放置补光灯来增大光源面积和光的强度。实验前水箱中的自由液面处于静止,且水箱处于室压室温状态,实验中将样本鱼放置于流场中。为了更好地观察尾涡情况,实验采用非牛顿流体,样本鱼在距离自由液面较近的区域游动,高速摄影设备固定在水箱上方,以每秒300帧的速度对样本鱼进行游动过程的拍摄。
|
图 3 实验装置示意图 Fig. 3 Sketch of experimental device |
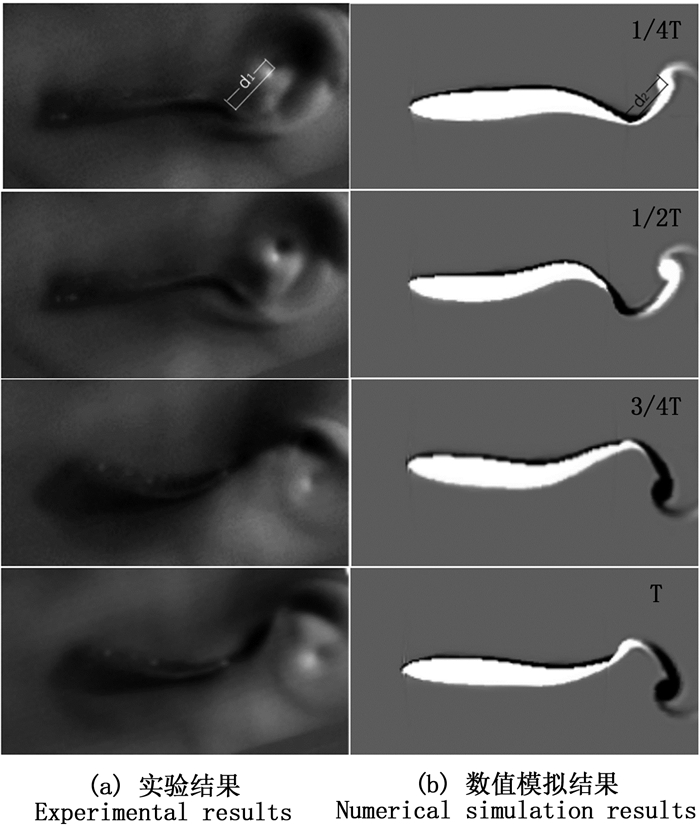
基于1.2节的实验方法,在若干次重复性实验的结果数据中选取一组较为稳定的一个摆动周期内的尾流场分布图作为验证结果,同时基于1.1节中的数值模型对该组实验进行1∶1尺度数值模拟,实验研究和数值研究所得结果的对比如图 4所示。
|
T.鱼游动时的一个完整摆动周期;d1.实验结果中鱼体后方尾涡中心距尾尖的距离;d2.数值模拟结果中鱼体后方尾涡中心距尾尖的距离。 T.A complete cycle of oscillation in fish swimming; d1. distance between the center of the rear vortex and the tip of the tail in the experiment results; d2. distance between the center of the rear vortex and the tip of the tail in the numerical simulation results. 图 4 实验与数值模拟结果对比 Fig. 4 Comparison of experimental and numerical simulation results |
图 4给出了生物鱼类游动实验和鱼类游动数值模拟实验在1个完整摆动周期T内4个特征时刻的鱼体形态,图中d1为实验结果中鱼体后方尾涡中心距尾尖的距离,d2为数值模拟结果中鱼体后方尾涡中心距尾尖的距离。从图中鱼体游动的基本形态以及尾涡位置的对比可以看出,研究建立的数值模型可以较为准确地还原BCF运动模式的鱼类在一个摆动周期内的运动及流场分布情况。在鱼体摆动过程中,鱼尾末端形成尾尖涡,且该涡会随尾尖的摆动而不断产生并向后脱落,随即形成推动鱼体向前游动的反卡门涡街。从尾尖涡的产生与脱落时刻及分布位置来看,数值模拟结果均与生物鱼类的实际游动结果呈现出较好的一致性。
在上图基础上,通过制图软件测得实验结果中鱼体后方尾涡中心距尾尖的距离d1与数值模拟结果中鱼体后方尾涡中心距尾尖的距离d2,并将两者进行对比如表 1所示,相对误差不超过7.5%,数值模型的有效性得到进一步验证。

|
表 1 鱼体后方尾涡中心距尾尖的距离对比 Tab.1 Comparison between experimental results and numerical simulation results |
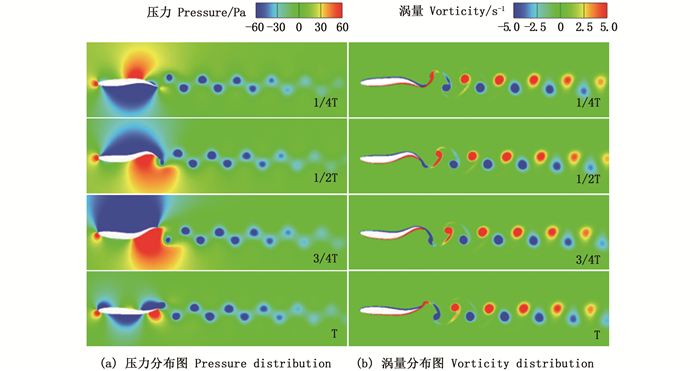
为了更清楚地观察鱼体摆动过程中的流场分布情况,图 5进一步给出了一个摆动周期内1/4 T、1/2 T、3/4 T和T等4个特征时刻鱼体附近流场压力及涡量场分布的数值模拟结果。从图 8中可以观察到,在鱼体摆动过程中,由于绕流作用,鱼体头部始终为高压区,而鱼体上下表面交替出现正、负压力分布。1/4 T~1/2 T时刻,鱼尾部拱起,尾尖向下,尾鳍上方首先形成一个顺时针涡旋,即启动涡,随后这一顺时针涡随着尾尖继续向下摆动而逐渐脱落;在1/2 T时刻时,尾鳍摆动到向下的最大幅值处,鱼身后1/3处形成高压中心,此时尾鳍的下方产生一个逆时针的涡,当尾鳍摆动至3/4 T时刻时,达到上方最大摆幅处,此后随着尾鳍继续摆动,逆时针的涡逐渐脱落;在T时刻,随着一个新的摆动周期的开始,尾尖处会形成一个新的顺时针的漩涡。在鱼体周期性的往复摆动下,尾迹区形成一串交错排列、旋向相反的反卡门涡街,涡街间的流动速度始终向后最终形成向后的射流,使鱼体获得向前的推进力。
|
T.鱼游动时的一个完整摆动周期。 T. A complete cycle of oscillation in fish swimming. 图 5 不同时刻流场中的压力和涡量分布 Fig. 5 Snapshots of the pressure field and vorticity field at different time instants |
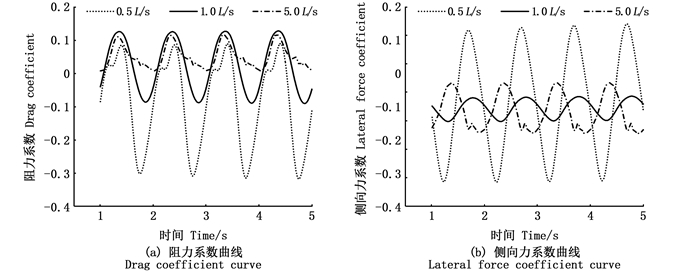
从图 6中可以看出,不同流速下(0.5 L/s,1.0 L/s,5.0 L/s)鱼体阻力系数与侧向力系数均呈现出明显的周期性,其中侧向力系数的时均值随游泳速度的变化不明显,基本在0左右,鱼体能够保持平稳游动,而阻力系数的时均值(CD)则随流速变化发生较为明显的改变。由于数值模型采用的是非自主游动模型,基于相对运动的原理设置流场来流速度,此时当鱼体阻力系数为非正数时即表示鱼体可以在该游动方式下获得相应的游速。当流速较小时,呈现负值,即表示鱼体可以在该游动方式下获得相应的游速;随着流速的增大,逐渐变为正值,即在当前摆动频率与摆动幅度下,鱼体无法在流场中获得足够的推进力。
|
图 6 不同来流速度下鱼体阻力系数与侧向力系数 Fig. 6 Drag coefficient and lateral force coefficient of fish at different velocity |
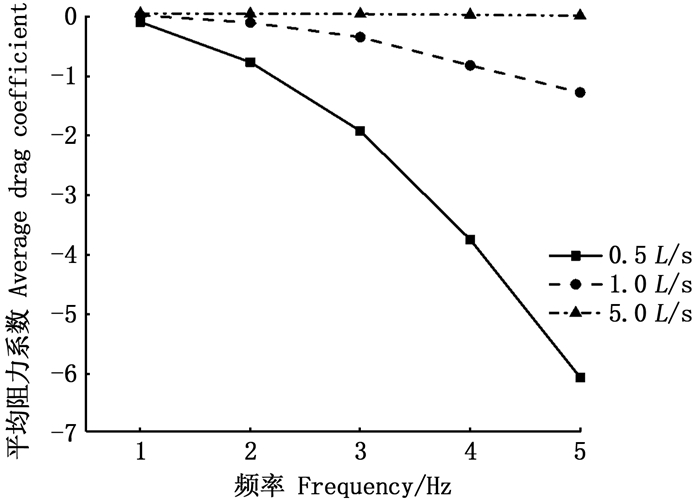
早期的鱼类行为研究学者通过大量的实验发现[23-24],鱼类的游泳能力与尾鳍的摆动频率密切相关。在上述计算分析的基础上,进一步给出了不同来流速度下CD随尾拍频率的变化情况,如图 7所示。从图 7中可以看出,当来流速度为0.5 L/s时,CD均为负值(即鱼尾摆动产生推进力),且绝对值随尾拍频率的增加显著增大,说明在1~5 Hz的摆频区间,鱼体均可以0.5 L/s的速度向前游动;来流速度为1.0 L/s时,CD在尾拍频率为2 Hz附近由正变负,此后绝对值随摆动频率的增加在一定程度上增大,即鱼体想要以1.0 L/s游动,需要将摆频增加至大约2 Hz才能向前游动;随着来流速度的增大,CD随尾拍频率的增加基本维持在0附近不变,此时鱼尾的摆动难以产生足够的推进力来抵抗流体阻力。
|
图 7 不同游动速度下阻力系数时均值随尾拍频率的变化 Fig. 7 Variation of drag coefficient with tail beat frequency at different velocity |
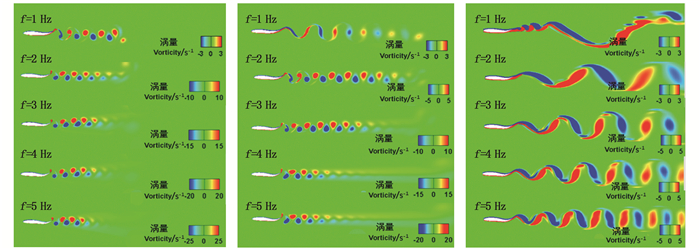
为深入探究尾拍频率对其游泳能力的影响机理,图 8进一步给出了不同来流速度下不同尾拍频率的鱼体附近流场涡量分布图。从图 8中可以看到在不同的来流速度下鱼体尾部在摆动时均会在尾流区形成反卡门涡街,随游动速度增加,尾流区的流动状态逐渐趋向湍流,因此鱼尾在摆动时身后涡的尺度也随之逐渐增大,但涡量值却随之逐渐减小,从而解释了图 7中CD由负变正的规律。在相同流速下时,随尾拍频率的增加,鱼体尾流区的涡街分布愈发密集,同时涡量值也随之逐渐增大,由此可知,鱼尾做高频摆动时,其产生的推进力要比低频摆动时更大,因此游泳速度也会更快,而这一规律在低流速的况下表现更为明显。
|
图 8 不同流速下不同尾拍频率鱼体附近流场涡量分布 Fig. 8 Vorticity distribution of the flow field near the fish body at different tail swing frequencies |
鲹科鱼类由于身体刚度较大,具有明显幅值的波动主要集中在身体后1/2部分,因此推进力主要由鱼尾摆动产生。在海洋中还有一类硬骨鱼类,其游泳方式在鲹科模式的基础上发展成了尾鳍做大幅摆动的游泳模式,即鲔科模式[24],这种模式通过尾鳍的运动可以产生近90%的推进力,是运动效率最高的一种尾鳍推进方式,代表性鱼类如金枪鱼、鲨鱼等。由此可见,尾鳍摆动幅度是影响鱼类游泳能力的一个重要因素。
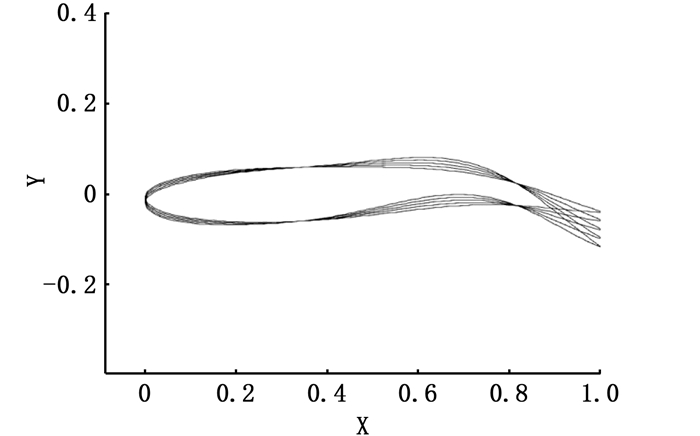
基于1.1.3节中公式(6)~(10)得到不同摆动幅值下的鱼体形态如图 9所示,通过自主编写并调用相应的UDF程序,计算分析鱼尾摆动幅度对游泳能力的影响。
|
图 9 不同摆幅的鱼体形态 Fig. 9 Fish body shape with different swing |
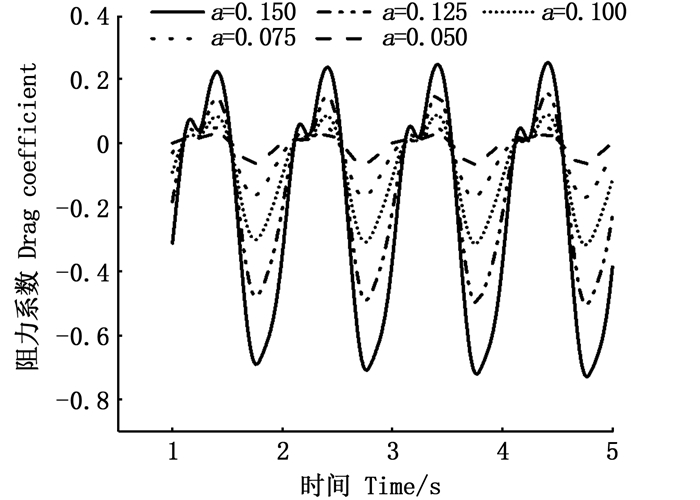
图 10给出了固定来流速度(0.5 L/s)下5 s内不同摆动幅值的鱼体阻力系数曲线。从图 10中看出,不同尾鳍摆动幅值下的鱼体阻力系数时均值均为负值,且阻力系数时均值的绝对值随摆动幅值的增加逐渐增大,即尾鳍摆动产生的推进力逐渐增大。由于计算工况中的鱼体尺寸及形态均相同,因此其获得的游动前进速度也随之增大。分析这一规律产生的原因是,随尾鳍摆动幅值的增加,鱼体尾部上下表面的正负压力值逐渐增大,这一正负压力差是鱼体推进力的主要成因,由此导致尾鳍摆动幅值的增加引起鱼类游动速度加快的现象。同时,随摆动幅值增加,尾流场中的涡尺度亦会随之增加,这也进一步带来了推进力的增大。
|
图 10 不同摆幅下的鱼体阻力系数曲线 Fig. 10 Fish body drag coefficient curves with different swing |
BCF推进模式从波动到振动的变化,又分为鳗鲡模式、亚鲹科模式、鲹科模式、鲔科模式和箱鲀模式[25]。而这几种不同的运动模式又因鱼体上的完整波形个数(或鱼体体波波长)不同,产生的推进效果也有显著差异,进而产生的游泳行为也不尽相同。
基于公式(2)改变鱼体体波波长后产生的鱼体形变如图 11所示。当λ=0.50 L时,整个身体的大部分都参与了大振幅的波动,此时的鱼体游动方式近似于鳗鲡式的运动模式;当λ=0.75 L时,推进运动主要发生在约身体后1/2的部分,此时的鱼体游动方式近似于典型的鲹科和亚鲹科鱼类BCF运动模式;当λ=1.00 L时,推进运动主要发生在约身体后1/3的部分,此时的鱼体游动方式近似于典型的鲔科鱼类BCF运动模式。

|
图 11 不同体波波长的鱼体计算模型 Fig. 11 Fish body calculation model for different body wave wavelengths |
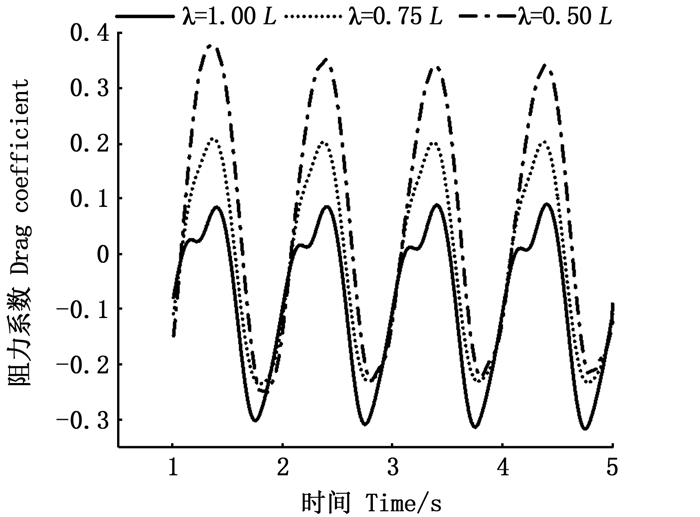
由图 12可以清楚地观察到,在相同的尾鳍摆动频率和幅值下,随着体波波长的减小,鱼体阻力系数在一个周期内的正波峰绝对值显著增加,而负波峰变化相对不明显,此时必然引起鱼体阻力系数的时均值随波长的减小出现由负值逐渐趋向于正值的变化趋势,意味着鱼体在尾鳍摆动时获得的推进力逐渐减小。当λ=0.75 L时,正负波峰的差值较小呈现负值且在0附近,而当体波波长减小至λ=0.50 L时,推进力转变为阻力,此时鱼体无法获得前进的动力,从另一个角度来说,意味着推进效率随鱼体波数的增加而呈降低趋势。结合图 11中不同体波波长对应的鱼类运动模式分析,鲹科和亚鲹科鱼类推进效率和游动速度都要较鳗鲡式的推进模式更高;而鲔科鱼类的推进效率和游动速度则要比鲹科鱼类更高,是3种BCF运动模式中效率最高的。
|
图 12 不同体波波长下的鱼体阻力系数曲线 Fig. 12 Fish body drag coefficient curves with different body wave wavelengths |
分析上述规律产生的原因,随着鱼体体波波长的增加(波数的减小),鱼体上下表面的压力差逐渐增大,同时鱼体后方的尾迹区涡的尺度也明显变大,因此会产生更高的推进力。当λ=0.50 L时,鱼体游泳方式类似于鳗鲡式运动,虽然身体大部分都参加了大幅波动,但是由于尾流区产生的涡尺度较小且不明显,因此推进效率并不高。而在λ=1.00 L时,由于体波波长被限制在身体的后1/3处,推力主要是由相对坚硬的尾鳍提供,侧向的水流流失和漩涡形成时的能量损失很少,推进效率大大提高。
2.2.5 鱼体体型对游泳行为的影响从流体力学角度分析,鱼体的体型与形状阻力(或压差阻力)大小密切相关,因此必然会对鱼类的游泳速度产生影响。鱼类在长期的进化中,体型发展成为适合其生活习性的形状,例如擅长高速游泳的鱼类往往具有纺锤型的体型,而游泳速度低的鱼类多半具有头大身体小的形态特征。研究根据真实鱼类的厚度系数,建立不同厚度系数的鱼体数值模型如图 13所示,在此基础上研究分析鱼体体型对其游泳行为的影响规律。

|
图 13 不同厚度系数的鱼体体型模型 Fig. 13 Fish body shape models with different thickness coefficients |
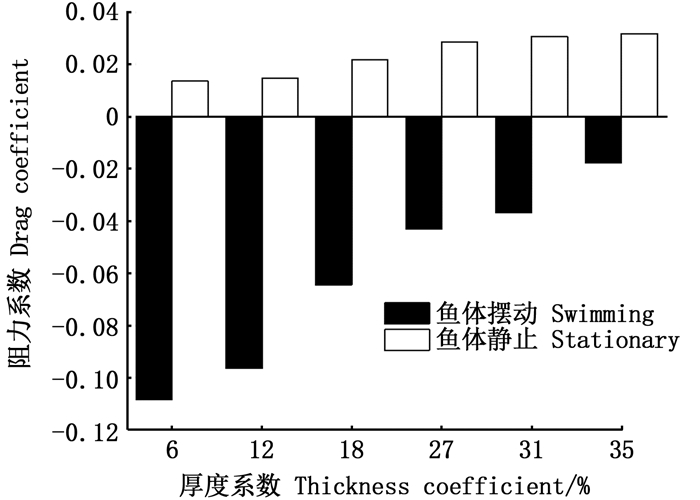
为了便于比较分析,图 14给出了鱼类游动与静止时随鱼体厚度系数的变化情况。从图 14中可以看到,静止时,鱼体绕流阻力随厚度系数的变化而逐渐增加,当鱼体厚度系数从27%增加至35%时,逐渐趋于稳定。在相同的摆动频率与幅值下,绝对值随鱼体厚度系数的增加而逐渐减小,即鱼体厚度较小的鱼类可以获得更高的推进力,反之头大身体小的大厚度系数鱼类则无法获得较快的速度。
|
图 14 游动和静止时不同鱼体厚度系数的阻力系数 Fig. 14 Drag coefficients of different fish body thickness coefficients when swimming and stationary |
鱼类经过长期的进化,从生态习性到游泳行为都对其生活环境产生了很好的适应性。作为水中的运动高手,其在游动时的水动力特性及推进机理成为生物学家及仿生学研究者的关注对象。在前人的研究基础上,采用CFD方法对BCF推进模式游动的鱼类进行数值计算分析,探究鱼类尾鳍摆动的推进机理,并在此基础上,结合鱼类的行为特性与生物学特性,通过改变尾鳍摆动频率、摆动幅值、鱼体体波波长及鱼体体型等运动参数与结构参数,研究了鱼类获得突进速度的机理、不同游泳方式的推进效率以及鱼体体型与游泳效率的关系,得出的主要结论如下:
(1) 在鱼体周期性的往复摆动下,尾迹区形成一串交错排列、旋向相反的反卡门涡街。对于鱼类来说,其游动由两部分组成,一是鱼体在水动力作用下的被动运动和变形,二是由鱼本身肌肉控制的主动变形[26],鱼类通过摆动躯体或尾鳍所产的反卡门涡街即是形成其前进推力的主要原因。
(2) 在固定的摆动频率与摆动幅值下,CD呈负值,鱼体可以获得向前游动的推进力;CD为正值时,意味着鱼体无法在流场中获得足够的前进动力。进一步分析,当鱼类所处的环境发生改变时(例如流速),其在游动过程中所获得的推进力会随之发生明显变化,而为了适应不同的环境,鱼类需要对其游泳行为(姿态、动作等)做出适当的调整,在不断的调整的过程中,其身体形态也可能会发生适应性的进化。
(3) 鱼体可以通过尾拍频率的增加获得更大的推进力从而提高游泳速度。当鱼类受惊逃逸或者捕食时,往往可以通过增加尾拍频率在短时间内获得更大的推力来完成加速,但由于摆动频率受限,这种方法不适合长时间的持续快速游动。
(4) 随着尾鳍摆动幅值的增加,鱼体尾部上下表面的正负压力值逐渐增大,同时尾流场中涡的尺度亦有较为明显的增加,在二者的共同作用下尾鳍摆动时产生的推进力随摆动幅值的增加显著增大。当鱼类在受惊逃逸或捕食等需要爆发高速运动的情况下,也会突然增加尾鳍的摆动幅值来获得更大推力。
(5) 鱼类尾鳍摆动时CD随波长的减小出现由负值逐渐趋向于正值的变化趋势,意味着鱼体在尾鳍摆动时获得的推进力逐渐减小,推进效率随鱼体上波数的增加而降低。结合分析可知,鲹科和亚鲹科鱼类的推进效率和游动速度要较鳗鲡式的推进模式更高,而鲔科鱼类的推进效率和游动速度则要较鲹科鱼类更高。
(6) 体型的变化对鱼类游泳能力的影响主要产生在压差阻力方面,在相同的尾摆频率与幅值下,头大身体小的鱼类推进效率及游泳速度较细长的流线型体型的鱼类低很多,这一结论在CHEN等[27]的研究中也得到了验证。这也从一定程度上解释了自然界中擅长高速游泳的鱼类往往具有细长的流线型体型,而游速较低或底栖鱼类则往往头大身小这一生物学现象。
| [1] |
WOLF Z, LAUDER G V. A soft robotic model to study the effects of stiffness on fish-like undulatory swimming[M]//PALEY D A, WERELEY D M. Bioinspired Sensing, Actuation, and Control in Underwater Soft Robotic Systems. Switzerland: Springer, 2021: 153-169.
|
| [2] |
SCARADOZZI D, PALMIERI G, COSTA D, et al. BCF swimming locomotion for autonomous underwater robots: a review and a novel solution to improve control and efficiency[J]. Ocean Engineering, 2017, 130: 437-453. DOI:10.1016/j.oceaneng.2016.11.055 |
| [3] |
钱卫国, 孔祥洪. 新型水下航行器——仿生机器鱼的设计与制作[M]. 北京: 科学出版社, 2018: 1-153. QIAN W G, KONG X H. Design and fabrication of a new type of underwater vehicle: biomimetic robotic fish Applied Fish Behavior[M]. Beijing: Science Press, 2018: 1-153. |
| [4] |
TRIANTAFYLLOU M S, TRIANTAFYLLOU G S. An efficient swimming machine[J]. Scientific American, 1995, 272(3): 64-70. DOI:10.1038/scientificamerican0395-64 |
| [5] |
LIGHTHILL M J. Note on the swimming of slender fish[J]. Journal of Fluid Mechanics, 1960, 9(2): 305-317. DOI:10.1017/S0022112060001110 |
| [6] |
YAN L, CHANG X H, TIAN R Y, et al. A Numerical simulation method for bionic fish self-propelled swimming under control based on deep reinforcement learning[J]. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 2020, 234(17): 3397-3415. DOI:10.1177/0954406220915216 |
| [7] |
SCHULTZ W, W W P. A Two-dimensional model of fish swimming[C] Mechanics and Physiology of Animal Swimming Meeting. Plymouth, U. K., 1991.
|
| [8] |
WOLFGANG M J, ANDERSON J M, GROSENBAUGH M A, et al. Near-body flow dynamics in swimming fish[J]. Journal of Experimental Biology, 1999, 202(17): 2303-2327. DOI:10.1242/jeb.202.17.2303 |
| [9] |
WEN L, WANG T M, WU G H, et al. Quantitative thrust efficiency of a self-propulsive robotic fish: experimental method and hydrodynamic investigation[J]. IEEE/ASME Transactions on Mechatronics, 2013, 18(3): 1027-1038. DOI:10.1109/TMECH.2012.2194719 |
| [10] |
GHOMMEM M, BOURANTAS G, WITTEK A, et al. Hydrodynamic modeling and performance analysis of bio-Inspired swimming[J]. Ocean Engineering, 2020, 197: 106897. DOI:10.1016/j.oceaneng.2019.106897 |
| [11] |
KRISHNADAS A, RAVICHANDRAN S, RAJAGOPAL P. Analysis of biomimetic caudal fin shapes for optimal propulsive efficiency[J]. Ocean Engineering, 2018, 153: 132-142. DOI:10.1016/j.oceaneng.2018.01.082 |
| [12] |
BORAZJANI I, DAGHOOGHI M. The fish tail motion forms an attached leading edge vortex[J]. Proceedings of the Royal Society B: Biological Sciences, 2013, 280(1756): 20122071. DOI:10.1098/rspb.2012.2071 |
| [13] |
WEI C, HU Q, LIU Y, et al. Performance evaluation and optimization for two-dimensional fish-like propulsion[J]. Ocean Engineering, 2021, 233: 109191. DOI:10.1016/j.oceaneng.2021.109191 |
| [14] |
CUI Z, GU X S, LI K K, et al. CFD studies of the effects of waveform on swimming performance of Carangiform Fish[J]. Applied Sciences, 2017, 7(2): 149. DOI:10.3390/app7020149 |
| [15] |
SUN X J, ZHANG J H, HUANG D G. Energy harvesting characteristics of an Inward-Type flow device undulating in a fish-Like motion[J]. European Journal of Mechanics - B/Fluids, 2020, 79: 419-427. DOI:10.1016/j.euromechflu.2019.10.008 |
| [16] |
VIDELER J J, HESS F. Fast continuous swimming of two pelagic predators, Saithe (Pollachius virens) and mackerel (Scomber scombrus): A kinematic analysis[J]. Journal of Experimental Biology, 1984, 109(1): 209-228. DOI:10.1242/jeb.109.1.209 |
| [17] |
BORAZJANI I, SOTIROPOULOS F. Numerical investigation of the hydrodynamics of Carangiform swimming in the transitional and inertial flow regimes[J]. The Journal of Experimental Biology, 2008, 211(Pt 10): 1541-1558. |
| [18] |
SUN P N, COLAGROSSI A, MARRONE S, et al. Multi-resolution Delta-plus-SPH with tensile instability control: towards high Reynolds number flows[J]. Computer Physics Communications, 2018, 224: 63-80. DOI:10.1016/j.cpc.2017.11.016 |
| [19] |
李寅凡. 鲫鱼(Carassius auratus Linnaeus)游泳行为的初步实验研究[D]. 上海: 上海海洋大学, 2011. LI Y F. Preliminary experimental study on swimming behavior of Crucian Carp[D]. Shanghai: Shanghai Ocean University, 2011. |
| [20] |
THEKKETHIL N, SHARMA A, Agrawal A. Self-propulsion of fishes-like undulating hydrofoil: a unified kinematics based unsteady hydrodynamics study[J]. Journal of Fluids and Structures, 2020, 93: 102875. DOI:10.1016/j.jfluidstructs.2020.102875 |
| [21] |
XIE O, SONG A G, YAO J, et al. Study on hydrodynamics of a flexible fishlike foil undulating in wall effect[J]. Engineering Applications of Computational Fluid Mechanics, 2020, 14(1): 593-606. DOI:10.1080/19942060.2020.1745891 |
| [22] |
VIDELER J J. Fish swimming[M]. London: Chapman & Hall, 1993.
|
| [23] |
周应祺. 鱼类最高游速的研究[J]. 水产学报, 1985(2): 105-120. ZHOU Y Q. Swimming behavior of fishes at high speed[J]. Journal of Fisheries of China, 1985(2): 105-120. |
| [24] |
BAINBRIDGE R. The speed of swimming of fish as related to size and to the frequency and amplitude of the tail beat[J]. Journal of Experimental Biology, 1958, 35(1): 109-133. DOI:10.1242/jeb.35.1.109 |
| [25] |
周应祺. 应用鱼类行为学[M]. 北京: 科学出版社, 2011. ZHOU Y Q. Applied fish behaviour[M]. Beijing: Science Press, 2011. |
| [26] |
王凯辉, 纪茹萱, 刘哲恒, 等. 鲫鱼在圆柱绕流尾迹中的卡门步态[J]. 生态学杂志, 2019, 38(12): 3771-3778. WANG K H, JI R X, LIU Z H, et al. Kármán gait of a Carassius auratus swimming in the wake of a circle cylinder[J]. Chinese Journal of Ecology, 2019, 38(12): 3771-3778. DOI:10.13292/j.1000-4890.201912.028 |
| [27] |
CHEN Z G, DOI Y. Numerical study on relaminarization in fish-like locomotion[J]. Journal of the Society of Naval Architects of Japan, 2002, 2002(191): 9-16. DOI:10.2534/jjasnaoe1968.2002.9 |
2. National Engineering Research Center for Oceanic Fisheries, Shanghai 201306, China;
3. Key Laboratory of Sustainable Exploitation, Ministry of Agriculture and Rural Affairs, Shanghai 201306, China;
4. School of Fishery, Zhejiang Ocean University, Zhoushan 316000, Zhejiang, China
 2022,
Vol. 31
2022,
Vol. 31


