海洋牧场是目前生态渔业发展的主要方式之一,其中投放人工鱼礁是海洋牧场建设中的一项重要技术手段[1]。作为一种人为放置于海底的构造物,人工鱼礁通过对水流的阻碍作用对礁体周围压力产生影响,形成新的流场分布,在礁体的上部形成局部上升流,在礁体的下部形成背涡流[2-3],促进水体垂直方向上的物质循环,将海底底层营养物带到表层,改善海洋生境,提高周围海域的初级生产力,实现渔业资源养护的目的。
随着声学技术在海洋牧场监测领域的应用,已有多项研究通过多波束、侧扫声呐等声学设备对不同人工鱼礁区进行调查评估,并发现各投放区内礁体均有不同程度的沉降现象[4-9]。当人工鱼礁发生沉降时,礁体周围流场效应会随沉降深度的增加产生一定变化,目前已有黄远东等[10]对多孔方型人工鱼礁周围流场进行了数值仿真研究,王佳浩等[11]在此基础上研究了布设间距对多孔方型人工鱼礁的流场影响,尚未涉及礁体沉降程度对多孔方型人工鱼礁流场效应影响的研究。
随着数值仿真技术的发展,国内外学者逐步证实CFD软件可以有效地进行流场效应分析[12-13]。为进一步研究礁体沉降程度对多孔方型人工鱼礁流场效应的影响,基于ANSYS 2020 R2平台,通过FLUENT流体仿真软件,模拟不同沉降程度下方型人工鱼礁周围流场效应,为礁体流场效应失效判别、礁体状态调整提供指导。
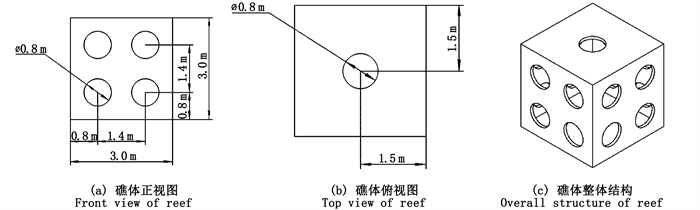
1 礁体结构与计算方法 1.1 礁体结构与计算区域本文采用礁体模型结构为边长3.0 m、壁厚0.1 m的空心多孔方型鱼礁,礁体的每个侧面上都开有4个直径为0.8 m的圆孔,同时顶盖中央开有一个直径为0.8 m的圆孔,底部闭合无开孔,见图 1。
|
图 1 人工鱼礁模型 Fig. 1 Artificial reef model |
郑延璇等[14]研究表明,在人工鱼礁数值仿真模拟中,对计算域长、宽、高的设定分别为礁体长度的9倍、礁体宽度的6倍和礁体高度的4倍,且当礁前、礁后距离分别为礁体长度3倍和5倍时,就能正确地反映人工鱼礁周围流场的情况。为了正确反映礁体周围流场效应兼顾计算成本,计算区域尺寸的长、宽、高分别定为45.00 m、30.00 m、18.00 m,即分别为礁体长度的15倍、10倍、6倍。礁体水平位置固定,以迎流面作为基准,礁前计算区域长度为18.00 m,礁后计算区域长度24.00 m。礁体两侧距离计算区域边界均为13.50 m,礁体底面与计算区域底面重合,整体布局如图 2所示。

|
图 2 计算区域 Fig. 2 Calculation area |
佟飞等[9]利用侧扫声呐技术对已建1年的人工鱼礁区进行现场勘测发现AR1型、AR2型鱼礁平均沉降率分别为19.20%、28.66%。赵刚等[7]通过侧扫声呐设备于2018年7月对海州湾海洋牧场示范区进行数据采集,发现于2017年6月投放的方型钢筋混凝土框架结构鱼礁平均沉降18%。本文礁体沉降深度h按照礁体高度的20%递增,分别为0、0.6、1.2、1.8、2.4 m,沉降程度分别占鱼礁整体的0%、20%、40%、60%、80%。
1.3 数学模型与控制算法水在礁体周围的绕流运动属于一种不可压缩的湍流运动,本研究中湍流模型选用带旋流修正的模型,该模型对圆柱射流的发散比率有着更精确的预测,同时它对于旋转流动、强逆压梯度的边界层流动、流动分离和二次流有很好的表现,近壁处理方式选用标准壁面函数(SWF)。
带旋流修正的湍动能k方程:
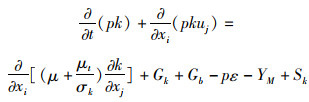 (1)
(1)
湍流耗散率ε:
 (2)
(2)
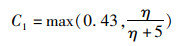 (3)
(3)
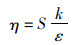 (4)
(4)
式中: ρ为流体密度;ui、uj为平均流速分量,i、j=1, 2, 3(i≠j)表示直角坐标系x, y, z三个方向;μ为动力黏度系数;C3ε=tanh|v/u|,v为流体平行于重力的速度分量,u为垂直于重力的速度分量;S为系数,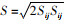
漩涡黏度μt:
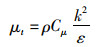 (5)
(5)
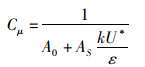 (6)
(6)
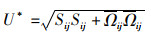 (7)
(7)
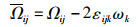 (8)
(8)
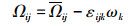 (9)
(9)
式中:Ω ij为柱坐标下带有角速度的ωk层流旋度AS= 
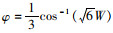

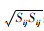
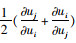
压力与速度耦合采用SIMPLEC,空间离散化梯度选择基于单元的格林高斯(Green-Gauss Cell Based),动量、湍流动能以及湍流耗散率均选用二阶迎风格式(Second order upwind),计算残差值选用10-6。
1.4 边界条件设置唐衍力等[3]研究表明,6种人工鱼礁(含方型)上升流面积和背涡流面积的大小与来流速度不相关,礁体的来流速度与上升流高度也不相关。黄远东等[15]研究发现,方型鱼礁上升流的最大速度与来流速度的比为定值,上升流的最大高度与礁体高度的比值同样几乎为定值。由于投放人工鱼礁的海域流速一般应小于1.0 m/s[16],为降低计算成本,本研究来流速度选为0.80 m/s定值。本研究计算区域入口选择速度入口,计算区域出口选择自由出口,计算区域底面及礁体各壁面选择无滑移边界条件,其他面选择对称边界条件。
1.5 网格划分方法及质量检测在以往的研究中,通常选择的网格划分方式为自适应的的四面体非结构化网格,此类方法在划分过程中可以较为快速的生成网格但是质量不高。本研究为了提高网格质量,将研究区域分为大量独立部分,实现六面体非结构化网格的建立。通过对礁体周围及孔洞位置进行网格几何尺寸调整,孔洞位置最大网格尺寸设为50 mm,礁体内部最大网格尺寸设为200 mm,其他区域最大网格尺寸设置为400 mm,最终整个计算区域网格数目在为200万~300万,网格节点数目略多于网格数量。整体网格划分效果、礁体周围局部网格情况分别如图 3、图 4所示。

|
图 3 整体网格划分 Fig. 3 Overall mesh rendering |

|
图 4 礁体周围网格 Fig. 4 Grid around reef |
以正交质量(Orthogonal quality)为检查标准,网格平均正交质量在0.995以上,最小值在0.249以上。计算收敛迭代次数为200~800次。
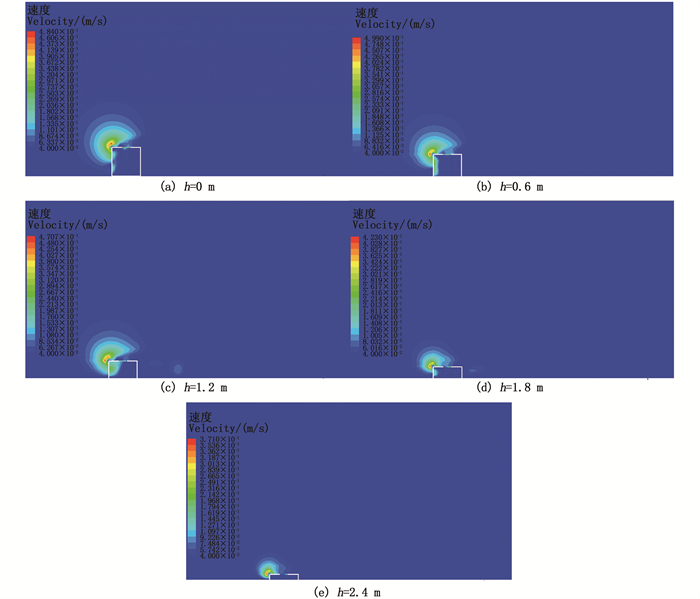
2 结果与分析 2.1 不同沉降程度对单体方型多孔人工鱼礁上升流的影响为分析不同沉降程度下多孔方型人工鱼礁的上升流情况,选取Z方向上速度分量与来流速度之比≥5%的水域为上升流研究区域[17]。通过CFD仿真,获得无沉降状态时单体方型多孔人工鱼礁在Y=0平面上的Z方向速度分量分布如图 5所示,负值表示z轴反方向。从图 5可以看出礁体周围的整体流场情况,在迎流面竖直方向靠近礁体上表面处有局部上升流,且上升流最大值位置处于迎流面与上表面交线附近,同时礁体内部存在明显涡流,背涡区与礁体背流面距离约为4 m。为较为准确的计算上升流高度,将速度分量取正值部分(速度大于0.04 m/s),并将速度分量大小划分为20份。5种不同沉降程度下的单体方型多孔人工鱼礁上升流云图如图 6所示。设无沉降状态为初始状态,通过仿真结果得出不同沉降程度下礁体的上升流大小、上升流高度与沉降深度、来流速度及初始状态之间关系见表 1。

|
图 5 无沉降状态时Y=0平面Z方向速度分量分布云图 Fig. 5 Cloud diagram of velocity component distribution in Z direction of Y=0 plane without settlement |
|
图 6 5种沉降深度下Y=0平面上的上升流分布 Fig. 6 Upwelling distribution on Y=0 plane at 5 settlement depths |
|
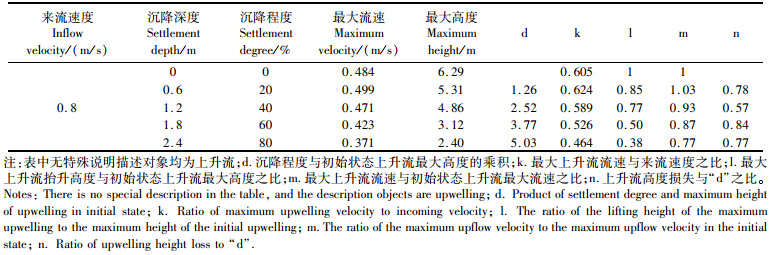
表 1 不同沉降程度对礁体上升流最大高度和上升流最大值影响 Tab.1 Effects of different subsidence degrees on maximum upwelling height and maximum upwelling size of reef |
当水流靠近鱼礁的迎流面时,由于礁体的阻碍作用,水流转向抬升后形成上升流。从图 6的仿真结果和表 1可以看出,在无沉降状态时,方型多孔鱼礁的上升流最大值约为0.48 m/s。在沉降程度为20%时,上升流流速最大值相较于无沉降状态时增加约0.015 m/s,之后随着沉降程度的逐渐增大,上升流速度最大值开始减小,从沉降程度为40%时开始上升流流速最大值降低速度明显加快,当沉降程度为80%时,上升流最大值为0.37 m/s,与来流速度比值约为0.46。从表 1可以算出,上升流最大流速随着沉降程度的每一次递增变化的差值分别0.015、-0.028、-0.048、-0.052 m/s,说明沉降对多孔方型人工鱼礁最大上升流流速在沉降40%以内影响较小,达到60%之后影响明显增大。
从表 1可以看出,方型多孔人工鱼礁最大上升流高度随着礁体沉降整体呈下降趋势,这是由于当水流撞击礁体迎流面时沿壁面垂直爬升的路径长度随沉降程度增加而减少。在无沉降状态时,上升流高度为6.29 m,上升流高度与鱼礁高度之比为2∶ 1,与王佳浩等[11]研究结果一致。随着沉降程度增加,最大上升流高度分别减少0.98、0.45、1.74、0.72 m,可以看出当沉降程度达到60%时,上升流最大高度减少最为明显。在沉降程度分别为20%、40%的情况下,礁体上升流最大抬升高度与初始状态比值分别为0.85和0.77,两者差值只有0.08,当沉降程度为60%该项值降低至0.5。在沉降程度40%时,礁体上升流最大高度损失与d的比值仅为0.57,说明此时沉降对方型多孔人工鱼礁上升流高度影响相较于其他沉降程度时较小。当沉降程度为80%时,礁体上升流最大高度为2.4 m,约为无沉降状态的40%。
从以上分析可知,对于单体方型多孔鱼礁来说,沉降程度在40%以内时,由于礁体阻流作用形成的上升流效应受沉降影响较小,甚至最大上升流流速在沉降20%时还略有增加。当礁体沉降程度达到60%时,礁体的上升流效应损失最为明显。
2.2 不同沉降程度对单体方型多孔人工鱼礁竖直方向涡流影响图 7是5种不同沉降程度下Y=0截面(过礁体中心)上的速度矢量分布图。从该图可以清楚地看出,当水流通过礁体孔隙进入礁体内部时,在沉降深度为0、0.6、1.2 m时鱼礁内均形成一个流速很小的顺时针涡旋,涡旋充斥整个礁体内部,涡旋中心水平方向大致位于礁体中心线上。从矢量线密集程度来看,在沉降深度为0.6 m时,礁体内腔涡量最大,之后随着沉降深度增加漩涡中心逐步靠近方型多孔鱼礁上侧开孔处,漩涡大小也随着礁体沉降逐步减少,当沉降深度为1.8 m时,礁体内部漩涡基本消失。

|
图 7 5种不同沉降程度下Y=0平面上的速度矢量分布 Fig. 7 Velocity vector distribution on Y=0 plane to five different settlement degrees |
从无沉降状态时方型鱼礁的速度矢量图可以看出,由于孔隙的透水性,在礁体的背流面处形成了一个与来流方向一致的水流速度很小的透水区域,同时由于流动分离,在距离背流面大约1.8 m处有一个较大范围的顺时针涡旋,该处即为背涡流区域,背涡流区域在Y轴方向长度大约为3倍礁体长度,漩涡中心高度约为1 m。在沉降深度为0.6 m时,透水区域与背涡流区域发生了明显的变化,透水区域范围扩大,背涡流中心水平位置沿来流方向移动约2 m,背涡流中心竖直高度及背涡流影响范围大小无明显变化。在沉降程度为1.2 m时,透水区域几乎消失,形成一个逆时针涡旋的趋势,同时在同一高度沿水流方向紧跟一个顺时针背涡流区域,顺时针背涡流影响范围减小。在礁体沉降深度为1.8和2.4 m状态时,礁体背涡流区域基本消失,沉降1.8 m时礁体背流面还有较为明显的一条狭长的透水区域,透水区最大高度约为1.6 m,透水区高度随距离背流面距离增大而逐步减少直至消失。当沉降深度为2.4 m时,礁体背流面仅剩范围较小的狭长透水区。
对比在不同沉降深度情况下的单体方型多孔人工鱼礁的内部及外部涡流情况可以发现,在沉降程度逐步达到40%左右时,由礁体结构产生的内部涡流及背涡流区域整体状态较好,鱼礁依旧发挥着稳定的流场效应,甚至在沉降20%左右的状态下背涡流区域变得更为复杂。在沉降程度大于40%时,礁体内部涡旋和外部背涡流开始减弱。在沉降程度达到60%时内部涡旋基本消失,背涡流区域和透水区域几乎融为一体,在礁体背流面已经没有明显的涡流。在沉降程度达到80%时,由方型多孔人工鱼礁形成的内部涡旋和背部背涡流区域已经消失不见,只存在流速较小的内部及背流区狭长区域。
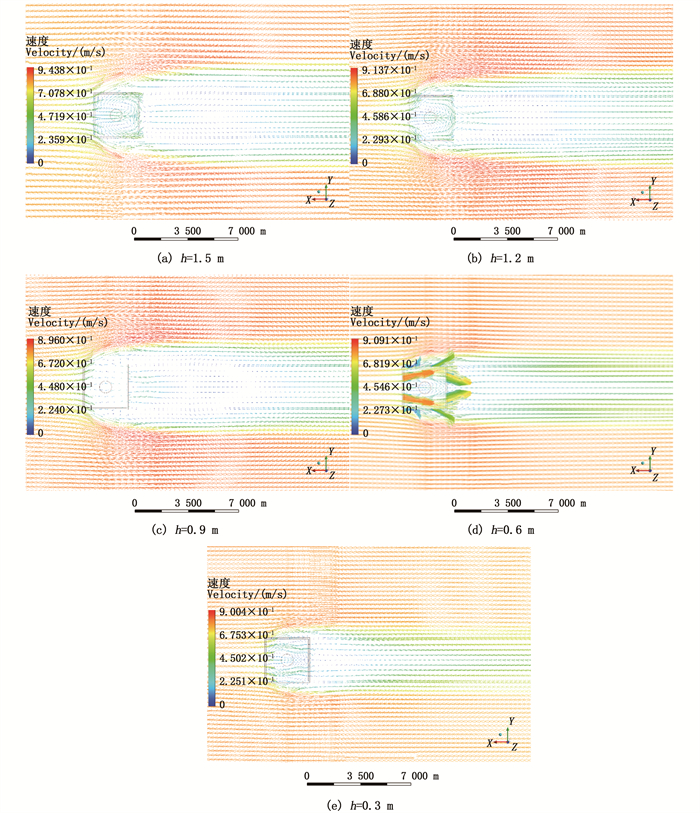
2.3 不同沉降程度对单体方型多孔人工鱼礁水平方向流态影响为了研究空心多孔方型人工鱼礁水平方向的内部及外部流态情况,选择不同沉降程度下裸露礁体高度的一半位置作为横切面进行后处理[17]。设横截面高度为H,5种不同沉降程度下对应的横截面高度H分别为1.5 m、1.2 m、0.9 m、0.6 m、0.3 m,各平面上的速度矢量分布见图 8。从图 8可以看出,当水流经过礁体时,由于礁体壁面的阻碍作用,水体流向向两侧偏转形成侧向流,同时流速有不同程度的增加,流速最大值出现的位置在X轴方向均处于礁体中心,整体呈两侧对称分布。在沉降深度为0 m、0.6 m、1.2 m时,最大值流域距礁体侧面距离约为1 m,并且通过图 8可以明显看出,在沉降深度为0.6 m时,礁体两侧流速增大区域范围明显增大,约为无沉降状态时1.5倍。从沉降程度60%开始,礁体流速增加区域明显靠近礁体两侧,且整体流速接近来流速度(0.8 m/s),在沉降深度达到80%时,礁体两侧流速增大区域基本消失,平均流速与来流速度基本相同。
|
图 8 5种沉降程度下对应横切面上的速度矢量分布 Fig. 8 Velocity vector distribution on the corresponding cross section to five settlement degrees |
沉降深度为1.8 m的横截面位置刚好截取方型人工鱼礁部分孔洞,从图 8可以明显看出,当水流通过礁体壁面孔洞进入礁体内部时,水体流向往礁体两侧偏转,此时平均流速大小与水流速度相同,同时由于方型多孔人工鱼礁的特殊构造,水流经过迎流面的孔洞后在礁体内部形成两个沿Y轴排列、方向相反的对称涡旋,涡旋整体流速较小。当水流从礁体两侧及背流面流出时,流速明显减小,其中从靠近迎流面的两侧对称孔洞流出的水流速度最小,流速在0.2 m/s以下,从远离迎流面的两侧孔洞流出的水流流速约为来流速度的一半。当水流从礁体背流面孔洞流出时,流向往礁体中心线偏转,流速有一定程度降低,之后在礁体背流面之后形成透水区和背涡流区域,整体分布范围与流态与图 6一致。
3 结论从仿真图像和数据可以看出,礁体沉降作为人工鱼礁投放后普遍发生的现象,对多孔方型人工鱼礁的流场效应有很大影响。由于多孔方型人工鱼礁特殊的构造,其内部和周围流态较为复杂,但通过仿真结果可以明显的看出上升流区域、内部涡流、外部流域等显著区域随着沉降深度变化而发生对应的流态改变。此外,无沉降状态时礁体内、外部流场情况以及礁体上升流最大高度、上升流影响范围与黄远东等[10]、王佳浩等[11]研究结果基本一致。通过对比分析5种不同沉降程度(0%、20%、40%、60%、80%)状态下多孔方型人工鱼礁周围的流场运动及变化情况,得出如下结果:
(1) 在沉降程度为20%时,方型多孔鱼礁最大上升流大小并未因礁体沉降而减少甚至增加约0.015 m/;沉降程度为40%时,最大上升流大小与初始状态相比基本相同,减少约0.01 m/s。
(2) 方型多孔鱼礁上升流最大高度随着沉降程度的增加而减少,但在沉降程度为40%以内,上升流最大高度减少量对比沉降程度降低趋势较缓,20%与40%两种沉降程度下礁体上升流最大高度差值约为0.45 m,当沉降程度达到60%时,上升流最大高度降低明显,相较于40%降低约1.74 m。
(3) 方型多孔鱼礁侧向流增大区域在沉降程度为20%明显增大,约为原来的1.5倍,同时礁体内部与礁后流场情况变得更加复杂,流场效应较好。在沉降程度为40%时,礁体背流面透水区域有形成一个逆时针涡旋的趋势,与背涡流区域涡旋方向相反,背流面整体流态复杂,人工鱼礁依旧发挥着较好的作用。
(4) 沉降程度从60%开始,方型多孔鱼礁最大上升流高度、上升流最大流速和礁体周围流场情况均开始有了明显损失。上升流最大抬升高度降低为原来的1/2,礁体侧向流接近来流流速,礁体背涡区域基本消失,只留下狭长透水区域。在沉降程度达到80%时,方型多孔鱼礁流场效应基本消失。
从以上结果可以得出,方型多孔鱼礁的某些流场特性并不是随着沉降现象的出现而一直降低,流场效应的损失也不是随着沉降程度增加呈线性变化。在沉降程度40%以内,礁体沉降对方型多孔鱼礁影响较小,礁体依旧发挥良好流场效应。在沉降程度为20%时,礁体周围流场情况从侧向流、最大上升流流速等角度来看甚至变得更加复杂,当沉降程度达到60%时多孔方型人工鱼礁的流场效应才出现各方面明显降低的情况。
本研究初步分析了沉降程度对多孔方型人工鱼礁内部及周围流场的影响,为鱼礁投放后礁体检测、修复及补充等研究工作提供一定参考。从研究结果可以推断,方型多孔人工鱼礁在对冲沉降影响方面与其结构的复杂性密切相关,沉降程度较低情况下礁体依旧发挥着较好的流场效应,因此在设计人工鱼礁时,增设开孔等镂空设计在一定程度上具有重要意义[18]。本研究以单体多孔方型人工鱼礁作为研究对象,还有一定的局限性,此外由于实际沉降现象复杂,礁体沉降形态也多种多样,数值仿真技术难以模拟完全真实情况,故需要结合实际考察等真实数据进行综合判断[19]。
| [1] |
李东, 侯西勇, 唐诚, 等. 人工鱼礁研究现状及未来展望[J]. 海洋科学, 2019, 43(4): 81-87. LI D, HOU X Y, TANG C, et al. A review on the progress of artificial reef research[J]. Marine Sciences, 2019, 43(4): 81-87. |
| [2] |
林军, 章守宇. 人工鱼礁物理稳定性及其生态效应的研究进展[J]. 海洋渔业, 2006, 28(3): 257-262. LIN J, ZHANG S Y. Research advances on physical stability and ecological effects of artificial reef[J]. Marine Fisheries, 2006, 28(3): 257-262. DOI:10.3969/j.issn.1004-2490.2006.03.015 |
| [3] |
唐衍力, 龙翔宇, 王欣欣, 等. 中国常用人工鱼礁流场效应的比较分析[J]. 农业工程学报, 2017, 33(8): 97-103. TANG Y L, LONG X Y, WANG X X, et al. Comparative analysis on flow field effect of general artificial reefs in China[J]. Transactions of the Chinese Society of Agricultural Engineering, 2017, 33(8): 97-103. |
| [4] |
方继红, 林军, 杨伟, 等. 双层十字翼型人工鱼礁流场效应的数值模拟[J]. 上海海洋大学学报, 2021, 30(4): 743-754. FANG J H, LIN J, YANG W, et al. Numerical simulation of flow field effect around the double-layer cross-wing artificial reef[J]. Journal of Shanghai Ocean University, 2021, 30(4): 743-754. |
| [5] |
逯金明. 基于多波束和侧扫声呐的人工鱼礁区对比分析[J]. 山东工业技术, 2018(5): 183. LU J M. Comparative analysis of artificial reef area based on multi beam and side scan sonar[J]. Shandong Industrial Technology, 2018(5): 183. |
| [6] |
李东, 唐诚, 邹涛, 等. 基于多波束声呐的人工鱼礁区地形特征分析[J]. 海洋科学, 2017, 41(5): 127-133. LI D, TANG C, ZOU T, et al. Terrain character analysis of artificial reefs area based on multibeam echo sounder[J]. Marine Sciences, 2017, 41(5): 127-133. |
| [7] |
赵刚, 李妍, 许祝华, 等. 侧扫声呐在人工鱼礁跟踪监测中的应用[J]. 地质学刊, 2020, 44(3): 307-311. ZHAO G, LI Y, XU Z H, et al. Application of side-scan sonar in artificial reef tracking and monitoring[J]. Journal of Geology, 2020, 44(3): 307-311. |
| [8] |
张硕, 张世东, 初文华, 等. 六边形开口方形人工鱼礁水动力性能模型实验[J]. 水产学报, 2020, 44(11): 1903-1912. ZHANG S, ZHANG S D, CHU W H, et al. Model experiment of hydrodynamic performance of square artificial reefs with hexagonal openings[J]. Journal of Fisheries of China, 2020, 44(11): 1903-1912. |
| [9] |
佟飞, 唐振朝, 贾晓平, 等. 基于侧扫声纳方法的框架式人工鱼礁测量[J]. 南方水产科学, 2018, 14(1): 99-104. TONG F, TANG Z C, JIA X P, et al. Frame-type artificial reef measurement by side-scan sonar[J]. South China Fisheries Science, 2018, 14(1): 99-104. |
| [10] |
黄远东, 赵树夫, 姜剑伟, 等. 多孔方型人工鱼礁绕流的数值模拟研究[J]. 水资源与水工程学报, 2012, 23(5): 15-18. HUANG Y D, ZHAO S F, JIANG J W, et al. Study on numerical simulation of water flow past a porous square artificial reef[J]. Journal of Water Resources and Water Engineering, 2012, 23(5): 15-18. |
| [11] |
王佳浩, 刘莉莉, 蔡新晨, 等. 布设间距对多孔方型人工鱼礁流场效应影响的数值模拟研究[J]. 渔业科学进展, 2020, 41(3): 40-48. WANG J H, LIU L L, CAI X C, et al. Numerical simulation study on influence of disposal space on effects of flow fieldaround porous square artificial reefs[J]. Progress in Fishery Sciences, 2020, 41(3): 40-48. |
| [12] |
KIM K P, AHMED M R, LEE Y H. Efficiency improvement of a tidal current turbine utilizing a larger area of channel[J]. Renewable Energy, 2012, 48: 557-564. |
| [13] |
FINNEGAN W, GOGGINS J. Numerical simulation of linear water waves and wave-structure interaction[J]. Ocean Engineering, 2012, 43: 23-31. |
| [14] |
郑延璇, 关长涛, 宋协法, 等. 星体型人工鱼礁流场效应的数值模拟[J]. 农业工程学报, 2012, 28(19): 185-193. ZHENG Y X, GUAN C T, SONG X F, et al. Numerical simulation on flow field around star artificial reefs[J]. Transactions of the Chinese Society of Agricultural Engineering, 2012, 28(19): 185-193. |
| [15] |
黄远东, 姜剑伟, 赵树夫. 方型人工鱼礁周围水流运动的数值模拟研究[J]. 水资源与水工程学报, 2012, 23(3): 1-3. HUANG Y D, JIANG J W, ZHAO S F. Study on numerical model of water flows past a square artificial reef[J]. Journal of Water Resources and Water Engineering, 2012, 23(3): 1-3. |
| [16] |
刘心媚, 郑艳娜, 陈昌平, 等. 框架型与沉箱型人工鱼礁绕流特性的数值模拟[J]. 大连海洋大学学报, 2019, 34(1): 133-138. LIU X M, ZHENG Y N, CHEN C P, et al. Numerical simulation of flow around frame and caisson artificial reef models[J]. Journal of Dalian Ocean University, 2019, 34(1): 133-138. |
| [17] |
LIU T L, SU D T. Numerical analysis of the influence of reef arrangements on artificial reef flow fields[J]. Ocean Engineering, 2013, 74: 81-89. |
| [18] |
姜昭阳, 郭战胜, 朱立新, 等. 人工鱼礁结构设计原理与研究进展[J]. 水产学报, 2019, 43(9): 1881-1889. JIANG Z Y, GUO Z S, ZHU L X, et al. Structural design principle and research progress of artificial reef[J]. Journal of Fisheries of China, 2019, 43(9): 1881-1889. |
| [19] |
KOMYAKOVA V, CHAMBERLAIN D, JONES G P, et al. Assessing the performance of artificial reefs as substitute habitat for temperate reef fishes: implications for reef design and placement[J]. Science of the Total Environment, 2019, 668: 139-152. |
 2023,
Vol. 32
2023,
Vol. 32

