2. 上海海洋可再生能源工程技术研究中心, 上海 201306
我国渔业产业结构调整,海洋捕捞业实施零增长战略,水产养殖业随之兴起,其中虾类养殖尤其是淡水虾类的养殖发展迅速[1]。随着虾类养殖规模的扩大,由于人工投饲的方式成本高、效率低,定点投饲机不适合虾塘的移动投饵,因此投饵船的研究开发是一个发展方向,符合当前国内水产养殖规模化、现代化和自动化的发展需求。
由于投饵船需要装载一定质量的饲料,比一般船体的重心要高,所以稳性差。目前投饵船的研究主要集中在结构设计、路径控制、投饵策略[2-11]等方面,未见稳性方面的研究,但稳性良好是船舶安全航行的前提,也是船舶设计的重要基础。目前投饵船在设计时仅对其初稳性进行理论计算,但计算结果仅表明其初稳性满足设计需求,且理论计算常基于投饵船正浮的状态,未考虑船舶浮态对船舶稳性的影响,而投饲机装载位置的不同、投饲过程中饲料质量的变化、下料过程中重心的变化都会极大影响投饵船的浮态,因此研究投饵船浮态和稳性的关系可以为投饵船和投饲机的设计、投饲机的装载位置提供一定的参考。
近年来计算流体动力学(computational fluid dynamics, CFD)方法逐渐成为研究船舶水动力方面的重要方法,国内外现已有诸多学者[12-17]应用CFD方法对船舶浮态进行研究。本文基于上海海洋大学工程学院研制的一款可均匀投饵的智能投饵船,利用Fluent软件对投饵船在空载、载重15 kg及满载时的浮态进行数值计算,基于各种载况下投饵船的浮态,对投饵船在不同横倾角下浮力及力矩进行数值计算,从而得到各浮态下的复原力臂曲线(复原力臂曲线指船舶在某一工况下复原力臂与横倾角的关系曲线,描述船舶在某一横倾角下船舶的抗倾覆能力),通过各浮态下的复原力臂曲线来分析投饵船浮态对稳性的影响。
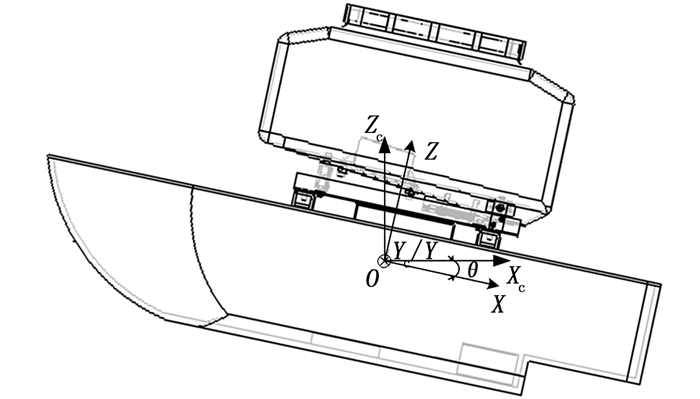
1 材料与方法 1.1 投饵船运动方程数值计算采用双重坐标系来描述投饵船浮态的变化,即惯性坐标系XC-O-ZC和随船坐标系X-O-Z,如图 1所示。惯性坐标系和随船坐标系的原点均取于投饵船空载时的重心坐标(0,0,0),此时重心距船尾480.5 mm,距投饵船上表面55.5 mm。随船坐标系的X轴指向投饵船船尾,Y轴指向右侧船体(箭头朝里),Z轴垂直指向甲板。θ表示纵倾角,绕Y轴顺时针旋转为艉倾,艉倾时θ为正,绕Y轴逆时针旋转为艏倾,艏倾时θ为负。
|
图 1 投饵船整体结构及其双重坐标系 Fig. 1 Overall structure of the bait boat and its dual coordinate system |
由于投饵船在设计过程中考虑了横向对称,因此在对投饵船静水浮态的数值模拟时仅考虑其垂荡及纵摇两自由度的作用,根据刚体六自由度运动理论[18-19]可知投饵船运动方程为
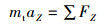 (1)
(1)
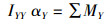 (2)
(2)
式中:mt为整船质量(船体和投饲机质量之和),kg;aZ为Z方向上的线加速度,m/s2;∑FZ为Z轴方向上的合力,即垂向力,N;IYY为关于Y轴的惯性矩,m4;αY为纵摇角加速度,rad/s2;∑MY为绕Y轴的合力矩,即纵摇力矩,N·m。
1.2 工况描述投饵船由船体和投饲机两部分组成,船体部分采用稳定性较好的双体船,空船总质量约为26.6 kg,船长为1.10 m,船宽为0.16 m,船高为0.61 m,双体船船距为0.24 m,投饵船在装载0、15和30 kg饲料时投饵船在随船坐标系中的重心坐标及质量如表 1所示。

|
表 1 投饵船在不同工况下重心坐标及质量 Tab.1 Gravity coordinates and quality of baitboat under various working conditions |
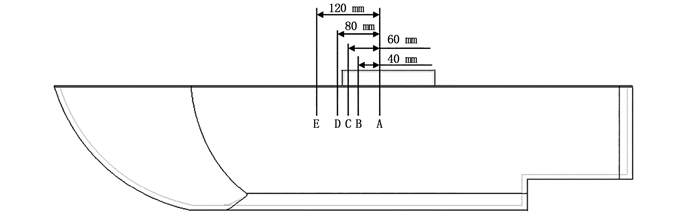
为研究投饵船在不同浮态下的稳性变化规律,选取空载、装载15 kg饲料以及满载30 kg饲料的投饲机安装在沿X轴方向上A(0,0,0)、B(-40,0,0)、C(-60,0,0)、D(-80,0,0)、E(-120,0,0)等5个位置进行浮态和复原力臂的数值计算,5个安装位置如图 2所示,Y坐标及Z坐标不变,则选取的3个工况下投饵船重心坐标的X坐标如表 2所示。
|
图 2 投饲机5个安装位置 Fig. 2 Five installation positions of feeding machine |

|
表 2 5个位置时投饵船重心X坐标
Tab.2 X coordinate of the center of gravity of the bait boat at 5 positions |
计算域取长×宽×高为8L×5L×5L的区域, 水面距计算域下表面为3L,其中L为船长。计算域四周及下表面为自由滑移壁面,上表面为压力出口边界,投饵船船体表面为非自由滑移壁面。数值计算的计算域及边界条件如图 3所示。
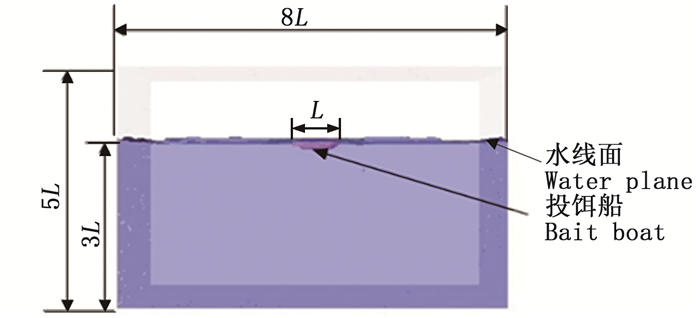
|
图 3 计算域及边界条件 Fig. 3 Computational domain and boundary conditions |
网格划分的本质是用有限个离散的点对连续的控制方程进行离散,是计算流体力学分析的基础,网格的数量和质量对数值计算结果的精确度起着决定性作用[20]。本文涉及投饵船的大幅度升沉及纵摇运动,为保证计算过程中的网格质量,故采用重叠网格。重叠网格由背景网格和部件网格组成,不同网格区域分别独立完成离散控制方程求解,通过边界点的插值来实现区域间的数据传递。本文主要求解船体所受力和力矩,为简化网格而省去料箱、连接件等部件,仅对两个船体进行网格划分,其中,小长方体网格为部件网格,大长方体网格为背景网格,投饵船船体附近生成边界层网格以更加准确求解流场,网格类型采用Poly-Hexcore形式的混合网格,网格划分如图 4所示。
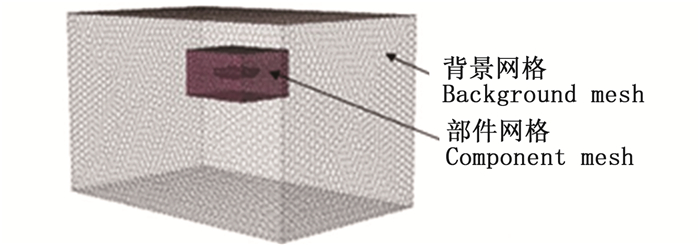
|
图 4 网格划分 Fig. 4 Mesh division |
在实际数值计算中,合适的网格数量不仅可以提高数值计算的精度,还可以节省计算时间,因此网格无关性验证是数值计算的重要环节[20]。在保证计算精度和网格质量的前提下,选取不同数量的网格对投饵船浮态进行数值模拟,不同网格数量下升沉量和纵倾角计算值如表 3所示,其中网格数量为背景网格数和部件网格数总数,误差为相邻两套网格下数值计算值之间的误差。

|
表 3 不同网格数量下升沉量和纵倾角的计算值 Tab.3 Calculated value of heave and trim angle with different numbers of grids |
从表 3可以看出,网格数达到440 085时,升沉量的数值计算值与前一套网格的计算误差在3%以内,纵倾角的数值计算值趋于稳定,此时数值计算精确度与网格数量的增加无关,因此选取网格数为375 992的混合网格作为数值计算网格。
1.5 数值计算可行性为检验数值模拟的可行性,在相同的条件下,分别进行仿真计算和现场实验,获取投饵船的浮态。实验时风力风向为西南风1级,投饵船升沉量和纵倾角由测量投饵船艏艉水线至投饵船甲板的距离计算得到,实验测量数据如图 5所示,实验时投饵船平衡后的浮态如图 6a所示。
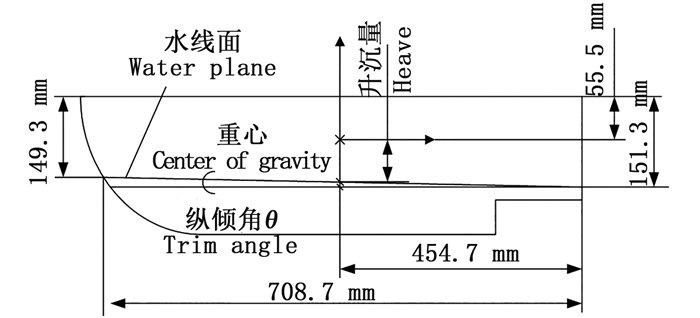
|
图 5 实验测量数据 Fig. 5 Experimental measurement data |
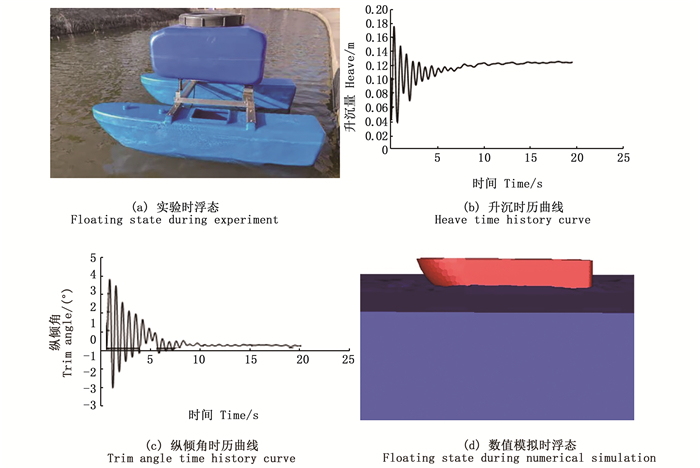
|
图 6 实验和数值模拟时浮态及时历曲线 Fig. 6 Floating state and time history curve during experiment and numerical simulation |
根据图 5可以得出:投饵船艏艉吃水差为2 mm,水线面与投饵船的交点的水平距离为708.7 mm,根据三角函数公式得出投饵船纵倾角θ为0.16°。投饵船升沉量:Z△为151.3-55.5-454.7×tanθ=94.4 mm。
投饵船浮态包括吃水线及纵倾角,数值模拟计算时设置初始吃水线为Z=0的位置,初始纵倾角为0°,即投饵船吃水线的计算转化为Z方向上升沉量的计算。图 6b、6c分别是与实验相同条件下的投饵船数值计算出的升沉时历曲线和纵倾时历曲线,均以衰减的形式达到稳定值。投饵船数值模拟的浮态如图 6d所示,数值计算结果如表 4所示。比较表 4中实验值和数值计算值,可以得到数值计算出的升沉量和纵倾角值的误差均在7%以内,说明数值模拟计算结果可靠,该数值计算方法可以用来代替实验进行研究。
|
表 4 实验及数值计算结果比较 Tab.4 Comparison of experimental and numerical calculation results |
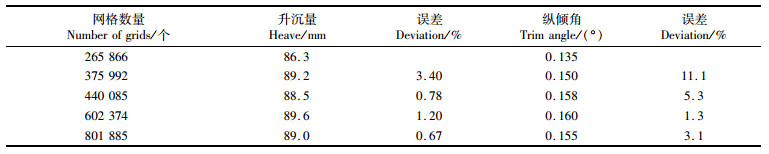
经浮态的数值模拟发现,在相同载重下,投饲机在不同安装位置时投饵船的升沉量几乎不变,因此仅对其纵倾角变化进行研究。图 7是投饵船在不同载重下通过数值计算得到的纵倾角曲线图。由图 7可知:在3种载重下,投饲机安装位置从A到E时,投饵船均从艉倾(正值)过渡到艏倾(负值);装载30 kg饲料的投饲机在A、D、E位置时已出现很大的纵倾角甚至是纵向倾覆的现象,因此该载重下在A、D、E这3个位置点没有研究意义。
|
图 7 纵倾角曲线图 Fig. 7 Curve of trim angle |
进行曲线拟合,得到纵倾角曲线拟合公式:空载时为y=0.028 3x+2.611;载重15 kg时为y=0.000 2x2+0.119 6x+5.924;载重30 kg时为y=0.365 5x+14.93。各拟合曲线与横坐标的交点(纵倾角为0°)就是投饵船处于正浮状态时投饲机的安装位置。由曲线拟合公式可知:载重不同,投饵船处于正浮时的投饲机安装位置(曲线与横坐标的交点)不同,投饵船在空载、装载15 kg和30 kg处于正浮状态时,投饲机的安装位置分别在H点(X=-92.26 mm)、G点(X=-56.12 mm)和F点(X=-40.85 mm)。
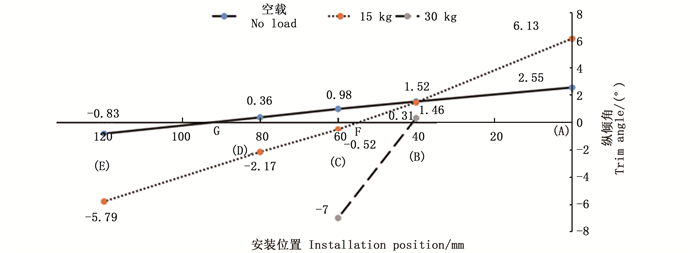
2.2 稳性计算结果及分析从浮态的计算结果分析可知,装载30 kg饲料时,投饲机安装在A、D、E这3个位置时,投饵船处于较大的纵倾角或者已经纵向倾覆,因此对其横稳性的研究已经没有意义,因此为了研究纵倾角和横稳性的关系,在稳性计算时只计算空载和装载15 kg饲料时在5个位置点(A、B、C、D和E)的复原力臂曲线。以浮态计算结果作为稳性计算的初始值,给予投饵船不同横倾角度置于流场中,计算在每一横倾角度下投饵船浮态达到稳定时所受力矩M和浮力F,根据力臂计算公式l=M/F得到在每一横倾角度下的复原力臂。复原力臂反映在相同载重下船舶抵抗倾覆的能力,复原力臂越大,其抗倾覆能力越强。最大复原力臂值是指投饵船所能抵抗的最大外力力臂,复原力臂曲线下面积为动复原力臂,即反映投饵船动稳性大小。图 8是空载和载重15 kg时的复原力臂曲线。
|
图 8 空载和载重15 kg时复原力臂曲线 Fig. 8 Curve of righting arm with no load and 15 kg |
分析图 8可以得出:
(1) 空载时,投饲机安装在A、B、C、D、E这5个位置时复原力臂曲线在横倾角较小(横倾角 < 5°)时基本重合,说明在横倾角小于5°时,纵倾角对投饵船的稳性没有明显影响。
(2) 空载时,在B位置(纵倾角为1.52°)时的最大复原力臂值比在其他位置的最大复原力臂值大,而在A位置(纵倾角为2.55°)时最大复原力臂明显减小,且在A、B、C位置时均在横倾角较大时出现复原力臂曲线急剧下降的现象。
(3) 载重15 kg时,投饲机安装在B、C、D、E这4个位置时复原力臂曲线在横倾角较小(横倾角 < 5°)时基本重合,说明在点B~E的位置区间,在横倾角小于5°时,纵倾角对投饵船的稳性没有明显影响。
(4) 载重15 kg时,在A、D、E位置相较于C位置(纵倾角为-0.52°)时的最大复原力臂值均减小,5个位置均出现复原力臂值达到最大值后急剧下降的现象,且出现该现象时的横倾角相较于空载时明显减小。
(5) 投饲机安装在A位置(纵倾角为6.13°)时,横倾角为10°左右复原力臂就急剧下降为0,最大复原力臂也远远小于其他几个位置的值。在E位置时,也有类似的情况,最大复原力臂和力臂为0时的横倾角也远小于B、C、D这3个位置。对照图 7纵倾角的情况可知:在A位置时各载荷下艉倾角的值大于B、C、D这3个位置,且载荷越大,艉倾角越大;而在E位置时各载荷下艏倾角的值大于B、C、D这3个位置,且载荷越大,艏倾角越大。这说明投饵船在较大的纵倾角时横稳性差,纵倾角越大,横稳性越差。进一步说明载重30 kg时除B位置外均有较大的纵倾角,对其横稳性的研究没有意义。
(6) 综合分析最大复原力臂和复原力臂曲线所围面积(动稳性力臂)可知:空载时,在B位置,虽然最大复原力臂比D、E位置略大,但动稳性力臂比D、E位置小,因此此时投饲机安装在D位置(纵倾角为0.36°)和E位置(纵倾角为-0.98°)时稳性最好。载重15 kg时,投饲机安装在C位置(纵倾角为-0.52°)时稳性最好,即同一载重下,投饵船越接近正浮(纵倾角为0°)时稳性越好。
(7) 根据以上分析和纵倾角拟合曲线方程可知:投饲机安装在F位置(X=-40.85 mm)时整体稳性最好,即满载时处于正浮状态或接近正浮状态时投饵船整体稳性最好,此时空载和载重15 kg时纵倾角较小。在投饵船整体布局时也应保证满载时投饵船处于正浮状态。
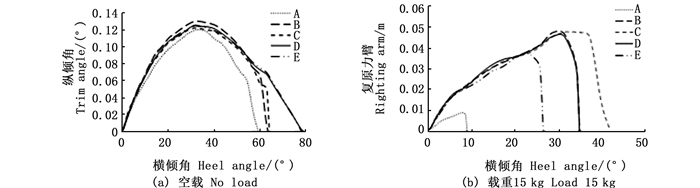
空载和载重15 kg时均在某一横倾角时发生复原力臂急剧下降的现象,进一步研究可知其原因在于:投饵船在横倾过程中伴随着纵倾角的变化,其变化趋势如图 9所示。在横倾角较小时,纵倾角变化幅度较小,且初始纵倾角越大,纵倾角随横倾角的变化越明显。在横倾角较大时,纵倾角急剧增大,发生纵向(绕Y轴旋转)倾覆现象,即出现复原力臂急剧下降的现象。
|
图 9 空载和载重15 kg时纵倾角变化曲线 Fig. 9 Trim angle change curves with no load and 15 kg |
本文基于CFD理论对投饵船进行初浮态和复原力臂数值模拟计算。采用重叠网格技术,耦合计算流体动力学控制方程和船舶运动方程,计算出投饵船在5个安装位置点的浮态和复原力臂曲线,综合分析得出以下结论:(1)在同一载重下,投饵船在出现艏倾或者艉倾角度较小时,对投饵船稳性影响较小,且投饵船越接近正浮(纵倾角为0°)时稳性越好。(2)本文仅分析投饲机安装位置对投饵船横稳性的影响,在其他零部件布局确定的前提下,投饲机安装在F点(X=-40.85 mm)时横稳性最优。但引起浮态变化的因素众多,因此在投饵船设计和整体布局时也应保证满载时纵倾角为0。(3)在稳性计算时,纵倾角随着横倾角的增大而增大,在横倾角较大时,会发生纵向倾覆,因此在稳性校核时,纵倾角是不可忽略的。
目前所设计的投饲机的安装位置是固定的,得到投饲机的最佳安装位置仅是保证在投饵过程中整体稳性保持良好的位置。由于投饵船在进行作业时需经历从满载到空载的过程,因此可以设计一款可根据投饵量实时调节投饲机位置的投饵船,使得投饵船在投饵过程中保持正浮状态,从而使得投饵船稳性保持最优。
| [1] |
黄玉玲. 我国虾类淡水养殖概述[J]. 水利渔业, 2003, 23(1): 1-3. HUANG Y L. An overview of freshwater shrimp aquaculture in my country[J]. Water Conservancy and Fisheries, 2003, 23(1): 1-3. DOI:10.3969/j.issn.1003-1278.2003.01.001 |
| [2] |
程文平. 智能型虾塘移动式投饵装置研发与试验[D]. 上海: 上海海洋大学, 2017. CHENG W P. Intelligent mobile shrimp pond feeding equipment development and testing[D]. Shanghai: Shanghai Ocean University, 2017. |
| [3] |
胡庆松, 郑波, 曹佳瑞, 等. 船载投饵装置平衡抖料系统设计与试验[J]. 上海海洋大学学报, 2020, 29(6): 131-140. HU Q S, ZHENG B, CAO J R, et al. Design and test of balance shaker system for ship-borne bait feeding device[J]. Journal of Shanghai Ocean University, 2020, 29(6): 131-140. |
| [4] |
REIS J, NOVRIADI R, SWANEPOEL A, et al. Optimizing feed automation: improving timer-feeders and on demand systems in semi-intensive pond culture of shrimp Litopenaeus vannamei[J]. Aquaculture, 2020, 519: 734759. DOI:10.1016/j.aquaculture.2019.734759 |
| [5] |
洪扬, 陈晓龙, 田昌凤, 等. 蟹、虾养殖池塘移动投饲装置的设计与试验[J]. 渔业现代化, 2018, 45(3): 9-14. HONG Y, CHEN X L, TIAN C F, et al. Design and test of a kind of moving feeding device for crab and shrimp ponds[J]. Fishery Modernization, 2018, 45(3): 9-14. DOI:10.3969/j.issn.1007-9580.2018.03.002 |
| [6] |
周达辉, 朱晓敏, 刘伟清. 基于PLC的自巡航虾塘投饲机研究[J]. 江苏农机化, 2016(4): 23-27. ZHOU D H, ZHU X M, LIU W Q. Research on feeding machine of self cruise shrimp pond based on PLC[J]. Agricultural Mechanization in Jiangsu, 2016(4): 23-27. DOI:10.3969/j.issn.1004-9908.2016.04.009 |
| [7] |
王真亮. 水面自主巡航式太阳能投饵船的设计与研究[D]. 合肥: 安徽工业大学, 2017. WANG Z L. The design and study on solar energy feeding ship based on autonomous cruise method[D]. Hefei: Anhui University of Technology, 2017. |
| [8] |
BÓRQUEZ-LOPEZ R A, CASILLAS-HERNANDEZ R, LOPEZ-ELIAS J A, et al. Improving feeding strategies for shrimp farming using fuzzy logic, based on water quality parameters[J]. Aquacultural Engineering, 2018, 81: 38-45. DOI:10.1016/j.aquaeng.2018.01.002 |
| [9] |
SIMÃO B R, BRITO L O, MAIA A S C, et al. Stocking densities and feeding strategies in shrimp and tilapia polyculture in tanks[J]. Pesquisa Agropecuária Brasileira, 2013, 48(8): 1088-1095. DOI:10.1590/S0100-204X2013000800039 |
| [10] |
郭俊. 基于图像与声音信息的养殖鱼群摄食规律与投饵技术研究[D]. 宁波: 宁波大学, 2018. GUO J. Research on feeding patterns and bait technology of fish culture based on information of image and sound[D]. Ningbo: Ningbo University, 2018. |
| [11] |
PARSONAGE K D, PETRELL R J. Accuracy of a machine-vision pellet detection system[J]. Aquacultural Engineering, 2003, 29(3/4): 109-123. |
| [12] |
CARRICA P M, FU H P, STERN F. Computations of self-propulsion free to sink and trim and of motions in head waves of the KRISO Container Ship (KCS) model[J]. Applied Ocean Research, 2011, 33(4): 309-320. DOI:10.1016/j.apor.2011.07.003 |
| [13] |
王凤琴. 基于CFD方法的舰船纵倾组合浮态阻力计算的研究[J]. 舰船科学技术, 2017, 39(22): 1-3. WANG F Q. Study on calculation of floating resistance of ship longitudinal assembly based on CFD method[J]. Ship Science and Technology, 2017, 39(22): 1-3. |
| [14] |
WEYMOUTH G D, WILSON R V, STERN F. RANS computational fluid dynamics predictions of pitch and heave ship motions in head seas[J]. Journal of Ship Research, 2005, 49(2): 80-97. DOI:10.5957/jsr.2005.49.2.80 |
| [15] |
邵江明, 应业炬, ZHOU Q, 等. 基于CFD的斜航船舶浮态数值预报[J]. 浙江海洋学院学报(自然科学版), 2015, 34(6): 559-564. SHAO J M, YING Y J, ZHOU Q, et al. CFD-based numerical prediction of the floating state of oblique ships[J]. Journal of Zhejiang Ocean University (Natural Science Edition), 2015, 34(6): 559-564. DOI:10.3969/j.issn.1008-830X.2015.06.011 |
| [16] |
吴明, 王骁, 应荣镕, 等. 船舶浅水航行下沉量和纵倾的数值计算[J]. 船舶, 2013, 24(3): 7-11. WU M, WANG X, YING R R, et al. Numerical calculation of ship sinkage and trim in shallow water[J]. Ship & Boat, 2013, 24(3): 7-11. |
| [17] |
石博文, 刘正江, 杨波. CFD方法的船舶骑浪稳性研究[J]. 哈尔滨工程大学学报, 2017, 38(7): 1035-1040. SHI B W, LIU Z J, YANG B. Study on the surf-riding stability of a vessel based on CFD[J]. Journal of Harbin Engineering University, 2017, 38(7): 1035-1040. |
| [18] |
李殿璞. 船舶运动与建模[M]. 2版. 北京: 国防工业出版社, 2008. LI D P. Ship motion and modeling[M]. 2nd ed. Beijing: National Defense Industry Press, 2008. |
| [19] |
贾欣乐, 杨盐生. 船舶运动数学模型——机理建模与辨识建模[M]. 大连: 大连海事大学出版社, 1999. JIA X L, YANG Y S. Mathematical model of ship motion——mechanism modeling and identification modeling[M]. Dalian: Dalian Maritime University Press, 1999. |
| [20] |
李鹏飞, 徐敏义, 王飞飞. 精通CFD工程仿真与案例实战[M]. 北京: 人民邮电出版社, 2011. LI P F, XU M Y, WANG F F. Proficient in CFD engineering simulation and case actual combat[M]. Beijing: People's Posts and Telecommunications Press, 2011. |
2. Shanghai Engineering Research Center of Marine Renewable Energy, Shanghai 201306, China
 2022,
Vol. 31
2022,
Vol. 31


