2. 中国水产科学研究院 渔业机械仪器研究所, 上海 200092
据《中国渔业年鉴2019》统计[1],2018年我国水产品总量6 457.66万t,比上年增长0.19%。其中,养殖产量4 991.06万t,同比增长1.73%,池塘养殖已成为中国水产养殖的主要形式和水产品供应的主要来源。随着我国的水产养殖向着高密度、集约化迅猛发展,越来越多的养殖废物在养殖环境中累积,造成养殖环境恶化,对生态环境造成了严重污染[2]。因此,提高养殖系统的水质净化效能对于改善养殖环境和保护生态环境有着重要意义。
为了减少传统池塘水产养殖造成的水体污染、水资源浪费、环境污染等问题,科研人员针对养殖池水体净化开展了大量研究[3-13]。刘乃硕等[7]针对CORNELL和WATERLINE提出的两种双通道圆形养殖池的内部流场特性进行了数值模拟,计算结果从理论上验证了两种池型底流比例的经验设计值在10%以内。赵乐[8]研究了虾养殖池及鱼类养殖池的集排污水动力特性,重点分析了不同射流角度和流速条件下养殖池的流场分布特性及污物的聚集特性。魏武[9]对圆形养殖池内部流场特性进行了数值模拟,分析了养殖池的结构与其自净化效能之间的关系,并根据两者的关系对圆形养殖池的结构参数进行了优化设计。李建平等[10]针对旋流分离装置内部的流动特性进行数值模拟,研究了旋流分离装置对水产养殖水体的分离效果,并通过试验数据对模拟结果进行了验证。SUMMERFELT等[11]对双通道排水养殖池在不同水体交换率、底流分流比、径深比的情况下进行了数值模拟,研究了养殖池几何形状、养殖池进出水结构对圆形池的颗粒冲洗和水力混合性能的影响。史明明等[12]对两种养殖系统的气液固三相三维流动进行了数值模拟研究,分析了两种养殖系统的内部流动特性并与实测数据对比,研究表明循环生物絮团系统能够解决原位生物絮团分布不均匀以及流场死角多等问题。LIU等[13]采用计算流体动力学方法研究了颗粒物的水动力学特性,并根据实验测量结果验证了模拟结果,对循环水产养殖系统的结构优化设计具有重要意义。
综上,关于养殖池底部结构对其净水效能影响的研究较少,尤其是针对养殖池底部坡度对其内部流场特性、颗粒物沉积与分布规律等问题需要进一步深入研究。本文以一种典型方形切角养殖池为研究对象,基于CFD数值计算理论和方法研究了养殖系统单个养殖池的液固两相流场特性,重点分析了不同水力条件和池塘底面坡度对养殖池集排污特性的影响机制,得到了方形切角养殖池底面结构与其水体净化效能的关系,并与现有的实验数据进行了对比分析。
1 养殖池液固两相流场数值计算模型 1.1 结构模型以一种应用较广泛的方形切角养殖池为研究对象,计算模型如图 1所示。养殖池的结构为方形切角型,切角角度为135°,切边长度为0.14 m;养殖池的长×宽×高为1.5 m×0.4 m×0.6 m,入水口距水面高度约为0.18 m;养殖池底面与水平面夹角为α,养殖池进水出水口的管道直径为0.22 m。

|
图 1 养殖池计算模型 Fig. 1 Calculation model of aquaculture pond |
采用欧拉-拉格朗日计算方法,将水中鱼类粪便、饲料等固体颗粒物视为球形粒子离散相,连续相为水。将连续相视为黏性不可压缩流体,离散相利用拉格朗日法进行粒子跟踪[14]。不考虑颗粒相的碰撞、溶解、破碎以及两相间的组分变化等。三维不可压缩非定常流动的N-S方程组为
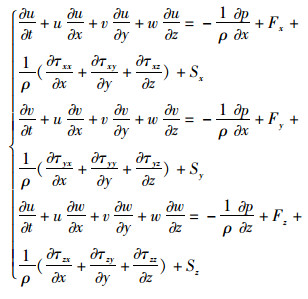 (1)
(1)
式中:ρ为流体压力;F为单位质量流体所受外部作用力,Fx、Fy、Fz是其在x、y、z方向上的分量;τ为黏性应力,τxx、τxy、τxz、τyx、τyy、τyz、τzx、τzy、τzz为其在对应x、y、z方向上的张量分量;S为流体质量源,Sx、Sy、Sz为其在x、y、z方向上的分量。
颗粒物的控制方程为
 (2)
(2)
式中:mi为颗粒质量;vi和ωi分别为颗粒平移速度和角速度;k为与粒子i相互作用的颗粒数;fn, ij和ft, ij分别为颗粒i和j之间的法向和切向接触力;ffp, i为颗粒与流体之间的相互作用力;Ii为转动惯量;Mi, ij和Mr, ij分别为作用在颗粒i、j上的切向和滚动摩擦力。
1.3 湍流模型养殖池水体循环过程中存在大应变率、旋流、液固分离等复杂流动问题,湍流模型采用SST k-ω湍流模型。相关研究表明:该湍流模型不需要使用容易失真的黏性衰减函数,特别适用于描述多相流动贴壁边界层区域内的复杂流动现象。
SST k-ω的k方程和ω方程分别为
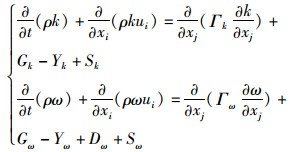 (3)
(3)
式中:k为湍流动能; ω为湍流频率; Γk、Γω分别为湍流扩散系数; Gk、Gω分别为湍流生成项; Yk、Yω分别为湍动能耗散项,Sk、Sω分别为自定义源项。
1.4 网格划分与计算参数划分合适数量的高质量网格是保证计算结果精度的关键之一。由于入水口相对其他部分较细以及需要重点分析出水口颗粒物质量浓度,这里对出水口和进水口进行局部网格加密。划分非结构化网格并通过网格无关性验证,确定网格划分数量约160万,相关计算参数如表 1所示。流场入水口设为速度进口边界条件,出口设为压力出口边界条件,其余壁面设为固壁边界条件。

|
表 1 计算参数 Tab.1 Calculation parameters |
养殖池塘净化效能指的是养殖池水质净化效能,与养殖池内部流动特性有一定关系。为研究不同底面坡度和水力条件下养殖池内部流场分布特性,设养殖池中心为坐标原点其中Y方向为重力加速度方向,XZ平面与水平面平行,取X=0纵截面和锥段上表面作为流场监测面监测两面的流场分布特性,纵截面和锥段上表面的交线设置为监测线,监测该线上的速度分布,出水口设置监测面监测该面上的出口粒子质量浓度,如图 2所示。

|
图 2 监测位置示意图 Fig. 2 Monitoring location diagram |
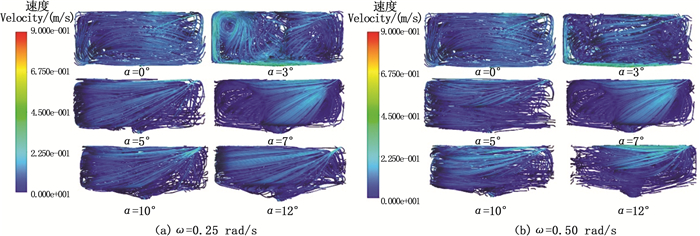
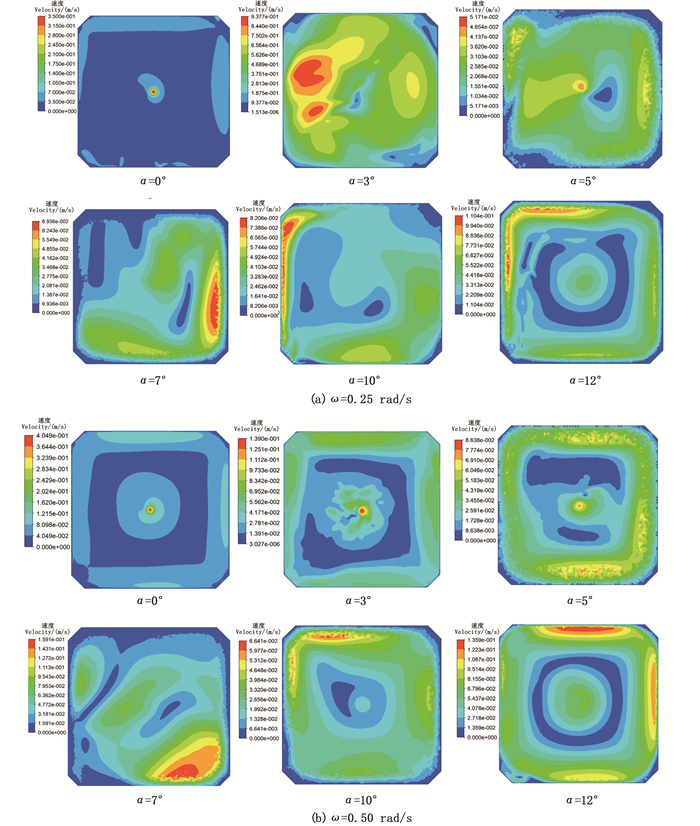
图 3为不同水流回转速度下的养殖池内部流线图,其中:图 3a为水流回转速度ω=0.25 rad/s下的内部流线图;图 3b为水流回转速度ω=0.50 rad/s下的内部流线图。图 4为不同水流回转速度下的养殖池锥段监测面的速度分布云图,图 4a为水流回转速度ω=0.25rad/s监测面上的速度分布云图;图 4b为水流回转速度ω=0.50 rad/s监测面上的速度分布云图。
|
图 3 不同水流回转速度下养殖池内部流线图 Fig. 3 Streamline diagrams of aquaculture ponds at different rotational angular velocities |
|
图 4 不同水流回转速度下锥段监测面速度云图 Fig. 4 Contours of velocity at different rotational angular velocities |
计算结果表明:养殖池底面与水平面夹角越大,有旋流动越明显即内部流动紊乱程度越小,养殖池内部流场湍流强度也会相应减少,这种情况下有利于固相颗粒物的沉降。当养殖池底面与水平面夹角为12°时,养殖池内部紊乱程度相对较小,有利于固体颗粒物在养殖池底部沉积。
压力分布对固相颗粒物的分布具有一定的影响,图 5为不同水流回转速度下监测线上的压力分布:图 5a为水流回转速度ω=0.25 rad/s养殖池内部流线;图 5b为水流回转速度ω=0.50 rad/s养殖池内部压力分布。从图 5可以看出:当水流回转速度ω=0.25 rad/s时,α越大该监测线上的压力分布就越小;当水流回转速度ω=0.50 rad/s时,监测线上的压力分布并不会随着α的改变呈线性变化。相关研究表明:养殖池内部压力越小,固相颗粒物受到的作用力越小,对颗粒物的沉积具有更好的效果。

|
图 5 不同水流回转速度下养殖池内部压力分布图 Fig. 5 Pressure distribution of aquaculture ponds at different rotational angular velocities |
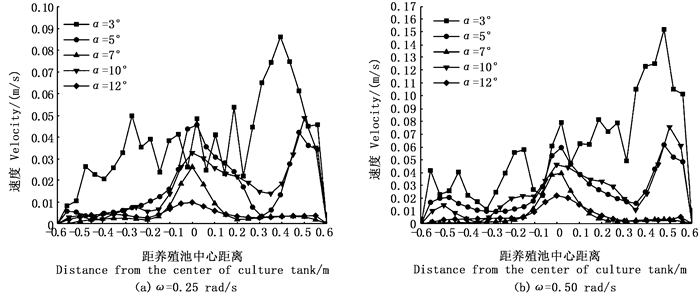
图 6为不同坡度养殖池在两种水流回转速度下监测线上的速度分布曲线。从图 6可以明显看出,α=12°该监测线上的速度分布较为均匀,并且在该情况下流速较小,有利于固体颗粒物的进一步沉积。
|
图 6 监测线上的速度分布曲线 Fig. 6 Speed distribution curves on the monitoring line |
边界出口的粒子质量浓度是评价养殖池净水性能的重要评估指标,出口粒子质量浓度越大,养殖池的净水效能越好。图 7为不同底面坡度养殖池在两种水流回转速度下的出口粒子质量浓度,计算结果表明:当水流回转速度为0.25 rad/s时,随着养殖池的底面坡度的增加,其净水效能逐渐增强,且当α=12°且ω=0.25 rad/s时,养殖池的净水效能相对最高。

|
图 7 不同坡度养殖池在两种水流回转速度下的出口粒子质量浓度 Fig. 7 Outlet particle mass concentration at different slopes of aquaculture ponds and two rotational angular velocities |
为了验证颗粒物输运数值计算结果的有效性,构建了长×宽×高为1.0 m×1.0 m×1.5 m的实验模型,研究了不同坡度下的养殖池颗粒物输运性即粒子逃逸率[15]。粒子逃逸率是指逃逸颗粒与入射颗粒的总质量的比值,是体现养殖池对颗粒物的输运性能和衡量净水效能的重要指标。为了验证本文所采取的数值计算方法的有效性,将此数值计算方法运用到文献[15]的实验模型中进行数值模拟,得到了不同底面坡度下的颗粒逃逸率,并与实验结果进行对比分析,如图 8所示。从图 8可以看出:通过数值计算得到底面不同坡度下的粒子逃逸率分别为8.32%、7.6%、9.5%、11%、9.3%,实验测试得到的不同底面坡度下粒子逃逸率分别为8.1%、7.9%、10.0%、10.8%、10.4%。对比分析发现,实验结果与数值计算结果基本接近,且整体变化趋势也基本一致,验证了本文数值计算方法的有效性和可靠性。

|
图 8 实验验证分析 Fig. 8 Experimental verification analysis |
通过数值研究养殖池的液固两相流动特性,分析不同水力条件和池塘底部坡度对颗粒物分离效率和水体净化效能的影响机制,并与现有的实验数据对比分析,主要得到以下结论:
(1) 随着养殖池的底面坡度增加,养殖池内部的流态紊乱程度逐渐减小,流场湍流强度也相应降低,有利于固相颗粒物的沉降。养殖池底面坡度越大,其底部出口附近压力越小,颗粒物受到的作用力就越小,越有利于固体颗粒物的沉积。
(2) 养殖池净水效能和底面坡度、养殖池水流回转速度存在一定关系。当水流回转速度一定时,随着坡度的增加,养殖池的净水效能逐渐增强。当水流回转速度为0.25 rad/s,且底部坡度为12°时,相对其他坡度养殖池净水效能最高。
(3) 数值计算结果与部分实验数据吻合较好,验证了本文所采取的数值计算方法的有效性。研究结果对于池塘生态养殖系统的结构优化设计,评价鱼类生存的水动力学条件,解决水循环效能低、集污/排污率差等问题具有重要科学意义和工程应用价值。
| [1] |
农业农村部渔业渔政管理局, 全国水产技术推广总站, 中国水产学会编制. 中国渔业统计年鉴[M]. 北京: 中国农业出版社, 2019. Fisheries and Fishery Administration Bureau of the Ministry of Agriculture and Rural Areas, National Aquatic Technology Promotion Center, Compiled by China Fisheries Association. China fishery statistical yearbook[M]. Beijing: China Agriculture Press, 2019. |
| [2] |
罗国芝, 朱泽闻, 包存宽. 中国水产养殖规划现状分析与对策[J]. 环境污染与防治, 2009, 31(2): 87-89. LUO G Z, ZHU Z W, BAO C K. The analysis and solutions to the China's aquaculture plan status[J]. Environmental Pollution & Control, 2009, 31(2): 87-89. DOI:10.3969/j.issn.1001-3865.2009.02.023 |
| [3] |
OCA J, MASALO I. Flow pattern in aquaculture circular tanks: influence of flow rate, water depth, and water inlet & outlet features[J]. Aquacultural Engineering, 2013, 52: 65-72. DOI:10.1016/j.aquaeng.2012.09.002 |
| [4] |
RASMUSSEN M R, MCLEAN E. Comparison of two different methods for evaluating the hydrodynamic performance of an industrial-scale fish-rearing unit[J]. Aquaculture, 2004, 242(1/4): 397-416. |
| [5] |
OCA J, MASAL I. Design criteria for rotating flow cells in rectangular aquaculture tanks[J]. Aquacultural Engineering, 2007, 36(1): 36-44. DOI:10.1016/j.aquaeng.2006.06.001 |
| [6] |
鲍伟君. 淡水池塘工程化循环水养殖系统性能评估及基于粒径分布的悬浮颗粒物去除研究[D]. 杭州: 浙江大学, 2019. BAO W J. Performance evaluation of an in-pond raceway system and study on suspended solids removal based on particle size distribution[D]. Hangzhou: Zhejiang University, 2019. |
| [7] |
刘乃硕, 刘思, 俞国燕. 两种双通道圆形养殖池水动力特性的数值模拟与研究[J]. 渔业现代化, 2017, 44(3): 1-6. LIU N S, LIU S, YU G Y. Numerical simulation of and research on hydrodynamic characteristics of two dual-channel circular aquaculture ponds[J]. Fishery Modernization, 2017, 44(3): 1-6. DOI:10.3969/j.issn.1007-9580.2017.03.001 |
| [8] |
赵乐. 管式射流驱动下的养殖池集污水动力学特性研究[D]. 舟山: 浙江海洋大学, 2017. ZHAO L. Study on the hydraulic characteristics of waste concentrated in the aquaculture pond equipped with a double pipe jet flow[D]. Zhoushan: Zhejiang Ocean University, 2017. |
| [9] |
魏武. 循环水圆形养殖池数值模拟及结构优化[D]. 湛江: 广东海洋大学, 2013. WEI W. Numerical simulation and structure optimization of circular culture tank for recirculating aquaculture systems[D]. Zhanjiang: Guangdong Ocean University, 2013. |
| [10] |
李建平, 吴康, 何相逸, 等. 基于CFD的养殖水体固液旋流分离装置数值模拟与验证[J]. 农业工程学报, 2019, 35(11): 182-187. LI J P, WU K, HE X Y, et al. Numerical simulation and validation of solid-liquid cyclone separation device for aquaculture water based on CFD[J]. Transactions of the Chinese Society of Agricultural Engineering, 2019, 35(11): 182-187. DOI:10.11975/j.issn.1002-6819.2019.11.021 |
| [11] |
SUMMERFELT S T, DAVIDSON J, TIMMONS M B. Hydrodynamics in the 'Cornell-Type' dual-drain tank[C]//Proceedings of the Third International Conference of Recirculating Aquaculture. Roanoke, VA, USA: Virginia Polytechnic Institute and State University, 2000: 160-166.
|
| [12] |
史明明, 阮赟杰, 刘晃, 等. 基于CFD的循环生物絮团系统养殖池固相分布均匀性评价[J]. 农业工程学报, 2017, 33(2): 252-258. SHI M M, RUAN Y J, LIU H, et al. Solid phase distribution simulation of culture pond with recirculating biofloc technology based on computational fluid dynamics[J]. Transactions of the Chinese Society of Agricultural Engineering, 2017, 33(2): 252-258. |
| [13] |
LIU Y, SONG X F, LIANG Z L, et al. Application of CFD modeling to hydrodynamics of CycloBio fluidized sand bed in recirculating aquaculture systems[J]. Journal of Ocean University of China, 2014, 13(1): 115-124. DOI:10.1007/s11802-014-2029-3 |
| [14] |
余康, 陈永灿, 林俊强, 等. 鱼卵漂流的欧拉-拉格朗日模型与产卵量估算[J]. 水力发电学报, 2019, 38(6): 56-68. YU K, CHEN Y C, LIN J Q, et al. Eulerian-Lagrangian modeling of riverine fish eggs drifting and improved estimation of spawning scale of fish with pelagic eggs[J]. Journal of Hydroelectric Engineering, 2019, 38(6): 56-68. |
| [15] |
孙由页, 刘飞. 以CFD-DEM为基础的养殖槽排污性能及底坡优化[J]. 水产学报, 2019, 39(4): 946-957. SUN D, LIU F. Pollution discharge performance and bottom slope optimization of aquaculture tanks for intensive pond aquaculture[J]. Journal of Fisheries of China, 2019, 39(4): 946-957. |
2. Fishery Machinery and Instrument Research Institute, Chinese Academy of Fishery Sciences, Shanghai 200092, China
 2021,
Vol. 30
2021,
Vol. 30

