2. 农业农村部大洋渔业开发重点实验室, 上海 201306;
3. 国家远洋渔业工程技术研究中心, 上海 201306;
4. 大洋渔业资源可持续开发教育部重点实验室, 上海 201306;
5. 农业农村部大洋渔业资源环境科学观测实验站, 上海 201306
柔鱼(Ommastrephes bartramii)是一种广泛分布于北太平洋海域的经济种类[1],是我国鱿钓渔船的重要捕捞对象[2]。目前,国内外学者已经在资源量时空分布[3]、资源评估管理[4-5]以及中心渔场预报[6-7]等方面对其进行了较为全面的研究。由于柔鱼是一种“生态机会主义”物种,其中心渔场分布与资源量大小极易受到海洋气候和环境条件的影响[8]。已有研究表明,环境和气候变化对北太平洋柔鱼的资源变动有着巨大影响,例如太平洋年代际震荡指数(pacific decadal oscillatio index, PDO)[9]、海表面温度(sea surface temperature, SST)[10]和叶绿素a质量浓度(chlorophyll a, Chl.a)[3]都与北太平洋柔鱼的资源变动有着密切的关系。所以,分析哪些因子对其影响更大,科学预测资源量的变动有助于掌握北太平洋柔鱼的资源现状,为以后的开发和管理提供依据。
灰色系统理论是一门不确定系统理论,其优点在于允许样本数量较少且服从任意分布,这对于缺乏数据的渔业科学来说,有很大的应用与发展前景[11]。目前,此方法已在渔场与海洋环境关系分析[12]、渔获量预测[13]等方面取得较好的效果,尤其是灰色预测模型在渔业资源量、资源丰度的预测方面应用比较广泛[14-16]。灰色预测模型通过对数量较少,信息不完整的原始数据序列进行处理,发现、掌握系统的发展规律,从而对系统的未来状态作出科学的定量预测。但是,用于预测的时间序列样本数据的长度该如何选择,不同阶数的灰色预测模型[GM(0,N)和GM(1,N)]哪个预测精度更好均未见报道。为此,采用不同时间序列长度的渔业生产数据与环境数据建立不同阶数的灰色预测模型,通过比较筛选出最优模型用于北太平洋柔鱼资源丰度的预测,为我国北太平洋鱿钓渔船科学生产提供参考。
1 材料与方法 1.1 数据来源数据包括渔业数据和环境数据。渔业生产统计数据来自上海海洋大学中国鱿钓技术组,时间为1998—2016年,空间范围为35°N~45°N和140°E~179°E,统计内容包括日期、经度、纬度、日产量和作业船数,空间分辨率为1°×1°。太平洋年代际振荡指数(PDO)来源于美国华盛顿大学大气与海洋研究联合研究所网站(http://research.jisao.washington.edu/pdo/PDO.latest),环境数据包括海表面温度(SST)和叶绿素a质量浓度(Chl.a),来源于NOAA的Oceanwatch网站(http://oceanwatch.pifsc.noaa.gov/erddap/index.html),时间为1998—2016年1—12月,空间范围分为产卵场和育肥场2个海域,产卵场海域数据时间为1—5月,范围为20°N~30°N、130°E~170°E[17];育肥场海域数据时间为7—11月,范围为35°N~50°N、150°E~175°E[17]。时间分辨率为月,空间分辨率为1°×1°。利用平均法计算各月产卵场和育肥场的平均SST和平均Chl.a。
1.2 CPUE标准化以单位捕捞努力量渔获量(catch per unit effort,CPUE)来表征柔鱼资源丰度。计算名义单位捕捞努力量渔获量(CPUE),其公式为
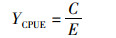 (1)
(1)
式中:YCPUE为单位捕捞努力量渔获量,t/(船·a);C为每年的渔获量,t/a;E为作业船数,船。
利用广义线性回归模型(generalized linear model,GLM)对名义CPUE进行标准化。由于CPUE受环境因子(SST)、渔场空间位置(渔场重心的经度Lon、纬度Lat)等因素影响,所以将其作为解释变量,CPUE作为响应变量,去除空间和环境因子对CPUE的影响,以标准化后的CPUE作为柔鱼资源丰度的指标。
渔场重心计算公式为
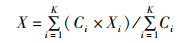 (2)
(2)
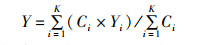 (3)
(3)
式中:X、Y分别为渔场重心的经度和纬度;Ci为i渔区的渔获量,t;Xi、Yi分别为渔区i的中心经纬度位置;K为渔区的总个数。
1.3 模型的构建 1.3.1 CPUE序列的选择对不同时间长度的CPUE序列建立GM(1,1)模型,在各个年份长度CPUE序列的预测模型中,计算不同起始年份CPUE序列建立的模型的预测值与真实值之间相对误差的平均值及方差,选择误差和方差相对小的CPUE序列作为后续建模的母序列。
1.3.2 环境因子的选择利用灰色关联法分析得到关键月份的环境及气候因子。以当年的CPUE为母序列,以产卵场与育肥场海域SST(分别简称为SGSST和FGSST)和Chl.a(分别简称为SGC和FGC)以及太平洋年代际震荡指数(PDO)为子序列,计算母序列与各个子序列之间的关联度,将各月指标中灰色关联度最大的一个作为资源丰度预测模型中的一个因子。灰色关联度计算方法见文献[18]。
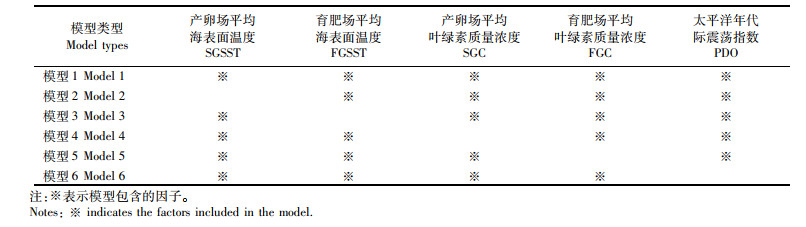
1.3.3 模型的建立与评价利用离散GM(0,N)和GM(1,N)模型对西北太平洋柔鱼资源丰度进行预测。其中数字0和1表示模型阶数,N=i+1(i为因子的个数)。模型的具体计算方法见文献[18]。考虑各种因子对资源丰度影响不同,拟建立6种不同模型来评价各种因子的重要性(表 1)。
|
表 1 多种因子组合的模型类型 Tab.1 Model types with multiple factor combinations |
通过模型预测的CPUE与真实的CPUE比较,计算出预测值与真实值之间的平均相对误差,并预留出构建模型样本数据的下一年数据用作验证数据,结合模型的拟合精度和预测精度来选择最优模型。
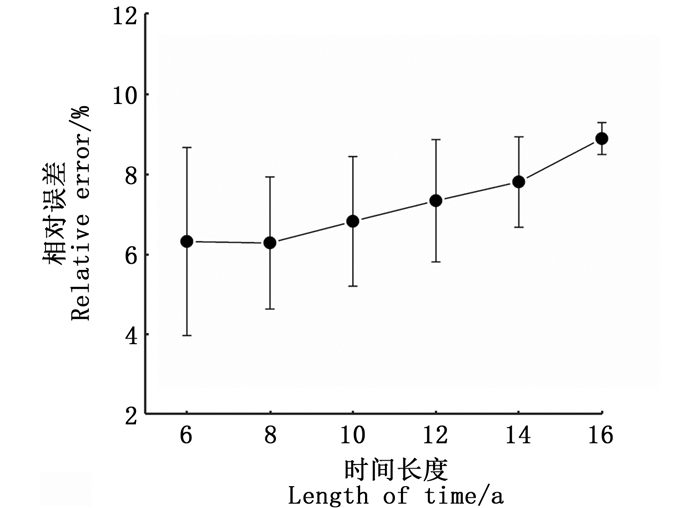
2 结果 2.1 CPUE序列的选择由图 1可知,随着CPUE序列时间长度的增加,GM(1,1)模型的平均相对误差基本上呈现增加的趋势,方差逐渐减小。8年CPUE序列的GM(1,1)模型的平均相对误差最小(6.28%),所以选择8年CPUE序列中相对误差最小的序列(1998—2005年)作为后续GM(0,N)和GM(1,N)模型的母序列,以期加入环境因子来提高模型预测的精度。
|
图 1 不同时间长度CPUE序列GM(1,1) 预测模型的相对误差 Fig. 1 Relative error of GM (1, 1) prediction model of CPUE sequence with different time length |
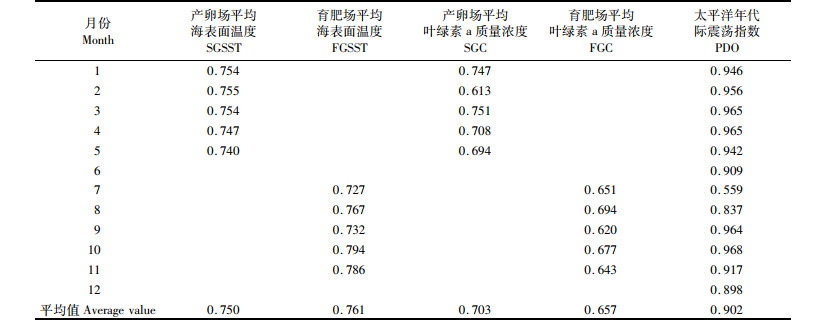
根据灰色关联分析的结果(表 2)来看,太平洋年代际振荡指数(PDO)的影响程度最大,其灰色关联度的平均值要远大于另外4个环境因子。按照关联度的平均值排序,各因子重要性从大到小的排序为:PDO,育肥场平均海表面温度(FGSST),产卵场平均海表面温度(SGSST),产卵场平均叶绿素a质量浓度(SGC),育肥场平均叶绿素a质量浓度(FGC)。
|
表 2 各环境因子子序列与当年CPUE母序列的灰色关联系数 Tab.2 Value of grey correlation indices between the environmental or climatic factors subsequence and the CPUE sequence |
各个环境因子对资源丰度影响最大的月份不同,其中10月的FGSST和PDO、2月SGSST、3月SGC、8月FGC与CPUE的灰色关联度最大,因此选择这5种因子作为西北太平洋柔鱼资源丰度预报模型的关键因子。
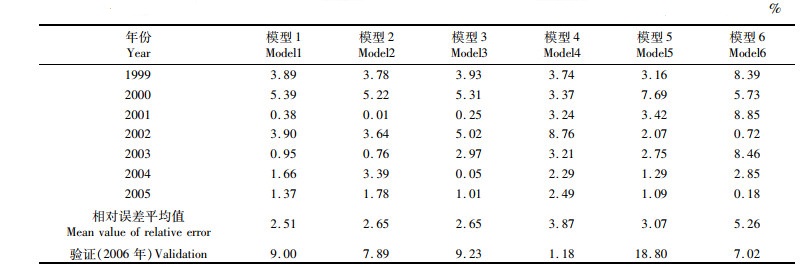
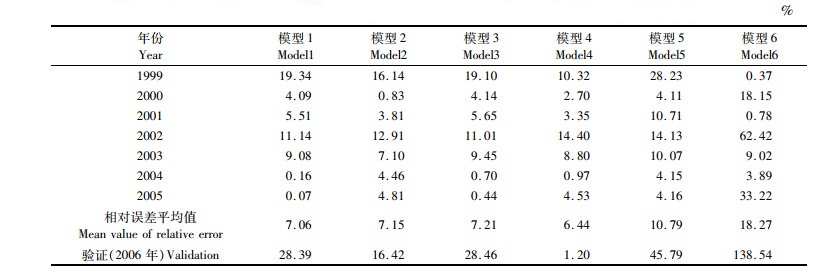
2.3 预测模型的比较与选择从模型的相对误差平均值(表 3,4)来看,GM(0,N)模型预测精度均高于GM(1,N)模型。从2006年模型验证的结果(表 3,4)来看,无论是GM(0,N)模型还是GM(1,N)模型,模型4的预测精度远高于其他模型,相对误差分别为1.18%和1.20%。由于GM(0,N)模型中各个模型拟合误差相差不大,且模型4验证结果远小于其他模型,所以选择不含有SGC因子的模型4作为西北太平洋柔鱼资源丰度预测的最佳模型。
|
表 3 西北太平洋柔鱼资源丰度GM(0,N)预测模型的相对误差 Tab.3 The relative error of Ommastrephes bartramii abundance calculated by GM(0, N)model |
|
表 4 西北太平洋柔鱼资源丰度GM(1,N)预测模型的相对误差 Tab.4 The relative error of Ommastrephes bartramii abundance calculated by GM(1, N)model |
通过灰色系统理论和方法,以产卵场和育肥场的环境因子与气候因子作为指标,对北太平洋柔鱼资源丰度进行了预测并得到了较好的结果。从灰色关联分析与预测模型的结果(表 2~4)可以看出,气候因子和环境因子的重要性与灰色关联结果基本上一致。无论GM(0,N)模型还是GM(1,N)模型,其模型6(不包含PDO)的相对误差均远大于包含所有因子的模型1和其他模型。这说明太平洋年代际振荡指数PDO是影响北太平洋柔鱼资源丰度的重要因子之一。如余为[19]认为,PDO作为以10年周期尺度变化的太平洋气候变化现象,其“冷、暖相位”的变化会对渔场环境产生影响。PDO暖期时,气候环境有利于柔鱼生长和繁殖,导致资源量上升,相反PDO冷期时,资源量骤减。而且,本研究数据采用的是1998—2005年的CPUE数据,刚好经历了一个PDO冷期(1998—2002)与一个PDO暖期(2003—2006)[20],所以PDO与年CPUE的灰色关联效果较好。
在环境因子上,从灰色关联分析的结果(表 2)来看,产卵场与育肥场的平均海表面温度对北太平洋柔鱼的资源丰度的影响最大。如:汪金涛[21]用产卵场的SST作为渔情预报模型的一个影响因子来预测柔鱼资源的补充量;余为等[22]利用产卵场和育肥场的SST距平值预测柔鱼的资源丰度。分别去除SGSST与FGSST的模型2与模型3,相比于包含所有因子的模型1,精度均降低,表明SST对柔鱼资源补充量的影响较大。产卵场与育肥场的平均Chl.a对年CPUE的影响最小,这与高雪等[23]的研究结果一致。不含有SGC的模型4不仅拟合效果好,预测精度也大大提升,原因可能是:(1)在没有清楚了解柔鱼的具体洄游路径的前提下,将产卵场与育肥场可能存在的所有范围求Chl.a平均值,这会弱化Chl.a的影响;(2)可能与卫星遥感数据的模拟算法有关。但有研究[24]认为,叶绿素峰区高生产海域形成了柔鱼良好的育肥场和索饵场,适合柔鱼仔鱼生长,从而提高资源的补充量。
灰色系统模型允许样本量少且不需要先验的优点,但从结果(图 1)可以看出,样本量的选择是有一定的适用范围,样本量过少和过多都会影响最终预测模型的精度。另外,不同阶数的GM模型预测的结果有一定的差异,结果显示GM(0,N)模型预测效果比GM(1,N)模型要好(图 2),但这不具有普适性,对于不同特征的CPUE序列的拟合精度结果可能存在不同[25]。从拟合值与真实值的关系(图 3)来看,CPUE的变化趋势基本上一致,并且模型预测的拟合值变化幅度较小,从预测模型的参数来看,发展系数-a为-1.71(表 5)满足中长期预报模型的条件(-a<0.3)[18]。针对灰色预测模型随着时间延续,预测精度不稳定的问题[26],本研究只预留出一年的数据进行验证,虽然预测精度较好,但对于是否适合长期预测需要进一步的研究,在今后的研究中扩大验证条件范围,加强模型残差的修正,以提高模型的稳定性和适用性。
|
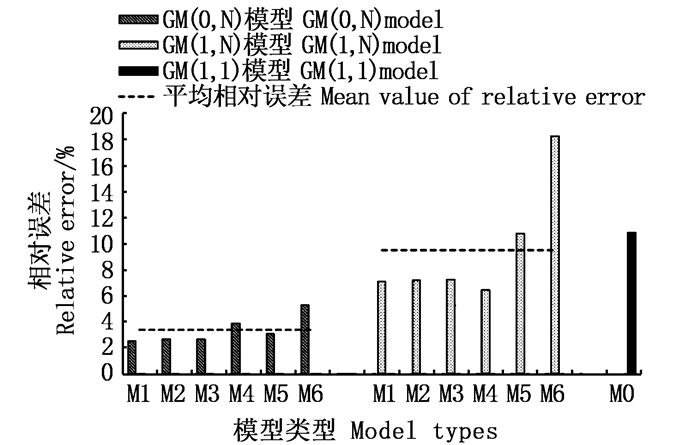
M0表示原始模型,即不加环境因子的GM(1,1)模型;M1~M6表示GM(1,N)和GM(0,N)模型中的模型1~模型6。 M0 represents the original model(the GM (1, 1) model without environmental factors).M1-M6 represents themodel 1 ~ model 6 by GM (1, N) and GM (0, N) models. 图 2 不同阶数预测模型的所有模型类型的平均相对误差 Fig. 2 Mean relative errors of all model types for different order prediction models |
|
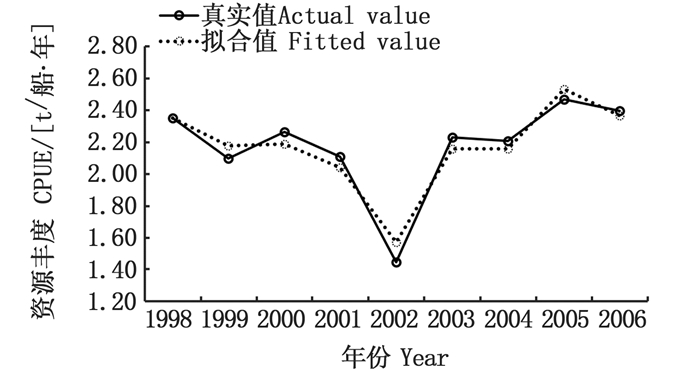
图 3 北太平洋柔鱼资源丰度最优预测模型[GM(0,N)模型4]拟合值与真实值的比较 Fig. 3 Comparison of the real CPUE and predict CPUE sequence based on Ommastrephes bartrami forecasting model[GM(0, N)model 4] |

|
表 5 GM(0,N)预测模型4因子的参数值 Tab.5 The parameters of GM (0, N) forecasting model 4 |
| [1] |
陈新军, 钱卫国, 刘必林, 等. 主要经济大洋性鱿鱼资源渔场生产性调查与渔业概况[J]. 上海海洋大学学报, 2019, 28(3): 344-356. CHEN X J, QIAN W G, LIU B L, et al. Productive survey and fishery for major pelagic economic squid in the world[J]. Journal of Shanghai Ocean University, 2019, 28(3): 344-356. |
| [2] |
陈新军. 世界头足类资源开发现状及我国远洋鱿钓渔业发展对策[J]. 上海海洋大学学报, 2019, 28(3): 321-330. CHEN X J. Development status of world cephalopod fisheries and suggestions for squid jigging fishery in China[J]. Journal of Shanghai Ocean University, 2019, 28(3): 321-330. |
| [3] |
唐峰华, 靳少非, 张胜茂, 等. 北太平洋柔鱼渔场时空分布与海洋环境要素的研究[J]. 中国环境科学, 2014, 34(8): 2093-2100. TANG F H, JIN S F, ZHANG S M, et al. Study for marine environmental elements on spatio-temporal distribution of neon flying squid in the north Pacific fishing ground[J]. China Environmental Science, 2014, 34(8): 2093-2100. |
| [4] |
陈新军, 曹杰, 刘必林, 等. 基于贝叶斯Schaefer模型的西北太平洋柔鱼资源评估与管理[J]. 水产学报, 2011, 35(10): 1572-1581. CHEN X J, CAO J, LIU B L, et al. Stock assessment and management of Ommartrephes bartramii by using a Bayesian Schaefer model in the Northwestern Pacific Ocean[J]. Journal of Fisheries of China, 2011, 35(10): 1572-1581. |
| [5] |
刘金立, 陈新军, 李纲, 等. 西北太平洋柔鱼资源综合配置模型及管理策略探讨[J]. 海洋与湖沼, 2014, 45(5): 1016-1022. LIU J L, CHEN X J, LI G, et al. Management strategy and comprehensive allocation model of Ommastrephes bartramii in the Northwestern Pacific Ocean[J]. Oceanologia et Limnologia Sinica, 2014, 45(5): 1016-1022. |
| [6] |
魏广恩, 陈新军, 李纲. 西北太平洋柔鱼洄游重心年际变化及预测[J]. 上海海洋大学学报, 2018, 27(4): 573-583. WEI G N, CHEN X J, LI G. Interannual variation and forecasting of Ommastrephes bartramii migration gravity in the northwest Pacific Ocean[J]. Journal of Shanghai Ocean University, 2018, 27(4): 573-583. |
| [7] |
魏联, 陈新军, 雷林, 等. 西北太平洋柔鱼BP神经网络渔场预报模型比较研究[J]. 上海海洋大学学报, 2017, 26(3): 450-457. WEI L, CHEN X J, LEI L, et al. Comparative study on the forecasting models of squid fishing ground in the northwest Pacific Oceanbased on BP artificial neural network[J]. Journal of Shanghai Ocean University, 2017, 26(3): 450-457. |
| [8] |
NISHIKAWA H, TOYODA T, MASUDA S, et al. Wind-induced stock variation of the neon flying squid(Ommastrephes bartramii) winter-spring cohort in the subtropical North Pacific Ocean[J]. Fisheries Oceanography, 2015, 24(3): 229-241. DOI:10.1111/fog.12106 |
| [9] |
余为, 陈新军, 易倩. 不同气候模态下西北太平洋柔鱼渔场环境特征分析[J]. 水产学报, 2017, 41(4): 525-534. YU W, CHEN X J, YI Q. Analysis of variations in the environmental conditions on the fishing ground of neon flying squid (Ommastrephes bartramii) in the Northwestern Pacific Ocean under different climate modes[J]. Journal of Fisheries of China, 2017, 41(4): 525-534. |
| [10] |
XU J, CHEN X J, CHEN Y, et al. The effect of sea surface temperature increase onthe potential habitat of Ommastrephes bartramii in the Northwest Pacific Ocean[J]. Acta Oceanologica Sinica, 2016, 35(2): 109-116. DOI:10.1007/s13131-015-0782-9 |
| [11] |
陈新军. 灰色系统理论在渔业科学中的应用[M]. 北京: 中国农业出版社, 2003: 1-32. CHEN X J. Grey system theory in fisheries science[M]. Beijing: China Agriculture Press, 2003: 1-32. |
| [12] |
王良明, 李渊, 张然, 等. 西北太平洋日本鲭资源丰度分布与表温和水温垂直结构的关系[J]. 中国海洋大学学报(自然科学版), 2019, 49(11): 29-38. WANG L M, LI Y, ZHANG R, et al. Relationship between the resource distribution of Scomber japonicus and seawater temperature vertical structure of Northwestern Pacific Ocean[J]. Periodical of Ocean University of China, 2019, 49(11): 29-38. |
| [13] |
杜小伟, 刘群. 灰色GM(1, 1)模型和Verhulst模型在青岛市海水养殖产量预测中的应用[J]. 浙江海洋学院学报(自然科学版), 2011, 30(5): 420-425. DU X W, LIU Q. Prediction of seawater aquaculture production of Qingdao city by using the GM (1, 1) model and the Verhulst model[J]. Journal of Zhejiang Ocean University(Natural Science), 2011, 30(5): 420-425. DOI:10.3969/j.issn.1008-830X.2011.05.010 |
| [14] |
王言丰, 陈新军, 陈芃, 等. 基于灰色系统西南大西洋阿根廷滑柔鱼资源丰度预测模型的构建[J]. 海洋学报, 2019, 41(4): 64-73. WANG Y F, CHEN X J, CHEN P, et al. Prediction of abundance index of Argentine shortfin squid in the Southwest Atlantic Ocean based on grey system model[J]. Acta Oceanologica Sinica, 2019, 41(4): 64-73. |
| [15] |
段丁毓, 陈芃, 陈新军, 等. 基于灰色系统的秘鲁鳀资源量预测模型的构建[J]. 上海海洋大学学报, 2018, 27(2): 284-290. DUAN D Y, CHEN P, CHEN X J, et al. The construction of biomass forecasting model for the anchoveta (Engraulis ringens) by the grey system model[J]. Journal of Shanghai Ocean University, 2018, 27(2): 284-290. |
| [16] |
解明阳, 陈新军, 汪金涛. 基于灰色系统的太平洋褶柔鱼冬春生群资源丰度变化研究[J]. 海洋渔业, 2018, 40(6): 641-648. XIE M Y, CHEN X J, WANG J T. On changes of abundance index of winter-spring cohort of Todarodes pacificus in the Northwest Pacific based on grey system theory[J]. Marine Fisheries, 2018, 40(6): 641-648. DOI:10.3969/j.issn.1004-2490.2018.06.001 |
| [17] |
CHEN X J, ZHAO X H, CHEN Y. Influence of El Niño/La Niña on the western winter-spring cohort of neon flying squid (Ommastrephes bartramii) in the Northwestern Pacific Ocean[J]. ICES Journal of Marine Science, 2007, 64(6): 1152-1160. DOI:10.1093/icesjms/fsm103 |
| [18] |
刘思峰, 杨英杰, 吴利丰, 等. 灰色系统理论及其应用[M]. 7版. 北京: 科学出版社, 2014. LIU S F, YANG Y J, WU L F, et al. Grey system theory and its application[M]. 7th ed. Beijing: China Science Press, 2014. |
| [19] |
余为. 西北太平洋柔鱼冬春生群对气候与环境变化的响应机制研究[D]. 上海: 上海海洋大学, 2016. YU W. Response mechanism of winter-spring cohort of neon flying squid to the climatic and environmental variability in the Northwest Pacific Ocean[D]. Shanghai: Shanghai Ocean University, 2016. |
| [20] |
杨龙奇, 许东峰, 徐鸣泉, 等. 黑潮入侵南海的强弱与太平洋年代际变化及厄尔尼诺-南方涛动现象的关系[J]. 海洋学报, 2014, 36(7): 17-26. YANG L Q, XU D F, XU M Q, et al. A study of correlation between Pacific Decadal Oscillation and El Niño-Southern Oscillation and the strength of Kuroshio intrusion into the South China Sea[J]. Acta Oceanologica Sinica, 2014, 36(7): 17-26. DOI:10.3969/j.issn.0253-4193.2014.07.003 |
| [21] |
汪金涛. 大洋性经济柔鱼类渔情预报与资源量评估研究[D]. 上海: 上海海洋大学, 2015. WANG J T. Fishery forecasting and stock assessment for commercial ocean Ommastrephid squid[D]. Shanghai: Shanghai Ocean University, 2015. |
| [22] |
余为, 陈新军. 西北太平洋柔鱼栖息地环境因子分析及其对资源丰度的影响[J]. 生态学报, 2015, 35(15): 5032-5039. YU W, CHEN X J. Analysis of environmental conditions and their influence on the abundance of neon flying squid in the Northwest Pacific Ocean[J]. Acta Ecologica Sinica, 2015, 35(15): 5032-5039. |
| [23] |
高雪, 陈新军, 余为. 基于灰色系统的西北太平洋柔鱼冬春生群资源丰度预测模型[J]. 海洋学报, 2017, 39(6): 55-61. GAO X, CHEN X J, YU W. Forecasting model of the abundance index of winter-spring cohort of Neon flying squid(Ommastrephes bartramii) in the Northwest Pacific Ocean based on grey system theory[J]. HaiyangXuebao, 2017, 39(6): 55-61. DOI:10.3969/j.issn.0253-4193.2017.06.006 |
| [24] |
ICHⅡ T, MAHAPATRA K, SAKAI M, et al. Changes inabundance of the neon flying squid Ommastrephes bartramii in relation to climate change in the central North Pacific Ocean[J]. Marine Ecology Progress Series, 2011, 441: 151-164. DOI:10.3354/meps09365 |
| [25] |
孟伟, 刘思峰, 方志耕, 等. 基于互逆分数阶算子的GM(1, 1)阶数优化模型[J]. 控制与决策, 2016, 31(4): 661-666. MENG W, LIU S F, FANG Z G, et al. GM(1, 1) with optimized order based on mutual fractional operators[J]. Control and Decision, 2016, 31(4): 661-666. |
| [26] |
曾亮. 改进的灰色多变量GM(1, N)模型及其应用[J]. 西南大学学报(自然科学版), 2019, 41(9): 68-76. ZENG L. An improved grey multivariable GM(1, N) model and its application[J]. Journal of Southwest University (Natural Science Edition), 2019, 41(9): 68-76. |
2. Key Laboratory of Oceanic Fisheries Exploration, Ministry of Agriculture and Rural Affairs, Shanghai 201306, China;
3. National Engineering Research Center for Oceanic Fisheries, Shanghai 201306, China;
4. Key Laboratory of Sustainable Exploitation of Oceanic Fisheries Resources, Ministry of Education, Shanghai 201306, China;
5. Scientific Observing and Experimental Station of Oceanic Fishery Resources, Ministry of Agriculture and Rural Affairs, Shanghai 201306, China
 2021,
Vol. 30
2021,
Vol. 30


