虾类是我国水产养殖的重要组成部分[1],2014年全国虾类养殖面积约50万公顷,其中南美白对虾产量290万t左右,产值1950余亿元[2]。投饵是养虾全过程的重要环节,由于虾类具有区域觅食的领地习性,要求饲料能均匀投入塘中,避免影响虾类的摄食和部分区域多余饲料污染水质 [3-5]。虾类养殖投饵目前仍主要以沿塘口或撑船人工抛洒为主,由于水产养殖类劳动力日渐匮乏和成本上升,实现饲料投喂自动化是一个必然趋势。鱼类养殖中采用定点投喂,不考虑饲料抛洒的均匀性,因此直接将鱼塘投饵机移到船体上不能解决问题。现有投饵机主要采用抛盘式投喂,利用偏心轮和铰链四杆机构,促使机构产生振动,从而达到均匀下料,饲料颗粒经下料口落入抛料转盘,借助电机的高转速带动转盘将饲料抛出。这种投饵方式在下料过程中会因抖料盘的振幅过大使得饲料颗粒跳动大,造成漏料,或者由于抖料盘振幅过小导致饲料滞留。另外,为实现一定的抛洒距离,不合理的抛料盘挡板会给饲料颗粒施加过大的撞击力,造成饲料破碎,导致饲料浪费和水体污染。
针对以上问题,本文对投饵机下料和抛料系统进行优化。对下料机构进行运动分析,导出偏心距和抖料盘振幅的关系,通过试验数据验证,获得最优值,实现下料量的精准控制。对抛料转盘进行优化设计,通过建立三维模型,改变抛盘挡板的折弯角度,分析饲料的运动轨迹,获得最优折弯角度,最后以现场抛料试验来验证优化效果。
1 移动式投饵系统总体方案上海海洋大学开发了具有自主导航功能的双体式移动虾塘投喂平台(图 1),船体采用玻璃钢材料,长1.8 m,宽1.1 m,最大航速3 m/s,饲料搭载量80 kg,可以满足10亩虾塘投喂需求。该平台通过手持遥控终端实现虾塘投喂路径的自主采集输入,巡航精度为0.9 m以内,满足实际投饵精度要求[6-7]。投饵机构位于图 1船体甲板箱体下部,饲料置于箱体上部。

|
图 1 双体式虾塘自主导航移动投喂平台
Fig. 1 Shrimp pond autonomous navigation mobile feeding catamaran
|
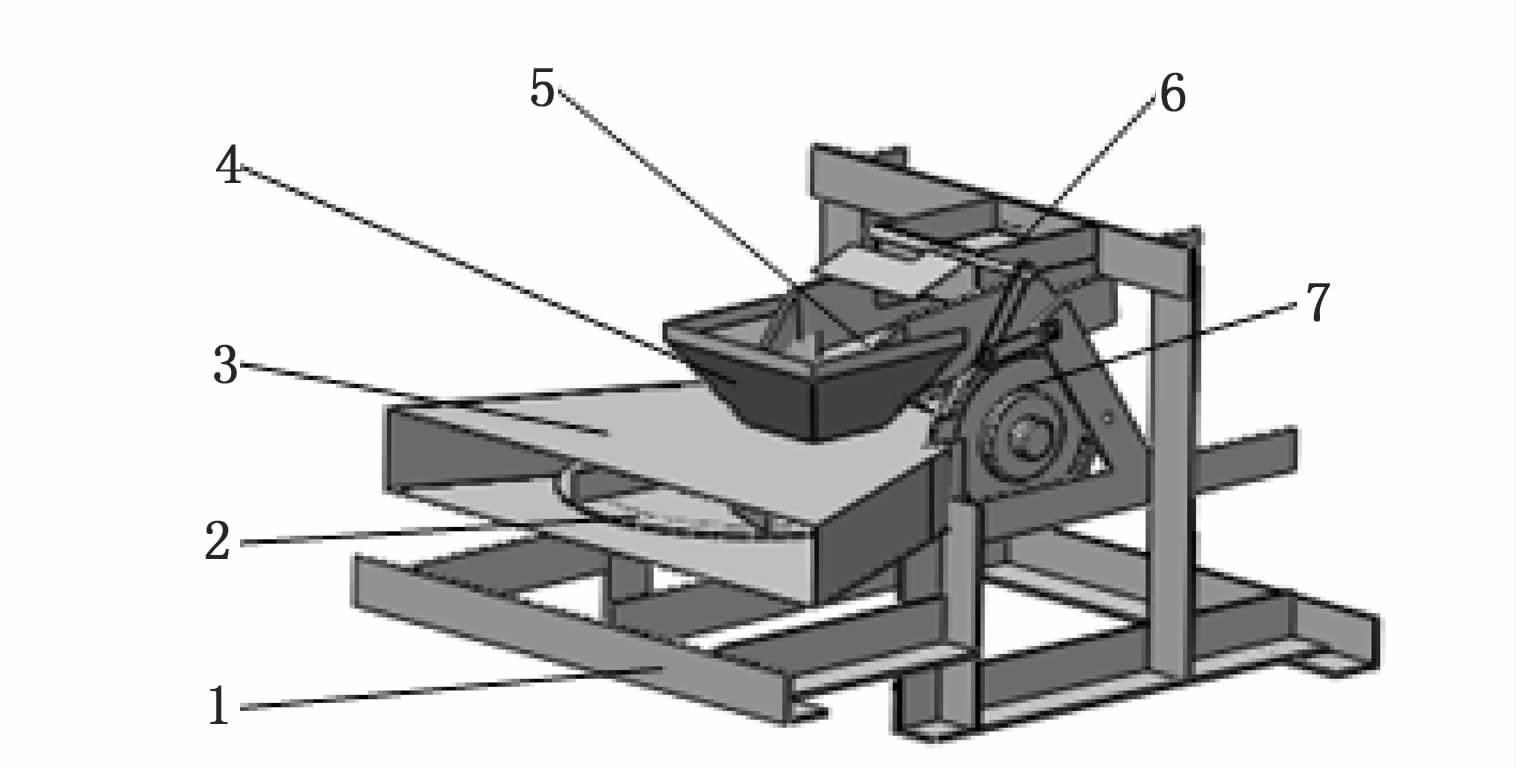
投饵机一般由框架体、抛料转盘、电机、下料口、抖料盘、偏心轴和偏心轴套等组成(图 2)。框架体主要用来固定各零部件,其设计应尽可能简单轻便;两个盘式电机额定转速1 350 r/min,一个用于带动抛料转盘的转动,另一个带动偏心轮用于抖料盘的振动,具有电流小、重量轻、节能等优势;抛料转盘用来抛洒饲料;抖料盘采用铸铁制造,主要通过抖动实现下料;通过挡板调节下料口大小控制饲料颗粒的下投速度,由养殖户根据需求进行料量的调节。偏心轴和偏心轴套实现抖料盘的振动,饲料经由落料口落入抖料盘当中,通过盘式电机带动偏心轮,促使抖料盘抖动,将饲料振动落入抛料转盘,转盘在电机的高速带动下,将饲料抛出,完成投饵。
|
图 2 投饵机结构图
Fig. 2 Structure diagram of feeding machine
1.框架体; 2.抛料转盘; 3.抛料器壳; 4.饲料通道; 5.抖料盘;6.落料口; 7.盘式电机。 1.Frame structure; 2.Bait rotary throwing tray; 3.Thrower box; 4. Bait filling funnel; 5. Shaking trays; 6. Bait filling hole; 7.Disc motor. |
投饵机下料主要是利用偏心轮运动过程中产生的位移变化带动抖料盘上下抖动,饲料颗粒随着抖料盘的抖动产生振动,由于抖料盘自身会有一定坡度,饲料颗粒在自身重力和料盘的抖动下经下料口落入抛料盘上,从而达到下料的目的。为使抛料均匀,必须保证落入抛料盘饲料量的均匀性。影响下料均匀性的主要因素是偏心轮运动过程中促使抖料盘产生的位移变化,即抖料盘振动幅度。
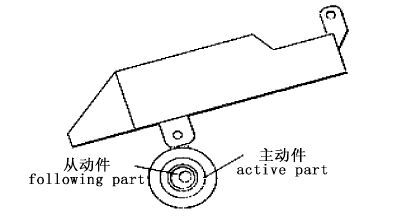
偏心轮是一种凸轮机构,根据从动件与主动件接触的形式,可分为尖顶从动件偏心凸轮机构和平顶从动件偏心轮机构[8]。尖顶从动件偏心凸轮机构的主、从动件间的接触点的位置始终相对从动件固定,而平顶从动件偏心轮凸轮机构的主、从动件间的接触点的位置相对从动件来回变化。基于此,可以根据需求选择合适运动规律的偏心凸轮机构。投饵机的抖料方式即为利用尖顶从动件偏心轮凸轮机构原理,再结合转动电机的高转速,促使抖料盘的高频率抖动,最终实现均匀下料。
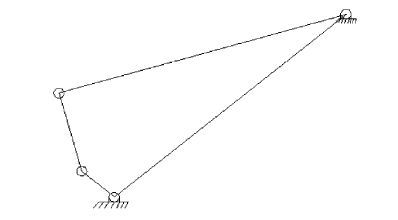
2.2 偏心抖料系统铰链四杆机构分析根据整个偏心抖料系统的结构和工作原理,可以把下料系统看成是一个铰链四杆机构。通过分析各杆的运动以及杆与铰链之间的相对关系,借助相关的数学分析方法对机构进行位置分析,得到变动的偏心距对抖料盘振幅的影响[9-11]。图 3是虾塘投饵机上的偏心抖料机构,简化后的铰链四杆结构见图 4。
|
图 3 投饵机偏心抖料系统
Fig. 3 Eccentric shaking system of feeding machine
|
|
图 4 铰链四杆机构简图
Fig. 4 Sketch of hinged four-bar mechanism
|
根据南美白对虾配合饲料规格可分为0、1、2、3号。其中0号呈粉末状,主要针对幼虾。1~3号主要针对体长为2.5 cm以上的成长期对虾,其中2号料使用时间最长,本文中相关试验均采用2号饲料进行。结合养殖经验及对虾本身食物摄取量得知,当投饵机在虾塘中的预设移动速度为0.8 m/s时,投饵机的最小下料量不得低于1 000 g/min,否则会导致投料量不足影响虾的生长;投饵机的最大下料量不得超过3 000 g/min,否则会造成饲料的过度抛洒,引发水体污染。为解决这一问题,需结合机构的高低档位(当时为低档,当时为高档)确定偏心距对抖料盘振幅的影响,获得最优偏心距和最优振幅区间。
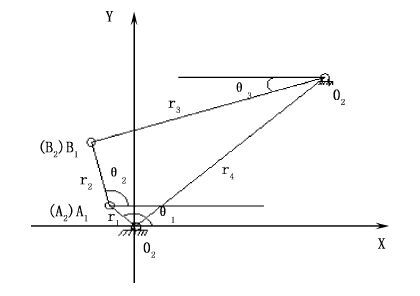
建立如图 5所示坐标系,采用封闭向量多边形法对铰链四杆机构进行机构位置分析。
|
图 5 铰链四杆机构数学模型
Fig. 5 Mathematical model of hinged four-bar mechanism
|
令r1、r2、r3、r4表示封闭向量多边形的各个向量,这里各向量均为复数。由图 5可知,位置解满足封闭向量多边形法则[12]。建立闭环方程:
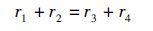 (1)
(1)
转化为复数的指数形式:
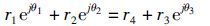 (2)
(2)
基于实部和虚部分解得到
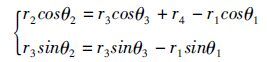 (3)
(3)
式(3)两边平方相加得:
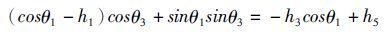 (4)
(4)
式中: 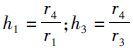
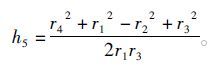
将上述方程变成二次多项式的形式,即
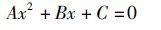 (5)
(5)
式中:A=-h1+(1-h3)cosθ1+h5;B=-2sinθ1;C=h1-(1+h3)cosθ1+h5 。
最后可求得:
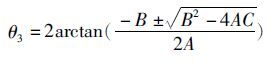 (6)
(6)
类似的方法可通过消去,求得
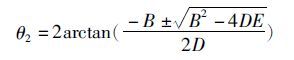 (7)
(7)
式中:D=-h1+(1+h2)cosθ1+h4 ;
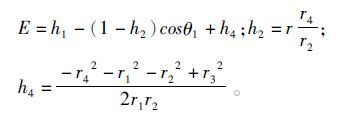
B1O2杆与水平方向的夹角为θ3,在O1A1的基础上增加不同的偏心距Δl(即改变r1的值),便可得到与之对应的θ3值,进而求得杆B1O2在点B1的位移变化(即抖料盘的振幅变化),计算方法如下:
当r1增加Δl时,即r1* =r1+Δl,将r1*带入公式(5)及(7)可得θ3*,于是得出B1O2杆角度的变化值:
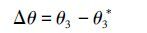 (8)
(8)
弧长与角度的换算公式:
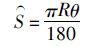 (9)
(9)
当改变中心距的值时,杆B1O2在B1的弧长变化为:
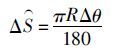 (1)
(1)
下面通过对不同档位测定5组不同的偏心距,分别为0.6、0.8、1.0、1.2、1.4,当偏心距为0.8 时,下料量在预期值范围内,且漏料量极少,故取偏心距0.8为最优值。根据公式可获得抖料盘的最优振幅区间为1.26~1.68。
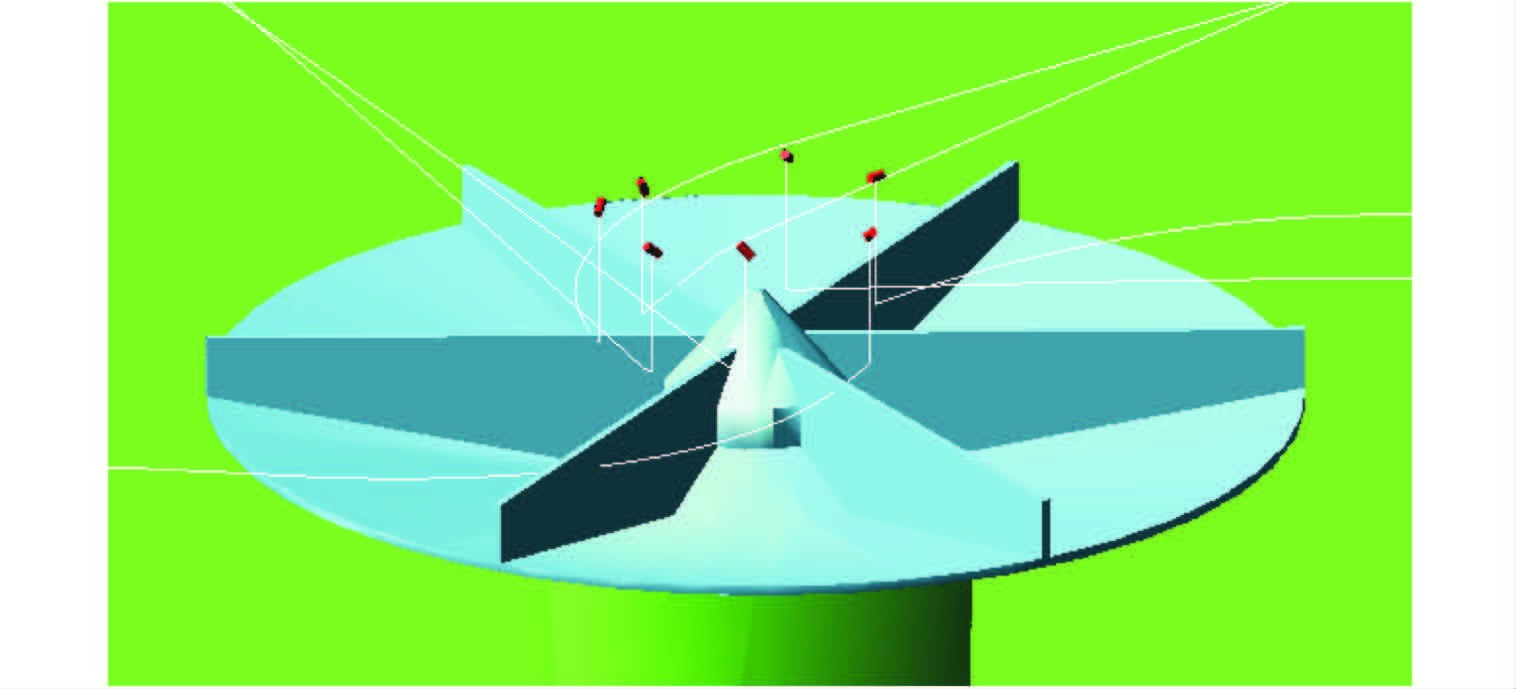
3 抛料系统的优化分析 3.1 基于ADAMS的运动仿真对抛料盘进行三维建模,如图 6所示。模型主要由底板、支撑柱和抛料盘3部分组成,其中支撑柱的高度按照实际抛料盘离地面的高度设定,以保证仿真效果的准确性[12-13]。
|
图 6 抛料盘运动仿真
Fig. 6 Motion simulation of bait throwing tray
|
将模型导入,对底板施加固定副,抛料转盘添加转动副。转动副的扭矩参数设定为165 ,将转动步数设为1 450,时长设为60 s。然后将饲料模型导入至叶轮叶片之间的扇形区域,并添加与抛料盘模型间的撞击关系,让抛料盘按照设定参数运转,从而得出饲料模型的运动轨迹及落地后的分布范围。
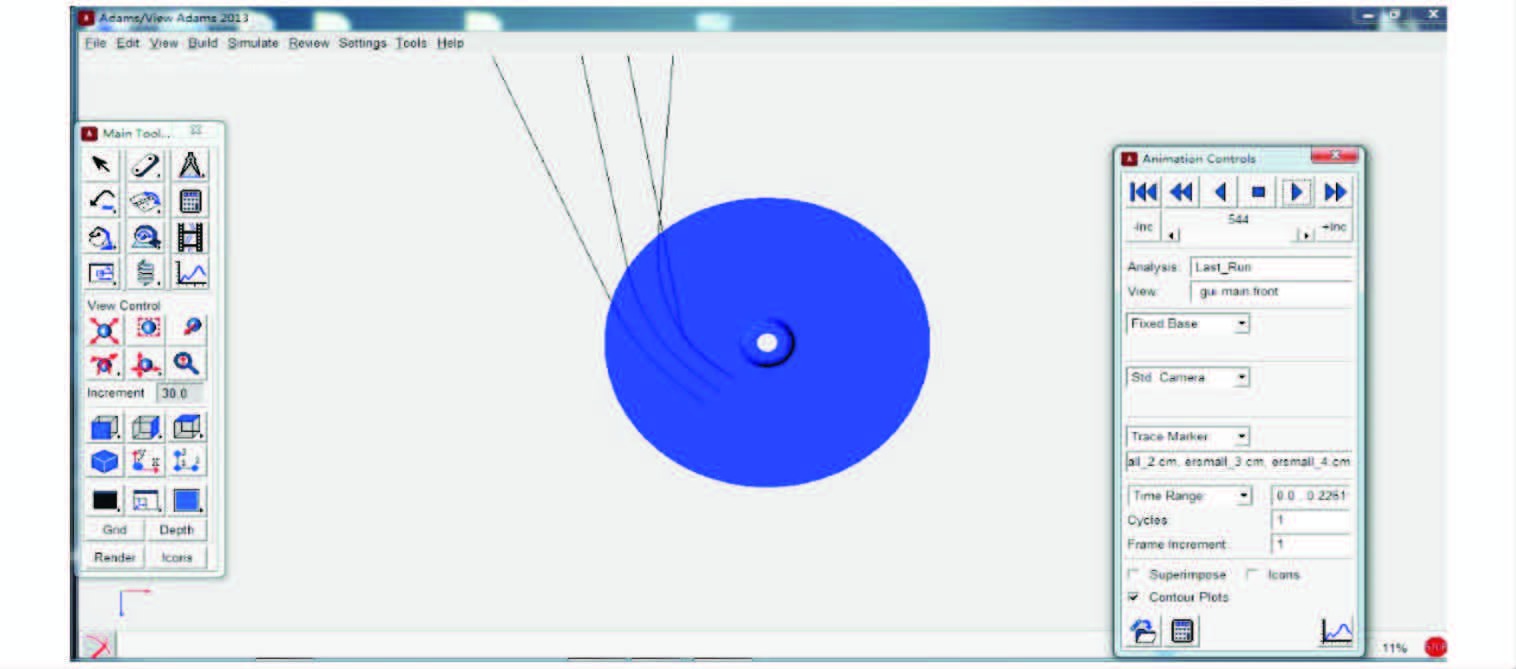
针对投饵机抛料盘存在抛料不均的问题,通过改变抛料盘叶轮叶片的折弯角度来分别进行运动仿真,观察不同折弯角度下饲料抛洒轨迹和抛洒范围。分别选取0°、6°、12°、18°4个折弯角度,参照已有投饵机抛料盘相对落料口的位置添加饲料模型及运动副和约束条件,实现不同模型的运动仿真。4个模型的运动仿真过程采用控制变量法,即折弯角度为唯一变量。通过仿真得出不同折弯角度对饲料轨迹及抛洒范围的影响,仿真效果如图 7所示,图中四条曲线代表饲料的抛洒轨迹及抛洒范围。
|
图 7 抛料效果图
Fig. 7 Chart of bait throwing effect
|
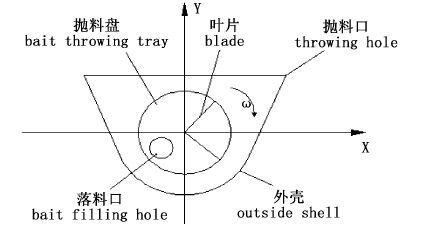
投饵机抛料系统示意图如图 8所示,设抛料盘以角速度进行运转,饲料由落料口落入叶轮叶片之间的扇形区域,由于离心力和叶轮叶片的撞击力作用,饲料会被料盘以一定的速度和轨迹抛洒出去。当折弯角度为0°时,饲料的抛洒轨迹明显偏向抛料出口的右侧,饲料抛洒过度集中;当折弯角度为6°时,饲料抛洒范围有明显改善,饲料抛洒轨迹相对0°轨迹整体向左偏移;当折弯角度为12°时,饲料的抛洒轨迹相对图 8中的Y轴成对称分布,且饲料路径轨迹分布均匀;当折弯角度为18°时,饲料的抛洒轨迹会相对Y轴向左侧偏移,使得饲料轨迹与抛料器左侧壳壁出现交叉,这说明有部分饲料会与壳壁发生碰撞,导致饲料的破碎。
|
图 8 抛料系统示意图
Fig. 8 Diagram of bait throwing system
|
综合分析可知,改变叶轮叶片折弯角度能有效校正饲料抛洒轨迹,使得饲料的分布范围增加,提高了饲料抛洒的均匀度。
4 投饵效果对比试验为验证对投饵机下料系统和抛料系统的优化效果,将投饵装置试验平台分别置于陆上和水面进行试验。
4.1 陆上对比试验及效果分析试验选用地表平整地面,试验区域为方形,面积为36 m2,装置选用优化前后投饵机各一台,饲料选用南美白对虾喂养专用2号饲料10 kg(经细孔隔筛板过滤后的重量,排除饲料原始破碎率的干扰),电子称一台(测量精度为0.1 g),60 cm见方的泡沫框一个,清理毛刷一支,秒表一块,如图 9所示。

|
图 9 陆上投饵试验
Fig. 9 Feeding test on land
|
饲料出口离地面0.6 m。投饵机每次试验饲料投放1 min,饲料抛出呈扇形分布,在离投饵机投饵出口2 m处等间距设定4个采样点,分别对每次试验进行采样,算出饲料分布密度。为减小误差,每组试验重复3次,取平均值进行对比。系统试验实施如图 10所示,A、B、C、D为4个采样区域。
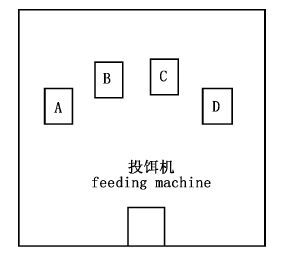
|
图 10 试验系统示意图
Fig. 10 Diagram of test system
|
装置优化前后对饲料抛洒进行统计分析,其分布密度分别如表 1、表 2所示。
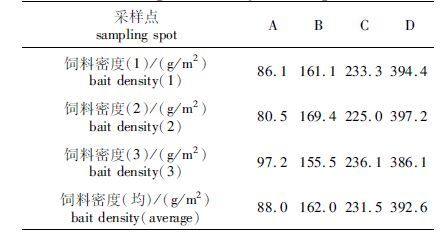
|
表 1 优化前投饵装置抛洒饲料密度 Tab.1 Bait spread density before optimization |
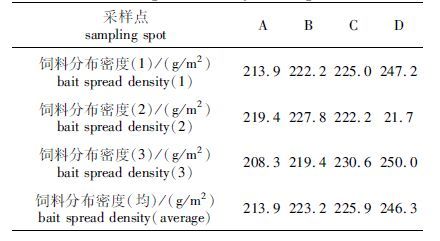
|
表 2 优化后投饵装置抛洒饲料分布密度 Tab.2 Bait spread density after optimization |
对双样本进行统计学t检验,验证4个样点饲料分布密度变化的显著性。经计算,表 1样本均值方差为16 900.77,表 2样本均值方差为186.44。由数据分析可知,样本值-0.134 64对应P=0.901 4>显著性水平0.1,显示提升效果显著。基于变异系数(标准差/平均数)进行分析,表 1样本均值标准差为130.88,平均数为218.50,其变异系数为59.5%;表 2样本均值标准差为13.7,平均数为227.33,其变异系数为6%。优化后装置抛洒饲料分布密度变异程度远小于优化前,饲料抛洒均匀性明显提高。
抛料盘的高速转动会造成饲料的破碎,为对破碎率进行测定,回收每组试验抛洒的饲料,采用细孔隔筛板将破碎的粉末饲料过滤称重,算出各自抛料后的破碎率。结果表明,优化前回收饲料净重为4.83 kg,破碎率为3.4%,优化后装置回收的颗粒饲料净重为4.92 kg,破碎率为1.6%,优化后的饲料破碎率明显降低。
4.3 虾塘水面投饵试验为了进一步验证投饵机下料系统和抛料系统优化后的实际使用效果,于2015年9月8日在上海市奉贤区某虾塘内进行了现场试验,水面试验如图 11所示。

|
图 11 虾塘投饵试验
Fig. 11 Bait casting test in shrimp pond
|
该虾塘长175 m,宽60 m,水深1.2 m,总面积约1.05 hm2。优化后的移动式投饵机按照系统设定的运行参数进行作业,并测算其投饵时长、总投饵量、船体速度及水面饲料分布密度均值等参数[14],作业次数为3次。优化后的投饵机在池塘投饵时,完成投饵的时长是 615 s,总投料量为36.54 kg,船速0.8 m/s,水面饲料分布密度均值为 3.48g/m2,与水平地面试验的饲料密度均值3.79 g/m2 相比,绝对误差0.31 g/m2 ,相对误差为8.2%,测试数据表明,优化后的投饵机在饲料投喂的均匀性上有了明显的改善,并且使得下料量更加合理,大大减少了饲料的浪费。
5 结论根据虾塘移动式投饵需要,对现有动力消耗较低、使用范围最广的抛盘式投饵机进行了优化设计。针对其主要存在漏料、投饵不均及高破碎率等问题,提出了对投饵机下料系统和抛料系统的优化方案。运用封闭向量多边形法对偏心下料系统铰链四杆机构进行运算分析,获得最优偏心距为0.8 mm。通过对抛料盘叶片的不同折弯角度进行运动仿真分析,模拟饲料抛洒路径,获得最优抛洒范围区间,选定折弯角度最优值为12°。
为验证理论分析结果的正确性,分别进行了陆上和水面抛料试验。通过装置优化前后对饲料分布密度、饲料破碎率的影响及现场试验数据,验证了投饵装置的优化效果。优化后的投饵装置提升了饲料抛洒的均匀性,降低了破碎率,其投饵效果相对优化前有显著提高。投饵装置的优化为实现智能型移动式投饵平台的推广应用打下了坚实的基础。
| [1] | NG W K, KOH C B, TEOH C Y, et al.Farm-raised tiger shrimp, Penaeus monodon, fed commercial feeds with added organic acids showed enhanced nutrient utilization, immune response and resistance to Vibrio harveyi challenge[J]. Aquaculture, 2015, 449: 69–77. DOI:10.1016/j.aquaculture.2015.02.006 |
| [2] | 农业部渔业渔政管理局.2015中国渔业统计年鉴[M].北京: 中国农业出版社, 2015. The Ministry of Agriculture Fishery and Fishery Administration.China fishery statistics yearbook 2015[M].Beijing: China Agriculture Press, 2015. |
| [3] | 袁凯, 庄保陆, 倪琦, 等.室内工厂化水产养殖自动投饲系统设计与试验[J]. 农业工程学报, 2013, 29(3): 169–176. YUAN K, ZHUANG B L, NI Q, et al.Design and experiments of automatic feeding system for indoor industrialization aquaculture[J]. Transactions of the Chinese Society of Agriculture Engineering, 2013, 29(3): 169–176. |
| [4] | 孙月平, 赵德安, 洪剑青, 等.河蟹养殖船载自动均匀投饵系统设计及效果试验[J]. 农业工程学报, 2015, 31(11): 31–39. SUN Y P, ZHAO D A, HONG J Q, et al.Design of automatic and uniform feeding system carried by workboat and effect test for raising river crab[J]. Transactions of the Chinese Society of Agriculture Engineering, 2015, 31(11): 31–39. |
| [5] | 王志勇, 谌志新, 江涛, 等.标准化池塘养殖自动投饵系统设计[J]. 农业机械学报, 2010, 41(8): 77–80. WANG Z Y, SHEN Z X, JIANG T, et al.Design of automatic feeding system in standardized pond culture[J]. Transactions of the Chinese Society for Agricultural Machinery, 2010, 41(8): 77–80. |
| [6] | HU G G, GAO S S, ZHONG Y M.A derivative UKF for tightly coupled INS/GPS integrated navigation[J]. ISA Transactions, 2015, 56: 135–144. DOI:10.1016/j.isatra.2014.10.006 |
| [7] | GUO W G, LIANG D N. The application of GPS/INS in airborne SAR motion compensation[C]//Proceedings of The 2002 International Conference on Control and Automation, 2002. Final Program and Book of Abstracts. Xiamen, Fujian Province, China: IEEE. 2015: 243. |
| [8] | 濮良贵, 纪名刚.机械设计[M].北京: 高等教育出版社, 2006. PU L G, JI M G.Mechanical design[M].Beijing: Higher Education Press, 2006. |
| [9] | CHEN Y, ASHOUR A F, GARRITY S W.Modified four-hinge mechanism analysis for masonry arches strengthened with near-surface reinforcement[J]. Engineering Structures, 2007, 29(8): 1864–1871. DOI:10.1016/j.engstruct.2006.09.023 |
| [10] | HU A P, KONG D J, ZHU W.Study on synthesis of hinged four-bar linkage straight-line mechanism using three symmetric points[J]. Key Engineering Materials, 2010, 426-427: 330–333. DOI:10.4028/www.scientific.net/KEM.426-427 |
| [11] | 于靖军, 郭卫东.机械原理[M].北京: 机械工业出版社, 2013. YU J J, GUO W D.Mechanical principles[M].Beijing: Machinery Industry Press, 2013. |
| [12] | 韩董董, 王成军, 陈蕾, 等.基于ADAMS的三维并联振动铸造机的仿真与优化[J]. 铸造技术, 2014, 35(11): 2721–2723. HAN D D, WANG C J, CHEN L, et al.Simulation and optimization of 3D parallel vibration casting machine based on ADAMS[J]. Foundry Technology, 2014, 35(11): 2721–2723. |
| [13] | 李团结, 朱超.基于虚拟样机技术的球形机器人运动仿真研究[J]. 系统仿真学报, 2006, 18(4): 1026–1029. LI T J, ZHU C.Research on motion simulation of spherical robot based on virtual prototype technology with ADAMS[J]. Journal of System Simulation, 2006, 18(4): 1026–1029. |
| [14] | 陈晓龙, 陈军, 唐荣, 等.对虾船载投饲机的研制[J]. 上海海洋大学学报, 2015, 24(1): 152–160. CHEN X L, CHEN J, TANG R, et al.Development of boat-borne feeding machine for shrimps[J]. Journal of Shanghai Ocean University, 2015, 24(1): 152–160. |
 2016,
Vol. 25
2016,
Vol. 25

