为了降低能耗和合理选材，需分析网具的总阻力及分析网具各部分的受力情况^[1]。为此，国内外学者以流体力学和弹性力学等为基础，对不同水流作用下渔具及其构件的水动力特性方面开展了大量的研究^{[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18]}。同时随着数学建模在网具研究中的广泛应用，数值模拟也用来分析网片的水动力^{[11, 12]}。可查到的最早的研究为前苏联学者巴拉诺夫^[1]、日本学者田内^{[3, 4, 5]}在天然水域进行实验，取得了与流向垂直的平面网片阻力公式。随着网具材料由传统的棉麻向合成材料转变，实验设备由天然水域向风洞和水槽转变。前苏联学者弗里特曼^[1]、日本学者寺田寅彦^[2]、宫本秀明^[6]等针对不同结构、线面积、缩结系数、材料以及不同工况下的网片进行测试，获得了一系列阻力计算的经验公式。今井健彦^{[1, 7]}采用C形框架研究小冲角时聚乙烯平面网片阻力，并对有结节网片和无结节网片的水阻力进行比较研究，研究发现有结节网片的水阻力和升力系数比无结节网片的要大10%。为了改善实验条件，王尔光^[8]设计出了水阻力小的流线型框架。随着新型方形和六角形网目网片的出现，孙满昌^[13]、许永久等^[14]分别对其进行了测试。

有结节菱形网片是大型竹筴鱼拖网的主要组成部分，本文对5种不同结构的有结节尼龙网片，通过水槽实验开展网片水动力特性的研究，分析了框架尾流对网片水动力性能的影响，研究结果可为拖网设计以及同种类型网片的设计和作业性能改进提供参考。

中国水产科学研究院东海水产研究所循环水槽。该水槽的主要技术参数为：工作段长1.8 m，宽0.5 m，高0.85 m，工作水深0.5 m，可提供的最大流速为2.5 m/s，如图1(左)所示。该水槽边界层为厘米级。测量网片的框架为圆截面的方形框架，由钛合金材料制成，边长为0.4 m,直径0.005 m，如图1(右)所示。测量仪器为日本共和电业制造的LSM-B-500NSA1-P 型三分力传感器，量程为500 N。

图1(Fig.1)

图1 动水槽(左)和方形框架(右) Fig.1 Flume tank (left) and framework(right)

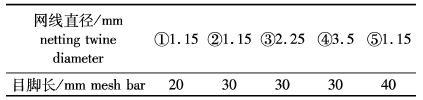
有结节尼龙网片，网片规格如表1所示。

表1(Tab. 1)

表1 实验网片的规格Tab. 1 Specification of nettings 网线直径/mmnetting twine diameter ①1.15 ②1.15 ③2.25 ④3.5 ⑤1.15 目脚长/mm mesh bar 20 30 30 30 40

表1 实验网片的规格 Tab. 1 Specification of nettings

将网片均匀固定在方形框架上，框架顶端与三分力天平相连接测量网片阻力，三分力天平的传感器与电脑连接，由电脑记录数据。

网片平面与水流的夹角为冲角。将框架固定到三分力天平的连接螺孔上，调节角度控制器，使网片的冲角分别为0°、5°、8°、10°、12°、15°、20°、25°、30°、45°、60°、75°、90°等十三档次，在每个角度下，断面平均流速分别设定为0.6 m/s、0.8 m/s、1.0 m/s和1.2 m/s等。网片的水平缩结系数E_T分别为0.3、0.5、0.707。在每个设定角度和流速下，当工况稳定、仪器显示稳定的读数下逐一测量记录框架的阻力，每个工况下记录5 s，共等间隔采样50个数据，取平均值。

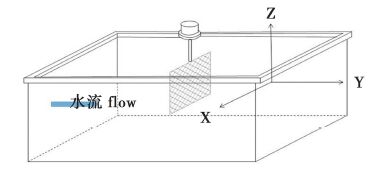
三分力天平测量的三个力的方向分别为网片平面的切向f_x、网片平面的法向f_y以及与z轴平行的方向。因此，在求解升阻力时，需要将所测量的f_x，f_y分解到x,y方向上，水槽示意图如图2所示。

图2(Fig.2)

图2 动水槽示意图 Fig.2 Schematic diagram of flume tank

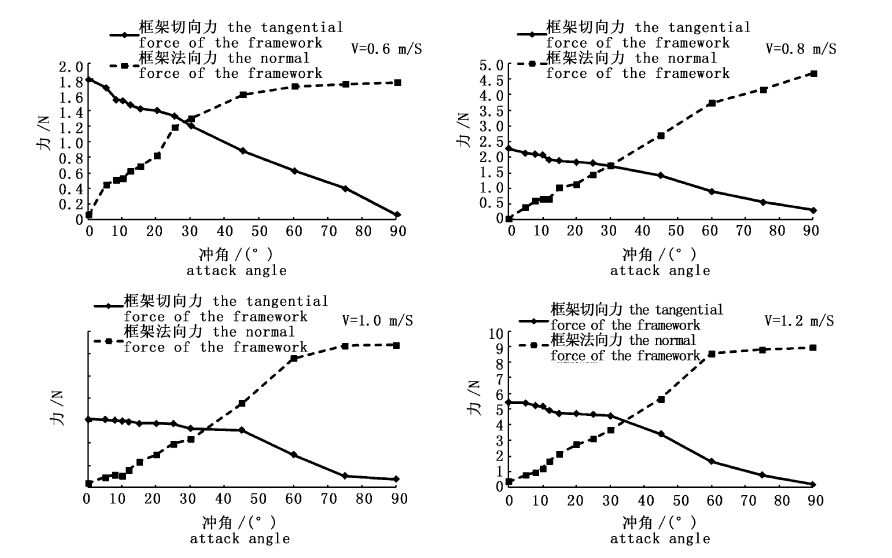
对实验测得每个工况下的50个数据取平均值。测量的未分解的框架的法向力(f_y)和切向力(f_x)如图3所示。将测试的网片与框架的阻力减去框架的阻力后，即为网片所受到的阻力，并计算网片的升力系数C_L、阻力系数C_d以及升阻力系数比K^[17]。

图3(Fig.3)

图3 框架受力 Fig.3 Force of framework

网片在流场中受到的总阻力为

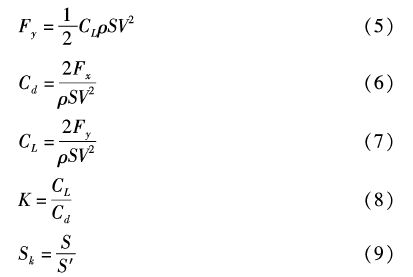
当缩结系数、网线直径、网目尺寸均不相同时，改进后的雷诺数^[1]计算如公式(10)(11)所示，则可以较好地表示相同网线直径、不同缩结系数、不同网目尺寸时的雷诺数。

根据升阻力系数随雷诺数、冲角、线面积系数的变化趋势，确定公式的表达形式，通过MATLAB面拟合函数进行多元非线性拟合得出升阻力系数的公式。

实验过程中，框架的阻挡作用使得作用在网片上的水动力有所改变，即尾流效应的影响。对框架的尾流效应影响计算。

计算尾流与冲角的关系如下^[1]。

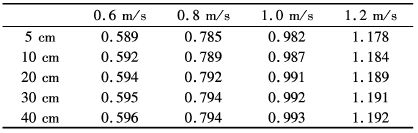
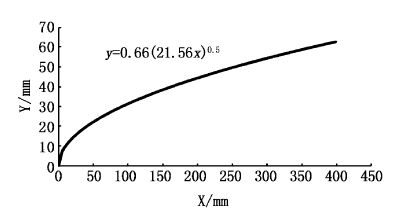
如表2所示。网片冲角在变化的过程中，冲角为9.1°时，整个网片40 cm都在尾流效应区间；当冲角为25.4°时，有5 cm长的网片在尾流效应区间内。在尾流区间内测得的网片的阻力比实际阻力稍小。图4即为尾流效应的函数区间，在函数下方即为尾流效应区间。表3所示，设定平均流速为0.6 m/s时，在框架正后方5 cm处的实际流速为0.589 m/s，相差1.8%；可见框架尾流的速度影响并不是很大。

表2(Tab. 2)

表2 尾流效应对网片长度的影响以及对应的冲角Tab. 2 The impact of wake effects on the length of the mesh and the corresponding attack angle 网片长度/cmlength of the netting 临界角度critical angle 40 9.1° 20 12.6° 10 17.9° 5 25.4°

表2 尾流效应对网片长度的影响以及对应的冲角 Tab. 2 The impact of wake effects on the length of the mesh and the corresponding attack angle

表3(Tab. 3)

表3 框架正后方的实际流速Tab. 3 The actual flow velocity behind the frame 0.6 m/s 0.8 m/s 1.0 m/s 1.2 m/s 5 cm 0.589 0.785 0.982 1.178 10 cm 0.592 0.789 0.987 1.184 20 cm 0.594 0.792 0.991 1.189 30 cm 0.595 0.794 0.992 1.191 40 cm 0.596 0.794 0.993 1.192

表3 框架正后方的实际流速 Tab. 3 The actual flow velocity behind the frame

图4(Fig.4)

图4 尾流效应的影响范围 Fig.4 Scope of wake effects

网线直径为1.15 mm、2.25 mm、3.5 mm，网目尺寸为60 mm，不同雷诺数对应的水动力系数如图5、图6所示。

图5(Fig.5)

图5 阻力系数与雷诺数的关系 Fig.5 The drag coefficient for the netting by Reynolds numbers

图6(Fig.6)

图6 升力系数与雷诺数的关系 Fig.6 The lift coefficient for the nettings by Reynolds numbers

由下图可知阻力系数随着雷诺数Re的增大总体呈减小的趋势。雷诺数Re<1 500时，阻力系数变化较大；冲角小于45°时，阻力系数随雷诺数增大而先增大后减小；冲角大于45°时，阻力系数随雷诺数的增大而减小。1 500<Re<2 800，冲角小于45°时，阻力系数随雷诺数的增大先增大后趋于稳定；冲角大于45°时，阻力系数随雷诺数的增大逐渐减小，趋于稳定。 Re>2 800时，阻力系数基本趋于稳定。

雷诺数500<Re<4 500时，升力系数没有明显的变化趋势，呈紊乱现象。网线直径不同、冲角相同时，升力系数总体上随着雷诺数的增大而减小。

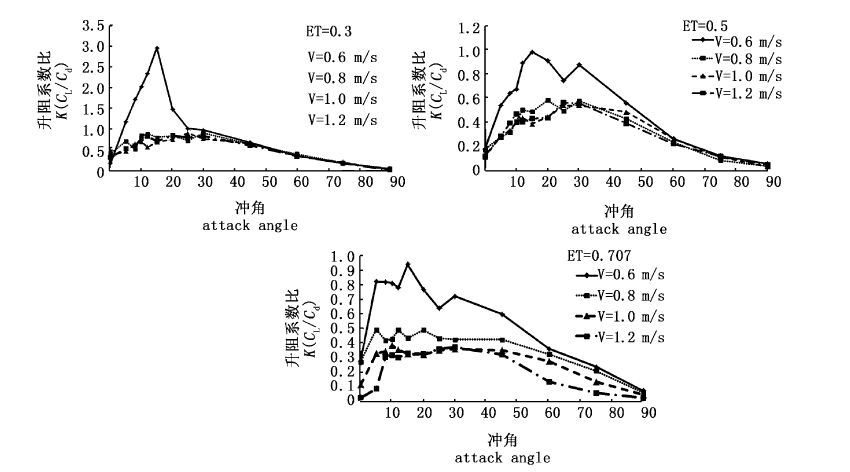
升阻系数比K，即空气动力学效率，反映了网片的流体力学特性。网目尺寸2a=60 mm的升阻系数比K如图7所示。升阻系数比K总体趋势是先增大后减小；但在0～30°时可能出现多个峰值波动，不太稳定。0～10°时，K值迅速增大,最大值出现在15°附近。30～90°之间，K值基本呈减小趋势。流速较小时，K值反而较大，最大K值为2.95。

图7(Fig.7)

图7 升阻系数比 Fig.7 The ratio of the lift and drag coefficients

①②③⑤网片，缩结系数为0.707，流速为0.8 m/s时的d/a与升阻力系数的关系如图8、9所示。在相同流速下的升阻力系数均随着d/a的增大呈现先增大后减小，d/a与升阻力的关系类似于二次抛物线。升力系数在冲角为15°、75°时较小，在冲角为45°、60°时较大。

图8(Fig.8)

图8 d/a与升力系数的关系(ET=0.707，V=0.8m/s) Fig.8 The relationship between lift coefficient and d/a (ET=0.707,V=0.8 m/s)

图9(Fig.9)

图9 d/a与阻力系数的关系(ET=0.707，V=0.8m/s) Fig.9 The relationship between drag coefficient and d/a(ET=0.707,V=0.8 m/s)

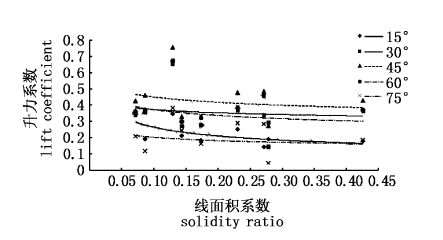
②③④号网片，缩结系数为0.3、0.5、0.707，不同的缩结系数对应的网片的线面积和缩结面积之比也不同，即线面积系数不同。线面积系数与升阻力系数的关系如图10、11所示。升阻力系数随线面积系数的增大而减小。

图10(Fig.10)

图10 线面积系数与升力系数的关系 Fig.10 The relationship between lift coefficient and solidity ratio

图11(Fig.11)

图11 线面积系数与阻力系数的关系 Fig.11 The relationship between drag coefficient and solidity ratio

网片在不同的缩结系数时，网线面积与缩结面积之比也不同，综合d/a、缩结系数、雷诺数等对网片升阻力系数的影响，针对不同线面积系数、不同雷诺数以及冲角的情况下进行多元非线性拟合。

网片阻力系数C_d、升力系数C_L分别为：

实验是在东海水产研究所动水槽进行。水槽工作水深为0.5 m，有效工作断面较小。实验框架0.4 m，边界层流和自由液面对测量结果可能有一定影响；此外，水流经导流片和整流栅后到达工作区时，同一断面上的流速也不可能完全相同，对测试精度也会产生影响。

但是，按明渠紊流的垂线流速指数分布公式^{[19, 20]}，在离水槽底5 cm处的流速为0.51 m/s，与平均流速相差15%，边界流速稍小于平均值0.6，可能使得测得的阻力偏小，从而水动力系数偏小，对于紊流，边界层很小^[19]，因此仍可以认为框架所处的断面流速合适。

雷诺数是表征流态的一个重要参数，缩结系数相同时，阻力系数随雷诺数的增大而减小(图5)。这与LEE^[15]在研究网目群化问题和詹杰民^[18]研究网片水动力实验中得出的结论一致，网片阻力系数随雷诺数的变化规律与圆柱体相同，但阻力系数大，说明网目与网目之间存在相互影响。若单纯使用R_e=dVυ(其中d为网线直径，V为来流速度)来表达流态不够准确，本文使用线面积系数雷诺数，既考虑了网线直径作为特征长度的影响，又考虑了网目与网目之间的相互影响以及缩结系数对阻力系数的影响，这种相互影响通过线面积系数反应出来，因此，本文中使用的线面积系数雷诺数更加合理。当雷诺数增大到一定程度，正好处在圆柱体(网线可视作粗糙圆柱体)的阻力曲线的“自动模型区”，此后雷诺数增大网片的阻力系数趋于稳定。

升阻力系数随d/a呈现先增大后减小的趋势，这与宫本秀明^[1]的研究结果相似。宫本秀明对不同类型结节的网片研究表明d/a与阻力系数为二次抛物线关系。本研究中共5种d/a，分别为1.15/40、1.15/30、1.15/20、2.25/30、3.5/30。前三组的网线直径相同，网目尺寸不同，网目数增多。虞聪达^[9]的研究表明阻力随d/a的增大而增大，d/a增大直接导致网片线面积增大，阻力增大。网片线面积越大即线面积系数越大，詹杰民^[18]对网片阻力系数的研究表明线面积系数越大阻力系数也越大，从图11可看出，本研究的结论和詹杰民的结论相近，阻力系数与线面积系数呈幂函数关系。随着网线直径的增大，雷诺数增大，而阻力系数减小。此外，网片的布置方向对阻力也存在一定影响。

LEE^{[21, 22]}通过网目群化的网片实验，总结出了升阻力系数与冲角和雷诺数的关系；IMAI^{[1, 22]}在1979对升阻力系数的研究中总结出了升阻力系数公式：

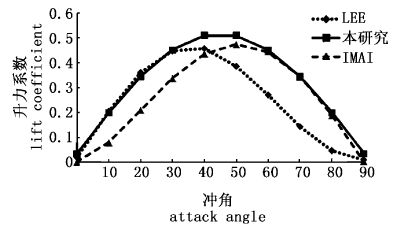
与本研究进行比较发现，LEE只考虑了冲角和雷诺数的关系，而IMAI只考虑了冲角对升阻力的影响，均未考虑线面积系数对升阻力系数的影响，本研究的公式综合了冲角、雷诺数以及线面积系数对升阻力的影响。本研究与LEE及IMAI的研究结果比较，如图12、13所示。

图12(Fig.12)

图12 升力系数比较 Fig.12 Comparison of the lift coefficient

图13(Fig.13)

图13 阻力系数比较 Fig.13 Comparison of the drag coefficient

本研究的升阻力系数均比LEE和IMAI的稍大。升力系数的最大值，本实验出现在40～50°之间，LEE的最大值出现在30～40°之间；IMAI的最大值出现在50～60°之间。LEE所用的框架为600 mm×600 mm，框架越大，网目数越多，结果可能越好；同时，水动力系数与水流断面流速的均匀程度有关。但本实验针对的缩结变化范围较大，水平缩结系数为0.3、0.5和0.707三组，缩结系数越小，网线越密；LEE所用实验材料的d/a最大值为0.048，而本实验中d/a的最大值为0.116，这也使得线面积系数增大；本实验中使用的是修正后的雷诺数，充分考虑到了网片线面积系数对雷诺数的影响，这种修正雷诺数能够能耗的表示流态的变化。LEE所针对的主要是金枪鱼围网网片，而金枪鱼围网网片是无结节网片，本实验中的网片为有结节的拖网网片；与IMAI的结果相比，本实验的阻力稍大，这可能与实验使用的框架和网片材料有关，本实验使用的是方形框架，而IMAI使用的是C形框架，框架阻力较小。材料、网片的工艺差别和线面积系数的差异使得作用在网片上的水动力差异较大，是导致本实验的水动力系数较大的主要原因。