关于渤海潮波系统的研究,尤其是数值模拟方面,前人已经累积了许多经验和成果。学者们通常将渤、黄、东海视为一个整体展开研究。沈育疆[1]首次对东中国海的潮汐做数值计算,研究东中国海传播规律及潮汐分布情况,给出了M2、S2、K1、O1 4个分潮的同潮图;赵保仁等[2]利用球坐标系中的二维非线性潮波方程组,对渤黄东海的M2和m1分潮的潮汐潮流进行数值模拟,计算结果与实测对比吻合较好,还证实或首次给出若干圆流点,最后讨论了M2和m1分潮的潮能通量传播、耗散情况;万振文等[3]、王凯等[4]也先后建立三维数值模式研究该区域的潮波系统,做了大量有意义的工作,使人们对渤、黄、东海潮汐潮流的认识不断完善,基本达到共识。
前人针对渤海区域的潮波数值研究工作取得不少成果,窦振兴等[5]采用Leedertse二维非线性长波模式模拟渤海潮流和余流,并绘制了M2和K1分潮同潮图;张占海[6]利用二维非线性潮波方程组,计算了渤海M2和K1分潮,分析渤海半日潮和全日潮波运动;于克俊[7]利用三维潮波方程,着重研究了M2分潮潮流的垂直变化。但是这些研究大多只考虑1~3个分潮,数据较少,通常是单独模拟不同的分潮,忽略了潮波传播过程当中不同分潮之间的非线性相互作用,并且模式精度比较低,对岸线拟合效果相对较差。因此,本文借助高精度的水深资料(2.5′×2.5′),基于POM研究渤海M2、S2、K1、O1 4个主要分潮,希望能对渤海潮波分布规律和传播特征有一个全面细致的了解。
1 模式介绍本文基于POM来建立渤海潮波数值模式,该模式目前已经被广泛地应用于海洋研究的很多领域。其基本特点是:水平和垂直方向分别采用正交曲线坐标系和随地形变化的sigma坐标系;自由表面可以模拟水位变化;垂直和水平方向的混合扩散分别采用2.5阶的Mellor-Yamada湍流闭合模式和Smagorinski模式;内外模态分别处理速度较慢的内重力波和速度较快的外重力波以提高整个模式计算效率等。本研究选取的模拟区域为(117.5°E~122.5°E,37°N~41°N),模式采用冷启动,初始场设为u=v=ω=η=0。水平计算域根据水深资料采用2.5′×2.5′的网格,垂直方向取10个sigma层。内外模态的时间步长分别取90 s和3 s,积分35 d,每小时记录一次水位和流速,前5天用于稳定场的建立,后30天的模拟结果进行调和分析,得到研究海区的潮汐调和常数。
2 模拟结果验证
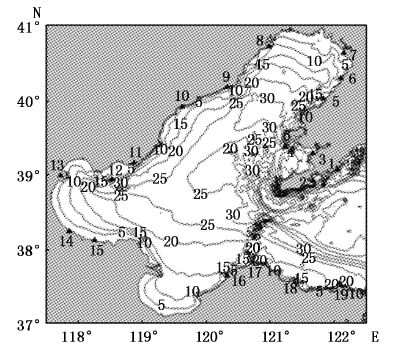
本文主要利用渤海沿岸 19 个验潮站(图1)调和常数资料[8]对模拟所得的M2、S2、K1、O1 4个分潮的调和常数进行了验证,首先采用了最常见的一种统计方法:考察振幅和迟角的模拟值与观测值之间的绝对平均偏差(MH,Mg),其计算公式为:
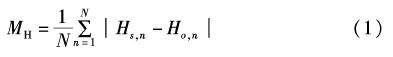
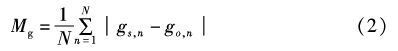
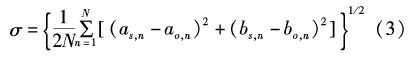
|
图1 渤海地形图及验潮站位图 Fig.1 Topography and tidal gauge stations in Bohai |

|
σ也常常被称为模拟值和观测值之间的距离,它表征了模拟值和观测值的偏离程度,而它与观测值变化性的相对偏离程度可用相对偏差

|
表示,其中,
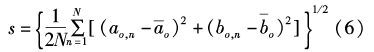
|
这里,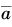 o和
o和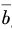 o分别为ao,n和bo,n的平均值。而
o分别为ao,n和bo,n的平均值。而

|
代表了模拟值和观测值的拟合程度,F相当于线性回归中的相关系数。
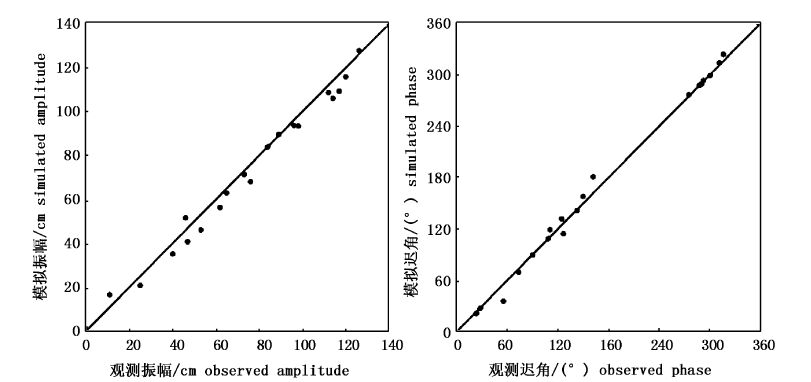
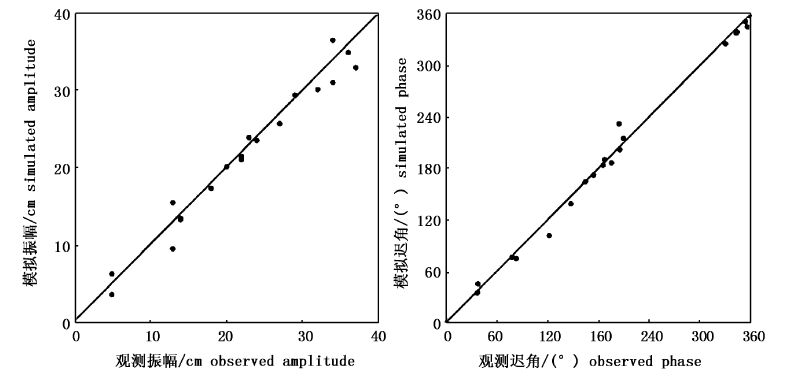
图2~图5,为M2、S2、K1、O1 4个分潮19个站位模拟值与观测值的比较,表1给出对应的误差对比。其中M2分潮的振幅绝对平均偏差为4.4 cm,迟角绝对平均偏差为5.2°,相对偏差12.4%,拟合程度高达98.5%,13号站位的振幅偏差最大,该站位位于渤海湾,水深受渤海湾常年围填海等活动影响变化较大,可能对部分验潮站调和常数存在影响 ,使模拟结果出现较大偏差,迟角偏差最大的为9号站位,由于靠近无潮点,迟角偏差达20°。S2分潮的振幅绝对平均偏差相比M2分潮较小,为1.5 cm,迟角绝对平均偏差为6.8°,相对偏差13.1%,拟合程度98.3%,振幅偏差最大区域出现在辽东湾顶,迟角偏差最大区域与M2分潮重合,原因同M2分潮。K1分潮的振幅绝对平均偏差为1.7 cm,迟角绝对平均偏差为3.0°,相对偏差15.7%,拟合程度97.5%,4号站位振幅偏差最大,为4 cm,11号站位迟角偏差最大,为16°。O1分潮的振幅绝对平均偏差偏小,为1.0 cm,迟角绝对平均偏差为4.0°,相对偏差12.4%,拟合程度98.5%。
|
图2 M2分潮模拟结果检验 Fig.2 Model validation for M2 tides |
|
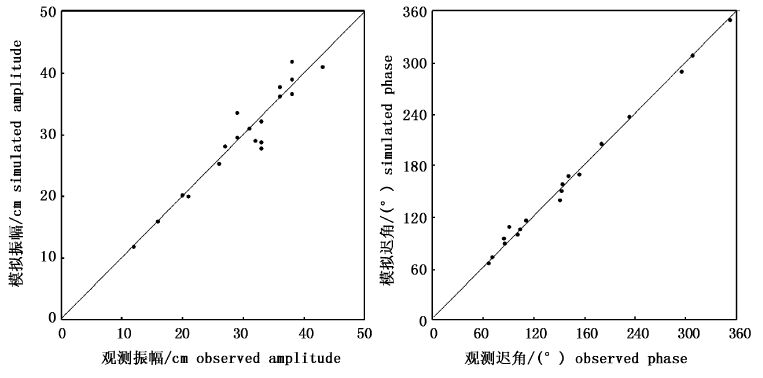
图3 S2分潮模拟结果检验 Fig.3 Model validation for S2 tides |
|
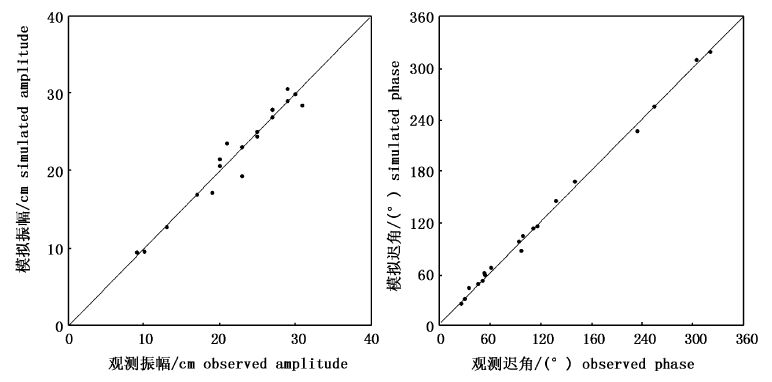
图4 K1分潮模拟结果检验 Fig.4 Model validation for K1 tides |
|
图5 O1分潮模拟结果检验 Fig.5 Model validation for O1 tides |
表1以上综合分析显示本模式对渤海潮波系统的模拟较为准确,对比该区域研究学者[2, 3]的模拟结果,发现本研究精度有所提高。可以用来分析研究渤海主要分潮的特征。
| 表1 M2、S2、K1、O1分潮模拟结果检验 Tab 1. Model validation for M2,S2,K1,O1 tides |
图6给出了渤海M2、S2、K1、O1分潮同潮图。由图6a和图6b可知,M2和S2分潮的分布特征类似,前进潮波经渤海海峡传入渤海,在向西传播过程中,受到渤海西岸的阻挡,发生反射,在地转效应的影响下,反射潮波与前进潮波叠加分别在辽东湾西南侧和渤海湾东南侧形成两个逆时针旋转的驻波系统,其对应无潮点分别位于秦皇岛外海和老黄河口附近。两个半日分潮的振幅在辽东湾和渤海湾湾顶最大,而在莱州湾内潮汐振幅是3个海湾中最小,渤海中部大片海区振幅相对比较小,振幅的模拟结果与前人相比都相差不大。其中M2分潮在这3个湾顶的振幅可达130 cm、110 cm和64 cm,在渤海潮波系统中占据主要地位。S2分潮振幅大约只有M2分潮的三分之一,在3个湾顶的振幅为39 cm、32 cm和22 cm。从图6b可以看到,老黄河口的S2分潮潮波系统出现一定程度的退化现象,无潮点已经退化到岸上,万振文等[3]、黄祖珂[10]、乐肯堂等[11]认为黄河三角洲水深和岸线演变是潮波系统运动变化的主要原因,王永刚等[12]的相关研究验证了黄河口海域水深和岸线变化对M2分潮无潮点位置和振幅的影响。

|
图6 M2、S2、K1、O1分潮同潮图:(a) M2 分潮,(b) S2 分潮,(c) K1分潮,(d) O1分潮 Fig.6 Simulated co-tidal charts for (a) M2 tide,(b) S2 tide,(c) K1 tide,(d) O1 tide |
K1 和O1分潮潮波系统两者也大致相似,在渤海海峡附近均有一个逆时针的旋转驻波系统,其无潮点位置位于渤海海峡附近。全日潮比较弱,渤海海区平均振幅约21 cm,随着水深变化,振幅由无潮点向渤海沿岸逐渐增大。K1分潮最大振幅在辽东湾湾顶,接近42 cm,渤海湾湾顶振幅次之,约37 cm(图6c)。O1分潮比K1分潮稍弱,振幅在辽东湾湾顶达到最大,约31 cm(图6d)。与前人的研究结果相比,K1和O1分潮无潮点位置基本一致,振幅的模拟结果略有差异,本文与王永刚等[9]的结果类似。
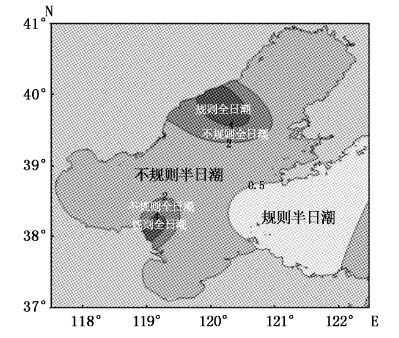
3.2 渤海潮汐类型分布潮汐类型是根据主要全日潮和半日潮振幅的比值来判别的。对于中国近海最主要的半日潮是M2分潮,而全日潮中K1和O1分潮大体相当,因此当0<(HK1+Ho1)/HM2≤0.5时潮汐类型为规则半日潮,当0.5<(HK1+Ho1)/HM2≤2.0是不规则半日潮,当2.0<(HK1+Ho1)/HM2≤4.0是不规则全日潮 ,当(HK1+Ho1)/HM2>4是规则全日潮。
渤海虽然是中国近海面积最小的海域,但是潮汐类型分布却最为复杂,涵盖四种潮汐类型,潮汐类型分布如图7所示,渤海大部分海区为不规则半日潮,由于K1分潮和O1分潮的无潮点同时出现在渤海海峡水域,全日潮振幅较弱,因此该处潮汐类型以规则半日潮为主。秦皇岛外海和老黄河口附近有M2驻波波节点分潮的无潮点,潮汐类型以规则全日潮和不规则全日潮为主,基本符合Fang等的研究成果[13]。
|
图7 渤海潮汐类型分布 Fig.7 Tidal type of Bohai |
由于渤海大部分海区潮汐类型半日潮,因此最大可能潮差选取如下计算公式:2×(1.29HM2+1.23HS2+HK1+Ho1。渤海最大可能潮差分布如图8所示,沿岸潮差大,中央海区潮差小,这主要是受到水深的影响;辽东湾湾顶潮差最大,超过5.5 m,渤海湾潮差次之,达到5 m,莱州湾潮差最小,最大潮差小于3.5 m,这与各分潮在海湾的振幅分布特征一致;由于渤海大部分海区潮汐类型半日潮,秦皇岛外海和老黄河口两个无潮点附近海域的潮差最小,均不超过1.5 m。

|
图8 渤海最大可能潮差(m)分布 Fig.8 Maximum possible tidal range (m) |
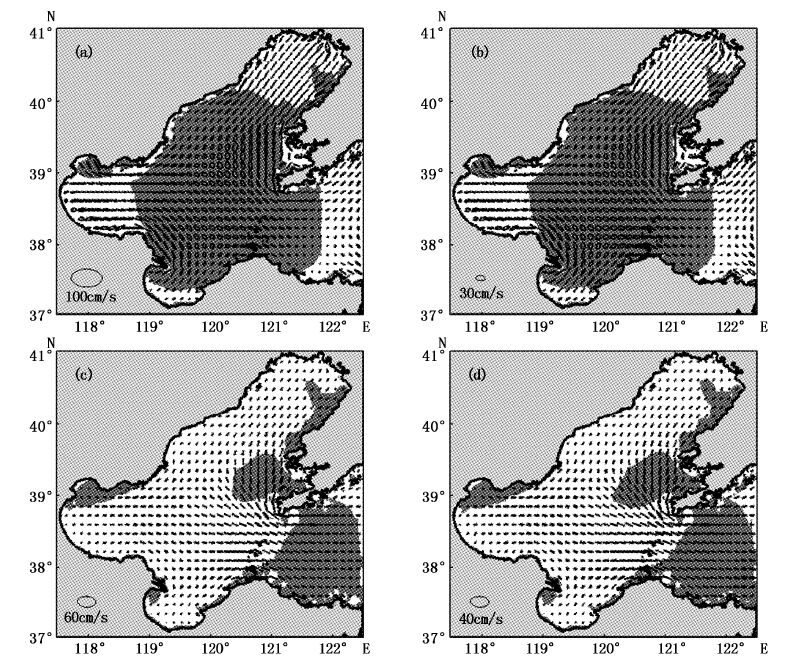
图9给出了渤海M2、S2、K1、O1分潮潮流的椭圆分布,阴影部分表示负旋度即潮流顺时针旋转。M2分潮潮流强流区出现在老铁山水道西侧、辽东湾南部和黄河口附近,尤其是老铁山水道附近最大流速达到96 cm/s,在强流区潮流椭圆几乎退化成直线,接近往复流形式;莱州湾和渤海中部海域流速相对较弱,流速多集中在20~40 cm/s,以顺时针旋转流为主,与王凯[4]的结果相吻合。S2分潮流速比M2潮流小很多,最大流速不超过30 cm/s,流速大多集中在10~20 cm/s,其潮流的旋转方向、强弱分布特征与M2基本一致,本文不做另外讨论。
|
图9 M2、S2、K1、O1分潮流椭圆分布图(a) M2 分潮,(b) S2 分潮,(c) K1分潮,(d) O1分潮 Fig.9 Simulated tidal flow ellipses for (a) M2 tide,(b) S2 tide,(c) K1 tide,(d) O1 tide |
K1分潮潮流强流区出现在渤海海峡附近,流速集中在20~30 cm/s,其中渤海海峡南北两侧流速最大,可超过40 cm/s,其他海域流速介于5~20 cm/s,分布特征大致与FANG[14]的结果一致。O1分潮流速分布与K1也大致相似,流速较K1分潮弱,最大流速在15~25 cm/s,其他海域为5~15 cm/s。两个分潮流在渤海中央大部分海域为逆时针旋转,仅在辽东湾东北部至金州湾沿岸、渤海湾北部和莱州湾西部沿岸为顺时针旋转,往复流主要分布在3个海湾。
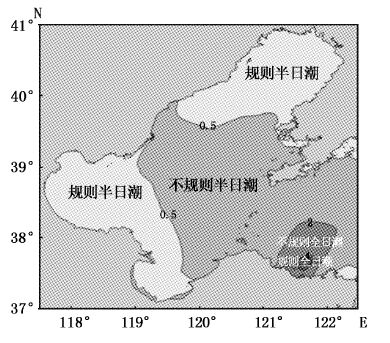
3.5 潮流类型和最大可能潮流流速分布潮流性质判别依据与潮汐类型划分类似,只不过以分潮最大潮流代替潮汐振幅。图10显示:渤海潮流是以半日潮流为主的混合潮流,辽东湾、渤海湾和莱州湾西南大部分海域为规则半日潮流,渤海中央海区为不规则半日潮流。比较图7和图10可以发现:烟台近海具有半日潮汐和全日潮流的特征,而秦皇岛外海具有全日潮汐和半日潮流的特征。可见对于同一海域,潮汐潮流的类型是可以不同的。
|
图10 渤海潮流类型分布 Fig.10 Tidal flow type of Bohai |
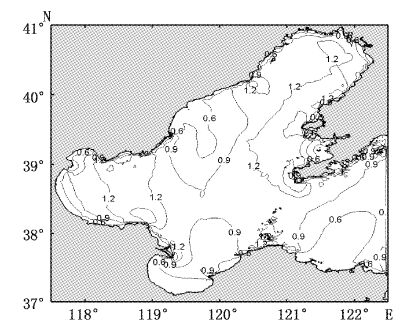
图11为渤海最大可能潮流流速分布图,在整个渤海存在3个强流区:老铁山水道及北侧海域、长岛和黄河口附近海域,最大可能流速可达2 m/s以上,对渤海的物质输运和混合过程将产生重要影响。
|
图11 渤海最大可能潮流流速分布 Fig.11 Maximum possible speed range of tidal flow |
本文基于POM模式,建立了渤海海域的高分辨率潮波数值模式,利用渤海沿岸验潮站的潮汐调和常数对模拟结果进行检验,结果显示模拟与观测资料吻合较好,M2、S2、K1、O1 4个分潮振幅绝对平均偏差为4.4 cm、1.5 cm、1.7 cm和1 cm,迟角绝对平均偏差为5.2°、6.8°、3.0°和4.0°,拟合程度分别为98.5%、98.3%、97.5%、98.5%。在此基础上,本文进一步分析了潮波的分布规律,结果表明:
(1)渤海潮汐以半日潮为主,其中M2分潮占主导地位,在辽东湾、渤海湾和莱州湾顶的振幅可达130 cm、110 cm和64 cm;
(2)渤海沿岸潮差大,中央海区潮差小;辽东湾湾顶潮差最大,渤海湾潮差次之,莱州湾潮差最小;
(3)渤海潮流是以半日潮流为主的混合潮流。在渤海中央海域潮流呈现为旋转流,在海湾多为往复流。最大可能潮流流速存在三个强流区,分别为:老铁山水道及北侧海域、长岛和黄河口附近海域。
| [1] | 沈育疆. 东中国海潮汐数值计算[J]. 山东海洋学院学报, 1980, 10(3): 26-35.SHEN Y J. Numerical computation of tides in the East China Sea[J]. Journal of Shandong College of Oceanology, 1980, 10(3): 26-35. |
| [2] | 赵保仁, 方国洪, 曹德明. 渤、黄、东海潮汐潮流的数值模拟[J]. 海洋学报, 1994, 16(5): 1-10.ZHAO B R, FANG G H, CAO D M. Numerical modelling of tide and tidal currents in the Bohai, Yellow and East China Sea[J]. Acta Oceanologica Sinica, 1994, 16(5): 1-10. |
| [3] | 万振文, 乔方利, 袁业立. 渤、黄、东海三维潮波运动数值模拟[J]. 海洋与湖沼, 1998, 29(6): 611-616.WAN Z W, QIAO F L, YUAN Y L. Three-dimensional numerical modelling of tidal waves in the Bohai, Yellow and East China Seas[J]. Oceanologia et Limnologia Sinica, 1998, 29(6): 611-616. |
| [4] | 王凯, 方国洪, 冯士笮. 渤海、黄海、东海M2潮汐潮流的三维数值模拟[J]. 海洋学报, 1999, 21(4): 1-13.WANG K, FANG G H, FENG S Z. A 3-D numerical simulation of M2 tides and tidal currents in the Bohai Sea, the Huanghai Sea and the East China Sea[J]. Acta Oceanologica Sinica, 1999, 21(4): 1-13. |
| [5] | 窦振兴, 罗远诠, 黄克辛, 等. 渤海潮流及湖余流的数值计算[J]. 海洋学报, 1981, 3(3): 355-369.DOU Z X, LUO Y Q, HUANG K X, et al. Numerical computation of tidal current and tide-induced residual circulation of the Bohai Sea[J]. Acta Oceanologica Sinica, 1981, 3(3): 355-369. |
| [6] | 张占海, 吴辉碇. 渤海潮汐和潮流数值计算[J]. 海洋预报, 1994, 11(1): 48-54.ZHANG Z H, WU H D. Numerical model of the tide and tidal current in the Bohai Sea[J]. Marine Forecasts, 1994, 11(1): 48-54. |
| [7] | 于克俊, 张法高. 渤海潮波运动的三维数值计算[J]. 海洋与湖沼, 1987, 18(3): 227-236.YU K J, ZHANG F G. A three-dimensional numerical model of the tidal motions in the Bohai Sea[J]. Oceanologia et Limnologia Sinica, 1987, 18(3): 227-236. |
| [8] | 高秀敏. 渤海潮波伴随同化研究[D]. 青岛: 国家海洋局第一海洋研究所, 2010.GAO X M. Data assimilation of tides in the Bohai Sea by using the adjoint method[D]. Qingdao: The First Institute of Oceanography, SOA, 2010. |
| [9] | 王永刚, 方国洪, 曹德明, 等. 渤、黄、东海潮汐的一种验潮站资料同化数值模式[J]. 海洋科学进展, 2004, 22(3): 253-274.WANG Y G, FANG G H, CAO D M, et al. Tides of the Bohai, Yellow and East China Seas by assimilating gauging station data into a hydrodynamic model[J]. Advances in Marine Science, 2004, 22(3): 253-274. |
| [10] | 黄祖珂. 渤海的潮汐余流[J]. 海洋湖沼通报, 1992, (3): 1-8.HUANG Z K. The tide-induced residual current in the Bohai Sea[J]. Transactions of Oceanology and Limnology, 1992, (3): 1-8. |
| [11] | 乐肯堂, 刘兴泉, 史久新. 黄河口的变迁对邻近海区潮波运动影响的数值研究[J]. 海洋科学集刊, 1995(36): 33-46.LE K T, LIU X Q, SHI J X. A numerical study on the effect of the changes of the Huanghe River estuary on the tidal wave movement in its adjacent sea area[J]. Studia Marina Sinica, 1995(36): 33-46. |
| [12] | 王永刚, 魏泽勋, 方国洪, 等. 黄河口及其邻近海域水深和岸线变化对M2分潮影响的数值研究[J]. 海洋科学进展, 2014, 32(2): 141-147.WANG Y G, WEI Z X, FANG G H, et al. A numerical study on the effect of changes in water depth and coastline on M2 tidal component near the Yellow River estuary[J]. Advances in Marine Science, 2014, 32(2): 141-147. |
| [13] | FANG G H, YANG J F. A two-dimensional numerical model of the tidal motions in the Bohai Sea[J]. Chinese Journal of Oceanology and Limnology, 1985, 3(2): 135-152. |
| [14] | FANG G H. Tide and tidal current charts for the marginal seas adjacent to China[J]. Chinese Journal of Oceanology and Limnology, 1986, 4(1): 1-16. |
 2015, Vol. 24
2015, Vol. 24


