圈养林麝生长曲线拟合

扩展功能

加入引用管理器

文章信息

蔡永华, 杨营, 付文龙, 朱萍, 冯达勇, 雷毅, 张明

CAI Youghua, YANG Ying, FU Wenlong, ZHU Ping, FENG Dayong, LEI Yi, ZHANG Ming

圈养林麝生长曲线拟合

Studies on Growth and Development Model of Captive Forest Musk Deer

四川动物, 2016, 35(): 238-242,248

Sichuan Journal of Zoology, 2016, 35(): 238-242,248

10.11984/j.issn.1000-7083.20150246

文章历史

收稿日期: 2015-08-11

接受日期: 2015-10-29

Abstract

PDF

Figures

Tables

引用本文

蔡永华, 杨营, 付文龙, 朱萍, 冯达勇, 雷毅, 张明. 圈养林麝生长曲线拟合[J]. 四川动物, 2016, 35(): 238-242,248. 复制到剪切板

CAI Youghua, YANG Ying, FU Wenlong, ZHU Ping, FENG Dayong, LEI Yi, ZHANG Ming. Studies on Growth and Development Model of Captive Forest Musk Deer[J]. Sichuan Journal of Zoology, 2016, 35(): 238-242,248. 复制到剪切板

圈养林麝生长曲线拟合

蔡永华¹, 杨营¹, 付文龙¹, 朱萍¹, 冯达勇¹, 雷毅², 张明^3*

1. 四川省养麝研究所, 四川都江堰 611845;
2. 四川农业大学旅游学院, 四川都江堰 611830;
3. 四川农业大学动物科技学院, 四川雅安 625014

收稿日期: 2015-08-11; 接受日期: 2015-10-29

基金项目: 四川省科技厅"'林麝饲养和活体取香技术'成果产业化配套技术的研究及推广应用"项目

作者简介: 蔡永华(1962-), 高级工程师

*通信作者: 张明, E-mail:zhm3000@163.com

摘要: 为探索圈养林麝Moschus berezovskii体质量、体尺的生产发育规律, 选用320只林麝(雄麝160只,雌麝160只),测定其1~400周龄的体质量和体尺(额宽、头长、耳长、脊柱长、胸围、肱骨长、大腿长和小腿长),并用Logistic、Bertalanffy、Gompertz模型进行生长曲线拟合。3种模型均能很好地拟合周龄与体质量之间的回归关系,根据回归方程决定系数判断,Bertalanffy对雄麝(R²=0.966)、雌麝(R²=0.954)体质量的拟合优于Logistic和Gompertz模型。体尺与周龄的拟合结果显示:Bertalanffy模型优于Logistic和Gompertz模型;肢体体尺与周龄的拟合度较高,头部体尺与周龄拟合度较低。在所检测的体尺指标中,Bertalanffy对雄麝(R²=0.927)、雌麝(R²=0.933)小腿长的拟合度最高。林麝体质量、体尺的生产发育规律可用Bertalanffy模型拟合。

关键词: 生长曲线林麝 Logistic模型 Bertalanffy模型 Gompertz模型

Studies on Growth and Development Model of Captive Forest Musk Deer

CAI Youghua¹, YANG Ying¹, FU Wenlong¹, ZHU Ping¹, FENG Dayong¹, LEI Yi², ZHANG Ming^3*

1. Institute of Breeding and Reproduction of Forest Musk Deer in Sichuan, Dujiangyan, Sichuan Province 611845, China;
2. College of Tourism, Sichuan Agricultural University, Dujiangyan, Sichuan Province 611830, China;
3. College of Animal Science and Technology, Sichuan Agricultural University, Ya'an, Sichuan Province 625014, China

Abstract: In order to explore the rule of growth and development of body weight and size of caotive forest musk deer (Moschus berezovskii), body weight and size (forehead width, head length, ear length, spine length, chest circumference, humerus length, thigh length and leg length) of 320 forest musk deer (males: 160, females: 160) were measured from the birth to the 400^th week, and the regression of the measured values and week-age were fitted with Logistic, Bertalanffy and Gompertz model, respectively. The results showed that the three tested models, Logistic, Bertalanffy and Gompertz, could fit the regression of body weight and week-age of forest musk deer. The fitting degree (R²) of Bertalanffy model was better than that of Logistic and Gompertz for males (R²=0.966) and females (R²=0.954). The results of the regression body size and week-age revealed that: Bertalanffy model was better than Logistic and Gompertz models; The fitting degree of limb size and week-age was high, whereas that of head size and week-age was low. In all parameters of body size, the fitting degree of leg length and week-age was the highest in males (R²=0.927) or females (R²=0.933) with Bertalanffy model. The rule of growth and development of body weight and size of forest musk deer could be fitted with Bertalanffy model.

Key words: growth curve forest musk deer Logistic model Bertalanffy model Gompertz model

动物生长曲线是动物个体生长发育规律的反映，通常采用非线性数学模型进行描述(Migon et al.，1990；盛志廉，吴常信，1995)。目前常用Logistic、 Bertalanffy和Gompertz模型来探讨动物的生长发育规律(Woolson & Leeper，1980；von-Rosen，1991;Nunez-Anton et al.，2001)。生长曲线模型可以用于预测动物的体质量、体尺等生长发育指标，并进一步以此判断动物的饲养管理和营养水平(李娟等，2009)。

林麝Moschus berezovskii是国家Ⅰ级保护动物(Yang et al.，2003；Meng et al. ，2006)，雄麝分泌的麝香具有极高的药用价值。随着林麝的人工驯养与繁殖的成功，已在林麝的基础生理学(姜海瑞等，2007；何迟酩等，2012)、行为学(Meng et al. ，2011)、遗传学(Xia et al. ，2006；Zhang et al. ，2007；Zhao et al. ，2008)和常见疾病(朱承嗣等，2012；周瑜等，2013)等方面进行了探索与研究。林麝体质量、体长和肩高(体高)的生长发育规律已有报道(竭航等，2014)，但已有的研究中，测量的个体数少，持续测定时间短，头长、耳长、胸围、大腿长和小腿长等体尺没有测定，而且使用的拟合模型不是经典模型。本研究利用Logistic、Bertalanffy和Gompertz模型对圈养林麝的体质量、额宽、头长、耳长、脊柱长、胸围、肱骨长、大腿长和小腿长的生长曲线进行拟合，为林麝生长发育研究提供更多的基础数据。

1 材料与方法 1.1 实验材料

四川省养麝研究所都江堰和马尔康养麝场的圈养林麝320只(雄麝160只，雌麝160只)。实验麝群自由采食、饮水。其他饲养管理措施参见程世国和邹真慧(1991)的研究。

1.2 测定指标

从出生到400周龄，每周测定实验林麝的空腹体质量，以及体尺指标：额宽、头长、耳长、脊柱长、胸围、肱骨长、大腿长和小腿长。

体尺指标定义如下：

额宽：两眼眶外侧突起点之间的距离；

头长：从两耳之间中部到鼻端的长度；

耳长：耳背根部到耳尖端的长度；

脊柱长：从头部枕骨后第一脊椎到尾根前第一尾椎之间，沿脊柱弯曲线的长度；

胸围：紧靠前肢腋下，垂直围绕胸部一周的长度；

肱骨长：前肢从肩关节凸出顶点到肘关节后端顶点间的直线距离；

小腿长：从后肢脚跟后端凸点到蹄冠后部间的直线距离；

大腿长：从后肢膝关节前段凸出顶点到脚跟后端突出点之间的直线距离。

1.3 生长曲线模型

采用3种最常见的动物生长曲线模型：Logistic、Bertalanffy和Gompertz(表 1)。

表 1 3种常用动物生长曲线模型 Table 1 Three kinds of common growth curve models

参数	Logistic	Bertalanffy	Gompertz
表达式	y_t=A/(1+Be^-Kt)	y_t=A(1-Be^-Kt)³	y_t=Ae^-Bexp(-Kt)
绝对生长率	d_y/d_t=ABKe^-Kt/(1+e^-Kt)²	d_y/d_t=3KA(1-Be^-Kt)²Be^-Kt	d_y/d_t=KABe^-Bexp(-Kt)e^-Kt
相对生长率	K(1-y_t/A)	3K	K(lnA-lny_t)
拐点(t_i,y_i)	t_i=(lnB)/K,y_i=A/2	t_i=(ln3B)/K,y_i=8A/27	t_i=(lnB)/K,y_i=A/e
最大增重(长)	Ky_i/2	3Ky_i/2	Ky_i
注： t为周龄, y_t为t周龄的体质量, A为成熟体质量, K为生长速率参数, e＝2.72, B为常数尺度, t_i为拐点周龄, y_i为拐点体质量。 Notes: t. week-age, y_t. body weight in the t week, A. body weight of adult, K. growing rate, e=2.72, B. constant, t_i. the week on the inflection point, y_i. the body weight on the inflection point.

表选项

1.4 数据处理

用SPSS 20拟合模型，建立生长曲线模型，推算出拐点体质量和最大增重、增长，并且根据拟合度(R²)对生长曲线模型进行评价。

2 结果分析 2.1 林麝体质量与周龄拟合

雌雄麝体质量的生长拟合方程和拟合度(R²)见表 2。结果显示：雄麝周龄与体质量的Logistic、Bertalanffy和Gompertz拟合方程决定系数分别为0.960、0.966和0.964，雌麝3种拟合方程的决定系数分别为0.938、0.954和0.950。结果表明：Logistic、Bertalanffy和Gompertz 3种模型均能很好拟合周龄与体质量的回归关系。但运用Bertalanffy模型计算雌麝的拐点周龄为0，因此相对较好的周龄-体质量拟合是Gompertz模型。

表 2 林麝体质量与周龄的3种拟合方程 Table 2 Three fitting equations of body weight-week of Moschus berezovskii

模型 Model	性别 Gender	拟合方程 Fitting equation	拟合度 Fitting degree (R²)	拐点周龄 Age of inflection value/w	拐点体质量 Body weight of inflection value/kg	最大周增重 Maximum weekly increase/kg
Logistic	♂		0.960	38.1	3.952	0.109
Logistic	♀		0.938	13.6	3.726	0.341
Bertalanffy	♂	Bw=8.040(1-0.544e^-0.028w)³	0.966	0.5	2.382	0.100
Bertalanffy	♀	Bw=7.861(1-0.563e^-0.030w)³	0.954	0.0	2.329	0.136
Gompertz	♂	Bw=7.986e^{-2.294e(-0.034w)}	0.964	20.0	2.890	0.125
Gompertz	♀	Bw=7.786e^{-2.364e(-0.043w)}	0.950	24.4	2.936	0.100
注: w. 周龄, e=2.72; 黑体表示指标与周龄在3个模型中具有最高的拟合度; 下同。 Notes: w. week-age, e=2.72; the bold represented the highest degree of fitting among the three models; the same below.

表选项

2.2 不同模型拟合的体质量生长曲线

利用Logistic、Bertalanffy和Gompertz回归方程绘制雌雄麝的体质量生长曲线(图 1)。

图 1 Logistic、Bertalanffy和Gompertz模型拟合的林麝体质量生长曲线 Fig. 1 Growth curves of body weight-week of Moschus berezovskii by Logistic, Bertalanffy and Gompertz model

图选项

在3种模型中，Bertalanffy模型在雌雄麝周龄- 体质量拟合中具有最高的拟合度。在Gompertz模型中，雌雄麝的初生体质量(0周龄)分别是1.236 kg和1.339 kg。实测雌雄麝初生体质量为0.48 kg±0.13 kg和0.53 kg±0.23 kg。在Logistic和Bertalanffy模型中，雌雄麝的初生体质量分别为0.567 kg、0.785 kg和0.866 kg、0.762 kg。

2.3 头部体尺与周龄的拟合

头部体尺指标额宽、头长和耳长与周龄的拟合方程和拟合度见表 3。结果显示：Logistic、Bertalanffy和Gompertz模型中，周龄与额宽拟合方程的决定系数为0.717~0.804，周龄与头长拟合方程的决定系数为0.860~0.899，周龄与耳长拟合方程的决定系数为0.810~0.941。雄麝周龄与额宽、头长和耳长拟合方程的决定系数分别为0.799~0.804、0.895~0.899和0.810~0.821，雌麝周龄与额宽、头长和耳长拟合方程的决定系数分别为0.717~0.721、0.860~0.866和0.939~0.941。综上所述，雌麝耳长与周龄用3种模型均能很好地拟合，而额宽和头长的拟合程度相对较低。以拟合度判断周龄与额宽、耳长的回归关系中，Bertalanffy模型具有最好的拟合度；雄麝头长与周龄，Logistic模型具有最好的拟合度，雌麝头长与周龄，Bertalanffy模型具有最好的拟合度。

表 3 林麝头部体尺与周龄的3种拟合方程 Table 3 Three fitting equations of head size-week of Moschus berezovskii

头部体尺 Head size	模型 Model	性别 Gender	拟合方程 Fitting equation	拟合度 Fitting degree (R2)	拐点周龄 Age of inflection value/w	拐点头部体尺 Head size of inflection value/cm	最大周生长 Maximum weekly increase/cm
额宽 Forehead width/cm	Logistic	♂		0.799	0.000	3.166	0.119
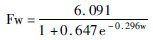	Logistic	♀		0.717	0.000	3.046	0.451
	Bertalanffy	♂	Fw=6.330(1-0.349e^-0.063w)³	0.804	0.489	2.382	0.100
	Bertalanffy	♀	Fw=6.130(1-0.155e^-0.027w)³	0.721	0.000	1.816	0.618
	Gompertz	♂	Fw=6.330e^{-0.422e(-0.069w)}	0.801	0.000	2.327	0.161
	Gompertz	♀	Fw=6.120e^{-0.504e(-0.243w)}	0.720	0.000	2.250	0.547
头长 Head length/cm	Logistic	♂		0.899	0.000	7.859	0.157
	Logistic	♀		0.860	0.000	7.533	0.166
	Bertalanffy	♂	Hl=15.806(1-0.500e^-0.026w)³	0.895	0.405	4.683	0.183
	Bertalanffy	♀	Hl=15.038(1-0.186e^-0.049w)³	0.866	0.000	4.456	0.267
	Gompertz	♂	Hl=15.754e^{-0.685e(-0.034w)}	0.897	0.000	5.792	0.191
	Gompertz	♀	Hl=15.042e^{-0.612e(-0.041w)}	0.864	0.000	5.530	0.227
耳长 Ear length/cm	Logistic	♂		0.810	1.000	4.929	0.283
	Logistic	♀		0.939	0.327	3.046	0.499
	Bertalanffy	♂	El=9.869(1-0.550e^-0.079w)³	0.821	0.500	2.924	0.347
	Bertalanffy	♀	El=10.016(1-0.252e^-0.090w)³	0.941	0.000	2.968	0.401
	Gompertz	♂	El=9.858e^{-0.772e(-0.097w)}	0.815	0.000	3.624	0.352
	Gompertz	♀	El=10.006e^{-0.865e(-0.100w)}	0.940	0.000	3.679	0.368

表选项

2.4 躯体体尺与周龄的拟合

躯体体尺指标：脊柱长和胸围与周龄的拟合方程和拟合度见表 4。结果显示：Logistic、Bertalanffy和Gompertz中，雄麝脊柱长与周龄的拟合方程决定系数分别为0.940、0.943和0.942，而雌麝脊柱长与周龄的拟合方程决定系数分别为0.865、0.869和0.868。Logistic、Bertalanffy和Gompertz 3种模型中，雄麝胸围与周龄的拟合方程决定系数分别为0.913、0.925和0.918，而雌麝胸围与周龄的拟合方程决定系数分别为0.893、0.897和0.896。但Bertalanffy和Gompertz模型中，均存在拐点周龄为0的情况。以拟合度判断，Bertalanffy模型在周龄与脊柱长和胸围回归关系中具有最好的拟合度。

表 4 林麝躯体体尺与周龄的3种拟合方程 Table 4 Three fitting equations of body size-week of Moschus berezovskii

躯体体尺 Body size	模型 Model	性别 Gender	拟合方程 Fitting equation	拟合度 Fitting degree (R2)	拐点周龄 Age of inflection value/w	拐点躯体体尺 Body size of inflection value/cm	最大周生长 Maximum weekly increase/cm
脊柱长 Spine length/cm	Logistic	♂		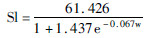0.940	5.408	30.713	1.029
	Logistic	♀		0.865	3.924	30.622	2.159
	Bertalanffy	♂	Sl=61.703(1-0.606e^-0.041w)³	0.943	0.000	18.282	1.124
	Bertalanffy	♀	Sl=61.392(1-0.295e^-0.095w)³	0.869	0.000	18.190	2.592
	Gompertz	♂	Sl=61.553e^{-0.908e(-0.053w)}	0.942	0.000	22.630	1.199
	Gompertz	♀	Sl=61.340e^{-1.036e(-0.106w)}	0.868	0.000	22.551	2.390
胸围 Chest circumference/cm	Logistic	♂		0.913	6.252	22.756	0.887
	Logistic	♀		0.893	4.831	23.630	1.465
	Bertalanffy	♂	Cc=46.140(1-0.637e^-0.040w)³	0.925	0.647	13.671	0.820
	Bertalanffy	♀	Cc=47.469(1-0.299e^-0.079w)³	0.897	0.000	14.065	1.667
	Gompertz	♂	Cc=45.869e^{-0.980e(-0.054w)}	0.918	0.000	16.864	0.911
	Gompertz	♀	Cc=47.391^{-0.084e(-0.022w)}	0.896	0.000	17.423	0.383

表选项

2.5 肢体体尺与周龄的拟合

表 5结果显示了林麝肢体体尺与周龄的3种拟合曲线。结果显示：周龄与肱骨长、大腿长和小腿长的拟合方程的决定系数分别为0.903~0.914、0.914~0.930和0.810~0.933。Logistic、Bertalanffy和Gompertz中，肢体体尺与周龄的拟合度分别为0.810~0.928、0.905~0.933和0.903~0.932。3种模型之间没有差异，但在肱骨和大腿与周龄的拟合中，Bertalanffy和Gompertz模型出现了拐点周龄为0的情况；在小腿与周龄拟合中，3种模型均出现了拐点周龄为0的情况。以拟合度判断，Bertalanffy 模型在周龄与肱骨长、大腿长和小腿长回归关系中具有最好的拟合度。

表 5 林麝肢体体尺与周龄的3种拟合方程 Table 5 Three fitting equations of limb size-week of Moschus berezovskii

肢体体尺 Limb size	模型 Model	性别 Gender	拟合方程 Fitting equation	拟合度 Fitting degree (R²)	拐点周龄 Age of inflection value/w	拐点肢体体尺 Limb size of inflecution value/cm	最大周生长 Maximum weekly increase/cm
肱骨长 Humerus length/cm	Logistic	♂		0.901	3.618	7.667	0.157
	Logistic	♀		0.910	2.166	7.612	0.346
	Bertalanffy	♂	Hul=15.356(1-0.550e^-0.029w)³	0.905	0.500	4.550	0.198
	Bertalanffy	♀	Hul=15.296(1-0.237e^-0.063w)³	0.915	0	4.532	0.428
	Gompertz	♂	Hul=15.340e^{-0.781e(-0.035w)}	0.903	0	5.640	0.197
	Gompertz	♀	Hul=15.274e^{-0.808e(-0.069w)}	0.914	0	5.615	0.387
大腿长 Thigh length/cm	Logistic	♂		0.923	1.989	10.647	0.447
	Logistic	♀		0.914	1.905	10.719	0.670
	Bertalanffy	♂	Tl=21.383(1-0.556e^-0.052w)³	0.930	0.425	5.482	0.592
	Bertalanffy	♀	Tl=21.474(1-0.246e^-0.092w)³	0.921	0	6.363	0.878
	Gompertz	♂	Tl=21.335e^{-0.793e(-0.066w)}	0.926	0	7.844	0.518
	Gompertz	♀	Tl=21.461e^{-0.839e(-0.100w)}	0.919	0	7.890	0.789
小腿长 Leg length/cm	Logistic	♂		0.810	0	9.250	0.476
	Logistic	♀		0.928	0.601	9.189	0.763
	Bertalanffy	♂	Ll=18.501(1-0.510e^-0.072w)³	0.927	0.425	5.482	0.592
	Bertalanffy	♀	Ll=18.419(1-0.226e^-0.125w)³	0.933	0	5.457	1.023
	Gompertz	♂	Ll=18.499e^{-0.697e(-0.087w)}	0.924	0	6.801	0.592
	Gompertz	♀	Ll=18.407e^{-0.761e(-0.135w)}	0.932	0	6.767	0.914

表选项

3 讨论

生长曲线分析实质是把不同时期体质量、体尺资料提供的信息综合成少数几个参数。动物生长中常用Logistic、Bertalanffy和Gompertz模型来探讨动物的生长发育规律(Woolson & Leeper，1980；von-Rosen，1991；Nunez-Anton et al.，2001)。因此本研究中仅用了Logistic、Bertalanffy和Gompertz模型拟合林麝体质量与体尺的回归关系。增重是一个连续的过程，在动物的整个生产过程中，动物的生长主要表现为“S”曲线，但“S”曲线必须在非限制饲养条件下(竭航等，2014)。在本研究中，林麝体质量与周龄在Logistic模型中呈“S”曲线，在Bertalanffy和Gompertz模型中接近幂函数型，本研究中Bertalanffy模型具有最好的拟合度。研究结果反映出林麝前期增重非常迅速，这与已有的研究结果一致(张保良，1982；程世国，1984；竭航等，2014)。在已有的研究中，体质量与日龄在Gompertz、Logistic模型中的拟合度分别为0.988、0.980(竭航等，2014)，与本研究的拟合度相比更高，其原因主要是研究的个体数少，个体生长发育体质量变异较小；另一方面使用的Logistic模型与本研究中经典的Logistic模型有差异。

林麝生产发育过程中体尺生长模型的研究很少，竭航等(2014)研究了肩高(体高、体长)与日龄的拟合曲线。本研究尝试用Logistic、Bertalanffy和Gompertz模型来探讨林麝体尺发育规律。结果表明Bertalanffy模型的拟合度相对较高，而且肢体体尺(肱骨长、大腿长和小腿长)与周龄的拟合度较高，头部体尺(额宽、头长和耳长)与周龄的拟合度较低，躯体体尺(脊柱长和胸围)与周龄的拟合度介于二者之间。在动物的体尺测量上：体长和肩高与动物站姿有关，胸围测量比较麻烦，因此通过测量林麝肢体体尺和头部体尺来估测林麝周龄对于其管理非常方便。

参考文献

程世国, 邹真慧. 1991. 麝的饲料和饲养[M]. 成都: 四川科技出版社: 4-32.

程世国. 1984. 麝的饲养[J]. 西南民族学院学报: 畜牧兽医版, 10(4): 45-49.

何迟酩, 林进生, 邓家波, 等. 2012. 林麝血液生理生化指标研究[J]. 四川动物, 31(3): 456-459.

姜海瑞, 徐宏发, 王晓黎, 等. 2007. 麝的生物学研究现状分析[J]. 生物学通报, 42(6): 4-6.

竭航, 封孝兰, 陈强, 等. 2014. 圈养林麝生长曲线拟合研究[J]. 四川农业大学学报, 32(1): 97-102.

李娟, 刘益平, 张明, 等. 2009. 大恒优质肉鸡早期体重发育规律[J]. 四川农业大学学报, 27(3): 345-349.

盛志廉, 吴常信. 1995. 数量遗传学[M]. 北京: 中国农业出版社: 114-115.

张保良. 1982. 麝的生长发育[J]. 野生动物, 4(4): 24-27.

周瑜, 赵克雷, 田永强, 等. 2013. 几种药物对圈养林麝化脓隐秘杆菌菌膜的影响[J]. 四川动物, 32(3): 330-333.

朱承嗣, 王方荣, 唐清山, 等. 2012. 家养林麝常见病诊断与防治研究[J]. 野生动物, 33(1): 3-4.

Meng XX, Zhao CJ, Hui CY, et al. 2011. Behavioral aspects of captive musk deer during non-mating season: gender differences and monthly pattern[J]. Asian-Australian Journal of Animal Science, 24(5): 707-712.

Meng XX, Zhou CQ, Hu JC, et al. 2006. Musk deer farming in China[J]. Animal Science, 82: 1-6.

Migon GS, Beaumont CL, Bihan DE, et al. 1990. Genetic parameters of growth curve parameter in male and female chicken[J]. British Poultry Science, 40(1): 44.

Nunez-Anton V, Zimmerman D, Gregoire TG, et al. 2001. Parametric modeling of growth curve data: an overview[J]. Test, 10(1): 1-73.

von-Rosen D. 1991. The growth curve model: a review[J]. Communications in Statistics-theory and Methods, 20(9): 2791-2822.

Woolson RF, leeper JD. 1980. Growth curve analysis of complete and incomplete logitudinal data[J]. Communications in Statistics-theory and Methods, 9(14): 1491-1513.

Xia S, Zou DF, Yue BS. 2006. Six microsatellite loci in forest musk deer, Moschus berezovskii[J]. Molecular Ecology Note, 6: 113-115.

Yang QS, Meng XX, Xia L, et al. 2003. Conservation status and causes of decline of musk deer (Moschus spp.) in China[J]. Biological Conservation, 109: 333-342.

Zhang SC, Yue BS, Zou FD. 2007. Isolation and characterization of microsatellite DNA marker from forest musk deer (Moschus berezovskii)[J]. Zoological Research, 18(1): 24-27.

Zhao SS, Chen X, Fang SG, et al. 2008. Development and characterization of 15 novel microsatellite markers from forest musk deer (Moschus berezovskii)[J]. Conservation Genetics, 9: 723-725.