2. 南京农业大学中国粮食安全研究中心, 江苏南京 210095
2. China Center for Food Security Studies, Nanjing Agricultural University, Nanjing 210095, China
一、引言
由于人口变迁一般规律和计划生育政策的双重作用,中国自20 世纪70 年代以来生育水平大幅度下降,进入90 年代后,总和生育率降至更替水平以下,2012 年的总和生育率仅为1. 246,然而,生育率的持续下降并没有带来人口的迅速减少,2012 年全国人口仍保持4. 95‰的正增长水平①。这主要是由于过去高生育水平积累起来的人口正增长惯性对中国人口总量的增长在发挥显著的促进作用,即人口年龄结构中育龄妇女占有较高比重,以及人口预期寿命延长带来的结果。长期的低生育水平必然会导致未来人口的减少,一旦人口正增长惯性的作用消失殆尽,负增长惯性取而代之发挥作用,便会加剧人口减少的速度。为避免因到时再来提高生育水平而无法有效及时地抑制人口负增长以及缓解人口老龄化问题,中国政府已经颁布并开始实施适当鼓励生育的计划生育政策,例如允许“双独”、“单独”家庭生育二胎。可见,探究掩盖于人口年龄结构之下的真正的人口增长水平以及蕴藏在人口年龄结构内部的人口增长惯性,对于清楚地了解人口长期发展趋势,完善计划生育政策的制定与实施具有重要的意义。
国内已有学者关注中国人口内在增长水平以及人口增长惯性问题,研究发现,早在1990 年人口内在自然增长率就已由正变负,人口负增长惯性正在逐渐积累起来[1, 2]。总体而言,这类研究基本是针对不同时期人口增长趋势的分析与模拟,尽管能够直观地给出具体一段时间内或某个时间点上的人口总量,但却需要建立在稳定人口的假设之上,即年龄别生育率与死亡率保持长期稳定不变[3],也就是要求同一时期各年龄人口具有相同的生育和死亡模式,显然这在现实中难以满足,尤其是在社会变迁比较明显的时期。
从本质上讲,人口内在自然增长率实际测度的是代际间的年均更替率。妇女终身生育率、出生婴儿性别比、妇女存活概率以及平均世代间隔是构成人口内在自然增长率的主要参数。但是,平常我们无法直接观察到未结束生育期的年龄组(队列) 妇女的终身生育率,而能够很容易地得到任一年份各年龄组(队列) 妇女当年生育率并加总得到总和生育率。这是很多研究会直接应用总和生育率分析时期角度的人口内在增长水平,而非应用终身生育率分析队列角度的人口内在增长水平的重要原因之一。但对于前者有两点值得注意: 一方面,应用前者所分析得到的结果无法代表任一真实人口队列的增长水平; 另一方面,总和生育率的较强波动性将难以对长期人口发展趋势进行稳定的预测。相反的,后者并不存在上述问题,虽然无法直接刻画出不同时期的人口规模,但至少能够作为时期人口内在增长水平研究的一个有益补充,根据各年龄人口的真实变化趋势分析具有不同年龄结构的人口的长期发展规律,有助于进一步了解未来人口的变化方向及增减速度。然而,一个亟待解决的问题便是如何缩短甚至消除终身生育率的时滞期限而令其具有更强的实际意义?
随着研究者们对总和生育率的深入认识和分析方法的不断改进,在一定条件下能够实现总和生育率对终身生育率的估计。邦戈茨(Bongaarts) 和菲尼(Feeney) 指出常规的总和生育率会因为时期生育年龄的变动(所谓的进度效应) 而产生显著的失真,因而提出了去进度效应总和生育率,简称B-F方法[4],该方法一经提出便引起了人口学界的广泛热议并催生出一系列的相关研究。一些研究对于这一指标到底在测量什么提出了质疑[5, 6, 7],因为它既不是对时期生育水平的估计又不是真正意义上的终身生育率[8]。邦戈茨和索博特卡(Sobotka) 新近提出了对该指标进一步改进的方法,并认为在一定条件下,比较去进度效应总和生育率和终身生育率是合理的,如用于队列生育率变化很慢,没有显著波动,而时期生育率的分布形状变化也很小的当代欧洲人口[9]。显然,这种转换方法也并不适用于任何一类人口群体。
笔者在一项研究中提出了利用初育年龄对终身生育率进行测度的尝试,并验证了该方法具有一定的可行性及合理性[10]。作为后续研究,本文将进一步以预测效率和稳定性为标准,比较初育年龄测度法与去进度效应总和生育率估计终身生育率的方法,并探讨上述两种方法在预测人口内在自然增长率方面的差异。以此为依据,本文将从队列视角揭示中国人口内在增长潜力,并结合人口年龄结构的变化特征探讨未来中国人口可能的发展趋势。目的在于与时期性质的人口变动水平进行对比,从另一个侧面为长期人口预测以至生育政策的制定提供科学合理的理论依据。 二、终身生育率两种估计方法的比较 1. 去进度效应总和生育率及其对终身生育率的估计
早在20 世纪50 年代,一些国外学者就已研究发现总和生育率无法准确反映生育数量的变化: 受生育时间变化的影响,即使实际队列的终身生育水平不发生改变,年度间的总和生育率也会被提高或降低。瑞得(Ryder) 首先提出应用一个人口中每个队列平均生育年龄的变化量对这一扭曲进行调整的思想[11],在此基础上,邦戈茨和菲尼进行了进一步的提炼,将这种扭曲称之为生育进度效应,并运用某一时期前后两年的分胎次平均生育年龄差异作为调整系数,试图用来消除该效应以得到真正的生育数量水平[4]。具体的调整思路可由如下的基本数学表达形式做出解释:
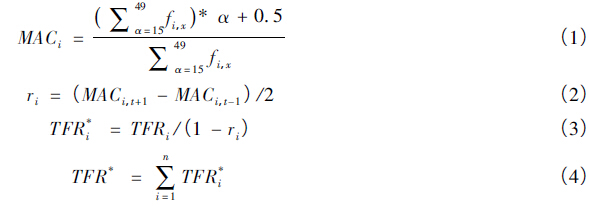
从上述公式可知,去进度效应总和生育率仅根据不同胎次年龄别生育率数据进行调整,并不需要额外的信息。其中,i 表示胎次,MACi表示分胎次的平均生育年龄,ri是调整系数,公式(2) 是经过整理后的简便表达形式,其计算依据是以当年及上一年生育年龄的平均数作为平均生育年龄年初值,以当年与下一年的均值作为年末值,最终用年末与年初的差值表示当年平均生育年龄的变动。如果当期的总体生育时间表现为向后推迟的状态,即ri > 0 ,那么得到的TFR* 将大于TFR ,也就是说实际的生育势能并没有在当期完全释放出来,而是向后累积,观察到的生育水平要低于真实的生育水平。
当然,可能会出现ri > 1 、TFR* 为负的异常现象,即平均生育年龄的变动幅度非常大。郝娟、邱长溶运用中国的经验数据证实的确会存在这种可能性[12]。虽然这与数据的质量有一定关系,但主要应是由于该方法要求年龄别生育率曲线形状不变、各年龄育龄妇女平均生育第i 孩年龄的年变化幅度相等,一旦现实与这一强假设条件相差较远,去进度效应总和生育率的稳定性会变得很差[13]。
随着对去进度效应总和生育率研究的不断深入,近期,邦戈茨等人在原方法的基础上将生育率替换为生育概率,提出了一种综合考虑孩次结构与进度效应的调整指标TFRp* ,并用欧洲多国的数据验证了其较TFR* 具有更强的稳定性[9]。一般来说,新指标的稳定性如何是多数研究探讨的焦点,因为并不存在一个真实的标准而难以对其效度进行评价。由于目前不完全具备计算所需的数据,因此,暂时难以将TFRp* 应用于中国生育研究中[14]。
不过,邦戈茨认为,在特殊条件下,调整的总和生育率与那些在同时期内已达平均生育年龄妇女队列滞后取得的终身生育率值还是可以比较的。例如,1965 年15 岁的育龄妇女队列的平均生育年龄为25 岁,那么该队列的终身生育率对应的是1975 年调整的总和生育率。值得注意的是,这里的总和生育率是5 年的移动平均值,而不是真正的终身生育率。尽管该方法较为粗糙,而且中国生育水平变化的实情确实很难满足二者的可比条件,但这却是目前为止最能够简单有效地将总和生育率转换为终身生育率的方法,可将其简称为总和生育率转换法。 2. 利用初育年龄对终身生育率的模拟
笔者在另一项研究中指出: 一生的生育是一个完整的过程,后一生育事件的发生必定建立在前一生育事件的基础上。因此,一方面遵循基本的生理规律,另一方面根据初次生育时间选择和终身生育数量的决策机制,推断属于前期生育行为的初育年龄与终身生育数量高度相关具有相当的合理性,而且在统计学上得到了强力支持[10]。该方法的具体思路是根据可获得的时期跨度较大的15-49 岁年龄别生育率数据,分别计算出不同队列的初育年龄与终身生育率,采用双对数模型进行模拟,另外需加入时间变量以捕捉其他因素对终身生育率的影响,基本模型如下:
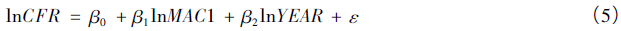
然而,过去高生育水平时期初育年龄与终身生育率的拟合结果并不意味着可以简单地用于更替水平以下时期的预测,关键在于人们对二胎生育的改变情况。如果同一年份出生的多数人的最少生育数量为两个孩子,那么当终身生育率降至2 附近时,很难再按照过去的水平随着初育年龄继续下降; 如果大部分人普遍能够接受1 个孩子的最少生育数量,那么二胎会同多胎一样与初育年龄的变化高度相关,而在接近1 的水平上放缓下降速度。在中国,农村人口人均收入水平低于城镇,同时计划生育政策也相对宽松,并且其生育观念也较为传统,2 个孩子仍可能是多数农村人口的最低生育数量需求。而在城镇,仅生育一胎的家庭则会更多。当然,随着农村人口不断地向城镇迁移,以及城乡间人口流动的加速,农村人口的生育行为会与城镇人口逐渐趋同。因此,可以模拟当社会总体的终身生育水平降至2 附近时,未来人口全部遵循城镇和农村人口两种极端情况下的生育水平变化趋势,并且根据农村和城镇人口比重对其进行加权平均,从而得到更可靠的预测结果。 3. 两种估计方法的结果比较
既然初育年龄测度法和总和生育率转换法均可以得到终身生育率的估计值,那么就能够以真实值为标准对不同方法的结果进行稳定性和有效性的检验。根据1950-2012 年中国育龄妇女年龄别生育率数据①,可以计算得到1950-1978 年开始进入生育期的29 个完整队列的终身生育率②。从数据上显示,随着时间的推移,实际终身生育率呈现稳定下降的趋势,而1977 年15 岁的育龄妇女队列的数值则出现了略微上升的现象,为考察这一变化是新的趋势还是数据的异常情况,我们进一步估计了1979 年妇女队列的终身生育率,假设其相应的缺失49 岁生育率数据对计算结果的影响可以忽略不计。因此,实际上是应用1950-1979 年30 个完整队列的终身生育率真实值对上述两种方法的结果进行评价,比较结果如图 1 所示。
① 数据来源: 1982 年全国1‰人口生育率抽样调查; 1988 年全国2‰人口生育节育抽样调查; 1992 年中国生育率抽样调查数据表; 历年《中国人口与就业统计年鉴》。1993 年、1994 年以及2010 年的缺失年龄别生育率数据用缺失年份前后两年的平均值来补充。② 1978 年15 岁的妇女在2012 年达到49 岁,完成了整个生育周期; 而1978 年以后满15 岁的妇女2012 年尚未完成生育周期。
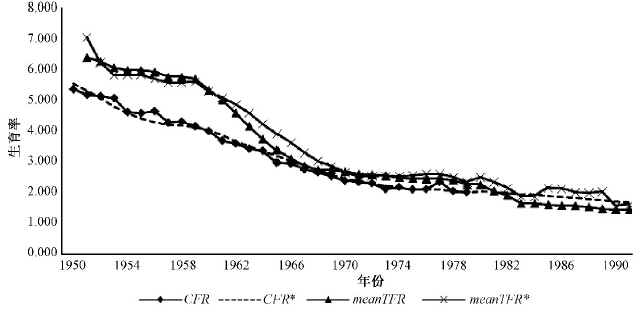 |
| 图 1 初育年龄测度法与总和生育率转换法估计值与真实值的比较 |
其中,CFR是30 个育龄妇女队列终身生育水平的真实值,CFR*是利用初育年龄测度得到的终身生育率估计值,meanTFR* 和meanTFR 分别表示去进度效应和常规总和生育率修匀值对应的队列终身生育率估计值。从稳定性的角度分析,很明显CFR*呈现出稳定的下降趋势,而meanTFR* 和meanTFR 的波动性较高,且偏离CFR。调整过的去进度效应总和生育率确实在一定程度上改善了常规总和生育率,体现为更加平稳的变化趋势,但仍然明显不如CFR*。从效度方面看,CFR*与真实值CFR保持高度一致,由常规和去进度效应的总和生育率预测得到的终身生育率估计值在1951-1967 年15 岁的17 个育龄妇女队列中与真实值的偏差较大,而这些队列的终身生育率估计值恰好对应的是20 世纪六七十年代总和生育率的修匀值,相对于其他时期而言,该时期总和生育率变化的起伏落差非常大。60 年代末期开始进入生育年龄的女性的终身生育率估计值与真实值之间的误差有所缩小,并且变化相对稳定,这与中国进入80 年代后总和生育率变动幅度小相关。反向预测表明,应用总和生育率估计终身生育率的效度并不高。
若以15-35 岁一胎年龄别生育率数据计算初育年龄,则可以预测出1980-1991 年进入生育期的12 个育龄妇女队列的终身生育率。从图 1 中可以清楚地看到,1980-1991 年15岁育龄妇女队列的终身生育水平继续平缓下降。虽然对于这部分预测值而言并不存在一个真实的终身生育率以验证预测的准确性,但可以与meanTFR*和meanTFR进行对比,结果显示由初育年龄预测得到的终身生育率估计值介于两者之间,并且更接近meanTFR*的平均变化趋势,说明其预测结果至少不会与总和生育率估计法产生较大偏差。
计算终身生育率的目的之一是测度相对稳定的人口内在自然增长率。从稳定性的角度看,CFR*在整个区间都远远优于meanTFR*和meanTFR。也即,与去进度效应和常规总和生育率修匀值相比,初育年龄法能提供对妇女终身生育率更稳定的预测值,因而更接近稳定的人口内在自然增长率。
过去的经验表明,由初育年龄预测得到的终身生育率估计值具有更高的准确性,但是,我们不仅无法观察到妇女未来的实际终身生育率,甚至无法统计1980 年以后年满15 岁的妇女的终身生育率,因而无法用实际观察值来验证预测值。然而,正因为无法得到观察值而又需要预测,我们才需要相对准确的方法。如果解释过去的能力可以合理延伸到预测未来,则初育年龄测度法不失为一种相对较好的方法。 三、人口内在自然增长率
尽管已有不少研究对时期人口内在自然增长率进行了分析,并将其与常规的人口自然增长率进行比较,说明隐藏在背后的人口内在增长势能[1, 3]。但从长期来讲,应用终身生育率等队列指标计算得到的人口内在自然增长率才是真正意义上的对人口增长潜力的表达。如前面所述,初育年龄测度法相比总和生育率估计法能够有效、稳定地对终身生育率进行预测,这一结果能否继续在人口内在自然增长率的分析中得以体现,队列角度的潜在人口增长水平究竟如何,这是进一步将要探讨的内容。 1. 涵义及计算方法
人口内在自然增长率r与净再生产率NRR 的计算需要相同的基本要素,即分年龄的女婴生育函数m(a) 和存活函数p(a) 。严格来说,有一点明显不同的是,人口内在自然增长率是稳定人口假设下测量人口增长潜力的时期性质的指标; 而人口的净再生产率则表示育龄妇女在生育期末平均生育的女孩数,也就是度量生育的妇女能否在数量上“复制她们自己”,似乎作为队列指标更为合理一些。若要将二者联系起来进行分析,首先必须统一研究对象为真实队列还是假设队列。由于本文的目的在于研讨真实人口队列的潜在增长水平,因此,人口内在自然增长率的涵义将被解释为两代人之间的年增长率,具体的计算参数也均应用相应的队列指标。
洛特卡将r与NRR 的关系表示为如公式(6) 所示,人口内在自然增长率等同于净再生产率的对数与平均世代间隔T之比:

净再生产率可以进一步分解为终身生育率CFR、出生婴儿中女婴所占比例S,以及育龄妇女存活到平均生育年龄的概率p(Am)三者的乘积[15],见公式(7) :
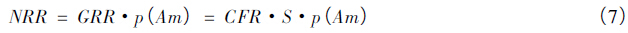
科尔(Coale) 证明平均世代间隔近似等于稳定人口和静止人口平均生育女儿年龄的均值,同时也证明了当死亡率曲线不是异常时(如战争、瘟疫) ,可以由年龄别生育率近似求得[16],具体表达形式如公式(8) 所示:

综合公式(6)-(8) ,人口内在自然增长率可以表示为:

根据基础的年龄别生育率数据、出生婴儿性别比以及引用的人口粗、净再生产率数据得到的用于计算人口内在自然增长率的各参数指标值如表 1所示。
由表 1 中的各参数值计算得到的人口内在自然增长率,即1950-1991 年进入生育期的育龄妇女到其生育下一代之间的年均人口自然增长率的变化趋势如图 2 所示。其中,r、r'和r*依次代表根据终身生育率真实值、利用初育年龄和去进度效应总和生育率预测得到的估计值计算的人口内在自然增长率。总体而言,图 2 中所显示的不同增长率曲线形状与各自对应的终身生育率曲线形状类似,说明与人们的预期一致,生育水平是衡量人口内在增长潜力的最主要的指标。然而,随着生育数量逐渐稳定维持在较低水平,平均世代间隔的延长会成为促进人口内在自然增长率下降的一个重要因素。
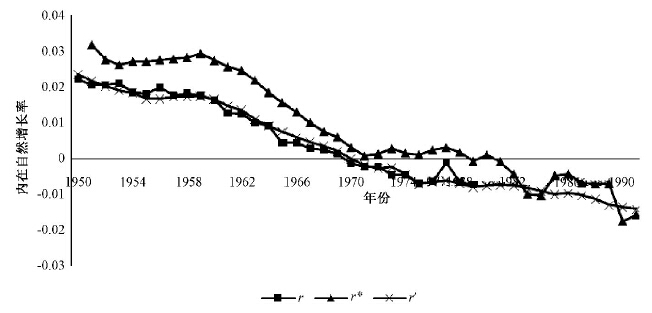 |
| 图 2 1950 - 1991 年15 岁的育龄妇女队列的人口内在自然增长率的变化趋势 |
从图 2 中可以看出,队列角度的人口潜在增长水平始终保持稳定下降的趋势,20 世纪50 年代15 岁的育龄妇女从其出生到生育下一代女孩期间,这两代女性人口以年均22‰的速度进行更替,直至1970 年出现负增长现象,也就是说从1970 年15 岁的育龄妇女这一代人开始,平均生育女孩的规模小于母亲这一代的规模。值得注意的是,70 年代初人口进入负增长时对应的女性终身生育率介于2. 2-2. 3 之间,高于普遍应用的2. 1 的更替水平,这主要与中国偏高的男女性别比有关,女婴比例过低会造成人口提前进入负增长时期,马瀛通在其研究中同样指出考虑高性别比在内的更替水平也应提高[17]。
对于整个20 世纪70 年代进入生育期的育龄妇女队列而言,真实的以及由初育年龄测度得到的人口内在自然增长率均为负值,代际之间的人口迅速减少; 而由去进度效应总和生育率转换法得到的数值则体现为接近零增长水平的长期波动,直至80 年代初期才开始出现负增长,明显这与在其他参数指标变化不显著时生育水平持续下降的事实相违背。虽然预测部分两种方法的估计值水平较为接近,但仍可以从人口内在自然增长率的变化态势中看出,初育年龄测度法比总和生育率转换法具有更强的稳定性。由初育年龄预测的20 世纪90 年代初15 岁的育龄妇女生育的下一代女孩数量在以年均15‰左右的速度减少。由于鼓励生育的政策只是在近期才开始实施,而且最多也仅放宽到二胎生育,因此,根据过去的发展趋势粗略外推,对于本文无法预测到的更年轻的育龄妇女队列而言,其人口内在自然增长率将会继续下降。 四、未来中国人口变化趋势的简要分析
结合前面对不同年代出生的育龄妇女的人口内在自然增长率的估计以及2010 年第六次全国人口普查的人口年龄结构,可以尝试对中国人口未来的变化趋势进行简要的分析。
如图 3 所示,根据第六次全国人口普查数据绘制的人口年龄金字塔形状并不规则,有几处明显的缺口,从上至下的第一个缺口是由于20 世纪60 年代初的三年自然灾害导致出生人口减少,然而随后便出现生育的反弹,经过周期性重复,80 年代出生的人口大量减少,并且伴随着计划生育政策的开展,第二个缺口有所扩大。值得注意的是,又经过一轮世代更替,第三个缺口已经并不明显,人口数量的变化趋于稳定。在这样一个人口结构中,2010 年处于生育期的育龄妇女(2010 年15 岁至1975年15 岁) 占有较高比重,对应类似于松柏型人口金字塔的向外最凸出部分。即便通过图 2 可知,从1970 年15 岁的队列开始,真实的人口增长就已进入负增长状态,但从传统的由出生率和死亡率决定的人口自然增长水平来看,中国人口至今仍表现为正增长。可见,父母一代的庞大基数掩盖了子女规模不断缩小的事实,从而保持总人口数逐年增加。另外,平均预期寿命的延长也是引起人口增长的一个重要因素,随着占总人口比重较高的人群逐渐进入老龄阶段,这一因素对人口增长的促进作用将会更为明显。
 |
| 图 3 2010 年全国人口年龄结构 数据来源: 《中国人口与就业统计年鉴2011》 注: 为方便结合队列人口内在自然增长率进行分析,这里的纵坐标解释为对应年份15 岁的人口队列。 |
然而,由过去高生育水平积累起来的人口正增长惯性正在慢慢消失,总人口中比重较高的人群逐渐退出生育期,比重较低的队列进入生育期,同时人口内在增长水平处于负增长阶段,因此,中国人口逐步减少是一个必然的结果,只是现阶段较低的生育水平又进一步为未来积累负的增长惯性,在两者的合力作用下,人口规模缩小的态势将会维持很长一段时间。例如,从2010 年开始推测15 年后的情况,也就是位于图 3 中人口金字塔底部的15 个队列整体进入生育期,即使终身生育率能够恢复到2. 1 的更替水平,也很难通过新生人口实现总人数的增长。正如前面所述,人们平均预期寿命的延长会对人口增长起到一定的正向作用,但恐怕到时也难以抵消负增长的势头,并且会加重人口老龄化问题。中国于20 世纪70 年代初实行的以控制人口过快增长为目的的计划生育政策,虽然在很大程度上成功降低了新生人数的增加,但却无法及时地抑制人口正增长惯性所产生的作用,以至于在政策实施的40 多年间中国人口规模仍在不断扩大。过去的历史经验告诉我们,生育水平固然是人口政策关注的重点,但由其带来的未来人口结构的变化会长期影响人口金字塔底部数量,更是不容忽视的。运用初育年龄估计终身生育率的方法可以将终身生育率的时滞期限缩短十几年,也就是说在2010 年的人口结构中,终身生育率以及人口内在自然增长率能够由已知的1979 年及更早年代进入生育期的队列推延到1991 年,甚至于可以进一步依据初育年龄的估计值预测更年轻的育龄妇女队列的人口内在自然增长率,进而再结合生育模式便能够模拟不同年龄结构下的人口变化情况。这样既可以对过去人口增长有一个更清晰的认识,也能够为预测未来人口变化提供一种较为科学的思路。 五、结论及建议
年度间的人口增长水平实际上包含真正的人口内在增长潜力和由年龄结构决定的人口增长惯性两方面的作用。为充分认识人口发展的内在规律,本文以真实的人口队列为研究对象,运用两种不同方法得到的终身生育率估计值,对中国人口的内在增长水平进行了初步分析。在已有研究的基础上,本文通过与邦戈茨等人新近提出的由去进度效应总和生育率对终身生育率估计的方法相比较,证明初育年龄测度法在反向“预测”过去时具有明显更高的精度,在描述现在和正向预测未来时具有更强的稳定性,因而更有利于进行长期人口预测。初育年龄测度法的最大优势在于有效缩短了终身生育率的时滞期限,增强了运用终身生育率分析队列人口内在增长水平的实际可能性。
研究同时证明,在估计人口内在自然增长率方面,初育年龄测度法同样要优于总和生育率估计法。研究表明,以队列为视角的中国人口内在增长水平从20 世纪70 年代初开始已经下降: 进入生育期的育龄妇女所生育女孩的规模已经小于其本身的规模,人口的内在增长水平进入负增长时期。根据我们的预测,90 年代初期进入生育期的育龄妇女,其生育的女儿数量以年均15‰左右的速度在减少。另外,研究还发现,对应正增长到负增长转换临界年份的育龄妇女队列的终身生育率为2. 28,高于普遍认为的2. 1 的更替水平。这与中国偏高的出生婴儿性别比相关,因为新生婴儿中女性比例偏低,只有妇女更高的终身生育率才能维持整个人口的替代率。
有关人口的决策一方面需要对人口的内在增长水平有一个清晰的认识,另一方面也不能忽视年龄结构作用的人口惯性增长。结合2010 年全国第六次人口普查绘制的人口年龄金字塔,可以看出,在目前生育水平很低的情况下,中国总人数仍呈增加态势的原因主要是处于育龄期的人口占有较高比重,以及人们预期寿命的延长,在未来后者可能会发挥更为重要的作用。因此,人口政策的调整不仅需要充分认清其对现有人口增长水平的作用,还要考虑到对未来年龄结构的影响。
人口再生产达到并稳定在更替水平是人口发展的理想模式,也是中国人口政策的目标。面对低生育水平的现实,过去人口政策中对生育数量的限制在现在被适当放宽。然而,本文的研究结论表明初育年龄与终身生育数量具有显著的负向关系,因此,生育政策的调整也应注意对生育时间的控制,如果人们的意愿生育时间越来越晚,即使政策上允许生育二胎,甚至多胎也难以达到预期的理想目标。一些欧洲人口的经验研究也同样主张尤其要阻止越来越晚的生育趋势来影响人口发展[18]。
| [1] | 王丰, 郭志刚, 茅倬彦. 21 世纪中国人口负增长惯性初探[J]. 人口研究, 2008 (6):7-17. |
| [2] | 茅倬彦. 60 年来中国人口惯性变化及趋势[J]. 人口与经济, 2010 (6):1-6. |
| [3] | 宋健, 范文婷. 惯性增长下的人口再生产:全国及省级变化[J]. 人口研究, 2013 (4):33-42. |
| [4] | BONGAARTS J, FEENEY G. On the quantum and tempo of fertility [J]. Population and Development Review, 1998 (2):271-291. |
| [5] | KIM Y J, SCHOEN R. On the quantum and tempo of fertility:limits to Bongaarts-Feeney adjustment [J]. Population and Development Review, 2000 (3):554-559. |
| [6] | VAN I E, KEILMAN N. On the quantum and tempo of fertility:comment [J]. Population and Development Review, 2000 (3):549-553. |
| [7] | ZENG Yi, KENNETH C L. Adjusting period tempo changes with an extension of ryder's basic translation equation [J]. Demography, 2002 (2):269-285. |
| [8] | 郭震威. 对"去进度效应总和生育率(TFR') 方法"的一点看法[J]. 人口研究, 2000 (1):19-21. |
| [9] | BONGAARTS J, SOBOTKA T. A demographic explanation for the recent rise in European fertility [J]. Population and Development Review, 2012 (1):83-120. |
| [10] | 王亚楠, 钟甫宁. 利用初育年龄测度终身生育率的探索[J]. 人口学刊, 2015 (2):5-14. |
| [11] | RYDER N B. Problems of trend determination during a transition in fertility [J]. Milbank Memorial Fund Quarterly, 1956, 34:5-12. |
| [12] | 郝娟, 邱长溶. 对去进度效应总和生育率的检验与讨论[J]. 人口研究, 2012 (3):81-88. |
| [13] | 曾毅. 对邦戈茨-菲尼方法的评述、检验与灵敏度分析[J]. 中国人口科学, 2004 (1):68-80. |
| [14] | 郭志刚. 常规时期生育率失真问题及调整方法的新进展[J]. 人口研究, 2012 (5):3-14. |
| [15] | SAMUEL H P, PATRICK H, MICHEL G. 人口统计学:人口过程的测量与建模[M]. 郑真真, 等译. 北京:社会科学文献出版 社, 2011:139-141. |
| [16] | 曾毅, 张震, 顾大男, 郑真真. 人口分析方法与应用[M]. 北京:北京大学出版社, 2011:242-243. |
| [17] | 马瀛通. 从稳定人口与人口再生产认识总和生育率真实涵义[J]. 中国人口科学, 2010 (2):24-34. |
| [18] | LUTZ W, O'NEILL B C, SCHERBOV S. Europe's population at a turning point [J]. Science, 2003, 299:1991-1992. |


