2. 计算机软件新技术国家重点实验室(南京大学), 江苏 南京 210043;
3. Applied Sciences Group, Microsoft, Redmond, WA 98034, USA
2. State Key Laboratory for Novel Software Technology (Nanjing University), Nanjing 210043, China;
3. Applied Sciences Group, Microsoft, Redmond, WA 98034, USA
强化学习(reinforcement learning, RL)是机器学习领域中的一种主要范式, 区别于以图像处理为代表的感知学习, 感知学习主要处理监督学习问题, 而强化学习的目标是解决带奖励的序贯决策问题. 强化学习算法以贝尔曼方程为基础, 通过在环境中不断试错、累积经验并学习改进, 从而得到在给定任务上的更优策略[1].近年来, 得益于深度学习强大的特征表示能力和函数拟合能力, 深度强化学习(deep reinforcement learning, DRL)在游戏、机器人等越来越多的场景中展现出惊人的能力, 其知名成果包括围棋中AlphaGo接连战胜人类世界冠军[2]、星际争霸Ⅱ中AlphaStar评分达到最顶尖的大师段位[3]、麻将中微软亚洲研究院开发的Suphx首次在专业日本麻将平台“天凤”上荣升至最顶尖的十段[4], 以及核聚变工程中DeepMind团队开发的灵活通用的托卡马克磁控制器架构[5]. 此外, 深度强化学习在各行各业也逐渐落地[6−8].
然而, 当前深度强化学习的成功很大程度上依赖海量的学习数据与计算资源: 国际象棋基准算法MuZero训练初具成效需要约106步数据[9], 按每秒60步采样需要约11天; DeepMind使用384个TPU并行运行约44天才完成星际争霸Ⅱ算法AlphaStar的强化学习训练[3]. 深度强化学习的训练成本高昂, 这使其应用范围受到很大限制. 该现象主要因为目前普遍采用的深度强化学习算法面对新任务总是从零开始学习或迁移训练的效率不高. 反观人类的学习过程, 人类在学会骑自行车后, 可以很快地学会骑电动滑板车, 因为人擅长将已掌握的知识类推到新任务并加以有效利用; 如果智能体能够在任务间高效迁移知识, 其在新任务上的训练成本同样有望显著降低[10], 从而拓展强化学习的应用边界, 同时推进相关领域向类人智能迈进. 为解决上述问题, 现有学者针对强化学习的样本高效利用[10]、强化学习的泛化[11]等需求开展研究.
元学习(meta-learning)可看作泛化研究的子领域, 相关工作致力于迁移已有知识并减少训练样本. 元学习也被称为学习如何学习(learning-to-learn), 其概念最早可追溯到上世纪[12], 而近年来该领域以MAML(model-agnostic meta-learning)框架[13]为热点引起了持续关注与研究浪潮. 元学习领域已有许多算法、扩展应用和综述[14−17], 但各方对“元学习”一词的定义与界限不完全统一. 本文主要遵循一种广义解释[15, 16], 认为元学习是一种机器学习范式: 给定多个任务或任务采样分布, 要求元强化学习算法学习“元”知识, 并提升算法在新任务上的学习效率.
元强化学习(meta-reinforcement learning, Meta-RL)概念来源于元学习和强化学习的结合, 期望解决当前强化学习算法中存在的诸多限制[18]. 元强化学习的研究门槛较高, 该研究领域的发展较元学习滞后. 据我们所知, 元强化学习综述多存在于强化学习综述[11, 19]、元学习综述[15, 16]及相关领域综述[20]中, 其系统性和参考价值较弱; 大篇幅综述元强化学习的工作已有3篇: 赵春宇和赖俊的工作[21]对元策略学习方法进行了扩展和总结, 谭晓阳和张哲的工作[18]从设计和分析元强化学习算法的学习经验(相关任务)、归纳偏置及学习目标这3个角度对元强化学习典型研究进行了归纳总结, Beck等人的工作[22]从元测试阶段样本量设定及其相关技术的角度对元强化学习研究进行了较细致的归纳总结. 但近两年学术界涌现出许多值得思考的新问题与代表算法, 现有工作已经构成更加整体的研究轮廓, 为元强化学习领域提供了新的理解与方向, 元强化学习领域需要一份针对前沿、关键问题的整体归纳总结工作, 从而更好地推动相关领域发展.
与现有元强化学习综述不同, 本文以元强化学习工作的研究对象与适用场景为脉络, 对元强化学习领域的研究进展进行了全面梳理. 本文第1节对深度强化学习、元学习两个相关背景作基本介绍. 第2节概述元强化学习研究范围, 包括元强化学习的形式化定义及常见的场景设置总结. 第3节按元强化学习研究成果的研究对象与适用场景展开介绍元强化学习的现有研究进展, 其中各小节按研究对象不同作进一步的细分介绍. 第4节针对现有元强化学习研究仍面临的一些关键问题, 提出领域中可能的研究挑战与展望. 最后, 第5节总结全文.
1 元强化学习背景简介元强化学习是强化学习与元学习的交叉领域, 涉及强化学习与元学习的研究背景. 本节简述元强化学习的研究背景, 包括第1.1节强化学习和第1.2节元学习.
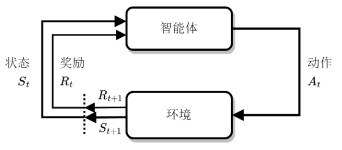
1.1 强化学习强化学习是机器学习的一种范式. 强化学习的框架如图 1所示, 其主要包含智能体(agent)和环境(environment)两部分. 强化学习的运行是智能体与环境两者不断交互的过程, 其中, 环境为智能体提供当前状态(state)和数值奖励(reward), 而智能体根据已有信息(通常是当前状态)向环境输出动作(action), 环境再给出执行动作后的状态和奖励. 如此循环, 直到任务终止(done). 在这一过程中, 智能体往往以最大化期望累积奖励为目标进行动作选择和策略学习.
|
图 1 强化学习框架 |
强化学习的环境模型普遍基于马尔可夫决策过程(Markov decision process, MDP)构建. MDP由一个四元组〈S, A, R, T〉定义, 其中, S是环境状态集合, A是可选动作集合, 状态转移函数T: S×A×S→[0, 1]给出由状态s和动作a转移到状态s′的概率, 奖励函数R: S×A×S→
智能体强化学习算法需要给出一个策略π, 策略在每个状态s决定动作a的执行与否(确定性策略)或执行概率(非确定性策略). 经典的强化学习算法认为环境的MDP模型是事先给定的, 策略π的优化目标为最大化期望累积折扣奖励. 设参数化策略πθ的参数为θ, 则算法计算最优参数θ*的公式为
| $ {\theta ^*} = \mathop {\arg \max }\limits_\theta {E_{{\pi _\theta }}}[\sum\nolimits_{t = 0}^T {{\gamma ^t}{r_t}} ] $ | (1) |
其中, T指代环境运行的时间步数; 折扣因子γ∈[0, 1]用于权衡长期奖励与短期奖励, 在T过大的环境中能显著稳定强化学习算法.
智能体强化学习算法主要分为基于值函数、基于策略梯度两类.
基于值函数的强化学习算法依据状态-动作值函数Qπ(s, a)决策. Qπ(s, a)指在状态s下执行动作a后, 继续依据策略π决策的期望累积奖励值. 因此, 最优动作a*即为状态s下取最大Qπ(s, a)的动作a:
| $ {a^*} = \mathop {\arg \max }\limits_a {Q^\pi }(s,a)|s $ | (2) |
Qπ(s, a)的计算则基于期望累积折扣奖励的表达式, 以贝尔曼最优方程(Bellman optimality equation)进行迭代, 具体如下:
| $ Q_{k + 1}^\pi (s,a) = {E_{s'}}[r + \gamma \mathop {\max }\limits_{a'} Q_k^\pi (s',a')|s,a] $ | (3) |
在基于值函数的深度强化学习算法中, Qπ(s, a)由神经网络构建, 并辅以一些设计以增强算法稳定性[23]. 该类算法在离散动作环境中表现更好, 但难以扩展到连续动作环境, 常用算法有深度Q网络(deep Q-network, DQN)[23]、双竞争深度Q网络(dueling double deep Q-network, D3QN)[24]、深度递归Q网络(deep recurrent Q-network, DRQN)[25]等.
基于策略梯度的强化学习算法直接对策略函数πθ(a|s)建模并优化. 同样从期望累积折扣奖励的优化目标出发, 策略参数θ的梯度为
| $ ∇_{θ}J(θ)=E_{π}[Q^{π}(s,a)∇_{θ}logπ_{θ}(a|s)] $ | (4) |
上式可以利用REINFORCE算法[26]近似估计, 其中, Qπ(s, a)由真实的采样轨迹(trajectory)计算, 但这样计算Qπ(s, a)的方差很大, 使策略难以提升. 演员-评论家(actor-critic, AC)框架将Qπ(s, a)作为独立的评论家模块学习, 评论家模块为演员策略提供参考. 经验表明, 该方法可显著提升策略训练效果. 基于策略梯度的常用算法均为演员-评论家架构, 该类算法在连续动作环境中表现更好, 包括深度确定性策略梯度算法(deep deterministic policy gradient, DDPG)[27]、近端策略优化算法(proximal policy optimization, PPO)[28]、柔性演员-评论家算法(soft actor-critic, SAC)[29]、双延迟深度确定性策略梯度(twin-delayed deep deterministic policy gradient, TD3)[30]等.
1.2 元学习元学习领域旨在解决传统神经网络模型泛化性能不足以及对新任务适应性较差的问题, 然而学术界对元学习的定义并不统一. 一些研究认为, 元学习的目标是学习一种通用的知识w, 元学习器(meta-learner)利用知识w针对任务生成基学习器(base learner), 使其能很好地泛化到新任务[13, 14, 31]; 另一些研究则将元学习视为机器学习的一种范式, 给定任务分布p(T), 要求算法优化在新任务上的训练效果[32−34]. 我们认为, 后者的定义更为合理, 其中有两个原因.
(1) 后者研究边界相对清晰. 前者的研究边界难以界定, 因为很多方法不显式提取通用知识w, 同时, 很多方法中元学习器与基学习器没有明确界限; 而与迁移学习、多任务学习、域泛化等概念相比, 后者的设定和优化目标有明显不同;
(2) 后者范畴包含前者. 若算法能够利用已有任务的训练提升在新任务上的效果, 表明算法内已经存在可迁移的知识.
因此, 下文中将更多地基于后者理解进行介绍.
任务(task)是元学习的主要概念之一. 任务的定义比较宽泛, 可以是分类、图像分割、强化学习MDP等等.在元学习的框架中存在两组任务: 元训练任务(meta-training task)和元测试任务(meta-testing task). 算法首先基于元训练任务进行学习, 然后在元测试任务中测试效果. 元训练任务以任务分布p(T)的形式给出: 在元训练开始时, 从任务分布p(T)中采样一定数量的元训练任务{Ttrain}, 即Ttrain~p(T). 在元训练过程中, 元测试任务是未知的, 因此理论上元学习的训练目标与评测准则随目标场景不同而不同. 在相关研究中[16], 一般假定元测试任务与元训练任务服从同一分布p(T), 由此可确定参数化算法的元训练目标为
| $ J(θ)=E_{T\sim p(T)}J_{T}(θ) $ | (5) |
其中, θ为元学习算法参数, JT(θ)为算法在单任务T中的目标函数. 上式中的期望ET~p(T)可通过任务采样近似, 从而使参数优化可实际计算并实现.
元学习算法类型繁多, 本文按实现思路主要分为基于优化、基于先验和基于度量这3类[14]. 3类方法切入角度不同, 并可以相互融合.
基于优化的方法主要源自模型无关的元学习算法(MAML)[13], 该工作针对元学习提出了新的优化目标, 希望找到一个初始化参数θ能快速、有效地适应给定任务分布. 关于参数θ的损失函数L(θ)为
| $ L(θ)=E_{T\sim p(T)}L_{T}(θ′) $ | (6) |
其中, θ′=θ−α∇θLT(θ)是在任务T上经过单步梯度下降更新的参数. 该类方法目前是元学习领域的热点话题, 已有许多基于MAML的改进工作, 如一阶优化算法Reptile[35]、近似概率推理元学习算法VERSA[36]等.
基于先验的方法针对特定领域的任务先验特征设计算法模型, 包括基于同质任务设计跨任务记忆模块的方法[37, 38]、设计超网络的方法[39, 40]等.
基于度量的方法将新任务与已有任务做距离度量, 从而一定程度上将问题转化为单对单的度量与迁移[41−43]. 该类方法有两个共同要素: (1) 样本特征提取, 归纳用于度量的特征; (2) 距离度量方法, 用于发现最相似的有标签样本.
2 元强化学习研究概述本节总体概述元强化学习研究, 包含元强化学习研究的定义范围和场景设置两部分, 为第3节元强化学习研究进展的展开作铺垫.
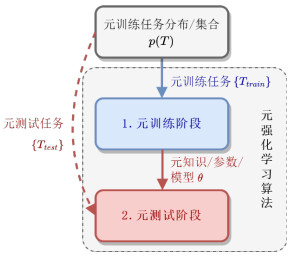
2.1 定义在“元强化学习”一词中, “元(meta)”是前缀词, “强化学习”是主要部分. 元强化学习领域将强化学习原本的单任务框架扩展到元学习的多任务框架, 以期提升强化学习的效果. 与元学习类似, 元强化学习在任务层面的流程分为两个阶段: 元训练阶段和元测试阶段. 该两阶段流程如图 2所示.
|
图 2 元强化学习两阶段流程 |
其中, 元训练任务和元测试任务中的每个任务T对应强化学习的一个环境模型, 该模型通常是MDP. 元训练任务的任务分布p(T)可能是任务场景中可调节的参数, 如物体大小、重力大小等, 这种参数以连续变量为主, 一般使用随机数进行采样; p(T)也可能基于预设的一系列任务定义, 如机械臂的抓取、开门等任务, 采样时随机选取离散的任务. 在元训练开始时, 从任务分布p(T)中采样一定数量的元训练任务{Ttrain}, 即Ttrain~ p(T). 元训练任务集合可能由一次采样固定, 也可能在多轮元训练中反复由采样生成. 在元训练阶段中, 算法基于元训练任务进行学习, 为下一阶段训练模型. 与元学习类似, 如果假定元测试任务与元训练任务服从同一分布p(T), 则参数化算法的元强化学习训练目标为公式(5), 其中, JT(θ)为算法在单个决策任务T中的强化学习目标函数. 在元测试阶段中, 已训练的元知识/参数/模型θ将在元测试任务{Ttest}上自适应运行, 并得到测试效果. 元测试任务的采样分布一般与元训练任务的任务分布p(T)一致, 即Ttest~p(T), 但元测试任务也可能被设定为特定任务.
现有工作在元测试阶段的评测指标主要分为两种: 零样本(zero-shot)适应性能和小样本(few-shot)适应性能. 零样本适应性能用于评价元训练模型在元测试任务上的决策能力, 常用指标为元训练模型在元训练任务上的采样步数-累积奖励曲线和在元测试任务上的平均累积奖励. 小样本适应性能用于评价元训练模型在元测试任务上的快速学习能力, 常用指标为元训练模型在元测试任务上的训练累积奖励曲线, 其横坐标轴多表示采样步数或训练轮数. 评测指标的选择主要和应用场景、算法设计目标相关, 例如: MAML算法的目标是利用少量样本适应新任务, 因此, MAML适用小样本适应性能进行评价, 而零样本适应性能无法反映其优势. 此外, 为进一步验证元强化学习方法的效果, 相关工作往往附加策略典型决策、编码特征分布或改进模块性能等更细节内容的可视化与分析.
与元强化学习类似, 迁移强化学习(transfer reinforcement learning)[10]、多任务强化学习(multi-task reinforcement learning)[44]、连续强化学习(continurous reinforcement learning)[45]、结合域适应(domain adaptation)、域泛化(domain generalization)的强化学习等领域都面向多个任务. 迁移强化学习将源任务上的学习经验迁移到目标任务中, 从而促进在目标任务下的学习; 在迁移强化学习中, 源任务和目标任务同时可见, 且通常不关注源任务的数量问题. 多任务强化学习则面向在多个任务上同时学习的需求, 其源任务和目标任务为给定的同一任务集. 连续强化学习也称为终身强化学习(lifelong reinforcement learning), 其面向目标任务持续到来的场景, 一般无法同时采样多个任务进行训练, 并往往针对任务分布漂移、知识灾难性遗忘等问题展开研究. 对于域适应[46]和域泛化[47], 若将强化学习的每个任务看作单独的域, 则域适应对应源任务和目标任务存在一定差异的迁移强化学习, 而域生成对应源任务和目标任务存在一定差异的元强化学习. 在域生成的定义中, 模型在有明显域差异的测试任务上直接测试而不进行迭代更新, 这与元强化学习学习元知识的目标相符, 而与其快速适应新任务的目标有所差异; 除此之外, 结合域生成的强化学习在任务层级上的定义和元强化学习非常相似, 因此可将结合域生成的强化学习研究看作元强化学习研究的一部分, 后文提到的一些相关工作即属于该范畴. 上述元强化学习相关领域对比总结见表 1.
| 表 1 元强化学习相关领域对比 |
2.2 场景设置
在元强化学习流程中, 元训练和元测试任务集的每个任务都作为独立的强化学习任务与智能体算法交互运行. 因此, 元强化学习以强化学习任务为基本单元. 本节介绍已有的元强化学习场景设置, 以便后续对比分析相关工作.
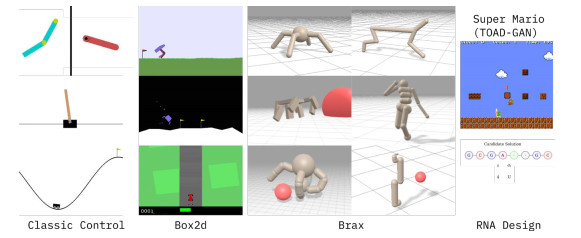
早期的元强化学习工作大多从状态、动作、奖励函数、转移函数等任务浅层特征入手构建任务. MAML工作[13]在MuJoCo机械仿真平台[48]上以半猎豹(half-cheetah)和蚂蚁(ant)两个模型作为智能体平台, 设定平台运动的目标速度不同或目标方向不同, 环境的奖励函数随之改变, 从而作为不同的任务. 与该设定相似, 有工作[49]将模型的一条腿质量或长度改变, 物理环境的状态转移随之改变, 从而获得不同的任务. 该类环境由传统强化学习环境简单修改得到, 部署方便且易于实验, 因此受到后续工作效仿[35, 36]. Benjamins等人发布的CARL环境集[50]整合了一系列经典环境, 如平衡杆和蚂蚁, 并将单环境中的一系列可控参数提取作为任务上下文变量, 其环境场景如图 3所示.
|
图 3 CARL环境集场景[50] |
一类元强化学习方法将环境抽象为部分可观测的马尔可夫决策过程(partially observable Markov decision process, POMDP). 在POMDP中, 观测状态ot由真实状态st映射得到, 并一般设定由观测状态无法反推得到真实状态, 在运行的大部分时间中智能体无法唯一确定真实状态st, 即无法唯一确定任务MDP, 因此, 强化学习算法求解MDP所给出的状态-动作映射应用到POMDP中效果较差, 由该问题延伸出多任务元学习算法.该类设定最早出现在RL2工作[51], 作者构建了第一人称视觉迷宫导航任务, 其中, 元训练任务的迷宫大小一致, 而不同任务的迷宫布局与目的地不同. 迷宫和导航任务具有容易实现和部署、元任务构建简单、展示直观等优点, 相关工作[32, 34]的实验场景均以迷宫、导航任务为主. 事实上, 大部分现实任务都存在部分可观测状态, 因此该类场景与算法也更加贴近应用.
还有一些工作以视频游戏为基础构建任务. OpenAI基于《刺猬索尼克》游戏构建任务集[52], 该任务集将原游戏按区域划分为11个任务场景, 所有任务的游戏规则基本相同, 但图像纹理、对象和通关策略不同. 次年, OpenAI发布视频游戏任务集CoinRun[53], 智能体的目标是控制小人达到硬币位置. 其环境场景(状态)如图 4中左图所示, 其中每个任务为难度不一的关卡, 并且背景纹理、对象纹理具有随机的显著视觉差异. 这些视频游戏同样蕴含着丰富的策略, 但高维输入使得元强化学习算法的训练和测试更难[54], 这可能是视频游戏环境应用相对较少的原因.
事实上, 很多强化学习环境具备场景的随机化功能, 同样符合元强化学习研究的任务需求. 在MiniGrid环境[56]中, 地图的大小与布局可随意配置从而生成不同的任务, 同时, 官方提供丰富的预设地图环境. 由FaceBook开源的强化学习游戏MiniHack可以自动随机生成各种游戏环境, 从怪物位置、类型到关卡、物体和地形, 用户可以控制地图中每一处细节[57].《我的世界》(Minecraft)作为开放沙盒游戏, 其随机生成的庞大初始世界可构成元任务集合, 同时, 游戏中复杂的通关步骤和极大的状态空间使智能体的训练面临较高难度[58].
最近的工作认为: 迁移方法与效果不仅与任务浅层特征相关, 还更多地与智能体策略学得的技能相关. 前述的实验场景虽然从MDP定义上属于不同任务, 但其中跨任务的元策略或技能相当局限, 这样的设定难以训练或验证元强化学习算法在更广泛任务上的泛化能力. OpenAI发布的视频游戏集合Procgen[55]包含16个风格各异的游戏, 包括CoinRun、迷宫、大鱼吃小鱼等, 各游戏的环境场景(状态)如图 4中右图所示. 其中, 各游戏的输入和输出统一格式, 这使得训练单一强化学习智能体玩所有游戏成为可能, 但游戏间策略显著差异与高维状态输入带来极大的训练难度. Yu等人提供了开源的元强化学习模拟环境Meta-World[59], 它由50个机器人操作任务组成, 各任务的环境场景如图 5中左图所示. 这些任务共享同一个桌面和机械手, 但其操作任务呈现出鲜明的技能特征, 如开窗户、开抽屉任务的策略为“抓取+直线运动”, 转盘、水龙头、开门任务的策略为“抓取+弧线运动”等. Meta-World正被越来越多的元强化学习工作选为实验场景[60−62]. DeepMind发布的3D视频游戏Alchemy[63]则考验智能体是否能基于元知识进行因果推断, 该游戏的目标是控制机械臂利用多个药水改变多个石头使石头总价值最高, 该环境场景(状态)如图 5中右图所示. 在Alchemy不同的任务中石头外观与分数对应关系不同, 且药水对石头的影响不同, 但药剂效果与颜色存在因果限制, 在同一回合内, 同种外观的石头及药水也具有同样的性质, 这使正确的因果推断能带来显著任务效益.
元强化学习研究正在向更具有挑战性的场景探索. 从设计者角度来看, 现有的研究仅仅通过实验结果验证场景难度, 在环境难易度、策略迁移难易度等方面尚缺少可以指导元任务设计的理论和框架.
3 元强化学习研究进展本节综述元强化学习的研究进展, 按元强化学习研究的研究对象与适用场景将现有工作分为元策略学习方法、强化学习模块元学习方法、元强化学习设定的新问题、元强化学习结合其他领域、元强化学习算法应用五层次展开, 脉络图如图 6所示.

|
图 6 元强化学习研究进展分类脉络图 |
上述顺序同时对应研究工作的大致时间先后顺序. 其中, 从元强化学习研究的定义与场景设置出发, 元学习研究大多面向单一端到端模型的训练, 类比在强化学习中则针对主要的策略模型端到端学习展开研究, 对应第3.1节的元策略学习方法. 除策略模型外, 强化学习框架中天然存在许多可学习的泛用模块, 相关工作元学习这些模块以提升智能体的表现, 对应第3.2节的强化学习模块元学习方法. 此外, 元强化学习不仅是一种新模型的训练方法, 其独特的任务设定也在强化学习的原有技术思路基础上引入了一些需要考虑的新问题. 该部分研究对应第3.3节的元强化学习设定的新问题, 相关工作基于已有元强化学习方法改进解决这些新问题. 接着, 元强化学习框架的泛用性使其容易与其他研究领域和落地应用结合, 用以提升原方法在目标问题上的迁移效果或泛化性能. 该部分研究分别对应第3.4节的元强化学习结合其他领域和第3.5节的元强化学习算法应用, 其中, 第3.4节的相关工作多基于第3.1节的元策略学习方法和第3.2节的强化学习模块元学习方法, 与第3.3节的元强化学习设定的新问题的结合方面还有待进一步研究.
3.1 元策略学习方法本节总结并介绍强化学习策略的元学习方法. 策略模块是强化学习智能体端到端模型的核心, 因此训练元策略的方向最受关注, 其中很多方法也成为其他元强化学习工作的基础. 本节内容按技术路线将现有工作分为基于MAML的方法、基于记忆和推断的方法、基于对比学习的方法、易泛化策略模型的构建方法这4个方面展开.
3.1.1 基于MAML的方法模型无关的元学习算法[13]是Finn等人提出的一种基于元目标梯度优化的元学习方法, 其能够同时适用于监督学习和强化学习. 该算法的目标是训练任务公共的元参数θ, 使新任务上的初始化模型仅用少量数据就能实现快速收敛. 这一目标形式化为公式(6). MAML采用梯度下降的方式优化参数θ, 其优化过程分为两层: 1) 内层在每个任务Ti上迭代任务参数θi, 其中典型的迭代方式为单步梯度下降, 即
| $ \theta ' = \theta - \beta {\nabla _\theta }\sum\nolimits_{{T_i} \sim p(T)} {{L_{{T_i}}}({{\theta '}_i})} . $ |
在强化学习中, 内层的损失函数是策略在任务上的期望累积奖励:
| $ {L_T}(\theta ) = - {E_{T,\theta }}\left[ {\sum\limits_t {{R_T}({x_t},{a_t})} } \right] $ | (7) |
内层损失函数的相关工作由强化学习算法完成, 并使用可微优化器以保留从θi到θ的梯度计算图; 外层优化可使用随机梯度下降(stochastic gradient descent, SGD). MAML算法用于强化学习中的伪代码如图 7所示.

|
图 7 强化学习MAML算法伪代码[13] |
MAML作为一种新的元学习框架, 其衍生出许多改进和扩展工作. 针对MAML的高阶求导带来训练不稳定、计算开销大的问题, Finn等人在MAML工作中提出仅使用一阶求导的简化算法FO-MAML; Nichol等人提出比FO-MAML更加泛用的一阶求导算法Reptile[35]. 一阶求导算法相比MAML的计算效率显著提升, 但一阶梯度估计不准确的问题从根本上限制了该类算法的性能上限. Antoniou等人对MAML的训练问题给出了较广泛的实验和结论[64]. Song等人提出的ES-MAML算法在外层优化中以进化算法替代求导[65], 该方法避开了二阶优化带来的问题, 但网络参数的进化算法也带来较大计算开销. 针对MAML应用在强化学习中的计算误差, Rothfuss等人提出的ProMP算法实现了更好的信用分配从而减小梯度估计方差[66]; Liu等人认为ProMP算法引入了额外的计算偏差, 其算法Taming MAML能够在外层梯度估计中减小方差而不引入偏差[67]. 这些工作进一步提升了基于MAML的元强化学习算法的鲁棒性. 理论分析方面, Fallah等人为非凸环境下的MAML和FO-MAML提供了收敛性分析[68], 并提出了具有与MAML相同理论性质的一阶算法Hessian-free MAML以替代FO-MAML; Khodak等人在在线凸环境下分析了MAML和Reptile算法的泛化边界[69]; Molybog和Lavaei分析了MAML在线性二次控制(linear quadratic regulator, LQR)决策任务集上的全局收敛性[70]; Wang等人建立了具有非凸元目标的MAML在强化学习中的全局最优性分析[71]; Fallah等人指出MAML-RL的分析更具挑战性, 构建了随机梯度下降的MAML-RL变体算法SG-MRL并数学分析SG-MRL的收敛性[72]; Ji等人在监督学习和强化学习两个场景中分析了多步MAML在一般非凸条件下的收敛速度和计算复杂性[73]. 这些工作提供了MAML在强化学习各场景中的理论保障.
总的来说, 基于MAML的元强化学习方法具有较强的理论基础和完善的研究脉络, 但相关工作的性能仍与基于推断和分层的元强化学习方法有一定距离, 因此, 近年来MAML多用于二阶求导目标的优化需求而不是模型泛化性能需求. 表 2总结了上述算法的技术特点和源码链接.
| 表 2 基于MAML的元策略学习算法小结 |
3.1.2 基于记忆和推断的方法
虽然强化学习问题的一般形式能有效地处理不确定性环境, 但传统强化学习方法与概率模型推理之间并未显式建立联系[20]. 基于记忆和推断的方法通常适用于POMDP任务.
● 从运行流程来看, 与MAML等其他元强化学习方法不同, 基于记忆和推断的方法一般不在测试任务上训练;
● 从参数更新方式来看, 基于记忆和推断的方法具备一种特别的学习方式: MAML在测试任务上更新整个模型, 而基于记忆和推断的方法通过编码历史来更新任务隐变量作为策略的更新参数.
在基于记忆的方法方面, 智能体通过记忆POMDP任务的历史来降低从观测推断状态的不确定性, 从而提升策略在未知任务上的表现. Duan等人提出了RL2算法[51], 该工作基于具有记忆的循环神经网络构建策略模型并在多任务间训练, 模型在同任务的轮次间传递隐状态而在不同任务间传递网络参数, 期望模型利用记忆优化跨任务能力. Wang等人首先将元强化学习定义为带历史信息的任务, 并构建了包含长短期记忆网络(long short-term memory, LSTM)的强化学习算法以及一系列多臂老虎机和导航任务, 以此探究元强化学习的特质[74]. Mishra等人提出将时序卷积和软注意力机制结合形成新的深度架构, 其算法SNAIL实验性能优于MAML和RL2[75]. 近年来, Transformer模型越来越多地用于深度强化学习的记忆功能, 并展现出远优于LSTM, GRU等传统记忆网络的泛化性能. Parisotto将基于注意力机制的Transformer模型[76]用作跨情节记忆模块, 其开发的算法CMRL可以显著降低模型在元强化学习环境中的训练成本和动作时延[77]. 基于记忆的方法并非针对POMDP任务设计, 但实验表明, 该类算法在第一人称视角迷宫导航等POMDP任务中表现良好.
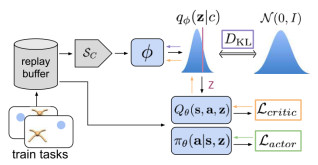
基于推断的方法更明确地将环境定义为POMDP, 智能体需要推断当前任务的特征, 基于任务特征将POMDP任务转化为MDP任务以构建策略. 在该流程中, 特征推断模块作为主要部分, 其输入主要是任务历史信息, 因此该类方法可看作基于记忆方法的延伸. Rakelly等人提出的PEARL算法[32]是其中的代表工作, 其训练流程如图 8所示.
|
图 8 PEARL算法训练流程[32] |
以下分为3部分介绍该工作.
1) 前向流程. PEARL将当前任务上t时刻的历史四元组信息c1:t={s, a, s′, r}1:t输入特征推断模块qϕ, 编码得到任务特征zt并输入强化学习流程. 从POMDP的视角看, 实际上, 任务特征zt与状态st合并成为某个MDP任务的状态[st, zt];
2) 训练流程. 强化学习的演员-评论家模块Q和π的训练与传统算法一致. 特征推断模块qϕ的损失函数由两部分构成: 一部分来自强化学习模块, 演员-评论家算法中一般评论家模块比演员模块稳定, 因此选择评论家模块的损失函数Lcritic; 另一部分源于信息论中的信息瓶颈(information bottleneck, IB), 用于驱使任务特征zt和历史c1:t的信息一致, 其形式为
| $ D_{KL}[q(z|c)||r(z)] $ | (8) |
其中, DKL为KL散度函数; r(z)为z的先验分布, 常用正态分布;
3) 特征推断模块qϕ. PEARL假设任务的历史信息具有时序无关性, 即时序上的置换不影响历史信息所表现的任务特征. 在该假设下, 对历史信息的编码可转为对每个四元组的编码:
| $ {q_\phi }(z|{c_{1:t}}) = \prod\limits_{n = 1}^t {{\psi _\phi }(z|{c_n})} $ | (9) |
其中, 令ψϕ输出服从高斯分布, 利用高斯分布的性质使qϕ输出始终服从高斯分布.
PEARL实际上将多POMDP任务的元强化学习转化为单MDP任务的强化学习. MAML需要on-policy更新, 而PEARL得以off-policy更新, 这使算法数据利用率得到提升. 此外, PEARL的特征推断模块避免了RNN的梯度回传层数过深问题, 训练更稳定. PEARL是目前元强化学习领域最热门的算法之一.
其他基于推断的方法中, Sæmundsson等人使用高斯过程和变分推断的方式建模任务隐变量, 并结合基于模型的强化学习算法实现快速元训练的算法ML-GP[78]; Zintgraf等人[79]和Lan等人[80]将MAML算法和任务上下文编码器结合得到性能提升; Humplik等人利用LSTM构建任务特征(文中称为信念)的推断模块, 并实现了类似PEARL的算法[81]. 这些工作可看作并行关系, 其中, PEARL因其性能优异、论文和源码质量高被后续工作广泛引用和跟随. 陆嘉猷等人构建了PEARL中SAC算法的温度系数自适应调节方法APE[82]. Fakoor等人利用门控循环单元(gated recurrent unit, GRU)作为历史编码器, 基于多任务目标训练强化学习算法MQL[33]. 算法没有设计任务特征相关的损失函数, 而实验表明MQL的表现与PEARL相近, 并在一些任务上表现更好. Raileanu等人提出的PD-VF算法利用预测环境累积奖励监督训练任务隐变量模块[83]; Zintgraf等人利用变分自动编码器(variational auto-encoder, VAE)训练任务特征推断模块, 并提出了VariBAD算法[34], 其中, VAE的重建编码器部分由奖励预测和状态预测两部分构成. VAE较PEARL的信息瓶颈理论更强、收敛结果更好但训练较慢. Zhang等人进一步将场景定义为隐参数块马尔科夫决策过程(hidden-parameter block MDP, HiP-BMDP), 其中每个任务MDP的转移函数由参数θ生成, 且观测状态o可唯一确定真实状态s. 该工作针对这些性质设计了任务转移函数模型及任务转移函数参数θ的预测模型[84].
基于推断的方法是目前元强化学习研究的主流方向, 相关工作较为成熟, 算法性能较好. 基于推断方法可以看作基于记忆方法的子类, 因任务推断模块不可避免地需要对历史信息进行记忆和编码, 该类方法只是引入了针对任务特征的训练方法, 并表现更好. 表 3总结了上述算法的技术特点和源码链接.
| 表 3 基于记忆和推断的元策略学习算法小结 |
3.1.3 基于对比学习的方法
对比学习(contrastive learning)是一种自监督学习方法, 用于在没有标签的情况下, 通过让模型对比相似或不同的数据来学习数据集的特征. 一般来说, 对比学习的目标是学习一个编码器f, 使得对任意数据x有:
| ${Dist}\left(f(x), f\left(x^{+}\right)\right)\ll{Dist}\left(f(x), f\left(x^{-}\right)\right) $ | (10) |
其中, x+是和锚点x相似的正样本, x−是和x不相似的负样本, Dist(⋅)是特征距离度量函数. 对比学习的实现难点在于如何构造正负样本, 为实现上述目标, Oord等人提出了InfoNCE损失函数[85]:
| $ {L_{NCE}} = - E\left[ {\log \frac{{\exp (f(x,{x^ + }))}}{{\sum\nolimits_i {\exp (f(x,{x_i}))} }}} \right] $ | (11) |
其中, xi∈X, X中非正样本x+的样本均视为负样本x−. Oord等人证明了最小化InfoNCE损失函数能最大化锚点x和正样本x+互信息的下界.
强化学习方面, Srinivas等人基于动量对比学习算法MoCo[86]构建了强化学习的无监督表征学习方法CURL[87], 其中, 正样本由对锚点图像应用常见图像扩充方法得到, 其他样本均为负样本.
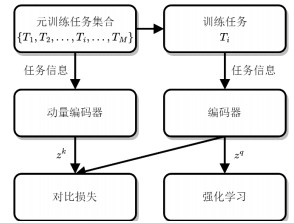
在元强化学习中, Fu等人认为, 同一任务不同时刻的任务特征应当相近, 不同任务的任务特征相对疏远, 而这一假定可用于构造对比学习的正负样本集[88]. Fu等人基于MoCo[86]和CURL[87]构建了CCM算法, 算法对比学习流程如图 9所示. 其中, 采样轨迹按任务分类存储在经验池中, 并在对比训练中将同任务特征作为正样本; 为使任务特征能更好地反映任务信息, CCM还基于信息增益单独训练用于探索的智能体, 其内在奖励加入了探索任务特征的信息增益, 且其训练梯度不回传到特征编码模块.
|
图 9 CCM[88]的对比学习流程 |
Wang等人提出了类似CCM的方法TCL, 其中, 正负样本按采样轨迹划分而不是任务类型[89]. Mu等人发现有限且复杂的元训练环境会使InfoNCE中的互信息的界限松弛并导致过低估计, 并设计了互信息分解优化方法DOMINO以解决该问题[90]. Raghu等人发现, 若将深度网络模型分为特征提取层和线性分类层两部分, 在MAML的内层更新中模型的线性分类层参数变动较大, 而特征提取层参数变动较小[91]. Kao等人更进一步发现, MAML算法在内层更新中冻结特征提取层时等同于带噪声的有监督对比学习器, MAML学习通用特征表示的能力得益于其内在的对比学习特性, 并给出了理论与实验分析[92]. 该工作拓宽了对比学习在元学习中的边界, 本文猜测, 对比学习在元强化学习中的应用还有更多开发潜力, 对比学习有望成为元强化学习的关键方法, 并可能具备优于MAML的泛化能力. 表 4总结了上述算法的技术特点和源码链接.
| 表 4 基于对比学习的元策略学习算法小结 |
3.1.4 易泛化策略模型的构建方法
在元强化学习中, 一种直观的思路是构建可有效迁移泛化的策略模型. 相比于前述元策略学习方法, 该类方法利用任务先验知识进行设计, 更加有效且具有可解释性. 相关工作可能不带有“元学习”关键词, 但其目的、思想与元学习一致.
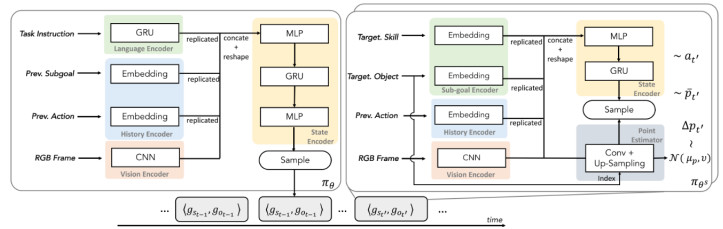
一种常见思路是构建分层策略模型, 使模型中某些模块功能可跨任务泛化, 从而实现元学习. 已有许多分层强化学习工作[93], 以下仅介绍一些元强化学习代表工作. 在《我的世界》游戏中, Tessler等人提出的H-DRLN算法首先将策略分为顶层策略和技能策略两部分, 其中, 顶层策略可选择自主行动或采用已有技能策略, 而技能策略可理解为游戏中通用的挖矿、合成、放置等操作, 由半马尔科夫决策过程(semi-Markov decision process, SMDP)相关工作训练给出[94]. Lin等人提出的JueWu-MC算法同样将策略分为高层控制策略和子任务策略, 其额外采用表征学习和自模仿学习加速子任务策略的训练, 最终算法获得遥遥领先的测试分数[58]. Fu等人提出的MGHRL算法同样在机械臂模拟环境中将策略分为两部分, 基于PEARL框架培训高级元策略, 并将如何实现子目标的其余部分作为独立的强化学习子任务[95]. 在导航任务中可构建类似的分层策略模型, Li等人提出的ULTRA算法将导航策略分为任务上层策略和通用子策略两层, 其中子策略由训练得到[96]. 为使交互机器人完成各类自然语言任务, Lu等人将子任务策略(文中称为原子技能)分为3种: 导航、问答和场景交互并针对性设计损失函数, 使其算法ASC学习有机组合子任务从而胜任全局任务[97]. 在上述两层策略的框架中, 底层技能策略通常为任务间共享的可迁移部分. ASC的两层策略框架如图 10所示, 这是一种较为通用的两层次策略结构.
|
图 10 ASC的两层策略框架[97] |
其他相关工作中, 聂凯和孟庆海将动态作战过程按情节划分为多个任务, 并针对设计了带情节记忆的多层策略模型[98]. Sohn等人提出了子任务图推理的分层任务问题, 其中, 分层任务为一个描述所有子任务及其依赖关系的图, 智能体完成子任务时将得到奖励, 并在该工作中提出了基于归纳逻辑编程的解决方法MSGI[99]. 该问题和方法可看作将策略模型拆分为子任务层及任务关系层. Peng等人将策略模型分为任务共享层和任务特有层, 其中, 任务特有层仅为一层神经网络, 并进一步设计适配器模型输出任务特有层参数以替代传统的梯度下降更新. 该工作采用多任务目标训练, 并在MuJoCo环境中取得了超越PEARL, MAML和MQL的效果[100]. 本文认为, 该工作的策略模型设计之所以有效, 其原因可能类似第3.1.3节所述的Raghu等人[91]和Kao等人[92]关于MAML算法的发现. Chua等人提出了一种具有理论保证的层次化元强化学习过程[101].
总的来说, 根据任务特性设计易泛化的功能模块并迁移是非常实用的思路, 其中以分层策略架构最为常用. 表 5总结了上述算法的技术特点和源码链接.
| 表 5 易泛化元策略模型的构建算法小结 |
3.2 强化学习模块元学习方法
强化学习框架中, 在策略模型外还有一系列可学习内容, 如探索策略、优化目标、环境动态(environment dynamics)模型、超参数等, 它们对智能体的性能表现同样有着重要影响. 以下本节按模块类别展开介绍研究进展.
3.2.1 探索策略元学习方法在强化学习中如何平衡探索和利用这一难题始终未有定论. 在与环境的序贯交互中, 智能体一方面需要利用已有信息选择最优动作, 以期提升累积回报奖励; 另一方面智能体也需要探索环境, 只有获取充分信息才能提升信息利用的效果. 在传统强化学习方法中, “利用”一般体现在强化学习智能体的最优决策过程, “探索”则一般对应非最优的决策噪声或目标函数[102].
现有工作的观点是: 虽然强化学习难以在传统的单一任务中学习探索与利用的平衡, 但容易将一些共通的探索策略在多个任务间迁移复用. 当迁移的探索策略能广泛地适用于不同任务时, 就可称其为元探索策略, 此时, 策略即代表探索相关的元知识. Stadie等人[103]将智能体与环境的交互过程分为探索和利用两个阶段, 在探索阶段中希望策略尽可能地探索任务信息, 其目标是使策略在利用阶段中的训练效果更好. 在上述两阶段设定下, 强化学习的目标函数梯度可作如下分解[103]:
| $ \begin{aligned} \frac{\partial }{{\partial \theta }}\iint {R(\tau )}{\pi _{U(\theta ,\bar \tau )}}(\tau ){\pi _\theta }(\bar \tau ){\text{d}}\bar \tau {\text{d}}\tau =& \iint {R(\tau )}\left[ {{\pi _\theta }(\bar \tau )\frac{\partial }{{\partial \theta }}{\pi _{U(\theta ,\bar \tau )}}(\tau ) + {\pi _{U(\theta ,\bar \tau )}}(\tau )\frac{\partial }{{\partial \theta }}{\pi _\theta }(\bar \tau )} \right]{\text{d}}\bar \tau {\text{d}}\tau \\ &\approx \frac{1}{T}\sum\limits_{i = 1}^T {R({\tau ^i})} \frac{\partial }{{\partial \theta }}\log {\pi _{U(\theta ,\bar \tau )}}({\tau ^i}) + \frac{1}{T}\sum\limits_{i = 1}^T {R({\tau ^i})} \frac{\partial }{{\partial \theta }}\log {\pi _\theta }({{\bar \tau }^i})\left| {\begin{array}{*{20}{c}} {} \\ {} \\ {{\tau ^i} \sim {\pi _{U(\theta ,\bar \tau )}}} \\ {{{\bar \tau }^i} \sim {\pi _\theta }} \end{array}} \right. \\ \end{aligned} $ | (12) |
其中, πθ是探索策略,
经过上述分解后, 目标函数梯度最终被分解为一个与MAML更新方式相同的项和一个探索提升最终回报的项. Stadie等人由此提出了E-MAML算法, 该算法能从多轮轨迹中自动学习探索策略如何优化更新后的利用策略. 该工作同时利用其思想的简化版本改进RL2工作[51], 并提出了E-RL2算法.
Gurumurthy等人认为[104], 更新前(探索)策略和更新后(利用)策略往往大相径庭, 这导致类似MAML使用少量梯度更新来适应任务的方法效果不理想. 与E-MAML使用同一策略分别进行探索与利用不同, 他们提出明确建模一个单独的探索策略, 以使探索策略更加灵活, 更容易适应任务. 他们提出了一种监督学习的探索策略目标, 其算法在多个任务上的收敛效果显著优于E-MAML. 为了解决DDPG探索较弱的问题, Xu等人构建了类似的元探索策略(又称教师策略)并设计其特有的内在奖励函数, 该策略的目标是为DDPG的训练采样优质经验数据[105].
还有一些相关工作从其他角度切入: Gupta等人希望结合不同但结构相似的先前任务的经验来学习探索策略, 他们提出的算法MAESN通过向策略模型注入带有时间相关性的噪声来促使策略进行随机化的探索, 该噪声的利用和采样方式由历史经验和元学习过程共同决定[106]; Alet等人设计了一种元学习的好奇心模块来为强化学习策略提供每一步的“伪奖励”, 并设计了丰富的面向深度网络的组件用于该模块的元架构搜索[107]; Hu等人利用任务表征的不确定性引导策略的探索学习[108].
总的来说, 目前探索策略的元学习方法较分散, 尚未形成体系和核心方法. 表 6总结了上述算法的技术特点和源码链接.
| 表 6 探索策略元学习算法小结 |
3.2.2 优化目标元学习方法
在深度强化学习中, 尽管已有许多数学推导得到的策略优化目标和更新公式, 如经典的DQN[23]和PG[109]算法, 但这些算法在实际优化中的稳定性和效果不尽人意, 并有诸多的优化目标改进工作, 其中包括D3QN[24], PPO[28], SAC[29]等久经考验的优秀算法. 然而, 当前优秀的优化目标均依赖人工实验改进, 缺少理论指导优化目标改进方向, 并因此很可能存在一些尚未被发现的更优秀的优化目标. 为寻找更好的优化目标, 可以利用深度学习自动优化强化学习的优化目标. 该过程正符合MAML框架“学习如何学习”的概念, 即是强化学习优化目标的元学习.
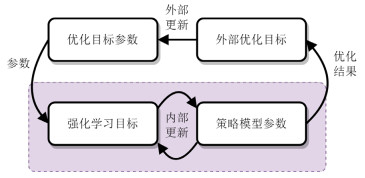
Houthooft等人首先为强化学习策略提出了一种两阶段的优化目标元学习框架与算法EPG[110], 该算法的示意图如图 11所示.
|
图 11 强化学习优化目标元学习算法框架[110] |
EPG算法由两个优化循环组成.
1) 内部循环(图 11下半部分)是传统强化学习过程. 在内部循环中, 环境从元训练任务分布中采样一些任务, 并让智能体通过最小化外部循环提供的损失函数来学习解决此任务. 其中, EPG使用随机梯度下降作为优化器优化智能体策略;
2) 外部循环(图 11上半部分)调整损失函数的参数, 希望最大化内环学习后的累积收益. 该工作认为, 外部循环的优化存在较大困难, 内环学习后的累积收益不能写成损失参数的显式函数, 因此使用进化策略(evolution strategy)作为黑盒优化器, 对损失函数的参数进行优化.
基于同样的两阶段优化思想, Kirsch等人为Actor-Critic框架的强化学习算法设计了一种可微的神经网络目标函数Lα(τ, πϕ, V), 其算法MetaGenRL因此得以结合MAML算法, 来完全基于梯度元训练优化目标预测网络[111]. 进一步地, Xu等人基于MetaGenRL将基于值函数和基于策略梯度强化学习算法的优化目标一并设计为带参可微的网络预测目标gη(τ)[112]. Zhou等人基于off-policyActor-Critic框架设计了与Critic模块并行的Meta-Critic模块, 并针对单任务训练设计了Meta-Critic的训练方法[113]. Oh等人改进利用LSTM对历史的动作和未来预测编码来生成优化目标, 额外的预测输入为其算法LPG带来了更强的泛化能力[114]. 特别地, Veeriah等人基于广义值函数(generalized value functions, GVFs)[1]设计了未来奖励的预测任务作为辅助的优化目标, 并利用MAML训练该预测目标参数的生成网络[115].
总的来说, 现有工作正致力于优化更加广泛的参数化优化目标, 其中多采用MAML算法以优化二阶求导目标. 表 7总结了上述算法的技术特点和源码链接.
| 表 7 优化目标元学习算法小结 |
3.2.3 奖励函数元学习方法
在强化学习框架中, 奖励用于引导智能体更快、更好地学习, 以在环境中达到人类的目标状态, 是环境马尔可夫过程中必需的一部分. 现有环境的奖励函数设计往往依赖人类先验, 而很多环境尚难以设计令人满意的奖励函数, 如: (1) 难以准确量化的用户满意度目标难以转化为有效的奖励函数; (2) 任务目标包含无法比较的多个子目标时难以组合成为单个奖励函数; (3) 围棋等游戏仅有终局目标的稀疏奖励, 将使智能体难以学习. 为替代人类手工设计, 容易想到使用学习的方法自动优化奖励函数, 在参数化奖励函数后即可根据智能体表现优化奖励函数参数; 而其中如果涉及MAML算法或元任务优化, 即可称为奖励函数的元学习方法.
Zheng等人首先参数化了一种内在奖励函数(intrinsic reward), 并基于梯度下降强化学习目标对内在奖励函数进行优化, 其算法LIRPG能够在多个环境中提升A2C和PPO算法的训练效果[116]. Yang等人面向无奖励的测试环境, 建模参数化的优势函数Aψ以预测环境奖励, 并利用MAML算法更新Aψ[117]. 逆强化学习是一类从示例样本中学习奖励函数的方法, Xu等人将最大熵逆强化学习算法(MaxEnt IRL)和MAML结合, 以训练多任务的元奖励函数, 但其算法MandRIL局限于表格MDP或已知任务分布[118]. Yu等人将MaxEnt IRL与基于任务隐变量推断的元强化学习算法结合, 提出了PEMIRL算法, 他们提供了算法的理论证明, 并在更广泛的场景上验证其效果[119]. Ghasemipour等人将MaxEnt IRL与基于记忆的元强化学习算法结合, 提出了算法SMILe, 该工作与PEMIRL相比更加着重于逆强化学习算法的设计[120]. Pong等人基于PEARL设计了一种两阶段式算法SMAC, 该算法利用离线数据集分布范围广的特点, 使用离线样本元训练奖励函数模型, 并将该模型迁移到在线无奖励样本中以照常训练[121].
总的来说, 现有工作元训练参数化的内在奖励函数有多种途径: 基于MAML和二阶优化目标、逆强化学习方法和基于推断方法中奖励的解码器. 表 8总结了上述算法的技术特点和源码链接.
| 表 8 奖励函数元学习算法小结 |
3.2.4 环境动态模型元学习方法
在已知环境的动态模型, 即状态转移函数T: S×A×S→[0, 1]时, 基于搜索的算法(如蒙特卡洛树搜索)和基于模型的强化学习算法(model-basedreinforcement learning)可以利用环境动态模型进行模拟的环境交互, 从而大幅减少强化学习训练所需的交互样本与训练时间, 提升智能体的学习效率. 但除围棋等已知全部规则的游戏环境之外, 大部分贴近现实环境的动态模型复杂程度极高, 如何构建准确可用的环境动态模型成为相关研究领域的挑战. 已有许多基于模型的强化学习算法研究环境动态模型的构建问题[122], 其中, MAML算法可以解决从优化目标到待优化参数的二阶梯度优化问题, 元任务优化方法可以提升所建立动态模型的任务泛化性能, 涉及MAML算法或元任务优化的方法即可称为环境动态模型的元学习方法.
Clavera等人基于MAML元训练环境动态模型并将其用于生成虚拟交互样本, 其算法MB-MPO在高维复杂四足运动机器人上仅需2小时就完成训练[123]. Mendonca等人基于历史隐变量的元强化学习构建算法MIER, 利用MAML与环境动态预测目标对隐变量编码模型进行元训练, 为提升深度模型的泛化能力, 该工作进一步提出了一种经验重新标记算法来提供分布外任务的大量训练样本[124]. 近年强化学习相关工作表明, 利用编码后状态替代原始状态进行动态模型的拟合具有更泛用的潜力[9]. Lee等人利用历史隐变量构建环境动态模型, 其算法CaDM在各类控制任务中表现出优异的泛化能力[49]. Wang和Hoof构建了一种图结构的代理模型GSSM, 以在隐空间编码任务特征, 利用任务特征构建环境动态模型, 并设计了一种元策略的快速更新方法APS以训练整套模型[125].
总的来说, 现有工作元训练环境动态模型有两种途径: 基于元策略学习方法训练带环境动态模型的策略、或基于任务表征重建环境动态; 根据任务特性决定环境动态参数是自然而高效的. 表 9总结了上述算法的技术特点和源码链接.
| 表 9 环境动态模型元学习算法小结 |
3.2.5 超参数元学习方法
深度强化学习算法具有学习率、训练频率、训练批数据大小、探索率等许多超参数, 这些超参数显著影响着算法训练结果的好坏. 超参数的选取往往依赖人工经验调试, 并需要反复运行测试效果. 为减少人工机械劳动, 提升调参能效, 容易想到使用学习的方法自动优化超参数, 在形式化超参数后即可根据智能体表现自动优化超参数; 而其中如果涉及MAML算法或元任务优化, 尤其将每次强化学习算法运行作为一次任务时超参数的调整, 是一种天然的多任务问题, 这种工作即可称为超参数的元学习方法.
Xu等人面向累积奖励相关的超参数η, 其中包括折扣因子γ和n步奖励累积加权系数λ, 首先提出了一种超参数的更新方法Meta-Gradient, 该方法将策略θ的目标函数作为超参数的元目标函数, 将超参数η作为策略参数θ的一部分, 并设计了一种近似算法以从策略参数θ传播更新梯度到超参数η[126]. Zahavy等人基于Meta-Gradient设计了STACX算法, 以自动优化LeakyV-Trace算法的6项超参数[127]. Wang和Ni基于Meta-Gradient设计了Meta-SAC算法, 以自动优化SAC算法的温度系数[128]. Beck等人基于VariBAD算法的任务表征训练超网络(hypernetwork), 以预测策略参数[129].
现有超参数元学习的方法关注于少量超参数的优化元学习, 更广泛超参数在更广泛算法、任务中的优化元学习是未来的研究方向. 表 10总结了上述算法的技术特点和源码链接.
| 表 10 超参数元学习算法小结 |
3.3 元强化学习设定的新问题
元强化学习不仅是一种新的强化学习训练方法, 其独特的任务设定也在强化学习的原有技术思路基础上引入了一些需要考虑的新问题. 以下按问题类别展开介绍研究进展.
3.3.1 元训练任务的设置问题与传统单任务强化学习和多任务强化学习不同, 元强化学习希望从多个元训练任务中学习得到的策略能够泛化应用在未知的元测试任务中. 训练数据的分布对测试性能影响很大, 同样, 元训练任务的分布也对算法在元测试阶段的效果有很大影响. 然而对元强化学习算法而言, 元测试任务是未知的, 算法难以根据元测试任务去衡量不同元训练任务的优劣, 因此, 如何设置元训练任务成为元强化学习领域的前沿探索方向之一.
Mehta等人面向MAML算法展开研究, 他们的工作首先利用简单的2D导航场景说明元训练任务分布可以广泛影响算法性能, 然后基于主动域随机化(active domain randomization, ADR)[130]和SVPG算法[131]筛选元训练任务[132]. Gutierrez和Leonetti提出了一种基于任务相关信息的任务选择算法ITTS, 并结合RL2和MAML算法验证了该算法的有效性[133]. Gupta等人通过设法在元任务上进行无监督探索, 提升了预训练算法对训练任务分布的鲁棒性[134]. 他们提出的算法UML-DIAYN首先结合基于技能多样性的无监督探索方法DIAYN[135]在给定元训练任务范围中进行元训练任务的选取, 并基于任务特征推理模块Dϕ(z|s)构建了任务多样性驱动的探索奖励rz(s)=log(Dϕ(z|s)), 该奖励用于在无监督任务中结合MAML进行元强化学习预训练. Jabri等人同样关注无监督的元训练任务选择问题, 其算法CARML假设任务由不同的奖励函数构建, CARML基于UML-DIAYN的探索奖励rz(s)加入最大化轨迹τ和任务表征z互信息的目标, 使得奖励函数根据任务所需技能动态调整[136]. Rimon等人探讨了确保高概率近似最优行为的元训练任务数量, 并提出一种算法使用密度估计技术直接学习任务分布, 然后针对该任务分布训练策略[137].
总的来说, 现有方法大多基于经验假设进行开环设计, 尚未完全解决元训练任务设置问题, 还有很大研究潜力. 表 11总结了上述算法的技术特点和源码链接.
| 表 11 元训练任务的设置算法小结 |
3.3.2 元知识复用的探索问题
在传统强化学习中, 智能体在单任务学习中需要平衡探索与利用; 而当智能体具备从其他任务迁移的先验知识时, 如何平衡旧知识的利用与新任务的探索成为新的问题. 在元强化学习中, 该问题更加突出: 智能体学习的元知识由多个元训练任务提供, 在元测试任务中时刻存在着能不能复用元知识、用哪个任务的知识、该怎么用元知识等问题, 而元强化学习算法往往将元参数或元模块整体复用, 相当于完全“利用”了元知识, 这使元强化学习算法在一些场景中的泛化性能较差. 为更好地利用元知识, 需要研究在元测试阶段探索如何灵活复用元知识的方法.
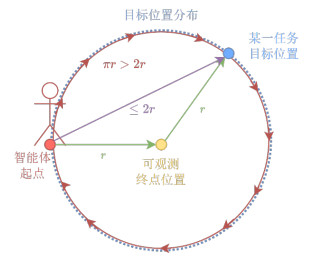
下面通过一个智能体寻路任务案例解释这个问题. 如图 12所示: 在这个任务中, 终点(蓝色)沿圆形场地边缘以均匀概率分布, 智能体起始不知道终点位置, 仅当智能体到达场地中央时获得终点位置. 在测试任务中, 智能体的最优策略为先走到场地中央(黄色)获得终点位置, 然后径直走向终点, 路径(绿色)长度期望为2r.然而在每个训练任务中, 智能体的最优解(紫色)均为径直走向未知的终点, 其策略的优化方向不会鼓励智能体获得终点位置, 因此智能体可能学到一种贪婪绕圈搜索的次优路径(红色)[60], 长度期望为(0+2πr)÷2=πr. 这种学到次优路径的现象可以归因于智能体在盲目复用元策略, 而没有有效利用“场地中央”这一元知识去探索更好地复用元策略的方法.
|
图 12 元知识复用的探索问题示意图 |
相关工作基于任务表征元知识, 通过探索完善测试任务的表征以选择契合任务的元策略. Zhang等人的MetaCURE工作构建了单独的任务特征探索策略πe, 探索策略首先在新任务中探索固定轮数获取任务表征z, 然后根据已获得的任务表征执行PEARL算法. 该探索策略由任务信息预测奖励r′(c: t+1, K)训练, 该奖励由最大化探索经验c: t+1和任务先验标签K之间的互信息计算得到[138]. Liu等人的工作DREAM构建了同样的探索策略
| 表 12 元知识复用的探索算法小结 |
总的来说, 现有方法研究了任务特征引导元知识的探索利用方法, 分为独立的任务特征探索策略和合并“超状态”两类方法, 但尚未形成体系, 有待进一步研究.
3.3.3 分布外任务泛化问题尽管现有元强化学习算法在一些任务环境上取得了成效, 但它们对任务分布变化非常敏感, 尤其当元测试任务分布与元训练任务分布不同, 即迁移到分布外(out-of-distribution, OOD)任务时, 算法的测试性能可能会显著下降.
现有工作从不同角度针对分布外任务泛化问题开展研究. Mendonca等人提出在元测试阶段重新标记训练时存储的任务样本, 以绕过分布不一致问题, 其算法MIER通过更新环境模型与任务标识来实现任务样本四元组(s, a, s′, r)的跨域转换[124]. Lin等人提出了基于模型的对抗式元强化学习算法AdMRL, 算法的新优化目标为策略在所有训练任务上的最坏表现, 并通过交替进行学习固定任务和寻找更难任务来对抗地迭代优化[140]. Lee和Chung提出的算法LDM基于VariBAD算法中的任务隐变量构建环境动力学模型, 并基于混合的环境模型生成模拟任务辅助训练, 以增强策略在任务级的泛化性能[141]. Xiong等人研究了元强化学习算法的理论一致性, 发现MAML是一种理论一致的算法并通常可以适应分布外任务, 然后将RL2和VariBAD算法改进为理论一致性算法并在实验中取得良好的泛化性能[142]. Fu等人针对孤立任务在MAML框架中难以学习导致任务泛化差的问题, 将任务分类为子集并基于子集开展训练[143]. Wang等人基于任务推断的元强化学习方法, 使用高斯混合空间作为任务表征以适应更广泛的任务变化[144].
综上, 现有相关工作的研究思路较为零散, 尚未形成体系和核心方法, 有待进一步研究. 表 13总结了上述算法的技术特点和源码链接.
| 表 13 分布外任务泛化算法小结 |
3.3.4 元任务特性问题
元强化学习相关研究往往选择非常相近的任务集进行训练和测试, 然而更加广泛的元任务设定将带来更多关于任务特性的机遇和挑战, 带来更多的研究空间. 现有工作针对样本任务可转化、动作映射变化两项元任务特性展开研究.
当不同任务的结构高度相似使得采样样本可在任务间转换时, 采样数据将具有更大的利用价值. Packer等人面向该场景, 类比事后经验重放(hindsight experience replay, HER)提出了一种样本增广算法HTR, 以适应稀疏奖励任务[145]. 当任务的不同仅体现在动作排序的变化时, 需要针对动作排序进行处理. Guo等人针对该场景提出了算法MCAT, 该算法在已有基于推断的元强化学习算法基础上加入了动作映射模块, 并设计了使映射后动作转移到同一状态的训练目标[146].
针对元任务特性的算法设计能有效地提升元强化学习算法落地业务场景的效果, 本文认为, 今后将涌现出更多探索、利用元任务特性的工作. 表 14总结了上述算法的技术特点和源码链接.
| 表 14 面向元任务特性的算法小结 |
3.4 元强化学习结合其他领域
元强化学习框架的泛用性使其容易与其他框架或问题结合, 用以提升原方法在目标问题上的迁移效果或泛化性能, 引入了一些需要考虑的新问题. 以下按问题类别展开介绍研究进展.
3.4.1 视觉元强化学习在元学习设定中, 任务样本的域变换后可看作一个不同的任务; 在元强化学习中, 也可将视觉图像状态的域变换看作不同的任务, 从而提升算法对视觉图像的泛化性能. OpenAI发布的视频游戏集合Procgen[55]是代表性的视觉元强化学习环境, 因其可将同一场景转换多种背景、贴图作为不同任务, 不同任务仅图像域发生变化而语义特征完全不变.
相关工作大多属于现有视觉泛化方法在元强化学习框架中的应用. Lee等人首先引入了用于随机扰动输入图像的随机神经网络, 通过增广输入范围提高深度强化学习智能体对图像状态的泛化能力[147]. Laskin等人引入了10种图像增广方法用于状态增广, 其算法RAD相比于传统算法取得了样本效率和训练效果的显著提升[148]. Hansen和Wang提出了一种软数据增强方法SODA, SODA对状态编码器加入增广数据和原始数据间隐变量互信息最大化的软约束, 依此获得比直接利用增广状态训练更好的样本效率、稳定性和鲁棒性[149].
综上, 视觉元强化学习的研究着力于在强化学习中引入视觉元学习的方法. 表 15总结了上述算法的技术特点和源码链接.
| 表 15 视觉元强化学习算法小结 |
3.4.2 离线元强化学习
离线元强化学习(offline meta-reinforcement learning, OMRL)相关工作研究如何利用离线数据完成元强化学习任务. Dorfman等人[150]第一个研究了离线元强化学习问题, 他们提出了MDP混淆(ambiguity)的问题概念, 即算法在离线数据下对任务特征的推断可能受离线样本分布限制而产生混淆, 并且无法像传统强化学习一样主动探索环境以降低任务特征的不确定性. 该工作针对上述问题, 基于VariBAD[34]构建算法. Mitchell等人提出了MACAW算法[62], 该算法基于结合演员-评论家算法的MAML框架, 采用面向离策略的优势函数加权回归方法改进实现仅利用离线样本计算MAML的外层优化部分. Li等人提出了MBML算法[151], 该算法基于PEARL算法, 采用离线强化学习中的批约束Q学习(batch constrained deep Q-learning, BCQ)作为强化学习模块以适应离线数据集, 并利用任务特征对比的优化目标修正离线数据分布偏差导致的任务特征偏差.
其他一些工作关注多任务之间的知识迁移与利用问题. 吴少波等人在基于相对熵的逆强化学习方法中引入元训练任务集和MAML方法以实现快速训练[152]. Li等人假设任意四元组样本(s, a, s′, r)的任务标签可以被唯一确定, 并依此设计了FOCAL算法[153]. Lin等人发现, 虚拟环境模型可以模拟交互从而探索离线数据之外的状态-动作对, 基于此提出了MerPO算法[154]. 该算法在已有数据和未知状态-动作对间做探索-利用均衡, 学习用于有效任务结构推断的元环境模型和用于安全探索分布外样本的元策略. Luo等人认为, 强化学习的安全探索问题契合离线元强化学习, 并进一步提出了安全适应元学习方法MESA[155]. Yuan和Lu提出离线数据的分布由采样策略和任务共同决定, 而现有离线元强化学习方法无法区分这些因素, 导致任务表示的训练不稳定, 并引入对比学习以增强编码的任务特征[156].
综上, 目前离线元强化学习研究有两个切入点: 1) 对基于任务特征推断的相关方法, 在离线数据下推断的任务样本特征较为模糊[150, 151, 156]; 2) 通过任务间信息互补提升策略训练效果[154]. 此外, 为提升样本效率, Nam等人从离线数据集中提取可重用技能和先验技能, 增强其泛用性并元学习上层策略[157]. 表 16总结了上述算法的技术特点和源码链接.
| 表 16 离线元强化学习算法小结 |
3.4.3 元模仿学习
模仿学习使智能体能够从专家演示样本中快速学习策略, 元模仿学习(meta-imitation learning)则期望利用多任务的专家演示样本快速学习元策略. 此外, 模仿学习能够很好地解决元强化学习中可能面临的稀疏奖励问题.
Mendonca等人针对MAML外层优化不稳定的问题, 巧妙地采用模仿学习的监督学习目标替代MAML外层原有的强化学习优化目标, 其算法GMPS在多项任务中的表现均大幅提升[158]. Zhou等人提出了算法WTL, 以加速元强化学习算法在稀疏奖励任务中的表现. WTL的训练流程分3个阶段: 首先, 利用专家样本构建探索策略; 然后, 利用探索策略采集任务样本; 最后, 利用专家样本和采集样本共同训练元策略[159]. 同样, 为加速元强化学习算法在稀疏奖励任务中的表现, Rengarajan等人提出的算法EMRLD将MAML的内层优化目标替换为强化学习目标和模仿学习目标的加权组合, 并针对次优演示数据提出了算法变体EMRLD-WS[160]. Bhutani等人提出了一种结合空间注意力的图像状态特征提取架构, 并采用元模仿学习范式进行训练[161].
综上, 目前离线元强化学习研究的切入点是, 采用专家样本和模仿学习替代MAML的一些模块以增强算法稳定性和学习效果. 此外, 因模仿学习的设定可以看作离线学习的一种, 其技术途径可以沿用离线元强化学习. 表 17总结了上述算法的技术特点和源码链接.
| 表 17 元模仿学习算法小结 |
3.4.4 持续元强化学习
在持续元强化学习(continual meta-reinforcement learning)的设定中, 多个任务接连到来, 智能体需要在每个当前任务执行元强化学习: 利用过去任务的知识完成当前任务, 并为未来的任务积累知识. 相关工作主要致力于利用元强化学习方法解决持续强化学习中的灾难性遗忘问题: Berseth等人设法在任务流中利用之前任务的离策略数据进行训练, 他们基于GMPS框架[158]提出了算法CoMPS, 其主要加入重要性采样来离策略训练内循环期间的策略参数[61]. Caccia等人使用基于重放和循环神经网络的强化学习算法3RL在MetaWorld环境中取得效果提升, 其中, RNN能够根据先前任务经验推断新任务的任务表征, 并缓解了持续学习的灾难性遗忘问题[162]. Kessler等人在持续强化学习中元学习世界模型, 该模型能够跨任务记忆经验并因此缓解灾难性遗忘[163].
综上, 一般算法难以部署到持续元强化学习的任务设定中, 因此, 相关工作致力于将元强化学习方法和持续学习方法有机地结合起来, 现有工作均采用了不同的技术思路. 表 18总结了上述算法的技术特点和源码链接.
| 表 18 持续元强化学习算法小结 |
3.4.5 多智能体元强化学习
现有多智能体元强化学习工作主要围绕多智能体特有的可泛化模块展开研究. 研究中常见的任务场景包括网格地图[164−167]、交通场景[166, 168]、粒子场景[169]、星际争霸[170]、棋牌博弈[171, 172]等. Rosa等人提出了为智能体学习负责智能体间通信的元专家策略, 该专家策略在变化的环境中展现出良好的泛化能力[173]; Zintgraf等人提出的算法MeLIBA将每个智能体的建模看作一个可泛化的任务, 并基于VAE元学习推断其他智能体动作的置信概率[174]; Huang等人为多演员-评论家架构的智能体构建了元演员-评论家模块, 该模块为每个智能体的演员模块提供更好的额外优化目标[175]; Schäfer等人针对智能体独立推断任务特征难的问题, 构建信息更全面的全局元任务特征解码器来帮助智能体训练[176]; Harris等人面向动态演变的多博弈求解场景设计并理论分析了元学习算法Meta-OGD[177]; Muglich等人为智能体信念建模设计了轻量的近似计算算法, 该算法同时具有良好的任务间泛化能力[178]; Yun等人元学习量子神经网络(quantum neural networks, QNN), 以快速适应多智能体带来的时变环境[179]. 表 19总结了上述算法的技术特点和源码链接.
| 表 19 多智能体元强化学习算法小结 |
3.5 元强化学习算法应用
强化学习在现实世界中的应用存在两大挑战: (1) 样本采样成本极高; (2) 意外扰动或未见场景会导致深度强化学习策略的测试效果急剧下降. 许多实际应用领域正逐步探索结合元强化学习的方法, 其中以交互式推荐、机械臂控制和具身视觉导航这3个典型任务为代表. 这些任务具有较为成熟的多任务仿真场景, 使得其中元强化学习算法的设计、迁移与验证易于实现. 以下本节按任务分别展开介绍研究进展.
3.5.1 机械臂控制仿真机械臂控制是强化学习中的经典任务, 同时, 其任务设置充分地丰富多变[48−50], 使得利用元强化学习实现真实机械臂控制兼具可行性与挑战性.
针对真实场景的视觉域变化问题, James等人提出了随机到规范自适应网络RCANs, 其算法将随机域图像统一映射到同一域并依此进行决策. 该工作在真实机械臂抓取任务中测试, 只需少量样本微调就能达到较高成功率[180]. Zhao等人设计了类似VariBAD的视觉元强化学习算法MELD, 该工作在真实机械臂以太网电缆的插入任务中测试, 在8小时采样训练后达到了较高成功率[181]. 为缓解强化学习现实应用的样本需求, 一些工作从仿真场景迁移知识到真实场景. Yu等人使用来自先前任务的人类和机器人演示数据, 利用元模仿学习建立先验知识, 并将先验知识结合人类视频演示进一步优化. 该工作在两种机械臂的放置、推动、拾取放置任务中进行测试, 机器人只需一段人类操作视频就可以学会完成相应任务[182]. Schoettler等人面向更加复杂的机械臂零件插入任务, 在虚拟场景中基于随机化工程参数的任务和PEARL算法进行元训练, 然后迁移到真实场景并展现出良好的泛化能力[183]. Arndt等人基于VAE构建了任务相关的轨迹生成模型以加速采样, 并使用MAML元训练适应各种动态的策略. 该工作在机器人将冰球击向目标的任务中测试, 在少量样本微调时取得了显著的性能提升[184]. Jang等人构建了一套面向机械臂的大规模交互式元模仿学习系统, 该系统融合了专家远程操作和机器自治过程, 能够高效地结合元模仿学习进行训练, 并在广泛的零样本和小样本任务中取得成效[185]. 针对真实机械臂的动力学受各种因素影响往往难以预测的问题, Harrison等人元学习动力学参数并与环境动态模型结合, 以快速适应真实环境动力学, 算法在四旋翼交付任务中的测试性能有显著提升[186]. Ghadirzadeh等人结合MAML和类似VariBAD的元强化学习算法, 并用于跨机械臂平台的快速策略适应[187]. Tiboni等人同样设计了虚实迁移算法DROPO, 算法将环境动力学参数作为任务域进行域随机化训练, 并将真实示例看作目标域做域拟合. 该工作在真实机械臂冰球击发和推物品两个任务中测试, 机器人只需5条现实场景轨迹就可以适应现实环境[188]. 语言大模型的能力在近年突飞猛进, Bing等人基于语言指示进一步加速了机械臂策略的元强化学习过程[189].
另一方面, 在控制领域中, 系统辨识(system identification)方法致力于辨识未知系统的模型结构与参数. 系统辨识往往应用在多任务或POMDP设定下, 因此其目标和基于推断的元强化学习方法相似. 相关工作包括Ross和Bagnell结合基于模型强化学习的方法DAgger[190]、Yu等人结合历史编码器的工作UP-OSI[191]、Liang等人以辨识系统参数为目标的主动探索策略方法[192]、Farid和Sakr结合变分推理学习的工作[193]等. 表 20总结了上述算法的技术特点和源码链接.
| 表 20 面向机械臂控制的元强化学习方法小结 |
总的来说, 现有机械臂控制的相关工作较多, 并已经能在真实场景的实验中达到比较好的效果, 已有许多工作向更具有挑战性、更广阔且更实用的具身机器人领域进发.
3.5.2 具身视觉导航具身机器人具有比机械臂更加广泛的用途, 将先前学习的技能(例如移动、推箱子等)应用于新任务(上下文或对象)的能力, 是下一代机器人的重要能力需求. 在具身机器人的诸多可能任务中, 视觉导航(visual navigation)是具身机器人必备的基础功能, 该功能已有成熟的传统方案, 但其效果有待进一步提升, 是当下热门的研究领域之一.
具身视觉导航已有高仿真的模拟环境[194, 195], 一些相关工作在其上展开实验. Wortsman等人提出了一种自适应视觉导航模型SAVN, 该模型借助MAML算法元学习策略损失函数, 从而实现在无奖励测试环境中的自适应训练[196]. Yan等人利用MAML和历史记忆元训练为导航机器人设计的多模态感知模型, 并在仿真语义导航任务中表现良好[197]. Li等人面向只有少数训练环境带有对象信息注释的场景, 基于Reptile算法提出了两个方法: (1) 任务课程的自动生成模块及其对抗学习方法; (2) 无监督分层强化学习方法, 用于在没有奖励时从无注释的环境中学习元技能(例如直行、转弯). 所提出的方法在有奖励环境中可以通过学习高级主策略来组合这些元技能, 从而快速适应视觉导航任务[96]. Luo等人将端到端策略网络分为感知网络和决策推理网络, 其中, 感知网络输出潜在特征, 并在冻结推理网络时利用MAML元训练感知网络. 实验表明, 其算法可以快速适应不同传感器配置和目标颜色未知的导航任务[198]. Hu等人面向能量受限无人机动态组建无线网络的问题, 提出了一种结合MAML元训练机制的值分解强化学习方案, 并在仿真场景中进行验证[199]. Wen等人结合MAML算法设计了机器人元强化学习算法dynamic-PMPO-CMA, 所训练的元策略能够在不同地图中避障导航, 并且其单智能体模型能适应多智能体机器人导航场景[200]. Lu等人设计了带有技能的多层策略网络及其训练和迁移方法, 其算法ASC在4个交互式任务中取得了较大性能提升[97]. Yu等人引入并改进了MAML算法, 使四旋翼无人机能在复杂的风扰动和碰撞环境中鲁棒地执行运动规划[201].
面向真实机器人, Nagabandi等人在基于模型的强化学习中元学习动力学模型, 分别采用了MAML和记忆模型作为元策略训练方法. 该算法在一个真实微型机器人中部署时, 能够快速在线适应腿的缺失、新的地形、姿态估计的误差以及载荷变动[202]. Song等人基于ES-MAML设计了改进元强化学习算法, 算法使真实机器人能快速适应动力学不断变化时的导航任务[203]. Asayesh等人基于MAML和类似VariBAD的元强化学习算法在多智能体机器人导航中训练预防碰撞策略, 并在真实环境中取得良好效果[204]. 表 21总结了上述算法的技术特点和源码链接.
| 表 21 具身视觉导航元强化学习方法小结 |
总的来说, 现有工作已能够初步用于一些机器人应用, 但对更广泛场景和任务的适应能力还有较大的提升空间. 此外, 现有工作多采用基于MAML的元强化学习方法, 其中, 关于元强化学习方法的运用较初级, 有待引入和设计更加强大的元强化学习方法.
3.5.3 交互式推荐交互式推荐方法能够在线适应用户推荐偏好, 是现今电子商务平台和视频网站的重要需求. 交互式推荐的执行流程天然契合强化学习框架, 强化学习已成为交互式推荐模型的主要训练方法之一[205−207]. 其中, 由于产品、用户和系统的频繁变动, 很难面对样本量少的新目标实行准确推荐, 这被称为推荐系统的冷启动问题. Zou等人首先聚焦于交互式推荐中的用户冷启动问题, 其算法NICF使用深度强化学习在适应用户档案和做出准确推荐间学习取得平衡, 并通过最大化每个用户的累积奖励来优化元模型[208]. Chu等人更加深入地引入了元强化学习方法, 该工作面向用户冷启动问题设计了3个协同的元模块: (1) 一个元探索策略, 用于通过探索性对话识别用户的偏好; (2) 一个基于Transformer的状态编码器, 用来模拟用户在对话中的积极和消极反馈; (3) 一个基于状态嵌入的自适应物品推荐器[209].
总的来说, 元强化学习已初步在交互式推荐的冷启动问题中展现作用, 有深入研究的潜力. 表 22总结了上述算法的技术特点和源码链接.
| 表 22 交互式推荐元强化学习方法小结 |
4 挑战与展望
元强化学习是近年新兴的领域, 其研究体系仍在不断改进完善, 这也为研究者提供了更多深入挖掘的机会. 从前述元强化学习研究进展中来看, 本文认为, 该领域主要面临以下几个问题和挑战.
4.1 基于对比学习的元策略学习挑战早期深度模型的元策略学习方法以MAML、记忆和推断为主, 而最新的工作更加青睐任务特征推断和特征对比学习两类方法, 这表明这两类方法的实用性相对更强. 其中, 任务特征推断的信息瓶颈和VAE架构已经定型一段时间, 相比之下, 特征对比学习作为一种新兴的热门技术, 其泛化理论和运用方法正在不断突破, 并潜在具有代替MAML框架的实用价值, 是值得关注的重要研究方向, 如何进一步挖掘对比学习的潜力成为挑战.
4.2 元强化学习的理论问题在元强化学习算法中, 近年已有一些关于MAML的理论分析研究, 但关于任务特征的推断方法及对比学习方法并没有完整的理论分析工作, 使得相关算法的设计、论证与应用涉及不确定性, 这一定程度上阻碍了元强化学习研究的发展.
4.3 元模块的泛化机理与性能分析问题除元模块如何训练的问题之外, 元模块承担的功能也显著影响着元知识的表达形式及其泛化能力. 已有的分层策略设计和各强化学习模块元学习方法均围绕元模块如何构建这一核心问题展开研究, 但现有方法的设计依赖直觉与实验效果, 各模块发挥元知识优势的机理与性能尚难以明确分析, 亟待研究该问题以为元模块的设计提供进一步指导.
4.4 面向更复杂任务场景的设计问题现有元强化学习工作大多围绕同一大类任务场景开展研究, 例如从视频游戏到视频游戏、从机械臂到机械臂等, 其中的任务差异相对局限. 然而, 广泛的现实任务迁移需求考虑更多、更复杂的任务差异性, 如控制目标差异、所处环境差异、动作语义差异、状态维度差异等, 目前尚无成熟的类似复杂任务场景, 现有元强化学习算法也不能很好地适应这类任务, 该方向亟待进一步探究以扩展元强化学习的适用领域.
4.5 元强化学习落地应用挑战元强化学习的范式与人类终身学习的过程相似, 元强化学习研究有望落地到更加广泛的实际应用中, 为人类生活增光添彩, 为世界带来新一轮的人工智能热潮. 但元强化学习落地应用面临着更多的严苛挑战, 包括虚实迁移、大跨度任务迁移、样本来源、训练与推理效率等种种要求与指标限制, 亟待研究者攻破层层难关, 早日让决策学习方法在更多领域开花结果.
5 总结本文对元强化学习研究的进展进行了广泛的回顾和总结. 本文首先介绍了元强化学习的相关概念及研究范围, 然后按研究问题从元策略学习方法、强化学习模块元学习方法、元强化学习设定的新问题、元强化学习结合其他领域和元强化学习算法应用这5个方面细分并总结了相关工作进展, 最后根据对相关工作进展的认识对元强化学习研究领域面临的关键挑战及发展展望进行了探讨.
| [1] |
Sutton RS, Barto AG. Reinforcement Learning: An Introduction. 2nd ed.. Cambridge: MIT Press, 2018.
|
| [2] |
Silver D, Huang A, Maddison CJ, et al. Mastering the game of Go with deep neural networks and tree search. Nature, 2016, 529(7587): 484-489.
[doi:10.1038/nature16961] |
| [3] |
Vinyals O, Babuschkin I, Czarnecki WM, et al. Grandmaster level in StarCraft Ⅱ using multi-agent reinforcement learning. Nature, 2019, 575(7782): 350-354.
[doi:10.1038/s41586-019-1724-z] |
| [4] |
Li J, Koyamada S, Ye Q, et al. Suphx: Mastering mahjong with deep reinforcement learning. arXiv: 2003.13590, 2020.
|
| [5] |
Degrave J, Felici F, Buchli J, et al. Magnetic control of tokamak plasmas through deep reinforcement learning. Nature, 2022, 602(7897): 414-419.
[doi:10.1038/s41586-021-04301-9] |
| [6] |
Dulac-Arnold G, Mankowitz D, Hester T. Challenges of real-world reinforcement learning. arXiv: 1904.12901, 2019.
|
| [7] |
Yu C, Liu J, Nemati S, et al. Reinforcement learning in healthcare: A survey. ACM Computing Surveys, 2021, 55(1): 1-36.
|
| [8] |
Gupta S, Singal G, Garg D. Deep reinforcement learning techniques in diversified domains: A survey. Archives of Computational Methods in Engineering, 2021, 28(7): 4715-4754.
[doi:10.1007/s11831-021-09552-3] |
| [9] |
Schrittwieser J, Antonoglou I, Hubert T, et al. Mastering Atari, Go, chess and shogi by planning with a learned model. Nature, 2020, 588(7839): 604-609.
[doi:10.1038/s41586-020-03051-4] |
| [10] |
Zhu Z, Lin K, Jain AK, et al. Transfer learning in deep reinforcement learning: A survey. arXiv: 2009.07888, 2020.
|
| [11] |
Kirk R, Zhang A, Grefenstette E, et al. A survey of zero-shot generalisation in deep reinforcement learning. Journal of Artificial Intelligence Research, 2023, 76: 201-264.
[doi:10.1613/jair.1.14174] |
| [12] |
Bock P. A perspective on artificial intelligence: learning to learn. Annals of Operations Research, 1988, 16(1): 33-52.
[doi:10.1007/BF02283734] |
| [13] |
Finn C, Abbeel P, Levine S. Model-agnostic meta-learning for fast adaptation of deep networks. In: Proc. of the Int'l Conf. on Machine Learning, Vol. 3. 2017. 1126−1135.
|
| [14] |
Finn C, Levine S. Meta-learning: From few-shot learning to rapid reinforcement learning. In: Proc. of the Int'l Conf. on Machine Learning. 2019.
|
| [15] |
Vanschoren J. Meta-learning: A survey. 2018: 1−29.
|
| [16] |
Huisman M, Van Rijn JN, Plaat A. A survey of deep meta-learning. Artificial Intelligence Review, 2021, 54(6): 4483-4541.
[doi:10.1007/s10462-021-10004-4] |
| [17] |
Li FC, Liu Y, Wu PX, et al. A survey on recent advances in meta-learning. Chinese Journal of Computers, 2021, 44(2): 422-446(in Chinese with English abstract).
https://www.cnki.com.cn/Article/CJFDTOTAL-JSJX202102012.htm |
| [18] |
Tan XY, Zhang Z. Review on meta reinforcement learning. Journal of Nanjing University of Aeronautics & Astronautics, 2021, 53(5): 653-663(in Chinese with English abstract).
https://www.cnki.com.cn/Article/CJFDTOTAL-NJHK202105001.htm |
| [19] |
Yadav P, Mishra A, Lee J, et al. A survey on deep reinforcement learning-based approaches for adaptation and generalization. arXiv: 2202.08444, 2022.
|
| [20] |
Levine S. Reinforcement learning and control as probabilistic inference: Tutorial and review. arXiv: 1805.00909, 2018.
|
| [21] |
Zhao CY, Lai J. Survey on meta reinforcement learning. Application Research of Computers, 2023, 40(1): 1-10(in Chinese with English abstract).
https://www.cnki.com.cn/Article/CJFDTOTAL-JSYJ202311001.htm |
| [22] |
Beck J, Vuorio R, Liu EZ, et al. A survey of meta-reinforcement learning. arXiv: 2301.08028, 2023.
|
| [23] |
Mnih V, Kavukcuoglu K, Silver D, et al. Human-level control through deep reinforcement learning. Nature, 2015, 518(7540): 529-533.
[doi:10.1038/nature14236] |
| [24] |
Wang Z, Schaul T, Hessel M, et al. Dueling network architectures for deep reinforcement learning. In: Proc. of the Int'l Conf. on Machine Learning, Vol. 48. 2016. 1995−2003.
|
| [25] |
Hausknecht M, Stone P. Deep recurrent Q-learning for partially observable mdps. In: Proc. of the AAAI Fall Symp. 2015. 29−37.
|
| [26] |
Willia RJ. Simple statistical gradient-following algorithms for connectionist reinforcement learning. Machine Learning, 1992, 8(3-4): 229-256.
[doi:10.1007/BF00992696] |
| [27] |
Lillicrap TP, Hunt JJ, Pritzel A, et al. Continuous control with deep reinforcement learning. In: Proc. of the Int'l Conf. on Learning Representations. 2016.
|
| [28] |
Schulman J, Wolski F, Dhariwal P, et al. Proximal policy optimization algorithms. arXiv: 1707.06347, 2017.
|
| [29] |
Haarnoja T, Zhou A, Abbeel P, et al. Soft actor-critic: Off-policy maximum entropy deep reinforcement learning with a stochastic actor. In: Proc. of the Int'l Conf. on Machine Learning, Vol. 80. 2018. 1856−1865.
|
| [30] |
Fujimoto S, Van Hoof H, Meger D. Addressing function approximation error in actor-critic methods. In: Proc. of the Int'l Conf. on Machine Learning. 2018. 1587−1596.
|
| [31] |
Finn C. Learning to Learn with Gradients. Berkeley: University of California, 2018.
|
| [32] |
Rakelly K, Zhou A, Finn C, et al. Efficient off-policy meta-reinforcement learning via probabilistic context variables. In: Proc. of the Int'l Conf. on Machine Learning. 2019. 5331−5340.
|
| [33] |
Fakoor R, Chaudhari P, Soatto S, et al. Meta-Q-learning. In: Proc. of the Int'l Conf. on Learning Representations. 2020.
|
| [34] |
Zintgraf L, Schulze S, Lu C, et al. VariBAD: Variational bayes-adaptive deep RL via meta-learning. The Journal of Machine Learning Research, 2021, 22(1): 13198-13236.
|
| [35] |
Nichol A, Achiam J, Schulman J. On first-order meta-learning algorithms. arXiv: 1803.02999, 2018.
|
| [36] |
Gordon J, Bronskill J, Nowozin S, et al. Meta-learning probabilistic inference for prediction. In: Proc. of the Int'l Conf. on Learning Representations. 2018.
|
| [37] |
Santoro A, Bartunov S, Botvinick M, et al. Meta-learning with memory-augmented neural networks. In: Proc. of the Int'l Conf. on Machine Learning. 2016. 1842−1850.
|
| [38] |
Ramalho T, Garnelo M. Adaptive posterior learning: few-shot learning with a surprise-based memory module. In: Proc. of the Int'l Conf. on Learning Representations. 2019.
|
| [39] |
Qiao S, Liu C, Shen W, et al. Few-shot image recognition by predicting parameters from activations. In: Proc. of the IEEE/CVF Conf. on Computer Vision and Pattern Recognition. IEEE, 2018. 7229−7238.
|
| [40] |
Gidaris S, Komodakis N, Paristech P, et al. Dynamic few-shot visual learning without forgetting. In: Proc. of the IEEE Computer Society Conf. on Computer Vision and Pattern Recognition, Vol. 9. 2018. 4367−4375.
|
| [41] |
Koch G. Siamese Neural Networks for One-Shot Image Recognition. University of Toronto, 2015.
|
| [42] |
Vinyals O, Blundell C, Lillicrap T, et al. Matching networks for one shot learning. In: Proc. of the Advances in Neural Information Processing Systems (NIPS). 2016. 3637−3645.
|
| [43] |
Snell J, Swersky K, Zemel R. Prototypical networks for few-shot learning. In: Proc. of the Advances in Neural Information Processing Systems, Vol. 30. 2017. 4077−4087.
|
| [44] |
Varghese NV, Mahmoud QH. A survey of multi-task deep reinforcement learning. Electronics, 2020, 9(9): 1363.
[doi:10.3390/electronics9091363] |
| [45] |
Khetarpal K, Riemer M, Rish I, et al. Towards continual reinforcement learning: A review and perspectives. Journal of Artificial Intelligence Research, 2022, 75: 1401-1476.
[doi:10.1613/jair.1.13673] |
| [46] |
Wang M, Deng W. Deep visual domain adaptation: A survey. Neurocomputing, 2018, 312: 135-153.
[doi:10.1016/j.neucom.2018.05.083] |
| [47] |
Zhou K, Liu Z, Qiao Y, et al. Domain generalization in vision: A survey. arXiv: 2103.02503, 2021.
|
| [48] |
Todorov E, Erez T, Tassa Y. MuJoCo: A physics engine for model-based control. In: Proc. of the IEEE Int'l Conf. on Intelligent Robots and Systems. 2012. 5026−5033.
|
| [49] |
Lee K, Seo Y, Lee S, et al. Context-aware dynamics model for generalization in model-based reinforcement learning. In: Proc. of the Int'l Conf. on Machine Learning. 2020. 5757−5766.
|
| [50] |
Benjamins C, Eimer T, Schubert F, et al. CARL: A benchmark for contextual and adaptive reinforcement learning. arXiv: 2110. 02102, 2021.
|
| [51] |
Duan Y, Schulman J, Chen X, et al. RL2: Fast reinforcement learning via slow reinforcement learning. arXiv: 1611.02779, 2016.
|
| [52] |
Nichol A, Pfau V, Hesse C, et al. Gotta learn fast: A new benchmark for generalization in RL. arXiv: 1804.03720, 2018.
|
| [53] |
Cobbe K, Klimov O, Hesse C, et al. Quantifying generalization in reinforcement learning. In: Proc. of the Int'l Conf. on Machine Learning. 2019. 1282−1289.
|
| [54] |
Alver S, Precup D. A brief look at generalization in visual meta-reinforcement learning. arXiv: 2006.07262, 2020.
|
| [55] |
Cobbe K, Hesse C, Hilton J, et al. Leveraging procedural generation to benchmark reinforcement learning. In: Proc. of the Int'l Conf. on Machine Learning. 2020. 2048−2056.
|
| [56] |
Chevalier-Boisvert M, Willems L, Pal S. Minimalistic Gridworld Environment for Gymnasium. 2018.
|
| [57] |
Samvelyan M, Kirk R, Kurin V, et al. MiniHack the planet: A sandbox for open-ended reinforcement learning research. In: Proc. of the Neural Information Processing Systems Track on Datasets and Benchmarks. 2021.
|
| [58] |
Lin Z, Li J, Shi J, et al. JueWu-MC: Playing minecraft with sample-efficient hierarchical reinforcement learning. In: Proc. of the Int'l Joint Conf. on Artificial Intelligence. 2022. 3257−3263.
|
| [59] |
Yu T, Quillen D, He Z, et al. Meta-World: A benchmark and evaluation for multi-task and meta reinforcement learning. In: Proc. of the Conf. on Robot Learning. 2019. 1094−1100.
|
| [60] |
Zintgraf L, Feng L, Lu C, et al. Exploration in approximate hyper-state space for meta reinforcement learning. In: Proc. of the Int'l Conf. on Machine Learning. 2021. 12991−13001.
|
| [61] |
Berseth G, Zhang Z, Zhang G, et al. CoMPS: Continual meta policy search. In: Proc. of the Int'l Conf. on Learning Representations. 2022.
|
| [62] |
Mitchell E, Rafailov R, Peng X Bin, et al. Offline meta-reinforcement learning with advantage weighting. In: Proc. of the Int'l Conf. on Machine Learning. 2021. 7780−7791.
|
| [63] |
Wang JX, King M, Porcel N, et al. Alchemy: A benchmark and analysis toolkit for meta-reinforcement learning agents. arXiv: 2102.02926, 2021.
|
| [64] |
Antoniou A, Storkey A, Edwards H. How to train your MAML. In: Proc. of the Int'l Conf. on Learning Representations. 2019.
|
| [65] |
Song X, Gao W, Yang Y, et al. ES-MAML: Simple hessian-free meta learning. arXiv: 1910.01215, 2019.
|
| [66] |
Rothfuss J, Lee D, Clavera I, et al. ProMP: Proximal meta-policy search. In: Proc. of the Int'l Conf. on Learning Representations. 2019.
|
| [67] |
Liu H, Socher R, Xiong C. Taming MAML: Efficient unbiased meta-reinforcement learning. In: Proc. of the Int'l Conf. on Machine Learning. 2019. 4061−4071.
|
| [68] |
Fallah A, Mokhtari A, Ozdaglar A. On the convergence theory of gradient-based model-agnostic meta-learning algorithms. In: Proc. of the Int'l Conf. on Artificial Intelligence and Statistics. 2020. 1082−1092.
|
| [69] |
Khodak M, Balcan MF, Talwalkar A. Provable guarantees for gradient-based meta-learning. In: Proc. of the Int'l Conf. on Machine Learning. 2019. 424−433.
|
| [70] |
Molybog I, Lavaei J. When does MAML objective have benign landscape? In: Proc. of the IEEE Conf. on Control Technology and Applications. 2021. 220−227.
|
| [71] |
Wang L, Cai Q, Yang Z, et al. On the global optimality of model-agnostic meta-learning. In: Proc. of the Int'l Conf. on Machine Learning. 2020. 9837−9846.
|
| [72] |
Fallah A, Georgiev K, Mokhtari A, et al. On the convergence theory of debiased model-agnostic meta-reinforcement learning. In: Proc. of the Advances in Neural Information Processing Systems, Vol. 34. 2021. 3096−3107.
|
| [73] |
Ji K, Yang J, Liang Y. Theoretical convergence of multi-step model-agnostic meta-learning. Journal of Machine Learning Research, 2022, 23: 1-41.
|
| [74] |
Wang JX, Kurth-Nelson Z, Tirumala D, et al. Learning to reinforcement learn. arXiv: 1611.05763, 2016.
|
| [75] |
Mishra N, Rohaninejad M, Chen X, et al. A simple neural attentive meta-learner. In: Proc. of the Int'l Conf. on Learning Representations. 2018.
|
| [76] |
Vaswani A, Shazeer N, Parmar N, et al. Attention is all you need. In: Proc. of the Advances in Neural Information Processing Systems, Vol. 30. 2017.
|
| [77] |
Parisotto E. Meta Reinforcement Learning through Memory. Carnegie Mellon University, 2021.
|
| [78] |
Sæmundsson S, Hofmann K, Deisenroth MP. Meta reinforcement learning with latent variable gaussian processes. In: Proc. of the Conf. on Uncertainty in Artificial Intelligence. 2018. 642−652.
|
| [79] |
Zintgraf L, Shiarlis K, Kurin V, et al. Fast context adaptation via meta-learning. In: Proc. of the 36th Int'l Conf. on Machine Learning (ICML 2019). 2019, 2019 (2018). 13262−13276.
|
| [80] |
Lan L, Li Z, Guan X, Wang P. Meta reinforcement learning with task embedding and shared policy. In: Proc. of the Int'l Joint Conf. on Artificial Intelligence. 2019. 2794−2800.
|
| [81] |
Humplik J, Galashov A, Hasenclever L, et al. Meta reinforcement learning as task inference. arXiv: 1905. 06424, 2019.
|
| [82] |
Lu JY, Ling XH, Liu Q, et al. Meta-reinforcement learning algorithm based on automating policy entropy. Computer Science, 2021, 48(6): 168-174(in Chinese with English abstract).
https://www.cnki.com.cn/Article/CJFDTOTAL-JSJA202106023.htm |
| [83] |
Raileanu R, Goldstein M, Szlam A, et al. Fast adaptation to new environments via policy-dynamics value functions. In: Proc. of the Int'l Conf. on Machine Learning. 2020. 7920−7931.
|
| [84] |
Zhang A, Sodhani S, Khetarpal K, et al. Learning robust state abstractions for hidden-parameter block mdps. In: Proc. of the Int'l Conf. on Learning Representations. 2021.
|
| [85] |
van den Oord A, Li Y, Vinyals O. Representation learning with contrastive predictive coding. 2018.
|
| [86] |
He K, Fan H, Wu Y, et al. Momentum contrast for unsupervised visual representation learning. In: Proc. of the IEEE Computer Society Conf. on Computer Vision and Pattern Recognition. 2020. 9726−9735.
|
| [87] |
Laskin M, Srinivas A, Abbeel P. CURL: Contrastive unsupervised representations for reinforcement learning. In: Proc. of the 37th Int'l Conf. on Machine Learning (ICML 2020). 2020, PartF16814(2018). 5595−5606.
|
| [88] |
Fu H, Tang H, Hao J, et al. Towards effective context for meta-reinforcement learning: An approach based on contrastive learning. Proc. of the AAAI Conf. on Artificial Intelligence, 2021, 35(8): 7457-7465.
[doi:10.1609/aaai.v35i8.16914] |
| [89] |
Wang B, Xu S, Keutzer K, et al. Improving context-based meta-reinforcement learning with self-supervised trajectory contrastive learning. arXiv: 2103.06386, 2021.
|
| [90] |
Mu Y, Zhuang Y, Ni F, et al. DOMINO: Decomposed mutual information optimization for generalized context in meta-reinforcement learning. In: Advances in Neural Information Processing Systems, Vol. 35. 2022. 27563−27575.
|
| [91] |
Raghu A, Raghu M, Bengio S, et al. Rapid learning or feature reuse? towards understanding the effectiveness of maml. In: Proc. of the Int'l Conf. on Learning Representations. 2020.
|
| [92] |
Kao CH, Chiu WC, Chen PY. MAML is a noisy contrastive learner. In: Proc. of the Int'l Conf. on Learning Representations. 2022.
|
| [93] |
Hutsebaut-Buysse M, Mets K, Latré S. ierarchical reinforcement learning: A survey and open research challenges. Machine Learning and Knowledge Extraction, 2022, 4(1): 172-221.
[doi:10.3390/make4010009] |
| [94] |
Tessler C, Givony S, Zahavy T, et al. A deep hierarchical approach to lifelong learning in minecraft. Proc. of the AAAI Conf. on artificial intelligence. arXiv: 1604.07255, 2017.
|
| [95] |
Fu H, Tang H, Hao J, et al. MGHRL: Meta goal-generation for hierarchical reinforcement learning. Distributed Artificial Intelligence. Vol. 12547. Springer, 2020. 29−39.
|
| [96] |
Li J, Wang X, Tang S, et al. Unsupervised reinforcement learning of transferable meta-skills for embodied navigation. In: Proc. of the IEEE Computer Society Conf. on Computer Vision and Pattern Recognition. 2020. 12120−12129.
|
| [97] |
Lu J, Salvador J, Mottaghi R, et al. ASC me to do anything: Multi-task training for embodied AI. arXiv: 2202.06987, 2022.
|
| [98] |
Nie K, Meng QH. Combat behavior evaluation based on hierarchical episodic meta-deep reinforcement learning. Command Control & Simulation, 2021, 43(2): 65-71(in Chinese with English abstract).
https://www.cnki.com.cn/Article/CJFDTOTAL-QBZH202102012.htm |
| [99] |
Sohn S, Woo H, Choi J, et al. Meta reinforcement learning with autonomous inference of subtask dependencies. In: Proc. of the Int'l Conf. on Learning Representations. 2020.
|
| [100] |
Peng M, Zhu B, Jiao J. Linear representation meta-reinforcement learning for instant adaptation. arXiv: 2101.04750, 2021.
|
| [101] |
Chua K, Lei Q, Lee J. Provable hierarchy-based meta-reinforcement learning. In: Ruiz F, Dy J, Van de Meent JW, eds. Proc. of the 26th Int'l Conf. on Artificial Intelligence and Statistics, Vol. 206. 2023. 10918−10967.
|
| [102] |
Amin S, Gomrokchi M, Satija H, et al. A survey of exploration methods in reinforcement learning. arXiv: 2109. 00157, 2021.
|
| [103] |
Stadie BC, Yang G, Houthooft R, et al. Some considerations on learning to explore via meta-reinforcement learning. In: Advances in Neural Information Processing Systems. 2018. 9280−9290.
|
| [104] |
Gurumurthy S, Kumar S, Sycara K. MAME : Model-agnostic meta-exploration. In: Proc. of the Conf. on Robot Learning. 2020. 910−922.
|
| [105] |
Xu T, Liu Q, Zhao L, et al. Learning to explore via meta-policy gradient. In: Proc. of the Int'l Conf. on Machine Learning. 2018. 5463−5472.
|
| [106] |
Gupta A, Mendonca R, Liu YX, et al. Meta-reinforcement learning of structured exploration strategies. In: Advances in Neural Information Processing Systems, Vol. 31. 2018. 5302−5311.
|
| [107] |
Alet F, Schneider MF, Lozano-Perez T, et al. Meta-learning curiosity algorithms. In: Proc. of the Int'l Conf. on Learning Representations. 2020.
|
| [108] |
Hu H, Huang G, Li X, et al. Meta-reinforcement learning with dynamic adaptiveness distillation. IEEE Trans. on Neural Networks and Learning Systems, 2023, 34(3): 1454-1464.
[doi:10.1109/TNNLS.2021.3105407] |
| [109] |
Silver D, Lever G, Heess N, et al. Deterministic policy gradient algorithms. In: Proc. of the Int'l Conf. on Machine Learning. 2014. 387−395.
|
| [110] |
Houthooft R, Chen RY, Isola P, et al. Evolved policy gradients. In: Advances in Neural Information Processing Systems, Vol. 31. 2018. 5400−5409.
|
| [111] |
Kirsch L, Van Steenkiste S, Schmidhuber J. Improving generalization in meta reinforcement learning using learned objectives. In: Proc. of the Int'l Conf. on Learning Representations. 2020.
|
| [112] |
Xu Z, Van Hasselt H, Hessel M, et al. Meta-gradient reinforcement learning with an objective discovered online. In: Advances in Neural Information Processing Systems, Vol. 33. 2020. 15254−15264.
|
| [113] |
Zhou W, Li Y, Yang Y, et al. Online meta-critic learning for off-policy actor-critic methods. In: Advances in Neural Information Processing Systems, Vol. 33. 2020. 17662−17673.
|
| [114] |
Oh J, Hessel M, Czarnecki WM, et al. Discovering reinforcement learning algorithms. In: Advances in Neural Information Processing Systems, Vol. 33. 2020. 1060−1070.
|
| [115] |
Veeriah V, Hessel M, Xu Z, et al. Discovery of useful questions as auxiliary tasks. In: Advances in Neural Information Processing Systems, Vol. 32. 2019.
|
| [116] |
Zheng Z, Oh J, Singh S. On learning intrinsic rewards for policy gradient methods. In: Advances in Neural Information Processing Systems, Vol. 31. 2018. 4644−4654.
|
| [117] |
Yang Y, Caluwaerts K, Iscen A, et al. NoRML: No-reward meta learning. In: Proc. of the Int'l Joint Conf. on Autonomous Agents and MultiAgent Systems, Vol. 1. 2019. 323−331.
|
| [118] |
Xu K, Ratner E, Dragan A, et al. Learning a prior over intent via meta-inverse reinforcement learning. In: Proc. of the Int'l Conf. on Machine Learning. 2019. 6952−6962.
|
| [119] |
Yu L, Yu T, Finn C, et al. Meta-inverse reinforcement learning with probabilistic context variables. In: Advances in Neural Information Processing Systems, Vol. 32. 2019. 1−15.
|
| [120] |
Ghasemipour SKS, Gu S, Zemel R. SMILe: Scalable meta inverse reinforcement learning through context-conditional policies. In: Advances in Neural Information Processing Systems, Vol. 32. 2019. 1−11.
|
| [121] |
Pong VH, Nair A, Smith L, et al. Offline meta-reinforcement learning with online self-supervision. In: Proc. of the Int'l Conf. on Machine Learning. 2022. 17811−17829.
|
| [122] |
Luo FM, Xu T, Lai H, et al. A survey on model-based reinforcement learning. arXiv: 2206.09328, 2022.
|
| [123] |
Clavera I, Rothfuss J, Schulman J, et al. Model-based reinforcement learning via meta-policy optimization. In: Proc. of the Conf. on Robot Learning. 2018. 617−629.
|
| [124] |
Mendonca R, Geng X, Finn C, et al. Meta-reinforcement learning robust to distributional shift via model identification and experience relabeling. arXiv: 2006.07178, 2020.
|
| [125] |
Wang Q, Van Hoof H. Model-based meta reinforcement learning using graph structured surrogate models and amortized policy search. In: Proc. of the Int'l Conf. on Machine Learning. 2022. 23055−23077.
|
| [126] |
Xu Z, Van Hasselt H, Silver D. Meta-gradient reinforcement learning. In: Advances in Neural Information Processing Systems, Vol. 31. 2018. 2396−2407.
|
| [127] |
Zahavy T, Xu Z, Veeriah V, et al. A self-tuning actor-critic algorithm. In: Advances in Neural Information Processing Systems, Vol. 33. 2020. 20913-20924.
|
| [128] |
Wang Y, Ni T. Meta-SAC: Auto-tune the entropy temperature of soft actor-critic via metagradient. arXiv: 2007.01932, 2020.
|
| [129] |
Beck J, Jackson MT, Vuorio R, et al. Hypernetworks in meta-reinforcement learning. In: Liu K, Kulic D, Ichnowski J, eds. Proc. of the 6th Conf. on Robot Learning, Vol. 205. 2023. 1478−1487.
|
| [130] |
Mehta B, Diaz M, Golemo F, et al. Active domain randomization. In: Proc. of the Conf. on Robot Learning. 2020. 1162−1176.
|
| [131] |
Pan X, Seita D, Gao Y, et al. Risk averse robust adversarial reinforcement learning. In: Proc. of the IEEE Int'l Conf. on Robotics and Automation. 2019. 8522−8528.
|
| [132] |
Mehta B, Deleu T, Raparthy SC, et al. Curriculum in gradient-based meta-reinforcement learning. arXiv: 2002.07956, 2020.
|
| [133] |
Gutierrez RL, Leonetti M. Information-theoretic task selection for meta-reinforcement learning. In: Advances in Neural Information Processing Systems, Vol. 33. 2020. 20532−20542.
|
| [134] |
Gupta A, Eysenbach B, Finn C, et al. Unsupervised meta-learning for reinforcement learning. arXiv: 1806.04640, 2018.
|
| [135] |
Eysenbach B, Ibarz J, Gupta A, et al. Diversity is all you need: learning skills without a reward function. In: Proc. of the Int'l Conf. on Learning Representations. 2019.
|
| [136] |
Jabri A, Hsu K, Eysenbach B, et al. Unsupervised curricula for visual meta-reinforcement learning. In: Advances in Neural Information Processing Systems, Vol. 32. 2019.
|
| [137] |
Rimon Z, Tamar A, Adler G. Meta reinforcement learning with finite training tasks -a density estimation approach. arXiv: 2206. 10716, 2022.
|
| [138] |
Zhang J, Wang J, Hu H, et al. MetaCURE: Meta reinforcement learning with empowerment-driven exploration. In: Proc. of the Int'l Conf. on Machine Learning. 2021. 12600−12610.
|
| [139] |
Liu EZ, Raghunathan A, Liang P, et al. Decoupling exploration and exploitation for meta-reinforcement learning without sacrifices. In: Proc. of the Int'l Conf. on Machine Learning. 2021. 6925−6935.
|
| [140] |
Lin Z, Thomas G, Yang G, et al. Model-based adversarial meta-reinforcement learning. In: Advances in Neural Information Processing Systems, Vol. 33. 2020. 10161−10173.
|
| [141] |
Lee S, Chung SY. Improving generalization in meta-RL with imaginary tasks from latent dynamics mixture. In: Advances in Neural Information Processing Systems, Vol. 34. 2021. 27222−27235.
|
| [142] |
Xiong Z, Zintgraf L, Beck J, et al. On the practical consistency of meta-reinforcement learning algorithms. arXiv: 2112.00478, 2021.
|
| [143] |
Fu Q, Wang Z, Fang N, et al. MAML2: Meta reinforcement learning via meta-learning for task categories. Frontiers of Computer Science, Springer, 2023, 17(4): 174325.
|
| [144] |
Wang M, Bing Z, Yao X, et al. Meta-reinforcement learning based on self-supervised task representation learning. Proc. of the AAAI Conf. on Artificial Intelligence, 2023, 37(8): 10157-10165.
|
| [145] |
Packer C, Abbeel P, Gonzalez JE. Hindsight task relabelling: Experience replay for sparse reward meta-RL. In: Advances in Neural Information Processing Systems, Vol. 34. 2021. 2466−2477.
|
| [146] |
Guo Y, Wu Q, Lee H. Learning action translator for meta reinforcement learning on sparse-reward tasks. Proc. of the AAAI Conf. on Artificial Intelligence, 2022, 36(6): 6792-6800.
|
| [147] |
Lee K, Lee K, Shin J, et al. Network randomization: A simple technique for generalization in deep reinforcement learning. In: Proc. of the Int'l Conf. on Learning Representations. 2020.
|
| [148] |
Laskin M, Lee K, Stooke A, et al. Reinforcement learning with augmented data. In: Advances in Neural Information Processing Systems, Vol. 33. 2020. 19884−19895.
|
| [149] |
Hansen N, Wang X. Generalization in reinforcement learning by soft data augmentation. In: Proc. of the IEEE Int'l Conf. on Robotics and Automation. 2021. 13611−13617.
|
| [150] |
Dorfman R, Shenfeld I, Tamar A. Offline meta reinforcement learning—Identifiability challenges and effective data collection strategies. In: Advances in Neural Information Processing Systems, Vol. 34. 2021. 4607−4618.
|
| [151] |
Li J, Vuong Q, Liu S, et al. Multi-task batch reinforcement learning with metric learning. In: Advances in Neural Information Processing Systems, Vol. 33. 2020. 6197−6210.
|
| [152] |
Wu SB, Fu QM, Chen JP, et al. Meta-inverse reinforcement learning method based on relative entropy. Computer Science, 2021, 48(9): 257-263(in Chinese with English abstract).
https://www.cnki.com.cn/Article/CJFDTOTAL-JSJA202109035.htm |
| [153] |
Li L, Yang R, Luo D. FOCAL: Efficient fully-offline meta-reinforcement learning via distance metric learning and behavior regularization. In: Proc. of the Int'l Conf. on Learning Representations. 2021.
|
| [154] |
Lin S, Wan J, Xu T, et al. Model-based offline meta-reinforcement learning with regularization. In: Proc. of the Int'l Conf. on Learning Representations. 2022.
|
| [155] |
Luo M, Balakrishna A, Thananjeyan B, et al. MESA: Offline meta-RL for safe adaptation and fault tolerance. In: Proc. of the Workshop at the Conf. on Neural Information Processing Systems. 2021.
|
| [156] |
Yuan H, Lu Z. Robust task representations for offline meta-reinforcement learning via contrastive learning. In: Proc. of the Int'l Conf. on Machine Learning. 2022. 25747−25759.
|
| [157] |
Nam T, Sun SH, Pertsch K, et al. Skill-based meta-reinforcement learning. In: Proc. of the Int'l Conf. on Learning Representations. 2022.
|
| [158] |
Mendonca R, Gupta A, Kralev R, et al. Guided meta-policy search. In: Advances in Neural Information Processing Systems, Vol. 32. 2019.
|
| [159] |
Zhou A, Jang E, Kappler D, et al. Watch, try, learn: Meta-learning from demonstrations and reward. In: Proc. of the Int'l Conf. on Learning Representations. 2020.
|
| [160] |
Rengarajan D, Chaudhary S, Kim J, et al. Enhanced meta reinforcement learning using demonstrations in sparse reward environments. In: Advances in Neural Information Processing Systems. 2022.
|
| [161] |
Bhutani V, Majumder A, Vankadari M, et al. Attentive one-shot meta-imitation learning from visual demonstration. In: Proc. of the IEEE Int'l Conf. on Robotics and Automation. IEEE, 2022. 8584−8590.
|
| [162] |
Caccia M, Mueller J, Kim T, et al. Task-agnostic continual reinforcement learning: In praise of a simple baseline. arXiv: 2205.14495, 2022.
|
| [163] |
Kessler S, Miłoś P, Parker-Holder J, et al. The surprising effectiveness of latent world models for continual reinforcement learning. arXiv: 2211.15944, 2022.
|
| [164] |
Iqbal S, Sha F. Actor-attention-critic for multi-agent reinforcement learning. In: Proc. of the Int'l Conf. on Machine Learning. 2019. 2961−2970.
|
| [165] |
Singh A, Jain T, Sukhbaatar S. Learning when to communicate at scale in multiagent cooperative and competitive tasks. In: Proc. of the Int'l Conf. on Learning Representations. 2019.
|
| [166] |
Koul A. Ma-Gym: Collection of Multi-Agent Environments based on Openai GYM. GitHub: GitHub Repository, 2019.
|
| [167] |
Papoudakis G, Christianos F, Schäfer L, et al. Benchmarking multi-agent deep reinforcement learning algorithms in cooperative tasks. In: Proc. of the Advances in Neural Information Processing Systems Track on Datasets and Benchmarks. 2021.
|
| [168] |
Li Q, Peng Z, Feng L, et al. MetaDrive: Composing diverse driving scenarios for generalizable reinforcement learning. IEEE Trans. on Pattern Analysis and Machine Intelligence, 2022.
|
| [169] |
Mordatch I, Abbeel P. Emergence of grounded compositional language in multi-agent populations. Proc. of the AAAI Conf. on Artificial Intelligence, 2018, 32(1): 1495-1502.
|
| [170] |
Samvelyan M, Rashid T, De Witt CS, et al. The StarCraft multi-agent challenge. In: Proc. of the Int'l Conf. on Autonomous Agents and MultiAgent Systems. 2019. 2186−2188.
|
| [171] |
Bergstrom CT, Godfrey-Smith P. On the evolution of behavioral heterogeneity in individuals and populations. Biology and Philosophy, 1998, 13(2): 205-231.
|
| [172] |
Brown N, Sandholm T. Superhuman AI for heads-up no-limit poker: Libratus beats top professionals. Science, 2018, 359(6374): 418-424.
|
| [173] |
Rosa M, Afanasjeva O, Andersson S, et al. BADGER: Learning to (learn [learning algorithms] through multi-agent communication). arXiv: 1912.01513. 2019.
|
| [174] |
Zintgraf L, Devlin S, Ciosek K, et al. Deep interactive bayesian reinforcement learning via meta-learning. In: Proc. of the Int'l Conf. on Autonomous Agents and MultiAgent Systems. 2021. 1712−1714.
|
| [175] |
Huang J, Huang W, Wu D, et al. Meta actor-critic framework for multi-agent reinforcement learning. In: Proc. of the Int'l Conf. on Artificial Intelligence and Pattern Recognition. Association for Computing Machinery, 2021. 636−643.
|
| [176] |
Schäfer L, Christianos F, Storkey A, et al. Learning task embeddings for teamwork adaptation in multi-agent reinforcement learning. 2022, 1−23.
|
| [177] |
Harris K, Anagnostides I, Farina G, et al. Meta-learning in games. arXiv: 2209.14110, 2022.
|
| [178] |
Muglich D, Zintgraf L, De Witt CS, et al. Generalized beliefs for cooperative AI. In: Proc. of the Int'l Conf. on Machine Learning. 2022. 16062−16082.
|
| [179] |
Yun WJ, Park J, Kim J. Quantum multi-agent meta reinforcement learning. Proc. of the AAAI Conf. on Artificial Intelligence, 2023, 37(9): 11087-11095.
|
| [180] |
James S, Wohlhart P, Kalakrishnan M, et al. Sim-to-real via sim-to-sim: Data-efficient robotic grasping via randomized-to-canonical adaptation networks. In: Proc. of the IEEE/CVF Conf. on Computer Vision and Pattern Recognition. 2019. 12627−12637.
|
| [181] |
Zhao Z, Nagabandi A, Rakelly K, et al. MELD: Meta-reinforcement learning from images via latent state models. In: Proc. of the Conf. on Robot Learning, Vol. 155. 2020. 1246−1261.
|
| [182] |
Yu T, Finn C, Xie A, et al. One-shot imitation from observing humans via domain-adaptive meta-learning. In: Proc. of the Int'l Conf. on Learning Representations—Workshop Track Proceedings. 2018.
|
| [183] |
Schoettler G, Nair A, Ojea JA, et al. Meta-reinforcement learning for robotic industrial insertion tasks. In: Proc. of the IEEE/RSJ Int'l Conf. on Intelligent Robots and Systems. 2020. 9728−9735.
|
| [184] |
Arndt K, Hazara M, Ghadirzadeh A, et al. Meta reinforcement learning for sim-to-real domain adaptation. In: Proc. of the IEEE Int'l Conf. on Robotics and Automation. 2020. 2725−2731.
|
| [185] |
Jang E, Irpan A, Khansari M, et al. BC-Z: Zero-shot task generalization with robotic imitation learning. In: Proc. of the Conf. on Robot Learning. 2022. 991−1002.
|
| [186] |
Harrison J, Sharma A, Calandra R, et al. Control adaptation via meta-learning dynamics. In: Proc. of the Workshop on Meta-Learning at the Conf. on Neural Information Processing Systems. 2018.
|
| [187] |
Ghadirzadeh A, Chen X, Poklukar P, et al. Bayesian meta-learning for few-shot policy adaptation across robotic platforms. In: Proc. of the IEEE/RSJ Int'l Conf. on Intelligent Robots and Systems. 2021(2): 1274−1280.
|
| [188] |
Tiboni G, Arndt K, Kyrki V. DROPO: Sim-to-real transfer with offline domain randomization. arXiv: 2201.08434, 2022.
|
| [189] |
Bing Z, Koch A, Yao X, et al. Meta-reinforcement learning via language instructions. In: Proc. of the 2023 IEEE Int'l Conf. on Robotics and Automation (ICRA). 2023. 5985−5991.
|
| [190] |
Ross S, Bagnell JA. Agnostic system identification for model-based reinforcement learning. In: Proc. of the Int'l Conf. on Machine Learning, Vol. 2. 2012. 1703−1710.
|
| [191] |
Yu W, Tan J, Liu CK, et al. Preparing for the unknown: learning a universal policy with online system identification. In: Proc. of the Robotics: Science and Systems, Vol. 13. 2017.
|
| [192] |
Liang J, Saxena S, Kroemer O. Learning active task-oriented exploration policies for bridging the sim-to-real gap. In: Proc. of the Robotics: Science and Systems. 2020.
|
| [193] |
Farid K, Sakr N. Few-shot system identification for reinforcement learning. In: Proc. of the Asia-Pacific Conf. on Intelligent Robot Systems. IEEE, 2021. 1−7.
|
| [194] |
Zhu Y, Mottaghi R, Kolve E, et al. Target-driven visual navigation in indoor scenes using deep reinforcement learning. In: Proc. of the IEEE Int'l Conf. on Robotics and Automation. 2017. 3357−3364.
|
| [195] |
Savva M, Kadian A, Maksymets O, et al. Habitat: A platform for embodied ai research. In: Proc. of the IEEE/CVF Int'l Conf. on Computer Vision. IEEE, 2019. 9339−9347.
|
| [196] |
Wortsman M, Ehsani K, Rastegari M, et al. Learning to learn how to learn: Self-adaptive visual navigation using meta-learning. In: Proc. of the IEEE/CVF Conf. on Computer Vision and Pattern Recognition. 2019. 6750−6759.
|
| [197] |
Yan L, Liu D, Song Y, et al. Multimodal aggregation approach for memory vision-voice indoor navigation with meta-learning. In: Proc. of the IEEE/RSJ Int'l Conf. on Intelligent Robots and Systems. 2020. 5847−5854.
|
| [198] |
Luo Q, Sorokin M, Ha S. A few shot adaptation of visual navigation skills to new observations using meta-learning. In: Proc. of the IEEE Int'l Conf. on Robotics and Automation. 2021. 13231−13237.
|
| [199] |
Hu Y, Chen M, Saad W, et al. Distributed multi-agent meta learning for trajectory design in wireless drone networks. IEEE Journal on Selected Areas in Communications, 2021, 39(10): 3177-3192.
|
| [200] |
Wen S, Wen Z, Zhang D, et al. A multi-robot path-planning algorithm for autonomous navigation using meta-reinforcement learning based on transfer learning. Applied Soft Computing, 2021, 110: 107605.
|
| [201] |
Yu Q, Luo L, Liu B, et al. Re-planning of quadrotors under disturbance based on meta reinforcement learning. Journal of Intelligent & Robotic Systems, 2023, 107(1): Article Number 13.
|
| [202] |
Nagabandi A, Clavera I, Liu S, et al. Learning to adapt in dynamic, real-world environments through meta-reinforcement learning. In: Proc. of the Int'l Conf. on Learning Representations. 2019.
|
| [203] |
Song X, Yang Y, Choromanski K, et al. Rapidly adaptable legged robots via evolutionary meta-learning. In: Proc. of the IEEE/RSJ Int'l Conf. on Intelligent Robots and Systems. 2020. 3769−3776.
|
| [204] |
Asayesh S, Chen M, Mehrandezh M, et al. Least-restrictive multi-agent collision avoidance via deep meta reinforcement learning and optimal control. In: Proc. of the Robot Intelligence Technology and Applications. 2023. 213−225.
|
| [205] |
Sun Y, Zhang Y. Conversational recommender system. In: Proc. of the Int'l ACM SIGIR Conf. on Research and Development in Information Retrieval. 2018. 235−244.
|
| [206] |
Lei W, He X, Miao Y, et al. Estimation-action-reflection: Towards deep interaction between conversational and recommender systems. In: Proc. of the Int'l Conf. on Web Search and Data Mining. 2020. 304−312.
|
| [207] |
Deng Y, Li Y, Sun F, et al. Unified conversational recommendation policy learning via graph-based reinforcement learning. In: Proc. of the Int'l ACM SIGIR Conf. on Research and Development in Information Retrieval. 2021. 1431−1441.
|
| [208] |
Zou L, Xia L, Gu Y, et al. Neural interactive collaborative filtering. In: Proc. of the Int'l ACM SIGIR Conf. on Research and Development in Information Retrieval. 2020. 749−758.
|
| [209] |
Chu Z, Wang H, Xiao Y, et al. Meta policy learning for cold-start conversational recommendation. In: Proc. of the ACM Int'l Conf. on Web Search and Data Mining. Association for Computing Machinery, 2023. 222−230.
|
| [17] |
李凡长, 刘洋, 吴鹏翔, 等. 元学习研究综述. 计算机学报, 2021, 44(2): 422-446.
https://www.cnki.com.cn/Article/CJFDTOTAL-JSJX202102012.htm |
| [18] |
谭晓阳, 张哲. 元强化学习综述. 南京航空航天大学学报, 2021, 53(5): 653-663.
https://www.cnki.com.cn/Article/CJFDTOTAL-NJHK202105001.htm |
| [21] |
赵春宇, 赖俊. 元强化学习综述. 计算机应用研究, 2023, 40(1): 1-10.
https://www.cnki.com.cn/Article/CJFDTOTAL-JSYJ202311001.htm |
| [82] |
陆嘉猷, 凌兴宏, 刘全, 等. 基于自适应调节策略熵的元强化学习算法. 计算机科学, 2021, 48(6): 168-174.
https://www.cnki.com.cn/Article/CJFDTOTAL-JSJA202106023.htm |
| [98] |
聂凯, 孟庆海. 基于层次情节性元强化学习的对抗行为评估. 指挥控制与仿真, 2021, 43(2): 65-71.
https://www.cnki.com.cn/Article/CJFDTOTAL-QBZH202102012.htm |
| [152] |
吴少波, 傅启明, 陈建平, 吴宏杰, 陆悠. 基于相对熵的元逆强化学习方法. 计算机科学, 2021, 48(9): 257-263.
https://www.cnki.com.cn/Article/CJFDTOTAL-JSJA202109035.htm |





