异质信息网络(也称为异质图)是由多种类型的实体与交互组成的网络结构, 常用于建模现实世界中实体间的复杂交互关系, 如知识图谱实体关系构建、社交网络多种角色建模等. 异质图表示学习通过将图中节点映射为低维且稠密的表示向量, 保留异质图中潜在的结构特性与语义信息, 对帮助人们理解实体复杂交互中的潜层结构关系与语义信息起到了关键的作用, 为不同的应用(如推荐系统^{[1, 2]}、异常用户检测^[3]、蛋白质作用预测^[4]、交通流量预测^[5]以及知识图谱信息表示^[6])提供了关键的特征信息支持. 图神经网络(graph neural networks, GNNs)作为一种有效的图表示学习工具, 因其强大的特征捕获能力, 近年来受到了众多研究人员的关注. 目前, 多数图神经网络(例如: GCN^[7]在谱域上定义了图的卷积操作, 通过归一化拉普拉斯矩阵与节点特征矩阵相乘, 实现节点表示的更新; GAT^[8]将注意力机制引入节点邻域特征的聚合过程, 在更新节点表示时区分了不同邻居的重要性), 其目标都是在同质图(只包含一种节点类型与一种边类型的图)上学习节点的表示, 无法在学习过程中区分异质图中多类型的节点与边所带来的不同影响, 因此不能直接将上述模型应用于异质图的表示学习中. 为了将图神经网络扩展至异质图, 用于抽取多类型复杂网络中的潜在特征, 例如知识图谱中的实体关联信息和社交网络中的多角色交互信息, 研究人员提出了异质图神经网络(heterogeneous graph neural network, HGNN), 并在异质图表示学习中取得了较优的表现, 为复杂信息系统提供了新的知识分析技术.

现有的HGNN模型, 如HAN^[9]、MAGNN^[10]以及HGT^[11], 使用了注意力机制加权的聚合目标节点的同类型内以及类型之间的邻域节点特征, 并将聚合后的特征作为目标节点更新的表征. 该类模型都遵从消息传递的方式(聚合节点的原始邻居或元路径邻居的表征)学习节点的表征. 在基于消息传递的HGNN模型中, 消息的传递是根据原始图中的交互关系执行的, 即原始图的结构(邻接矩阵)直接决定了一个节点该聚合哪些节点的表征作为自身的表征. 而从现实的复杂交互中构建的异质图, 通常会由于人为采集数据过程中的不规范操作或采集标准不统一等因素, 使得构建的异质图中存在与实际情况不相符的噪声连接并且缺失必要的连接.例如图 1所示的DBLP异质学术网络, 该异质学术网络包含了3位作者A₁、A₂与A₃, 3篇文章P₁、P₂与P₃以及文章所属的两种会议C₁和C₂. 图 1(a)展示了这些实体在现实中真实的连接关系, 而在数据采集的过程中, 由于数据构建错误导致构建的异质图中丢失了一部分交互(如A₃与P₂之间的交互)且添加了噪声交互(如P₃原本属于C₂, 但由于数据记录不当, 产生出了与C₁的交互). 此类存在拓扑结构错误的图数据可以视为受到了结构干扰或结构攻击, 使得神经网络聚合具有误导性的特征, 产生了错误的预测结果, 严重影响了图神经网络模型的学习性能^{[12, 13]}. 这样存在交互错误的异质图结构同样也会直接输入到现有的HGNN模型中, 作为其消息传递的范式, 引导节点特征的聚合. 而现有的HGNN既无法消除原始图中的噪音交互, 也无法补全图中的缺失交互, 使得模型学习的节点表征没有聚合正确的邻域特征, 进一步导致学习到的节点表征存在特征偏差, 严重影响了HGNN模型在下游任务(如节点分类、节点聚类)上的表现. 因此, 如何学习出优化的异质图结构, 抑制错误交互带来的不相关特征, 是提升HGNN模型性能表现的关键问题.

图结构学习(graph structure learning, GSL)旨在使用GNN模型学习节点表征的同时, 联合优化输入的原始图结构, 以解决因邻域交互错误导致的节点特征聚合偏差. 因其可以有效地剔除原始图中存在的噪声交互且补全原始图中的缺失交互, 解决了交互错误导致的消息传递偏差^{[14, 15]}, 近两年吸引了大量的关注. 目前, 多数图结构学习模型用于学习优化同质图的原始交互结构, 并以节点分类任务为目标, 将节点的标签作为监督信号, 引导图结构与GNN参数的更新优化. 这类同质图结构学习方法无法区分不同类型的节点与边所产生的不同影响, 将其应用于异质图结构优化会丢失异质图中的重要语义信息. 如何对异质图结构进行学习优化, 修正异质图中的结构错误, 成为了异质图神经网络中的热点研究. 此外, 上述方法都依托于节点分类任务来优化图结构, 即需要在节点标签信息的监督下联合优化图结构与模型参数的方式来进行图结构学习. 当面临的学习场景中没有可利用的节点标签时, 上述方法无法有效地优化图结构. 因此, 如何在不依赖节点标签的情况下实现异质图的图结构学习, 是异质图研究中急需解决的问题.

为了解决上述两个问题: (1) 现有大多数模型只能学习优化同质图结构, 针对异质图结构学习的模型少; (2) 仅有的异质图结构学习模型在学习时需要监督信息作为指引, 无法应用于无监督信息的场景之中. 本文提出了多视图对比增强的异质图结构学习(multi-view contrastive enhanced heterogeneous graph structure learning, MV-HGSL)方法, 实现了在不借助额外的监督信息(如节点的标签信息), 仅利用数据自身的特性, 学习完整的异质图结构.

● 首先, 为了保持异质图中由多种节点类型与边类型产生的异质信息, 该模型使用元路径, 将原始异质图转化为多个记录了元路径邻居的元路径图; 然后, 该模型使用多层感知机(multi-layer perception, MLP)生成节点的表征, 根据节点表征计算节点间的特征相似度, 生成相似度图, 使用节点的特征相似性来优化图结构;

● 其次, 为了在无监督信息的场景下实现图结构学习, MV-HGSL使用对比学习的方式, 将元路径图与相似度图视为两种不同的视图, 通过最大化两种视图之间的互信息, 令学习到的相似度图保持了异质图中的结构特性与语义信息;

● 最后, 通过将相似度图与原始图加权相加, 利用相似度图中的交互去抑制原始图中的噪声交互且补全缺失的交互的方式, 以实现图结构的优化.

此外, 由于模型在训练初期的表示能力较弱, 生成的相似度图中存在错误的相似度交互. 为解决该问题, 本文设计了一种渐进式图结构融合方法, 逐步增加相似度图与元路径图聚合的比例, 抑制因模型学习能力弱所产生的交互偏差. 在4种真实数据集上的实验结果表明本文提出的MV-HGSL是可行且有效的. 本文的贡献总结如下.

(1) 针对目前异质图中有存在噪声交互并且缺失部分交互, 使得异质图神经网络聚合的邻域特征存在偏差的问题, 本文提出了一种基于图对比学习优化异质图交互结构的图结构学习模型MV-HGSL. 针对异质图数据包含多种节点类型与复杂交互关系的特性, MV-HGSL使用元路径用于保持异质图中的结构与语义信息, 并通过自监督的图对比学习方式, 最大化对比学习视图之间的互信息, 实现了利用数据自身的特性引导异质图结构的优化, 令图结构学习模型摆脱了对节点标签信息的依赖, 能够在无监督信息的场景下进行异质图结构学习;

(2) 本文提出了一种渐进式的图结构融合方法, 随着模型的训练次数, 逐步地递增图结构加权相加时相似度图结构所占的比例, 渐进地优化输入的异质图结构, 解决了因神经网络模型在训练初期表示能力弱、生成的节点表征不能准确地表达对应节点的拓扑特征, 从而导致相似度图中包含错误交互的问题;

(3) 本文在4种真实异质图数据集上, 以节点分类和节点聚类为目标任务进行了丰富的实验. 同时选择了9种对比方法, 包括同质图神经网络模型、异质图神经网络模型、图结构学习模型以及异质图对比学习模型, 与本文提出的MV-HGSL进行比较, 以验证本文方法的可行性与有效性. 实验结果展示出了本文提出的MV-HGSL在节点分类以及节点聚类任务上的效果均优于对比方法. 在节点分类任务上, MV-HGSL与最优对比方法相比, 在Micro-F1与Macro-F1两个指标下取得了1%−1.5%的性能提升. 在节点聚类任务中, MV-HGSL同样取得了优于对比模型的聚类效果, 在NMI与ARI两个聚类指标下, 取得了1%−2%的聚类性能提升.

本文第1节介绍异质图神经网络以及图结构学习的相关方法和研究现状. 第2节介绍本文所应必备的基础知识, 包括异质图及其结构学习的定义. 第3节介绍本文构建的多视图对比学习增强的异质图结构学习模型. 第4节通过对比实验验证所提模型的有效性. 最后总结全文.

1 相关工作

为了清晰地介绍本文提出的MV-HGSL模型的目标任务, 本节将介绍与本文提出的MV-HGSL密切相关的3个研究领域, 分别为异质图神经网络、图结构学习以及图对比学习, 并对每个领域的研究现状进行总结.

1.1 异质图神经网络

为了将深层神经网络应用于异质图的表示学习, 研究人员提出了异质图神经网络(HGNN). 现有的异质图神经网络模型可分为人为设定元路径的模型与自动学习元路径的模型. 人为设定元路径的模型是通过专家的领域知识来设定元路径, 以捕获异质图中的特定高阶语义, 并通过聚合节点的元路径邻居更新节点的表征.例如, Wang等人^[9]提出的HAN使用层次注意机制来捕获节点和语义重要性. 该模型包括3个部分: 节点级注意力机制、语义级注意力机制和预测. 节点级注意力的目的是利用自注意力机制^[16]来学习某一元路径下邻居的重要性; 然后, 由于不同的元路径会捕获不同的异构语义信息, 因此, HAN设计了语义级注意力机制来计算多条元路径之间的重要性; 最后, 以节点分类为目标任务优化整个模型. Fu等人^[10]设计的HGNN模型MAGNN使用了与HAN相同的层次的注意力机制, 不同于HAN在节点级聚合时仅仅聚合了元路径末端节点的表征而忽略了路径当中的节点所携带的信息, MAGNN在聚合元路径邻居时不仅聚合了该路径末端节点的表征, 还聚合了路径当中所有节点的表征. Zhou等人^[17]提出的HAHE采用了与HAN相同的层次结构来学习节点的表征, 其不同在于, HAHE使用了cosine相似度而非注意力机制来计算元路径邻居的重要性.

虽然基于元路径的模型在异质图节点表示学习上取得了较优的效果, 但这些模型都依赖于人为设定的元路径, 而元路径设定又需要一定的领域知识. 如何摆脱元路径设定的束缚, 成为HGNN中的研究重点. 因此, 研究人员提出了许多自动学习元路径的模型. 例如, 由Yun等人^[18]提出的GTN提出了一种可自动学习元路径的异质图卷积模型. 该模型首先根据交互的类型, 将异质图划分为多个关系子图, 并使用多通道的卷积网络学习出每种关系的重要度; 然后组合每一层网络中重要度最高的关系, 作为学习到的元路径. Hong等人^[19]设计的HetSANN和Hu等人^[11]提出的HGT都将一种类型的节点作为目标类型来计算其周围其他类型节点的重要性, 通过这种方法, 不仅可以捕获不同类型节点之间的交互, 而且在聚合过程中为邻居分配不同的权值, 权重值最高的交互就作为当前网络层中最重要的交互. 组合多层网络中每一层最重要的交互, 就能捕获任意长度的元路径. HetSANN与HGT的不同之处在于: HGT在消息聚合的过程中使用与交互类型对应的对角矩阵来表示节点之间的交互所特有的特征; 而HetSANN则直接聚合了节点特征, 忽略了节点之间的交互特征. Yang等人^[20]设计的ie-HGCN提出了针对异质图的图卷积网络, 该方法使用点积注意力计算不同类型的邻居的重要度, 并根据重要度选取有用的元路径.

1.2 图结构学习

图结构学习的主要目的是, 在学习GNN参数的同时学习出干净的图结构. 现有的图结构学习方法可分为三大类, 分别是基于度量学习的模型、基于概率的模型与直接优化的模型. 基于度量的模型主要是利用节点间属性的相似度作为两点之间的边权重, 并根据权重大小更改每一个节点的邻域, 以此来更新图结构. 例如, Li等人^[14]提出的AGCN首先使用马氏距离衡量节点对在特征空间中的距离, 然后通过高斯核函数将距离映射为相似度并更新图结构. 由Jiang等人^[15]提出的GLCN则是使用了一层注意力网络计算节点之间的相似度, 并将相似度值作为节点之间的边权重来生成新的图结构. 由Yu等人^[21]提出的GRCN将节点的特征两两做内积, 作为节点间的相似度, 并将相似度作为优化的图结构中的边权重. Wang等人^[22]提出的图结构学习模型AM- GCN则是使用了cosine相似度来计算节点间的相似程度, 然后利用注意力机制, 将基于特征相似度生成的图与原始图聚合形成最终优化的图结构. Chen等人^[23]提出了一种迭代优化图结构的模型IDGL, IDGL在每一次迭代中都使用上一次迭代产生的节点表征生成特征图, 并将其与原始邻接矩阵组合形成优化的图结构, 再通过2层GCN学习到当前迭代中的节点表征, 直至生成的图结构满足设定的条件. Zhao等人^[24]提出的HGSL首次在异质图上进行图结构学习, 针对异质图中的每一种关系子图, 它首先使用加权的cosine相似度计算节点间的结构相似度与语义相似度, 并生成结构相似度图与语义相似度图; 然后通过注意力机制融合二者作为学习到的图结构, 并以节点分类任务为目标, 利用节点的标签信息引导图结构的优化. Liu等人^[25]提出的SUBLIME使用了图对比学习的方式学习图结构, 该方法首先计算节点之间的特征相似度, 并根据相似度大小生成相似度图; 然后使用图对比学习, 最大化学习图与原始图之间的互信息, 利用原始图数据所包含的结构与特征信息来优化学习的图结构.

基于概率的模型认为, 原始的图结构是从某一个概率分布中采样得到的. 这类模型通过计算出采样的概率分布, 并使用该分布来获得更优的图结构用于更新模型参数或是采样出多张图用来更新模型参数. 例如, Franceschi等人^[26]设计的LDS-GNN使用伯努利分布作为节点之间的边所服从的分布, 并将图结构学习看作是一个二元优化的问题; 然后使用超梯度近似求解该问题以获得采样服从的分布, 进而采样出干净的图结构. 由Zheng等人^[27]提出的NeuralSparse通过图的稀疏化任务来实现图结构的更新, 它使用深层神经网络计算节点间边的概率, 然后使用Gumbel-Softmax去近似采样的分布. Zhang等人^[28]设计了一种贝叶斯方法称为BGCN, 它将现有的图看作是从一个随机图簇中采样得到的样本, 从图簇中采集出N张图; 然后, BGCN利用蒙特卡罗dropout对模型中的可学习参数在每个生成的图上进行多次抽样, 并最大化节点表征的后验概率, 得到更新的节点表征用于半监督分类. BGCN的图结构学习是通过在多张采样图上进行参数更新而实现, 代替了生成图再进行参数学习的过程. 类似地, 由Elinas等人^[29]提出的vGCN也使用贝叶斯方法实现图结构学习, 与BGCN不同的是, 该方法使用变分推断去近似后验概率求解的过程.

直接优化的模型是将输入的原始邻接矩阵看作是待更新的特征矩阵, 通过GNN的层级更新, 将其与节点表征一同进行优化. 这类模型通常会在优化中加入对图结构的限制, 如保持图中的稀疏性、低秩性、特征平滑性等, 使学习得到的图结构符合真实图数据的特性. 例如, Yang等人^[30]提出的GCN-GT通过在损失函数中加入标签平滑性的限制, 利用神经网络模型直接优化图结构. Gao等人^[31]设计的GLNN在神经网络直接学习图结构的过程中, 保证了学习得到的图结构具有稀疏性与特征平滑性. Jin等人^[32]提出的Pro-GNN是在学习图结构的同时, 通过在目标优化函数中添加限制项, 从而保持了图结构的稀疏性、低秩性与特征平滑性. Wan等人^[33]提出的GSML则是通过图的稀疏化任务来实现图结构学习, 该模型将图的稀疏化定义为一个二元优化问题, 并使用元学习中的元梯度对该问题进行求解, 从而去除图结构中的噪声冗余交互.

1.3 图对比学习

对比学习是自监督学习中的一种重要技术, 是指对输入的原始数据进行增广变换, 生成在多种视角下的不同的数据形式, 通过对比不同视图之间的差异, 来捕获数据自身的深层信息. 近年来, 在计算机视觉^{[34, 35]}与自然语言处理^{[36, 37]}上取得了优异的性能表现. 由于图结构数据在现实生活中普遍存在, 众多研究人员致力于将对比学习用于图数据特征的挖掘, 逐渐成为了图机器学习中的研究热点. 图对比学习模型大致可分为3种类型: 节点级对比、全局对比以及节点-全局对比. Zhu等人^[38]提出了一种节点级的图对比方法GRACE, 该方法使用两种数据增广方式, 分别是边移除与特征掩盖, 对图数据进行增广变换, 并使用同一个图编码器在两种视图上学习节点的表示. 最后定义节点级的损失函数, 使用温度系数的交叉熵损失来衡量正负样本之间的差距. Peng等人^[39]提出了节点级图对比方法GMI, 将视图之间的互信息扩展为从节点特征与拓扑结构两方面同时计算. 在GMI中, 每一个节点都将作为中心节点, 计算该中心节点与该节点的邻域节点在特征维度与结构维度的互信息, 并最大化互信息, 实现多视图下的对比学习, 抽取图数据的特征与拓扑信息. Velickovic等人^[40]提出的DGI模型通过对比图中节点的局部邻域结构与高阶邻域结构, 实现了节点-全局的对比学习框架, 并使用最大化对比互信息的方式构造对比损失用于优化网络. You等人^[41]提出了全局范围对比的图对比模型GraphCL, 其定义了4种类型的数据增广方式, 分别是节点失活、边扰动、特征掩盖以及子图划分, 以此获得更加丰富的增广视图, 充分挖掘了图数据中隐层的模式, 并通过对比最大化原始图与增广视图之间的互信息来学习图的表示向量. Zeng等人^[42]提出的图对比学习模型CSSL遵循与GraphCL相似的对比方式, 不同之处在于数据增广的方式, 除了删除节点外, CSSL还将节点插入视为一种重要的增广策略. Park等人^[43]将DGI的思想扩展到多关系图, 提出了针对多关系图的对比学习模型DMGI. 对于每一种连接关系, DMGI首先使用图神经网络学习该关系下的节点表示, 并将节点表示聚合成该关系图的表示; 随后, 在节点表示与图表示之间执行对比学习. Ren等人^[44]提出的HDGI模型将DGI的对比方式拓展至异质图的表示学习当中, 利用双层的注意力机制学习节点的局部邻域表示, 并与全局的节点表示进行对比优化.

现有的图对比学习都是通过对图数据进行数据增广生成同一图数据的多种视图, 并将最大化不同视图之间的互信息作为优化目标, 利用了图数据自身蕴含的潜在特性来学习包含了邻域的结构信息和属性信息的节点表征或图表征. 由于图对比学习不依赖监督信号的指引, 其相比于监督学习的图神经网络模型具有更广泛的应用场景.

2 基础知识

为了清晰且形式化地表述本文提出的MV-HGSL模型, 本节首先给出异质图的形式化定义以及异质图的关系子图、网络模式和元路径的基本概念的介绍. 本节最后给出形式化的异质图结构学习的定义, 用于描述异质图结构学习的目标.

定义1(异质图). 异质图G=(V, E, T, R, φ, ϕ)是由多种类型的节点和边组成的图, 其中, V是节点集合; E是边集合; T与R分别表示节点类型与边类型的集合, 且|T|+|R|≥2; φ表示节点类别映射函数φ: V→T; ϕ表示边类别映射函数ϕ: E→R. 令V_t⊆V表示类型为t的节点集合, 则节点特征矩阵可表示为集合:

$ X = \{ {\boldsymbol{X}_t}, t \in T\} , {\text{ }}{\boldsymbol{X}_t} \in {\mathbb{R}^{|{V_t}| \times {d_t}}}, $

其中, d_t为t类型节点特征的维度.

定义2(关系子图). 给定异质图G=(V, E, T, R, φ, ϕ), 其关系子图$ {G_r} = ({V_{{t_{head(r)}}}}, {V_{{t_{tail(r)}}}}, {E_r}) $定义为只包含了边类型为r的子图, 其中, $ {V_{{t_{head(r)}}}} $与$ {V_{{t_{tail(r)}}}} $分别表示子图中由关系r确定的头节点与尾节点的集合, E_r表示所有类型为r的边的集合. 关系子图G_r的邻接矩阵记为${\boldsymbol{A}_r} \in {\mathbb{R}^{|{V_{{t_{head(r)}}}}| \times |{V_{{t_{tail(r)}}}}|}}, $当节点${v_i} \in {V_{{t_{head(r)}}}}$与节点${v_j} \in {V_{{t_{tail(r)}}}}$之间有边时, A_r[i, j]=1; 否则, A_r[i, j]=0. 从而异质图的邻接矩阵可以使用所有关系子图的邻接矩阵组成的集合A加以表示, 即A={A_r, r∈R}.

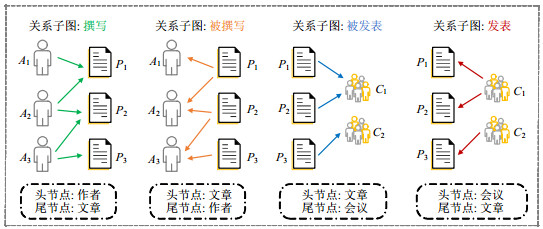
以图 1中展示的DBLP异质网络为例, 抽取该网络中所有的关系子图, 结果如图 2所示. 该异质网络中共包含4种类型的交互, 分别是撰写(write)、被撰写(written)、发表(publish)以及被发表(published). 网络中的每一种交互都有固定的头节点类型与尾节点类型, 例如: 当交互类型为撰写时, 其头节点为作者, 尾节点为文章; 而当交互为被撰写时, 其头节点为文章, 尾节点为作者.

定义3(网络模式). 给定异质图G=(V, E, T, R, φ, ϕ), 图G的网络模式定义为一个有向图S_G=(T, R), 其节点集合为T, 边集合为R网络模式可看作是异质图G的元模式, 其中的节点与边对应着异质图中的节点类型与边类型. 网络模式记录了异质图中不同类型节点之间的每一种交互, 是异质图的高阶抽象表示.

以图 1所示的DBLP异质学术网络为例, 图 3(b)给出了该DBLP异质网络的网络模式, 由3个节点与4条边组成, 对应于该网络中3种类型的节点和4种类型的边. 通过图 3(b)所示的网络模式, 可知该DBLP异质网络中包含了3种节点与4种交互. 其中, 图 3(a)表示DBLP异质学术网络; 图 3(b)表示该异质学术网络的网络模式, 其中节点对应于异质图中的节点类型, 边对应于异质图中的边类型; 图 3(c)表示在该学术异质网络上定义的两种元路径: APA与APCPA.

定义4(元路径). 元路径p是定义在网络模式S_G上的一条路径, 通常用于描述节点之间的高阶语义关系, 记为$ p = {t_1}\xrightarrow{{{r_1}}}{t_2}\xrightarrow{{{r_2}}}...\xrightarrow{{{r_k}}}{t_{k + 1}}, $可简写为t₁t₂…t_k+1, 其中, k表示元路径p的长度.

元路径p描述了不同类型的节点t₁与t_k+1之间的高阶语义关系. 例如, 图 3(c)给出了在DBLP异质网络上定义的两条元路径, APA与APCPA. 基于元路径APA的邻居表示了具有合著关系的作者, 而基于元路径APCPA的邻居则表示了两位作者有文章发表在同一个会议上.

定义5(元路径的生成). 给定异质图的关系子图, 元路径图可以通过连乘关系子图的邻接矩阵来获得, 计算过程如公式(1)所示:

$ \boldsymbol{A}_p=\boldsymbol{A}_1 \boldsymbol{A}_2 \ldots \boldsymbol{A}_r, r \in R $

(1)

其中, ${\boldsymbol{A}_p} \in {\mathbb{R}^{|{V_{{t_{sta(p)}}}}| \times |{V_{{t_{end(p)}}}}|}}$表示基于元路径p的邻接矩阵, t_sta(p)表示元路径p开始的节点的类型, t_end(p)表示该路径结束的节点的类型. 例如: 图 3(c)所示生成的元路径APA与APCPA, 其头节点类型都为作者(author), 尾节点类型同样为作者(author). 通过构建元路径邻接矩阵, 本文保持了异质图中的复杂高阶异质信息. 例如: 元路径APA可以表达作者之间的合著关系, 可由关系子图的邻接矩阵A_write(A-P)与A_written(P-A)相乘获得, 并生成元路径APA的邻接矩阵A_APA.

此外, 为了保证能够全面捕获异质图中多样的高阶语义信息, 本文将定义多条元路径并记为集合P= (p₁, p₂, …, p_M), 其中, P是元路径集合, M为定义的元路径数量, 则元路径邻接矩阵可以记为集合:

$ {A_P} = \{ {\boldsymbol{A}_{{p_1}}}, {\boldsymbol{A}_{{p_2}}}, ..., {\boldsymbol{A}_{{p_M}}}\} . $

定义6(异质图结构学习). 给定异质图G、元路径邻接矩阵A_P以及节点特征X, 异质图结构学习的目的是获取去除了冗余交互并且补足了缺失交互的元路径邻接矩阵$A_P^*$, 并将该邻接矩阵作为下游任务的输入.

3 多视图对比增强的异质图结构学习

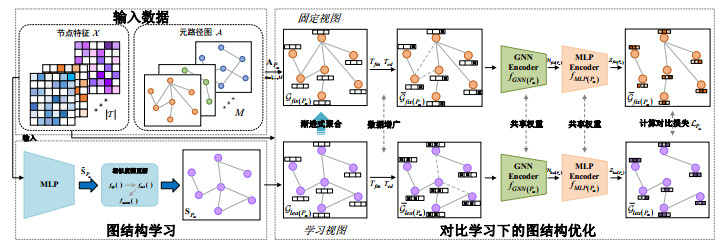
针对先前提出的两个问题, 本文提出了MV-HGSL, 该方法由4个步骤组成, 分别是相似度图计算、相似度图更新、多视图对比下的图结构优化以及渐进式图结构更新. 图 4所示的模型框架图展示了MV-HGSL学习图结构的步骤.

(1) 为了利用节点特征优化图结构, MV-HGSL利用MLP生成包含了结构与特征信息的节点表征, 而后计算节点表征之间的cosine相似度, 并将相似度值作为交互权重生成相似度图;

(2) 由于计算了所有节点对之间的特征相似度, 生成的相似度图为全连接图, 不符合实际的交互情形(稀疏且边权重非负). 因此, 设置相似度图更新步骤, 将生成的相似度图稀疏化、非负化并归一化, 使其符合真实图数据的特性. 其中, 归一化的目的是方便在对比学习中利用GCN学习节点表征;

(3) 为实现在无标签信息的监督下优化相似度图, MV-HGSL利用多视图对比学习, 将相似度图与元路径图看作两种不同的视图, 分别称为“学习视图”与“固定视图”, 并以最大化两种视图之间的互信息的方式, 令相似度图保留元路径图中的关键拓扑信息;

(4) 为了利用生成的相似度图结构优化原有的图结构, MV-HGSL通过将相似度图与原始图加权相加的方式, 利用相似度图中的交互去抑制原始图中的噪声交互且补充缺失交互. 此外, 为了减少训练初始时模型生成的交互错误, MV-HGSL设计了随训练可变融合比例的渐进式图结构融合方法, 将相似度图以融合比例递增的方式与元路径图相加, 从而获得优化的异质图结构.

下文将详细介绍MV-HGSL的每一个步骤.

3.1 相似度图计算

一般地, 图数据中具有连接关系的两个节点, 其特征也会相似^{[24, 32]}, 即节点之间的特征相似度可以看作是该节点对之间存在交互的可能性大小. 因此, 节点之间的特征相似度可以自然而然地用于判断当前节点之间的交互是否合理. MV-HGSL的第1个步骤: 相似度图计算, 即使用cosine相似度计算两两节点之间的特征相似度, 并将相似度值作为交互权重, 构建相似度图. 该图结构记录了根据节点特征相似性构建的交互关系, 将该图与元路径图融合, 即实现了利用节点特征之间的关系来优化元路径图的拓扑结构.

相似度图计算首先利用MLP学习节点的表征, 并使用cosine相似度函数计算节点表征之间的相似度. 然后, 将表征相似度作为节点之间的交互权重, 生成相似度图. 由于异质图中的节点具有多种类型, 不同类型节点的特征属于不同的特征空间, 为了计算节点间的特征相似度, 需要将不同类型节点的特征映射至同一特征空间中, 节点特征的映射过程如公式(2)所示:

$ \boldsymbol{H}_t^{(0)} = {\boldsymbol{X}_t}{\boldsymbol{W}_t}, {\text{ }}t \in T $

(2)

其中, ${\boldsymbol{W}_t} \in {\mathbb{R}^{{d_t} \times d}}$是节点类型特定的映射矩阵, d是所有类型节点映射后的特征维度, $ \boldsymbol{H}_t^{(0)} $为经过映射后的类型为t的节点特征. 本文使用L层MLP用于学习节点的表征向量, MLP的输入为经过映射后的节点特征$ \boldsymbol{H}_t^{(0)}$, 则第l层网络学习节点表征的过程如公式(3)所示:

$ \boldsymbol{H}_t^{(l)} = \sigma (\boldsymbol{H}_t^{(l - 1)}{\boldsymbol{W}^{(l)}}) $

(3)

其中, $\boldsymbol{W}^{(l)} \in \mathbb{R}^{d \times d}$是第l层网络的参数矩阵. 由于不同类型的节点特征已经映射到了同一特征空间当中, 所以对每一种类型的节点的特征使用相同的参数矩阵. σ为非线性激活函数, 本文使用ReLU函数作为MLP中的非线性激活函数.

节点的原始特征经过映射和MLP更新之后, 获得包含丰富语义信息的节点表征. 然后, 本文使用cosine相似度计算节点间的特征相似度, 并生成相似度图. 给定元路径p_m, m=1, 2, …, M, 相似度图计算过程如公式(4)所示:

$ {\tilde {\boldsymbol{S}}_{{p_m}}} = \cos (\boldsymbol{H}_{{t_{sta({p_m})}}}^{(l)}, \boldsymbol{H}_{{t_{end({p_m})}}}^{(l)}) $

(4)

其中, cos为cosine相似度计算函数, $ \boldsymbol{H}_{{t_{sta({p_m})}}}^{(l)} $与$ \boldsymbol{H}_{{t_{end({p_m})}}}^{(l)} $为元路径p_m的两端的节点所对应的特征, $ {\tilde{\boldsymbol{S}}_{{p_m}}} $表示生成的与元路径邻接矩阵${\boldsymbol{A}_{{p_m}}}$相同维度的相似度图. 针对预先设定的所有元路径P=(p₁, p₂, …, p_M), 都使用相似度计算函数分别学习出每条元路径对应的相似度图, 并记为$ \tilde S = \{ {\tilde {\boldsymbol{S}}_{{p_1}}}, {\tilde {\boldsymbol{S}}_{{p_2}}}, ..., {\tilde {\boldsymbol{S}}_{{p_m}}}\} . $

3.2 相似度图更新

在生成相似度图的过程中, 由于MV-HGSL计算了所有节点对之间的特征相似度, 并将其作为边权重, 使得相似度图为全连接图. 而真实图数据中的交互通常是稀疏的, 相似度图的交互分布不符合现实图数据交互分布. 因此, 本文需要去除全连接的相似度图中过多的冗余交互. 此外, 由于cosine相似度的取值范围为[−1, 1], 使得图中的边权重存在负值, 而实际中的图数据边权重通常不存在负值, 与实际中图的边权重取值不符. 为了解决上述问题, MV-HGSL设置了相似度图更新步骤, 使相似度图符合真实图结构的特性(稀疏、对称且边权重非负).

相似度图更新的目标是: 将生成的相似度图$ \tilde S $变为稀疏的、非负的和归一化的图结构S. 在相似度图更新中共有3个处理步骤, 分别是稀疏化、非负化以及归一化, 依次对$ \tilde S $进行处理, 令其符合真实图数据的特性.

(1) 稀疏化

为了将全连接的相似度图$ \tilde S $稀疏化, 去除大量的冗余交互信息, 降低后续模型计算的代价, MV-HGSL使用KNN图实现对相似度图的稀疏化. 对于每一个节点, 只保留k个与其最相似的邻居, 将与其余的交互权重设置为0. 对于每一条元路径下的相似度图$ {\tilde{\boldsymbol{S}}_{{p_m}}}, $稀疏化的过程如公式(5)所示:

$ \tilde{\boldsymbol{S}}_{i j\left(p_m\right)}^{(s p)}=f_{s p}\left(\tilde{\boldsymbol{S}}_{i j\left(p_m\right)}\right)= \begin{cases}\tilde{\boldsymbol{S}}_{i j\left(p_m\right)}, & \tilde{\boldsymbol{S}}_{i j\left(p_m\right)} \in {top}-k\left(\tilde{\boldsymbol{S}}_{i\left(p_m\right)}\right) \\ 0, & \tilde{\boldsymbol{S}}_{i j\left(p_m\right)} \notin {top}-k\left(\tilde{\boldsymbol{S}}_{i\left(p_m\right)}\right)\end{cases} $

(5)

其中, top-k是k最近邻居选择函数, 用于选择行向量中k个最大值; $ {\tilde {\boldsymbol{S}}_{i({p_m})}} $是相似度图邻接矩阵的第i行; f_sp表示稀疏化函数. 在经过稀疏化操作后, MV-HGSL获得了只保留k个最相似邻居的相似度图:

$ \tilde{S}^{(s p)}=\left\{\tilde{\boldsymbol{S}}_{p_1}^{(s p)}, \tilde{\boldsymbol{S}}_{p_2}^{(s p)}, \ldots, \tilde{\boldsymbol{S}}_{p_M}^{(s p)}\right\} . $

(2) 非负化

在生成了稀疏化的相似度图$ \tilde{S}^{(s p)}=\left\{\tilde{\boldsymbol{S}}_{p_1}^{(s p)}, \tilde{\boldsymbol{S}}_{p_2}^{(s p)}, \ldots, \tilde{\boldsymbol{S}}_{p_M}^{(s p)}\right\} $后, 为了去除图中权重为负值的交互, MV-HGSL使用激活函数将相似度图中的边权重非负化, 以保证边权重值在非负的取值范围内. 对于每一条元路径下的相似度图$ \tilde{\boldsymbol{S}}_{{p_m}}^{(sp)}, $其非负化过程如公式(6)所示:

$ \tilde{\boldsymbol{S}}_{p_m}^{(a c t)}=f_{a c t}\left(\tilde{\boldsymbol{S}}_{p_m}^{(s p)}\right)={ReLU}\left(\tilde{\boldsymbol{S}}_{p_m}^{(s p)}\right) $

(6)

其中, f_act表示非负化函数. MV-HGSL使用ReLU激活函数用于非负化相似度图中的边权重, 得到经过稀疏化与非负化的相似度图$ {\tilde S^{(act)}} = \{ \tilde {\boldsymbol{S}}_{{p_1}}^{(act)}, \tilde {\boldsymbol{S}}_{{p_2}}^{(act)}, ..., \tilde {\boldsymbol{S}}_{{p_M}}^{(act)}\} . $

(3) 归一化

为了将相似度图中的边权重取值置于[0, 1]范围之间, MV-HGSL对每一条元路径下的相似度图$ \tilde {\boldsymbol{S}}_{{p_m}}^{(act)} $执行

归一化操作, 计算过程如公式(7)所示:

$ \boldsymbol{S}_{p_m}=f_{ {norm }}\left(\tilde{\boldsymbol{S}}_{p_m}^{(a c t)}\right)=\left(\tilde{\boldsymbol{D}}_{p_m}^{(a c t)}\right)^{-\frac{1}{2}} \tilde{\boldsymbol{S}}_{p_m}^{(a c t)}\left(\tilde{\boldsymbol{D}}_{p_m}^{(a c t)}\right)^{-\frac{1}{2}} $

(7)

其中, $ \tilde {\boldsymbol{D}}_{{p_m}}^{(act)} $为相似度图$ \tilde {\boldsymbol{S}}_{{p_m}}^{(act)} $的节点度矩阵, 其形式为对角矩阵, 对角线元素为对应节点的度. 输出的$ {{\boldsymbol{S}}_{{p_m}}} $为相似度图的归一化拉普拉斯矩阵.

最终, 相似度图更新输出了经过稀疏化、非负化以及归一化的相似度图$ S = \{ {{\boldsymbol{S}}_{{p_1}}}, {{\boldsymbol{S}}_{{p_2}}}, ..., {{\boldsymbol{S}}_{{p_M}}}\} , $用于在后续步骤中学习节点表征并优化原始图结构. 此时在得到的相似度图中, 每个节点具有相同的度, 与现实世界中互联的实体的度分布存在差异. 本文通过后续迭代地对比学习训练, 令生成的相似度图逐渐靠近真实的图结构, 即节点之间关键的交互会被保留放大, 非关键交互则会被抑制, 通过模型的迭代优化体现出不同节点的度差异, 消除与真实图结构之间的差异, 使其能够保留原始图中的重要拓扑结构特性(如节点度的分布).

3.3 多视图对比下的图结构优化

通过相似度图更新, MV-HGSL获得了稀疏、非负且归一化的相似度图结构. 为了在不使用节点标签的情况下实现对学习得到的相似度图进行优化, MV-HGSL使用对比学习的方式, 利用数据自身的特性作为监督信号, 从而摆脱对节点标签的依赖. 如何从图数据自身中挖掘监督信号, 成为本文实现在无标签情形下学习图结构中的重点问题. 在图对比学习中, 通过设置多种形式的数据增广, 对原有数据进行变换, 生成了每一种视图下掩盖了不同信息的图数据, 并构建正负样本作为引导信息, 指引模型的优化学习. 本文选择最大化不同视图之间的互信息作为监督信号, 通过最大化元路径图与相似度图间的互信息, 将不同视图下同一节点的表征作为正样本, 不同节点的表征作为负样本, 用于指引图结构的学习与优化.

3.3.1 对比学习视图设置

多视图对比学习首先需要构建可对比的视图. 在本文中, MV-HGSL将输入的元路径图与生成的相似度图作为两种不同的视图进行对比学习. MV-HGSL将相似度图构建的视图称为学习视图, 将元路径图构建的视图称为固定视图. 选择将相似度图与元路径图设置为对比视图进行对比的原因是: 通过最大化两者之间的互信息, 可令相似度图最大程度地保留元路径图中的高阶异质语义信息.

(1) 学习视图: 学习视图由处理过后的相似度图$ S = \{ {\boldsymbol{S}_{{p_1}}}, {\boldsymbol{S}_{{p_2}}}, ..., {\boldsymbol{S}_{{p_M}}}\} $与节点特征X={X_t, t∈T}组成. 对于每一条元路径下的相似度图, 都构建其对应的学习视图, 记为${G_{lea({p_m})}} = ({\boldsymbol{S}_{{p_m}}}, X);$

(2) 固定视图: 固定视图则由元路径图${A_P} = \{ {\boldsymbol{A}_{{p_1}}}, {\boldsymbol{A}_{{p_2}}}, ..., {\boldsymbol{A}_{{p_M}}}\} $与节点特征X={X_t, t∈T}组成, 用于在对比学习中为相似度图提供异质图的高阶语义信息. 对每一条元路径下的元路径图, 都构建其对应的固定视图, 记为${G_{fix({p_m})}} = ({\boldsymbol{A}_{{p_m}}}, X).$

3.3.2 数据增广

为了从原始图数据生成与原数据具有差异的增广数据用于对比学习, 本文选择了两种在图对比学习中常用的数据增广方式: 特征掩码和边丢弃^[45], 两者分别从特征与结构的角度来生成不同的增广数据.

(1) 基于特征掩盖的数据增广

为了给节点特征添加扰动, 本文随机选择节点特征的一部分维度, 使用掩码向量将其掩盖(将值设置为0). 由于异质图中不同类型的节点具有不同类型的特征维度, 因此, 针对不同维度的特征, MV-HGSL使用了类型特定的特征掩码向量. 给定节点特征X={X_t, t∈T}, 对于每一类的特征X_t, 都以p^(f)的概率掩盖其特征维度, 生成其对应的特征掩码向量$\boldsymbol{m}_t^{(x)} \in {\mathbb{R}^{1 \times {d_t}}}, $特征掩盖过程如公式(8)所示:

$ \overline{\boldsymbol{X}}_t={Tr}_{f m}\left(\boldsymbol{X}_t\right)=\left[\boldsymbol{x}_{t 1} \odot \boldsymbol{m}_t^{(x)}, \boldsymbol{x}_{t 2} \odot \boldsymbol{m}_t^{(x)}, \ldots, \boldsymbol{x}_{t\left|V_t\right|} \odot \boldsymbol{m}_t^{(x)}\right] $

(8)

其中, x_ti, i=1, 2, …, |V_t|为第i个t类型的节点的特征, $\odot$表示哈达玛乘积, Tr_fm(⋅)是特征掩码函数, $ {\bar {\boldsymbol{X}}_t} $是数据增广后的特征矩阵.

(2) 基于边掩盖的数据增广

为了产生图结构上的扰动, 本文选择丢弃图结构中的交互. 具体来说, 对于每一条元路径下的元路径图与相似度图, 本文生成与元路径图和相似度图相同维度的图结构掩码矩阵${\boldsymbol{K}_{{p_m}}} \in {\mathbb{R}^{|{V_{{t_{sta({p_m})}}}}| \times |{V_{{t_{end({p_m})}}}}|}}, $以p^(a)的概率丢弃两种视图中的边. 对于每一条元路径下的边丢弃过程如公式(9)所示:

$ \overline{\boldsymbol{A}}_{p_m}=T r_{e d}\left(\boldsymbol{A}_{p_m}\right)=\boldsymbol{A}_{p_m} \odot \boldsymbol{K}_{p_m}, \overline{\boldsymbol{S}}_{p_m}=T r_{e d}\left(\boldsymbol{S}_{p_m}\right)=\boldsymbol{S}_{p_m} \odot \boldsymbol{K}_{p_m} $

(9)

其中, $\odot$表示哈达玛乘积, Tr_ed(⋅)是边丢弃函数, $ {\bar {\boldsymbol{A}}_{{p_m}}} $与$ {\bar {\boldsymbol{S}}_{{p_m}}} $是数据增广后的邻接矩阵.

本文对设置的两种视图都执行上述的特征掩盖与边丢弃增广操作, 生成经过节点特征与交互结构变换的图数据, 其过程如公式(10)所示:

$ {\bar G_{lea({p_m})}} = (T{r_{fm}}(X), T{r_{ed}}({\boldsymbol{S}_{{p_m}}})), {\text{ }}{\bar G_{fix({p_m})}} = (T{r_{fm}}(X), T{r_{ed}}({\boldsymbol{A}_{{p_m}}})) $

(10)

其中, $ {\bar G_{lea({p_m})}} $与$ {\bar G_{fix({p_m})}} $分别是在元路径p_m下经过数据增广后的学习视图和固定视图.

3.3.3 基于多视图对比学习的图结构优化

获得了经过数据增广的两种视图后, 本文执行节点级的图对比学习, 通过最大化两种视图节点表征之间的互信息来优化生成的相似度图. 由于本文从节点表征的角度计算对比损失, 因此在多视图对比下的图结构优化当中, 首先需要学习节点的表示, 进而构造对比损失函数以优化获得的相似度图.

(1) 节点级表示学习

本文使用GNN模型用于在增广后的两个视图上学习节点的表示. 对于在元路径p_m下的两种视图$ {\bar G_{lea({p_m})}} $与$ {\bar G_{fix({p_m})}}, $其节点表示学习过程如公式(11)所示:

$ {H_{lea({p_m})}} = {f_{GNN({p_m})}}({\bar G_{lea({p_m})}}, X), {\text{ }}{H_{fix({p_m})}} = {f_{GNN({p_m})}}({\bar G_{fix({p_m})}}, X) $

(11)

其中, $ {f_{GNN({p_m})}} $是学习节点表示的GNN模型. 集合${H_{lea({p_m})}} = \{ {\boldsymbol{H}_{lea(t)({p_m})}}, t \in T\} $与${H_{fix({p_m})}} = \{ {\boldsymbol{H}_{fix(t)({p_m})}}, t \in T\} $分别表示在两种视图$ {\bar G_{lea({p_m})}} $与$ {\bar G_{fix({p_m})}} $下学习到的节点表示, 其中, ${\boldsymbol{H}_{lea(t)({p_m})}}$与${\boldsymbol{H}_{fix(t)({p_m})}}$分别表示在两种视图上学习到的第t种类型节点的特征矩阵. 在本文中, MV-HGSL使用了GCN^[7]作为GNN模型以用于学习节点表示.

通过GCN获得节点表征之后, 本文使用MLP将学习得到的两种视图下的节点表示映射至同一特征空间中, 以用于计算节点级的对比损失. 对于在元路径p_m下学习到的两种节点表示, 其MLP映射过程如公式(12)所示:

$ {Z_{lea({p_m})}} = {f_{MLP({p_m})}}({H_{lea({p_m})}}), {\text{ }}{Z_{fix({p_m})}} = {f_{MLP({p_m})}}({H_{fix({p_m})}}) $

(12)

其中, $ {f_{MLP({p_m})}} $是节点表征的映射函数. 集合${Z_{lea({p_m})}} = \{ {\boldsymbol{Z}_{lea(t)({p_m})}}, t \in T\} $与${Z_{fix({p_m})}} = \{ {\boldsymbol{Z}_{fix(t)({p_m})}}, t \in T\} $分别表示经过MLP映射后的两种视图下的节点表征.

(2) 构建对比损失函数

本文使用temperature-scaled cross-entropy loss^{[46, 47]}函数作为不同视图之间的对比损失, 用于衡量两个视图间的互信息大小. 通过最大化视图间的互信息, 相似度图就可以保持元路径图中的异质高阶语义交互, 并优化整个MV-HGSL模型. 在元路径p_m下的对比损失计算如公式(13)所示:

$ \left\{ \begin{gathered} {L_{{p_m}}} = \frac{1}{{2(|{V_{{t_{sta({p_m})}}}}| + |{V_{{t_{end({p_m})}}}}|)}}\sum\limits_{i = 1}^{|{V_{{t_{sta({p_m})}}}}| + |{V_{{t_{end({p_m})}}}}|} {[l({\boldsymbol{z}_{lea, i({p_m})}}, {\boldsymbol{z}_{fix, i({p_m})}}) + l({\boldsymbol{z}_{fix, i({p_m})}}, {\boldsymbol{z}_{lea, i({p_m})}})]} \\ l({\boldsymbol{z}_{lea, i({p_m})}}, {\boldsymbol{z}_{fix, i({p_m})}}) = \log \frac{{{{\text{e}}^{\cos ({\boldsymbol{z}_{lea, i({p_m})}}, {\boldsymbol{z}_{fix, i({p_m})}})/tem}}}}{{\sum\limits_{k = 1}^{|{V_{{t_{sta({p_m})}}}}| + |{V_{{t_{end({p_m})}}}}|} {{{\text{e}}^{\cos ({\boldsymbol{z}_{lea, i({p_m})}}, {\boldsymbol{z}_{fix, k({p_m})}})/tem}}} }} \\ \end{gathered} \right. $

(13)

其中, cos表示cosine相似度计算函数; tem是温度控制参数, 用于缩放相似度值; $ {\boldsymbol{z}_{lea, i({p_m})}} $与$ {\boldsymbol{z}_{fix, i({p_m})}} $分别表示节点i在学习视图以及固定视图上的表征向量.

通过最大化公式(13)中的对比损失函数, 使得同一节点的表征在不同视图上的差距越小, 不同节点的表征在不同视图上的差距就越大, 保持了图数据自身的潜在结构信息与特征信息, 并以此数据特有的信息为监督信号, 指引图结构学习的优化方向.

3.3.4 渐进式图结构融合

本文通过将相似度图与元路径图进行加权融合, 即通过迭代地将两种图结构加权相加, 使得对下游任务重要的交互的权重越来越大, 冗余交互的权重越来越小, 实现了将学习得到的相似度图用于优化原始图结构. 此外, 在模型训练开始时, 其信息抽取能力较弱, 使得学习得到的相似度图会包含一定的错误交互. 例如在SUBLIME^[25]中, 在训练开始时, 每c次都以固定的比例将相似度图融合进原始图结构, 而初始训练时, 神经网络对数据的信息抽取能力不足, 不能准确地挖掘出正确交互, 使得生成的相似度图中依旧包含冗余交互或是缺失关键交互. 此时, 将相似度图以固定比例与元路径图融合, 会给图结构带来新的交互偏差.

为了解决现有工作^{[25, 35]}中存在的上述问题, 本文设计了渐进式的图结构融合方法, 可以随着训练次数的变化改变相似度图融合比例. 对于每一条元路径, 计算过程如下:

$ \boldsymbol{A}_{{p_m}}^* = (1 - \hat \tau ){\boldsymbol{A}_{{p_m}}} + \hat \tau {\boldsymbol{S}_{{p_m}}}, {\text{ }}\hat \tau = \min \left\{ {(1 - \tau ), \frac{{(1 - \tau )}}{{step}} \times q} \right\} $

(14)

其中, τ∈[0, 1]是融合率; step是将设定的融合率分步更新的次数; q=1, 2, …, Q是模型当前训练的迭代次数, Q为模型总的训练迭代次数; $ \hat \tau $表示由模型训练次数控制的融合率. 在模型开始训练时, q的取值从1开始, 且小于设定的分布更新次数step, 此时, $ \hat \tau $取值为远远小于设定的τ值, 仅将很小比例的相似度图与元路径图进行了融合. 随着训练次数的增加, 模型的拟合能力逐渐增强, 再以逐渐增加的比例将相似度图与元路径图进行融合, 使得最后得到的优化的图结构中避免因训练初期模型拟合能力弱所导致的结构偏差问题. 经过对每一个元路径图进行学习优化, 最后将优化的元路径图$A_P^* = \{ \boldsymbol{A}_{{p_1}}^*, \boldsymbol{A}_{{p_2}}^*, ..., \boldsymbol{A}_{{p_m}}^*\} $用于下游的节点分类以及节点聚类任务.

4 实验分析

为了验证本文方法的有效性, 本文以节点分类以及节点聚类任务为目标任务, 在4种异质图数据集上评估本文的模型. 在执行节点分类任务时, 本文选择了9种现有图表示学习模型作为基准模型与其进行性能比较, 并使用Macro-F1与Micro-F1作为分类结果的评价指标. 选择节点聚类作为目标任务时, 本文选择5种图表示学习模型来学习节点表示, 并使用K-means算法对节点进行聚类. 在节点聚类任务中, 使用归一化互信息(normalized mutual information, NMI)与调整兰德指数(adjusted Rand index, ARI)作为聚类评价指标.

4.1 实验数据与评价指标

本文选择了4种异质信息网络数据集: ACM、DBLP、IMDB以及Freebase, 来验证本文方法的有效性. 4个数据集共分为两种类别, 其中, ACM与DBLP为异质学术信息网络, IMDB与Freebase则为异质电影信息网络. 下面对4种数据集进行详细描述, 并在表 1中给出了4种数据集的统计信息.

(1) ACM: ACM为异质学术信息网络, 该网络包含了3种类型的节点, 分别是文章(P)、作者(A)以及类别(S), 以及4种类型的交互, 分别为文章-作者(P-A)、作者-文章(A-P)、文章-类别(P-S)和类别-文章(S-P). 该网络中, 文章(A)类型的节点是带有标签信息的目标节点, 共分为3个类别: 数据挖掘(data mining)、数据库(database)和计算机网络(computer network);

(2) DBLP: 与ACM网络类似, DBLP同样为异质学术信息网络, 该网络包含了4种类型的节点, 记为文章(P)、作者(A)、会议(C)和分组(T), 以及6种类型的边, 分别是文章-作者(P-A)、作者-文章(A-P)、文章-会议(P-C)、会议-文章(C-P)、文章-组别(P-T)、组别-文章(T-P). 其中, 作者(A)类型的节点带有节点标签, 共分为4种类型, 分别为数据挖掘、数据库、机器学习(machine learning)和信息检索(information retrieval);

(3) IMDB: IMDB是一个由电影及其主演、导演等信息组成的异质电影信息网络, 其中包含了4种类型的节点: 电影(M)、演员(A)、用户(U)与导演(D), 以及6种类型的交互: 电影-演员(M-A)、演员-电影(A-M)、电影-用户(M-U)、用户-电影(U-M)、电影-导演(M-D)与导演-电影(D-M). 其中, 电影(M)类型的节点带有标签信息, 其标签类别为: 喜剧片(comedy)、纪录片(documentary)、歌剧片(drama)以及恐怖片(horror);

(4) Freebase: Freebase同样为异质电影信息网络, 该网络中共有4种类型的节点, 分别是电影(M)、演员(A)、导演(D)与制片人(P), 以及6种类型的边: 电影-演员(M-A)、演员-电影(A-M)、电影-导演(M-D)、导演-电影(D-M)、电影-制片人(M-P)与制片人-电影(P-M). 该网络中, 电影类型节点为目标节点, 带有标签信息. 其标签共有3个类别, 分别是动作片(action)、喜剧片(comedy)以及歌剧片(drama).

为了充分验证本文提出的MV-HGSL模型的有效性, 在对比实验中, 本文提出的MV-HGSL将与5种类型共9个基准模型, 并以节点分类以及节点聚类为目标任务进行性能对比. 选择的9种对比模型分别是GCN^[7]、GAT^[8]、Metapath2Vec^[48]、HAN^[9]、HGT^[11]、RGCN^[49]、AM-GCN^[23]、HGSL^[24]以及HDGI^[44]. 其中, GCN与GAT为学习普通同质图节点表示的GNN模型, 这两种模型作为经典的GNN框架, 可以在忽略了异质图中的多种类型信息后, 学习异质图中节点的表示. Metapath2Vec(简写为M2V)为基于随机游走的异质图表示学习模型, 该模型利用了异质Skip-Gram方法学习节点表示. 对比的模型中还包含了3个异质图神经网络模型: HAN、HGT、RGCN以及两种图结构学习模型: AM-GCN与HGSL. HDGI为异质图对比学习模型, 通过对比节点的邻域特征与全局特征学习节点的表示. 在以节点聚类任务为目标任务时, 本文选择了GCN、GAT、Metapath2Vec、HAN、RGCN、HGT以及HDGI作为对比模型, 学习节点的表示向量, 并使用K-means对节点进行聚类. 在分类任务中, 对比的图结构学习模型AM-GCN与HGSL都需要利用节点的标签信息作为监督信号, 并以最小化模型输出与标签之间的差距为优化目标, 无法执行聚类任务. 因此在节点聚类中, 选择上述7种模型与本文模型进行比较.

当本文选择以节点分类作为目标任务以验证本文模型的有效性时, 使用Micro-F1与Macro-F1作为分类性能的评价指标. 公式(15)给出了Micro-F1与Macro-F1的定义:

$ Macro{\text{ - }}F1 = \sum\limits_{i = 1}^n {\frac{{2 \times T{P_i}}}{{2 \times T{P_i} + F{N_i} + F{P_i}}}} , {\text{ }}Micro{\text{ - }}F1 = \frac{{\sum\nolimits_{i = 1}^n {2 \times T{P_i}} }}{{\sum\nolimits_{i = 1}^n {[2 \times T{P_i} + F{N_i} + F{P_i}]} }} $

(15)

其中, TP_i、FN_i与FP_i分别表示i个类别下True Positive、False Positive以及False Negative的数量.

在节点聚类任务中, 本文选择归一化互信息NMI与调整兰德指数ARI作为评价指标, 以验证本文模型在聚类任务上的有效性.

● 公式(16)给出了NMI的定义:

$ NMI(X, Y) = \frac{{I(X, Y)}}{{\sqrt {H(X)H(Y)} }} $

(16)

其中, X与Y为随机变量, I(X, Y)表示X与Y的互信息, H(X)与H(Y)分别为X与Y的信息熵;

● 公式(17)给出了ARI的定义:

$ ARI = \frac{{RI - E(RI)}}{{\max (RI) - E(RI)}} $

(17)

其中, RI表示兰德指数(Rand index), E(RI)表示兰德指数的期望值. 公式(18)给出了兰德指数E(RI)的定义:

$ RI = \frac{{TP + TN}}{{TP + FP + FN + TN}} $

(18)

其中, TP为两个同类样本点在同一类中的情况数量, FP为两个非同类样本点在同一类中的情况数量, FN表示两个同类样本点分别在两个类中的情况数量, TN表示两个非同类样本点分别在两个类中的情况数量.

4.2 节点分类对比实验

在得到优化了的元路径图之后, 本文将其输入HAN模型以执行节点分类任务, 用于验证学习得到的图结构可提升节点分类任务的性能. 为了与同质图神经网络模型(GCN、GAT以及AM-GCN)进行性能比较, 当本文用上述同质图模型学习4个异质图数据中的节点表示时, 忽略了网络中由多种类型的节点与交互构成的异质关系, 将异质网络转换为同质网络. 对于每一种模型, 本文将其运行5次取平均值, 并将实验结果记录在了表 2之中.

本文以模型在下游任务中的性能提升程度来评价图结构优化的有效性. 从表 2中的实验结果可以看出, MV-HGSL模型在4种异质图数据集上基本都取得了最优的分类效果. 与对比的方法中分类性能最优的模型相比, 在两个分类评价指标上均有0.8%−1.5%的性能提升. 该结果验证了在无法使用节点标签作为监督信息的情况下, 通过挖掘数据自身所包含的结构信息与特征信息, 并将其作为监督信号, 也能够有效地指引图结构学习的优化方向, 学习到结构完整的异质图结构, 明显提升了神经网络模型在下游分类任务上的性能. HGSL的节点分类结果仅次于本文提出的MV-HGSL, 说明相比于只通过消息传递学习节点表征的图神经网络模型, 对图结构进行优化的HGSL可以有效地提升神经网络在下游任务中的表现. 从表中可以看到: 在训练数据比例为0.8时, HGSL在ACM以及IMDB数据上的分类效果略好于本文模型. 可说明在节点标签信息足够多的情况下, 以监督学习形式学习图结构的HGSL能够取得较优的效果, 但此条件也限制了HGSL的应用范围. AM-GCN的分类效果不仅在两种评价指标上低于本文模型以及HGSL约2%−3%, 甚至低于HAN以及HGT两个异质图神经网络模型. 其原因为: AM-GCN是学习同质图结构的模型, 当该方法在4种异质图数据上执行时, 忽略了异质图中的多类型关系, 使得AM-GCN无法捕获异质图中的多类型异构信息, 丢失了异质图中的潜在语义特性, 降低了其节点分类的性能.

在3种对比的HGNN模型中, HGT取得了高于HAN和RGCN的分类效果. 其原因为: HGT利用注意力机制计算邻居的重要性, 可以自动地学习出与节点分类任务最相关的多类型邻域特征, 而非人为地预设定元路径, 可避免获得与目标任务有偏差的高阶邻域特征信息. HGDI取得了与HGT以及HAN近似的分类性能, 证明了不使用节点标签作为监督信息的对比方式, 通过最大化不同视角下节点的互信息, 也可以有效地捕获异质图中的结构与语义信息. 由于GCN与GAT是用于学习同质图中节点表示的GNN模型, 无法区分异质图中由多类型节点与交互所产生的不同影响, 因此, GCN与GAT在4种异质图数据上的节点分类性能低于上述3种HGNN模型约4%−10%左右. 由于Metapath2Vec是通过随机游走和异质Skip-Gram来捕获异质信息, 学习异质图中节点的表征, 没有深层的神经网络结构, 即无法提取节点邻域中的高阶非线性特征, 因此在所有模型中, Metapath2Vec的分类效果最差. 此外, 从表 2所示结果可以发现: 在4种数据集上执行分类任务, 所有模型在IMDB与Freebase数据集上的分类准确性远远低于ACM与DBLP. 其原因是: 在两种电影数据集中, 其目标节点的标签与ACM以及DBLP中的相比划分得较为混乱, 标注质量较低, 明显降低了所有模型在两种电影数据集上的分类效果.

本文模型在以自监督方式学习更新图结构之后, 使用了HAN模型学习节点的表征向量, 并用于下游任务. 因此, MV-HGSL与HAN的分类对比结果直接反映了输入经过图结构优化的图数据与直接输入原始图数据在节点分类任务上的性能差异. 该结果显示: 本文提出的MV-HGSL相比于HAN, 在4种数据集上取得了2%−3%的性能提升. 证明了利用节点特征以及自监督对比学习能够优化原始图的连接结构, 更新节点的局部邻域交互, 有效地提升了模型在下游任务上的性能表现.

4.3 节点聚类对比实验

与节点分类任务类似, 在得到优化了的元路径图之后, 本文将其输入HAN模型, 并使用K-means算法执行节点聚类任务. 与同质图学习模型比较时, 同样将异质图转换为同质图. 为了降低聚类时不同的初始化赋值带来的不稳定影响, 本文重复执行5次聚类过程, 并将两种指标的平均值记录在了表 3之中.

从表 3的实验结果可知: 与7种对比模型相比, 本文提出的MV-HGSL在4种异质图数据上取得了最优的节点聚类效果; 与效果最优的对比模型HGT相比, 均有2%的聚类性能提升. 证明了本文提出的MV-HGSL模型能够有效地抽取异质图中的复杂信息, 抑制不准确的拓扑结构对神经网络学习性能的影响, 获得具有表现力的节点表示, 提升了节点聚类任务的性能. 与节点分类任务中的效果趋势类似, 3种异质图神经网络模型(HAN、RGCN与HGT)以及对比学习模型HDGI取得了明显高于同质图模型(GCN、GAT)和Metapath2Vec的聚类性能. 其原因为: GCN与GAT在学习节点表示的过程中忽略了异质图的多种类型信息, 而Metapath2Vec由于使用人为设定长度的随机游走来捕获邻域结构, 且使用异质Skip-Gram模型学习节点的向量表示, 对节点的高阶非线性特征捕捉能力不足, 使其在节点聚类任务中的效果为对比模型中最差.

从4种数据集上的实验结果可以看出: 所有模型在IMDB以及Freebase数据集上的聚类效果, 相比于两种异质学术网络有明显的下降. 其原因为: 在执行聚类任务时, 本文将聚类中簇的数量设置为节点类别的数量, 而IMDB与Freebase数据集中混乱的标注使得节点难以划分至正确的簇当中, 令聚类的效果大幅下降. 与节点分类任务中的效果类似, MV-HGSL在节点聚类任务上也取得了优于HAN的聚类效果, 同样证明: 经过优化的图结构能够有效地提升下游任务的性能表现.

4.4 参数敏感性分析

本节实验将讨论模型中设置的4个重要超参数, 分别为丢弃概率p^(f)与p^(a)、KNN邻居数量k以及图结构融合调整率τ, 对实验效果的影响. 实验分析中选取节点分类任务作为目标任务. 丢弃概率p^(f)与p^(a)的大小直接决定了在对比学习中模型能够获取到的图数据特征信息与结构信息的多少, 影响着模型从数据自身挖掘到的监督信号的质量, 进而影响了图结构是否能够得到正确充分的优化; 邻居数量k的多少则决定了相似度图的交互稀疏程度, 影响着节点在消息传递过程中能否聚合正确且完备的邻域特征, 进而决定了在节点分类任务下的性能; 调整率τ的大小则决定着在最终用于节点分类的图结构当中, 保留了多少原始元路径图的信息, 且融合了多少学习得到的相似度图的信息.

本文为上述每一个超参数设置多种取值, 并记录了在不同取值下模型的节点分类性能表现. 下面将对实验结果进行详细介绍.

(1) 邻居数量k

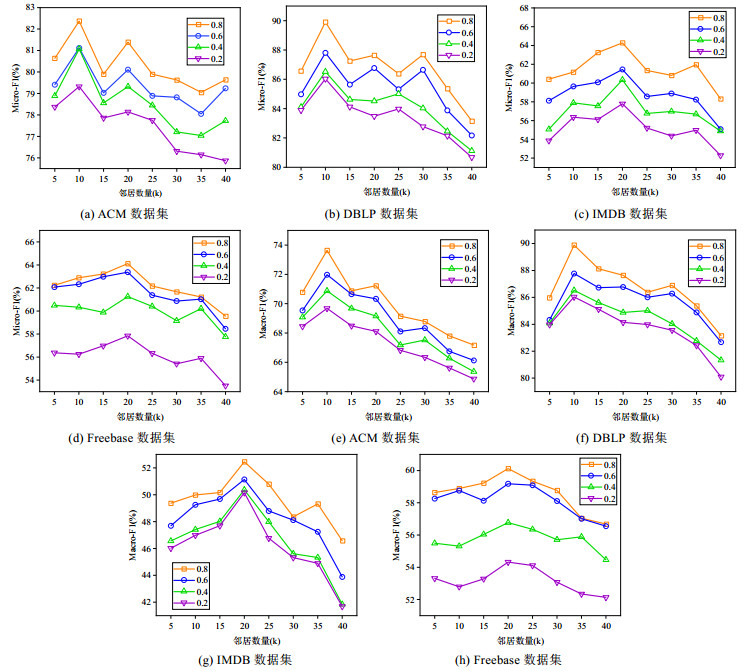
在使用KNN图对生成的相似度图进行稀疏化时, k的大小直接影响着相似度图的交互稀疏度, 决定了图中每个节点的邻域大小. 本文将邻居数量k的取值放置在[5, 40]的范围内, 并以5为步长分别选择k值, 以发现在4种数据集中的最优邻居数量k. 实验结果如图 5所示.

从图 5中的结果可以看出: 在ACM与DBLP数据集上, 当邻居数量k都为10时, 模型取得了最优的分类效果; 而在IMDB与Freebase数据集上, 当邻居数量k为20时, 模型在节点分类上的效果最优. 其原因可能是由于电影数据集的标签混乱, 使得目标节点需要聚合较多的邻域特征, 模型才能判断其所属的类别. 随着选择的邻居数量k越来越大, 模型的分类性能逐渐下降. 其原因为: 真实的图数据中的交互应是稀疏的, 而相似度图中每个节点连接的邻居越多, 与真实交互的偏差越大. 即: 在学习节点表征时, 过多的邻域交互会使节点聚合了本不是自身邻居的节点的表征, 从而降低了模型在节点分类上的性能. 而当k值的选择较小时, 每个节点与应有的邻居没有充分的连接, 导致学习的节点表征聚合的邻域特征不足, 同样使得模型的分类性能较低.

(2) 丢弃概率

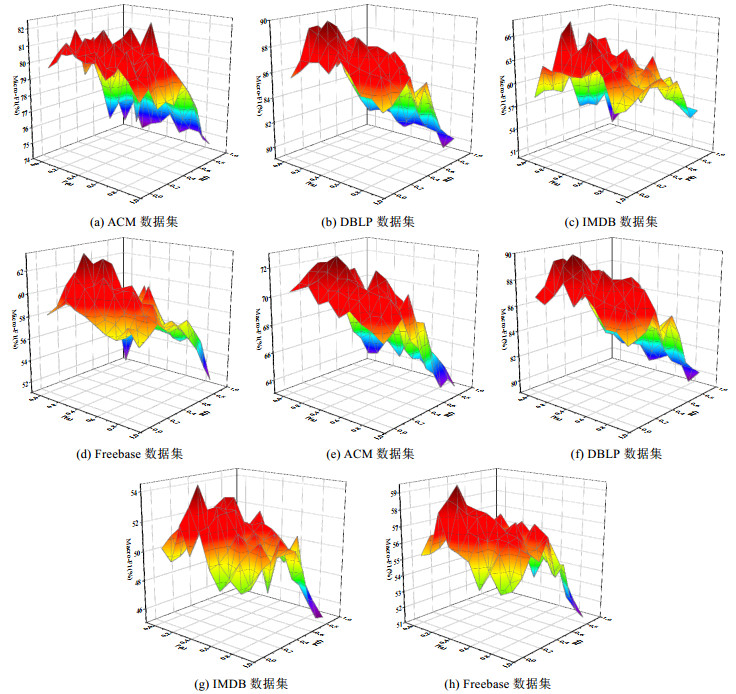
为了探究在对两个视图进行数据增广时, 掩盖的节点特征与交互的多少对节点分类效果的影响, 本文在4个数据集上, 将节点特征丢弃概率p^(f)与边丢弃概率p^(a)分别设置在[0, 0.9]的范围内, 并以0.1为步长依次递增, 探究最优的丢弃概率值. 实验结果如图 6所示.

如图 6所示: 在ACM数据集上, 当特征丢弃概率与边丢弃概率分别为0.3和0.3时, 分类效果达到最优; 而在DBLP、IMDB以及Freebase数据集上, 最优的分类结果在特征丢弃概率与边丢弃概率分别取0.2和0.2时达到. 在4种数据集上的丢弃概率的对比实验结果都呈现出: 随着丢弃概率的增大, 得到的图结构用于节点分类任务的性能越差的趋势, 即学习到的图结构质量越差. 说明掩盖的特征与结构信息越多, 学习得到的图结构与真实交互情况的偏差越大, 令模型的分类性能越差. 此外, 从图 6中还可以看出: IMDB数据集对丢弃概率的敏感性更高, 在丢弃概率的变化范围内, 其分类的结果相差最大. 其原因为: 由于IMDB的节点标签较为混乱, 划分不佳, 在丢弃了更多的原始特征与交互信息后, 保留下来的信息不足以作为节点类别划分的判断依据, 即节点特征的维度减少, 交互减少, 导致原有可分的数据在降维之后变得不可分, 使得分类效果下降幅度较大. 而ACM与DBLP对丢弃概率的敏感度较相似, 都是当丢弃概率在区间[0, 0.5]时分类结果较优; 当概率高于0.5时, 分类效果有明显降低.

(3) 融合参数τ

最后, 本文将讨论融合参数τ与更新步长step对模型分类性能的影响. 虽然输入的元路径图中存在交互错误, 但仍然包含了许多关键的交互结构. 本文采用了神经网络模型常用的等比增加参数选择方式来选择融合参数τ, 记为[1, 0.99999, 0.9999, 0.999, 0.99, 0.9], 探究相似度图融合的多少对分类结果的影响. 此外, 设置更新步长step为[0, 250, 500, 750, 1000, 1250], 模型训练总的迭代次数Q为1 500次. 实验结果如图 7所示.

从图 7所示的实验结果可知: 在ACM与DBLP数据集中, 当τ值取0.999 9时, 模型的分类效果最优; 而在IMDB与Freebase数据集中, 当τ值取0.999时, 模型的分类效果最优, 说明电影数据集相比于学术网络, 更需要以节点特征相似度生成的相似度图来优化原始交互结构. 随着τ值的减小, 原始的元路径图中融合的相似度图结构越来越多, 模型的分类性能有一定程度的下降. 该结果说明, 虽然原始图结构中包含了冗余交互以及缺失部分交互, 但其中的大部分交互信息还是对节点表示学习以及下游的分类任务起到了重要的作用, 不断地将相似度图的结构信息放大并与元路径图融合会覆盖原有的某些关键交互结构, 从而导致了分类效果的降低. 此外, 当更新步长step在ACM与DBLP数据上设置为250时分类的效果最优, 在IMDB上设置为500时效果最优, 而在Freebase数据集上选取更新750步时分类性能最优. 即, 不同数据集到达最优效果的更新距离不同. 由图 7中实验结果可得, 当更新步长step为0时的分类效果明显低于分步更新图结构时的效果, 说明本文提出的随训练次数提升聚合比例的方式可以有效地增加模型在分类任务上的效果, 验证了渐进式的图结构融合可以有效地避免在训练初期网络学习能力弱的情况下, 将相似度图中存在的错误结构信息融入到元路径图中.

4.5 消融实验

本文提出的异质图结构学习模型MV-HGSL包含了4个主要步骤, 分别是相似度图计算、图结构处理、基于多视图对比的图结构优化以及渐进式图结构更新. 为了验证模型中相似度图计算、图结构处理以及渐进式图结构更新步骤的有效性, 本节将设计消融实验, 替换MV-HGSL原有步骤中的计算方式, 并以节点分类任务为目标进行实验. 下面将对MV-HGSL与3种其变体形式的消融实验给出详细介绍.

(1) 基于特征相似度的图学习有效性分析

首先验证MV-HGSL中使用的基于MLP与cosine相似度计算图结构的有效性. 本文将基于MLP的图结构学习模块替换为随机初始化相似度图的方式, 将该MV-HGSL的变体形式记为w/o-MLP, 以验证利用节点特征之间的相似度来优化原始图中的交互是否能够得到更优的图结构. 在4种数据集上的实验结果见表 4.

由表 4的分类结果可知: 在4种数据集上, 使用MLP学习节点表征并利用节点表征计算节点之间的特征相似度而生成的图结构, 在节点分类任务上取得了比随机初始化相似度图更优的分类效果, 在两种评价指标下的性能提升在1%−1.5%左右. 该实验结果表明, 使用相似度度量函数计算节点特征之间的相似度, 并利用相似度的大小生成节点间交互的方式, 可以提供正确且有效的交互信息, 用于去除原始元路径图中的冗余交互且补全原始元路径图中缺失的交互(即特征相似的节点之间应存在交互, 非相似节点间不存在交互), 有效地提升了节点分类的效果. 此外, 从表 4的结果可以看出: 利用MLP计算特征相似度生成的图结构在节点分类上的性能仅优于随机初始化的图结构约1%−1.5%, 没有因随机初始化带来的噪声而产生大幅的性能下降.其原因为: 本文模型以输入的元路径图作为对比学习中的对比视图, 其记录着节点之间的高阶交互关系. 随着模型的训练, 将初始化的相似度图进行迭代优化, 使其趋近于输入的元路径图. 这样, 相似度图在保留了真实的节点高阶交互的同时, 也逐步消除了其初始化带来的交互误差.

(2) 图结构处理步骤有效性分析

随后, 本文设计实验来验证将相似度图处理为稀疏、非负且归一化的图结构处理步骤的有效性. 在该实验中, 本文将得到的全连接相似度图不经过任何处理, 直接输入到图对比学习中进行图结构优化, 用于验证经过稀疏化、非负化和归一化的相似度图可以有效地补充原始元路径图结构, 获得结构干净且完备的元路径图结构. 本文将该变体模型记为w/o-GP, 在4种数据集上的实验结果见表 5.

从表 5中的实验结果可以看到: MV-HGSL在4种数据集上的节点分类效果均优于去除了图结构处理步骤后的变体形式w/o-GP, 在两种评价指标下的分类效果相比w/o-GP有3%−5%的提升. 该实验结果表明: 图结构处理步骤能够有效地剔除生成的全连接相似度图中的冗余交互信息, 保留每个节点最重要的邻域关系, 并将相似度图边权重归一标准化, 令模型在使用相似度图去优化原始元路径图的过程中, 不会在图结构优化时引入新的结构偏差, 有效地提升了MV-HGSL在节点分类任务上的性能.

(3) 渐进式图结构融合有效性分析

最后, 本文通过实验来验证MV-HGSL中, 随模型训练可变图结构融合比例的渐进式图结构更新的有效性. 实验中, 将随模型训练次数可变比例的图结构融合方式替换为以固定比例融合图结构的方式, 以验证本文提出的渐进式图结构融合的有效性, 并将该变体形式记为w/o-Progre. 在4种数据集上的实验结果见表 6.

由表 6中的分类结果可得: MV-HGSL在4种数据集上的分类效果均优于以固定比例融合图结构的变体形式w/o-Progre, 在两种评价指标下的性能均高于w/o-Progre约1%−2%. 表 6中的实验结果表明: 本文提出的随训练可变比例的渐进式图结构融合方法能够有效地避免因训练初期神经网络学习能力弱, 生成的节点表征没有获取到完备的节点结构与特征信息, 令节点之间的相似度大小不能真实地反映其特征相似情况, 进而产生的相似度图结构偏差的问题. 通过随训练增加图结构融合比例的方式, 有效地去除了相似度图中的计算错误交互, 提升了模型在节点分类上的效果.

5 总结

为了消除异质图数据中的噪声交互与缺失交互对异质图数据神经网络的影响, 本文提出了多视图对比增强的异质图结构学习方法MV-HGSL, 以自监督的方式学习无噪声且完备的异质图结构. 该模型首先通过元路径来保持异质图中的高阶异构语义信息, 然后计算节点之间的特征相似度生成相似度图, 以节点之间的特征相似性来修正原有的错误交互; 其次, 最大化相似度图与元路径图之间的互信息, 在无需标签信息的监督下, 利用异质图数据自身的结构和特征信息优化学习到的相似度图; 最后, 为了避免在对比学习过程中让学习得到的图结构再次融入错误交互, 该模型设计了渐进式的图结构融合方式, 有效地避免了在模型开始训练时聚合新生成的错误交互. 在4种异质图数据集上的实验结果表明: 本文提出的多视图对比增强的异质图结构学习方法能够有效地优化异质图中的交互结构, 学习出结构准确的异质图, 明显地提升了模型在节点分类以及节点聚类任务上的性能.

在未来的工作当中, 可以从以下两个方面继续深入研究异质图结构学习: (1) 可以通过优化理论定性定量地分析经过学习优化的图结构对噪声交互的去除以及缺失交互的补足的精准性如何; (2) 可以从概率分布的角度出发, 将异质图结构视为采样数据, 通过KL散度等方法计算异质图结构之间的交互分布差异, 衡量优化的异质图结构的质量, 保证图结构学习时的理论可靠性.