不经意传输协议研究综述

引用本文

高莹, 李寒雨, 王玮, 刘翔, 陈洁. 不经意传输协议研究综述[J]. 软件学报, 2023, 34(4): 1879-1906. http://www.jos.org.cn/1000-9825/6692.htm

Gao Y, Li HY, Wang W, Liu X, Chen J. Survey on Oblivious Transfer Protocols[J]. Journal of Software, 2023, 34(4): 1879-1906(in Chinese). http://www.jos.org.cn/1000-9825/6692.htm

不经意传输协议研究综述

高莹^1,2,3 , 李寒雨² , 王玮² , 刘翔² , 陈洁⁴

1. 公共大数据国家重点实验室(贵州大学), 贵州贵阳 550025;
2. 北京航空航天大学网络空间安全学院, 北京 100191;
3. 空天网络安全工业和信息化部重点实验室, 北京 100191;
4. 华东师范大学软件工程学院, 上海 200062

收稿时间: 2021-12-10; 修改时间: 2022-01-27; 采用时间: 2022-04-14; jos在线出版时间: 2022-07-22

基金项目: 北京市自然科学基金(M21033); 国家自然科学基金(61932011, 61972017, 61972156); 腾讯微信犀牛鸟基金

作者简介: 高莹(1977-), 女, 博士, 副教授, 博士生导师, CCF高级会员, 主要研究领域为隐私计算, 密码学应用;
李寒雨(1996-), 男, 硕士生, 主要研究领域为隐私集合求交, 不经意传输协议;
王玮(1998-), 女, 硕士生, 主要研究领域为多方隐私集合求交;
刘翔(2000-), 男, 硕士生, 主要研究领域为代理隐私集合求交;
陈洁(1985-), 男, 博士, 研究员, 博士生导师, CCF专业会员, 主要研究领域为公钥密码学.

通讯作者: 高莹, E-mail: gaoying@buaa.edu.cn.

摘要: 在互联网快速发展、大数据的挖掘与应用已渗透到各行各业的今天, 如何安全且高效地共享、使用海量数据成为新的热点研究问题. 安全多方计算是解决该问题的关键技术之一, 它允许一组参与方在不泄露隐私输入的前提下进行交互, 共同计算一个函数并得到输出结果. 不经意传输协议, 也叫茫然传输协议, 是一种保护隐私的两方通信协议, 消息发送者持有两条待发送的消息, 接收者选择一条进行接收, 事后发送者对接收者获取哪一条消息毫不知情, 接收者对于未选择的消息也无法获取任何信息. 不经意传输协议是安全多方计算技术的关键模块之一, 其效率优化可有效推动安全多方计算技术的应用落地, 对于特殊的两方安全计算协议如隐私集合交集计算尤为重要. 总结了不经意传输协议的分类及几种常见的变体, 分别阐述了基于公钥密码的不经意传输协议的构造和研究进展, 以及不经意传输扩展协议的构造和研究进展, 由此引出不经意传输扩展协议的效率优化研究的重要性. 同时, 在半诚实敌手和恶意敌手这两种敌手模型下, 分别对不经意传输协议和不经意传输扩展协议的效率优化研究进展进行了全面梳理. 另一方面, 从应用角度对不经意传输协议和不经意传输扩展协议在工程实现中常用的优化技术进行了系统化分析. 最后, 总结了不经意传输协议和不经意传输扩展协议研究目前所面临的主要问题及未来发展趋势.

关键词: 不经意传输不经意传输扩展协议效率优化安全多方计算隐私集合交集计算

Survey on Oblivious Transfer Protocols

GAO Ying^1,2,3 , LI Han-Yu² , WANG Wei² , LIU Xiang² , CHEN Jie⁴

1. State Key Laboratory of Public Big Data (Guizhou University), Guiyang 550025, China;
2. School of Cyber Science and Technology, Beihang University, Beijing 100191, China;
3. Key Laboratory of Aerospace Network Security, Ministry of Industry and Information Technology, Beijing 100191, China;
4. Software Engineering Institute, East China Normal University, Shanghai 200062, China

Abstract: With the rapid development of the Internet and the penetration of big data mining and applications into all walks of life, how to share and use massive data securely and efficiently has become a new hot research issue. Secure multi-party computation is one of the key technologies to solve this problem. It allows a group of participants to interact compute a function together, and get the output without revealing private inputs. Oblivious transfer is a privacy-protected two-party communication protocol in which a sender holds two messages to be sent, and a receiver selects one to receive, but after that, the sender knows nothing about which message the receiver gets, and the receiver cannot get any information about the unselected message. Oblivious transfer has become one of the key modules of secure multi-party computation, and its efficiency optimization can effectively promote the application of secure multi-party computation, especially for special two-party secure computation protocols such as private set intersection. This paper summarizes the classification of oblivious transfer and several common variants, and respectively describes the construction and research progress of the oblivious transfer protocol based on public key cryptography and oblivious transfer extension, which leads to the importance of the efficiency optimization research of oblivious transfer. At the same time, this paper comprehensively reviews the research progress of efficiency optimization of oblivious transfer and oblivious transfer extension from the perspectives of semi-honest adversary and malicious adversary. On the other hand, in practical application, this paper systematically summarizes the optimization technologies used in the engineering implementation of oblivious transfer and oblivious transfer extension protocols. Finally, this paper points out the main problems and future works of oblivious transfer and oblivious transfer extension protocols.

Key words: oblivious transfer oblivious transfer extension protocol efficiency optimization secure multi-party computation private set intersection

随着云计算、大数据和人工智能技术的迅速发展与应用, 数据安全和隐私保护成为全球关注的热点问题. 2018年, 欧盟出台《通用数据保护条例》(general data protection regulation, GDPR)用于保护欧盟境内的个人隐私数据. 2021年, 我国通过了《中华人民共和国数据安全法》和《中华人民共和国个人信息保护法》, 旨在从立法层面规范全面构筑我国信息与数据安全领域的法律框架. 与传统数据使用方式相比较, 隐私计算可以平衡数据利用和安全, 实现数据的“可用不可见”, 可为数据安全和隐私保护问题提供了较为有效的解决方案.

不经意传输协议(oblivious transfer, OT)是隐私计算领域重要技术之一, 最早由Rabin提出^[1], 是指发送方向接收方发送2条消息, 接收方通过1位选择比特能够选择性地接收其中一条消息, 同时发送方无法确定接收方的选择比特, 接收方对未选择消息一无所知. OT协议^[1−6]是通信双方用来传递秘密信息的协议, 它不仅是密码学理论中最基本、最重要的原语之一, 早期多用于构建公平秘密交换协议^{[1, 2]}、抛币协议^{[2, 7, 8]}、公平电子合同签署协议^[2−4]、零知识证明协议^{[6, 9]}等.

OT协议是安全多方计算协议中需要大量使用的关键构建模块. 1988年, Kilian^[6]提出了著名的结论: 拥有一个实现不经意传输的黑盒就可以完备地构建任何一个安全计算协议. 安全多方计算(secure multi-party computation, SMPC)是指两方或多方将各自拥有的不愿泄露的秘密信息作为输入共同计算某个函数, 并在不泄露任何一方秘密信息的情况下得到函数的计算结果, 同时参与方也无法通过输出推断出其他任何一方的秘密信息.

1996年之前, OT协议均基于公钥密码学原语建立, 这使得OT协议的计算效率较低. 1989年, Impagliazzo和Rudich^[10]指出: 完全摆脱公钥密码学原语(如整数分解、离散对数), 仅基于对称密钥原语(如伪随机数生成器(pseudorandom generator, PRG)、哈希函数)去构造OT协议的困难程度相当于证明P≠NP. 虽然后来Beaver^[11]提出可通过线下预计算等量的随机OT (random OT, ROT)实例的方式换取线上阶段OT协议执行的高效性, 但是在预计算中, ROT也是基于公钥实现的, 并未能从根本上解决问题. 1996年, Beaver提出OT扩展(OT extension, OTE)协议^[12], 将公钥密码学原语和对称密码学原语结合使用, 成功突破了文献[10]中理论上的限制. OT扩展协议仅需执行少量基于公钥原语的“种子OT”, 再结合对称密钥原语进行扩展即可产生大量OT实例. 经过后续研究的不断改进^[13−25], 目前大多数已知实际有效的通用和专用SMPC协议均基于OT扩展协议构建.

作为SMPC协议中被大量使用的构建模块, OT协议和OT扩展协议的效率在很大程度上决定着整个SMPC协议的效率. 在实际应用方面, 除了几种最实用有效的通用SMPC协议^[26−33]是基于OT协议构建的之外, 在其他协议比如平衡场景(参与双方集合大小、计算能力相近)下的隐私集合交集计算(private set intersection, PSI)协议中, 目前最高效的方案^[34−44]也是基于OT实现的. 同时, OT协议在当下隐私计算领域具备广泛应用前景, 如共同好友发现^{[45, 46]}、广告转化率计算^[47−49]、机器学习隐私保护^[50−53]等.

另一方面, 考虑到不同OT协议变体的计算效率以及应用需求, 目前学术界关注度最高的OT变体主要是2-选-1 OT^{[2, 9, 54−59]}及其扩展协议^{[12−25, 39]}、n-选-1 OT^{[5, 54, 60]}及其扩展协议^{[13, 14, 18, 61]}, 二者有着不同的应用场景和构造方式, 前者一般用于PSI协议^{[34−36, 39, 42, 43]}、SMPC协议^{[17, 27−33, 45, 51−53, 62, 63]}, 后者则在PSI协议^{[13, 14, 37, 38, 40, 41, 44]}、对称私有信息检索(symmetric private information retrieval, SPIR)协议^[64]、不经意采样^[64]和不经意多项式求值(oblivious polynomial evaluation, OPE)^[65]等都有应用. 随着应用场景越复杂, 所需执行的OT实例数量也就越多, 使用高效的OT扩展协议可使基于OT构造的安全协议在实际应用中保持较低廉的开销.

Phong^[66]曾在2011年对几种基于公钥加密构造的OT协议进行总结, 但是对OT协议各类变体、OT扩展协议及相关应用研究进展的梳理并不全面. 本文对OT协议及各种变体进行总结, 重点围绕OT协议和OT扩展协议的效率优化及相关应用场景进行梳理和归纳, 对OT协议和OT扩展协议在效率优化上的挑战以及前人工作进行全面整理.

由于篇幅原因, 本文省去了对安全性相关定义的阐述, 包括但不限于敌手模型^[67−69](半诚实敌手、恶意敌手、隐蔽敌手)、协议执行环境^[70−73](独立模型、通用组合模型)以及安全模型^{[13, 15, 74, 75]}(标准模型、随机谕言机模型)与假设(Diffie-Hellman假设、关联鲁棒性假设及LPN假设等)等相关内容.

本文第1节概述OT协议基本知识, 给出OT协议及各种变体的分类, 以及构造OT协议的基本框架. 第2节梳理基于公钥的基础OT协议相关研究成果和效率优化进展, 并对其进行比较分析. 第3节梳理OT扩展协议的研究进展与相关成果, 并对其进行比较分析. 第4节对工程实现上的OT扩展优化思路以及相关技术的研究进展进行总结. 第5节概括OT协议的使用需求和使用场景. 最后, 在第6节总结目前OT协议效率研究方面存在的问题以及未来发展趋势.

1 OT协议概述 1.1 OT协议的分类

OT协议是一种保证通信双方信息隐私性的通信协议, 协议中有两个参与方, 一是信息持有方, 即发送方S (下文均用S表示), 二为接收方R (下文均用R表示). 本节给出目前存在的不同OT协议及其变体.

(1) 原始OT协议

1981年, Rabin^[1]基于二次剩余求解困难性假设首次提出不经意传输协议, S向R发送某个1比特消息$b \leftarrow\{0, 1\}$, R有1/2的机会能拿到b, 同时S无法得知最终R是否收到了b.

(2) 2-选-1 OT协议

1985年, Even等人^[2]基于单向陷门置换函数的存在性假设(可基于RSA假设实现)提出了一种更实用的2-选-1 OT协议, 发送方S持有消息M₀和M₁, R持有选择比特r∈{0, 1}, R将收到M_r, S无法推断出选择比特r的值, 同时R也无法获知M_1−r的任何信息. 该协议通常用$\left( \begin{gathered} 2 \\ 1 \\ \end{gathered} \right){\mathit{ - OT}}$表示.

1987年, Crépeau^[76]证明了Rabin的原始OT协议与Even等人^[2]提出的$\left( \begin{gathered} 2 \\ 1 \\ \end{gathered} \right){\mathit{ - OT}}$是等价的, 二者能够互相转化. $\left( \begin{gathered} 2 \\ 1 \\ \end{gathered} \right){\mathit{ - OT}}$目前通常作为OT扩展协议的“Base OT阶段”(见第1.3.1节)用于交换秘密种子信息. 因为必须基于公钥密码学原语构造, 后续有很多对其效率进行优化^[54−59]的方案, 其中, 2019年Döttling等人^[57]首次提出了陷门哈希函数原语, 结合陷门哈希函数构造了具有高通信效率的rate-1 OT(即传输的密文消息与发送方实际明文消息的长度比值近似为1的OT协议)方案, 并为基于DDH、LWE、二次剩余等假设构建rate-1 OT提供了一种框架, 该构造使rate-1 OT在近几年备受关注, 可用于构造分支程序同态加密协议以及通信高效的私有信息检索协议.

2020年, Garg等人^[58]提出了范围陷门哈希函数的概念, 将rate-1字符串OT的接收方通信复杂度从O(n²)个群元素优化为O(n) (n为OT消息长度). 2021年, Chase等人^[59]考虑到rate-1 OT协议通常需要多次执行, 而前人方案不同OT实例之间的通信相互独立且不可复用, 故提出均摊rate-1 OT (amortized rate-1 OT)原语, 在双线性群上基于标准假设进行实现, 将接收方的计算分成线下和线上阶段, 实现消息复用, 降低不可复用的通信开销, 优化rate-1 OT协议在多次执行场景下接收方的通信效率, 与前人方案相比, 通信效率优势随着OT执行次数的增加而显著.

(3) n-选-1 OT协议

1986年, Brassard等人^[5]通过调用$\left( \begin{gathered} 2 \\ 1 \\ \end{gathered} \right){\mathit{ - OT}}$来提出的OT协议中, 发送方S输入消息${M_0}, ..., {M_{n - 1}}, $ R输入秘密值$r \in \{ 0, ..., n - 1\} , $ R将收到M_r, S无法推断出R的秘密值r, 同时R也无法获知其余n−1条消息的任何信息, 该协议通常用$\left( \begin{gathered} {\mathit{n}} \\ 1 \\ \end{gathered} \right){\mathit{ - OT}}$表示.

Brassard等人^[5]是通过调用n次$\left( \begin{gathered} 2 \\ 1 \\ \end{gathered} \right){\mathit{ - OT}}$来实现$\left( \begin{gathered} {\mathit{n}} \\ 1 \\ \end{gathered} \right){\mathit{ - OT}}, $并给出了从传输比特消息的$\left( \begin{gathered} {\mathit{n}} \\ 1 \\ \end{gathered} \right){\mathit{ - OT}}$协议归约为传输较长字符串的$\left( \begin{gathered} {\mathit{n}} \\ 1 \\ \end{gathered} \right){\mathit{ - OT}}$的实现方式. 1999年, Naor、Pinkas^[64]对该协议进行改进, 提出了仅需logn次$\left( \begin{gathered} 2 \\ 1 \\ \end{gathered} \right){\mathit{ - OT}}$ (相当于logn次指数运算)以及O(n)次伪随机函数计算即可实现的$\left( \begin{gathered} {\mathit{n}} \\ 1 \\ \end{gathered} \right){\mathit{ - OT}}$协议. 2001年, Naor和Pinkas^[54]基于DDH假设在随机谕言机模型下直接构造出效率更优的$\left( \begin{gathered} {\mathit{n}} \\ 1 \\ \end{gathered} \right){\mathit{ - OT}}$协议, 其线上计算开销约等于只进行1次指数运算, 以及O(n)次伪随机函数计算. 在2002年, Tzeng^[60]基于DDH假设构造了一个$\left( \begin{gathered} {\mathit{n}} \\ 1 \\ \end{gathered} \right){\mathit{ - OT}}$协议, 虽然计算上没有^[54]高效, 但该协议结合秘密共享可以很容易地扩展为分布式的门限OT. 另外还可以通过密码学技术(如DDH假设、格密码)直接构造$\left( \begin{gathered} {\mathit{n}} \\ 1 \\ \end{gathered} \right){\mathit{ - OT}}$^{[54, 60, 77, 78]}.

(4) 随机OT协议

假设有两个参与方S和R, R输入选择比特b←{0, 1} (也可由协议本身随机生成), 发送方S输入随机选取的消息对(m₀, m₁), 因此该消息对也可以由协议本身随机生成返回给S, 正确执行随机OT后, R将获得消息m_b, S无法推断出R的选择比特b, R无法获知m_1−b的任何信息, 该协议通常简称为ROT^[11].

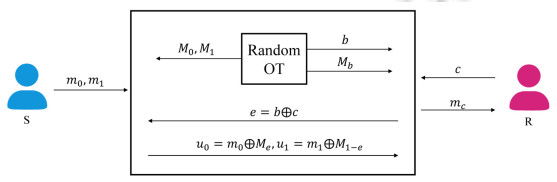
ROT最早在1995年由Beaver^[11]提出, 并指出ROT可以很容易地转化为OT协议. 该转化过程将OT协议分为线下和线上阶段, 双方可先在线下阶段交互生成大量ROT实例. 在线上阶段, R只需发送1比特信息c, 而S则只需发送两条消息m₀和m₁, 便能将1个ROT实例转为1个OT实例, 如图 1所示, 该构造虽然没有直接优化OT协议本身, 但保证了协议在线上阶段的通信与计算效率, 具备较好实用性.

图 1 从随机OT到OT协议的转化

(5) OT扩展协议

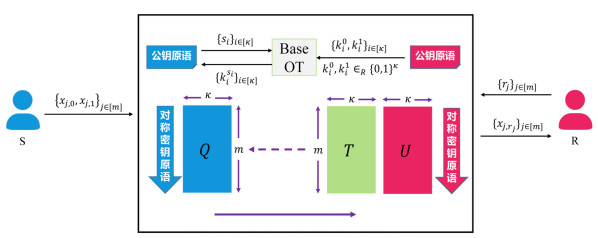
在1996年, Beaver提出OT扩展(OT extension, OTE)协议^[12], 当参与双方需要执行大量(m次)OT协议时, 只需将少量的κ (安全参数)个基于公钥原语构造的OT实例与对称密钥原语(如伪随机数生成器, 伪随机函数等)结合, 即可产生m (m≫κ)个OT实例的密码学协议. 如图 2所示.

图 2 OT扩展协议

(6) 广义OT协议

广义OT协议(简称GOT)最早在1997年由Ishai和Kushilevitz^[79]提出, 在GOT协议中, 发送方S持有一个有n个消息的集合$U = \{ {M_1}, ..., {M_n}\} , $并将U的非空子集组成的单调递减集合作为检索结构A. 设B∈A, 接收方R允许获取消息集合B的任意子集, 其余信息均无法得到, 同时S无法得知R所做的选择. 后来Tassa^[80]提出了一种采用了秘密共享的简单高效的GOT协议. GOT技术主要有两种应用场景: 带价格的OT (priced oblivious transfer)以及多元多项式的不经意求值(oblivious evaluation of multivariate polynomials).

(7) n-选-k OT协议

在1999年Naor等人^[65]提出了比k次执行$\left( \begin{gathered} {\mathit{n}} \\ 1 \\ \end{gathered} \right){\mathit{ - OT}}$协议更高效的$\left( \begin{gathered} {\mathit{n}} \\ k \\ \end{gathered} \right){\mathit{ - OT}}$协议, 发送方S输入消息${M_0}, ..., {M_{n - 1}}, $接收方R输入秘密选择向量$ r = \{ {r_0}, ..., {r_{k - 1}}\} \in {\{ 0, ..., n - 1\} ^k}, $ R将收到$\{ {M_{{r_0}}}, ..., {M_{{r_{k - 1}}}}\} , $ S无法推断出R的秘密选择向量r, 同时R也无法获知其余n−k条消息的任何信息, 该协议通常用$\left( \begin{gathered} {\mathit{n}} \\ k \\ \end{gathered} \right){\mathit{ - OT}}$表示.

对于$\left( \begin{gathered} {\mathit{n}} \\ k \\ \end{gathered} \right){\mathit{ - OT}}, $在1989年Bellare等人^[9]首次提出了一个n取n−1的OT协议构造, 但不算一般意义上的$\left( \begin{gathered} {\mathit{n}} \\ k \\ \end{gathered} \right){\mathit{ - OT}}{\mathit{.}}$ $\left( \begin{gathered} {\mathit{n}} \\ k \\ \end{gathered} \right){\mathit{ - OT}}$的构造思路同样主要有两种: 一种是通过并行化执行k个$\left( \begin{gathered} {\mathit{n}} \\ 1 \\ \end{gathered} \right){\mathit{ - OT}}$协议实例得到^[60], 另一种则是通过密码学技术(如DDH假设、双线性映射、椭圆曲线密码)直接构造^{[64, 81−83]}. 目前通信上最高效的$\left( \begin{gathered} {\mathit{n}} \\ k \\ \end{gathered} \right){\mathit{ - OT}}$方案在2018年由Lai等人^[84]基于新提出的两个假设构造, S到R的通信量为n+1个群元素, 而R到S通信量固定为3个群元素, 独立于n和k.

因为$\left( \begin{gathered} {\mathit{n}} \\ k \\ \end{gathered} \right){\mathit{ - OT}}$完全基于公钥原语构造, 而且长期没有像OT扩展协议(见定义7)结合对称密钥原语对大规模$\left( \begin{gathered} {\mathit{n}} \\ k \\ \end{gathered} \right){\mathit{ - OT}}$实例高效生成的方案, 所以该类变体与$\left( \begin{gathered} 2 \\ 1 \\ \end{gathered} \right){\mathit{ - OT}}, $ $\left( \begin{gathered} {\mathit{n}} \\ 1 \\ \end{gathered} \right){\mathit{ - OT}}$相比应用场景会受限一些, 但近两年在隐私集合交集计算领域中$\left( \begin{gathered} {\mathit{n}} \\ k \\ \end{gathered} \right){\mathit{ - OT}}$扩展的思想得到了实现与发展(见第5.2节).

(8) 自适应OT协议

1999年, Naor等人^[85]又提出了一种$\left( \begin{gathered} {\mathit{n}} \\ k \\ \end{gathered} \right){\mathit{ - OT}}$的变体, 被称为自适应OT (adaptive oblivious transfer, adaptive OT). 与$\left( \begin{gathered} {\mathit{n}} \\ k \\ \end{gathered} \right){\mathit{ - OT}}$不同的是, 在自适应OT中R不再一次性获得k个选择的查询结果, 而是能根据前i−1个值的情况来决定第i次要查询的值. 方案包括两个阶段: 承诺阶段和传输阶段. 在承诺阶段S对所有的消息秘密承诺交给R, 然后R在传输阶段对秘密逐个做查询.

自适应OT方案有很多应用场景, 比如不经意搜索、不经意数据库查询、私有信息检索等. 后续也有一些对自适应OT的通信效率进行优化的方案^{[81, 86−90]}, 或是在更强的安全性定义下保证效率, 如Camenisch等人^[91]提出的两种分别基于随机谕言机模型和标准模型的满足全模拟安全性的自适应OT构造, Green等人^[92]基于q-hidden LRSW问题提出的在通用可组合模型下安全的自适应OT协议, Jarecki^[93]等人基于CDR (composite decisional residuosity)和q-DHI (q-decisional Diffie-Hellman inversion)假设构造的满足全模拟安全的自适应OT协议, 和Kurosawa等人^[94]基于简单的DDH假设构造的满足全模拟安全性的自适应OT协议.

(9) 门限OT (也叫分布式OT)协议

2000年由Naor和Pinkas^[95]提出的一种OT协议, 是将发送方的任务通过秘密共享的方式分派给多个服务器, 此协议要求一定数量的服务器不合谋, 且接收方需要与至少门限数量个服务器交互、得到秘密信息, 才能最终获得正确的OT输出. 其主要优势在于计算更加高效, 因为仅涉及相对较小域上的多项式计算(无需指数计算), 所以其计算更加高效. 此协议在信息论意义下保证安全性.

(10) 相关OT协议

相关OT协议在2013年由Asharov等人提出^[19], 接收方R输入选择比特b←{0, 1}, 发送方S输入一个相关函数${f_\Delta }( \cdot ), $ (比如${f_\Delta }({x_0}) = {x_0} \oplus \Delta $)由协议本身生成随机消息x₀, 返回消息对$({x_0}, {x_1} = {f_\Delta }({x_0}))$给S, 正确执行Correlated OT后, R获得消息x_b, S无法推断出R的选择比特b, R无法获知x_1−b的任何信息, 该协议通常简称为COT.

COT在很多SMPC协议的预处理阶段中都作为核心构建模块存在^{[15, 17, 23, 25, 33, 51−53, 96, 97]}, 可用于生成比特乘法分享、认证比特和Beaver乘法三元组, 这些过程占据了协议的主要开销. 进一步地, 参与双方只需要对自己拿到的输出通过关联鲁棒性函数进行哈希, 便能将COT转化为ROT, 进而由ROT也可以很容易地转化为OT协议实例^[11].

(11) 其他变体协议

变体协议的研究让OT协议本身的特性得到更多挖掘与关注, 也使其在更多应用场景下发挥作用, 比如Wolf等人^[98]设计的对称OT构造, 能够仅基于1个OT实例、1比特通信量和1个附加的随机比特构造1个反方向OT实例, 这一归约表明了OT的对称特性, 解决了Crépeau等人^[99]提出的公开问题; 黄琼等人^[100]首次基于公开密钥公开随机性(public-key public-randomness, PKPR)模型提出独立的不经意传输协议, 当双方执行大量OT协议时, 单个OT实例的信息泄露不会威胁到其他OT实例的安全性, 且对于拥有无限计算能力的接收方能够保证安全性; 隗云等人^[101]首次提出基于非交换辫群上的共轭搜索问题和多重共轭搜索问题的OT协议, 能够抵抗量子分析; 张艳硕等人^[102]提出的概率型OT协议构造方案, 能使接收方以一般的概率恢复出自己选择的秘密消息.

1.2 基础构造框架 1.2.1 Base OT协议基础构造

本节分别在半诚实敌手和恶意敌手两种模型下介绍Base OT协议的构造. Base OT协议即基于公钥密码学实现的$\left( \begin{gathered} 2 \\ 1 \\ \end{gathered} \right){\mathit{ - OT}}$协议, 可基于多种不同的假设构造: 陷门置换函数存在性假设^[2]、大整数因子分解困难性假设^[1]、Diffie-Hellman假设^{[9, 54]}、RSA假设^{[3, 4]}、格上困难问题^{[16, 77, 103]}等.

(1) 半诚实敌手

1989年Bellare和Micali^[9]提出的非交互式$\left( \begin{gathered} 2 \\ 1 \\ \end{gathered} \right){\mathit{ - OT}}$协议, 接收方是半诚实敌手. 其特点在于除去公钥参数协商阶段, 接收方仅需被动接收消息, 无需做额外交互. 基于公钥密码学的安全性, 该构造在半诚实敌手模型下是安全的, S因为无法仅通过两个公钥$(p{k_0}, p{k_1})$推断出R的选择, 所以无法作恶. R也无法求出随机选取的公钥pk′对应的私钥. 要注意的是这一半诚实协议无法抵御恶意的接收方R: R可以生成2对公私钥$(p{k_0}, s{k_0})$和$(p{k_1}, s{k_1}), $并发送$(p{k_1}, s{k_1})$给S, 这样R就可以同时解密出$({x_0}, {x_1}).$

协议构造思路^{[9, 67]}如图 3所示.

图 3 半诚实敌手下构造$\left( \begin{gathered} 2 \\ 1 \\ \end{gathered} \right){\mathit{ - OT}}$协议框架

(2) 恶意敌手

为了应对接收方R作恶的情形, 必须要求R只能知道其中一个公钥所对应的私钥, 为实现这一目的, 可令R随机生成的公钥$P{K_{1 - \sigma }}$由S发送的随机元素C决定, 这使得R只能确定其中一个公钥所对应的私钥, 进而抵御R的恶意行为. 这一构造思想首先由Bellare和Micali^[9]在1989年提出, 并在随机谕言机模型下基于DDH假设进行构造, 之后由Naor和Pinkas^[54]对其进行了通信开销和计算开销的改进优化, 最后便有了到目前仍在使用的经典Base OT原语. 可采用图 4所示的恶意敌手下$\left( \begin{gathered} 2 \\ 1 \\ \end{gathered} \right){\mathit{ - OT}}$协议构造思路.

图 4 恶意敌手下$\left( \begin{gathered} 2 \\ 1 \\ \end{gathered} \right){\mathit{ - OT}}$协议框架

1.2.2 OT扩展协议基础框架

(1) 半诚实敌手

OT扩展协议由Beaver^[12]提出, Beaver将仅需单向函数存在性假设的PRG与OT协议放在一起使用, 构造了计算上安全且高效的OT协议, 只需根据计算安全参数κ执行少量公钥密码操作, 再结合高效的对称密码学原语, 即可产生多项式数量级的m(m≫κ)个OT协议, 并保证半诚实敌手模型下安全, 这对于Impagliazzo和Rudich^[10]提出的“基于更弱的假设构造OT协议是十分困难的”这一结论而言无疑是巨大的进步.

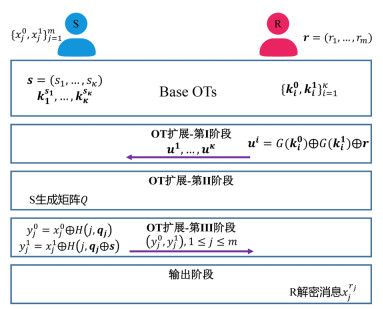
然而, 由于Beaver的协议基于Yao的混淆电路非黑盒地实现了PRG, 所以协议非常低效, 难以应用于实际. Ishai和Kilian等人^[15]针对Beaver的协议存在的效率问题黑盒地使用随机谕言机对κ次Base OT所交换的短种子信息进行长度扩展, 提出了一种半诚实敌手模型下高效的OT扩展协议, 此协议被简记为IKNP协议, 该协议是半诚实敌手模型下OT扩展协议的经典框架, 该框架如图 5所示.

图 5 半诚实敌手下的IKNP OT扩展协议框架

IKNP协议主要可分为3阶段: Base OT阶段、OT扩展阶段和输出阶段, 其中, OT扩展阶段可进一步分为3部分, 包含2次交互. 即对$OT_\kappa ^\kappa $按列进行长度扩展得到$OT_m^\kappa , $然后对$OT_m^\kappa $按行进行长度扩展便得到$ OT_\ell ^m. $更具体的构造方式如图 6所示.

图 6 半诚实敌手下OT扩展协议的构造思路

IKNP协议的核心技巧在于OT扩展阶段的步骤(b), S是通过计算qⁱ按列生成矩阵Q, 生成后再按行看矩阵Q, 会发现${q_j} = {t_j} \oplus (s \cdot {r_j}), $简单移项后可得式(1).

$ {\boldsymbol{{t_j}}} = \left\{ {\begin{array}{*{20}{c}} {{\boldsymbol{{q_j}}} \oplus {\boldsymbol{s}}, \;\;({\boldsymbol{{r_j}}} = 1)} \\ {{\boldsymbol{{q_j}}}, \;\;({\boldsymbol{{r_j}}} = 0)} \end{array}} \right. $

(1)

由式(1), S可用H(j, q_j)和H(j, q_j⊕s)作为对称密钥加密消息$ {\boldsymbol{x_j}}^0, \;{\boldsymbol{x_j}}^1. $使用H函数一方面是为了进行长度扩展, 另一方面是为了破坏混淆q_j和q_j⊕s之间的关系. 又因为t_j只等于q_j和q_j⊕s中的一个, 且R不知道s, 也无法通过H(j, q_j)和H(j, q_j⊕s)中的一个推断出另一个的原象值, 所以R只能解密消息${\boldsymbol{x_j^{{r_j}}}}.$

IKNP协议使用对称密码学原语的OT扩展思想, 既保证消息加解密的效率, 又限制了接收方解密的能力.

(2) 恶意敌手

由于IKNP协议对恶意的发送方和半诚实的接收方是安全的. 因此如果要实现恶意敌手下的OT扩展协议, 只需考虑如何抵御接收方的恶意行为即可.

首先, 接收方R可采取的有效攻击行为非常有限: 因为中途退出协议、发送不真实的选择向量r这样的攻击行为并不能帮助R获取到S的秘密信息, 而且也无法通过密码学方法去约束, 所以不在恶意安全协议所考虑的范围内. 因此, 恶意敌手下的OT扩展协议主要考虑抵御的是以下恶意行为:

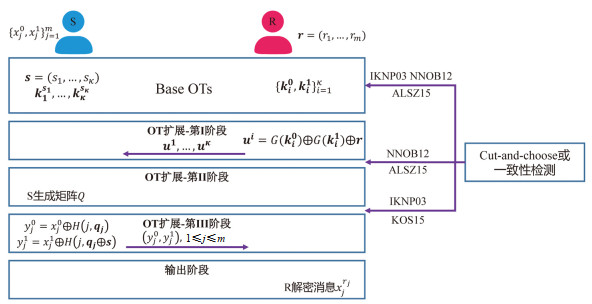
在OT扩展阶段, R需要发送${\boldsymbol{{u^i}}} = {\boldsymbol{{t^i}}} \oplus {\boldsymbol{G}}({\boldsymbol{k_i}}^1) \oplus {\boldsymbol{r}}, \;1 \leqslant {\boldsymbol{i}} \leqslant \kappa , $如果考虑R是半诚实敌手, 则R需要遵守协议, 每次使用的r都应该是相同的; 若R是恶意敌手, R便可将每个uⁱ中的r都替换为不同的值(经过专门构造的值)发送给S, 进而可提取出S的选择向量s, 并解密其他秘密消息${\boldsymbol{x_j}}^{1 - {\boldsymbol{{r_j}}}}.$因为uⁱ之间各不相同且伪随机, S无法分析出R发送的uⁱ是否都采用了相同的r, 所以为抵御R的这一恶意行为需要引入一致性检测, 即让S相信R使用的是同一个r. 目前大多数实现恶意敌手下安全的OT扩展协议构造都是基于半诚实的IKNP协议在不同阶段增加不同类型的一致性检测来抵御恶意行为, 经过归纳后的恶意敌手下安全OT扩展协议框架如图 7所示.

图 7 恶意敌手下安全的OT扩展协议框架

由图 7的框架可以看出, 恶意敌手下安全的OT扩展协议都是在IKNP协议的Base OT阶段、OT扩展阶段加入cut-and-choose或一致性检测来保证恶意安全性. cut-and-choose技术最初由IKNP协议的作者引入, 一致性检测则是后来Nielsen和Nordholt等人^[17]提出通过哈希MAC对Base OT阶段传输的字符串进行哈希以实现恶意安全性的技术. 后者大大降低了实现恶意安全性带来的额外的通信开销、计算开销. 基于文献[17]中的MAC一致性检测思想, Asharov等人^[21]对一致性检测所需的哈希函数执行次数进行了分析和进一步优化. 再后来, Keller等人^[20]则提出了一种更简洁的无需额外增加Base OT数量的一致性检测方法来构造恶意敌手下安全的OT扩展协议, 该检测方法所带来的额外开销较低, 使得目前恶意安全的OT扩展协议开销及运行时间已经近似等同于半诚实敌手下安全的IKNP协议的开销和运行时间, 更多相关细节将在第3节进一步讨论.

2 Base OT协议研究进展

Base OT协议在SMPC协议和OT扩展协议中都是最基础、最核心的密码学原语. 目前广泛使用的Base OT原语以及后续工作都是基于恶意敌手模型下安全的, 故本节对Base OT协议进展的总结也将仅在恶意敌手模型下展开.

但因为现实中不存在真正的随机函数, 学术界认为随机谕言机模型在实现时仍存在安全隐患, 并且以上两个方案^{[9, 54]}只在恶意敌手下实现了对参与方输入隐私的保护, 无法保证执行结果的正确性. 因此后来有很多学者致力于在并发环境下基于更高级别、更为严格的安全定义——UC模型安全性去构建OT协议^{[16, 104, 105]}, 从而不需要依赖于随机谕言机模型, 这虽然带来了更强的安全性, 却也使协议变得过于低效, 例如Peikert等人^[16]提出的协议中需要每个$\left( \begin{gathered} 2 \\ 1 \\ \end{gathered} \right){\mathit{ - OT}}$实例都进行11次指数运算, 并生成一个公共随机字符串(该字符串必须在协议开始阶段由某个可信的随机源生成).

2013年, Asharov等人^[19]将Base OT中有限域上的公钥运算转化为椭圆曲线上的公钥运算, 无论是从密钥长度还是计算速度上, 都使得Base OT阶段的计算开销、通信开销得到了进一步优化.

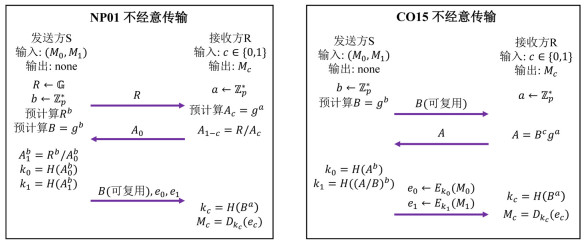
2015年, Chou和Orlandi^[55]基于DH密钥交换协议的变体和随机谕言机模型构造了一种非常简洁的恶意敌手下安全的$\left( \begin{gathered} 2 \\ 1 \\ \end{gathered} \right){\mathit{ - OT}}$协议(简称CO15协议), 通过巧妙地复用消息, 对文献[54]中Base OT协议的通信开销实现了进一步优化, CO15协议与NP01协议流程的对比如图 8所示.

图 8 NP01协议与CO15协议对比图

由图 8易知, 与NP01协议^[54]的3轮通信方案相比, CO15协议^[55]精简了协议所需的数据, 移除不可复用的消息R, 引入可复用消息B, 不但降低了通信开销, 还使得在执行多次OT时, 每次OT只需进行2轮通信, 并且在广域网(wide area networks, WAN)环境下CO15协议的运行速度也会更具优势; 在计算开销上, CO15协议对数据的精简使得协议双方所需执行的运算也得到减少; 在实现上, CO15协议从有限域密码学运算转换到基于椭圆曲线实现公钥操作, 选用了扭曲爱德华兹曲线进行实现, 使得$\left( \begin{gathered} 2 \\ 1 \\ \end{gathered} \right){\mathit{ - OT}}$协议的运算效率与文献[19]的协议中的Base OT相比, 要快1个数量级.

在安全性上, CO15协议^[55]作者一开始声称该方案在UC模型下实现了安全性, 并且可以抵御动态的恶意敌手, 这是一个非常强的安全性, 再加上效率上的优势, 该方案引起了学术界的高度关注, 后来多位学者指出CO15协议的UC安全性证明存在问题^[106−109], 证明了CO15协议并没有达到UC安全性, 其中, 文献[107]指出CO15协议无法在CDH假设下保证UC安全, 也许需要引入一个DDH谕言机才能保证安全性, 这一问题后来由Hauck和Loss使用GapDH假设得到解决^[74], 使得CO15协议在GapDH假设、随机谕言机模型下能够实现UC安全, 并抵御静态恶意敌手的攻击. 此外, 文献[74]也在CO15协议的基础上, 另又提出了一个仅基于CDH假设且满足完全UC安全性的高效$\left( \begin{gathered} {\mathit{n}} \\ 1 \\ \end{gathered} \right){\mathit{ - OT}}$协议.

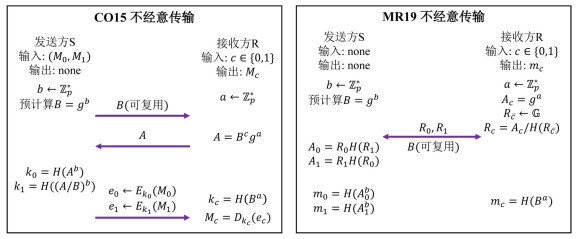
2019年, Masny和Rindal^[56]提出了一个新的基于模拟的安全性概念: 地方性安全(endemic security), 这一安全性概念与已有的OT协议和OT扩展协议所依赖的安全性概念如均匀消息安全性、发送人消息选择安全性相比都要更弱, 其特点在于不再限定参与方提供的消息满足均匀分布, 无论是哪个恶意敌手都可以任意决定消息的分布, 随之换来的是协议通信轮数的降低和协议效率的提升, 并且采用这一安全性概念后仍可结合各种安全性假设来构造OT协议. 作者引入地方性安全概念后, 基于DDH假设和随机谕言机模型构造的OT协议仅需1轮通信即可实现, 并达到了完全可模拟安全性(后简称MR19协议), 而此前CO15协议则需要2轮通信, 且未能实现完全可模拟安全性. 文献[56]中的实验结果表明, MR19协议在WAN环境下的运行速度要明显优于CO15协议, MR19协议与CO15协议流程的对比如图 9所示.

图 9 CO15协议与MR19协议对比图

2020年, Canetti等人^[110]从OT扩展协议轮数的角度分析了前人Base OT协议在扩展为OTE协议时存在的不足, 他们指出基于CO15协议构造OTE协议时通信轮数为4轮, 轮数上并不高效; 而基于MR19协议^[56]构造OTE协议时虽然通信轮数为3轮, 但安全性变弱, 同时每个OT实例所需的指数运算也有所增加, OTE协议的实现效率较低. Canetti等人^[110]以构造最高效的“对OTE协议友好的(OTE-friendly) Base OT协议”为出发点, 提出了一种与CO15效率相近的Base OT协议(后简称CSW20协议), CSW20协议基于可观测随机谕言机(observable random oracle, ORO)模型和CDH假设构造, CSW20与Keller等人^[20]的协议结合构造, 得到的OTE协议的通信轮数为3轮且满足UC安全性, 与CO15和Keller等人^[20]的协议结合构造的4轮OTE协议相比, 通信轮数更少, 这得益于CSW20协议的特点: 最后两轮消息可以安全地与OTE协议的消息并行发送, 从而形成3轮OTE协议, 与CO15协议的实验对比也证明了这一点. CSW20协议与CO15协议流程的对比如图 10所示.

图 10 CO15协议与CSW20协议对比图

现以执行κ次OT为例, 设素数阶乘法循环群G上元素的长度为1 024比特, 传输的消息长度为λ比特, 计算开销只考虑指数运算的次数和需要线上计算的部分, 上述几种不同Base OT协议的对比情况见表 1.

表 1 Base OT协议对比

目前大多数OT协议都是基于传统密码体制提出的, 而自1994年Shor^[111]提出结合量子计算机高效破解离散对数问题以及大整数因子分解的算法以来, 后量子OT协议的设计也一直是重要的研究方向.

现有的后量子OT协议主要可分为两类: 一类是依赖于统计安全构造的后量子OT协议, 基于比如噪声信道存在性(existence of noisy channels)^[112−119]、预分布的关联数据(pre-distributed correlated data)^{[120, 121]}、密码门(cryptogates)^{[122, 123]}等假设构造. 然而这些构造(除了基于可信初始值的构造以外)的假设普遍缺乏实用性, 因此后量子OT协议的研究目前更侧重另一类依赖于计算安全的构造, 比如基于带噪声学习奇偶校验(learning parity with noise, LPN)^[22−25]、带差错学习(learning with errors, LWE)^[124]、伴随式译码问题(syndrome decoding problem, SDP)^[125]等计算困难问题, 其中很多协议能够保证UC模型下的安全性.

David等人^[126]首次提出基于LPN假设的UC模型下安全的OT协议. Peikert等人^[16]首次提出了双模密码系统(dual-mode cryptosystem), 为轮数最优的UC模型下安全的OT协议提供了一个在公共参考字串(common reference string, CRS)模型下的通用框架, 该框架能够基于DDH假设、二次剩余假设、LWE假设进行有效实例化. 刘沫萌^[103]则结合量子平移定理及相关定理对Peikert等人^[16]进行量子安全分析, 进一步证明了该协议在量子敌手环境下的安全性, 并基于环上带差错学习(ring learning with errors, RLWE)假设和随机谕言机模型构建了格上UC安全的OT协议, 其优势在于RLWE假设利用理想格的特殊代数结构能够降低基于LWE假设时的计算、通信开销.

基于伴随式译码问题困难性假设的UC模型下安全OT协议最早由Bernardo等人^[127]提出, 后来Barreto等人^[128]也提出了一种随机谕言机模型下轮最优的UC安全的OT协议框架, 该框架能够基于多种编码或者格的假设(低噪声LPN, SDP, LWE等)进行实例化, 并且基于LPN及SDP假设初始化的OT协议与前人UC模型下安全的方案^{[126, 127]}相比, 实现了数量级的效率优化. 后续也有基于不同的假设(如基于椭圆曲线的同源密码(isogeny-based cryptography)体制)或者模型(如可编程的随机谕言机模型)构造UC模型下安全高效的后量子OT协议、OT扩展协议等工作^[129−131].

3 OT扩展协议研究进展

OT扩展协议的提出主要是为了解决在执行大量OT协议时公钥密码学原语所带来的巨大开销, 其主要思想为参与双方先执行少量Base OT协议交换“种子”信息, 然后通过高效的对称密钥原语(如哈希函数、伪随机数生成器(PRG)、伪随机函数(PRF)等)对种子信息进行长度扩展, 进而生成大量OT实例.

从OT扩展协议的构造方式角度来进行划分, 目前OT扩展协议的构造方式主要可分为: 基于IKNP的OT扩展框架(IKNP-style OTE)和基于伪随机相关生成器(pseudorandom correlation generators, PCG)的OT扩展框架(PCG-style OTE).

其中, 最基础的协议框架是2003年Ishai等人^[15]提出的IKNP协议(见第1.3.2节)框架(IKNP-style OTE), 且后续有关OT扩展协议的很多研究也都是基于IKNP协议开展的.

而基于PCG的OT扩展框架则源自Boyle等人^{[22, 23]}基于dual-LPN假设, 结合PCG技术构造的Silent OT扩展协议, 该协议主要实现的是对于COT的高效扩展, COT不仅是很多SMPC协议预处理阶段的核心构造模块, 也能高效地转换为可选择输入的标准OT扩展协议^[11]. 基于PCG的OT扩展协议框架(PCG-style OTE)因为其通信开销仅和输出的COT数量呈次线性级相关, 成为一种有潜力取代IKNP框架的构造方式, 也为今后OT扩展协议的发展提供了新的研究思路.

3.1 2-选-1 OT扩展协议 3.1.1 半诚实敌手

2013年, Asharov等人^[19]指出在WAN环境下IKNP协议的瓶颈在于通信开销, 并将IKNP协议中的$OT_m^\kappa $原语部分进行了优化, 使得$OT_m^\kappa $原语的通信开销降低了一半, 并且从工程实现的角度对OT扩展协议的实现效率, 比如矩阵转置操作、并行化处理等方面进行了优化, 更多的工程优化方法将在第4节展开介绍.

同年, Kolesnikov和Kolesnikov^[18]注意到IKNP协议中的矩阵U可分解为两个矩阵的异或: $ {\boldsymbol{T}} \oplus {\boldsymbol{R}}, $其中, 矩阵R是由选择向量r重复κ次排列而成, R的每一行都是选择向量r中某一位r_j的简单重复, r_j的取值0或1, 相应地被映射为${0^\kappa }, {1^\kappa }.$所以每一行可看做是对r_j的一个简单重复编码. 为让κ比特能承载更多信息, 作者对R的每一行重新编码, 让r_j可以取自更大的值域$\{ 1, ..., n\} , $设编码方式为C, 即: ${r_j} \to C({r_j}) \in {\{ 0, 1\} ^\kappa }, $将r_j映射成κ比特长的字符串, 在不改变原矩阵的大小的前提下使得r_j的取值范围变大了, 基于此便可实现$\left( \begin{gathered} {\mathit{n}} \\ 1 \\ \end{gathered} \right){\mathit{ - OT}}$扩展协议, 同时这也使$\left( \begin{gathered} 2 \\ 1 \\ \end{gathered} \right){\mathit{ - OT}}$扩展协议的实现更加高效. 通过引入编码思想, $\left( \begin{gathered} 2 \\ 1 \\ \end{gathered} \right){\mathit{ - OT}}$扩展协议的通信开销实现了O(logn) (采用Walsh-Hadamard纠错码, n最大可取到256)数量级因子的优化.

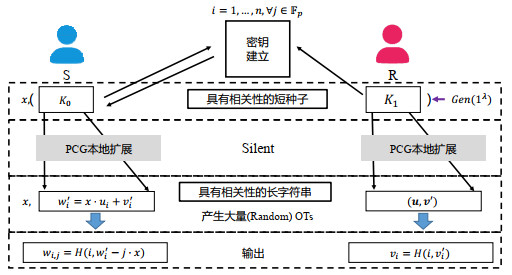
2019年, Boyle等人^[22]提出了半诚实敌手下安全的Silent OT扩展协议, 该协议依赖于dual LPN (dual learning parity with noise)困难性假设和关联鲁棒性(CR)假设. 不同于IKNP协议框架, 该协议是基于2018年Boyle等人^[132]设计的高效伪随机相关生成器(pseudorandom correlation generators, PCG)方案所构造. 协议流程示意图如图 11所示.

图 11 Silent OT扩展协议示意图

Silent OT扩展协议主要分为“种子密钥建立分发”阶段、“本地伪随机长度扩展”阶段和“输出”阶段, 其最大的特点在于: 参与双方仅需在建立阶段执行少量OT协议交换种子信息, 而在OT扩展阶段则无需通信, 在本地执行PCG扩展算法即可将具有相关性的短种子信息扩展为具有相关性的长伪随机比特串, 其扩展长度可达多项式级, 这使Silent OT扩展协议无论是在通信开销还是存储压力方面都具备显著优势, 在图 11中, K₀, K₁为种子密钥, (u, v′)是接收方R的选择向量和私有随机向量, x相当于S的选择向量, 发送方S用$(x, {w'_i})$构建伪随机输出${w_{i, j}} = H(i, {w'_i} - j \cdot x), $ R的输出满足$ H(i, {v'_i}) = {w_{i, {u_i}}}. $经测试, 在不同数量规模的OT协议计算中, Silent OT扩展协议每个ROT实例的平均通信开销仅为0−3比特, 但其存在的问题在于密钥建立阶段的计算复杂度较大, 并且在dual-LPN假设下也不能做到很高效的编码. 因此Silent OT扩展协议仅在通信开销和网络环境为瓶颈的应用场景下可作为IKNP扩展协议的替换方案.

为了降低Silent OT扩展协议在密钥建立阶段以及dual-LPN假设所带来的较大计算开销, Schoppmann等人^[133]提出采用GGM tree技术实现参与双方的密钥建立, 并改用primal-LPN假设进行构造, primal-LPN假设支持更简单高效的编码方式, 这带来了较高的计算效率, 但同时也带来了更多的通信开销.

后来Yang等人^[25]针对文献[133]中存在的通信效率问题进行了一系列优化, 最终根据噪声向量分布特点的不同, 分别构造了半诚实敌手下安全的Ferret Regular和Ferret Uniform两种OT扩展协议, 这两种协议都具备次线性级别的通信复杂度和线性级别的计算复杂度. 与Schoppmann等人^[133]的工作相比, 除去建立阶段, 通信效率提升了大约15倍, 计算效率也有所提升, 建立阶段的开销较大, 但生成较大数量的COT后平均开销也可忽略不计. 与Silent OT扩展协议相比, 在大于50 Mb/s带宽的网络环境中, Ferret OT扩展协议在运行时间上都要比其快至少9倍. 与IKNP类型的协议相比, 因为不需要矩阵转置操作, 在计算上也更为高效.

Silent OT扩展协议的提出开辟了一种新的OT扩展协议构造框架, 这种构造能够对COT进行高效扩展, COT广泛应用于混淆电路协议中, 而且也能很容易地转化为可选择的标准OT (chosen-input OT), 用来构造PSI协议. 基于Silent OT构造的PSI协议^[43]已由Rindal等人在2021年欧密会上提出, 并且基于Vector-OLE和PaXoS数据结构提出了一种新的批量不经意伪随机函数(oblivious pseudorandom function, OPRF)构造, 经过实验验证, 该协议的通信开销非常低, 在低带宽的通信环境下效率都要大幅优于此前最高效的PSI协议^{[13, 41, 42]}.

3.1.2 恶意敌手

恶意敌手下安全协议的最终设计目的是在满足恶意安全性的同时, 其效率尽可能接近半诚实敌手下安全协议的效率.

Ishai等人^[15]在提出半诚实敌手下安全的IKNP协议的同时, 也给出了抵御恶意敌手的方案, 为保证恶意安全性, 该方案引入了cut-and-choose技术, 为保证s比特的统计安全性, 此协议相当于在并发执行s次普通半诚实OT扩展协议的基础上增加了发送方发起挑战、接收方公开相应秘密值、接收方发送消息纠正位、发送方发送纠正后的最终密文信息这一系列通信过程. 在当时, 采用cut-and-choose技术^[134]不但能够抵抗恶意敌手攻击, 而且避免了零知识证明这样复杂低效的操作, 此外, 后续还有很多工作专注于优化cut-and-choose技术所带来的额外开销^{[29, 32, 135−141]}.

近年来, 恶意敌手下安全的OT扩展协议的运行成本已经大大降低, 并优化至固定开销.

2012年, Nielsen等人^[17]在随机谕言机模型下构造了UC安全的、可抵御恶意敌手的高效OT扩展协议(简称NNOB12协议). 其主要贡献在于首次引入信息论意义下的消息认证码来完成对双方隐私输入的一致性检测, 以抵抗恶意敌手替换输入信息的恶意行为. 与此前对每个扩展后得到的OT进行一致性检测的方案^{[142, 143]}不同, NNOB12协议^[17]是对每个Base OT进行一致性检测, 通过哈希函数实现, 共需$\left\lceil {\frac{8}{3}\kappa } \right\rceil (\kappa = 128)$个恶意安全的Base OT实例, 进一步地, 可通过PRG将这些Base OT实例高效扩展为大量恶意安全的OT实例, 从而实现OT扩展协议, 这也成为当时最高效的恶意敌手下安全的OT扩展协议.

用哈希函数实现一致性检测的思想在后来得到沿用与改进. 2015年, Asharov等人^[21]在NNOB12协议的基础上给出了一种进一步降低计算及通信开销的恶意敌手下安全的OT扩展协议(简称ALSZ15协议), 他们首先移除了NNOB12协议中“公开一半数量Base OT”的步骤, 移除后仅需$\ell = \kappa + \rho = 168$个Base OT实例, 但随之换来的是一致性检测数量的增加. 如果将每个Base OT实例看作是一个顶点, 每次一致性检测看作是不同顶点之间的边, 则$\ell {\mathit{ = }}168$时所构成的完全图需要14 028次一致性检测, 计算开销过大, 于是一致性检测的数量成为新的瓶颈. 作者通过证明发现发送方只需对每个待检测节点都随机生成一个μ-正则图(μ取值较小, 如μ=3或甚至μ=2), 并让接收方提供相应μ-正则图的检测哈希值进行一致性检测, 即可保证“坏点集合”与“好点集合”之间至少有ρ(ρ=40)个顶点相匹配, 这一结论能大大减少一致性检测的次数, 并且使敌手通过一致性检测的成功率不超过2^−ρ, 这一优化思想的示意图如图 12所示.

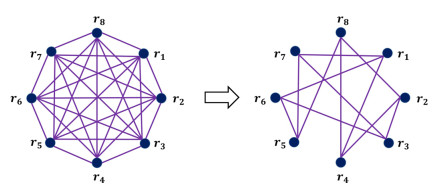
图 12 ALSZ15协议一致性检测优化示意图

进一步地, 作者考虑在此结论的基础上增加少量的Base OT来降低一致性检测的数量, 通过调整参数$\ell , {\mathit{ }}\mu $及实验对比, 在LAN环境下可取$\ell = 190, {\mathit{ }}\mu = 2, $一致性检测数量仅需380次, 与半诚实的IKNP协议相比, 仅额外增加了20%的运行时间和50%的通信开销.

同样是在2015年, Keller等人^[20]提出了一种更为简洁高效的一致性检测方法(作者也称其为“相关性检测”), 在随机谕言机模型下构造了恶意敌手下安全的$\left( \begin{gathered} 2 \\ 1 \\ \end{gathered} \right){\mathit{ - OT}}$扩展协议(简称KOS15协议), 与半诚实敌手下安全的IKNP协议相同, 该协议仅需执行κ次Base OT实例, 再在OT扩展阶段通过PRG额外扩展出κ+s (s为统计安全参数)个ROT实例即可实现. 与半诚实的IKNP协议相比, 增加的通信复杂度仅为O(κ), 并且一致性检测的通信开销与生成的OT实例数量相独立. 最终实现结果表明该协议运行时间与IKNP协议相比不超过5%, 是IKNP框架目前最高效的恶意敌手下安全的$\left( \begin{gathered} 2 \\ 1 \\ \end{gathered} \right){\mathit{ - OT}}$扩展协议, 后来Keller等人^[33]用其构造高效的恶意敌手下安全的两方算术电路协议MASCOT, MASCOT预处理阶段基于OT实现, 与此前基于部分同态加密技术实现预处理阶段的SPDZ协议^[144]相比效率提升了200倍以上.

另一方面, 在低带宽的WAN网络环境下, 如何降低通信开销是OT扩展协议亟需解决的又一问题. Boyle等人^[23]分析了Silent OT扩展协议^[22]的局限性在于: (1) 建立阶段需${\mathit{O}}\left( {\log \frac{{4m}}{t}} \right)$(m为OT数量, t为噪声向量的汉明重量)轮通信, 轮数过高; (2) 协议仅在半诚实敌手下安全; (3) 对协议效率的估计缺乏具体工程实现的实验数据支撑. 其中, “通信轮数过高”以及“仅在半诚实敌手下安全”这两点局限是由协议采用的分布式点函数(distributed point function, DPF)密钥生成协议^[145]所决定的. 于是作者将此前协议中使用的DPF替换为更简单的基于GGM tree的可穿孔伪随机函数PPRF (puncturable pseudorandom function)原语, 构造了恶意敌手下安全且仅需2轮通信的Silent OT扩展协议, 并给出了具体实现, 该协议成为当时恶意敌手下安全的在低带宽WAN网络环境中最高效的$\left( \begin{gathered} 2 \\ 1 \\ \end{gathered} \right){\mathit{ - OT}}$扩展协议.

至此, Silent OT协议的瓶颈问题从通信开销转移到了建立阶段的计算开销. Schoppmann等人^[133]通过引入primal-LPN假设实现了计算效率的优化, 但是仅构造了半诚实敌手下安全的协议, 如何在此基础上扩展为恶意安全成为了新的问题. 后来Yang等人^[25]对这一问题给出了解决方案, 不但在文献[133]中提到的方案的基础上很好地平衡了计算开销与通信开销, 还采用高效的检测技术保证协议正确性和一致性, 仅需额外生成κ个COT实例, 即可将提出的半诚实OT扩展协议Ferret Regular和Ferret Uniform都分别扩展为恶意敌手下安全的协议. 最后实验表明平均每个COT实例上的耗时仅比半诚实协议的COT实例耗时增加了1−3 ns, 与KOS15协议类似, 该检测技术的构造已经近似于最优.

由于文献[19]通过算法优化很好地降低了OT扩展协议的计算开销, 并指出目前OT扩展协议的主要瓶颈在于通信开销, 即低带宽WAN环境下的协议效率, 因此下面仅从通信开销的角度对不同OT扩展协议进行了对比, 分析对比情况见表 2. 表 2中, 设OT扩展协议产生m个ROT/COT实例, 计算安全参数$\kappa = 128, $统计安全参数s=40, 文献[18]的编码取值范围为[n], t为文献[22]中噪声向量的汉明重量, μ为文献[21]中的一致性检测中正则图的度数. c为Ferret-Uni和Ferret-Reg协议的迭代轮数, 如果COT的实例是按需生成则c会按需增加, 而如果要生成的COT数量已知, 则c=1. 通信开销不考虑Base OT部分, 仅考虑生成m个ROT/COT实例所需的通信开销, 通信轮数比较中统一将Base OT记为1轮, 并且仅考虑生成ROT/COT所需的通信轮数.

表 2 OT扩展协议通信开销分析比较

3.2 n-选-1 OT扩展协议 3.2.1 半诚实敌手

如第3.1节中所提到的, 2013年Kolesnikov等人^[18]对IKNP协议引入的编码框架扩展将$\left( \begin{gathered} 2 \\ 1 \\ \end{gathered} \right){\mathit{ - OT}}$扩展协议推广为$\left( \begin{gathered} {\mathit{n}} \\ 1 \\ \end{gathered} \right){\mathit{ - OT}}$扩展协议(简称KK13协议). 2016年, Kolesnikov等人^[13]对KK13协议^[18]中的编码进行了改进, 他们注意到: (1) KK13协议中的编码方式C不需要解码功能; (2) C只需保证对任意不同的$r, {\mathit{ }}r', $ $C(r) \oplus C(r')$的汉明重量不小于计算安全参数κ.

进一步地, 作者认为只需保证$C(r) \oplus C(r')$的汉明重量小于κ的概率是可忽略的即可, 于是将编码C替换为随机函数C, 该随机函数对于任意长度的输入r, 都可以得到一个相应的输出C(r), 并且在安全性方面, 设HW(⋅)为汉明重量, 需保证:

$ \Pr [HW(C(r) \oplus C(r'))] \leqslant {2^{ - \kappa }} $

(2)

即不同的$C(r), {\mathit{ }}C(r')$之间的汉明距离小于安全参数κ的概率是可忽略的, 作者证明了当随机函数C的输出长度至少为3.5κ时, 可以保证安全性.

由于r取值任意, 故相当于n=∞, 且该协议所实现的实质上为ROT, 因此文献[13]中的协议便成功地将$\left( \begin{gathered} {\mathit{n}} \\ 1 \\ \end{gathered} \right){\mathit{ - OT}}$扩展协议推广为随机$\left( \begin{gathered} \infty \\ 1 \\ \end{gathered} \right){\mathit{ - OT}}$扩展协议, 基于该OT扩展协议可高效地实现OPRF模块, 从而构造出在当时最高效的半诚实PSI协议(后简称KKRT16协议), 并且其最大优势在于计算效率, 到目前为止, 该PSI协议都是在LAN运行环境下最高效的PSI协议.

3.2.2 恶意敌手

2017年, Orrù等人^[14]基于Kolesnikov等人^[18]提出的半诚实敌手下安全的KK13协议, 设计了恶意敌手下安全的$\left( \begin{gathered} {\mathit{n}} \\ 1 \\ \end{gathered} \right){\mathit{ - OT}}$扩展协议(简称OOS17协议). OOS17协议就是在KK13协议的基础上增加了简单的一致性检测从而实现了主动安全性. 但在实际构造过程中仍面临着一些技术上的挑战, 与基于IKNP协议的恶意敌手下安全的KOS15协议不同, KOS15协议的一致性检测是为验证所有的字符串都是$({x_i}, {x_i} + b)$的形式, 且b固定不变, 而OOS17协议必须要确保字符串形式为${x_i} + b \odot C({m_i}), $其中, C通过纠错码对m_i进行编码, 故KOS15协议的方法无法直接应用于这一情形. 最终, OOS17协议通过选用二元线性码, 利用其加法同态性质解决了一致性检测的构造问题.

另一方面, 通过使用合适的二元线性码, n可以取至安全参数的指数级大小, 这远远超出了KK13协议中使用的WH编码的取值范围(n≤256), 而在整体开销上与半诚实协议相比只增加了5%−30%, OOS17协议是目前为止最高效的恶意敌手下安全的$\left( \begin{gathered} {\mathit{n}} \\ 1 \\ \end{gathered} \right){\mathit{ - OT}}$扩展协议.

2020年, Pinkas等人^[41]基于OOS17协议构造了一个高效且恶意安全的PSI协议, 其运行效率与半诚实敌手下安全的KKRT16协议^[13]相近.

4 OT扩展协议的实现效率优化进展

本节以图 5的IKNP协议为基础框架, 从实现效率角度出发, 围绕OT扩展协议中的几个模块: Base OT、OT扩展-第Ⅰ阶段、OT扩展-第Ⅱ阶段、OT扩展-第Ⅲ阶段依次介绍工程实现上的计算和通信效率优化方法.

4.1 Base OT阶段

Base OT阶段的主要特点是基于公钥密码学构造, 在实现时计算效率较低、通信开销较大, 因此在实现上可考虑通过将有限域上的模幂运算转换为椭圆曲线上的倍点运算以降低计算和通信开销, 也可结合多线程技术进行计算效率的优化.

4.1.1 椭圆曲线密码学优化Base OT

对于Base OT阶段的公钥密码运算, 文献[146]在实现过程中发现将基于有限域密码学(finite field cryptography, FFC)的运算换成椭圆曲线密码学(elliptic curve cryptography, ECC)的运算后虽然降低了通信开销, 但计算开销反而比FFC要大, 作者分析原因是Java虚拟机本身带来的额外开销使得ECC执行效率太低, 根据NIST的推荐^[147], 对称加密算法(SYM)、FFC、ECC三者的密钥长度及安全性对应关系见表 3.

表 3 安全性参数和推荐的密钥长度

为更好地进行比对, 后来Asharov等人^[19]通过C++调用Miracl函数库实现ECC, 并采用性能表现最好的Koblitz曲线, 同时用C++调用GMP库实现FFC, 最终实验数据表明, 在中等密钥长度以及长密钥长度下, ECC在计算速度上均要优于FFC, 同时通信开销也大大降低.

2015年, Chou和Orlandi^[55]提出的CO15协议简洁高效, 并在实现时选用了安全性和性能都得到进一步改进的基于扭曲爱德华曲线的Ed25519签名算法来实现$\left( \begin{gathered} 2 \\ 1 \\ \end{gathered} \right){\mathit{ - OT}}$协议, 在长密钥的安全级别下, 与文献[19]基于随机谕言机模型假设下的Base OT实现结果相比, CO15协议中Base OT的运算效率要快1个数量级.

4.1.2 多线程Base OT

当需要实现大量OT时, 一个很自然的优化思路便是并行计算, 通过将运算任务分配给多个不同的线程并行处理, 以实现计算效率的优化, Henecka和Schneider^[146]基于FastGC框架^[148]对其中的Base OT进行了并行计算的优化, 提出对κ次Base OT实现分组并行化, 作者将计算集中的公钥操作分配给N个线程, 这样每个线程只需要执行κ/N个Base OT, 并且彼此独立. 其实验结果表明当在双核处理器下采用4线程执行Base OT时, 计算效率较单线程提升了接近1倍.

4.1.3 批处理Base OT

批处理Base OT (batching Base OT)一般的实现方式是借助Base OT协议中发送方提供的可复用的消息(如第2节所示), 接收方在本地构造出128个OT实例密文, 然后一次性批量发送给发送方, 通过两轮交互即可完成Base OT阶段. 但在2021年亚密会上McQuoid等人^[149]指出前人通过简单地重用协议消息来批量生成OT实例的实现方式通常是不安全的, 并且会对某些OT扩展协议(如OOS17协议^[14])的安全性造成影响, McQuoid等人通过在不同OT实例之间实施域分离(domain separation)技术, 即在哈希函数中包含该OT实例的索引来解决这一安全性问题, 并对更改后的安全性进行了证明, 能够保证方案原有的安全性. 最后, 对现有Base OT方案^{[54−56, 150]}实现了安全批处理改进和实验分析, 以文献[56]为例, 结合批处理技术后在低延迟和高带宽环境下运行效率分别优化了18%和11%.

4.2 OT扩展-第Ⅰ阶段

对于OT扩展-第Ⅰ阶段, 主要的瓶颈在于较为繁重的通信开销, 而对该部分并行化处理是一个可行的通信效率优化思路, Henecka和Schneider^[146]提出对需要发送m条消息的OT扩展协议按M=128为单位进行分组, 共分为B=m/M组, 逐组完成OT扩展, 同时每组的运算过程并行处理, 以降低内存的占用率, 虽然整个OT扩展协议的内存占用率得到了优化, 但是相比于之前的FastGC框架^[148]这一处理增加了通信的轮数.

针对这一问题, 文献[19]对整个OT扩展协议进行了分块, 交由N个线程并行处理, 每个线程处理m/N个输入, 并在发送方和接收方之间为每个线程都单独开设Socket, 由操作系统完成调度, 以实现通信上的并行化.

4.3 OT扩展-第Ⅱ阶段

OT扩展-第Ⅱ阶段的主要操作为发送方S根据第Ⅰ阶段收到的消息生成矩阵Q, 该过程在实现上一方面可通过矩阵转置实现算法的优化来提升计算效率, 另一方面可通过PRG的实现效率优化来提升矩阵按列扩展时的计算效率.

4.3.1 矩阵转置实现优化

密码协议的计算复杂度通常是通过计算密码原语的调用次数来衡量的, 这是因为它们的开销往往在运行时占主导地位. Asharov等人^[19]则认为非密码学运算开销也可能对计算开销造成较大的影响, 最终他们发现OT扩展协议中的矩阵转置操作成为了计算效率上的瓶颈.

注意到在IKNP协议中, 接收方R生成的两个m×κ阶矩阵T和U是按列生成、按列存储的, 发送方S收到的m×κ阶矩阵Q也是按列接收、按列存储的. 但是在最后一步S发送消息$(y_j^0, y_j^1)$给R, 其中, $y_j^0 = x_j^0 \oplus $ $H(j, {q_j}), y_j^1 = x_j^1 \oplus H(j, {q_j} \oplus s), $以及最后R解密消息${z_j} = y_j^{{r_j}} \oplus H(j, {t_j}), $却均是在按行读取矩阵的元素, 按行进行哈希计算, 这一前后读取方式的不同, 可能会使计算机频繁发生缺页中断, 执行页面调度操作, 这将大大降低读取过程的效率, 而先进行矩阵转置, 再读取元素便能很好地利用空间局部性原理避免这一问题, 因此矩阵转置运算对于OT扩展协议十分必要.

经过实验, Asharov等人^[19]得到了OT扩展协议的主要计算开销分布, 见表 4.

表 4 OT extension主要计算开销占比^[19]

由表 4可知矩阵转置运算在OT扩展中是一项很重要的开销, 作者便对OT扩展中的矩阵转置算法进行优化, 采用了复杂度仅为O(nlogn)的Eklundh算法^[151], 然后通过在一个寄存器中加载多个比特来并行执行多个交换操作, 将该算法复杂度降为${\mathit{O}}\left( {\left\lceil {\frac{n}{r}} \right\rceil \log n} \right)$(r为CPU的寄存器大小, 这里r=64), 在作者的实验结果中, 矩阵转置部分的耗时从7.1 s缩短为0.76 s.

后来在文献[13]中, Kolesnikov等人对KKRT16协议的实现也沿用了Asharov等人^[19]的代码中通过Eklundh算法优化OT扩展协议的矩阵转置操作. 因此采用高效的矩阵转置算法也已经成为OT扩展协议实现优化的重要手段.

4.3.2 PRG的实现优化

对于PRG, 可以考虑3种实现方式: CTR-模式的分组密码、流密码和哈希函数. 其中最常用的是通过分组密码实现, 这是因为现代CPU的硬件支持, AES的实现比SHA-1、SHA-256更高效, 故在2013年, Henecka和Schneider^[146]将用于长度扩展的PRG的输出分成多块并分别用AES在CTR-模式下加密, 然后又采用了电路门数更少的AES电路, 提高了运算效率; 进一步地, 作者也尝试性地提出或许可将AES进一步替换为安全性略低, 但是效率可以大大提升的超轻量分组密码算法PRESENT.

后来在2015年的欧密会上, Albrecht等人^[152]提出了针对SMPC协议、零知识证明以及全同态加密的高效计算而设计的分组密码算法: LowMC. 与AES相比, LowMC算法具有相当少的与门数量和较小的电路深度. 作者分别对SMPC协议和全同态加密协议两个场景进行不同分组密码算法的实现比较, 表明了当加密大量数据时, LowMC的计算和通信效率是使用AES算法时的5倍. 2019年Kales等人^[46]所设计的移动端PSI协议中便将GC-PSI中实现PRF所需的AES算法替换为LowMC算法, 经过合适的参数选取, 将原有协议的通信开销优化了8.2倍.

4.4 OT扩展-第Ⅲ阶段

OT扩展-第Ⅲ阶段中发送方S加密消息对的安全性依赖于RO假设或CRH假设, 其中CRH假设是比RO假设更弱的安全性假设. 通常在协议设计和分析时都会用哈希函数来模拟RO和CRH以保证实现的安全性.

就哈希函数的实现效率而言, 可以考虑采用BLAKE2哈希算法^[153]来优化. 该算法的计算速度比常见的MD5、SHA-1、SHA-2、SHA-3都要快, 并且其安全性与SHA-3相当. 在2017年, Orrù等人^[14]提出的恶意安全$\left( \begin{gathered} {\mathit{n}} \\ 1 \\ \end{gathered} \right){\mathit{ - OT}}$扩展协议的实现中便采用了这一算法. 2020年, O’Connor等人首次在Real World Crypto 2020上发布了最新的研究成果: BLAKE3哈希算法, 并对其进行开源. 就现有攻击而言, BLAKE3是同时保证安全性与效率的最优哈希算法, 因此在以后的研究工作中也可以考虑使用BLAKE3进一步提升OT扩展协议的实现效率.

由于AES具备良好的硬件实现支持, 它的实现效率是一般哈希函数(SHA-3, SHA256等)的15−50倍^[75], 很多SMPC协议对于RO和CRH并不是采用哈希函数进行实例化, 而是采用固定密钥的AES算法, 以保证计算效率. 但这些协议的实现的方式通常各不相同, 且没有充分的安全性证明支撑, 这是因为采用固定密钥的AES的实现依赖的是随机置换模型假设下的安全性, 并不能从理论上直接保证这是一种安全的实现方式.

针对这一问题, Guo等人^[75]发现很多SMPC领域的知名代码库(比如libOTe, EMP等)中对于OT扩展协议和混淆电路的RO、CRH实例化代码都存在着安全问题. 进一步地, 他们针对不同OT扩展协议中H函数的安全性需求考虑了几种关联鲁棒性的变体概念, 并针对不同假设给出基于固定密钥的AES(随机置换)的H函数构造. 现假设固定密钥为k的随机置换$\pi = {F_k}:{\{ 0, 1\} ^{128}} \to {\{ 0, 1\} ^{128}}, $ OT扩展协议中H函数的安全构造方式见表 5, 其中, TCR为可调关联鲁棒性(tweakable correlation robustness, TCR)假设.

表 5 OT扩展协议中H函数的安全构造方式

5 OT协议的应用

OT协议最早用于构建公平的秘密交换协议^[1]、抛币协议^{[7, 8]}、公平电子合同签署协议^[2]、消费者网上购物的隐私保护协议^[154]、零知识证明协议^{[6, 9]}等安全计算协议, 这里主要介绍近年来与实际应用场景结合较紧密的OT协议应用: SMPC协议、隐私集合交集计算、私有信息检索和不经意多项式求值.

5.1 安全多方计算

19世纪80年代末, 有两个重要的SMPC协议被提出: Yao的混淆电路协议^[15]以及GMW^[63]协议. 这两个协议都使用了OT协议作为其中基础且重要的密码学原语, 以实现关键隐私信息的交换.

混淆电路协议(garbled circuit, GC)是基于大整数分解的困难性问题提出的一种通用的半诚实敌手模型下的安全两方计算协议, 其核心思想是将函数看作布尔电路来实现. 布尔电路与算术电路相比, 虽然在算术运算上, 特别是乘法运算, 不如算术电路执行高效, 但它可以很容易地实现比较运算^[155]. 并且因为混淆电路协议可以非交互式地完成, 所以协议能在常数轮内执行完毕^[156]. 后来Lindell和Pinkas^[157]首次对混淆电路的构造进行了完整详细的阐述以及严格的安全性证明. 在混淆电路协议中发送方负责生成混淆电路、每个电路门对应的“混淆计算表”, 以及每个输入对应的密钥; 接收方需要通过OT协议从发送方获取每个电路门与自己输入对应的密钥, 因为这样才能防止发送方知道接收方的输入比特, 并防止接收方获得输入比特所对应密钥以外的信息, 保护发送方与接收方的隐私.

而Goldwasser等人^[63]提出的GMW协议, 则是基于布尔电路的另一种SMPC协议的实现方案. GMW协议分别讨论了异或(XOR)、非(NOT)、与门(AND)的安全计算的实现方法, 其中与门(AND)的安全计算需要知道彼此的隐私信息才能完成计算, 所以每个与门(AND)的实现都需要执行4-选-1 OT协议来保证隐私信息的安全交换, 故GMW协议的运算复杂度与电路的大小(与门数)正相关, 电路规模越大, GMW协议的开销就越大, 且该协议是交互式的; 而Yao的混淆电路协议的复杂度只与参与方的输入比特长度正相关, 并且对于每个电路门的计算都是对称加密运算, 速度快, 此外协议是非交互的, 因此能在常数轮通信运行完毕. 所以通常混淆电路协议要比GMW协议更高效, 也更容易被应用在大规模且复杂的场景中^[105].

在混淆电路协议与GMW协议提出后, Kilian^[6]展示了如何通过OT协议建立一般的安全两方计算协议, 更表明了, 给定一个理想的OT协议谕言机, 就可以在不依赖其他复杂理论假设的条件下, 无条件地、安全地构造一个安全两方计算协议. 而后续Crépeau等人^[158]又将该结论推广到SMPC协议中. 但要注意的是这些构造并不高效, 所以应该侧重把它们看作是可行性意义上的结论^[159].

随着安全多方计算技术的不断发展, 为了满足不同的场景需求, 安全多方计算协议也被不断地优化并产生了各种各样的协议变体. 对于安全多方计算协议的设计者来说, 将合适的安全协议应用到相匹配的场景中是较容易的, 但是对于非专家来讲, 为特定的部署场景选择合适并高效的计算协议仍存在困难. Daniel等人^[15]基于OT协议提出了一个安全两方计算框架ABY. ABY框架是一个混合协议框架, 涉及算术共享、布尔共享和Yao共享3种共享方案, 主要解决共享方案之间的转化问题, 可以实现对这3种方案的自动化选择. 在ABY中, 为了提高算术共享的计算效率, 他们使用COT扩展协议代替同态加密来构造算术乘法三元组. 通过实验对比发现, COT扩展协议的使用可以显著缩短计算时间且降低通信开销.

ABY框架、混淆电路协议在近几年机器学习隐私保护方案中得到广泛应用与进一步发展, 比如基于秘密共享的SecureML^[51]、ABY^3[52]和基于混淆电路、OT协议的QUOTIENT^[53]. SecureML基于秘密共享来实现随机梯度下降过程, 用于实现两方训练的线性/逻辑回归和深度神经网络(deep neural network, DNN)模型训练, 在ABY框架基础上开发了新技术来支持秘密共享的定点整数运算, 并提出对非线性函数(如sigmoid和softmax)的MPC友好替代方案. ABY³则是首次提出了一个恶意敌手下安全的三方ABY框架, 支持算术、二进制、混淆电路之间的高效转换, 提供了新的线性/逻辑回归和DNN训练方法. QUOTIENT是2019年提出的利用OT协议、混淆电路的安全两方DNN模型训练方法, 结合最先进的DNN训练的关键组件, 如层规范化(normalization)和自适应梯度(adaptive gradient)方法进行优化, 与此前最优的DNN训练方案SecureML相比, 在WAN环境下整体效率提升了50倍, 在绝对准确率上提升了6%.

综上, OT协议及相关变体已成为SMPC协议的关键基础构件, 并得到广泛应用, 而OT协议及相关变体本身的效率, 也往往成为了使用它的协议的性能瓶颈^[105], 所以对OT协议及相关变体的每一步研究与优化都将换来SMPC相关研究方向及协议框架的实现效率上的提升.

5.2 隐私集合交集计算

隐私集合交集计算作为SMPC领域一个热门问题, 具备十分广泛的应用前景, 如: 联系人发现^{[15, 46]}、广告转化率计算^{[37, 47−49]}、安全的人类基因检测^[160]等. 基于OT扩展协议构造的PSI协议要比基于代数和公钥技术构造的PSI协议更加高效, 无论是基于混淆电路^[15]、GMW协议^[63]实现还是近几年主流且高效的PSI协议^{[13, 35, 37, 39]}都需要OT协议来完成构造, 因为无论是$\left( \begin{gathered} 2 \\ 1 \\ \end{gathered} \right){\mathit{ - OT}}, $ $\left( \begin{gathered} {\mathit{n}} \\ 1 \\ \end{gathered} \right){\mathit{ - OT}}$还是$\left( \begin{gathered} {\mathit{n}} \\ k \\ \end{gathered} \right){\mathit{ - OT}}, $都等价于OPRF这一概念, 并且基于OT的PSI^[35−43]本质就是接收方对每个输入元素以不经意的方式求PRF后再与发送方输入元素的PRF值进行比对求交集的过程. 因此如何以更低的计算开销、通信开销实现OPRF是OT优化的重要方向. $\left( \begin{gathered} 2 \\ 1 \\ \end{gathered} \right){\mathit{ - OT}}$扩展协议^{[15, 19, 21]}和$\left( \begin{gathered} {\mathit{n}} \\ 1 \\ \end{gathered} \right){\mathit{ - OT}}$扩展协议^{[13, 18]}的发展都使得需要生成大量OT实例的PSI协议的计算开销、通信开销得到了很好的优化^{[13, 35, 37, 40, 43]}, 并且近两年$\left( \begin{gathered} {\mathit{n}} \\ k \\ \end{gathered} \right){\mathit{ - OT}}$也成为了构造高效PSI协议^{[39, 42]}的重要模块, 它等价于多点不经意伪随机函数(multi-point OPRF).

5.3 私有信息检索

私有信息检索协议^[161]允许用户从数据库中检索所选项目, 同时向拥有数据库的服务器隐藏该项目的标识. 但PIR只要求对用户隐私进行保护, 对数据库的隐私保护没有要求, 为了能进一步保护数据库的隐私, 便有了对称私有信息检索协议SPIR^[162], SPIR是具有附加限制的PIR协议, “对称”是指在检索的过程中客户端和服务端都具有隐私保护的需求.

$\left( \begin{gathered} {\mathit{n}} \\ 1 \\ \end{gathered} \right){\mathit{ - OT}}$协议能够很好地满足这一需求去构造SPIR^[64], 并且SPIR协议与$\left( \begin{gathered} {\mathit{n}} \\ 1 \\ \end{gathered} \right){\mathit{ - OT}}$协议之间可以很容易地进行相互转化^{[162, 163]}.

5.4 不经意多项式求值

不经意多项式求值的研究始于Naor和Pinkas在1999年提出的方案^[64], 通过OT协议的变体: $\left( \begin{gathered} {\mathit{n}} \\ 1 \\ \end{gathered} \right){\mathit{ - OT}}$协议来完成构造, 并且OPE也能够用于解决PSI问题, 比如文献[164−166], 而基于OPE实现的PSI协议并没有直接基于OT协议实现的PSI协议高效^[35].

6 总结与展望

综上所述, 从Base OT协议, 到$\left( \begin{gathered} 2 \\ 1 \\ \end{gathered} \right){\mathit{ - OT}}$扩展协议、$\left( \begin{gathered} {\mathit{n}} \\ 1 \\ \end{gathered} \right){\mathit{ - OT}}$扩展协议, 无论是侧重于效率优化的半诚实敌手模型, 还是效率较低的恶意敌手模型, 协议本身的改进加上工程实现技术的成熟使得近年来OT协议、OT扩展协议在安全性和实用性上都取得了显著的研究进展, 推动了SMPC技术在不同应用场景下的落地, 比如隐私保护集合交集运算. 相信在不久的将来我们有望看到可靠高效的SMPC技术在日常生活中得到普及应用, 为数据安全与隐私保护领域作出更多贡献.

结合当前OT协议和OT扩展协议的研究进展, 目前可进一步研究的问题包括但不限于.

(1) 满足UC安全性的高效OT扩展协议、COT扩展协议的设计及其在不同安全多方计算协议中的应用和测试;

(2) 将解决了通信开销瓶颈的Silent OT扩展协议和Ferret OT扩展协议应用到不同SMPC协议以及机器学习隐私保护方案中, 并做进一步的开销对比以及可用性分析;

(3) 基于PCG的OT扩展协议框架构造高效的$\left( \begin{gathered} {\mathit{n}} \\ 1 \\ \end{gathered} \right){\mathit{ - OT}}$扩展协议;

(4) 结合分布式的思想实现OT扩展协议;

(5) rate-1 OT的计算和通信效率优化、rate-1 OT思想与OT扩展协议的结合以及其他变体应用的研究.

使用已有的最新可用的工程优化技术进行实现对比, 并探索更多易普及的工程优化思路.

参考文献

[1]	Rabin MO. How to exchange secrets with oblivious transfer. IACR Cryptol. ePrint Arch., 2005, 2005(187).
[2]	Even S, Goldreich O, Lempel A. A randomized protocol for signing contracts. Communications of the ACM, 1985, 28(6): 637-647. [doi:10.1145/3812.3818]
[3]	Líšková L, Stanek M. Efficient simultaneous contract signing. In: Proc. of the IFIP Int'l Information Security Conf. Boston: Springer, 2004. 441-455.
[4]	Staneková L, Stanek M. Fast contract signing with batch oblivious transfer. In: Proc. of the IFIP Int'l Conf. on Communications and Multimedia Security. Berlin, Heidelberg: Springer, 2005. 1-10.
[5]	Brassard G, Crépeau C, Robert JM. All-or-nothing disclosure of secrets. In: Proc. of the Conf. on the Theory and Application of Cryptographic Techniques. Berlin, Heidelberg: Springer, 1986. 234-238.
[6]	Kilian J. Founding cryptography on oblivious transfer. In: Proc. of the 20th Annual ACM Symp. on Theory of Computing. 1988. 20-31.
[7]	Blum M. Coin flipping by telephone a protocol for solving impossible problems. ACM SIGACT News, 1983, 15(1): 23-27. [doi:10.1145/1008908.1008911]
[8]	Harn L, Lin HY. An oblivious transfer protocol and its application for the exchange of secrets. In: Proc. of the Int'l Conf. on the Theory and Application of Cryptology. Berlin, Heidelberg: Springer, 1991. 312-320.
[9]	Bellare M, Micali S. Non-interactive oblivious transfer and applications. In: Proc. of the Conf. on the Theory and Application of Cryptology. New York: Springer, 1989. 547-557.
[10]	Impagliazzo R, Rudich S. Limits on the provable consequences of one-way permutations. In: Proc. of the 21st Annual ACM Symp. on Theory of Computing. 1989. 44-61.
[11]	Beaver D. Precomputing oblivious transfer. In: Proc. of the Annual Int'l Cryptology Conf. Berlin, Heidelberg: Springer, 1995. 97-109.
[12]	Beaver D. Correlated pseudorandomness and the complexity of private computations. In: Proc. of the 28th Annual ACM Symp. on Theory of Computing. 1996. 479-488.
[13]	Kolesnikov V, Kumaresan R, Rosulek M, et al. Efficient batched oblivious PRF with applications to private set intersection. In: Proc. of the 2016 ACM SIGSAC Conf. on Computer and Communications Security. 2016. 818-829.
[14]	Orrù M, Orsini E, Scholl P. Actively secure 1-out-of-n OT extension with application to private set intersection. In: Proc. of the Cryptographers' Track at the RSA Conf. Cham: Springer, 2017. 381-396.
[15]	Ishai Y, Kilian J, Nissim K, et al. Extending oblivious transfers efficiently. In: Proc. of the Annual Int'l Cryptology Conf. Berlin, Heidelberg: Springer, 2003. 145-161.
[16]	Peikert C, Vaikuntanathan V, Waters B. A framework for efficient and composable oblivious transfer. In: Proc. of the Annual Int'l Cryptology Conf. Berlin, Heidelberg: Springer, 2008. 554-571.
[17]	Nielsen JB, Nordholt PS, Orlandi C, et al. A new approach to practical active-secure two-party computation. In: Proc. of the Annual Cryptology Conf. Berlin, Heidelberg: Springer, 2012. 681-700.
[18]	Kolesnikov V, Kumaresan R. Improved OT extension for transferring short secrets. In: Proc. of the Annual Cryptology Conf. Berlin, Heidelberg: Springer, 2013. 54-70.
[19]	Asharov G, Lindell Y, Schneider T, et al. More efficient oblivious transfer and extensions for faster secure computation. In: Proc. of the 2013 ACM SIGSAC Conf. on Computer & Communications Security. 2013. 535-548.
[20]	Keller M, Orsini E, Scholl P. Actively secure OT extension with optimal overhead. In: Proc. of the Annual Cryptology Conf. Berlin, Heidelberg: Springer, 2015. 724-741.
[21]	Asharov G, Lindell Y, Schneider T, et al. More efficient oblivious transfer extensions with security for malicious adversaries. In: Proc. of the Annual Int'l Conf. on the Theory and Applications of Cryptographic Techniques. Berlin, Heidelberg: Springer, 2015. 673-701.
[22]	Boyle E, Couteau G, Gilboa N, et al. Efficient pseudorandom correlation generators: Silent OT extension and more. In: Proc. of the Annual Int'l Cryptology Conf. Cham: Springer, 2019. 489-518.
[23]	Boyle E, Couteau G, Gilboa N, et al. Efficient two-round OT extension and silent non-interactive secure computation. In: Proc. of the 2019 ACM SIGSAC Conf. on Computer and Communications Security. 2019. 291-308.
[24]	Schoppmann P, Gascón A, Reichert L, et al. Distributed vector-OLE: Improved constructions and implementation. In: Proc. of the 2019 ACM SIGSAC Conf. on Computer and Communications Security. 2019. 1055-1072.
[25]	Yang K, Weng C, Lan X, et al. Ferret: Fast extension for correlated OT with small communication. In: Proc. of the 2020 ACM SIGSAC Conf. on Computer and Communications Security. 2020. 1607-1626.
[26]	Nielsen J B, Orlandi C. LEGO for two-party secure computation. In: Proc. of the Theory of Cryptography Conf. Berlin, Heidelberg: Springer, 2009. 368-386.
[27]	Shelat A, Shen CH. Fast two-party secure computation with minimal assumptions. In: Proc. of the 2013 ACM SIGSAC Conf. on Computer & Communications Security. 2013. 523-534.
[28]	Frederiksen TK, Jakobsen TP, Nielsen JB, et al. MiniLEGO: Efficient secure two-party computation from general assumptions. In: Proc. of the Annual Int'l Conf. on the Theory and Applications of Cryptographic Techniques. Berlin, Heidelberg: Springer, 2013. 537-556.
[29]	Huang Y, Katz J, Kolesnikov V, et al. Amortizing garbled circuits. In: Proc. of the Annual Cryptology Conf. Berlin, Heidelberg: Springer, 2014. 458-475.
[30]	Lindell Y, Pinkas B. An efficient protocol for secure two-party computation in the presence of malicious adversaries. Journal of Cryptology, 2015, 28(2): 312-350. [doi:10.1007/s00145-014-9177-x]
[31]	Lindell Y, Riva B. Blazing fast 2PC in the offline/online setting with security for malicious adversaries. In: Proc. of the 22nd ACM SIGSAC Conf. on Computer and Communications Security. 2015. 579-590.
[32]	Lindell Y. Fast cut-and-choose-based protocols for malicious and covert adversaries. Journal of Cryptology, 2016, 29(2): 456-490. [doi:10.1007/s00145-015-9198-0]
[33]	Keller M, Orsini E, Scholl P. MASCOT: Faster malicious arithmetic secure computation with oblivious transfer. In: Proc. of the 2016 ACM SIGSAC Conf. on Computer and Communications Security. 2016. 830-842.
[34]	Dong C, Chen L, Wen Z. When private set intersection meets big data: An efficient and scalable protocol. In: Proc. of the 2013 ACM SIGSAC Conf. on Computer & Communications Security. 2013. 789-800.
[35]	Pinkas B, Schneider T, Zohner M. Faster private set intersection based on OT extension. In: Proc. of the 23rd USENIX Security Symp. 2014. 797-812.
[36]	Rindal P, Rosulek M. Improved private set intersection against malicious adversaries. In: Proc. of the Annual Int'l Conf. on the Theory and Applications of Cryptographic Techniques. Cham: Springer, 2017. 235-259.
[37]	Pinkas B, Schneider T, Segev G, et al. Phasing: Private set intersection using permutation-based hashing. In: Proc. of the 24th USENIX Security Symp. 2015. 515-530.
[38]	Pinkas B, Schneider T, Zohner M. Scalable private set intersection based on OT extension. ACM Trans. on Privacy and Security, 2018, 21(2): 1-35.
[39]	Pinkas B, Rosulek M, Trieu N, et al. Spot-light: Lightweight private set intersection from sparse OT extension. In: Proc. of the Annual Int'l Cryptology Conf. Cham: Springer, 2019. 401-431.
[40]	Pinkas B, Schneider T, Tkachenko O, et al. Efficient circuit-based PSI with linear communication. In: Proc. of the Annual Int'l Conf. on the Theory and Applications of Cryptographic Techniques. Cham: Springer, 2019. 122-153.
[41]	Pinkas B, Rosulek M, Trieu N, et al. PSI from PaXoS: Fast, malicious private set intersection. In: Proc. of the Annual Int'l Conf. on the Theory and Applications of Cryptographic Techniques. Cham: Springer, 2020. 739-767.
[42]	Chase M, Miao P. Private set intersection in the internet setting from lightweight oblivious PRF. In: Proc. of the Annual Int'l Cryptology Conf. Cham: Springer, 2020. 34-63.
[43]	Rindal P, Schoppmann P. VOLE-PSI: Fast OPRF and circuit-PSI from Vector-OLE. Cryptology ePrint Archive, Report 2021/266, 2021. https://eprint.iacr.org/2021/266
[44]	Kolesnikov V, Matania N, Pinkas B, et al. Practical multi-party private set intersection from symmetric-key techniques. In: Proc. of the 2017 ACM SIGSAC Conf. on Computer and Communications Security. 2017. 1257-1272.
[45]	Kiss Á, Liu J, Schneider T, et al. Private set intersection for unequal set sizes with mobile applications. PoPETs, 2017, 2017(4): 177-197. [doi:10.1515/popets-2017-0044]
[46]	Kales D, Rechberger C, Schneider T, et al. Mobile private contact discovery at scale. In: Proc. of the 28th USENIX Security Symp. 2019. 1447-1464.
[47]	Ion M, Kreuter B, Nergiz E, et al. Private intersection-sum protocol with applications to attributing aggregate ad conversions. IACR Cryptol. ePrint Arch., 2017, 2017: 738.
[48]	Lv S, Ye J, Yin S, et al. Unbalanced private set intersection cardinality protocol with low communication cost. Future Generation Computer Systems, 2020, 102: 1054-1061. [doi:10.1016/j.future.2019.09.022]
[49]	Ion M, Kreuter B, Nergiz AE, et al. On deploying secure computing: Private intersection-sum-with-cardinality. In: Proc. of the 2020 IEEE European Symp. on Security and Privacy. IEEE, 2020. 370-389.
[50]	Demmler D, Schneider T, Zohner M. ABY-A framework for efficient mixed-protocol secure two-party computation. NDSS, 2015.
[51]	Mohassel P, Zhang Y. SecureML: A system for scalable privacy-preserving machine learning. In: Proc. of the 2017 IEEE Symp. on Security and Privacy. IEEE, 2017. 19-38.
[52]	Mohassel P, Rindal P. ABY 3: A mixed protocol framework for machine learning. In: Proc. of the 2018 ACM Conf. on Computer and Communications Security. ACM, 2018. 35-52.
[53]	Agrawal N, Shahin Shamsabadi A, Kusner M J, et al. QUOTIENT: Two-party secure neural network training and prediction. In: Proc. of the 2019 ACM SIGSAC Conf. on Computer and Communications Security. 2019. 1231-1247.
[54]	Naor M, Pinkas B. Efficient oblivious transfer protocols. In: Proc. of the 2001 ACM SODA. 2001, 448-457.
[55]	Chou T, Orlandi C. The simplest protocol for oblivious transfer. In: Proc. of the Int'l Conf. on Cryptology and Information Security in Latin America. Cham: Springer, 2015. 40-58.
[56]	Mansy D, Rindal P. Endemic oblivious transfer. In: Proc. of the 2019 ACM SIGSAC Conf. on Computer and Communications Security. 2019. 309-326.
[57]	Döttling N, Garg S, Ishai Y, et al. Trapdoor hash functions and their applications. In: Proc. of the Annual Int'l Cryptology Conf. Cham: Springer, 2019. 3-32.
[58]	Grag S, Hajiabadi M, Ostrovsky R. Efficient range-trapdoor functions and applications: Rate-1 OT and more. In: Proc. of the Theory of Cryptography Conf. Cham: Springer, 2020. 88-116.
[59]	Chase M, Grag S, Hajiabadi M, et al. Amortizing rate-1 OT and applications to PIR and PSI. In: Proc. of the Theory of Cryptography Conf. Cham: Springer, 2021. 126-156.
[60]	Tzeng WG. Efficient 1-out-n oblivious transfer schemes. In: Proc. of the Int'l Workshop on Public Key Cryptography. Berlin, Heidelberg: Springer, 2002. 159-171.
[61]	Patra A, Sarkar P, Suresh A. Fast actively secure OT extension for short secrets. arXiv: 1911.08834, 2019.
[62]	Yao ACC. How to generate and exchange secrets. In: Proc. of the 27th Annual Symp. on Foundations of Computer Science. IEEE, 1986. 162-167.
[63]	Goldwasser S. How to play any mental game, or a completeness theorem for protocols with an honest majority. In: Proc. of the 19th Annual ACM STOC 1987. 1987. 218-229.
[64]	Naor M, Pinkas B. Computationally secure oblivious transfer. Journal of Cryptology, 2005, 18(1): 1-35. [doi:10.1007/s00145-004-0102-6]
[65]	Naor M, Pinkas B. Oblivious transfer and polynomial evaluation. In: Proc. of the 21st Annual ACM Symp. on Theory of Computing. 1999. 245-254.
[66]	Phong LT. A survey on oblivious transfer protocols. Journal of the National Institute of Information and Communications Technology, 2011, 58(3): 181-186.
[67]	Evans D, Kolesnikov V, Rosulek M. A pragmatic introduction to secure multi-party computation. Foundations and TrendsⓇ in Privacy and Security, 2017, 2(2-3).
[68]	Shen LY, Chen XJ, Shi JJ, et al. Survey on private preserving set intersection Technology. Journal of Computer Research and Development, 2017, 54(10): 2153(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-JFYZ201710005.htm
[69]	Aumann Y, Lindell Y. Security against covert adversaries: Efficient protocols for realistic adversaries. In: Proc. of the Theory of Cryptography Conf. Berlin, Heidelberg: Springer, 2007. 137-156.
[70]	Green M, Hohenberger S. Blind identity-based encryption and simulatable oblivious transfer. In: Proc. of the Int'l Conf. on the Theory and Application of Cryptology and Information Security. Berlin, Heidelberg: Springer, 2007. 265-282.
[71]	Lindell AY. Efficient fully-simulatable oblivious transfer. In: Proc. of the Cryptographers' Track at the RSA Conf. Berlin, Heidelberg: Springer, 200. 52-70.
[72]	Canetti R. Universally composable security: A new paradigm for cryptographic protocols. In: Proc. of the 42nd IEEE Symp. on Foundations of Computer Science. IEEE, 2001. 136-145.
[73]	Blazy O, Chevalier C. Generic construction of UC-secure oblivious transfer. In: Proc. of the Int'l Conf. on Applied Cryptography and Network Security. Cham: Springer, 2015. 65-86.
[74]	Hauck E, Loss J. Efficient and universally composable protocols for oblivious transfer from the CDH assumption. IACR Cryptol. ePrint Arch., 2017, 2017: 1011.
[75]	Guo C, Katz J, Wang X, et al. Efficient and secure multiparty computation from fixed-key block ciphers. In: Proc. of the 2020 IEEE Symp. on Security and Privacy. IEEE, 2020. 825-841.
[76]	Crépeau C. Equivalence between two flavours of oblivious transfers. In: Proc. of the Conf. on the Theory and Application of Cryptographic Techniques. Berlin, Heidelberg: Springer, 1987. 350-354.
[77]	Wang FH, Hu YP, Liu ZH. Lattice-based oblivious transfer protocol. Journal on Communications, 2011, 32(3): 125-130(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-TXXB201103017.htm
[78]	Li Z, Zhang Y, Zhang F, et al. Ideal lattice-based oblivious transfer protocol of provably secure. Application Research of Computers, 2017, 34(1): 242-245(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-JSYJ201701056.htm
[79]	Ishai Y, Kushilevitz E. Private simultaneous messages protocols with applications. In: Proc. of the Fifth Israeli Symp. on Theory of Computing and Systems. IEEE, 1997. 174-183.
[80]	Tassa T. Generalized oblivious transfer by secret sharing. Designs, Codes and Cryptography, 2011, 58(1): 11-21. [doi:10.1007/s10623-010-9378-8]
[81]	Chu CK, Tzeng WG. Efficient k-out-of-n oblivious transfer schemes. Journal of Universal Computer Science, 2008, 14(3): 397-415.
[82]	Xu YJ, Li DS, Chen ZH. Efficient oblivious transfer protocol based on bilinear pairing. Computer Engineering, 2013, 39(6): 166-169(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-JSJC201306038.htm
[83]	Xu YJ, Li DS, Wang DS, et al. Oblivious transfer based on elliptic curve public key cryptosystems. Computer Science, 2013, 40(12): 186-191(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-JSJA201312040.htm
[84]	Lai J, Mu Y, Guo F, et al. Efficient k-out-of-n oblivious transfer scheme with the ideal communication cost. Theoretical Computer Science, 2018, 714: 15-26. [doi:10.1016/j.tcs.2017.12.019]
[85]	Naor M, Pinkas B. Oblivious transfer with adaptive queries. In: Proc. of the Annual Int'l Cryptology Conf. Berlin, Heidelberg: Springer, 1999. 573-590.
[86]	Ogata W, Kurosawa K. Oblivious keyword search. Journal of Complexity, 2004, 20(2-3): 356-371. [doi:10.1016/j.jco.2003.08.023]
[87]	Chu CK, Tzeng WG. Efficient k-out-of-n oblivious transfer schemes with adaptive and non-adaptive queries. In: Proc. of the Int'l Workshop on Public Key Cryptography. Berlin, Heidelberg: Springer, 2005. 172-183.
[88]	Green M, Hohenberger S. Practical adaptive oblivious transfer from simple assumptions. In: Proc. of the Theory of Cryptography Conf. Berlin, Heidelberg: Springer, 2011. 347-363.
[89]	Kurosawa K, Nojima R, Phong LT. Efficiency-improved fully simulatable adaptive OT under the DDH assumption. In: Proc. of the Int'l Conf. on Security and Cryptography for Networks. Berlin, Heidelberg: Springer, 2010. 172-181.
[90]	Kurosawa K, Nojima R, Phong LT. Generic fully simulatable adaptive oblivious transfer. In: Proc. of the Int'l Conf. on Applied Cryptography and Network Security. Berlin, Heidelberg: Springer, 2011. 274-291.
[91]	Camenisch J, Neven G. Simulatable adaptive oblivious transfer. In: Proc. of the Annual Int'l Conf. on the Theory and Applications of Cryptographic Techniques. Berlin, Heidelberg: Springer, 2007. 573-590.
[92]	Green M, Hohenberger S. Universally composable adaptive oblivious transfer. In: Proc. of the Int'l Conf. on the Theory and Application of Cryptology and Information Security. Berlin, Heidelberg: Springer, 2008. 179-197.
[93]	Jarecki S, Liu X. Efficient oblivious pseudorandom function with applications to adaptive OT and secure computation of set intersection. In: Proc. of the Theory of Cryptography Conf. Berlin, Heidelberg: Springer, 2009. 577-594.
[94]	Kurosawa K, Nojima R. Simple adaptive oblivious transfer without random oracle. In: Proc. of the Int'l Conf. on the Theory and Application of Cryptology and Information Security. Berlin, Heidelberg: Springer, 2009. 334-346.
[95]	Naor M, Pinkas B. Distributed oblivious transfer. In: Proc. of the Int'l Conf. on the Theory and Application of Cryptology and Information Security. Berlin, Heidelberg: Springer, 2000. 205-219.
[96]	Frederiksen TK, Keller M, Orsini E, et al. A unified approach to MPC with preprocessing using OT. In: Proc. of the Int'l Conf. on the Theory and Application of Cryptology and Information Security. Berlin, Heidelber: Springer, 2015. 711-735.
[97]	Hazay C, Scholl P, Soria-Vazquez E. Low cost constant round MPC combining BMR and oblivious transfer. Journal of Cryptology, 2020, 33(4): 1732-1786. [doi:10.1007/s00145-020-09355-y]
[98]	Wolf S, Wullschleger J. Oblivious transfer is symmetric. In: Proc. of the Annual Int'l Conf. on the Theory and Applications of Cryptographic Techniques. Berlin, Heidelberg: Springer, 2006. 222-232.
[99]	Crépeau C, Sántha M. On the reversibility of oblivious transfer. In: Proc. of the Workshop on the Theory and Application of Cryptographic Techniques. Berlin, Heidelberg: Springer, 1991. 106-113.
[100]	Huang Q, Zhao YM. Independent oblivious transfer. Ruan Jian Xue Bao/Journal of Software, 2007, 18(4): 1015-1025. http://www.jos.org.cn/jos/article/abstract/20070423?st=search [doi:10.1360/jos181015]
[101]	Wei Y, Xiong GH, Zhang XK, et al. Oblivious transfer protocols over braid groups. Application Research of Computers, 2010, 27(8): 3042-3044(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-JSYJ201008064.htm
[102]	Zhang YS, Zhao HS, Chen HY, Yang YT. On scheme design of probabilistic 1 out of 2 oblivious transfer protocol. Journal of Cryptologic Research, 2021, 8(2): 282-293(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-MMXB202102008.htm
[103]	Liu MM. Analysis and design of lattice-based oblivious transfer protocols[Ph. D. Thesis]. Xi'an: Xidian University, 2018 (in Chinese with English abstract).
[104]	Damgård I, Nielsen J B, Orlandi C. Essentially optimal universally composable oblivious transfer. In: Proc. of the Int'l Conf. on Information Security and Cryptology. Berlin, Heidelberg: Springer, 2008. 318-335.
[105]	Hazay C, Lindell Y. Efficient secure two-party protocols: Techniques and constructions. Springer Science & Business Media, 2010.
[106]	Li B, Micciancio D. Equational security proofs of oblivious transfer protocols. In: Proc. of the IACR Int'l Workshop on Public Key Cryptography. Cham: Springer, 2018. 527-553.
[107]	Genç ZA, Iovino V, Rial A. "The simplest protocol for oblivious transfer" revisited. Information Processing Letters, 2020, 105975.
[108]	Byali M, Patra A, Ravi D, et al. Fast and universally-composable oblivious transfer and commitment scheme with adaptive security. IACR Cryptol. ePrint Arch., 2017, 2017: 1165.
[109]	Doerner J, Kondi Y, Lee E, et al. Secure two-party threshold ECDSA from ECDSA assumptions. In: Proc. of the 2018 IEEE Symp. on Security and Privacy. IEEE, 2018. 980-997.
[110]	Canetti R, Sarkar P, Wang X. Blazing fast OT for three-round UC OT extension. In: Proc. of the 23rd IACR Int'l Conf. on the Practice and Theory of Public-key Cryptography, PKC 2020. Springer, 2020. 299-327.
[111]	Shor PW. Algorithms for quantum computation: Discrete logarithms and factoring. In: Proc. of the 35th Annual Symp. on Foundations of Computer Science. IEEE, 1994. 124-134.
[112]	Crépeau C, Kilian J. Achieving oblivious transfer using weakened security assumptions. In: Proc. of the 29th Annual Symp. on Foundations of Computer Science. IEEE Computer Society, 1988. 42-52.
[113]	Crépeau C. Efficient cryptographic protocols based on noisy channels. In: Proc. of the Int'l Conf. on the Theory and Applications of Cryptographic Techniques. Berlin, Heidelberg: Springer, 1997. 306-317.
[114]	Damgård I, Kilian J, Salvail L. On the (im) possibility of basing oblivious transfer and bit commitment on weakened security assumptions. In: Proc. of the Int'l Conf. on the Theory and Applications of Cryptographic Techniques. Berlin, Heidelberg: Springer, 1999. 56-73.
[115]	Stebila D, Wolf S. Efficient oblivious transfer from any non-trivial binary-symmetric channel. In: Proc. of the IEEE Int'l Symp. on Information Theory. IEEE, 2002. 293.
[116]	Crépeau C, Morozov K, Wolf S. Efficient unconditional oblivious transfer from almost any noisy channel. In: Proc. of the Int'l Conf. on Security in Communication Networks. Berlin, Heidelberg: Springer, 2004. 47-59.
[117]	Nascimento ACA, Winter A. On the oblivious-transfer capacity of noisy resources. IEEE Trans. on Information Theory, 2008, 54(6): 2572-2581.
[118]	Pinto ACB, Dowsley R, Morozov K, et al. Achieving oblivious transfer capacity of generalized erasure channels in the malicious model. IEEE Trans. on Information Theory, 2011, 57(8): 5566-5571.
[119]	Dowsley R, Nascimento ACA. On the oblivious transfer capacity of generalized erasure channels against malicious adversaries: The case of low erasure probability. IEEE Trans. on Information Theory, 2017, 63(10): 6819-6826.
[120]	Beaver D. Commodity-based cryptography. In: Proc. of the 29th Annual ACM Symp. on Theory of Computing. 1997. 446-455.
[121]	Rivest R. Unconditionally secure commitment and oblivious transfer schemes using private channels and a trusted initializer. Unpublished manuscript, 1999.
[122]	Kilian J. More general completeness theorems for secure two-party computation. In: Proc. of the 22nd Annual ACM Symp. on Theory of Computing. 2000. 316-324.
[123]	Beimel A, Malkin T, Micali S. The all-or-nothing nature of two-party secure computation. In: Proc. of the Annual Int'l Cryptology Conf. Berlin, Heidelberg: Springer, 1999. 80-97.
[124]	Regev O. On lattices, learning with errors, random linear codes, and cryptography. Journal of the ACM, 2009, 56(6): 1-40.
[125]	McEliece RJ. A public-key cryptosystem based on algebraic. Coding Thv., 1978, 4244: 114-116.
[126]	David B, Dowsley R, Nascimento ACA. Universally composable oblivious transfer based on a variant of LPN. In: Proc. of the Int'l Conf. on Cryptology and Network Security. Cham: Springer, 2014. 143-158.
[127]	David BM, Nascimento ACA, Müller-Quade J. Universally composable oblivious transfer from lossy encryption and the mceliece assumptions. In: Proc. of the Int'l Conf. on Information Theoretic Security. Berlin, Heidelberg: Springer, 2012. 80-99.
[128]	Barreto PSLM, David B, Dowsley R, et al. A framework for efficient adaptively secure composable oblivious transfer in the ROM. arXiv: 1710.08256, 2017.
[129]	Lai YF, Galbraith SD, de Saint Guilhem CD. Compact, efficient and UC-secure isogeny-based oblivious transfer. In: Proc. of the Annual Int'l Conf. on the Theory and Applications of Cryptographic Techniques. Cham: Springer, 2021. 213-241.
[130]	Barreto P, Nascimento A, Oliveira G, et al. Supersingular isogeny oblivious transfer. arXiv: 1805.06589, 2018.
[131]	Vitse V. Simple oblivious transfer protocols compatible with supersingular isogenies. In: Proc. of the Int'l Conf. on Cryptology in Africa. Cham: Springer, 2019. 56-78.
[132]	Boyle E, Couteau G, Gilboa N, et al. Compressing vector OLE. In: Proc. of the 2018 ACM SIGSAC Conf. on Computer and Communications Security. 2018. 896-912.
[133]	Schoppmann P, Gascón A, Reichert L, et al. Distributed vector-OLE: Improved constructions and implementation. In: Proc. of the 2019 ACM SIGSAC Conf. on Computer and Communications Security. 2019. 1055-1072.
[134]	Pinkas B. Fair secure two-party computation. In: Proc. of the Int'l Conf. on the Theory and Applications of Cryptographic Techniques. Berlin, Heidelberg: Springer, 2003. 87-105.
[135]	Lindell Y, Pinkas B. An efficient protocol for secure two-party computation in the presence of malicious adversaries. In: Proc. of the Annual Int'l Conf. on the Theory and Applications of Cryptographic Techniques. Berlin, Heidelberg: Springer, 2007. 52-78.
[136]	Lindell Y, Pinkas B. Secure two-party computation via cut-and-choose oblivious transfer. Journal of Cryptology, 2012, 25(4): 680-722.
[137]	Shen C. Two-output secure computation with malicious adversaries. In: Proc. of the Annual Int'l Conf. on the Theory and Applications of Cryptographic Techniques. Berlin, Heidelberg: Springer, 2011. 386-405.
[138]	Huang Y, Katz J, Evans D. Efficient secure two-party computation using symmetric cut-and-choose. In: Proc. of the Annual Cryptology Conf. Berlin, Heidelberg: Springer, 2013. 18-35.
[139]	Mohassel P, Riva B. Garbled circuits checking garbled circuits: More efficient and secure two-party computation. In: Proc. of the Annual Cryptology Conf. Berlin, Heidelberg: Springer, 2013. 36-53.
[140]	Lindell Y, Riva B. Cut-and-choose based two-party computation in the online/offline and batch settings. IACR Cryptol. ePrint Arch., 2014, 2014: 667.
[141]	Kolesnikov V, Kumaresan R. On cut-and-choose oblivious transfer and its variants. In: Proc. of the Int'l Conf. on the Theory and Application of Cryptology and Information Security. Berlin, Heidelberg: Springer, 2015. 386-412.
[142]	Harnik D, Ishai Y, Kushilevitz E, et al. OT-combiners via secure computation. In: Proc. of the Theory of Cryptography Conf. Berlin, Heidelberg: Springer, 2008. 393-411.
[143]	Nielsen JB. Extending oblivious transfers efficiently-How to get robustness almost for free. IACR Cryptol. ePrint Arch., 2007, 2007: 215.
[144]	Damgård I, Keller M, Larraia E, et al. Practical covertly secure MPC for dishonest majority–or: breaking the SPDZ limits. In: Proc. of the European Symp. on Research in Computer Security. Berlin, Heidelberg: Springer, 2013. 1-18.
[145]	Doerner J, Shelat A. Scaling ORAM for secure computation. In: Proc. of the 2017 ACM SIGSAC Conf. on Computer and Communications Security. 2017. 523-535.
[146]	Henecka W, Schneider T. Faster secure two-party computation with less memory. In: Proc. of the 8th ACM SIGSAC Symp. on Information, Computer and Communications Security. 2013. 437-446.
[147]	Barker E, Barker W, Burr W, et al. NIST Special Publication 800-57 Recommendation for Key Management–Part 1: General. 2012.
[148]	Huang Y, Evans D, Katz J, et al. Faster secure two-party computation using garbled circuits. In: Proc. of the USENIX Security Symp. 2011, 201(1): 331-335.
[149]	McQuoid I, Rosulek M, Roy L. Batching Base Oblivious Transfers. In: Proc. of Advances in Cryptdogy-ASIACRYPT 2001. 2001. 281-310.
[150]	McQuoid I, Rosulek M, Roy L. Minimal symmetric PAKE and 1-out-of-n OT from programmable-once public functions. In: Proc. of the 2020 ACM SIGSAC Conf. on Computer and Communications Security. 2020. 425-442.
[151]	Eklundh JO. A fast computer method for matrix transposing. IEEE Trans. on Computers, 1972, 100(7): 801-803.
[152]	Albrecht MR, Rechberger C, Schneider T, et al. Ciphers for MPC and FHE. In: Proc. of the Annual Int'l Conf. on the Theory and Applications of Cryptographic Techniques. Berlin, Heidelberg: Springer, 2015. 430-454.
[153]	Aumasson JP, Neves S, Wilcox-O'Hearn Z, et al. BLAKE2: Simpler, smaller, fast as MD5. In: Proc. of the Int'l Conf. on Applied Cryptography and Network Security. Berlin, Heidelberg: Springer, 2013. 119-135.
[154]	Aiello B, Ishai Y, Reingold O. Priced oblivious transfer: How to sell digital goods. In: Proc. of the Int'l Conf. on the Theory and Applications of Cryptographic Techniques. Berlin, Heidelberg: Springer, 2001. 119-135.
[155]	Pinkas B, Schneider T, Smart NP, et al. Secure two-party computation is practical. In: Proc. of the Int'l Conf. on the Theory and Application of Cryptology and Information Security. Berlin, Heidelberg: Springer, 2009. 250-267.
[156]	Schneider T, Zohner M. GMW vs. Yao? Efficient secure two-party computation with low depth circuits. In: Proc. of the Int'l Conf. on Financial Cryptography and Data Security. Berlin, Heidelberg: Springer, 2013. 275-292.
[157]	Lindell Y, Pinkas B. A proof of security of Yao's protocol for two-party computation. Journal of Cryptology, 2009, 22(2): 161-188.
[158]	Crépeau C, van de Graaf J, Tapp A. Committed oblivious transfer and private multi-party computation. In: Proc. of the Annual Int'l Cryptology Conf. Berlin, Heidelberg: Springer, 1995. 110-123.
[159]	Ishai Y, Prabhakaran M, Sahai A. Founding cryptography on oblivious transfer–efficiently. In: Proc. of the Annual Int'l Cryptology Conf. Berlin, Heidelberg: Springer, 2008. 572-591.
[160]	Baldi P, Baronio R, De Cristofaro E, et al. Countering gattaca: Efficient and secure testing of fully-sequenced human genomes. In: Proc. of the 18th ACM Con. on Computer and Communications Security. 2011. 691-702.
[161]	Chor B, Goldreich O, Kushilevitz E, et al. Private information retrieval. In: Proc. of the IEEE 36th Annual Foundations of Computer Science. IEEE, 1995. 41-50.
[162]	Gertner Y, Ishai Y, Kushilevitz E, et al. Protecting data privacy in private information retrieval schemes. Journal of Computer and System Sciences, 2000, 60(3): 592-629.
[163]	Di Crescenzo G, Malkin T, Ostrovsky R. Single database private information retrieval implies oblivious transfer. In: Proc. of the Int'l Conf. on the Theory and Applications of Cryptographic Techniques. Berlin, Heidelberg: Springer, 2000. 122-138.
[164]	Freedman MJ, Nissim K, Pinkas B. Efficient private matching and set intersection. In: Proc. of the Int'l Conf. on the Theory and Applications of Cryptographic Techniques. Berlin, Heidelberg: Springer, 2004. 1-19.
[165]	Kissner L, Song D. Privacy-preserving set operations. In: Proc. of the Annual Int'l Cryptology Conf. Berlin, Heidelberg: Springer, 2005. 241-257.
[166]	Hazay C, Nissim K. Efficient set operations in the presence of malicious adversaries. In: Proc. of the Int'l Workshop on Public Key Cryptography. Berlin, Heidelberg: Springer, 2010. 312-331.
[68]	申立艳, 陈小军, 时金桥, 等. 隐私保护集合交集计算技术研究综述. 计算机研究与发展, 2017, 54(10): 2153. https://www.cnki.com.cn/Article/CJFDTOTAL-JFYZ201710005.htm
[77]	王凤和, 胡予濮, 刘振华. 格基不经意传输协议. 通信学报, 2011, 32(3): 125-130. https://www.cnki.com.cn/Article/CJFDTOTAL-TXXB201103017.htm
[78]	李子臣, 张亚泽, 张峰娟, 等. 理想格上可证明安全的不经意传输协议. 计算机应用研究, 2017, 34(1): 242-245. https://www.cnki.com.cn/Article/CJFDTOTAL-JSYJ201701056.htm
[82]	徐彦蛟, 李顺东, 陈振华. 基于双线性对的高效不经意传输协议. 计算机工程, 2013, 39(6): 166-169. https://www.cnki.com.cn/Article/CJFDTOTAL-JSJC201306038.htm
[83]	徐彦蛟, 李顺东, 王道顺, 等. 基于椭圆曲线公钥系统的不经意传输协议. 计算机科学, 2013, 40(12): 186-191. https://www.cnki.com.cn/Article/CJFDTOTAL-JSJA201312040.htm
[101]	隗云, 熊国华, 张兴凯, 等. 辫群上的不经意传输协议. 计算机应用研究, 2010, 27(8): 3042-3044. https://www.cnki.com.cn/Article/CJFDTOTAL-JSYJ201008064.htm
[102]	张艳硕, 赵瀚森, 陈辉焱, , 等. 张艳硕, 赵瀚森, 陈辉焱, 等. 概率型2选1不经意传输协议的方案设计. 密码学报, 2021, 8(2): 282-293. https://www.cnki.com.cn/Article/CJFDTOTAL-MMXB202102008.htm
[103]	刘沫萌. 格上不经意传输协议的分析与设计[博士学位论文]. 西安: 西安电子科技大学, 2018.