基于分解的演化多目标优化算法综述

引用本文

高卫峰, 刘玲玲, 王振坤, 公茂果. 基于分解的演化多目标优化算法综述[J]. 软件学报, 2023, 34(10): 4743-4771. http://www.jos.org.cn/1000-9825/6672.htm

Gao WF, Liu LL, Wang ZK, Gong MG. Survey on Multiobjective Optimization Evolutionary Algorithm Based on Decomposition[J]. Journal of Software, 2023, 34(10): 4743-4771(in Chinese). http://www.jos.org.cn/1000-9825/6672.htm

基于分解的演化多目标优化算法综述

高卫峰¹ , 刘玲玲¹ , 王振坤^2,3 , 公茂果⁴

1. 西安电子科技大学数学与统计学院, 陕西西安 710126;
2. 南方科技大学系统设计与智能制造学院, 广东深圳 518055;
3. 南方科技大学计算机科学与工程系, 广东深圳 518055;
4. 西安电子科技大学电子工程学院, 陕西西安 710071

收稿时间: 2020-09-07; 修改时间: 2021-04-13; 采用时间: 2021-07-28; jos在线出版时间: 2022-05-24

基金项目: 国家自然科学基金(61772391, 62106186); 陕西省自然科学基础研究计划(2022JQ-670, 2020JM-178)

作者简介: 高卫峰(1985－), 男, 博士, 教授, 博士生导师, 主要研究领域为最优化方法, 进化计算理论及应用;
刘玲玲(1997－), 女, 硕士生, 主要研究领域为多目标演化优化算法及应用;
王振坤(1990－), 男, 博士, 副研究员, 博士生导师, CCF专业会员, 主要研究领域为计算智能与先进制造;
公茂果(1979－), 男, 博士, 教授, 博士生导师, CCF高级会员, 主要研究领域为计算智能理论与方法, 网络信息感知, 隐私保护, 雷达与遥感智能系统.

通讯作者: 公茂果, E-mail: gong@ieee.org.

摘要: 基于分解的演化多目标优化算法(MOEA/D)的基本思想是将一个多目标优化问题转化成一系列子问题 (单目标或者多目标)来进行优化求解. 自2007年提出以来, MOEA/D受到了国内外学者的广泛关注, 已经成为最具代表性的演化多目标优化算法之一. 总结过去13年中关于MOEA/D的一些研究进展, 具体内容包括: (1)关于MOEA/D的算法改进; (2) MOEA/D在超多目标优化问题及约束优化问题上的研究; (3) MOEA/D在一些实际问题上的应用. 然后, 实验对比几个具有代表性的MOEA/D改进算法. 最后, 指出一些MOEA/D未来的研究方向.

关键词: 多目标优化演化算法分解 MOEA/D

Survey on Multiobjective Optimization Evolutionary Algorithm Based on Decomposition

GAO Wei-Feng¹ , LIU Ling-Ling¹ , WANG Zhen-Kun^2,3 , GONG Mao-Guo⁴

1. School of Mathematics and Statistics, Xidian University, Xi’an 710126, China;
2. School of System Design and Intelligent Manufacturing, Southern University of Science and Technology, Shenzhen 518055, China;
3. Department of Computer Science and Engineering, Southern University of Science and Technology, Shenzhen 518055, China;
4. School of Electronic Engineering, Xidian University, Xi’an 710071, China

Abstract: The basic concept of the multiobjective optimization evolutionary algorithm based on decomposition (MOEA/D) is to transform a multiobjective optimization problem into a set of subproblems (single-objective or multiobjective) for optimization solutions. Since MOEA/D was proposed in 2007, it has attracted extensive attention from Chinese and international scholars and become one of the most representative multiobjective optimization evolutionary algorithms. This study summarizes the research progress on MOEA/D in the past thirteen years. The advances include algorithm improvements of MOEA/D, research of MOEA/D on many-objective optimization and constraint optimization,and application of MOEA/D in some practical issues. Then, several representative improved algorithms of MOEA/D are compared through experiments. Finally, the study presents several potential research topics of MOEA/D in the future.

Key words: multiobjective optimization evolutionary algorithm decomposition MOEA/D

很多现实世界的工程优化问题都需要同时考虑多个相互冲突的目标, 这些问题通常都被建模成多目标优化问题(multiobjective optimization problem, MOP). 一个连续MOP可以表述为:

$ \left\{\begin{aligned} & {\mathrm{minmize }}\;F(x) = {({f_1}(x), \ldots, {f_m}(x))^{\rm{T}}} \in {R^m} \\ & {\mathrm{s.t.}}\;x = {({x_1}, {x_2}, \ldots, {x_n})^{\rm{T}}} \in \Omega \\ \end{aligned}\right. $

(1)

其中, $\Omega \subset {R^n}$ 为决策空间, ${R^m}$ 为目标空间, $F(x):\Omega \to {R^m}$ 是具有 $m$ 个目标函数值的目标向量. 这里的 $\Omega \subset {R^n}$ 是一个连通的闭集.

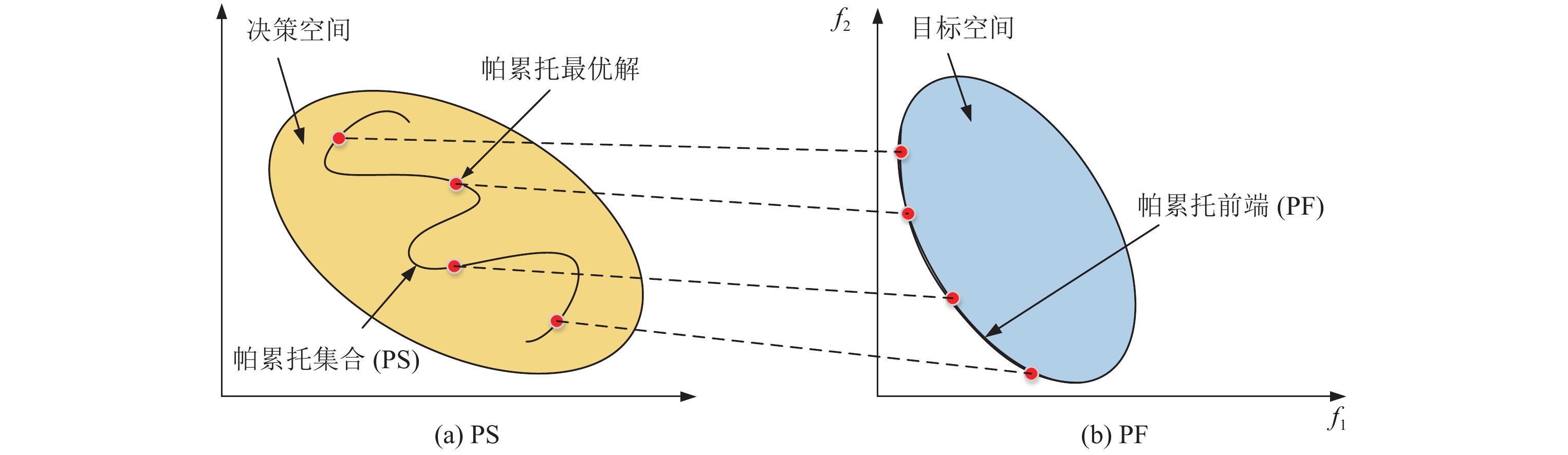
通常一个MOP不存在一个唯一的最优解, 取而代之的是一组折衷最优解. 这组折衷最优解在决策空间被称为帕累托集合(Pareto set, PS) , 在目标空间称为帕累托前端(Pareto front, PF). 下面给出几个相关的概念.

定义1. 支配关系. ${x_1}$ , ${x_2}$ 为决策空间 $\Omega $ 中的两个决策变量, ${x_1}$ 支配 ${x_2}$ (记为 ${x_1} \succ {x_2}$ ), 当且仅当对于所有的 $i = 1, 2, \ldots, m$ 都有 ${f_i}({x_1}) \leqslant {f_i}({x_2})$ , 且存在一个 $j = 1, 2, \ldots, m$ 使得 ${f_j}({x_1}) < {f_j}({x_2})$ .

定义2. 帕累托最优解. 如果不存在任何一个决策向量 $x \in \Omega $ 能够使得 $x \succ {x^*}$ , 则 ${x^*}$ 是一个帕累托最优解(Pareto optimal solution).

定义3. 帕累托集合. 所有帕累托最优解组成的集合称为帕累托集合.

定义4. 帕累托前端. 所有帕累托最优解映射到目标空间中的目标向量组成的集合称为帕累托前端.

如图1所示, PS为多目标优化问题在决策空间的最优解集合, PF为对应于目标空间中的最优解集合.

Fig. 1 Diagram of PS and PF 图 1 PS和PF 示意图

在没有先验信息的情况下, 决策者(decision maker, DM)需要得到整个帕累托前端的近似解集合, 后续再根据需求从中选出一个最适合的. 演化多目标优化算法(multiobjective optimization evolutionary algorithms, MOEAs)一次运行就可以逼近整个PF, 并且MOEAs不受限于目标函数的不连续性、不可微性等性质^[1-4]. 这些优良的性质使得MOEAs受到了越来越多的关注. 当前的MOEAs主要可大致分为以下3类.

(1) 基于支配关系的演化多目标优化算法

基于支配关系的演化多目标优化算法利用支配关系将种群中的个体分为不同的层级. 越靠近底部层级的个体, 适应度值越高, 在进行环境选择的时候被选中的机会就越大. 同一层级中的个体互不支配, 需要通过拥挤度距离或小生境等机制来选择个体. 代表性的算法有NSGA-II^[5]、PESA-II^[6]和SEPA2^[7]等. 基于支配关系的演化多目标优化算法在目标个数为2–3个时有比较好的性能. 然而, 随着目标个数的增加, 种群中非支配解的数量急剧上升, 最后种群中绝大多数的个体都是非支配解. 这会导致基于层级的选择机制失效. 同时, 由于目标空间增大, 为了确定种群中解的拥挤程度, 需耗费很大的计算量. 因此在高维情况下, 基于支配关系的演化多目标优化算法面临很大的挑战.

(2) 基于性能指标的演化多目标优化算法

基于性能指标的演化多目标优化算法通过性能指标来指导整个种群的演化优化. 超体积(hyper volume, HV)指标由于具有良好的理论支撑, 成为最常用的指标之一. 然而, 随着目标个数的增加, HV指标的计算代价会呈指数级增长, 这阻碍了HV在高维多目标优化问题上的应用. 为了解决这一问题, 学者们提出一些快速计算HV的方法^[8,9], 但截至目前, 仍然没有一个特别有效的算法来显著地降低其在高维多目标优化问题上的计算复杂度.

(3) 基于分解的演化多目标优化算法(MOEA/D)

MOEA/D^[10]的核心是通过分解方法将一个多目标优化问题分解成一系列子问题来进行求解, 这些子问题可以是单目标优化问题也可以是多目标优化问题. 然后利用子问题之间的邻域关系, 以协作的方式同时优化所有的子问题, 并得到整个PF的近似解集合. 这类算法通常使用子问题的目标函数值作为适应度值, 有效避免了随着目标个数的增加个体的选择压力失效的状况. 此外, 子问题目标函数值计算不会呈现指数级增长.

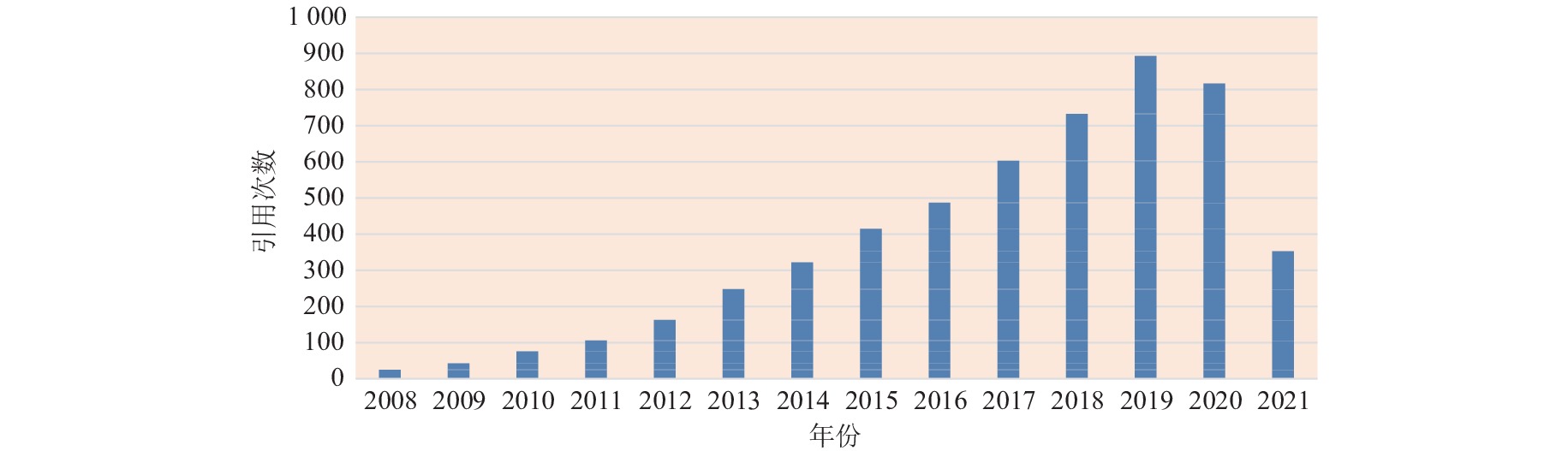
MOEA/D自提出以来, 吸引了越来越多学者的关注, 出现了许多MOEA/D的改进算法, MOEA/D也被应用到许多问题上. 根据谷歌学术中的统计, 到目前为止MOEA/D被SCI他引已经高达4643次. 图2是MOEA/D每年被引次数的统计情况, 可以看到近年来MOEA/D被引次数一直在不断地增长. Trivedi等人^[11]在2016年对这些算法进行了总结. 然而, 从2016年至今, 一些新颖的MOEA/D改进版本被提出, 这些改进算法解决了不同领域的一些通用问题. Xu等人^[12]在2020年进一步对MOEA/D的改进以及近几年来新的发展进行了系统的研究. 而国内还没有对这类算法进行总结的文章, 鉴于MOEA/D近年来发展迅速以及在许多实际问题上的成功应用, 本文我们对MOEA/D的发展做出详细讨论. 与已有综述文章相比, 本文的工作主要有以下4个贡献: (1)结合MOEA/D近年来的发展, 对MOEA/D的基本框架进行总结; (2)对MOEA/D的演化过程进行划分, 并给出明确的定义; (3)详细介绍MOEA/D在6项典型实际问题中的具体应用; (4)给出6个具有代表性的算法在多组测试问题上的对比实验.

Fig. 2 Cited quantities of MOEA/D 图 2 MOEA/D被引次数

本文第1节简要介绍MOEA/D的基本框架. 第2节对MOEA/D的研究方向进行详细地讨论. 第3节介绍关于MOEA/D的热点研究. 第4节介绍MOEA/D在一些实际问题上的应用. 第5节实验分析具有代表性MOEA/D改进算法性能. 第6节提出一些MOEA/D需进一步研究的方向和问题.

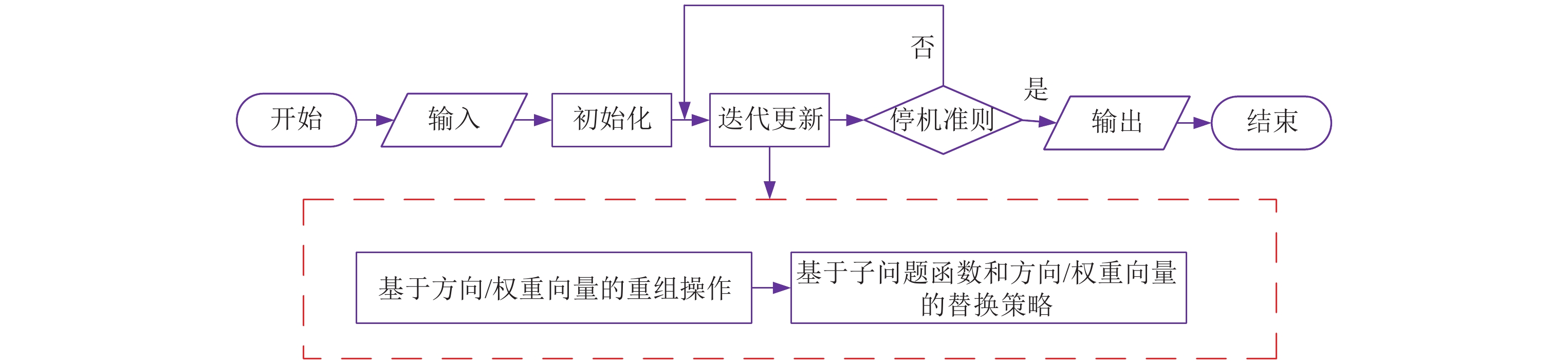
1 MOEA/D概述 1.1 MOEA/D基本框架

如图3所示, 在MOEA/D的初始化阶段, 需要预先生成一组均匀分布的方向/权重向量. 这组方向/权重向量通常由单纯形网格设计方法^[13]生成. 利用这些方向向量/权重向量, MOEA/D可以将一个多目标优化问题转换成一组单目标优化问题(如线性加权^[14])或者一组简单多目标优化问题(如空间划分^[15]).

Fig. 3 MOEA/D flowchart 图 3 MOEA/D流程图

在MOEA/D的迭代阶段, 算法往往利用方向/权重向量之间的邻域关系以及它们与种群分布的关系来执行重组操作. 这里重组操作可以是 $u + 1$ 的, 即稳态(steady state)模式, 也可以是 $u + u$ 或 $u + \lambda $ 的, 即代际(generational)模式. 稳态演化模式是指产生一个新解后就更新整个种群. 代际演化模式是指生成整个子代种群后再与父代种群竞争得到下一代种群. 在新的子代产生以后, 算法执行替换策略. 这里的替换原则通常是基于种群个体的子问题目标函数值以及它们与方向/权重向量的距离来执行的.

算法不断迭代直至达到停机条件. 达到停机条件之后, 算法输出获得的非支配解, 并将其作为这个多目标优化问题的近似解.

1.2 常用的分解方法

在迭代更新过程中, 使用不同的分解方法能够得到不同的子问题函数, 在MOEA/D中, 常用的分解方法有以下3种.

(1) 加权和(weighted sum, WS)方法

假设 $\lambda = {({\lambda _1}, \ldots, {\lambda _m})^{\rm{T}}}$ 是一个权重向量, 满足 ${\lambda _i} \geqslant 0, \displaystyle\sum\nolimits_{i = 1}^m {{\lambda _i}} = 1, i = 1, \ldots, m$ . ${({f_1}(x), \ldots, {f_m}(x))^{\rm{T}}}$ 为目标向量, 则加权和方法定义的子问题如下:

$ \left\{\begin{aligned} & {\min}\;{g^{ws}}(x|\lambda ) = \sum\nolimits_{i = 1}^m {({\lambda _i}{f_i}(x))} \\ & {\mathrm{s.t.}}\;x \in \Omega \\ \end{aligned} \right.$

(2)

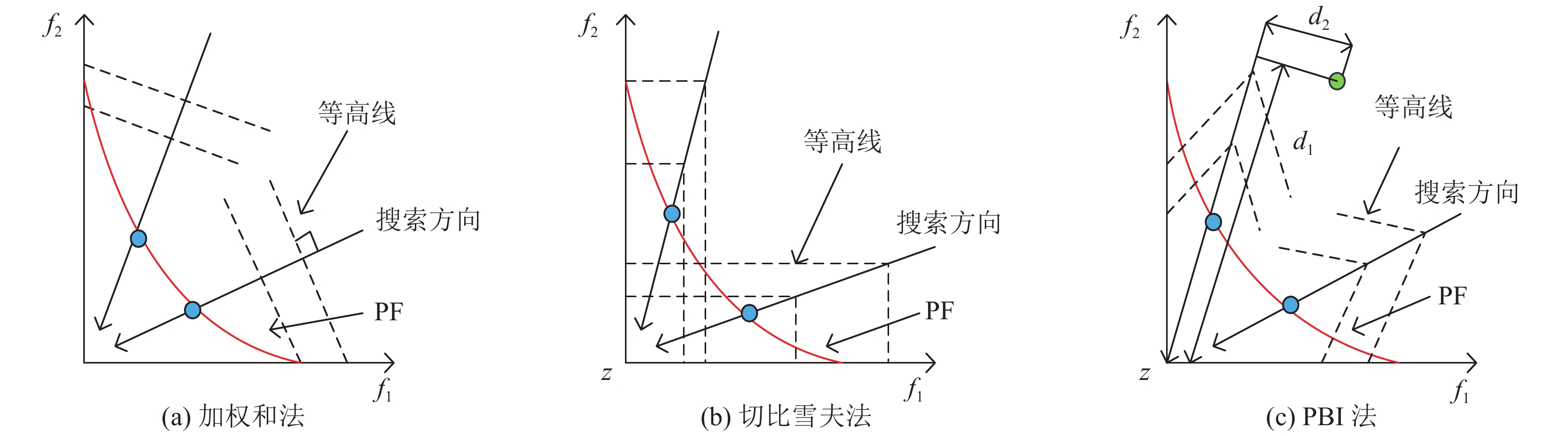
使用不同的权重向量, 可以得到一组不同的子问题. 在问题具有凸PF的情况下, 该方法具有良好的性能. 然而, 在非凸PF的情况下, 并不是每个帕累托最优解都可以通过该方法得到.

(2) 切比雪夫(Tchebycheff, TCH)方法

切比雪夫方法可以求解任意PF形状的MOP, 所以在许多MOEA/D改进算法中得到了广泛使用. 切比雪夫方法构造的子问题如下:

$ \left\{\begin{aligned} & {\min}\;{g^{te}}(x|\lambda , \textit{z}) = \mathop {\max }\limits_{1 \leqslant i \leqslant m} \{ {\lambda _i}|{f_i}(x) - \textit{z}|\} \\ & {\mathrm{s.t.}}\;x \in \Omega \\ \end{aligned}\right. $

(3)

其中, $\textit{z} = {({\textit{z}_1}, \ldots, {\textit{z}_m})^{\rm{T}}}$ 是参考点, 满足 $\forall i = 1, \ldots, m, \;{\textit{z}_i} < \min \{ {f_i}(x)|x \in \Omega \}$ .在温和条件下, 每一个帕累托最优解 ${x^*}$ , 必存在一个权重向量 $\lambda $ 使得公式(3)的最优解就是 ${x^*}$ , 反过来公式(3)的每一个最优解都对应MOP的一个帕累托最优解. 因此, 通过改变权重向量, 可以得到不同的帕累托最优解.

(3) 基于惩罚的边界交叉(penalty-based boundary intersection, PBI)方法

PBI方法构造的子问题如下:

$ \left\{\begin{aligned} & {\min}\;{g^{pbi}}(x|\lambda , \textit{z}) = {d_1} + \theta {d_2} \\ & {d_1} = \frac{{||F(x) - \textit{z}{)^{\rm{T}}}\lambda ||}}{{||\lambda ||}} \\ & {d_2} = \left\|F(x) - \left(\textit{z} + {d_1}\frac{\lambda }{||\lambda ||}\right)\right\| \\ & {\mathrm{s.t.}}\;x \in \Omega \\ \end{aligned}\right. $

(4)

其中, z与公式(3)中相同, $\theta > 0$ 是一个预先设定的惩罚参数. ${d_1}$ 为解映射到目标空间中的目标向量在权重向量 $\lambda $ 上的投影距参考点的距离, ${d_2}$ 为解映射到目标空间中的目标向量距权重向量的距离. 因此具有更小的 ${d_1}$ 和 ${d_2}$ 值的解被认为是更好的解. ${d_1}$ 和 ${d_2}$ 的平衡通过参数 $\theta $ 控制, 对于不同的MOP设置合适的 $\theta $ 值能优化PBI方法性能.

如图4所示, 是对应3种分解方法分解机制示意图.

Fig. 4 Diagram of three decomposition methods 图 4 3种分解方法示意图

2 研究方向

MOEA/D因其简单高效的特点吸引了许多学者对它进行研究. 最初版本的MOEA/D考虑的是一组具有2–3个目标的无约束优化问题和一组具有2–4个目标的背包问题. 随着测试问题的多样性增加和复杂性提高, 出现了许多基于MOEA/D的改进算法. 这些算法主要针对问题的不同特性, 对最初版本的MOEA/D进行改进. 具体地, 关于这方面的研究可总结为5个方向: (1) 权重向量; (2) 分解方法; (3) 重组策略; (4) 替换策略; (5) 计算资源分配机制. 下面将对这5个方向逐一展开介绍.

2.1 权重向量

MOEA/D的一个关键特征是, 种群的多样性由一组权重向量(或一组由权重向量决定的参考点/参考向量)引导. 每个权重向量定义一个子问题, 在理想情况下, 每个子问题的最优解为一个帕累托最优解. 对于不同的优化问题, 经典的权重向量生成方法^[13]存在以下问题.

(1) 生成权重向量的数量受目标函数个数的限制, 无法产生任意指定数量的权重向量.

(2) 对于PF规则的多目标优化问题, 均匀分布的权重向量能够引导PF近似解的一致性; 当优化问题的PF不规则(如不连续的、退化的等)时, 均匀分布的权重向量所引导的近似解在PF上不一定是一致分布的.

(3) 在高维目标空间中, 生成的方向/权重向量大多集中在目标空间的边界, 分布并不均匀. 将目标个数达到4个及以上的优化问题称为超多目标优化问题(many-objective optimization problem, MaOP).

针对上述问题, 从以下两个方面对权重向量的研究进行总结: (1)生成均匀分布的权重向量策略; (2)自适应权重向量生成方法.

2.1.1 生成均匀分布的权重向量

Tan等人^[16]提出了基于均匀设计的MOEA/D (uniform design MOEA/D, UMOEA/D)算法, 该算法通过构造均匀设计的混合实验(uniform design for experiments with mixtures, UDEM)来生成权重向量. 在UDEM中, 设置了一个参数M作为权重向量非一致性的度量, M的值越小, 权重向量的分布越均匀, 在该方法下, 生成的权重向量分布偏差最小, 与单纯形网格设计方法相比, 得到的权重向量在目标空间中分布更均匀.

针对利用MOEA/D求解MaOP时, 权重向量主要分布在权重空间的边界, Ma等人^[17]提出了一种权重向量初始化方法, 该方法下可以生成任意数量的均匀分布权重向量, 进而发展了MOEA/D-UDM算法. 该算法结合UDEM^[16]和单纯形网格设计方法, 生成备选的权重向量. 将权重向量主要产生在权重空间的内部, 部分留在边界. 然后, 从备选权重向量中选择所需权重向量数量. Li等人^[18]提出生成双层权重向量, 使用单纯形网格设计方法, 分别在目标空间的边界和内部生成一组大小分别为 ${N_1}$ 和 ${N_2}$ 的权重向量. 然后利用坐标变换, 缩小内部权重向量的坐标. 最终的权重向量集合为边界和内部所有的权重向量.

2.1.2 自适应权重向量生成方法

Harada等人^[19]提出为难求解的子问题自适应增加权重向量的方法. 首先通过EP (外部存档, 用于存储非支配解)和已有的权重向量找到比较难搜索到的子问题, 然后分配多个权重向量给这个子问题, 将该子问题进一步细分为更多的子问题, 使得更多的计算资源用于该子问题. Li等人^[20]提出通过识别浪费计算资源的权重向量来自适应的调整权重向量. 具体地, 当子问题对应的解在目标空间中的向量陷入局部最优或者处于PF的不连续区域时, 继续优化该子问题会浪费计算资源, 此时就需要对权重向量进行调整.

Jiang等人^[21]提出一种基于帕累托自适应的权重向量生成方法. 该算法根据问题的PF特征自动调整权重向量. 它有两个重要的特点: (1)采用混合均匀设计方法^[22], 生成任意数量的权重向量; (2)利用超体积指标^[4]评估权重向量与PF的交点, 调整权重向量使得超体积达到最大和交点沿PF的分布更均匀. 进一步, Jiang等人^[23]提出了一种具有快速超体积存档的新型MOEA/D算法, 用于自适应调整权重向量以适应PF形状的变化. 该算法定义了一个存档, 存储演化过程中产生的非支配解, 并通过最大化存档集合的超体积更新存档, 最后根据存档中的解周期性地调整权重向量.

Gu等人^[24]提出了一种基于自组织映射(self-organizing map, SOM)的权重向量设计方法. 具体地, 该算法利用N (N为种群大小)个当前个体的目标向量训练SOM网络中的神经元, 然后根据神经元的权值更新权重向量, 这样权重向量是根据种群中个体分布进行的调整, 因而得到的解在不完整的PF上分布也是均匀的. 该方法可以与大多数基于分解的MOEAs结合求解MaOP.

针对PF形状不连续, 有尖峰或低尾的问题, Qi等人^[25]提出了一种采用自适应权重向量调整的改进算法(MOEA/D with adaptive weight adjustment, MOEA/D-AWA). 该算法提出一个两阶段策略调整权重向量的生成. 在第1阶段, 根据TCH方法生成的权重向量和最优解之间的几何关系, 提出了一种权重向量初始化方法: WS变换. WS变换将一个子问题的权重向量进行映射, 由WS变换的可逆性, 可得到一组均匀分布在超平面 ${f_1} + {f_2} + \ldots + {f_m} = 1$ ( $m$ 为目标函数数量)的权重向量. 但当问题的PF与超平面 ${f_1} + {f_2} + \ldots + {f_m} = 1$ 不一致时, 子问题权重向量的均匀性并不能保证PF上最优解的一致性. 故在第2阶段, 提出使用自适应权重向量调整策略(adaptive weight adjustment, AWA), 使得生成的权重向量与PF形状相适应. AWA策略主要通过离解最近的m个邻居解来判断PF上解的稀疏性. 进一步, Qi等人^[26]使用狄洛尼三角网为子问题定义了一种新的邻域关系, 其PF上解的稀疏性由解之间的欧式距离和解之间的分布共同决定.

Li等人^[27]提出一种在演化过程中逐步调整权重向量的方法(approach to adapt weights, AdaW). 该方法根据种群在演化过程中产生的信息周期性地更新权重向量, 为给定的问题寻找合适的权重向量. 具体地, 当种群迭代一定次数后, 对权重向量进行更新, 生成新的权重向量, 删除解拥挤处的权重向量. 此外, 当算法接近演化过程的终点时, 权重向量的变化可能会导致沿着指定的搜索方向(权重向量)演化不够充分. 因此, 该方法不会在最后的10%代评估期间更新权重向量.

2.1.3 小　结

基于分解的算法中最终近似解集的分布和权重向量的分布是密不可分的. 因此, 如何根据问题特点生成均匀分布的权重向量是这一部分工作的研究目标. 根据上面的讨论, 可以得到以下结论.

(1) MOEA/D-UDM^[17]和双层权重向量生成方法^[18], 不仅使得权重向量的生成摆脱了目标数量的限制, 而且克服了在高维目标情况下边界解稀少的局限性. 但它们在进化过程中权重向量是固定的, 只能在问题PF规则的情况下有较好的性能.

(2) 如何在不预先知道问题的PF情况下确定一组合适的权值是一个开放问题, 利用进化过程中的信息自适应的调整权重向量是主要的解决方法. 其中, 进化过程中的信息包括子问题的求解程度^[19]、问题PF特征^{[21, 23]}、种群分布情况^{[24, 25]}等.

(3) 值得注意的是AdaW方法^[27], 该方法通过细化权重自适应过程中的几个关键部分, 即权重生成、权重添加、权重删除和权重更新频率, 逐步为给定问题分配合适的权重. 实验结果表明, AdaW适用于PF形状非常复杂的问题, 包括高度非线性, 不连续的, 退化的问题等.

2.2 分解方法

传统的3种分解方法(即WS、TCH、PBI), 在求解一些MOP时存在一定的缺陷, 如解的改进区域过大, 种群多样性被破坏. 近年来不少学者对分解方法进行了深入研究, 这些研究主要可分为以下3个方面: (1) 改进法; (2) 混合法; (3) 划分目标区域法. 下面对这3类算法进行简要概述.

2.2.1 改进法

分解方法的效果往往受所优化问题的影响. 由于优化问题的复杂性和多样性, 传统的分解方法在求解一些问题时存在一定的缺陷. 改进法即根据演化搜索过程中的特点, 对传统分解方法进行改进以更好地求解不同的优化问题.

在TCH、PBI分解方法中, 种群中的解在目标空间中朝着参考点z演化(通常z是在搜索过程中找到的理想点). 当种群趋向于PF的某一区域时, 搜索找到的理想点和真实的理想点之间的距离会变大, 导致最后得到的种群无法逼近整个PF. 针对这一个问题, Sato^[28]对传统的PBI分解方法进行扩展, 提出了反向PBI (inverted PBI, IPBI)分解方法. 与传统的PBI通过最小化子问题函数值使得解向理想点z演化相反, IPBI以当前种群中最差目标值构造的w为参考点, 通过最大化子问题函数值演化解. 在该方法中, 随着权重向量的改变, 最大子问题函数值对应的解也会改变, 使得IPBI能够搜索目标空间中更广泛的区域. 另外, 与PBI类似, IPBI也通过参数 $\theta $ 来平衡种群收敛性和多样性.

PBI方法的一个缺点是惩罚参数 $\theta $ 需要用户指定, 没有唯一的 $\theta $ 适用于不同类型的问题. Yang等人^[29]根据对PBI中惩罚参数进行分析, 提出了两种新的惩罚策略来平衡种群收敛性和多样性. 一种为自适应惩罚方案(adaptive penalty scheme, APS), APS对所有子问题分配相同的惩罚值, 但惩罚值随着搜索进行不断增加. 因此, 在搜索早期, 惩罚值较小, 有利于快速收敛; 在搜索后期, 惩罚值变大, 更强调多样性. 另一种为基于子问题的惩罚方案(subproblem-based penalty scheme, SPS), SPS根据不同子问题权重向量的位置指定不同惩罚值, 对边界子问题采取严格惩罚, 对中间子问题采取宽松惩罚, 从而边界解得到保留, PF上解的分布更广泛. 对两种策略进行比较的实验结果表明, SPS策略优于APS. 进一步将SPS融入两个MOEA/D改进算法(即MOEA/D-ACD^[30]和MOEA/D-STM^[31])中, 验证了SPS的有效性.

Wang等人提出的MOEA/D-ACD^[30]中定义子问题 $i$ 的当前解 ${x_i}$ 在目标空间中改进区域为所有优于 ${x_i}$ 的解向量构成的集合. 分析表明, 对于传统的分解方法(WS, TCH, PBI), 解的改进区域对一些问题来说过大, 导致一个新的解可以取代几个旧的解, 使得多个不同子问题有相同的解, 破坏了种群多样性. 为了克服这个问题, 提出了约束分解方法, 即对子问题添加约束. 该方法通过控制参数 ${\theta ^i}$ 来调整子问题 $i$ 的改进区域, 其中 ${\theta ^i}$ 的值在演化过程中自适应调整, 达到平衡种群收敛性和多样性的作用. Cai等人^[32]提出一种基于网格的约束分解方法(constrained decomposition with grids, CDG), 该方法将目标空间划分成多个网格. 在划分的网格系统中, 通过约束分解定义了 $m \times {K^{m - 1}}$ 个子问题( $m$ 为目标函数的数量, K为划分的区间数), 其中相同的解最多可以分配给 $m$ 个子问题, 有效缩小了解的改进区域. 另外, 网格系统很容易反映解之间的邻域关系, 使得解之间的匹配选择更有效.

Ma等人^[33]提出基于方向向量 ${l_p}$ 范数约束的切比雪夫分解方法( $p$ -Tch). 在该方法中每个子问题由方向向量的 ${l_p}$ 范数构成. 分析表明, $p$ 值的增加能够使得对各子问题改进区域的划分更均匀. 进一步, 通过分析 $p$ -Tch和其他切比雪夫分解方法之间的关系, 定义了一个广义子问题, 这个广义子问题可以在竞争中调整子问题的重要性, 使得偏好的子问题获得更多更新机会, 从而提高算法性能.

聚合函数等高线的形状和位置, 对算法搜索起着至关重要的作用^[34]. Jiang等人^[35]提出两种等高线可控的聚合函数, 分别为乘法标量化函数(multiplicative scalarizing function, MSF)和基于惩罚的标量化函数(penalty-based scalarizing function, PSF). 在MSF和PSF中, 均设置了一个参数 $\alpha $ 调整解的改进区域大小, 其中更小的 $\alpha $ 值有利于算法收敛, 对应解的改进区域更大. 所以在搜索的不同阶段调整 $\alpha $ 值, 能够有效改进算法性能. 此外, 当 $\alpha = 0$ 时, 两种标量化函数都退化为TCH.

2.2.2 混合法

不同的分解方法具有不同的搜索特性. 混合法就是将两种或者及以上的分解方法相结合, 以充分利用不同分解方法的搜索特性来有效解决MOP. 如何选择不同的分解方法进行合理地融合是这类算法的关键.

Ishibuchi等人^[14]提出同时使用TCH和WS分解方法计算个体适应度值. 并提出两种方式对这两种分解方法进行组合. 一种是多网格策略, 其中每个分解方法都有各自完整的权重向量网格系统. 另一种是单网格策略, 交替为网格中的权重向量分配这两种不同的分解方法. Zhend等人^[36]提出直接将WS和TCH进行加权组合得到一个新的加权混合方式(weighted mixture-style, WM)的分解方法, 由于WS方法集中于全局搜索, 而TCH方法关注个体搜索, 从而WM方法能够充分利用搜索信息, 有效提高算法性能.

传统的WS和TCH方法对目标函数尺度比较敏感, 结合文献[13]中基于方向的分解方法: 正常边界交叉方法(normal boundary intersection, NBI)和传统的TCH方法, Zhang等人^[37]提出了一种新的分解方法: NBI方式的切比雪夫方法, 用于处理目标函数尺度不同的MOP. 该方法根据目标空间中的极值点(即对应单个目标函数值最小的点), 生成了一组在极值点连线上均匀分布的参考点. 然后通过最小化解距参考点的最大距离使得解向参考点演化, 进而逼近PF.

WS方法适合问题PF为凸的情况, 当问题PF非凸时需要选择其他的分解方法. Ishibuchi等人^[38]提出了一种自动选择WS和TCH方法策略. 该方法的特点是, 在每一代, 若解的目标向量位于PF的非凸区域则使用TCH方法. 否则, 使用WS方法. 融合该方法的MOEA/D算法在改进的非凸PF多目标背包问题上进行了实验, 验证了该方法的有效性. MOEA/D对问题PF的形状很敏感, 主要是因为分解方法中参考点和子问题公式的设置对各种问题适应能力不强. Wu等人^[39]提出学习分解(learning-to-decomposition, LTD)范式, 首次在基于分解的MOEAs中同时自适应地设置子问题公式中的参考点, 等高线和搜索方向. 具体地, LTD范式由两个相互依赖的部分组成, 即: 学习模块和优化模块. 学习模块使用优化模块中的非支配解作为训练集, 通过高斯回归(GP)^[40]学习估计PF的模型. 然后通过学习模型中的信息, 优化模块自适应地设置: (1)符合估计PF形状的有效参考点; (2) 合适的等高线和搜索方向. 优化模块可以是任何一种基于分解的MOEAs.

Wang等人^[41]分析了一类常用分解方法的性质: ${L_p}$ 加权方法. 在 ${L_p}$ 加权方法中, 当 $p = 1$ 时, 即为WS方法; 当 $p \to \infty $ 时, 即为TCH方法. 分析表明, 随着 $p$ 值的增加, ${L_p}$ 的搜索性能下降, 但在PF几何上的鲁棒性增加, 即 $p$ 值可用于调节 ${L_p}$ 方法搜索性能及其PF几何上鲁棒性之间的平衡. 进一步, 如果知道PF几何结构, 则可通过PF的曲率来确定一个合适的 $p$ 值, 这验证了文献[42]中最优分解方法的存在性. 基于这个观点, 提出基于帕累托自适应分解方法的MOEA/D改进算法, 该算法首先初始化一组 $p$ 值, 然后在每一代, 使用参考曲线族^[21]近似PF来评估每个子问题的 $p$ 值, 将不同的子问题与不同的 $p$ 值联系起来. 在此基础上, Wang等人^[43]中提出了一种在线改进方法: PaS逼近, 用于选择最优的 $p$ 值. 该方法并不需要对PF进行评估, 更简单高效.

2.2.3 划分目标区域法

MOEA/D及其改进版本大多数通过子问题的多样性来实现种群的多样性. 在更新过程中, 新解是否替换旧解完全取决于它们的聚合函数值. 在某些情况下, 这种替代会错过一些搜索区域, 导致种群多样性丢失. 另外, 这些算法取得好的性能需要选择适当的分解方法和权重向量, 这对于很多问题来说并不容易. 为了减缓这些缺陷, Liu等人^[15]提出一种将多目标优化问题分解为一组多目标优化子问题的方法. 该方法推广了MOEA/D的框架, 得到的算法为MOEA/D-M2M. 具体地, 首先选择K个单位向量, 将目标空间划分为K个子区域. 然后将种群中的解分配到这K个不同的子区域. 基于这种划分, 将多目标优化问题转化为K个带约束的多目标优化子问题, 其中目标函数不发生改变, K个子区域定义了这K个子问题的约束空间.

2.2.4 小　结

分解方法决定了算法在演化过程中的搜索行为, 根据上述研究, 将现有工作总结如下.

(1) 分解方法主要由参考点^[28]、控制参数^{[29, 33]}、等高线的位置和形状^{[34, 35]}等因素决定. 通过调整这些因素, 能够有效提高算法性能.

(2) 为了打破传统分解方法的限制, MOEA/D-ACD^[30]、CDG^[32]通过添加约束的方式提出了新的分解机制, 能够更加灵活地调整旧解被新解替换的范围. 这类方法的关键是制定合适的约束方案以适应不同的优化问题.

(3) 不同的分解方法具有不同的搜索特性, 充分利用不同分解方法的优点, 将分解方法的特点与演化过程相匹配, 融合多种分解方法可有效提高算法求解问题的性能.

(4) MOEA/D-M2M^[15]提出的空间划分策略拓展了分解的定义, 该方法利用权重向量将目标空间划分为一组子区域, 为研究分解方法提供了新的思路.

2.3 重组策略

关于重组策略的研究主要包括两部分: 第1部分是父本的选择方式; 第2部分是子代的产生方式. 最初版本的MOEA/D根据目标空间中权重向量之间距离定义子问题邻域结构, 每个解的匹配父本是在其邻域解中随机选择的.

Li等人^[44]提出允许父本以 $1 - \delta $ 的概率从整个种群中选择来提高种群多样性, 得到的算法为MOEA/D-DE. 在此基础上, Chiang等人^[45]进一步提出一种自适应策略来调整父本选择范围. 在该策略中, 首先根据子问题在连续 $\alpha $ 代的改进情况, 将子问题分为已解决的和未解决的, 在演化过程中只选择未解决的子问题进行演化. 同时, 为了保证收敛性和多样性, 保持了 $\;\beta $ 个拥挤度距离最大的解总是被选择. 然后, 在 $\gamma Gen$ 代后开始调整父本选择范围( $Gen$ 为最大迭代次数), 根据当前解之间的欧式距离确定邻域结构, 而不是根据目标空间中权重向量之间距离, 从而避免了在目标空间中接近的解可能在决策空间中相距很远的情况, 实现了更有效的局部调整.

基于邻域的选择可能会产生一些重复解, 导致种群多样性下降. Jiang等人^[46]引入小生境技术来指导父本选择. 该方法计算每个解在T个邻域解中小生境计数, 如果一个解的小生境计数超过了给定阈值, 意味着这个解与其邻域解很相似, 此时选择邻域外的解作为父本, 避免了产生重复解, 增加了种群多样性.

选择好父本后, 需要对父本进行重组操作产生新解. MOEA/D采用模拟二进制交叉(simulated binary crossover, SBX)和多项式变异(polynomial mutation, PM)作为重组算子产生新解. 由于不同算子搜索行为不同, 对算法的影响也不同. 已有不少算子被提出应用于MOEA/D框架中.

Li等人^[44]提出使用差分算子(differential evolution, DE)作为杂交算子来处理PS复杂的MOP. Huang等人^[47]进一步研究了各种DE策略对MOEA/D性能影响, 这些DE策略包括DE/best/1、DE/rand/1、DE/best/2、DE/rand/2和DE/rand-best/1. 实验结果表明各种DE策略关键不同在于父本的选择, 但没有一种DE策略适合所有问题.

Li等人^[48]提出基于适配率等级的多臂强盗(fitness-rate-rank-based multiarmed bandit, FRRMAB)策略来自适应地选择重组算子. 为了减轻直接使用适应度改进导致算法鲁棒性弱的问题, FRRMAB使用适应度改进率(fitness improvement rates, FIR)衡量算子在最近搜索过程中的表现, 并用一个固定大小的滑动窗口来存储最近使用算子的FIR值, 每个算子的奖励为当前滑动窗口中该算子所有FIR值总和. 然后, 引入一个衰退机制, 为所有算子分配信用值来指导算子选择. 将FRRMAB方法融入MOEA/D的一个改进算法(MOEA/D-DRA^[49])中, 选择4种常用的交叉算子作为候选算子(即DE/rand/1, DE/rand/2, DE/current-to-rand/1和DE/current-to-rand/2), 测试了算法在UF^[50]测试实例上的性能. 实验结果表明, 算法在该测试实例上显著提高了MOEA/D-DE^[44]、MOEA/D-DRA^[49]和ENS-MOEA/D^[51]的性能.

Ke等人^[52]将MOEA/D与蚁群算法结合来构造解. 提出的算法将一个多目标优化问题分解为 $N$ 个单目标优化子问题, 每个单目标优化子问题由一只蚂蚁负责. 在搜索过程中, 每只蚂蚁利用当前解, 邻域信息素矩阵和自身启发式信息矩阵组成的函数来构造一个新解, 使得构造的解充分利用全局和局部信息, 更可能为子问题的一个较好的解, 加速算法收敛.

Zhou等人^[53]提出利用高斯模型产生解. 其基本思想是围绕MOEA/D中的解建立一个多元高斯模型, 从建立的高斯模型中采样一个新的试验解, 然后用多项式变异算子进行变异. 该算法在每一代建立的多元高斯模型与子问题数目相同, 所以与一般的算子相比, 计算量更大. Shim等人^{[54, 55]}提出把分布式估计算法(estimation of distribution algorithm, DEA)融入MOEA/D中来产生解. 算法通过估计决策空间中解的总体分布来预测未知解的分布, 然后采样选择解.

Martínez等人^[56]提出在MOEA/D中融入局部搜索算子, 进一步获得局部更优解. Ke等人^[57]将一个两阶段局部搜索方法(two phase Pareto local search, 2PPLS)与MOEA/D结合, 提出一种基于分解的模因算法(memetic algorithm based on decomposition, MOMAD). 算法的每一代在每个解的邻域利用帕累托局部搜索方法产生新解. Shi等人^[58]提出基于分解的并行帕累托局部搜索算法(parallel Pareto local search based on decomposition, PPLS/D), 与2PPLS不同, 该算法将原始的搜索空间分解为L个子区域, 然后在这L个子区域同时执行并行搜索.

Ma等人^[59]将一个改进的Baldwinian学习算子融入MOEA/D框架中. 该算法将当前父代种群分为K个不相交的簇, 在每个簇中建立局部分布模型, 从而得到当前种群的分段分布模型. 然后, 结合父代个体进化历史和得到的分布模型, 构造后代的下降方向. 在下降方向的指导下, 算法的收敛速度显著增加.

Wang等人^[60]研究了两种不同算子的搜索行为, 分别为差分进化, 多项式变异算子和邻域学习, 反转突变算子. 分析表明前者在找到分布广泛的解上更有潜力, 而后者能找到质量更高的解. 将这两种具有不同搜索特征的算法融入MOEA/D-GR^[61], 更有效地平衡了种群收敛性和多样性, 提高了算法性能.

依据演化过程中的特点, 本文将重组策略定义为两部分: 第1部分是父本的选择方式; 第2部分是子代的产生方式. 根据已有工作, 可以得到如下结论.

(1) 通过设置选择父本的邻域范围, 可以有效维持种群的多样性. MOEA/D-DE^[44]通过参数 $ \mathrm{\delta } $ 控制从邻域选择父本的概率. 但这种选择方式可能会产生一些重复解. 文献[46]引入小生境技术选择父本可有效避免了这一问题, 为种群多样性维持提供了新的方法.

(2) 许多产生子代解的方式已经融入分解的框架中, 主要有采用新的算子(如: 差分算子^[44]、局部搜索算子^[56]、改进的Baldwinian学习算子^[59]等)、利用其他的启发式方法^[52]和概率模型^[53]. 另外, 考虑到不同算子的特点, 根据算法性能需求融合多种算子可以有效平衡种群收敛性和多样性.

2.4 替换策略

在MOEA/D中, 一个新解可以替换多个较差的邻域解, 可能破坏种群的多样性. 不少研究通过制定不同的替换原则来克服这个问题.

Li等人^[44]提出通过限定一个新解替换旧解的个数来避免种群多样性被破坏. 在MOEA/D中, 子问题i产生的新解 $x_{\rm new}^i$ 是否取代其邻域子问题对应的解完全依赖于聚合函数值, 并没有保证解 $x_{\rm new}^i$ 对取代的子问题来说是最合适的, 从而产生下面两个问题: (1)若在搜索早期产生一些高质量的解, 将会取代大多数当前解, 使得许多子问题陷入局部最优; (2)解 $x_{\rm new}^i$ 虽然不适合子问题i的邻域子问题, 但可能适合其他子问题. 而这种情况的解, 在MOEA/D中会被舍弃, 降低了算法收敛效率. 故Wang等人^[61]提出一种全局替换(global replacement, GR)策略来调整解的替换范围. 具体地, 首先为解 $x_{\rm new}^i$ 找到最合适的子问题j, 然后选择 ${T_r}$ 个距子问题j最近的子问题组成替换邻域, 其中替换邻域大小 ${T_r}$ 可以控制种群收敛性与多样性平衡. 文献[62]进一步对GR策略进行拓展, 提出在演化过程中动态调整替换邻域大小的方法, 有效平衡了搜索过程中种群收敛性和多样性.

Wang等人^[30]提出一种约束分解方法来限制旧解的改进, 该方法通过对子问题增加约束来减小子问题改进区域. 根据搜索过程中得到的信息, 文章进一步提出一种自适应调整约束因子策略, 有效平衡了算法在不同搜索阶段种群收敛性和多样性.

在替换过程中, 有希望的解和子问题之间的相互选择可以看作是一个双边匹配问题, 即子问题对解的选择具有偏好, 反之亦然. 而MOEA/D中并没有明确考虑解对子问题的偏好. Li等人^[31]提出一个简单有效的稳定匹配(effective stable matching, STM)模型协调选择过程. 每个子问题根据聚合函数值对所有解进行排序, 此时子问题偏好聚合函数值更小的解, 因此子问题的偏好促进了算法收敛. 另外, 每个解根据其与子问题方向向量的距离对所有子问题进行排序, 此时解偏好距离最近的子问题, 解的偏好促进了多样性. 利用STM为每个子问题分配一个解, 平衡子问题和解的偏好, 进而平衡了演化搜索过程中种群收敛性和多样性.

Li等人^[18]提出融入帕累托支配关系进行替换的方法. 在该方法中, 解的替换是分层进行的, 依次考虑的是帕累托支配关系, 局部密度估计和聚合函数. 此外, 为了进一步提高种群多样性, 不会替换与一个孤立子区域相关联的最差解.

替换策略也是分解算法框架中重要的一步, 该策略通过解的替换来达到平衡种群收敛性和多样性的目的. 主要的原则有: (1)合理限定新解和旧解的替换范围; (2)将解和子问题之间进行精准匹配, 为每个子问题选择最合适的解.

2.5 计算资源分配

MOEA/D通过固定权重向量定义分解子问题, 这意味着定义了一组不变的子问题, 且在演化过程中每个子问题得到的计算资源是相等的. 然而对于复杂问题, 不同的子问题优化的难易程度是不同的, 对不同的子问题分配相同的计算资源, 使得计算资源并没有得到有效的利用. 在基于计算资源分配的MOEA/D改进算法中, 致力于将更多的计算资源分配给进化潜力更大的子问题, 以充分利用计算资源.

Zhang等人^[49]在MOEA/D的框架下提出一种为不同子问题自动分配计算资源的算法(MOEA/D-DRA). 在该算法中, 为每个子问题 $i$ 定义了一个效用函数 ${\pi ^i}$ , 并根据每50代计算的目标函数值相对减少量更新 ${\pi ^i}$ . 接着引入10-竞标赛选择机制选择效用函数值更大的一组子问题进化, 实现了计算资源动态分配. 进一步, MOEA/D-GRA^[63]在MOEA/D-DRA基础上进行扩展. 该算法定义了一个概率向量P, 并将子问题与P中不同元素相关联. 然后提出两种资源分配策略更新向量P. 这两种策略分别为离线资源分配(offline resource allocation, OFRA), 在线资源分配(online resource allocation, OBRA). OFRA表示离线度量, 即向量P中的元素根据子问题难易程度事先设定. ONRA表示在线度量, 即向量P根据搜索过程中子问题难易程度动态调整. 实验测试表明, ONRA策略更加实用.

Cai等人^[64]提出了一种新的算法. 该算法利用外部存档指导计算资源在子问题之间动态分配. 算法融合了多目标演化优化的两种基本策略, 分别为基于支配排序和分解的策略, 用于求解具有2个或3个目标的组合优化问题. 算法维持了两个种群, 一个为内部种群, 另一个为外部存档, 其中基于分解的策略用于演化内部种群, 使用NSGA-II中的非支配排序和拥挤度距离更新外部存档. 算法通过记录前L代中每个子问题演化所得的解进入外部存档的数量, 决定子问题分配计算资源的概率.

Li等人^[65]提出引入随机权重向量的MOEA/D改进算法. 该算法在MOEA/D-DE^[44]的基础上进行改进, 在考虑使用固定权重向量的同时, 引入随机权重向量, 用于求解具有不规则PF的MOP. 具体地, 当算法中固定权重向量定义的子问题i在G次函数求值中都没有得到改进时, 则从外部种群中选择个体生成新解 $y$ , 并更新在 $y$ 上改进最大的子问题. 子问题更新通过外部存档中非支配解产生随机权重向量实现.

计算资源分配主要思想是为不同难度的子问题分配不同的计算资源, 以期实现计算资源的高效合理分配. 实现的方式有: (1)定义效用函数来评价子问题难易程度, 如何根据演化过程在线更新效用函数是这类方法的关键^{[49, 64]}; (2)利用外部存档存储演化过程中得到的非支配解, 来指导计算资源分配^[65]; (3)根据演化过程中的信息调整权重向量^[66], 该方法在求解PF不规则的问题上具有较好的性能.

3 研究热点

自20世纪90年代以来, 许多学者致力于研究求解目标数量为2–3个的无约束多目标优化问题算法. 然而许多实际应用不仅涉及的目标达到4个或以上, 而且一般都具有一定的限制条件, 使得优化问题的求解难度大大增加. 近年来, 目标个数达到4个及以上的超多目标优化问题(MaOP)和含有约束限制的约束优化问题(constrained optimization problem, COP)已成为优化领域的热点研究课题. 受基于分解算法思想和技术的启发, 许多研究在求解MaOP和COP上做出了一些成果.

3.1 在超多目标优化问题(MaOP)上的研究

在MaOP中, 随着目标维数的增加, 优化过程中搜索能力、重组效率和分布性评价等难度急剧增加. 而基于分解的算法中简单有效的个体比较方式以及良好的多样性维持机制有希望解决MaOP中存在的困难. 不少研究已经做出了一些探索. 本节主要从以下3个方面进行总结, 分别是: (1)参考点/参考向量的设置; (2)分解技术与其他方法结合; (3)偏好信息表达.

3.1.1 参考点/参考向量的设置

基于参考点/参考向量设置的方法主要通过定义一组分布在目标空间中的参考点/参考向量指导种群在不同区域搜索.

Deb等人^[66]在NSGA-II的框架下提出了一种基于参考点的超多目标演化算法(NSGA-III)来求解MaOP. 该算法主要通过一组参考点将目标空间分解, 然后将解与参考点相关联来指导解的选择. 而一组固定的参考点可能会出现帕累托最优解和参考点不匹配的情况. 故文献[67]进一步对NSGA-III进行改进, 提出了一种自适应参考点方法, 即如果一个参考点与多个解相关联, 则认为该参考点是拥挤的, 需要在该参考点附近加入新的参考点. 反之, 如果一个参考点没有相关联的解, 则将该参考点删除.

文献[68]在MOEA/D-M2M^[15]的基础上, 设计了一种自适应区域分解策略来处理PF退化的MaOP. 自适应区域分解由自适应参考向量实现, 该策略根据种群在演化过程中的变化趋势及时调整参考向量来划分区域, 弥补了PF退化的MaOP在采用固定且均匀分布参考向量的不足之处.

Cheng等人^[69]提出了一种基于参考向量指导的演化算法(reference vectors-guided evolutionary algorithm, RVEA). 该算法主要特点是: (1)设计了一种新的基于角度惩罚距离(angle-penalized distance, APD)聚合方法来动态平衡算法收敛性和多样性; (2)针对目标函数没有很好归一化情况, 提出了一种自适应调整参考向量策略, 以得到一个均匀分布的帕累托最优子集.

Asafuddoula等人^[70]提出了一种基于分解的改进算法(improved decomposition-based evolutionary algorithm, I-DBEA). 该算法使用PBI方法中的两种距离度量 ${d_1}$ 和 ${d_2}$ 来维持种群收敛性与多样性平衡. 与PBI方法中通过额外参数控制不同, 算法采用了简单的优先原则, 先考虑 ${d_2}$ 度量再考虑 ${d_1}$ 度量. Yuan等人^[71]提出利用目标空间中解到参考向量的垂直距离明确地维持高维空间中解的多样性.

3.1.2 分解技术与其他方法结合

Cai等人^[72]提出一种基于排序和选择的MOEA/D改进算法(variant of MOEA/D with sorting-and-selection, MOEA/D-SAS)求解MaOP. 算法引入两个独立部分来平衡收敛性和多样性, 即基于分解的排序(decomposition-based-sorting, DBS)和基于角度的选择(angle-based-selection, ABS). DBS只对每个子问题的L个最接近的解进行排序, 以控制收敛性和降低计算量. ABS利用目标空间中解之间的角度信息来精确的保持多样性. 此外, 该算法允许一个子问题与任意数量的解相关联, 这使得它能更灵活处理PF形状不同的问题.

Li等人^[18]提出一种结合帕累托支配和分解策略的算法(MOEAs combines the dominance- and decomposition-based approaches, MOEA/DD)来求解MaOP. 算法主要利用支配和分解方法的优势来平衡演化过程中收敛性和多样性. 分解策略用于限制每个解只能与一个子区域相关联, 并通过对子区域的局部密度估计管理多样性. 算法的特点是采用稳态分层方式, 依次基于帕累托支配, 局部密度估计和聚合函数进行更新操作.

NSGA-III强调的是接近参考点的非支配解, 当目标数量较大时, NSGA-III依赖的帕累托支配关系仍然缺乏足够的选择压力将种群拉向PF, 此时NSGA-III更强调多样性而忽略了收敛性. 而MOEA/D即使在高维目标空间中, 通常也可以通过基于聚合函数的选择算子很好地逼近PF. 故Yuan等人^[73]提出了一种新的支配关系: $\theta $ -支配. 该支配关系考虑了NSGA-III与MOEA/D的优势, 利用MOEA/D中基于聚合函数的适应度评价方案来增强NSGA-III在高维空间中的收敛能力, 从而更好地兼顾收敛性和多样性.

3.1.3 偏好信息表达

多目标优化最终目的是为DM提供更多偏好解. 随着目标数量的增加, 为DM提供大量近似整个PF的折中解, 不仅增加了DM的工作量, 而且给决策过程带来了许多不相关甚至是有噪声的信息. 特别的, 当目标空间较大时, 以有限大小的种群来获得整个PF上具有代表性子集是不现实的. 为了方便决策过程, 利用DM偏好信息指导搜索过程, 找到DM感兴趣的区域不仅能够节省大量的计算资源, 而且更具有实际意义.

基于参考点的多目标演化算法可以通过指定参考点指导特定区域搜索. NSGA-III对整个PF生成一组均匀分布的参考点, 若用DM指定的参考点代替均匀参考点, 也可以聚焦于PF上偏好区域. 文献[69]提出通过DM提供一个中心向量和半径来指定一个偏好区域. Li等人^[31]提出通过选择指定参考点附近的权重向量来定义子问题, 驱动搜索及计算资源集中于偏好区域. Mohammadi等人^{[74, 75]}提出基于参考点的分解多目标演化算法(reference point based multiobjective evolutionary algorithm with decomposition, R-MEAD)及其改进算法R-MOEAD2. 算法以DM决定的一组参考点代表其偏好区域. 与直接利用参考点定义子问题不同, 算法引入了一组基本权重向量, 所谓基本权重向量指的是与每个参考点最接近点对应的权重向量. 然后, 通过半径参数围绕基本权重向量生成一组新的权重向量. 在满足终止条件之前, 动态循环更新与每个参考点相关的权重向量, 使算法收敛于偏好区域.

Li等人^[76]提出了一种系统方法, 以先验或交互的方式将DM偏好信息整合到基于分解的演化算法中. 其基本思想是通过一种非均匀映射策略(nonuniform mapping scheme, NUMS), 将标准单纯形上原本均匀分布的参考点映射到接近DM提供的期望向量, 使得越接近DM指定的期望向量区域参考点的数量越多, 从而能够直接或交互地引导搜索过程朝着感兴趣区域方向. 这里NUMS决定了映射后参考点的分布, 如何进一步根据DM需求采取不同的映射策略是值得进一步研究的问题.

Pilat等人^[77]提出将用户偏好融入MOEA/D中的协同演化算法(co-evolution-based algorithm which incorporates user preferences into MOEA/D, cwMOEA/D). 算法的主要思想是利用权重向量与用户偏好协同演化. 该算法中用户偏好通过定义偏好函数表达, 然后在每一代, 对偏好解和非偏好解使用标准差不同的高斯突变来动态调整权重, 探索用户更偏好的解.

Xiong等人^[78]提出了一种区域偏好混合交互式超多目标演化算法. 算法结合目标区域和参考点构造了反映DM偏好的模型. 为了在集中于偏好区域搜索同时保持区域内良好收敛性和多样性, 引入三层排序准则, 在搜索过程的不同阶段使用不同的排序. 在交互式方法中使用模糊理论使DM在优化过程中进一步表达偏好程度, 并将更多的计算资源分配到目标空间中感兴趣区域.

3.2 在约束优化问题(COP)上的研究

约束多目标优化问题(constrained multiobjective optimization problem, CMOP)在包含多个相互冲突的目标的同时还需要满足一定的约束条件. 由于约束条件的存在, 导致产生了许多不可行解. 如何处理搜索过程中不可行解与可行解之间的关系, 实现计算资源的有效利用是求解这类问题的关键. 近年来, 许多复杂的约束处理方法被有机地集成到MOEA/D框架中, 成功地解决了各种CMOP. 这些方法主要可分为3类, 分别是惩罚函数, 目标和约束分离, 修复方法. 下面对这3类方法进行总结. 另外, 运用MOEA/D的分解思想求解单目标约束优化问题也有一些研究^[79].

3.2.1 惩罚函数

基于惩罚函数的约束处理方法是处理约束优化问题常用的一种方法, 其主要思想是在目标函数中加入惩罚项构造惩罚适应度函数, 将约束优化问题转化为无约束优化问题, 从而很多无约束优化方法可以被修正来处理约束优化问题.

Jan等人^[80]对MOEA/D-DE^[44]更新策略进行修正, 提出了一种新的约束处理方法, 该方法通过在适应度函数中加入惩罚项构造一个惩罚函数来惩罚不可行解. 具体地, 算法计算了每个解 $x$ 的约束违反值 $V(x)$ , 如果 $V(x) = 0$ ,说明 $x$ 是可行解, 否则是不可行解. 并根据解 $x$ 当前匹配更新邻域中解的最大约束违反值和最小约束违反值, 定义一个阈值 $\tau $ 控制解 $x$ 的惩罚量. 当解 $x$ 的约束违反值大于阈值 $\tau $ 时, 罚函数的惩罚量大幅度增加, 解 $x$ 更新其他解的机会大大降低, 使得算法更倾向于搜索解的可行区域和可行区域附近的不可行区域.

Fan等人^[81]提出了一种推拉搜索(push and pull search, PPS)框架, 并将该框架与MOEA/D结合求解CMOP. 具体地, PPS将搜索过程分为两个不同的阶段: 推进和拉回阶段. 在推进阶段, 不考虑约束对搜索空间进行搜索, 使得解可以快速跨越PF前不可行区域, 逼近无约束PF. 此外, 在推进阶段可以对约束信息进行探测和估计, 用于拉回阶段的参数设置. 当种群中理想点和最低点之间的最大变化率小于或等于一个预先定义的阈值时, PPS转换到拉回阶段, 该阶段采用改进的 $\varepsilon $ 约束处理技术, 将推进阶段得到的不可行解拉回到可行和非支配区域. 在基于惩罚技术的约束优化算法中, 惩罚参数的设置决定了不可行解的惩罚程度, 会影响约束优化问题最优解的搜索. 进一步, Fan等人^[82]提出一种自适应参数设置方法. 受机器学习中学习率的启发, 设计了一个采用指数衰减模型的惩罚函数, 该模型整合了约束违反值、目标值、当前迭代计数和最大迭代次数的信息, 能够自适应的生成惩罚因子. 与 $\varepsilon $ 约束处理机制^[81]中先考虑约束违反值, 再考虑目标值不同, 该惩罚函数同时考虑了约束违反值和目标值, 能更好地维持种群多样性.

3.2.2 目标和约束分离

在惩罚函数方法中, 寻找一个理想的惩罚因子并不容易. 约束与目标分离的机制将目标和约束分开处理, 不需要额外的参数.

Fan等人^[83]对 $\varepsilon $ 约束处理方法^[84]进行改进, 用于处理CMOP. 与原 $\varepsilon $ 约束处理方法中 $\varepsilon $ 水平值递减不同, 在改进的方法中, 当种群中可行解的比例大于一个给定的阈值时, 增加 $\varepsilon $ 水平值, 从而增加了对不可行区域的搜索偏好, 在一定程度上提高了算法性能. 此外, 在该算法中, 以 $\varepsilon $ 水平值作为参数, 定义了一个基于 $\varepsilon $ 水平值比较的准则, 新生成的解根据 $\varepsilon $ 水平值比较准则与邻域中的解进行比较, 并取代更差的解.

Fan等人^[85]对约束支配原则(constrained dominance principle, CDP)^[86]进行改进, 提出了一种基于角度的约束支配原则(angle-based constrained dominance principle, ACDP). 在CDP中, 考虑不可行解与可行解时, 认为不可行解总是比可行解更好, 忽略了不可行区域的一些有用信息. 考虑不可行解与不可行解时, 仅依赖于解的约束违反, 使得当种群中大部分的解都为不可行解时, 种群的多样性难以维持. 而在ACDP中, 在比较解时, 还考虑了比较的解在目标空间中的角度以及当前种群中可行解比例, 即当比较的解中存在不可行解时, 如果解之间的角度小于一个给定的阈值, 则认为可行解是更好的, 否则, 解之间是不可比较的. 改进后的方法融入MOEA/D中, 显著改进了种群收敛性和多样性.

文献[87]回顾了一类常用的约束多目标进化算法, 其中基于分解的约束多目标进化算法有MOEA/D-CDP^[88], MOEA/D-SR^[88]和MOEA/D-IEpsilon^[83]. 并在23个约束问题上对这些算法进行了测试, 实验结果表明, 在基于分解的约束多目标进化算法中, MOEA/D-IEpsilon性能最好, 这得益于在进化过程中, 算法在工作种群中维持了一小部分不可行解, 在一定程度上增强了MOEA/D-IEpsilon的性能.

3.2.3 修复方法

这类算法利用修复算子将不可行解转化为可行解.

文献[89]提出了一种相反的修复算子, 来修复违反上下界约束的解. 算子的提出受对立学习(OBL)^[90]概念启发, 当解违反上界约束时, 将解的修复值设置为下界. 反之, 设置为上界. 即对解进行相反的估计, 那么根据OBL原理, 这个算子有可能增加种群多样性.

4 在实际问题中的应用

许多工程应用和工业生产问题都可以转化为多目标优化问题, MOEA/D作为最具代表性的MOEAs之一, 已成功应用于许多实际问题. 本节主要介绍6项MOEA/D在实际问题中的典型应用.

4.1 图像分割问题

图像分割在计算机视觉和图像理解中起着重要作用. 图像分割的定义是将一幅图像分割成具有相似特征(如颜色、纹理、灰度等)的多段图像. 近年来, 各种基于演化算法的模糊聚类方法被提出用于图像应用. Zhang等人^[91]提出一种多目标演化模糊聚类方法, 该方法考虑在图像分割中保持图像细节和抑制噪声的平衡, 采用MOEA/D中WS分解方法, 将两个目标优化问题分解为多个单目标优化子问题, 每个子问题代表一个具有不同权重集的模糊聚类问题, 从而兼顾了保留图像细节和抑制噪声这两个目标的不同平衡. 然而, 在一些复杂的问题中, 特别是非凸聚类问题, WS分解方法并不适合作为分解策略. 融合更有效的策略来处理图像分割中复杂聚类问题是未来可进一步研究的问题.

4.2 调度问题

柔性制造系统(flexible manufacturing system, FMS)是指由有限资源组成, 可处理多种作业的计算机控制的制造系统. 与作业车间和流水车间等传统生产环境不同, FMS由于具有高度的路由灵活性和资源共享能力, 经常会遇到死锁问题. 一旦出现死锁, 整个或部分系统将被无限期锁住, 无法完成制造任务. 在实践中, 开发有效的控制和调度方法在避免死锁的同时优化系统性能是至关重要的. Wang等人^[92]针对有死锁倾向FMS多目标调度问题, 在所研究系统Petri网(Petri net, PN)模型基础上, 结合分解方法和离散化差分演化(discrete differential evolution, DDE)算法, 提出了一种新的调度算法(DMOEA/D), 该算法将一个多目标调度问题分解为若干单目标子问题, 并在一次运行中优化所有子问题, 其中子问题的解由DDE算法生成.

4.3 传感器问题

近年来, 无线传感器网络(wireless sensor networks, WSNs)的应用越来越广泛, 其中最重要的应用之一是入侵检测. 无线传感器屏障覆盖的目的就是检测试图穿越特定区域的入侵者, 在这些区域有限功率的传感器是以随机方式远程分布. Zhang等人^[93]考虑沿线性域部署范围可调的有限功率传感器, 以形成检测入侵事件的屏障. 具体地, 引入了个最小化目标: (1)满足全覆盖情况下的总耗能; (2)主动传感器的数量; (3)主动传感器节点的最大感知范围. 为了在这3个目标之间取得更好的平衡, 提出了多目标框架PS-MOEA/D (problem specific MOEA/D). 此外, 将问题的背景知识融入局部搜索中, 使得相邻子问题在搜索过程中能更好地相互协作. 由于传感器的功率是有限的, 节能是延长无线屏障使用寿命的一个关键问题. 节能WSNs设计的关键是需要决定位置(部署)和感兴趣区域传感器部署的传输功率^[94], 来最大化网络覆盖和生命周期. Konstantinidis等人^[95]定义了WSNs中密集部署和功率分配问题(dense deployment and power assignment problem, d-DPAP), 提出了一种混合分解和广义子问题依赖启发式(generalized subproblem-dependent heuristic, GSH)算法, 该算法将d-DPAP分解为若干个单目标子问题, 并利用邻域信息和问题背景知识并行地对子问题进行优化, GSH依概率在6种d-DPAP策略之间交替, 这些策略是基于各种不同WSNs概念和对子问题的偏好设计的.

4.4 航空航天工程问题

随着全球商业、通讯和旅游业迅速发展, 航空运输业的重要性也明显提高. 然而, 飞机和机场运营的扩展面临一个相当大的问题是机场附近社区的抗议. 因为噪声, 污染物排放等对环境负面影响的显著增加, 直接影响了机场周边社区的日常生活. 因此, 如何减少航空运输带来的不利影响, 是实现航空运输可持续发展的关键. 文献[96]将MOEA/D技术应用于飞机终端降噪航线的优化设计. 综合各方面因素, 制定了噪声和油耗双目标优化问题. 然后, 利用MOEA/D求解这些问题. 此外, 为了保证在优化过程中垂直剖面的设计空间始终可行, 采用了一种轨迹参数化技术, 该技术有效减少了MOEA/D模型评价数量, 大大降低了计算成本.

航空发动机管道布线也是一个典型的多目标优化问题. Jiao等人^[97]提出一种基于改进的MOEA/D多目标管道布线方法, 以自动生成三维空间和发动机旋转空间中管道布局的非支配解. 该方法设计了一种适用于三维空间中直线布线问题的编码方式, 将管道长度, 管道安装方便度和管道数指定为布线的目标, 并将避障约束整合到每个目标函数中. 根据管道布线问题的特点, 通过集成一个离散化算子来修正MOEA/D, 并用它来求解管道布局的Pareto集. 进一步可将该布线方法推广到表面的情况, 以满足航空发动机旋转表面铺设管道的要求. 最后, 分别在三维模型和简化后的航空发动机模型上进行了管道布线计算, 验证了该方法的有效性.

4.5 能源供应问题

功率变换器是智慧城市时代重要的可再生能源供应系统, 为了实现高效的可再生能源供应, 必须考虑两个问题. 第1个是最大功率点跟踪(maximum power point tracking, MPPT)^[98-100]: 通过调节系统参数, 功率变换器尝试从光伏输入中提取最大平均功率; 第2个是系统运行稳定^[101-103]: 通过对系统参数调整, 功率变换器试图稳定瞬时输入功率的周期轨道. 以这两个问题作为目标函数, Togawa等人^[104]提出了改进的MOEA/D进行求解, 其中以TCH作为分解方法, BLX- $ \mathrm{\alpha } $ ^[105]为交叉算子. 通过数值实验, 得到了目标空间中两个目标函数和系统控制参数的帕累托前端. 这一结果表明文献[102, 103]中的权衡结果是PF的一部分, 为实现可再生能源的高效供应、发展经济与可持续能源供应的合作提供了基础.

4.6 机器学习

在机器学习和认知科学中, 自步学习(SPL)是最近提出的一种学习范式, 用于避免求解非凸优化任务时, 得到一个不好的局部最优解. SPL问题可以很自然地表述为一个标准的双目标优化问题, 即损失函数和自步调节器. 文献[106, 107]中提出了一个多目标自步学习(multiobjective self-paced learning, MOSPL)方法来求解SPL问题, 利用MOEA/D对这两个目标同时进行优化. 由于每个解都可以使用来自其邻域解的信息, 并进行自动校正. 故提出的MOSPL方法对初始化具有很强的鲁棒性. 此外, MOSPL引导解收敛到帕累托前端, 以最快的速度接近整个求解路径, 有利于对SPL问题进行更进一步的理解.

深度卷积神经网络(deep convolutional neural networks, DCNNs)近十几年来在计算机视觉任务中取得了显著的效果. 为了在文献[108, 109]等海量数据集上实现更高的精度, 设计超大规模的网络已成为一种趋势. 然而, 由于在测试评估过程中需要进行数以千万计的乘加运算, 计算复杂度巨大, 阻碍了DCNNs在计算资源有限的平台上的部署. Zhang等人^[110]提出在MOEA/D的框架下, 以精度和计算成本为两个相互冲突的目标, 同时进化多个染色体, 这些染色体代表预先训练的卷积神经网络不同的结构. 利用基于MOEA/D的剪枝方法, 通过启发式搜索演化卷积结构, 主动找到卷积核的关键结构. 该方法显著降低了神经网络计算复杂度, 在网络结构优化等机器学习任务中显示出巨大的潜力. Lu等人^[111]将MOEA/D用于卷积神经网络中超参数优化, 有效平衡了提出的神经网络结构的预测精度、模型紧凑性和模型效率.

在连续机器人控制问题的多目标强化学习中, Xu等人^[112]表明多目标机器人控制最佳性能折中的有效表示是由不同策略族组成的帕累托集. 为了找到这个帕累托集的表示, 提出了一种计算帕累托策略集的有效算法. 该算法借鉴了MOEA/D中的分解思想, 通过加权和聚合, 将多目标优化问题分解为了多个单目标子问题.

多任务学习(multi-task learning, MTL)旨在同时学习多个相关任务, 是机器学习领域的热门研究课题. 通过共同解决多个相关任务, MTL可以进一步提高每个任务的求解性能, 减少执行所有任务所需时间. MTL已经在计算机视觉^[113]、自然语言处理^[114]和语音识别^[115]等领域取得了很好的效果. Lin等人^[116]提出了一种基于帕累托的多任务学习(Pareto MTL)算法, 与以往找到单一解来优化所有任务不同, Pareto MTL结合MOEA/D-M2M^[15]和基于梯度的思想, 获得了一组在各任务之间进行不同权衡的代表性解. 统计结果表明, 提出的算法能有效求解超高维(神经网络训练, 可达百万维及以上)优化问题. Pareto MTL中的偏好方向虽然可以基于用户偏好, 但得到的解并不能保证与偏好的一致性. 故Mahapatra等人^[117]进一步提出了精确Pareto最优(exact Pareto optimal, EPO)搜索方法, 寻找满足某一偏好的帕累托最优解, 得到PF上更多样化的解.

模糊系统是一种将输入、输出和状态变量定义在模糊集上的系统. 模糊系统设计中有两个目标: 最大化准确性和最大化可解释性, 这两个目标通常是相互矛盾的. 因此, 无法设计一个理想的基于模糊规则系统对这两个目标来说都是最优的, 即模糊系统设计可看作是找到准确性和可解释性之间一个折中方案. Nojima等人^[118]提出了一种新的聚合函数-精度定向函数(accuracy-oriented function, AOF), 将其融入MOEA/D中, 并应用于演化模糊系统中模糊分类器设计. 在多目标基于模糊遗传的机器学习(fuzzy genetics-based machine learning, FGBML)^[119]中的测试, 表明对训练数据使用AOF能显著提高MOEA/D搜索能力. 基于MOEA/D的多目标FGBML得到了更简单的分类器, 在保持测试数据准确性的同时, 计算时间更短.

5 代表性MOEA/D改进算法性能对比

本节实验比较了6种MOEA/D改进算法性能, 分别是MOEA/D-DE^[44]、MOEA/D-DRA^[49]、MOEA/D-M2M^[15]、MOEA/D-AWA^[25]、MOEA/D-GR^[61]和MOEA/D-AGR^[62]. 这6种对比算法主要是根据MOEA/D的改进方向进行选择的, 具体的算法介绍见第5.1节. 测试函数选择了8组测试问题, 分别是: ZDT^[120]、DTLZ^[121]、DTLZ^{–1 [122]}、mDTLZ^[123]、WFG1–WFG4^[124]、UF1–UF9^[50]、MOP1–MOP7^[15]和RE21–RE25, RE31–RE37^[125]问题.

5.1 算法介绍

(1) MOEA/D-DE、MOEA/D-DRA

MOEA/D-DE是基于DE算子进行演化的MOEA/D改进算法. MOEA/D-DRA是在MOEA/D的框架下提出的一种为不同子问题自动分配计算资源的算法, 算法定义了一个效用函数来指导演化子问题的选择, 实现计算资源的动态分配.

(2) MOEA/D-M2M

MOEA/D-M2M拓展了MOEA/D的框架, 该算法将目标空间划分为K个子区域, 然后将种群中的解分配到这K个子区域, 实现了将一个多目标优化问题转化为K个带约束的多目标优化子问题.

(3) MOEA/D-AWA

MOEA/D-AWA针对的是PF形状不规则的问题(如不连续、有尖峰或低尾问题)提出的改进算法, 算法采用一个两阶段策略来实现PF上最优解均匀分布. 第1阶段初始化得到均匀分布的权重向量; 第2阶段引入自适应调整权重向量策略, 使得权重向量分布与PF形状相一致.

(4) MOEA/D-GR、MOEA/D-AGR

MOEA/D-GR采用一种全局策略来调整解的替换范围, 为当前解匹配合适的子问题及相应的替换邻域. MOEA/D-AGR进一步对MOEA/D-GR中的策略进行拓展, 在演化过程中采用动态调整替换邻域大小方法, 有效平衡了搜索过程中收敛性和多样性.

5.2 测试问题介绍

ZDT是一组2目标测试问题, 其决策变量维度可扩展. DTLZ测试问题的决策变量维度和目标函数维度都可以进行扩展, 这两组测试问题的决策变量可分且PS是线性的. DTLZ^–1是DTLZ测试问题进行稍微改变得到的, 即将DTLZ中最小化目标函数改为最大化目标函数. mDTLZ是对DTLZ进行修正得到的测试问题, 得到的mDTLZ测试问题具有几乎不占主导位置的边界. WFG测试问题也是可扩展的问题, 这组测试问题包含各种属性: 凸的、凹的、不可分和多峰等. UF是一组PS形状复杂的测试问题. MOP是一组距离函数不均衡的测试问题. 这几组测试问题都是合成的, 特点比较直观. RE是一组由现实问题组成的测试问题, 其目标维度和决策变量维度都是不可扩展的.

5.3 实验设置

(1) 种群大小N: 实验中, 对于相同的测试问题每个算法种群大小设置相同. 对于ZDT、MOP1–MOP5和RE21–RE25问题, N=100; 对于DTLZ、UF1–UF9、WFG1–WFG4、MOP6–MOP7、DTLZ^–1和mDTLZ问题, N=300; 对于RE31-RE37问题, N=105.

(2) 最大评价次数: ZDT问题, 最大评价次数设置为25000; DTLZ、WFG1–WFG4、DTLZ^–1、mDTLZ和RE问题, 最大评价次数设置为100000; UF1–UF9, 最大评价次数设置为150000; MOP1–MOP5, 最大评价次数设置为300000; MOP6–MOP7, 最大评价次数设置为900000.

(3) 独立运行次数: 30次.

(4) 性能评价指标: 选择一个常用的指标—反向世代距离(inverted generational distance, IGD)指标来评价算法性能.

IGD指标^[126]: 令 ${P^*}$ 为从真实PF上均匀采样得到的一组解; P为一个算法终止时获得的一组近似解. 则IGD值的计算如下:

$ IGD({P^*}, P) = \frac{{\displaystyle\sum\nolimits_{v \in {P^*}} {d(v, P)} }}{{|{P^*}|}} $

(5)

其中, $v = {({v_1}, \ldots, {v_m})^{\rm{T}}}$ 表示 ${P^*}$ 中的一个解, $d(v, P)$ 表示v到P中最近点的欧式距离. IGD指标值越小, 表示这个算法得到的近似解P的质量越好.

5.4 实验结果及分析

表1为6个算法求解的8组测试问题IGD统计结果. 图5–图9为6个算法中平均IGD最小的算法, 在30次独立运行时得到的IGD最小时PF近似图. 由表1中IGD统计结果可知, 对于ZDT, DTLZ这两组测试问题, MOEA/D-AWA性能最好. MOEA/D-DRA和MOEA/D-M2M次之. 由图5的PF近似图可以看到, 最好的算法在DTLZ2和DTLZ4测试问题上表现是欠佳的.

表 1 6种算法求解选择的测试问题时, 30次独立运行得到的IGD度量值

Problem	MOEA/D-DE	MOEA/D-DRA	MOEA/D-M2M	MOEA/D-AWA	MOEA/D-GR	MOEA/D-AGR
Problem	mean (std)	mean (std)	mean (std)	mean (std)	mean (std)	mean (std)
ZDT1	2.3923E−2 (6.75E−3)	6.8684E−3 (4.03E−3)	6.8292E−3 (3.74E−4)	3.9987E−3 (9.84E−5)	6.9234E−3 (2.30E−3)	6.824E−3 (1.70E−3)
ZDT2	1.4810E−2 (5.58E−3)	2.7626E−2 (3.01E−2)	7.0759E−3 (3.50E−4)	6.0739E−3 (1.00E−2)	6.154E−3 (1.23E−3)	6.527E−3 (9.91E−4)
ZDT3	3.5688E−2 (1.74E−2)	1.0176E−1 (4.63E−2)	1.7213E−2 (2.15E−3)	8.6876E−3 (4.15E−3)	1.7934E−2 (6.12E−3)	1.2526E−2 (2.44E−4)
ZDT4	4.2971E−1 (2.41E−1)	3.1790E+0 (3.13E+0)	9.9562E+0 (4.18E+0)	1.1497E−2 (1.36E−2)	2.7215E+1 (1.17E+1)	7.2450E−2 (1.04E−3)
ZDT6	3.1371E−3 (1.15E−4)	3.1143E−3 (1.65E−5)	6.0482E−3 (3.33E−4)	3.1920E−3 (5.09E−5)	4.8237E−3 (1.92E−3)	4.4724E−3 (1.62E−3)
DTLZ1	1.5206E−2 (3.25E−5)	1.5191E−2 (5.96E−5)	6.5052E−1 (5.69E−1)	1.0832E−2 (8.17E−5)	1.2041E−2 (5.78E−4)	1.1245E−2 (1.47E−5)
DTLZ2	3.8063E−2 (1.47E−4)	3.7961E−2 (2.31E−4)	8.4632E−2 (3.99E−3)	2.9116E−2 (9.74E−5)	3.1024E−2 (3.21E−4)	3.0431E−2 (4.03E−4)
DTLZ3	5.4607E−2 (5.80E−2)	6.4726E−2 (6.81E−2)	3.1659E+1 (1.15E+1)	3.0183E−2 (3.95E−4)	7.0570E+0 (1.65E+1)	4.5621E−2 (7.7182E−3)
DTLZ4	4.9766E−2 (3.91E−2)	8.5263E−2 (1.27E−1)	4.8311E−2 (1.36E−3)	9.7475E−2 (1.77E−1)	3.8132E−1 (2.71E−1)	3.8174E−1 (1.69E−1)
DTLZ1⁻¹	2.9440E+2 (7.73E+0)	3.1046E+2 (6.72E+0)	2.8668E+2 (8.11E+0)	3.1753E+2 (4.37E+0)	6.9848E+1 (2.23E+1)	1.9624E+2 (2.13E+1)
DTLZ2⁻¹	2.4993E+0 (1.28E−3)	2.4985E+0 (1.73E−3)	2.3754E+0 (3.05E−2)	2.4985E+0 (2.67E−3)	7.2601E−1 (1.08E−1)	2.4975E+0 (1.87E−2)
DTLZ3⁻¹	1.9567E+3 (4.80E+1)	2.0081E+3 (3.71E+1)	1.8589E+3 (7.25E+1)	2.1729E+3 (2.19E+1)	7.4275E+2 (3.60E+1)	2.0402E+3 (2.57E+1)
DTLZ4⁻¹	2.4923E+0 (4.35E−3)	2.4938E+0 (2.39E−3)	2.3689E+0 (2.86E−2)	2.4979E+0 (3.15E−3)	1.8945E+0 (5.44E−1)	2.4908E+0 (4.862E−1)
mDTLZ1	3.7395E−1 (3.31E−1)	3.0537E−1 (1.70E−1)	1.7462E+4 (1.32E+2)	1.7547E−2 (1.94E−4)	3.8001E−1 (3.05E−1)	2.6712E−2 (1.97E−1)
mDTLZ2	5.9440E−2 (1.45E−3)	5.8766E−2 (1.67E−3)	9.1315E−2 (4.34E−3)	3.6228E−2 (1.68E−3)	5.7218E−2 (2.20E−3)	6.2431E−2 (1.20E−3)
mDTLZ3	4.0521E−1 (3.23E−1)	4.3291E−1 (5.21E−1)	2.2231E+4 (2.36E+2)	5.2756E−2 (1.00E−3)	5.5057E−1 (1.72E−1)	6.0391E−2 (2.67E−2)
mDTLZ4	2.0174E−1 (1.22E−1)	2.1648E−1 (1.11E−1)	8.5298E−2 (2.95E−3)	1.6943E−1 (7.91E−2)	1.9501E−1 (1.16E−1)	9.1521E−2 (1.52E−2)
WFG1	1.4072E+0 (4.83E−2)	1.0782E+0 (1.37E−1)	1.2685E+0 (5.87E−2)	1.0062E−1 (2.48E−3)	1.4507E+0 (2.08E−2)	1.4491E+0 (1.61E−2)
WFG2	1.6345E−1 (5.55E−3)	1.6558E−1 (6.14E−3)	1.5418E−1 (5.98E−3)	1.0812E−1 (4.91E−3)	1.4272E−1 (2.10E−3)	1.5413E−1 (6.93E−3)
WFG3	4.3992E−2 (1.50E−3)	4.3698E−2 (2.39E−3)	1.3206E−1 (1.41E−2)	2.6940E−2 (9.09E−4)	1.317E−1 (5.91E−3)	5.5521E−2 (4.09E−3)
WFG4	2.1764E−1 (4.67E−3)	2.1932E−1 (8.86E−3)	2.0798E−1 (7.00E−3)	1.2575E−1 (2.51E−3)	1.9071E−1 (1.84E−3)	1.8764E−1 (7.12E−3)
UF1	3.1263E−3 (3.18E−4)	5.2004E−2 (6.86E−2)	2.7171E−2 (4.96E−3)	1.5171E−1 (9.27E−2)	3.6123E−3 (4.17E−4)	3.6110E−3 (4.16E−4)
UF2	1.1299E−2 (2.00E−3)	9.7983E−3 (4.63E−3)	1.0300E−2 (9.12E−4)	4.4294E−2 (2.14E−2)	3.6762E−3 (5.33E−4)	3.6521E−3 (2.42E−4)
UF3	1.5070E−2 (1.72E−2)	9.6843E−2 (4.11E−2)	3.5622E−2 (8.98E−3)	3.2982E−1 (5.21E−2)	1.9012E−2 (1.40E−2)	1.6128E−2 (1.34E−3)
UF4	6.7425E−2 (6.07E−3)	7.0000E−2 (8.05E−3)	4.7085E−2 (1.45E−3)	5.0666E−2 (5.32E−3)	6.7312E−2 (5.91E−3)	6.1372E−2 (1.31E−2)
UF5	4.2309E−1 (9.96E−2)	5.1743E−1 (1.28E−1)	3.8792E−1 (7.02E−2)	5.0210E−1 (1.58E−1)	3.2573E−1 (4.88E−2)	2.5513E−1 (1.62E−2)
UF6	1.3585E−1 (8.93E−2)	3.8852E−1 (1.03E−1)	1.8234E−1 (2.52E−2)	5.4788E−1 (3.16E−1)	1.5281E−1 (9.57E−2)	1.5372E−1 (9.20E−2)
UF7	5.8005E−3 (1.62E−3)	3.6628E−1 (1.92E−1)	1.3647E−2 (3.26E−3)	2.4234E−1 (1.79E−1)	5.9123E−3 (1.46E−3)	5.9021E−3 (2.11E−4)
UF8	9.0957E−2 (1.07E−2)	1.6060E−1 (6.75E−2)	2.1219E−1 (4.96E−2)	1.5933E−1 (6.98E−2)	9.9912E−2 (7.31E−3)	9.8321E−2 (1.95E−2)
UF9	1.4936E−1 (6.56E−2)	2.1486E−1 (2.30E−2)	2.4333E−1 (5.66E−2)	2.2266E−1 (6.08E−2)	1.5523E−1 (6.82E−2)	6.5636E−2 (6.20E−4)
MOP1	1.7844E−1 (7.88E−2)	2.8553E−1 (9.21E−2)	1.8717E−2 (7.11E−4)	6.5686E−1 (1.56E−1)	2.8312E−2 (2.74E−3)	2.7613E−2 (4.23E−3)
MOP2	2.4559E−1 (6.02E−2)	2.1902E−1 (3.71E−2)	1.7538E−2 (8.37E−3)	6.9944E−1 (2.31E−1)	3.7643E−2 (5.10E−2)	7.3183E−2 (4.72E−2)
MOP3	5.1497E−1 (8.56E−2)	6.7173E−1 (1.99E−1)	2.0662E−2 (7.45E−3)	9.1616E−1 (1.01E−1)	2.4037E−2 (1.45E−2)	1.5672E−2 (9.62E−3)
MOP4	2.6603E−1 (2.59E−2)	2.5917E−1 (2.83E−2)	8.9837E−3 (1.15E−3)	3.0528E−1 (1.03E−1)	3.6946E−2 (4.11E−2)	9.0412E−2 (2.87E−2)
MOP5	3.1677E−1 (6.45E−3)	3.0113E−1 (3.68E−2)	2.5137E−2 (1.22E−3)	3.0467E−1 (1.99E−2)	2.6821E−2 (3.51E−3)	2.1352E−2 (2.14E−3)
MOP6	2.3505E−1 (2.77E−2)	2.7607E−1 (3.63E−2)	6.9555E−2 (3.30E−3)	3.0934E−1 (5.77E−6)	5.7183E−2 (8.29E−4)	5.7512E−2 (8.16E−4)
MOP7	3.1251E−1 (6.09E−2)	3.1416E−1 (2.42E−2)	1.1580E−1 (1.31E−2)	3.5704E−1 (3.54E−5)	8.5821E−2 (8.21E−3)	1.6643E−1 (7.31E−3)
RE21	1.8695E+2 (8.10E−1)	1.8646E+2 (2.52E−1)	2.0322E+1 (4.30E+0)	1.0322E+1 (6.04E+0)	3.0563E+2 (5.28E+0)	3.0473E+2 (2.43E−1)
RE22	1.8663E+2 (1.31E−1)	1.8592E+2 (8.15E−1)	6.5538E+1 (2.24E+1)	9.9476E+0 (4.06E+1)	2.0672E+0 (1.30E−1)	2.0338E+0 (3.53E−2)
RE23	2.5338E+5 (4.96E+1)	2.5339E+5 (6.70E+1)	6.0987E+4 (7.46E+3)	6.0322E+3 (5.07E+2)	2.4857E+5 (7.66E+2)	2.4891E+5 (4.80E+2)
RE24	2.7575E+1 (1.14E−1)	2.7428E+1 (3.32E−2)	9.5062E+0 (2.80E+0)	1.6655E+0 (6.11E−1)	2.7173E+1 (2.50E−2)	2.7133E+1 (6.40E−3)
RE25	5.4280E+3 (2.13E−6)	5.4280E+3 (2.25E−6)	3.3321E+4 (7.60E+4)	3.6584E+3 (1.62E−2)	6.6225E+3 (4.71E−3)	6.6225E+3 (4.44E−4)
RE31	5.3064E+6 (8.78E+5)	5.5712E+6 (8.00E+5)	9.7124E+5 (2.19E+5)	7.6751E+5 (5.89E+5)	6.5123E+6 (2.91E−1)	6.5121E+6 (2.10E−1)
RE32	1.3176E+8 (4.90E+3)	1.3175E+8 (4.89E+3)	1.1691E+7 (2.35E+6)	1.2442E+8 (2.24E+7)	1.1496E+08 (2.23E+07)	1.1387E+8 (1.14E+7)
RE33	3.5196E+7 (6.85E+0)	3.5196E+7 (7.41E+0)	3.5158E+7 (8.66E+4)	3.5196E+7 (3.43E+2)	3.5196E+7 (6.26E−2)	3.5195E+7 (1.32E+3)
RE34	1.2879E+0 (3.07E−1)	1.1850E+0 (1.50E−1)	1.4836E+0 (2.41E−1)	6.9948E−1 (2.41E−1)	1.2968E+0 (4.20E−1)	1.3604E+0 (3.15E−2)
RE35	1.8693E+2 (2.01E+1)	1.7747E+2 (2.77E+0)	1.2839E+2 (1.67E+1)	3.3512E+1 (2.24E+0)	9.3806E+1 (5.27E+0)	8.4014E+1 (8.02E+0)
RE36	1.7567E+0 (3.94E−1)	1.7398E+0 (3.79E−1)	1.1303E+0 (2.54E−1)	4.0191E+0 (6.49E−1)	2.2979E+0 (4.58E−1)	1.5811E+0 (5.43E−1)
RE37	6.1498E−1 (1.56E−4)	6.1498E−1 (1.61E−4)	6.2749E−1 (1.41E−3)	6.1459E−1 (4.88E−4)	7.1231E−1 (8.41E−3)	7.0463E−1 (1.68E−2)

表 1 6种算法求解选择的测试问题时, 30次独立运行得到的IGD度量值

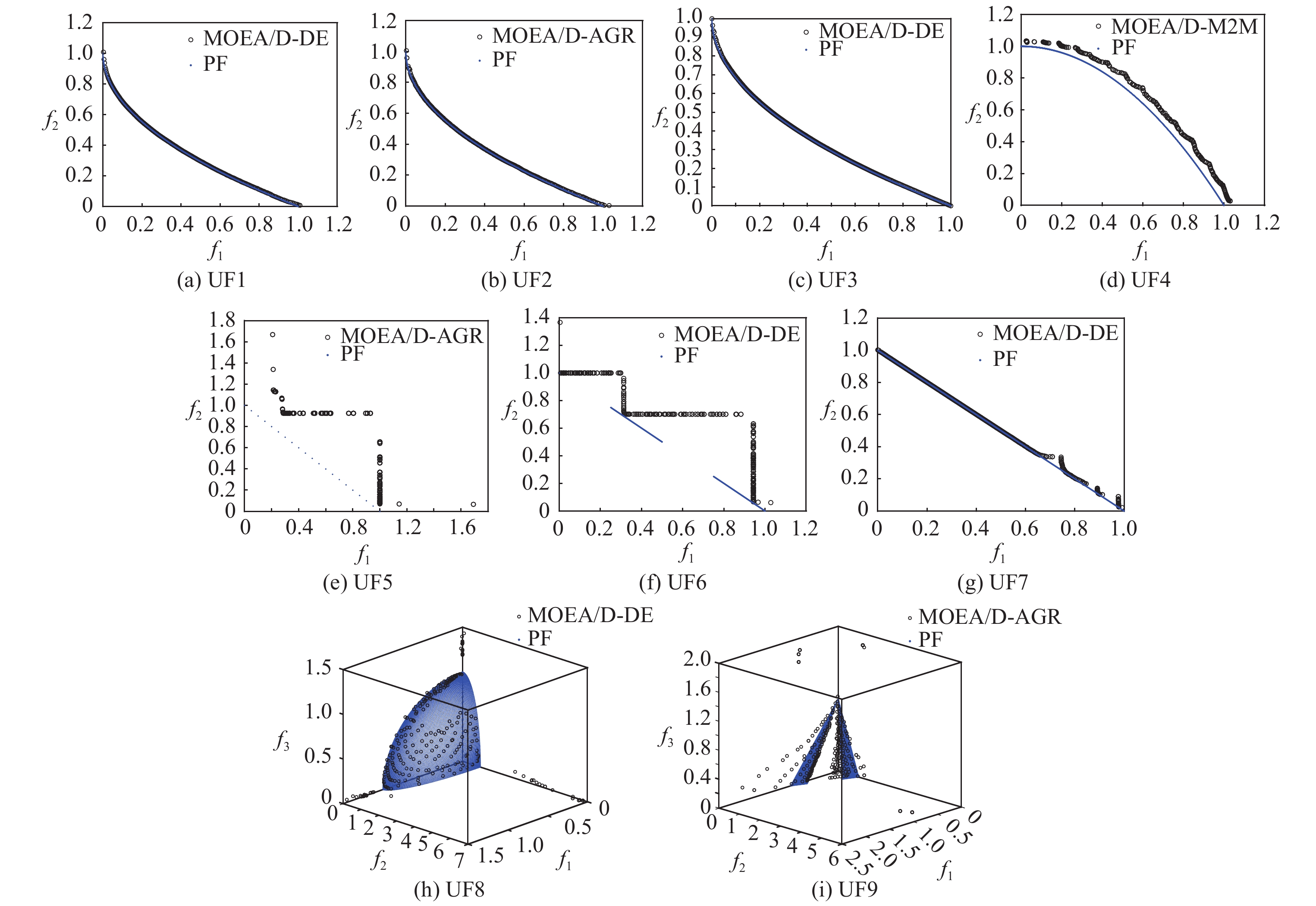
Fig. 7 PF’s approximate plots about the UF test problems 图 7 UF测试问题PF近似图

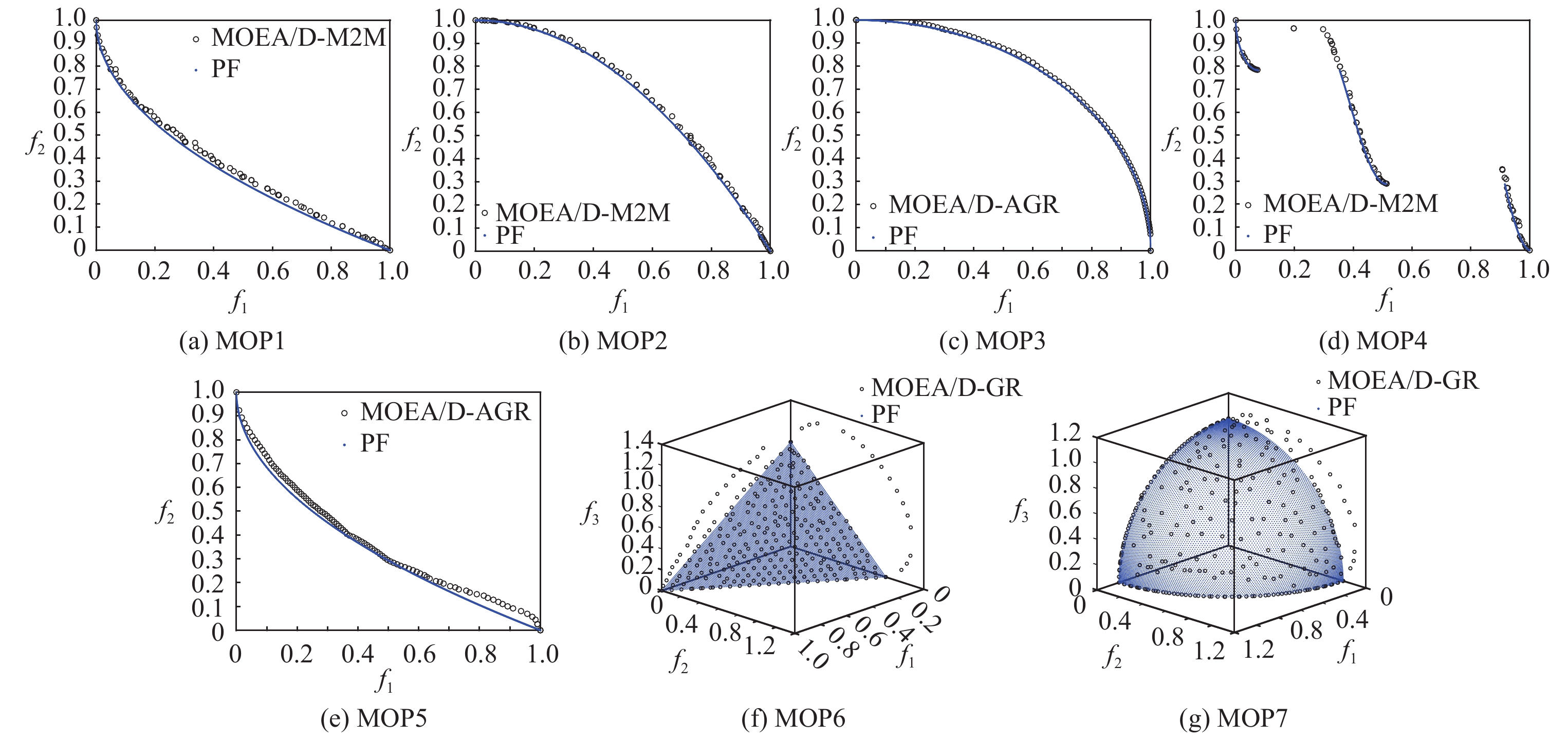
Fig. 8 PF’s approximate plots about the MOP test problems 图 8 MOP测试问题PF近似图

对于DTLZ^–1测试问题MOEA/D-GR性能最好, 对于mDTLZ和WFG测试问题MOEA/D-AWA性能最好. 而通过图6的PF近似图可以看到, 6个算法对DTLZ^–1、mDTLZ1、MDTLZ3、WFG3测试问题效果均不理想.

图 6 $ {\mathrm{D}\mathrm{T}\mathrm{L}\mathrm{Z}}^{-1} $ , mDTLZ和WFG测试问题PF近似图

对于UF测试问题, MOEA/D-DE性能最好, MOEA/D-AGR次之. 由图7中PF近似图可以看到, 6个算法在UF5、UF6、UF8和UF9测试问题上表现不好.

对于MOP测试问题, MOEA/D-M2M性能最好, MOEA/D-GR和MOEA/D-AGR性能相似.

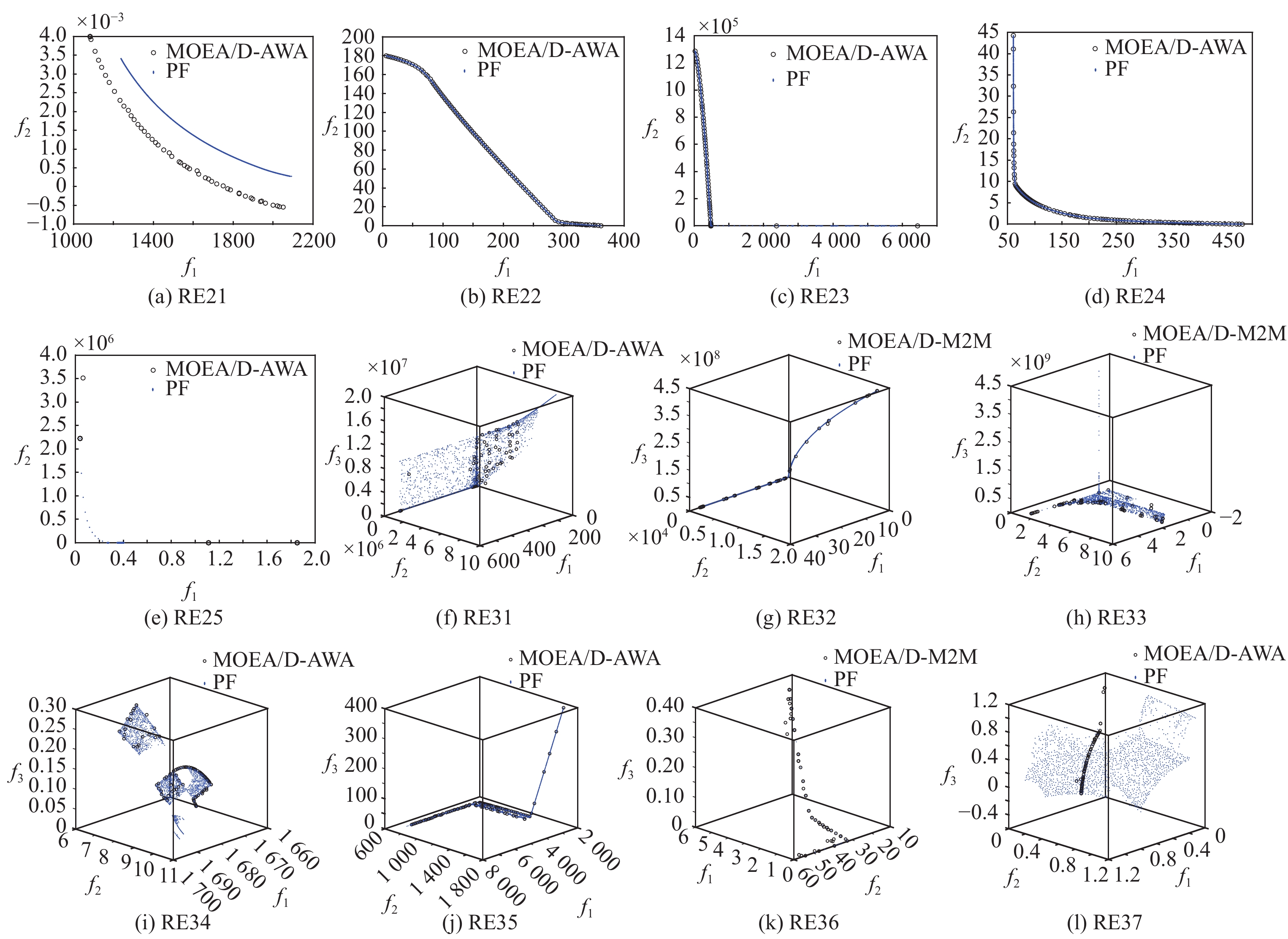
对于RE测试问题MOEA/D-AWA性能最好, MOEA/D-M2M次之. 由图9可以看到, 6个算法在除RE22测试问题外, 在这组其他测试问题上效果均不是很理想.

Fig. 5 PF’s approximate plots about the ZDT and DTLZ test problems 图 5 ZDT和DTLZ测试问题PF近似图

根据测试问题的性质, 对比算法的特点和实验结果, 可以得到如下一些比较显然的分析结果.

(1) MOEA/D-DE、MOEA/D-DRA主要用来求解PS形状复杂的多目标优化问题. 在UF1–UF9这组测试问题上, MOEA/D-DE的总体性能优于MOEA/D-DRA, 原因是计算资源的动态分配过程中, 优先选择潜力大的子问题, 使得早期演化过程中解比较集中, 在一定程度上忽略了种群的多样性, 增加了算法求解问题的成本. 另外, 可以观察到MOEA/D-AGR在处理这组测试问题时性能仅次于MOEA/D-DE, 这表明自适应调整解的替换范围可以有效平衡种群收敛性和多样性.

(2) MOEA/D-M2M在MOP1–MOP5这组测试问题上性能表现比较突出, 这是一组距离函数偏置不均衡的问题, 其特点是一些高质量的解往往在演化早期就被找到, 很容易把整个种群吸引进入一些局部最优区域. 因此, 这组问题主要测试算法多样性保持能力. 另外, 可以观察到MOEA/D-GR和MOEA/D-AGR在处理这组测试问题时也有一定的优势.

Fig. 9 PF’s approximate plots about the RE test problems 图 9 RE测试问题PF近似图

(3) MOEA/D-AWA提出采用自适应权重向量调整策略来求解PF不规则(如PF不连续、存在尖峰或低尾)问题. 根据实验结果, 可以观察到算法在8组测试问题中的5组上性能最好, 分别是ZDT、DTLZ、mDTLZ、WFG和RE测试问题. 这表明, 该算法根据演化过程中种群分布信息对权重向量进行调整, 对PF规则和不规则的问题均有一定的优势, 并且在处理现实问题上也比较有效. 值得注意的是mDTLZ这组测试问题, 虽然MOEA/D-AWA在这组测试问题上表现最好, 但据图6所示, 最终得到的解集离PF比较远, 特别是在mDTLZ1和mDTLZ2上, 可能的原因是测试问题中存在的难以支配的边界解对权重向量的调整产生了一定的误导作用. 根据文献[123], 采用广义分解方法能在一定程度上缓解上述问题.

Fig. 6 PF’s approximate plots about the $ {\mathrm{D}\mathrm{T}\mathrm{L}\mathrm{Z}}^{-1} $ , mDTLZ and WFG test problems 图 6 ${\mathrm{D}\mathrm{T}\mathrm{L}\mathrm{Z}}^{-1} $ , mDTLZ和WFG测试问题PF近似图(续)

(4) DTLZ1^–1–DTLZ4^–1这组测试问题主要用于验证算法对PF形状和大小的敏感性. 据表1所示, MOEA/D-GR在这组测试问题上性能最好, 这表明通过调整解的替换范围来平衡种群的收敛性和多样性是一个稳定且有效的策略.

总的来说, 不同算法在不同测试问题上的性能并不相同, 没有算法在所有测试问题上都表现良好. 上述的分析结果, 可以进一步指导在实际工程应用中算法的选择.

对实际工程应用中建立的多目标优化模型进行求解时, 可以根据优化模型的一些先验信息来指导算法的选择: (1)能够预先判断模型PS可能的几何结构, 如果PS形状是比较复杂的, 优先考虑MOEA/D-DE, MOEA/D-AGR次之; (2)能够预先判断PF可能的几何结构, 如果PF是不规则的, 优先考虑MOEA/D-AWA, 若进一步需要考虑到算法的稳定性, 则MOEA/D-GR是一个有效的算法. (3)如果模型在求解过程中, 出现一些高质量的解在演化早期就被找到, 导致演化停滞的现象, 则可以考虑MOEA/D-M2M. 若不能得到有用的先验信息, 由于MOEA/D-AWA在所有测试问题上总体性能最好, 优先考虑MOEA/D-AWA.

6 展　望

虽然MOEA/D在演化多目标优化领域已经取得了一些不错的成果, 但经过上述讨论, MOEA/D仍有许多值得进一步研究的方向.

(1) 算法层面

目前关于MOEA/D的算法改进主要集中在权重向量调整, 以及分解方法的研究上. 对如何利用历史信息、种群分布信息来产生新解的研究相对较少. 以及对如何进行计算资源的分配和如何替换解的研究也相对缺乏. 如何将单目标技术更高效地融入MOEA/D的框架中, 提高算法的性能也是一个非常值得关注的研究课题. 另外关于算法的收敛性分析的研究也有待开展.

(2) 应用层面

多目标优化问题在工程应用与科学研究中非常普遍, 这些问题的各个目标往往相互冲突, 在对其优化时, 需要对各个目标进行折中处理. 在多目标优化问题的广泛应用前景下, MOEAs应运而生, 目前已经成为比较成熟的解决多目标优化问题的一门技术, 并在许多行业得到了应用, 如: 通信与网络、机器人、航空航天工程、管理工程、机械设计与制造、金融, 以及科学研究中的物理、化学、医学、计算机科学等领域. MOEA/D及其改进算法作为一类求解最优化问题的高效算法, 已成功应用于许多实际应用, 如无线传感器屏障覆盖^[93-95]、车间调度^[92]、飞机终端降噪航线的优化设计^[96]、航空发动机管道布线^[97]、单脉冲天线设计^[127]、机器人路径规划^[128]、能源供应问题^[98-105]、机器学习^[106-119]等, 进一步将MOEA/D应用于更多的实际问题将是未来研究的方向之一.

致谢　向张青富老师表示深深的敬意和衷心的感谢, 感谢张老师在论文写作期间提出的宝贵意见和建议.

参考文献

[1]	Miettinen K. Nonlinear Multiobjective Optimization. Boston: Kluwer Academic Publishers, 1999.
[2]	Deb K. Multi-objective Optimization Using Evolutionary Algorithms. New York: John Wiley & Sons, 2001.
[3]	Coello CAC, Van Veldhuizen DA, Lamont GB. Evolutionary Algorithms for Solving Multi-objective Problems. New York: Kluwer Academic, 2002.
[4]	Zitzler E, Thiele L. Multiobjective evolutionary algorithms: A comparative case study and the strength Pareto approach. IEEE Trans. on Evolutionary Computation, 1999, 3(4): 257-271. [doi:10.1109/4235.797969]
[5]	Deb K, Pratap A, Agarwal S, Meyarivan T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. on Evolutionary Computation, 2002, 6(2): 182-197. [doi:10.1109/4235.996017]
[6]	Corne DW, Jerram NR, Knowles JD, Oates MJ. PESA-II: Region-based selection in evolutionary multiobjective optimization. In: Proc. of the 3rd Annual Conf. on Genetic and Evolutionary Computation. San Francisco: ACM, 2001. 283–290.
[7]	Zitzler E, Laumanns M, Thiele L. SPEA2: Improving the strength Pareto evolutionary algorithm. In: Evolutionary Methods for Design, Optimization and Control with Applications to Industrial Problems. Berlin: Springer, 2001.
[8]	Bader J, Zitzler E. HypE: An algorithm for fast hypervolume-based many-objective optimization. Evolutionary Computation, 2011, 19(1): 45-76. [doi:10.1162/EVCO_a_00009]
[9]	While L, Bradstreet L, Barone L. A fast way of calculating exact hypervolumes. IEEE Trans. on Evolutionary Computation, 2012, 16(1): 86-95. [doi:10.1109/TEVC.2010.2077298]
[10]	Zhang QF, Li H. MOEA/D: A multiobjective evolutionary algorithm based on decomposition. IEEE Trans. on Evolutionary Computation, 2007, 11(6): 712-731. [doi:10.1109/TEVC.2007.892759]
[11]	Trivedi A, Srinivasan D, Sanyal K, Ghosh A. A survey of multiobjective evolutionary algorithms based on decomposition. IEEE Trans. on Evolutionary Computation, 2017, 21(3): 440-462. [doi:10.1109/TEVC.2016.2608507]
[12]	Xu Q, Xu ZQ, Ma T. A survey of multiobjective evolutionary algorithms based on decomposition: Variants, challenges and future directions. IEEE Access, 2020, 8: 41588-41614. [doi:10.1109/ACCESS.2020.2973670]
[13]	Das I, Dennis JE. Normal-boundary intersection: A new method for generating the Pareto surface in nonlinear multicriteria optimization problems. SIAM Journal on Optimization, 1998, 8(3): 631-657. [doi:10.1137/S1052623496307510]
[14]	Ishibuchi H, Sakane Y, Tsukamoto N, Nojima Y. Simultaneous use of different scalarizing functions in MOEA/D. In: Proc. of the 12th Annual Conf. on Genetic and Evolutionary Computation. Portland: ACM, 2010. 519–526.
[15]	Liu HL, Gu FQ, Zhang QF. Decomposition of a multiobjective optimization problem into a number of simple multiobjective subproblems. IEEE Trans. on Evolutionary Computation, 2014, 18(3): 450-455. [doi:10.1109/TEVC.2013.2281533]
[16]	Tan YY, Jiao YC, Li H, Wang XK. MOEA/D+uniform design: A new version of MOEA/D for optimization problems with many objectives. Computers & Operations Research, 2013, 40(6): 1648-1660. [doi:10.1016/j.cor.2012.01.001]
[17]	Ma XL, Qi YT, Li LL, Liu F, Jiao LC, Wu JS. MOEA/D with uniform decomposition measurement for many-objective problems. Soft Computing, 2014, 18(12): 2541-2564. [doi:10.1007/s00500-014-1234-8]
[18]	Li K, Deb K, Zhang QF, Kwong S. An evolutionary many-objective optimization algorithm based on dominance and decomposition. IEEE Trans. on Evolutionary Computation, 2015, 19(5): 694-716. [doi:10.1109/TEVC.2014.2373386]
[19]	Harada K, Hiwa S, Hiroyasu T. Adaptive weight vector assignment method for MOEA/D. In: Proc. of the 2017 IEEE Symp. Series on Computational Intelligence (SSCI). Honolulu: IEEE, 2017. 1–9.
[20]	Li ZX, He L, Chu YJ. An improved decomposition multiobjective optimization algorithm with weight vector adaptation strategy. In: Proc. of the 13th Int’l Conf. on Semantics, Knowledge and Grids (SKG). Beijing: IEEE, 2017. 19–24.
[21]	Jiang SW, Cai ZH, Zhang J, Ong YS. Multiobjective optimization by decomposition with Pareto-adaptive weight vectors. In: Proc. of the 7th Int’l Conf. on Natural Computation. Shanghai: IEEE, 2011. 1260–1264.
[22]	Fang KT, Ma CX. Orthogonal and Uniform Experimental Design. Beijing: Science Press, 2001 (in Chinese).
[23]	Jiang SW, Feng L, Yang DZ, Heng CK, Ong YS, Zhang ANS, Tan PS, Cai ZH. Towards adaptive weight vectors for multiobjective evolutionary algorithm based on decomposition. In: Proc. of the 2016 IEEE Congress on Evolutionary Computation (CEC). Vancouver: IEEE, 2016. 500–507.
[24]	Gu FQ, Cheung YM. Self-organizing map-based weight design for decomposition-based many-objective evolutionary algorithm. IEEE Trans. on Evolutionary Computation, 2018, 22(2): 211-225. [doi:10.1109/tevc.2017.2695579]
[25]	Qi YT, Ma XL, Liu F, Jiao LC, Sun JY, Wu JS. MOEA/D with adaptive weight adjustment. Evolutionary Computation, 2014, 22(2): 231-264. [doi:10.1162/EVCO_a_00109]
[26]	Qi YT, Ma XL, Yin ML, Liu F, Wei JX. MOEA/D with a Delaunay triangulation based weight adjustment. In: Proc. of the 2014 Companion Publication of the Annual Conf. on Genetic and Evolutionary Computation. Vancouver: ACM, 2014. 93–94.
[27]	Li MQ, Yao X. What weights work for you? Adapting weights for any Pareto front shape in decomposition-based evolutionary multiobjective optimisation. Evolutionary Computation, 2020, 28(2): 227-253. [doi:10.1162/evco_a_00269]
[28]	Sato H. Analysis of inverted PBI and comparison with other scalarizing functions in decomposition based MOEAs. Journal of Heuristics, 2015, 21(6): 819-849. [doi:10.1007/s10732-015-9301-6]
[29]	Yang SX, Jiang SY, Jiang Y. Improving the multiobjective evolutionary algorithm based on decomposition with new penalty schemes. Soft Computing, 2017, 21(16): 4677-4691. [doi:10.1007/s00500-016-2076-3]
[30]	Wang LP, Zhang QF, Zhou AM, Gong MG, Jiao LC. Constrained subproblems in a decomposition-based multiobjective evolutionary algorithm. IEEE Trans. on Evolutionary Computation, 2016, 20(3): 475-480. [doi:10.1109/TEVC.2015.2457616]
[31]	Li K, Zhang QF, Kwong S, Li MQ, Wang R. Stable matching-based selection in evolutionary multiobjective optimization. IEEE Trans. on Evolutionary Computation, 2014, 18(6): 909-923. [doi:10.1109/TEVC.2013.2293776]
[32]	Cai XY, Mei ZW, Fan Z, Zhang QF. A constrained decomposition approach with grids for evolutionary multiobjective optimization. IEEE Trans. on Evolutionary Computation, 2018, 22(4): 564-577. [doi:10.1109/tevc.2017.2744674]
[33]	Ma XL, Zhang QF, Tian GD, Yang JS, Zhu ZX. On Tchebycheff decomposition approaches for multiobjective evolutionary optimization. IEEE Trans. on Evolutionary Computation, 2018, 22(2): 226-244. [doi:10.1109/TEVC.2017.2704118]
[34]	Derbel B, Brockhoff D, Liefooghe A, Verel S. On the impact of multiobjective scalarizing functions. In: Proc. of the 13th Int’l Conf. on Parallel Problem Solving from Nature. Ljubljana: Springer, 2014. 548–558.
[35]	Jiang SY, Yang SX, Wang Y, Liu XB. Scalarizing functions in decomposition-based multiobjective evolutionary algorithms. IEEE Trans. on Evolutionary Computation, 2018, 22(2): 296-313. [doi:10.1109/TEVC.2017.2707980]
[36]	Zheng W, Tan YY, Meng LL, Zhang HX. An improved MOEA/D design for many-objective optimization problems. Applied Intelligence, 2018, 48(10): 3839-3861. [doi:10.1007/s10489-018-1183-5]
[37]	Zhang QF, Li H, Maringer D, Tsang E. MOEA/D with NBI-style Tchebycheff approach for portfolio management. In: Proc. of the 2010 IEEE Congress on Evolutionary Computation. Barcelona: IEEE, 2010. 1–8.
[38]	Ishibuchi H, Sakane Y, Tsukamoto N, Nojima Y. Adaptation of scalarizing functions in MOEA/D: An adaptive scalarizing function-based multiobjective evolutionary algorithm. In: Proc. of the 5th Int’l Conf. on Evolutionary Multi-criterion Optimization. Nantes: ACM, 2009. 438–452.
[39]	Wu MY, Li K, Kwong S, Zhang QF, Zhang J. Learning to decompose: A paradigm for decomposition-based multiobjective optimization. IEEE Trans. on Evolutionary Computation, 2019, 23(3): 376-390. [doi:10.1109/TEVC.2018.2865931]
[40]	Rasmussen CE, Williams CKI. Gaussian Processes for Machine Learning. Cambridge: MIT Press, 2006.
[41]	Wang R, Zhang QF, Zhang T. Pareto adaptive scalarising functions for decomposition based algorithms. In: Proc. of the 8th Int’l Conf. on Evolutionary Multi-criterion Optimization. Guimarães: Springer, 2015. 248–262.
[42]	Giagkiozis I, Fleming PJ. Methods for multi-objective optimization: An analysis. Information Sciences, 2015, 293: 338-350. [doi:10.1016/j.ins.2014.08.071]
[43]	Wang R, Zhang QF, Zhang T. Decomposition-based algorithms using Pareto adaptive scalarizing methods. IEEE Trans. on Evolutionary Computation, 2016, 20(6): 821-837. [doi:10.1109/TEVC.2016.2521175]
[44]	Li H, Zhang QF. Multiobjective optimization problems with complicated Pareto sets, MOEA/D and NSGA-II. IEEE Trans. on Evolutionary Computation, 2009, 13(2): 284-302. [doi:10.1109/TEVC.2008.925798]
[45]	Chiang TC, Lai YP. MOEA/D-AMS: Improving MOEA/D by an adaptive mating selection mechanism. In: Proc. of the 2011 IEEE Congress of Evolutionary Computation (CEC). New Orleans: ACM, 2011. 1473–1480.
[46]	Jiang SY, Yang SX. An improved multiobjective optimization evolutionary algorithm based on decomposition for complex Pareto fronts. IEEE Trans. on Cybernetics, 2016, 46(2): 421-437. [doi:10.1109/TCYB.2015.2403131]
[47]	Huang WB, Li H. On the differential evolution schemes in MOEA/D. In: Proc. of the 6th Int’l Conf. on Natural Computation. Yantai: IEEE, 2010. 2788–2792.
[48]	Li K, Fialho Á, Kwong S, Zhang QF. Adaptive operator selection with bandits for a multiobjective evolutionary algorithm based on decomposition. IEEE Trans. on Evolutionary Computation, 2014, 18(1): 114-130. [doi:10.1109/TEVC.2013.2239648]
[49]	Zhang QF, Liu WD, Li H. The performance of a new version of MOEA/D on CEC09 unconstrained MOP test instances. In: Proc. of the 2009 IEEE Congress on Evolutionary Computation. Trondheim: IEEE, 2009. 203–208.
[50]	Zhang QF, Zhou AM, Zhao SZ, Suganthan PN, Liu WD, Tiwari S. Multiobjective optimization test instances for the CEC 2009 special session and competition. Technical Report, CES-487, 2008. 1–30.
[51]	Zhao SZ, Suganthan PN, Zhang QF. Decomposition-based multiobjective evolutionary algorithm with an ensemble of neighborhood sizes. IEEE Trans. on Evolutionary Computation, 2012, 16(3): 442-446. [doi:10.1109/TEVC.2011.2166159]
[52]	Ke LJ, Zhang QF, Battiti R. MOEA/D-ACO: A multiobjective evolutionary algorithm using decomposition and antcolony. IEEE Trans. on Cybernetics, 2013, 43(6): 1845-1859. [doi:10.1109/TSMCB.2012.2231860]
[53]	Zhou AM, Zhang QF, Zhang GX. A multiobjective evolutionary algorithm based on decomposition and probability model. In: Proc. of the 2012 IEEE Congress on Evolutionary Computation. Brisbane: IEEE, 2012. 1–8.
[54]	Shim VA, Tan KC, Cheong CY. A hybrid estimation of distribution algorithm with decomposition for solving the multiobjective multiple traveling salesman problem. IEEE Trans. on Systems, Man, and Cybernetics, Part C (Applications and Reviews), 2012, 42(5): 682-691. [doi:10.1109/TSMCC.2012.2188285]
[55]	Shim VA, Tan KC, Tan KK. A hybrid adaptive evolutionary algorithm in the domination-based and decomposition-based frameworks of multi-objective optimization. In: Proc. of the 2012 IEEE Congress on Evolutionary Computation. Brisbane: IEEE, 2012. 1–8.
[56]	Martínez SZ, Coello CAC. A direct local search mechanism for decomposition-based multi-objective evolutionary algorithms. In: Proc. of the 2012 IEEE Congress on Evolutionary Computation. Brisbane: IEEE, 2012. 1–8.
[57]	Ke LJ, Zhang QF, Battiti R. Hybridization of decomposition and local search for multiobjective optimization. IEEE Trans. on Cybernetics, 2014, 44(10): 1808-1820. [doi:10.1109/TCYB.2013.2295886]
[58]	Shi JL, Zhang QF, Sun JY. PPLS/D: Parallel Pareto local search based on decomposition. IEEE Trans. on Cybernetics, 2020, 50(3): 1060-1071. [doi:10.1109/TCYB.2018.2880256]
[59]	Ma XL, Liu F, Qi YT, Li LL, Jiao LC, Liu MY, Wu JS. MOEA/D with Baldwinian learning inspired by the regularity property of continuous multiobjective problem. Neurocomputing, 2014, 145: 336-352. [doi:10.1016/j.neucom.2014.05.025]
[60]	Wang ZK, Zhang QF, Li H. Balancing convergence and diversity by using two different reproduction operators in MOEA/D: Some preliminary work. In: Proc. of the 2015 IEEE Int’l Conf. on Systems, Man, and Cybernetics. Hong Kong: IEEE, 2015. 2849–2854.
[61]	Wang ZK, Zhang QF, Gong MG, Zhou AM. A replacement strategy for balancing convergence and diversity in MOEA/D. In: Proc. of the 2014 IEEE Congress on Evolutionary Computation (CEC). Beijing: IEEE, 2014. 2132–3139.
[62]	Wang ZK, Zhang QF, Zhou AM, Gong MG, Jiao LC. Adaptive replacement strategies for MOEA/D. IEEE Trans. on Cybernetics, 2016, 46(2): 474-486. [doi:10.1109/TCYB.2015.2403849]
[63]	Zhou AM, Zhang QF. Are all the subproblems equally important? Resource allocation in decomposition-based multiobjective evolutionary algorithms. IEEE Trans. on Evolutionary Computation, 2016, 20(1): 52-64. [doi:10.1109/TEVC.2015.2424251]
[64]	Cai XY, Li YX, Fan Z, Zhang QF. An external archive guided multiobjective evolutionary algorithm based on decomposition for combinatorial optimization. IEEE Trans. on Evolutionary Computation, 2015, 19(4): 508-523. [doi:10.1109/TEVC.2014.2350995]
[65]	Li H, Ding M, Deng JD, Zhang QF. On the use of random weights in MOEA/D. In: Proc. of the 2015 IEEE Congress on Evolutionary Computation (CEC). Sendai: IEEE, 2015. 978–985.
[66]	Deb K, Jain H. An evolutionary many-objective optimization algorithm using reference-point-based nondominated sorting approach, Part I: Solving problems with box constraints. IEEE Trans. on Evolutionary Computation, 2014, 18(4): 577-601. [doi:10.1109/TEVC.2013.2281535]
[67]	Jain H, Deb K. An evolutionary many-objective optimization algorithm using reference-point based nondominated sorting approach, Part II: Handling constraints and extending to an adaptive approach. IEEE Trans. on Evolutionary Computation, 2014, 18(4): 602-622. [doi:10.1109/TEVC.2013.2281534]
[68]	Liu HL, Chen L, Zhang QF, Deb K. An evolutionary many-objective optimisation algorithm with adaptive region decomposition. In: Proc. of the 2016 IEEE Congress on Evolutionary Computation (CEC). Vancouver: IEEE, 2016. 4763–4769.
[69]	Cheng R, Jin YC, Olhofer M, Sendhoff B. A reference vector guided evolutionary algorithm for many-objective optimization. IEEE Trans. on Evolutionary Computation, 2016, 20(5): 773-791. [doi:10.1109/TEVC.2016.2519378]
[70]	Asafuddoula M, Ray T, Sarker R. A decomposition-based evolutionary algorithm for many objective optimization. IEEE Trans. on Evolutionary Computation, 2015, 19(3): 445-460. [doi:10.1109/TEVC.2014.2339823]
[71]	Yuan Y, Xu H, Wang B, Zhang B, Yao X. Balancing convergence and diversity in decomposition-based many-objective optimizers. IEEE Trans. on Evolutionary Computation, 2016, 20(2): 180-198. [doi:10.1109/TEVC.2015.2443001]
[72]	Cai XY, Yang ZX, Fan Z, Zhang QF. Decomposition-based-sorting and angle-based-selection for evolutionary multiobjective and many-objective optimization. IEEE Trans. on Cybernetics, 2017, 47(9): 2824-2837. [doi:10.1109/TCYB.2016.2586191]
[73]	Yuan Y, Xu H, Wang B, Yao X. A new dominance relation-based evolutionary algorithm for many-objective optimization. IEEE Trans. on Evolutionary Computation, 2016, 20(1): 16-37. [doi:10.1109/TEVC.2015.2420112]
[74]	Mohammadi A, Omidvar MN, Li XD. Reference point based multi-objective optimization through decomposition. In: Proc. of the 2012 IEEE Congress on Evolutionary Computation. Brisbane: IEEE, 2012. 1–8.
[75]	Mohammadi A, Omidvar MN, Li XD, Deb K. Integrating user preferences and decomposition methods for many-objective optimization. In: Proc. of the 2014 IEEE Congress on Evolutionary Computation. Beijing: IEEE, 2014. 421–428.
[76]	Li K, Chen RZ, Min GY, Yao X. Integration of preferences in decomposition multiobjective optimization. IEEE Trans. on Cybernetics, 2018, 48(12): 3359-3370. [doi:10.1109/TCYB.2018.2859363]
[77]	Pilat M, Neruda R. Incorporating user preferences in MOEA/D through the coevolution of weights. In: Proc. of the 2015 Annual Conf. on Genetic and Evolutionary Computation. Madrid: ACM, 2015. 727–734.
[78]	Xiong MH, Xiong W, Liu CX. A hybrid many-objective evolutionary algorithm with region preference for decision makers. IEEE Access, 2019, 7: 117699-117715. [doi:10.1109/ACCESS.2019.2931742]
[79]	Wang BC, Li HX, Zhang QF, Wang Y. Decomposition-based multiobjective optimization for constrained evolutionary optimization. IEEE Trans. on Systems, Man, and Cybernetics: Systems, 2021, 51(1): 574-587. [doi:10.1109/TSMC.2018.2876335]
[80]	Jan MA, Zhang QF. MOEA/D for constrained multiobjective optimization: Some preliminary experimental results. In: Proc. of the 2010 UK Workshop on Computational Intelligence (UKCI). Colchester: IEEE, 2010. 1–6.
[81]	Fan Z, Li WJ, Cai XY, Li H, Wei CM, Zhang QF, Deb K, Goodman E. Push and pull search for solving constrained multi-objective optimization problems. Swarm and Evolutionary Computation, 2019, 44: 665-679. [doi:10.1016/j.swevo.2018.08.017]
[82]	Fan Z, Ruan J, Li WJ, You YG, Cai XY, Xu ZL, Yang Z, Sun FZ, Wang ZJ, Yuan YT, Li ZC, Zhu GJ. A learning guided parameter setting for constrained multi-objective optimization. In: Proc. of the 1st Int’l Conf. on Industrial Artificial Intelligence (IAI). Shenyang: IEEE, 2019. 1–6.
[83]	Fan Z, Li H, Wei CM, Li WJ, Huang H, Cai XY, Cai ZQ. An improved epsilon constraint handling method embedded in MOEA/D for constrained multi-objective optimization problems. In: Proc. of the 2016 IEEE Symp. Series on Computational Intelligence (SSCI). Athens: IEEE, 2016. 1–8.
[84]	Laumanns M, Thiele L, Zitzler E. An efficient, adaptive parameter variation scheme for metaheuristics based on the epsilon-constraint method. European Journal of Operational Research, 2006, 169(3): 932-942. [doi:10.1016/j.ejor.2004.08.029]
[85]	Fan Z, Fang Y, Li WJ, Cai XY, Wei CM, Goodman E. MOEA/D with angle-based constrained dominance principle for constrained multi-objective optimization problems. Applied Soft Computing, 2019, 74: 621-633. [doi:10.1016/j.asoc.2018.10.027]
[86]	Deb K. An efficient constraint handling method for genetic algorithms. Computer Methods in Applied Mechanics and Engineering, 2000, 186(2–4): 311-338. [doi:10.1016/S0045-7825(99)00389-8]
[87]	Fan Z, Fang Y, Li WJ, Lu JW, Cai XY, Wei CM. A comparative study of constrained multi-objective evolutionary algorithms on constrained multi-objective optimization problems. In: Proc. of the 2017 IEEE Congress on Evolutionary Computation (CEC). Donostia: IEEE, 2017. 209–216.
[88]	Jan MA, Khanum RA. A study of two penalty-parameterless constraint handling techniques in the framework of MOEA/D. Applied Soft Computing, 2013, 13(1): 128-148. [doi:10.1016/j.asoc.2012.07.027]
[89]	Fan Z, Huang H, Li WJ, Xie SX, Cai XY, Goodman E. An opposition-based repair operator for multi-objective evolutionary algorithm in constrained optimization problems. In: Proc. of the 11th Int’l Conf. on Natural Computation (ICNC). Zhangjiajie: IEEE, 2015. 330–336.
[90]	Ma XL, Liu F, Qi YT, Gong MG, Yin ML, Li LL, Jiao LC, Wu JS. MOEA/D with opposition-based learning for multiobjective optimization problem. Neurocomputing, 2014, 146: 48-64. [doi:10.1016/j.neucom.2014.04.068]
[91]	Zhang MX, Jiao LC, Ma WP, Ma JJ, Gong MG. Multi-objective evolutionary fuzzy clustering for image segmentation with MOEA/D. Applied Soft Computing, 2016, 48: 621-637. [doi:10.1016/j.asoc.2016.07.051]
[92]	Wang XN, Xing KY, Yan CB, Zhou MC. A novel MOEA/D for multiobjective scheduling of flexible manufacturing systems. Complexity in Manufacturing Processes and Systems 2019, 2019, 5734149. [doi:10.1155/2019/5734149]
[93]	Zhang X, Zhou Y, Zhang QF, Lee VCS, Li MM. Problem specific MOEA/D for barrier coverage with wireless sensors. IEEE Trans. on Cybernetics, 2016, 47(11): 3854-3865. [doi:10.1109/TCYB.2016.2585745]
[94]	Tharmarasa R, Kirubarajan T, Peng JM, Lang T. Optimization-based dynamic sensor management for distributed multitarget tracking. IEEE Trans. on Systems, Man, and Cybernetics, Part C (Applications and Reviews), 2009, 39(5): 534-546. [doi:10.1109/TSMCC.2009.2022175]
[95]	Konstantinidis A, Yang K. Multi-objective energy-efficient dense deployment in wireless sensor networks using a hybrid problem-specific MOEA/D. Applied Soft Computing, 2011, 11(6): 4117-4134. [doi:10.1016/j.asoc.2011.02.031]
[96]	Ho-Huu V, Hartjes S, Geijselaers LH, Visser HG, Curran R. Optimization of noise abatement aircraft terminal routes using a multi-objective evolutionary algorithm based on decomposition. Transportation Research Procedia, 2018, 29: 157-168. [doi:10.1016/j.trpro.2018.02.014]
[97]	Jiao GS, Liu Q, Mao L, Guo X. Pipe routing for aero-engine using modified MOEA/D. In: Proc. of the 10th Int’l Symp. on Computational Intelligence and Design (ISCID). Hangzhou: IEEE, 2017. 59–63.
[98]	Peng BR, Ho KC, Liu YH. A novel and fast MPPT method suitable for both fast changing and partially shaded conditions. IEEE Trans. on Industrial Electronics, 2018, 65(4): 3240-3251. [doi:10.1109/tie.2017.2736484]
[99]	Li H, Yang D, Su WZ, Lü JH, Yu XH. An overall distribution particle swarm optimization MPPT algorithm for photovoltaic system under partial shading. IEEE Trans. on Industrial Electronics, 2019, 66(1): 265-275. [doi:10.1109/TIE.2018.2829668]
[100]	Selvakumar S, Madhusmita M, Koodalsamy C, Simon SP, Sood YR. High-speed maximum power point tracking module for PV systems. IEEE Trans. on Industrial Electronics, 2019, 66(2): 1119-1129. [doi:10.1109/TIE.2018.2833036]
[101]	Banerjee S, Verghese GC. Nonlinear Phenomena in Power Electronics: Bifurcations, Chaos, Control, and Applications. New York: IEEE Press, 2001.
[102]	Kimura D, Saito T. A trade-off between the maximum power point and stability. IEICE Trans. on Fundamentals of Electronics, Communications and Computer Sciences, 2011, E94-A(7): 1513-1518. [doi:10.1587/transfun.E94.A.1513]
[103]	Matsushita H, Saito T. Application of particle swarm optimization to parameter search in dynamical systems. Nonlinear Theory and Its Applications, IEICE, 2011, 2(4): 458-471. [doi:10.1587/nolta.2.458]
[104]	Togawa T, Kunii Y, Yasukawa S, Saito T. Application of MOEA/D to a trade-off problem between maximum power point and stability. In: Proc. of the 2019 IEEE Congress on Evolutionary Computation (CEC). Wellington: IEEE, 2019. 3221–3226.
[105]	Eshelman LJ, Schaffer JD. Real-coded genetic algorithms and interval-schemata. Foundations of Genetic Algorithms, 1993, 2: 187-202. [doi:10.1016/B978-0-08-094832-4.50018-0]
[106]	Li H, Gong MG, Meng DY, Miao QG. Multi-objective self-paced learning. In: Proc. of the 30th AAAI Conf. on Artificial Intelligence. Phoenix: ACM, 2016. 1802–1808.
[107]	Gong MG, Li H, Meng DY, Miao QG, Liu J. Decomposition-based evolutionary multiobjective optimization to self-paced learning. IEEE Trans. on Evolutionary Computation, 2019, 23(2): 288-302. [doi:10.1109/TEVC.2018.2850769]
[108]	Szegedy C, Liu W, Jia YQ, Sermanet P, Reed S, Anguelov D, Erhan D, Vanhoucke V, Rabinovich A. Going deeper with convolutions. In: Proc. of the 2015 IEEE Conf. on Computer Vision and Pattern Recognition (CVPR). Boston: IEEE, 2015. 1–9.
[109]	He KM, Zhang XY, Ren SQ, Sun J. Deep residual learning for image recognition. In: Proc. of the 2016 IEEE Conf. on Computer Vision and Pattern Recognition (CVPR). Las Vegas: IEEE, 2016. 770–778.
[110]	Zhang QY, Li B, Zhang F. A MOEA/D approach to exploit the crucial structure of convolution kernels. In: Proc. of the 10th Int’l Conf. on Advanced Computational Intelligence (ICACI). Xiamen: IEEE, 2018. 643–648.
[111]	Lu ZC, Deb K, Boddeti VN. MUXConv: Information multiplexing in convolutional neural networks. In: Proc. of the 2020 IEEE/CVF Conf. on Computer Vision and Pattern Recognition (CVPR). Seattle: IEEE, 2020. 12044–12053.
[112]	Xu J, Tian YS, Ma PC, Rus D, Sueda SJ, Matusik W. Prediction-guided multi-objective reinforcement learning for continuous robot control. In: Proc. of the 37th Int’l Conf. on Machine Learning. ACM, 2020. 10607–10616.
[113]	Kokkinos I. UberNet: Training a universal convolutional neural network for low-, mid-, and high-level vision using diverse datasets and limited memory. In: Proc. of the 2017 IEEE Conf. on Computer Vision and Pattern Recognition. Honolulu: IEEE, 2017. 6129–6138.
[114]	Subramanian S, Trischler A, Bengio Y, Pal CJ. Learning general purpose distributed sentence representations via large scale multi-task learning. In: Proc. of the 6th Int’l Conf. on Learning Representations. Vancouver: OpenReview.net, 2018.
[115]	Huang Z, Li JY, Siniscalchi M, Chen IF, Wu J, Lee CH. Rapid adaptation for deep neural networks through multi-task learning. In: Proc. of the 16th Annual Conf. of the Int’l Speech Communication Association. Dresden: ISCA, 2015. 3625–3629.
[116]	Lin X, Zhen HL, Li ZH, Zhang QF, Kwong S. Pareto multi-task learning. In: Proc. of the 33rd Int’l Conf. on Neural Information Processing Systems. Vancouver: ACM, 2019. 32.
[117]	Mahapatra D, Rajan V. Multi-task learning with user preferences: Gradient descent with controlled ascent in Pareto optimization. In: Proc. of the 37th Int’l Conf. on Machine Learning. ACM, 2020. 6597–6607.
[118]	Nojima Y, Arahari K, Takemura S, Ishibuchi H. Multiobjective fuzzy genetics-based machine learning based on MOEA/D with its modifications. In: Proc. of the 2017 IEEE Int’l Conf. on Fuzzy Systems (FUZZ-IEEE). Naples: IEEE, 2017. 1–6.
[119]	Ishibuchi H, Nojima Y. Analysis of interpretability-accuracy tradeoff of fuzzy systems by multiobjective fuzzy genetics-based machine learning. Int’l Journal of Approximate Reasoning, 2007, 44(1): 4-31. [doi:10.1016/j.ijar.2006.01.004]
[120]	Zitzler E, Deb K, Thiele L. Comparison of multiobjective evolutionary algorithms: Empirical results. Evolutionary Computation, 2000, 8(2): 173-195. [doi:10.1162/106365600568202]
[121]	Deb K, Thiele L, Laumanns M, Zitzler E. Scalable test problems for evolutionary multiobjective optimization. In: Abraham A, Jain L, Goldberg R, eds. Evolutionary Multiobjective Optimization. London: Springer, 2005. 105–145.
[122]	Ishibuchi H, Setoguchi Y, Masuda H, Nojima Y. Performance of decomposition-based many-objective algorithms strongly depends on Pareto front shapes. IEEE Trans. on Evolutionary Computation, 2017, 21(2): 169-190. [doi:10.1109/tevc.2016.2587749]
[123]	Wang ZK, Ong YS, Ishibuchi H. On scalable multiobjective test problems with hardly dominated boundaries. IEEE Trans. on Evolutionary Computation, 2019, 23(2): 217-231. [doi:10.1109/TEVC.2018.2844286]
[124]	Huband S, Hingston P, Barone L, While L. A review of multiobjective test problems and a scalable test problem toolkit. IEEE Trans. on Evolutionary Computation, 2006, 10(5): 477-506. [doi:10.1109/TEVC.2005.861417]
[125]	Tanabe R, Ishibuchi H. An easy-to-use real-world multi-objective optimization problem suite. Applied Soft Computing, 2020, 89: 106078. [doi:10.1016/j.asoc.2020.106078]
[126]	Zitzler E, Thiele L, Laumanns, Fonseca CM, Da Fonseca VG. Performance assessment of multiobjective optimizers: An analysis and review. IEEE Trans. on Evolutionary Computation, 2003, 7(2): 117-132. [doi:10.1109/TEVC.2003.810758]
[127]	Pal B, Das S, Basak A, Suganthan PN. Synthesis of difference patterns for monopulse antennas with optimal combination of array-size and number of subarrays: A multi-objective optimization approach. Progress in Electromagnetics Research B, 2010, 21: 257-280. [doi:10.2528/PIERB10033107]
[128]	Waldock A, Corne D. Multiple objective optimisation applied to route planning. In: Proc. of the 13th Annual Conf. on Genetic and Evolutionary Computation. Dublin: ACM, 2011. 1827–1834.
[22]	方开泰, 马长兴. 正交与均匀试验设计. 北京: 科学出版社, 2001.