1 引　言

逆向强化学习(inverse reinforcement learning, IRL)作为一种学习专家策略的模仿学习算法, 已成功应用于汽车导航^[1]、路径规划^{[2, 3]}、行为预测^[4-8]和机器最优控制^[9-11]等领域. 近年来, 鉴于以上任务的复杂性和应用前景, 逆向强化学习已成为强化学习领域和模仿学习领域的研究热点. 本文旨在梳理逆向强化学习发展脉络, 介绍前沿研究进展和分析关键问题.

逆向强化学习方法将模仿学习问题抽象为马尔可夫决策过程, 应用强化学习方法模仿专家策略. 与强化学习依据奖赏函数求解最优策略不同, 逆向强化学习方法包含依据专家样本求解奖赏函数过程, 因其与强化学习方法学习过程相反, 被称为逆向强化学习算法.

强化学习(reinforcement learning, RL)起源于最优控制领域, 是一种通过与环境交互求解最优策略的方法, 广泛应用于工业制造^[12]、机器人最优控制^[13]、游戏博弈^{[14, 15]}、优化与调度^[16-18]和仿真模拟^[19]等领域. 强化学习方法基于马尔可夫决策过程, 通过智能体与环境交互获得奖赏, 并根据累积奖赏更新策略以选取最优动作, 具有对环境探索的自学能力. 算法在执行过程中持续探索环境和利用环境反馈信息, 使智能体的策略逐步迭代收敛至最优策略. 此外, 强化学习方法中的奖赏函数由人工设定, 作为设计人员与智能体之间的沟通媒介, 奖赏函数中蕴含设计人员所期望目标的全部信息, 而智能体通过与环境交互获得奖赏的方式“解码”奖赏函数, 完成期望任务.

模仿学习是一种通过专家样本模仿专家策略的方法^{[20, 21]}, 包括行为克隆方法(behavioral cloning, BC)和逆向强化学习方法.

行为克隆^{[22, 23]}方法直接学习状态或标签到动作或路径的映射, 无需建立奖赏函数, 一般通过监督学习方法实现. 对于小状态空间问题, 行为克隆是一种十分高效的方法. 但在连续状态-动作空间或大状态-动作空间问题中, 因为行为克隆方法只考虑在每个状态采取的动作与专家样本是否匹配, 不考虑未来收益, 所以若与环境交互路径很长且专家样本不足, 则行为克隆方法会将细微误差在连续决策中逐步放大, 甚至环境发生一点变化, 都会极大影响算法性能, 这被称为行为克隆方法中的复合误差问题^{[24, 25]}.

逆向强化学习也被称为逆向最优控制(inverse optimal control, IOC)^{[26, 27]}, 最初由Russell于1998年提出^[28]. 与强化学习方法相同, 逆向强化学习方法基于马尔可夫决策过程, 通过智能体与环境交互求解最优策略. 在一般强化学习问题中, 奖赏函数由人工设定, 而在许多复杂问题中, 很难设计出精确的奖赏函数, 此时却很容易通过专家策略采样专家样本, 例如汽车驾驶^[29]和操纵机器打结等^{[30, 31]}. 针对这类问题, 逆向强化学习方法抛弃人工设定奖赏函数过程, 直接通过专家样本重建奖赏函数, 并依据所得奖赏函数求解最优策略, 达到模仿专家策略的目的^[32].

相比行为克隆方法, 逆向强化学习方法具有更好的泛化性和鲁棒性^{[33, 34]}, 若环境改变或在专家样本状态-动作空间之外, 仍可保证算法性能. 此外, 由于逆向强化学习方法通过最大化累积奖赏值求解最优策略, 所以逆向强化学习方法方法不存在行为克隆方法中的复合误差问题.

逆向强化学习方法的奖赏函数最初为线性函数, 由Ng等人于2000年提出^[35], 此后基于学徒学习的逆向强化学习算法^[36]、最大边际算法^[37]、最大熵算法^[38]和相对熵算法^[39]等被相继提出. 这类算法假设状态或状态-动作对特征的线性组合为奖赏函数, 算法的最终目标为求解每个特征的系数, 当特征系数确定, 奖赏函数随之确定. 逆向强化学习方法中多个奖赏函数均可求解专家策略, 这被称为非适定(ill-posed)问题, 算法仍需在满足条件的奖赏函数集合中选择最优解. Ng等人基于启发式搜索思想要求奖赏函数满足约束条件的同时还需满足额外目标函数, 这一思想可用线性规划或二次规划数学模型表示. 因此, 早期逆向强化学习方法使用线性规划或二次规划方法求解奖赏函数, 且奖赏函数为线性基函数, 依据不同目标函数, 基于基函数的算法分为3类: 基于最大边际思想的算法、基于概率模型思想的算法和基于结构化分类思想的算法. 上述3类算法要求奖赏函数满足基本约束条件, 在此基础之上, 基于最大边际思想的算法要求奖赏函数尽可能区分专家策略(最优策略)与次优策略, 即专家策略平均回报尽可能大于次优策略平均回报. 基于概率模型思想的算法将问题抽象为概率模型, 每个奖赏函数对应的最优路径(trajectory)都满足各自的概率分布^[40]. 因此最大熵算法要求奖赏函数在满足基本约束条件的同时, 保证其所对应最优路径概率分布的熵值最大, 类似还有基于交叉熵^{[41, 42]}、相对熵和最大似然估计^[43]等算法. 基于结构化分类思想的算法通过多个线性参数化分类器求解奖赏函数, 以使每个状态的累积回报尽可能大. 总体来说, 基于线性奖赏函数的逆向强化学习算法在一些小状态空间和离散状态空间问题中取得了不错的效果, 且应用到汽车导航问题中. 这类算法除相对熵算法外都是基于模型的算法, 因此需要提供环境模型(状态转移概率), 在一定程度上限制了算法的应用. 另外, 由于所有的奖赏函数都是特征的线性组合, 导致以下问题: (1)特征需要凭借人的经验来选取, 增加了算法的难度和不稳定性; (2)线性奖赏函数形式简单, 存在表达能力有限的问题.

为克服线性奖赏函数的局限性, 基于非线性奖赏函数的逆向强化学习算法被提出, 包括基于贝叶斯的非参数化特征构建算法^[44]和基于神经网络的非线性逆向强化学习算法. 基于贝叶斯的非参数化特征构建算法用高斯过程(Gaussian processes, GPs)^[45]构建非线性奖赏函数, 在一定程度上解决了线性奖赏函数表征能力不足的问题, 但同时也需要提供大量专家样本. 传统逆向强化学习算法(例如学徒学习算法、最大边际算法、最大熵算法、相对熵算法)与神经网络结合, 将神经网络作为奖赏函数, 取得了很好的效果. 这类算法可以通过神经网络自动提取状态特征, 具有更强的表征能力. 目前, 在游戏、自动驾驶、路径导航和机器控制领域取得了一定成果.

Ho等人将在计算机视觉领域取得优秀成果的生成对抗网络(generative adversarial network, GAN)^[46]与逆向强化学习结合, 提出生成对抗模仿学习算法(generative adversarial imitation learning, GAIL)^[47]. 该算法将逆向强化学习过程抽象为求解奖赏函数的IRL过程和求解最优策略的RL过程, 并指出两个过程的交替迭代为零和博弈问题, 因此可用生成对抗思想解决. 相比非线性逆向强化学习算法, GAIL具有更小的计算量和更高的性能, 但也存在训练不稳定、模态崩塌(mode collapse)^[48]和生成样本利用率低的问题^{[49, 50]}.

近年来, 逆向强化学习方法在机器最优控制领域、状态动作信息不完全领域、多智能体领域和提高专家样本利用率等领域都取得了进展, 也有学者将专家样本最优性假设进行扩展, 解决专家样本非最优问题^[51-53], 此外还有指导逆向强化学习方法研究等^[54-60].

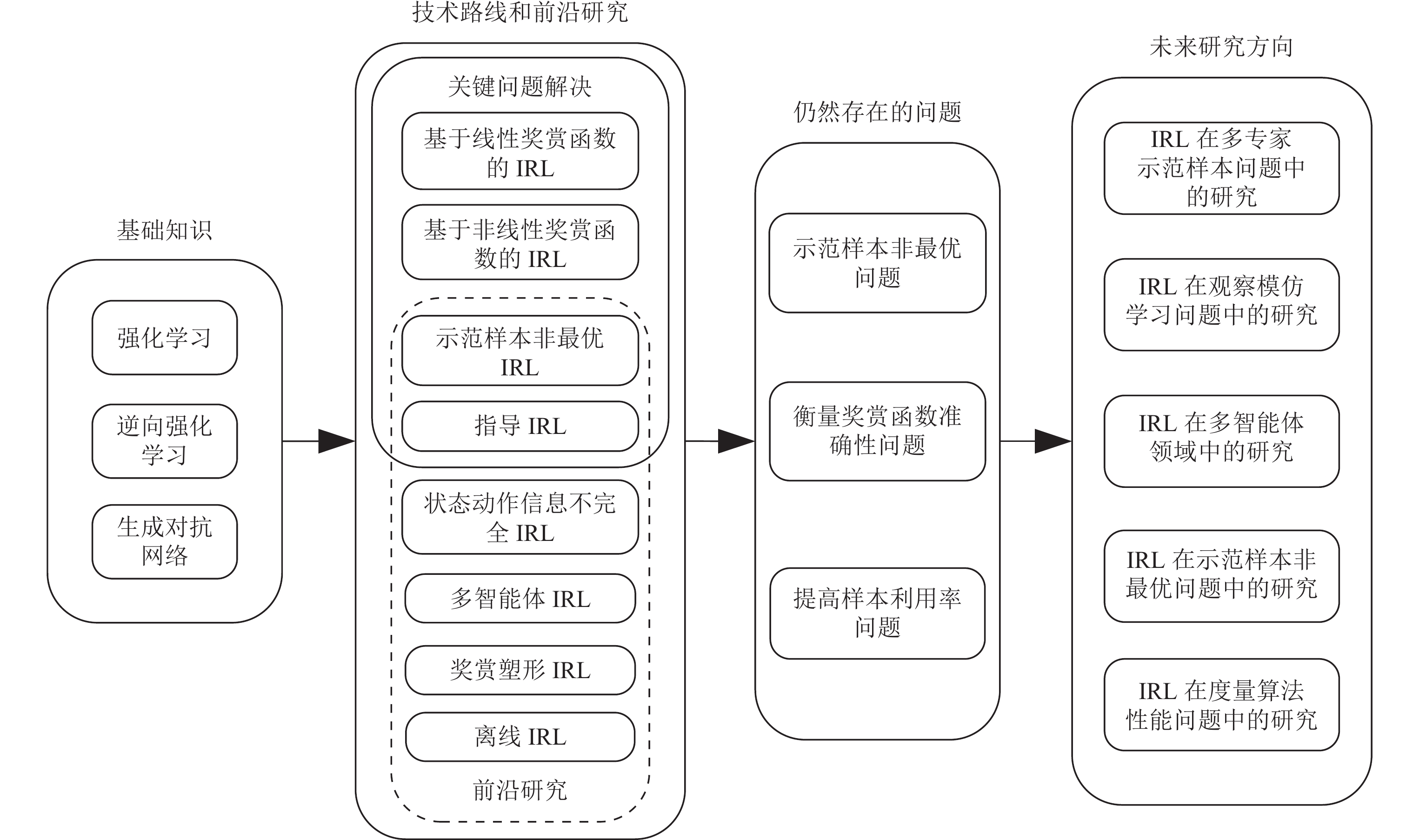
逆向强化学习方法发展至今, 已成为模仿学习方法中最重要的实现方式. 本文将基于以上分类, 梳理逆向强化学习的发展脉络, 分析其发展的内部机理, 探讨其优势和不足, 并总结未来可能的发展方向. 本文的结构框架如后文图1所示, 我们将按照图1结构, 介绍逆向强化学习领域的关键论文和最新进展.

2 预备知识

介绍IRL的基本知识, 包括数学定义、常用概念和基本算法, 提供与后续章节相关的简单背景知识.

2.1 强化学习

强化学习^{[61, 62]}起源于最优控制领域, 是一种持续与环境交互获得奖赏, 并根据累积奖赏采取最优动作的算法. 其本质为通过不断试错的方法与环境交互获取信息, 并利用所获取信息进行策略优化. 算法将与环境交互过程抽象为马尔可夫决策过程(Markov decision process, MDP)^[63], 定义MDP为五元组 $(S, A, R, \gamma , P)$ , 智能体在每个状态的动作选择符合马尔可夫性, 即所采取动作只与当前状态有关, 与之前状态无关. MDP五元组的具体含义如下.

(1) $S$ : 表示环境中的所有状态集合;

(2) $A$ : 表示智能体的所有动作集合;

(3) $R$ : 表示智能体从环境中获得的奖赏函数集合, 依据在不同环境中奖赏函数因变量的不同, 奖赏函数分别为: $r(s, a, s')$ 、 $r(s, a)$ 和 $r(s)$ . 其中, $r(s, a, s')$ 表示在状态 $s$ 采取动作 $a$ 到达 $s'$ 所得奖赏, $r(s, a)$ 表示在状态 $s$ 采取动作 $a$ 所得奖赏, $r(s)$ 表示到达状态 $s$ 所得奖赏;

(4) $\gamma $ : 表示折扣因子, 强化学习在每个状态选择动作会考虑长远影响, 但是, 算法无法考虑无限远的影响, 这不仅导致状态值无穷大, 也无法实现. 目前有两种解决方法: 设置最大时间步长T; 设置折扣因子 $\gamma $ , $\gamma $ 越接近于0, 算法越注重短期奖赏, 反之, $\gamma $ 越接近于1, 算法越重视长期奖赏, 因此, 可通过调节 $\gamma $ 平衡算法在短期奖赏和长期奖赏之间的取舍;

(5) P: 表示环境的状态转移概率, 依据在不同环境中状态转移概率函数因变量的不同, 可分为: $p(s', r|s, a)$ 和 $p(s'|s, a)$ . 其中, $p(s'|s, a)$ 表示智能体在状态 $s$ 采取动作 $a$ 后, 到达状态 $s'$ 的概率; $p(s', r|s, a)$ 表示智能体在状态 $s$ 采取动作 $a$ 后, 到达状态 $s'$ 并获得奖赏r的概率.

策略 $\pi (a|s)$ 表示状态到动作的映射, 强化学习中策略分为确定性策略和随机策略, 确定性策略表示在每个状态选择的动作确定且唯一, $\pi :S \to A$ . 最优策略 ${\pi ^*}$ 即为所选动作 $ a = \arg {\max _a}q(s, a) $ 在当前状态选择收益最大, $q(s, a)$ 为状态-动作值函数. 随机策略表示在每个状态的动作选择满足一个概率分布, $\pi :S \to {{prob}}(A)$ , 策略 $\pi $ 下的状态值函数 ${v_\pi }(a|s)$ 和动作值函数 ${q_\pi }(s, a)$ 的迭代形式如公式(1)和公式(2)所示.

$ {v_\pi }(s) = \sum\limits_a {\pi (a|s)\sum\limits_{s', r} {p(s', r|s, a)} } [r(s, a, s') + \gamma {v_\pi }(s')] $

(1)

$ {q_\pi }(s, a) = \sum\limits_{s', r} {p(s', r|s, a)[r(s, a, s') + \gamma {v_\pi }(s')]} $

(2)

强化学习算法分为表格式算法、值函数逼近算法和策略梯度算法. 早期的动态规划、蒙特卡罗和时序差分等算法属于表格式算法, 这类算法适用于离散动作问题和小状态空间问题. 以深度Q网络(deep Q-network, DQN)^[64]算法为代表的值函数逼近算法, 将适用范围扩展到大状态空间和连续状态空间问题, 用深度神经网络代替表格, 输入为状态和动作, 输出为状态-动作对的值 $q(s, a)$ .

另外一种算法为策略梯度算法, 解决了DQN无法表示连续动作的问题, 该算法用深度神经网络表示策略函数 $\pi $ , 输入为状态, 输出为该状态采取的动作. 策略梯度算法的目标函数针对不同问题有3个目标函数: 起始价值、平均价值和时间步平均奖赏, 分别如公式(3)–公式(5)所示.

$ J(\theta ) = {v_\pi }({s_0}) = {\mathbb{E}_\pi }[{v_0}] $

(3)

其中, ${s_0}$ 表示初始状态, ${v_0}$ 表示起始价值, $\theta $ 表示策略 $\pi $ 的参数向量:

$ J(\theta ) = \sum\limits_{s \in S} {{d_\pi }(s){v_\pi }(s)} $

(4)

其中, ${d_\pi }(s)$ 表示在策略 $\pi $ 下关于状态 $s$ 的静态分布:

$ J(\theta ) = \sum\limits_{s \in S} {{d_\pi }\sum\limits_{a \in A} {\pi (a|s)} } r(s, a, s') $

(5)

其中, ${d_\pi }$ 表示在策略 $\pi $ 下状态的概率分布, $\pi \left( {a|s} \right)$ 为状态 $s$ 下按照策略 $\pi $ 执行动作 $a$ 的概率, $ r(s, a, s') $ 为状态 $s$ 下执行动作 $a$ 到达下一状态 $s'$ 所获得的即时奖赏.

因为策略梯度算法基于回合更新, 存在策略评估效率低下和方差较高问题, 所以行动者-评论家(actor-critic)算法将策略梯度算法与值函数逼近算法结合, 以增加算法偏差为代价减少方差, 实现算法单步更新、灵活选择动作, 其代表算法为A2C (advantage actor-critic)和A3C (asynchronous advantage actor-critic)^[65]. 基于随机策略梯度的算法还包括实现算法稳步更新的TRPO (trust region policy optimization)算法^[66]. 此外还有基于行动者-评论家架构的PPO (proximal policy optimization algorithms)算法^[67], 用于解决连续动作空间问题. 以上几种随机策略梯度算法需要对动作采样, 当动作维度很高时效率较低, 此时可采用DDPG (deep deterministic policy gradient)算法^[68].

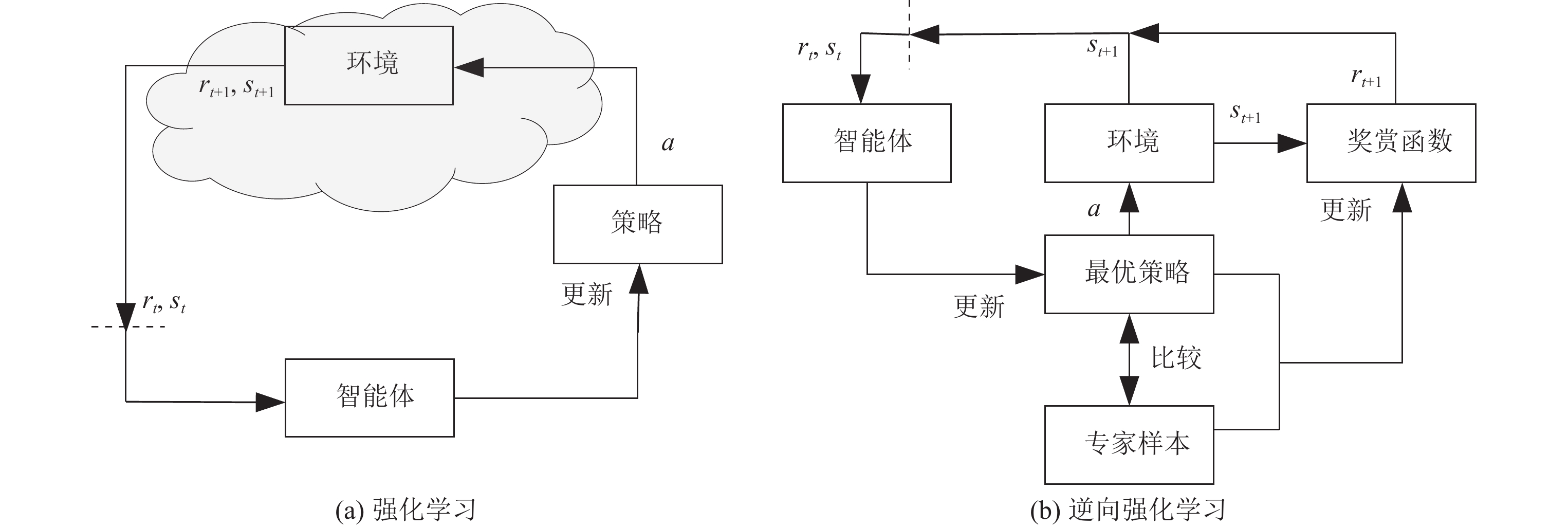
2.2 逆向强化学习

逆向强化学习方法通过专家样本求解奖赏函数, 再根据奖赏函数学习最优策略, 原理如图2所示. 为准确定义逆向强化学习问题, 以马尔科夫决策过程作为问题框架, 假设专家策略在MDP下进行动作选择. 定义MDP为五元组 $(S, A, R, \gamma , P)$ , S表示由状态组成的集合, A表示由动作组成的集合, $P:S \times A \to {{prob(}}S)$ 表示状态转移概率, R表示奖赏函数集合, 奖赏函数与上文强化学习中的定义相同, $\gamma $ 表示折扣因子. 另外, 奖赏函数定义为特征的线性组合, 特征向量 $\phi $ 可为表示状态的特征向量 $ \phi :S \to {[0, 1]^{\left| S \right|}} $ , 也可为表示状态-动作对的特征向量 $ \phi :S \times A \to {[0, 1]^{\left| S \right| \times \left| A \right|}} $ .

逆向强化学习的定义如下, 给定:

(1) 智能体在环境中的专家样本;

(2) 若需要, 则给定传感器所得数据;

(3) 若可行, 则给定物理环境的模型(包括智能体自身).

确定: 使智能体的策略最优的奖赏函数.

逆向强化学习方法通过由专家轨迹 $\tau $ 组成的专家样本 $D = \{ {\tau _1}, \ldots, {\tau _N}\}$ 求解奖赏函数 $r(s, a, s')$ . 假设专家策略 ${\pi _E}(a|s)$ 为最优策略 ${\pi ^*}(a|s)$ , 专家样本由专家策略与环境交互采样得到. 策略的平均回报定义为: $ {\mathbb{E}_\pi }\left[r(s, a, s')\right] \triangleq \mathbb{E}\left[\displaystyle\sum\nolimits_{t = 0}^\infty {{\gamma ^t}r({s_t}, {a_t}, {{s'}_t})} \right] $ , 其中 $a \sim \pi ( \cdot |{s_t})$ , ${s_{t + 1}} \sim P( \cdot |{s_t}, {a_t})$ . 逆向强化学习方法的优化目标定义为:

$ \mathop {{\max}}\limits_{r \in R} {\kern 1pt} \;\left( {\mathop {\min }\limits_{\pi \in \Pi } \; - H(\pi ) - {\mathbb{E}_\pi }[r(s, a, s')]} \right) + {\mathbb{E}_{{\pi _E}}}[r(s, a, s')] $

(6)

其中, $ H(\pi ) \triangleq {\mathbb{E}_\pi }[ - \log \pi (a|s)] $ 表示策略 $\pi $ 基于 $\gamma $ 折扣的因果熵^[69]. 公式(6)的目标为寻找奖赏函数使得专家策略的平均回报尽可能大于其他策略的平均回报. 逆向强化学习算法中依据当前奖赏函数求解最优策略的目标函数定义为:

$ {\mathrm{RL}}(r) = \mathop {\arg \max }\limits_{\pi \in \Pi } \; - H(\pi ) + {\mathbb{E}_\pi }[r(s, a, s')] $

(7)

求解最优策略的目标为最大化策略 $\pi $ 的平均回报和熵值. 逆向强化学习算法通常通过迭代方法^[70]计算其所确定的二次规划问题, 算法的总体流程如下.

(1) 初始化奖赏函数.

(2) 根据当前奖赏函数, 利用强化学习算法求解最优策略.

(3) 所得最优策略与专家策略比较, 计算特征期望匹配程度.

(4) 改进奖赏函数.

逆向强化学习方法的目的为通过从专家样本中求解奖赏函数模仿专家策略, 然而, 一个策略可以是多个奖赏函数的最优策略, 因此求解奖赏函数的问题为非适定问题. 为获得奖赏函数的唯一解, 一些算法增加目标函数, 例如最大边际算法和最大熵算法等^[71-73].

不同逆向强化学习算法实现以上流程的方式各不相同, 基于模型算法需要环境信息(状态转移概率)计算状态访问概率和最优策略. 当环境模型已知时, 这种基于模型的算法实现相对简单, 但较难应用于非线性环境中. 无模型算法则通过采样实现以上功能, 可以应用到非线性环境模型中. 另外, 有些无模型算法需要从环境中采样轨迹, 并计算轨迹的分布概率, 这导致算法的时间复杂度较高. 基于奖赏函数的最优策略以强化学习算法求解.

2.3 生成对抗网络

生成对抗网络(generative adversarial network, GAN)^[46]在计算机视觉领域取得了很好的成果. GAN可以被看作一种基于结构化学习(structure learning)的方法, 即: 对于给定的输入, 传统的算法输出为一个数值(例如识别图片中的数字), 或者输出为一个类别(例如给出输入属于哪一类别), 而GAN的输出为一串序列(向量、矩阵、图片等).

生成对抗网络由生成器(generator, G)和判别器(discriminator, D)组成. 生成器和判别器都为深度神经网络. 以图像生成任务为例, 对于给定的图像输入, 生成器的功能为生成与输入相似的图像, 而判别器的功能为判断生成器输出图像与输入图像是否相似. 因此生成器和判别器组成了一个零和博弈问题, 生成器从随机噪声中生成与数据集中样本尽可能相似的图像, 尽可能使判别器认为生成图像为真实样本, 而判别器的功能为抽象真实图像中特征, 并用抽象特征区分真实图像与生成图像, 两者在持续博弈中逐步优化, 直至收敛. 实际上, 真实样本在每个像素点和像素点之间的颜色满足一定的概率分布, 而GAN的目标为: 最小化真实样本概率分布与生成样本概率分布之间的距离. 博弈的目标函数如公式(8)所示:

$ \mathop {\min }\limits_G \mathop {\max }\limits_D {L_{\rm GANs}}(D, G) = {\mathbb{E}_x}[\log D(x)] + {\mathbb{E}_\textit{z}}[\log (1 - D(G(\textit{z})))] $

(8)

其中, $x$ 表示真实样本, $\textit{z}$ 表示噪声输入, $G(\textit{z})$ 表示生成器产生的样本, $D( \cdot )$ 表示判别器判断样本为真实样本的概率.

3 逆向强化学习研究进展 3.1 基于线性奖赏函数的逆向强化学习

在逆向强化学习方法发展初期, 用状态-动作对特征的线性组合表示奖赏函数. 因为奖赏函数的不确定性, 传统逆向强化学习方法致力于通过启发式搜索选择最优奖赏函数, 依据其不同实现方式, 分为最大边际方法、概率模型方法和结构化分类方法. 本节从基于线性奖赏函数的逆向强化学习方法出发, 介绍传统逆向强化学习算法对奖赏函数的初选和择优问题的解决.

3.1.1 最大边际方法

逆向强化学习算法可以有效解决行为克隆算法中泛化性差和复合误差问题, 同时也存在非适定问题, 即依据专家样本求得满足条件的奖赏函数存在多个, 难以确定唯一解. 为解决这一问题, Ng等人^[35]依据最大边际(maximum margin)思想选择最优奖赏函数, 使专家策略平均回报尽可能大于其他次优策略平均回报. 算法简化奖赏函数, 定义奖赏函数为只与当前状态特征有关、与选取动作和下一状态无关的线性方程, 并给出了奖赏函数求解方法. 该算法在逆向强化学习方法发展早期有重要意义, 但是, 当 $R = 0$ (或为常数向量)或每个状态的奖赏非常接近时, 该方法效果并不明显.

基于已有的学徒学习思想^[74], Abbeel等人提出基于学徒学习的逆向强化学习算法^[36], 算法假设奖赏函数为关于状态的线性奖赏函数, 首次提出特征期望(feature expectation)概念, 定义特征值的折扣累加为 $\mu (\pi )$ . 算法证明, 若当前策略与专家策略的特征期望匹配, 则当前策略为专家策略. 因此, 算法虽然不能保证求解正确的奖赏函数, 但可以求解与专家策略同样最优的策略, 并且可以测量策略之间的距离. 由于逆向强化学习的非适定性, 如何从所有满足要求的奖赏函数集合中筛选最优解, 一直是该领域的研究重点. Ratliff等人^[37]引入学徒学习思想, 正式提出最大化专家策略和次优策略距离的最大边际算法.

3.1.2 概率模型优化方法

为了从满足要求的奖赏函数集合中筛选最优解, 与最大边际方法不同, 概率模型方法选取最优策略的熵值为目标函数. 首先, 该方法基于当前奖赏函数计算最优策略, 然后通过最优策略进行采样获得样本轨迹. 最大熵逆向强化学习算法^[38]是一种完全基于概率模型的算法. 在满足通过奖赏函数计算出的策略奖赏等于专家策略奖赏的前提下, 利用最大熵方法对奖赏函数集合进行筛选^[75-77]. Boularias等人^[39]提出基于相对熵的逆向强化学习算法, 通过当前最优样本的概率分布与专家样本概率分布之间的KL散度学习奖赏函数.

在基于最大熵逆向强化学习算法的基础上, Scobee等人^[78]提出了基于最大似然约束推断的逆向强化学习算法. 算法要求提供基于最优策略的专家样本和粗糙的奖赏函数, 通过在马尔可夫决策过程中增加约束(constraint), 逐步最大化关于专家样本的似然函数, 即最大化专家样本的出现概率. 该算法通过增加约束的方式最大化专家样本发生的概率, 为解决逆向强化学习问题提供了新的视角, 但是目前只能应用于确定性环境, 且需要提供粗糙设计的奖赏函数. Shehryar等人^[79]基于增加约束的方法提出了ICRL算法, 算法的两个主要步骤为: (1)基于约束集合(由神经网络表示), 学习最优策略; (2)优化约束集合, 使得专家样本发生的概率最大(样本概率通过最大熵算法求解). 算法依据以上两步迭代求解, 直至收敛. 基于以上改进, ICRL算法可以应用于连续高维环境中, 但仍然需要奖赏函数信息.

3.1.3 结构化分类方法

逆向强化学习算法的目的是: 寻找一种策略使得智能体的特征期望与专家策略的特征期望相等. 关于这一点, 上文的逆向强化学习算法中已有介绍, 具体体现在算法提出的二次规划方程的约束条件中. 这一约束条件的本质含义为: 依据算法学习所得策略生成的路径, 其路径分布概率应与专家样本的路径分布概率尽可能相等. 所有这些算法都需重复的通过强化学习过程求解当前最优策略, 因此算法的时间复杂度很大. 为解决这一问题, Klein等人^[80]提出了基于结构化分类的逆向强化学习算法(structured classification based IRL, SCIRL).

SCIRL算法抛弃传统逆向强化学习算法从状态到奖赏函数再到最优动作的求解路线, 直接建立状态到动作的映射关系, 即根据动作的不同对状态分类. 在基于结构化分类的逆向强化学习算法中, 状态-动作对依然表示为特征的线性组合, 与上文算法不同, SCIRL算法将线性状态-动作对特征方程的参数直接作为奖赏函数的参数. 这样定义的优点为: 状态-动作对的值函数与特征期望相等, 对每个特征期望的约束等价于对该特征下状态-动作对的约束, 这直接建立了状态与动作的映射关系. 因此, 问题转变为: 在每个特征下, 状态为样本, 动作为标签, 训练样本为专家样本, 训练算法可以用多类分类算法, 例如: 多类SVM (multi class SVM)分类算法.

作为SCIRL的扩展, Klein等人^[81]结合分类和回归两类算法, 提出了级联监督逆向强化学习(cascaded supervised IRL, CSI)算法. 在MDP环境中, 奖赏函数与状态-动作值函数一一对应, 因此可先求解满足专家样本的状态-动作值函数, 该过程为监督学习算法. 进一步, 根据贝尔曼方程, 状态-动作值函数已知, 若求解奖赏函数, 需提供状态转移概率. 状态转移概率信息包含在专家样本的路径中, 通过最小二乘逼近器求解, 可最终得到奖赏函数.

3.1.4 对比分析

因为逆向强化学习方法的非适定性, 算法需要在所有满足要求的奖赏函数中筛选最优解. 基于启发式搜索思想要求奖赏函数满足约束条件的同时, 还需满足额外目标函数. Ng等人在算法中运用最大边际思想^[35], 被Ratliff等人在最大边际算法中正式提出^[37]. 此外还包括最大熵和结构化分类思想^{[80, 82, 83]}.

3.1.4.1 解决奖赏函数的非适定问题

在Ng等人所提出算法中, 要求专家样本的所有状态-动作值之和尽可能大于对应状态的次优状态-动作值之和. 这一方法有助于算法筛选最优奖赏函数, 但其只看重整体之和, 未考虑每个状态-动作对所占比例关系, 对于出现概率较高的状态-动作对, 应希望其状态-动作值尽量高于次优状态-动作对的值; 另外, 状态-动作对的概率分布与策略也存在对应关系. 因此, 学徒学习对专家样本的状态-动作对求特征期望, 并要求基于该特征期望的奖赏大于次优策略的奖赏. 此后正式提出最大边际思想的最大边际算法也基于这一方法, 更进一步在对应状态所选动作与专家动作不一致时, 增加惩罚项.

概率模型方法从信息角度出发, 提出一种基于熵的奖赏函数选择方法. 若想选择最优奖赏函数, 算法需依据最优问题约束条件求解奖赏函数. 最大熵逆向强化学习算法认为, 所有满足条件的奖赏函数中所含额外信息最少的奖赏函数为最优奖赏函数. 算法通过奖赏函数所对应最优策略与环境交互, 采样策略轨迹, 并计算轨迹的概率分布, 其中轨迹概率分布熵值最大的奖赏函数即为最优奖赏函数. 进一步, 相对熵算法将应用范围拓展至无模型问题, 通过轨迹概率分布与专家轨迹概率分布的相对熵筛选最优奖赏函数. 与最大边际方法相比, 概率模型方法可以应用到更大的状态空间问题. 基于最大似然约束推断的逆向强化学习算法直接通过增加约束的方式优化奖赏函数, 更有利于在实际任务中应用.

结构化分类方法通过多分类算法求解奖赏函数, 研究多集中于离散状态-动作空间任务, 同时动作空间不能过大. 因此, 最终策略的泛化性不如最大边际方法和概率模型方法, 但该方法可以节省大量计算资源.

3.1.4.2 衡量奖赏函数准确性

吴恩达提出的算法依据贝尔曼方程推导奖赏函数需满足一定条件, 通过该方式计算奖赏函数, 需要大量计算资源, 同时也难以应用于大状态-动作空间问题.

学徒学习算法要求与当前奖赏函数所对应最优策略的特征期望尽可能等于专家样本的特征期望, 目前大多数逆向强化学习算法都以此(或略有改变)作为奖赏函数是否满足要求的判据, 并在此基础上对奖赏函数作进一步改进.

概率模型方法同样基于特征期望相等这一思想, 但该方法以样本轨迹为计算单元. 概率模型方法所确定最优问题的约束条件要求基于轨迹概率的所有状态-动作对的特征期望尽可能与专家样本的特征期望相等.

结构化分类方法通过对应状态所选动作与专家样本是否一致衡量奖赏函数的准确性, 与监督学习方法类似, 这导致该方法的样本泛化性较差.

3.1.4.3 基于模型和无模型

逆向强化学习算法分为两类: 基于模型(model-based)算法和无模型(model-free)算法. 基于模型算法需要知道环境信息, 通常为状态转移概率. 因为在奖赏函数迭代过程中需要用状态转移概率计算状态访问概率和最优策略, 以帮助提升奖赏函数. 但是, 若环境信息未知, 需要通过与环境交互采样学习环境模型, 面对大状态空间甚至连续状态空间问题, 难以学习准确模型. 无模型算法主要用于解决环境信息未知问题, 一般通过大量的采样获得情节的分布概率, 这也带来了更高的方差和更多的计算量.

学徒学习算法最小化最坏情况下学习所得特征期望与专家策略特征期望之间的差值, 最大边际算法通过次梯度方法最小化代价函数, 最大熵算法求解所有满足约束的模型中熵值最大模型. 以上算法在其运算过程中都需使用MDP模型计算最优策略, 相对熵算法通过重要性采样方法求解损失函数, 属于无模型算法.

3.2 基于非线性奖赏函数的逆向强化学习

在传统逆向强化学习算法中, 由于线性奖赏函数表达能力不足, 限制了算法的应用. 在解决连续高维状态-动作空间问题时, 线性奖赏函数难以准确表征真实奖赏函数. 因此需要将线性奖赏函数变为非线性函数, 提高其表达能力^{[84, 85]}.

另外, 算法设计时, 特征需凭借设计人员经验选取, 所选特征的范围和正确性直接影响算法性能^[1], 增加了算法的难度和不稳定性.

3.2.1 高斯过程拟合奖赏函数

基于高斯过程^[86]的非线性逆向强化学习算法(Gaussian process inverse reinforcement learning, GPIRL)用高斯过程学习非线性奖赏函数^[87], 并且确定了不同特征之间的相关性, 因为高斯过程基于概率的特点, 算法允许专家样本为次优策略.

高斯过程回归需要输入-输出对, 在基于值函数的近似算法中也有应用^{[88, 89]}. 而基于高斯过程的逆向强化学习算法只有动作输入没有奖赏输入, 因此需要扩展高斯过程模型, 建立动作和潜在奖赏的随机关系. 学习所得高斯核函数参数既可确定奖赏函数, 也包含不同特征之间的相关性信息.

逆向强化学习期望求解使得其最优策略与专家样本的特征期望相匹配^[90]的奖赏函数, 因此专家策略应为最优策略, 而在实际问题中, 有时示范样本由次优策略产生或包含部分次优样本. 学习次优策略的一种方法为建立动作选择的概率模型. GPIRL采用最大熵算法, 该算法中选择某一路径 $\tau $ 的概率与该路径奖赏的指数次方成正比.

3.2.2 深度熵优化模型

目前线性奖赏函数算法存在表征能力有限, 且其特征需要人工设定的问题. 以汽车导航为例, 算法为实现汽车之间保持安全距离^[2]的目标, 提出用神经网络近似复杂、非线性奖赏函数, 取得了很好的效果, 所用神经网络为全卷积神经网络(fully convolutional neural networks, FCNNs). 基于最大熵的深度逆向强化学习算法(maximum entropy deep inverse reinforcement learning, MEDIRL)^[91]用神经网络表示奖赏函数, 目标函数与最大熵算法相同. 由于神经网络的灵活性, MEDIRL算法中奖赏函数的特征无需人工设定, 但算法所解决问题局限于离散状态空间问题. 与最大熵逆向强化学习算法相同, MEDIRL算法要求所求最优策略的状态访问概率与专家样本尽可能相等^[92]. 奖赏函数求得最优策略的路径满足公式(9).

$ p(\tau |r){\rm{\backslash }} \propto \exp \left\{ \sum\limits_{s,a \in \zeta } {r(s,a)} \right\} $

(9)

因为在复杂问题中状态的维度非常大, 所以奖赏函数无法与表格式方法一样准确确定每个状态的奖赏, 该算法用参数为 ${\theta _{1, 2, \ldots , n}}$ 的全连接卷积神经网表示奖赏函数. 并用最大后验估计(maximum a posteriori probability estimate, MAP)方法, 最大化专家样本和参数 $\theta $ 的联合概率.

当奖赏函数为线性函数时, 联合对数似然方程对参数 $\theta $ 可微^[93], 可用梯度下降法求解. 当前问题的目标函数为求最大熵, 奖赏函数为深度神经网络, 同样具有这一性质.

3.2.3 逻辑回归方法

基于逻辑回归的逆向强化学习算法^{[94, 95]}采用逻辑回归方法求解非线性奖赏函数, 是一种无模型算法. 算法通过线性可解马尔可夫决策过程(linearly solvable Markov decision processes, LMDP)将逆向强化学习问题转变为密度比例(density ratio)预测问题, 密度比例为最优状态转移(optimal state transition)和基准状态转移之比. 密度比例通过值函数和奖赏函数组成的二分类逻辑回归(binomial logistic regression)分类器求解, 分类器的目的是区分最优策略和基准策略. 因为最优策略为专家策略且基准策略已知, 可通过监督学习求解神经网络表示的值函数和奖赏函数. 根据所得奖赏函数和值函数初始化可得状态-动作值网络, 进而可求解最优策略.

算法在LMDP框架下通过贝叶斯规则定义密度比例的对数形式如下:

$ \ln \frac{{\pi (s'|s)}}{{b(s'|s)}} = \ln \frac{{\pi (s)}}{{b(s)}} + \beta q(s) + \gamma V(s') - \beta V(s) $

(10)

其中, $s$ 为当前所在状态, $s'$ 为在状态 $s$ 采取动作 $a$ 后到达的状态, $q(s)$ 为状态独立奖赏函数(state-dependent reward function), $V(s)$ 为在状态 $s$ 的值函数.

作者提出通过强化学习方法求解最优策略, 使用DQN预测状态-动作值函数 $Q(s, a)$ , 并且使用dueling network构建神经网络^[96], 由状态值和优势函数两部分组成. 在正向强化学习过程中, 神经网络的输入为当前状态, 输出为状态-动作值, 神经网络由3部分构成: 奖赏网络 $r(s, {w_r})$ , 状态值函数网络 $V(s, {w_V})$ , 偏好函数网络(preference network).

3.2.4 生成对抗模仿学习 3.2.4.1 生成对抗模仿学习框架

逆向强化学习方法依据示范样本模仿专家策略, 要求最优策略逼近专家策略的状态-动作对概率分布. GAN算法^[46]在逼近概率分布问题中有优异性能^[97]. 因此, Ho等人基于GAN提出生成对抗模仿学习算法^[47], 以最大因果熵为损失函数, 直接从专家策略学习.

给定 ${\mathbb{E}_\pi }(c(s, a)) \triangleq \mathbb{E}\left[\displaystyle\sum\nolimits_{t = 0}^\infty {\gamma c({s_t}, {a_t})} \right]$ 为策略 $\pi $ 下代价函数的期望, 代价函数为 $c \in C$ , ${\pi _E}$ 表示专家策略且已知, 假设最大因果熵存在, 最优问题定义为:

$ \mathop {\max }\limits_{c \in C} (\mathop {\min }\limits_{\pi \in \Pi } - H(\pi ) + {\mathbb{E}_\pi }[c(s, a)]) - {\mathbb{E}_{{\pi _E}}}[c(s, a)] $

(11)

其中, ${H_\pi } \triangleq {\mathbb{E}_\pi }[ - \log \pi (a|s)]$ 为策略 $\pi $ 的因果熵, 即在状态 $s$ 已发生条件下, 所采取策略概率分布的条件熵.

生成对抗模仿学习算法从占用率度量(occupancy measure)角度出发, 将逆向强化学习问题分解为正向强化学习(RL)过程和逆向强化学习(IRL)过程. 在RL过程中, 最优化问题的约束条件为所求策略与专家策略占用率度量相匹配, 目的为依据当前奖赏函数寻找策略 $\pi $ , 满足 $ {\rm{RL}}(c) = \arg {\min _{\pi \in \Pi }} - H(\pi ) + {\mathbb{E}_\pi }[c(s, a)] $ , 即最大化因果熵, 最小化代价期望. IRL过程为RL过程的对偶问题, 目的为寻找代价函数, 使得专家策略代价尽可能小, 次优策略代价尽可能大.

生成对抗模仿学习算法在目标函数(11)中加入为凸函数的正则函数 ${\psi ^*}$ , 并通过凸共轭函数变换, 将目标函数的强化学习过程转换为如下等价形式:

$ {\mathrm{RL}} \circ {\mathrm{IRL}}({\pi _E}) = \mathop {\arg \min }\limits_{\pi \in \Pi } - H(\pi ) + {\psi ^ * }({\rho _\pi } - {\rho _{{\pi _E}}}) $

(12)

其中, ${\psi ^*}$ 为正则函数的凸共轭函数, $\;{\rho _\pi }$ 为当前策略的状态-动作对占用率度量, ${\rho _{{\pi _E}}}$ 为专家策略的状态-动作对占用率度量.

此处, 与深度学习中用正则函数防止过拟合不同, ${\psi ^*}$ 用作衡量所求策略与专家策略的差异, 对算法性能有很大影响, 因此选择正确的正则函数十分关键. 算法分析了3种正则函数: 常数正则化函数、示性正则化函数和熵正则化函数. 应用常数正则化函数难以处理大状态空间问题, 应用示性正则化函数的学徒学习算法难以精确匹配占用率度量, 只有熵正则化函数与上文提出模型等价. 基于以上结论, GAIL算法采用一种新的正则化函数, 最终所得目标函数为:

$ {\mathbb{E}_{{\pi _\theta }}}[\log {D_\omega }(s, a)] + {\mathbb{E}_{{\pi _E}}}[\log (1 - {D_\omega }(s, a))] - \lambda H(\pi ) $

(13)

解决公式(13)的关键在于寻找鞍点 $({\pi _\theta }, {\kern 1pt} {\kern 1pt} {D_\omega })$ , 其中策略 ${\pi _\theta }$ 和 ${D_\omega }$ 用函数逼近器表示. $\omega $ 利用Adam梯度算法使公式(13)增加, $\theta $ 利用TRPO算法使公式(13)下降, TRPO能够保证 ${\pi _{{\theta _{t + 1}}}}$ 不远离 ${\pi _{{\theta _t}}}$ . GAIL算法的判别器为D, 其所提供奖赏值被用来区分专家策略与次优策略, 与GAN中的判别器训练方法相同. 在得到D中的奖赏后, 利用TRPO算法进行策略学习, 改进生成器, 直到算法收敛.

与传统逆向强化学习算法相比, GAIL算法具有更强的表征能力和更高的计算效率^[98], 能够解决大状态空间问题. 但是也存在模态崩塌问题(model collapse)^[48]、训练不稳定问题和生成样本利用率低问题(low sample efficiency in terms of environment interaction)^{[49, 50]}.

3.2.4.2 生成对抗模仿学习算法性能分析

目前, 当能够采样足够专家样本时, BC算法依然是最佳选择. 但在绝大多数模仿学习任务中, 由于任务危险或采样成本高, 难以获取足够的专家样本. 在这些专家样本较少的模仿学习任务中, GAIL算法的性能优于BC算法. 然而, 目前对这一现象的理论分析依然很少. 假设通过GAIL算法或BC算法优化所得最优策略为 ${\pi ^*}$ , 专家策略为 ${\pi _E}$ , 策略在起始状态 ${s_0}$ 的值函数分别为 ${V_{{\pi _E}}}({s_0})$ 和 $ {V_{{\pi ^*}}}({s_0}) $ , 用以评价策略的性能.

Xu等人^[99]理论分析证明, 在BC算法中, 若最优策略 ${\pi ^*}$ 与专家策略 ${\pi _E}$ 之间的KL散度满足 ${\mathbb{E}_{s \sim {\pi _E}}}[{D_{KL}}({\pi _E}( \cdot |s), {\pi ^*}( \cdot |s))] \leqslant \varepsilon $ , 则 ${V_{{\pi _E}}}({s_0})$ 和 $ {V_{{\pi ^*}}}({s_0}) $ 的差值满足公式(14).

$ {V_{{\pi _E}}}({s_0}) - {V_{{\pi ^*}}}({s_0}) \leqslant \frac{{2\sqrt 2 {R_{\max }}}}{{{{\left( {1 - \gamma } \right)}^2}}}\sqrt \varepsilon $

(14)

其中, ${R_{\max }}$ 表示奖赏函数的约束: $\left| {r(s, a)} \right| \leqslant {R_{\max }}$ .

在GAIL算法中, 若最优策略 ${\pi ^*}$ 与专家策略 ${\pi _E}$ 之间的f-散度满足 ${D_f}({\rho _{{\pi ^*}}}, {\rho _{{\pi _E}}}) \leqslant \varepsilon $ , 则 ${V_{{\pi _E}}}({s_0})$ 和 $ {V_{{\pi ^*}}}({s_0}) $ 的差值满足公式(15).

$ {V}_{{\pi }_{E}}({s}_{0})-{V}_{{\pi }^{*}}({s}_{0})\leqslant \mathcal{O}\left(\frac{1}{1-\gamma }\sqrt{\varepsilon}\right) $

(15)

由公式(14)、公式(15)可知, 在BC算法中 ${V_{{\pi _E}}}({s_0})$ 和 $ {V_{{\pi ^*}}}({s_0}) $ 的复合误差(compounding error)随着由 $\gamma $ 控制的序列长度增加呈指数增加, 复合误差在GAIL算法中呈线性增加.

3.2.4.3 生成对抗模仿学习中的模态崩塌问题

模态指专家样本中存在的一些特征. 例如, 在自动驾驶问题中, 专家样本中可能存在两种模态: 车辆在高速公路中以高速行驶; 在市区中以相对低速行驶. 逆向强化学习算法一般假设专家样本为单一模态, 但是, 在实际问题中, 专家样本通常由多个专家产生或某一专家依据不同偏好产生, 即专家样本存在多个子分布. 然而, 在GAIL算法中生成器所生成样本只能满足专家样本的某一子分布, 无法满足全部的专家样本分布. 针对这一问题, 目前的改进方向有: 多模态改进^{[11, 100, 101]}和模型改进^{[102, 103]}.

(1) 基于最大互信息的生成对抗模仿学习

Li等人^[101]提出了基于最大互信息的生成对抗模仿学习(information maximizing generative adversarial imitation learning, InfoGAIL)算法, 通过最大化策略轨迹与模态隐变量之间的互信息, 学习多模态策略. 算法假设模态隐变量 $c$ 为隐藏在专家样本集合中的离散变量, 策略 $\pi $ 关于该变量的条件概率分布为 $p(\pi |c)$ , 可通过训练得到. 为最大化利用模态隐变量 $c$ 中信息, InfoGAIL算法要求最大化 $c$ 与状态-动作对之间互信息, 互信息表达式如下所示:

$ I{\left( {c;s, a} \right)_{a = \pi (s, a)}} = H\left( c \right) - H\left( {c, \left( {s, a} \right)} \right) .$

因为模态隐变量关于状态-动作对的后验概率 $q(c|s, a)$ 未知, 算法将互信息缩放为其变分的最小值, 在生成对抗网络模型中增加推断器, 用以逼近后验概率. 推断器的输入为生成器产生的状态-动作对, 输出为后验概率 $q$ , 随着算法训练, 判别器逐渐收敛到使互信息最大的模态隐变量.

(2) 基于辅助选择器的生成对抗模仿学习

在实际任务中, 专家样本通常由多种模态策略或技能生成. 以自动驾驶问题为例, 专家策略通常使用3个技能: 保持直行、变道左侧车道和变道右侧车道. 为使算法能够依据当前状态自主选择技能, Fei等人^[103]提出一种新的多模态生成对抗框架, Triple-GAIL算法. Triple-GAIL中专家样本带有技能标签, 算法将Triple-GAN算法扩展, 增加辅助选择器, 与Triple-GAN增加通过半监督方法训练的分类器不同, Triple-GAIL中选择器具有重要作用, 不只用于区分技能标签, 还可以根据当前状态自动生成技能标签, 实现同时学习选择标签和重建多模态策略的功能.

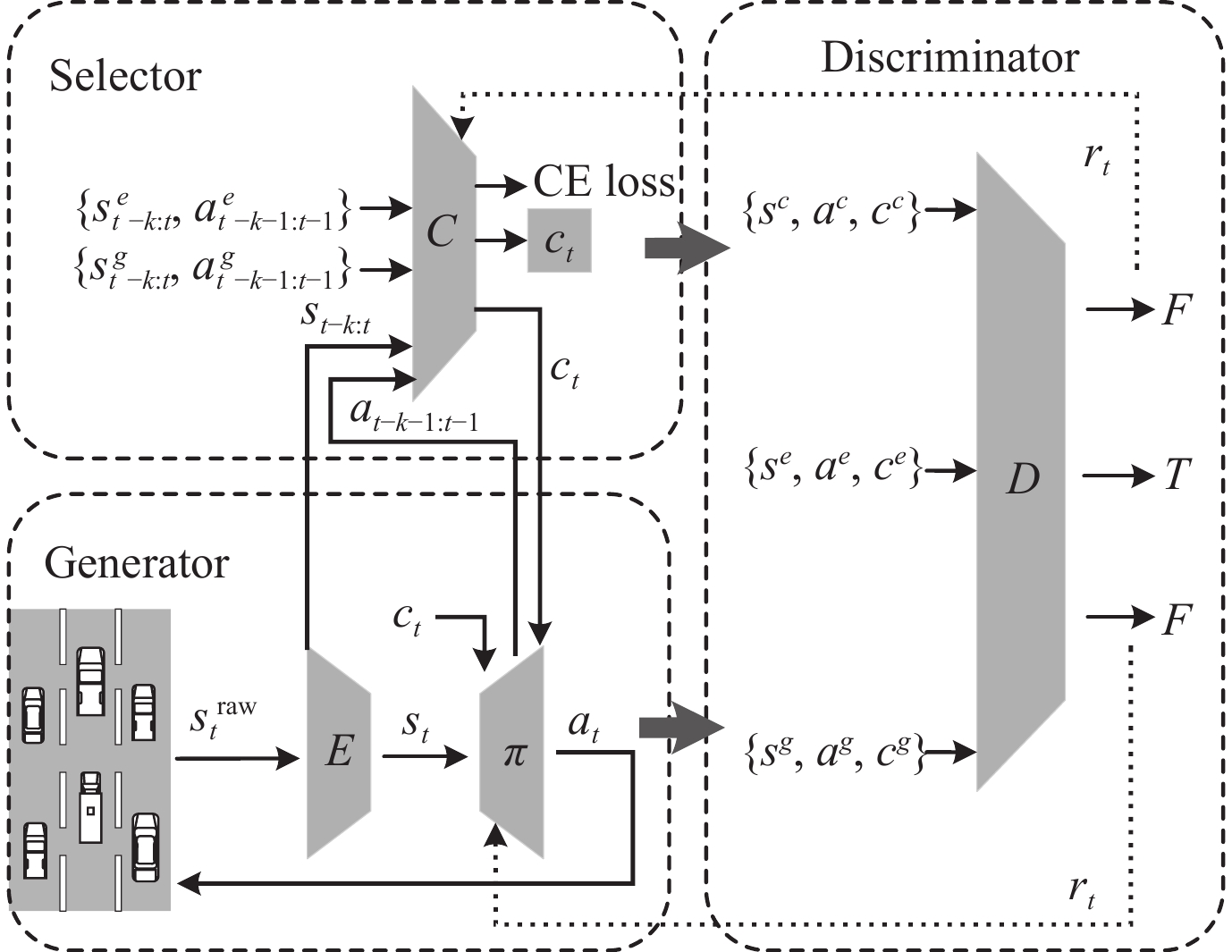
如图3所示, Triple-GAIL模型由3部分组成: 选择器、生成器和判别器. 选择器输入为专家样本 $\{ s_t^e, a_t^e\} $ 和生成器样本 $\{ s_t^g, a_t^g\} $ , 输出为技能标签 ${c_t}$ , 生成器基于算法训练设定技能和当前状态选择动作, 判别器判断当前状态-动作-标签样本是否来自属于特定模态的专家样本. 无论专家示范样本中是否有状态-动作-标签样本, 选择器和基于条件分布的生成器都可以输出状态-动作对和状态-标签对.

基于标签的监督学习方法通过在已知分布的专家样本中随机采样学习模态变量, 一旦训练完成, 模型输出动作与人工设定的标签一一对应. 而Triple-GAIL算法可以根据环境逐步学习技能.

Triple-GAIL的目标函数如公式(16)所示.

$ \mathop {\max }\limits_{\alpha , \theta } \mathop {\min }\limits_\omega {\mathbb{E}_{{\pi _E}}}[\log (1 - {D_\omega }(s, a, c))] + \gamma {\mathbb{E}_{{\pi _\theta }}}[\log {D_\omega }(s, a, c)] \; + (1 - \gamma ){\mathbb{E}_{{C_\alpha }}}[\log {D_\omega }(s, a, c)] + {\lambda _E}{R_E} + {\lambda _G}{R_G} - {\lambda _H}H({\pi _\theta }) \\ $

(16)

其中, $\alpha $ 、 $\theta $ 和 $\omega $ 分别为选择器、生成器和判别器的参数, ${R_E} = {\mathbb{E}_{\pi E}}[ - \log {p_{{c_\alpha }}}(c|s, a)]$ , ${R_E}$ 表示确保选择器收敛到专家样本轨迹概率分布的监督学习损失, ${R_G} = {\mathbb{E}_{\pi_\theta }}[ - \log {p_{{c_\alpha }}}(c|s, a)]$ , ${R_G}$ 表示选择器条件概率分布 ${p_{{c_\alpha }}}(c|s, a)$ 与生成器条件概率分布 ${p_{{\pi _\theta }}}(c|s, a)$ 之间的散度.

3.2.4.4 生成对抗模仿学习中的不稳定问题

目前, 前沿的逆向强化学习算法大多基于对抗模仿学习算法(adversarial imitation learning). 在这类算法中, 生成器和判别器以对抗博弈的方式交替更新, 因此, 所有对抗模仿学习算法核心是解决最大最小优化问题, 这导致算法训练不稳定、对超参数敏感和样本利用率低. Dadashi等人^[104]提出了不依赖对抗训练的基于Wasserstein距离的模仿学习算法(primal Wasserstein imitation learning, PWIL). 在实际算法中, 需要等待智能体与环境交互并生成轨迹后计算Wasserstein距离, 为解决这一问题, 作者提出利用Wasserstein距离的上限代替距离计算. 因此, 虽然PWIL算法的奖赏函数与对抗模仿学习一样不是稳定常数, 但并不通过智能体与环境交互确定, 当专家样本确定后, 奖赏函数可以通过离线方式确定. 因为避免了求解最大最小优化问题, 相比对抗模仿学习算法, PWIL算法具有较高的稳定性和样本利用率. 另外, PWIL算法构建了智能体策略与专家策略之间距离的度量方法, 且无需提供环境的真实奖赏函数, 因此, 其可以用于真实环境中的训练效果评测.

3.2.5 引导代价学习方法

逆向强化学习算法可以解决高维任务中的模仿学习问题, 但由于最优示范样本通常难以获得和高维任务的复杂性, 存在策略模型容易陷入局部最优的问题. 此外, 算法为提升自身策略性能, 需要进行大量试错, 导致收敛速度慢, 环境样本利用率低.

解决以上问题的一个方法是建立近似模型^[105], 利用模型引导算法在状态空间中探索, 环境的近似模型可以人为建立, 也可以通过已知数据建立. 引导策略搜索(guided policy search, GPS)算法利用差分动态规划方法(differential dynamic programming, DDP)生成合适的引导样本(guiding samples), 引导样本指导算法在高回报区域搜索, 同时避免陷入局部最优. GPS算法通过正则化的重要性采样利用引导样本进行策略搜索.

该算法主要应用于通过专家样本学习最优策略的机器人控制领域^[9]. 实现过程分为两步: 第1步, 根据专家样本的最优路径概率分布求解代价函数; 第2步, 根据代价函数求解其对应最优路径的概率分布.

(1) 根据最优路径概率分布求解代价函数

首先假设示范样本是专家在奖赏函数不确定的环境中采取最优策略生成的样本, 且依据最大熵模型, 示范样本中的路径 ${\tau _i}$ 满足如下分布.

$ \left\{\begin{aligned} & p(\tau ) = \frac{1}{Z}\exp ( - {c_\omega }(\tau )) \\ & Z = \int {\exp \left( { - {c_\omega }({\tau _j})} \right)d\tau } \\ \end{aligned}\right. $

(17)

其中, $\tau = {s_1}, {a_1}, \ldots, {s_T}, {a_T}$ 表示单个路径样本, ${s_t}$ 和 ${a_t}$ 分别是在时间 $t$ 的状态和动作, ${c_\omega }(\tau ) =\displaystyle \sum\nolimits_t {{c_\omega }(\tau )} $ 为由参数 $\omega $ 组成且未知的代价函数, $p\left( \tau \right)$ 为路径 $\tau $ 发生的概率.

公式(17)的含义为根据最大熵模型, 当知道环境的代价函数时, 其基于最优策略的路径分布可通过公式(17)求出, 显然当前代价函数产生的路径分布与示范样本路径分布越接近代价函数越好. 当示范样本给定, 可通过求似然估计函数的最大值确定最优代价函数.

抽样概率分布 $q(\tau )$ 是基于抽样的IOC (inverse optimal control)算法成功的关键. 预测 $Z = \int {\exp ( - {c_\omega }(\tau ))}d\tau $ 的最优分布为 $q(\tau ) \propto {\text{exp}}( - {c_\omega }(\tau ))$ , 因此在代价函数未知的情况下确定分布 $q(\tau )$ 是十分困难的. 可以通过迭代的方式逐步完善 $q(\tau )$ 的分布, 选取当前代价函数下的最优路径和示范样本共同组成 $q(\tau )$ 分布, 首先在当前路径分布 $q(\tau )$ 下根据最大似然原理优化代价函数 ${c_\omega }$ , 然后根据当前代价函数优化路径分布 $q(\tau )$ . 因为该算法是基于抽样方法实现, 所以可以用于无模型环境.

(2) 根据代价函数求最优路径概率分布

在单次迭代过程中代价函数 ${c_\omega }(\tau )$ 已知, 目标是尽可能准确表达当前代价函数下最优策略所产生路径的高斯分布. 为使该算法应用于无模型环境中, 可通过 $\hat q(\tau )$ 采样所得路径分布 ${D_{\rm traj}}$ 建立环境的局部模型, 但这会导致当搜索区域距离当前样本过远时误差变大, 可添加约束缓解该问题.

$\left\{ \begin{aligned} & \mathop {\min }\limits_{\omega , q(\tau )} {\mathbb{E}_q}[{c_\omega }(\tau )]\quad \\ & {\text{s}}{\text{.t}}{\text{.}}\;\; {D_{KL}}(q({u_t}|{x_t})\parallel \hat q({u_t}|{x_t})) < \varepsilon \\ \end{aligned} \right.$

(18)

其中, $\hat q(\tau )$ 为上一次迭代过程中的路径概率分布.

采用拉格朗日乘子法可将公式(18)有约束问题变为无约束问题:

$ {L_{\rm traj}}(q(\tau ), \eta ) = {\mathbb{E}_q}[{c_\omega }(\tau )] + \eta ({D_{KL}}(q\parallel \hat q) - \varepsilon ) $

(19)

3.2.6 对比分析

基于线性奖赏函数的传统逆向强化学习方法致力于以更好地算法选择奖赏函数和衡量奖赏函数的准确性. 但是, 线性奖赏函数算法存在表征能力有限, 状态特征需要人工设定的问题. 因此, 本节算法提出使用高斯过程或神经网络近似复杂、非线性奖赏函数, 取得了很好的效果.

3.2.6.1 具体分析

Levine等人^[87]用高斯过程表示奖赏函数. 然而该算法需要大量的专家样本和实验奖赏样本才能完成奖赏函数的训练^[106], 且算法仍然需要状态的特征作为输入.

相比传统逆向强化学习算法, 基于最大熵的深度逆向强化学习算法可以表示更复杂的奖赏函数, 不需要人工设计状态特征, 该算法在行人导航中进行了实验验证. 但同时, 该算法仍局限于解决格子世界环境中本质为离散状态空间问题的路径规划任务, 并未测试算法在连续状态空间问题中的性能.

基于逻辑回归的逆向强化学习算法用二分类逻辑回归方法解决了IRL过程, 并且不需要完全求解正向强化学习过程. IRL过程中求出了奖赏函数和状态值函数, 相比之前的算法, 状态值函数大大加快了收敛过程, 因为在正向强化学习过程中dueling network可以直接利用状态值函数的信息初始化自己的参数. 另外, 因为输入样本不包含动作信息, 所以算法可用于连续动作问题, 但需将DQN算法换为TRPO算法.

生成对抗模仿学习方法为具有复杂内部关联结构的高维数据分布建模提供了一种很有发展前景的方法, 本质上是一种监督学习方法, 因为其考虑数据之间的关系, 使得算法具有很好的泛化性, 现已成为逆向强化学习领域的经典算法. 但也存在以下两个问题.

(1) 训练不稳定问题

生成器和判别器的训练是零和博弈问题, 需要控制判别器强度. 若判别器明显比生成器强, 会导致生成器改进梯度变小, 同样若判别器比生成器弱, 也不利于生成器改进.

生成器面临梯度消失问题, 因为当判别器远比生成器性能好时, 判别器相当于Sigmoid函数, 中间陡峭, 两边分别无限接近于0和1, 且斜率接近于0. 此时判别器保持稳定, 输入样本处于Sigmoid函数的左右两部分, 即使输入样本存在扰动也可以准确区分. 但这也带来一个问题, 因为Sigmoid函数左右两个部分的斜率接近于零, 会使得生成器改进梯度消失.

(2) 模态崩塌问题

针对模态崩塌问题, 按照专家样本中模态标签是否确定, 目前的改进方法可分为无监督学习方法和监督学习方法. InfoGAIL通过最大化模态隐变量和观测状态-动作对的互信息模仿专家策略. VAE-GAIL^[102]引入变分自编码器推断模态变量. 以上算法可以从无标签专家样本中学习, 但是因为缺少标签信息, 这些算法只能推断隐含的标签信息, 而缺乏对文本和具体任务的分析.

CGAIL^[11]将标签信息直接输入生成器和判别器, 求解关于标签的策略和奖赏函数. ACGAIL^[100]在生成对抗模型中增加了辅助分类器, 而判别器的任务只是判定样本是否来自专家样本, 在ACGAIL中, 分类器与判别器共享参数, 两者共同向生成器提供对抗损失.

Triple-GAIL中的专家样本由多个专家生成, 且带有技能标签. 与上文提到的算法不同, Triple-GAIL算法可以根据当前状态自动选择技能标签, 先人工确定模态, 然后重新建立多模态策略.

PWIL算法利用Wasserstein距离以离线方式确定奖赏函数, 将IRL算法缩减为一个强化学习过程, 极大提高了算法稳定性和样本利用率.

引导代价学习算法致力于解决现实问题中的高维复杂问题, 并在2D导航模拟器和现实机械臂环境中实验. 另外, 因为算法基于抽样方法实现, 所以可用于无模型环境.

3.2.6.2 仍然存在的共同问题

(1) 需要大量计算资源和专家样本

逆向强化学习是一个在若干约束条件中搜索奖赏函数的过程, 影响算法求解难度的主要因素为单次迭代复杂度和问题本身复杂度. 对于问题本身来说, 若最优问题为凸函数, 则求解速度呈线性. 反之, 若最优函数不为凸函数, 则需要重点分析单次迭代复杂度, 单次迭代过程为通过当前奖赏函数求解最优策略的强化学习过程. 另外, 非线性逆向强化学习方法用于解决高维复杂问题, 相比于线性问题状态-动作空间指数增加. 同时, 非线性奖赏函数所表示函数集合空间也很大. 这要求专家示范更多的样本满足需求^[107].

(2) 样本利用率低

逆向强化学习算法每次迭代更新奖赏函数都需要进行一次强化学习过程, 计算基于当前奖赏函数的最优策略, 因此逆向强化学习算法与环境交互次数远多于强化学习算法. 当算法为采用随机策略的无模型算法时, 这一问题更加严重^[49]. 当算法在模拟环境中实验时, 这一缺点并不明显, 但在机器人控制领域, 机械手臂需要与环境交互, 导致采样代价较高. 由于逆向强化学习方法存在生成样本利用效率低的问题, 该方法很难应用在这些领域.

目前, 结构化分类方法和基于逻辑回归的逆向强化学习算法引入监督学习思想, 通过减少强化学习过程的方法, 减少了与环境的交互次数. 引导代价学习算法利用差分动态规划建立模型, 生成训练样本, 既可以引导策略, 又可以提高样本利用率. 同样, PWIL和SQIL算法^[108]将IRL算法缩减为强化学习过程, 提高了算法稳定性和样本利用率.

4 示范样本非最优逆向强化学习

逆向强化学习方法假设专家样本由最优策略产生, 限制了该方法的应用. 在一些任务中, 因为环境的危险性或采样成本高昂无法产生足够数量的专家样本, 只能以非最优样本辅助算法学习. 或者, 因为专家策略的不稳定和泛化性差, 导致专家样本中含有非最优样本.

为解决这类问题, Brown等人^[52]提出了基于路径排序的奖赏函数推测算法(trajectory-ranked reward extrapolation, T-REX). 算法首先将专家样本按从差到优排序, 如公式(20)所示.

$ {\tau _{\text{1}}} \prec {\tau _{\text{2}}} \prec \ldots \prec {\tau _T} $

(20)

算法通过深度神经网络表示奖赏函数, 路径之间的距离通过交叉熵表示, 并将交叉熵通过Softmax函数归一化, 表示一个路径比另一个路径好的概率. 如公式(21)所示.

$ P(\hat J({\tau _i}) < \hat J({\tau _j})) \approx \frac{{\exp \displaystyle\sum\limits_{s \in {\tau _j}} {\hat r(s)} }}{{\exp \displaystyle\sum\limits_{s \in {\tau _i}} {\hat r(s)} + \exp \displaystyle\sum\limits_{s \in {\tau _j}} {\hat r(s)} }} $

(21)

将算法应用于基于观察的MuJoCo实验和雅达利游戏, 实验证明, 算法性能比传统算法好一个数量级. 另外, 也有一些强化学习算法, 利用不是最优的示范样本辅助算法学习. 例如, Gao等人^[53]提出NAC (normalized actor-critic)算法, 利用SAC (soft actor-critic)模型^[51]实现了算法从差样本中学习.

完全最优的专家样本通常很难获取, 而衡量专家样本的置信度得分(confidence scores)比获取最优专家样本容易. 因此Wu等人^[109]提出2IWIL (two-step importance weighting imitation learning)算法和IC-GAIL (generative adversarial IL with imperfect demonstration and confidence)算法用于解决非最优专家样本问题, 该算法假设专家样本中存在非最优样本, 且部分样本具有置信度得分, 其中置信度得分表示该策略为最优策略的概率, 同时算法允许专家样本由不同专家生成. 2IWIL算法首先通过带有置信度得分标签的数据训练概率分类器, 然后预测未带标签数据的置信度得分, 将所有专家样本的置信度得分标签补全, 并以此训练最优策略. 由于2IWIL算法可能存在错误累加问题, IC-GAIL算法继续采用GAIL算法中的占用率度量(occupancy measure)思想, 将算法收敛目标设置为最小化当前策略与专家策略的占用率度量分布散度.

在逆向强化学习算法的许多应用领域, 算法不仅可以获取接近最优的专家策略, 还可以观测专家的学习过程. 专家学习过程所生成的样本虽然不由最优策略生成, 但也包含有价值的信息, 例如: 在智能体学习环路驾驶问题中, 通过观察专家训练, 智能体能够区分有益状态和有害状态, 这可以帮助智能体在以非最优策略访问状态空间时, 优化算法策略, 提升算法稳定性.

Jacq等人^[110]对这类问题归纳总结, 提出了从学习者中学习问题(learning from learner, LfL). LfL问题包含两个智能体: 学习者(learner)和观察者(observer), 其中观察者可以获得学习者在学习过程中产生的轨迹, LfL问题的两个假设如下: (1)学习者的策略基于环境奖赏函数; (2)学习者通过与环境交互获得奖赏改进自身策略. 为解决LfL问题, Jacq等人假设学习者用基于熵正则化的强化学习算法学习, 当奖赏函数只与状态-动作对相关时, 算法虽无法求解真实奖赏函数, 但可以解得与真实奖赏函数等效的奖赏函数. 若问题简化, 当奖赏函数只与状态有关时, 算法可以解得真实奖赏函数. 总结来说, Jacq等人提出了逆向强化学习中的新问题, 并给出了求解算法, 这类问题有助于我们研究如何使观测者超越学习者. 然而, 该算法并未完全解决LfL问题, 算法假设学习者的策略为单调改进的策略, 且需要提供环境中状态转移概率.

在之前的从学习者中学习算法中, 学习者通过强化学习算法学习最优策略, 而算法要求学习者所生成样本轨迹的策略性能单调递增, 这在强化学习算法中很难被保证. 为解决这一问题, Ramponi等人^[111]提出了基于梯度的从非专家学习者中学习的算法(learning observing a gradient not-expert learner, LOGEL). LOGEL算法假设观测者可以获得学习者的策略参数、策略迭代的学习率和轨迹样本. 另外, 因为即使是基于值迭代的传统Q-learning算法也与策略梯度算法紧密相关, 所以LOGEL算法假设学习者通过梯度下降方法更新策略. 算法中观测者以求解最能解释学习者策略迭代原因的奖赏函数为目标. 具体实现为: 在每次迭代中, LOGEL算法所求解的最优奖赏函数应尽可能缩小学习者的策略参数与依据当前奖赏所求策略参数之间的欧氏距离. 算法在离散状态-动作空间的格子世界和连续状态-动作空间的MuJoCo环境中取得了一定的效果, 但由于需要学习者的策略参数和梯度, 导致算法难以应用于实际任务中.

目前, 专家样本非最优问题存在以下两个特点: (1)专家无法以最佳方式完成任务, 导致样本中含有非最优样本; (2)由于环境的危险性导致专家样本少且泛化性差. 针对以上两点, 目前算法从两个方向提出解决方法: (1)提供额外辅助信息(表示样本优劣的标签). 此类方法利用专家样本中的辅助信息进行奖赏函数优化或求解最优策略. (2)推测专家目标. 此类算法用于解决最优样本稀少的问题, 为了求解最优策略, 算法通过失败样本辅助成功样本学习, 虽然失败样本没有完成任务, 但至少包含两点信息: 哪些动作不符合最优策略和哪些动作可以采取(即使其不是最优动作). 因此, 可通过观测学习过程, 理解专家意图, 进而优化奖赏函数和当前策略.

与传统的假设专家样本全为最优样本组成的逆向强化学习算法相比, 基于示范样本非最优的逆向强化学习算法具有更广的应用范围. 引入专家样本中辅助信息和通过次优样本预测专家意图, 以学习环境信息, 二者相辅相成, 保证算法准确优化奖赏函数, 学习最优策略. 另外, 逆向强化学习算法通常通过特征期望的匹配程度衡量奖赏函数的优劣, 因此传统算法难以应用到示范样本非最优问题. 目前针对这一问题的研究仍处于初始阶段, 在如何利用非最优样本提升特征期望的匹配程度方面仍考虑较少. 此外, 专家更愿意以多种方式表达他们的意图和偏好, 而不仅通过专家样本, 此类问题仍有待研究.

5 指导逆向强化学习

逆向强化学习算法假设示范样本独立同分布, 因此在训练过程中, 算法通常随机选择示范样本. 而在人类教学过程中, 并不随机抽取示范样本, 其会潜在地多次选择相似样本或选择具有对比性的样本. 基于这一思想, 研究者思考如何建立最优示范样本序列, 或提供信息量最高的示范样本集合.

Odom等人^[54]借鉴主动学习思想提出基于逆向强化学习算法的主动搜寻建议算法. 主动学习(active learning或query learning)已广泛应用于监督学习领域, 算法优化目标为寻找一批数量少但具有代表性的专家示范样本, 以更好地提升算法性能. 主动学习算法寻找最大信息量集合的标准为筛选信息量最大的状态集合(通常用熵或其他不确定性度量方法). 与监督学习类似, 逆向强化学习算法也通过专家样本学习最优策略, 因此, 作者将主动学习应用于逆向强化学习领域, 但仍有一些问题需要解决. 逆向强化学习中状态到动作映射的概率分布即为智能体所需从专家样本中获取的信息, 主动学习算法希望专家样本集合中包含尽可能多的此类信息, 这一信息既与奖赏函数有关也与最优策略有关. 但是, 因为逆向强化学习问题中一个最优策略可由多个奖赏函数确定, 所以此类信息与奖赏函数的相关性和与最优策略的相关性并不等价. 为解决这一问题, 作者将两种相关性的加权求和作为动作关于状态分布的不确定性标准. 算法在每一次迭代后, 返回最希望专家样本提供的状态集合, 并以此指导智能体学习奖赏函数. 算法首次引入主动学习思想, 研究了逆向强化学习中如何利用专家示范样本指导智能体学习的问题, 具有一定开创性.

Brown等人^[55]引入机器教学(machine teaching)算法用以提高智能体从专家样本中的学习效率和性能. 机器教学算法的优化目标为: 选择具有最小教学代价的样本集合进行训练, 决定教学代价的两个指标为训练样本数量和教学风险. 算法依据机器教学理论定义逆向强化学习问题. 首先定义损失函数如公式(22)所示.

$ {{Loss(}}{\omega ^*}{\text{, }}\hat \omega {\text{) = }}{\omega ^*}^{\text{T}}\left[ {\mathbb{E}\left( {\sum\limits_{t = 0}^\infty {{\gamma ^t}\phi ({s_t})} |{\pi ^*}} \right)} \right. - \left. {\mathbb{E}\left( {\sum\limits_{t = 0}^\infty {{\gamma ^t}\phi ({s_t})} |\hat \pi } \right)} \right] $

(22)

其中, ${\omega ^ * }$ 为真实奖赏函数系数, $\hat \omega $ 为当前奖赏函数系数, ${\pi ^ * }$ 为最优策略, $\hat \pi $ 为当前策略, $\phi \, (s)$ 为状态 $s$ 的特征向量. 损失函数表示当前策略和最优策略在真实奖赏函数中的奖赏差值.

机器教学在逆向强化学习问题中的定义为:

$\left\{ \begin{aligned} & \mathop {\min }\limits_D \;\;{\mathrm{ TeachingCost}}(D) \\ & {\text{s.t.}}\;\;{Loss(\omega ^*}, \hat \omega ) \leqslant \varepsilon,\;\hat \omega { = \mathrm{IRL}(}D{{)}} \end{aligned}\right. $

(23)

其中, D为专家示范样本集合, 问题目标为该线性规划的最优解.

本文用机器指导方法解决逆向强化学习中如何利用专家示范样本指导智能体学习的问题, 具有一定创新性, 但公式(23)线性规划问题需提供真实奖赏函数. 因此作者将主动学习方法与机器指导方法结合, 利用贝叶斯方法估计状态集合信息, 但局限于解决离散状态空间问题.

Haug等人^[56]利用机器指导方法解决专家特征空间与学习者特征空间不匹配问题, 通过引入教学风险(teaching risk)指标, 衡量当前所学策略为专家次优策略的程度. 实验证明, 当教学风险较小时, 即使学习者策略与专家策略之间存在特征空间不匹配问题, 也可以训练逼近最优策略. 基于这一发现, Haug等人提出TR-Greedy算法(feature and demo based teaching with TR-greedy feature selection), 通过专家不断提高学习者的特征空间, 逐渐减小教学风险. 作者将TR-Greedy算法在格子世界问题中实验, 并与其他选择特征空间的方法比较, 验证了算法的有效性, 但该算法并不能用于解决连续空间问题.

与TR-Greedy算法用于解决特征不匹配问题不同, Kamalaruban等人^[57]从教学者视角出发, 提出了一种应用更广泛的交互式教学算法, 以提升学习者策略性能. 算法将问题分为两类: (1)假设教学者拥有全局视野, 可以观测学习者的当前策略; (2)假设教学者不知道学习者的动态环境, 只能观察到学习者带有噪音的当前策略. 基于这两类问题, 作者将之前算法中专家策略到学习者策略的教学简化为参数教学. 作者引入软贝尔曼策略(soft Bellman policies), 通过MCE-IRL^[60]方法更新奖赏函数梯度, 并借鉴机器教学思想^{[58, 59]}提供专家示范样本, 原则为尽可能缩小学习者与教学者之间的奖赏函数参数. 作者在基于离散空间的汽车驾驶模拟环境中进行实验, 验证了算法的有效性, 但仍然缺乏对连续空间问题的研究.

本节介绍了通过建立最优示范样本序列, 或提供信息量最高的示范样本集合进行策略优化的指导逆向强化学习算法. 这类算法主要通过两种方法提供最能协助智能体学习最优策略的信息: 基于主动学习的方法和基于粗糙奖赏函数的方法. 两种方法目标一致, 但实现方式不同. 基于主动学习的方法在每次迭代中, 通过筛选信息量最大的专家样本集合优化当前策略. 而基于粗糙奖赏函数的方法通过引入额外指标筛选信息量最大的专家样本集合.

与传统逆向强化学习算法相比, 指导逆向强化学习算法具有更好的鲁棒性、更快的收敛速度和更高的样本利用率. 但现有的指导学习方法多集中在与监督学习方法结合的初级阶段, 依然存在许多问题. 由于基于主动学习的方法需要不断与专家交互, 极大增加了人力成本. 而基于粗糙奖赏函数的方法需要人工设计奖赏函数, 这在复杂问题中难以被满足. 另外, 现有的指导逆向强化学习算法只能适用于离散空间问题或低维状态-动作空间问题中, 在连续高维状态-动作空间问题中的应用仍有待研究.

6 状态动作信息不完全逆向强化学习

状态或动作信息不完全问题指: 智能体对状态-动作-下一状态序列只有非完全的观测. 包括部分可观察逆向强化学习问题、观察模仿学习(imitation learning from observation, IfO)问题和基于状态信息的逆向强化学习问题.

6.1 部分可观察逆向强化学习

部分可观察逆向强化学习问题表示, 在马尔可夫决策过程(partially observable Markov decision process, POMDP)中, 难以观测状态的完整信息, 或者观测与状态之间满足一定函数关系. 在POMDP问题中, 智能体在时间步t, 只能获得观测 ${o_t} = o({s_t})$ , 其中 $o:{s_t} \to {o_t}$ 是一个固定观测函数. IRL算法可用于解决POMDP问题^[112], 并且在图像识别^[73]和机器人控制^[113]等领域取得了一定进展.

在图像识别领域, 有时传感器输入的图像带有噪声, 识别这些图像即为部分可观察问题. Kitani等人^[73]引入基于最大熵的逆向强化学习思想, 通过隐变量马尔可夫决策过程(hidden variable Markov decision process)建模, 求解观测状态概率分布熵值的最大值. 在机器人领域, 物体之间的欧几里得距离较为容易获取, 因此Boularias等人^[113]引入马尔可夫随机场模型(Markov random fields), 通过关键物体之间距离判断状态是否相似, 在相似状态采取相同动作, 并将算法成功应用在导航和抓取任务中, 但该算法计算量较大.

6.2 观察模仿学习

在一些问题中, 模仿者只能获取专家生成的状态信息, 无法获取动作信息, 例如: 从视频中学习. 因此, IfO算法是一种只通过状态信息进行学习的模仿学习算法. 目前IfO问题的研究方向可分为: 视频感知和动作控制. 随着卷积神经网络和视觉识别技术的提升, 视频感知方向可以实现直接从专家视频资源中学习, 但仍然存在示学体不匹配(embodiment mismatch)和观察视角不同(viewpoint difference)的问题^[114].

动作控制方向的研究可分为基于模型方法和无模型方法两个分支. 基于模型方法将学习模型分为逆向动态模型(inverse dynamic model)和前向动态模型(forward dynamic model). 逆向动态模型以当前状态和下一状态为输入, 输出为当前状态的动作^[115], 即为求解当前状态-动作对关于当前状态和下一状态的条件概率分布. 前向动态模型的输入为状态-动作对, 输出为下一状态, Edwards等人^[116]基于这一模型提出观察模仿隐策略(imitation latent policies from observation, ILPO)算法, 该算法可用于离线(off-line)学习专家策略.

无模型方法分为两类: 奖赏函数设计方法和对抗方法. 奖赏函数设计方法依据专家示范样本设计奖赏函数, 通过强化学习算法进行训练. IfD (imitation learning from demonstration)表示通过包含状态-动作信息的专家样本学习专家策略的模仿学习算法. 其中, GAIL算法通过最小化当前策略与专家策略之间状态-动作对度量分布的KL散度^[117], 在模仿学习任务中取得优异性能, 现已成为IfD领域的代表算法. 基于对抗方法的IfO算法采用生成对抗模仿学习框架, 通过状态到状态的信息, 推断最优策略. 为最小化当前策略与专家策略之间状态-下一状态对度量分布的KL散度, Yang等人^[118]提出IDDM (inverse dynamics disagreement minimization)算法, 在传统IfO方法的基础上缩小IfO与IfD的差距(推断隐藏在状态迁移中的动作信息). 并在GAIL框架下, 证明了IfO和IfD之间存在由因果熵表示的差距IDD (inverse dynamics disagreement), 且差距的上界可在model-free下减小, 但IDDM算法只能用于确定性环境.

6.3 基于状态信息的逆向强化学习算法

在逆向强化学习算法中, 通常假设模仿者与专家之间的物理结构和应用环境相同, 然而在一部分实际问题中, 这一假设难以被满足, 例如: 在迷宫中, 专家策略可以快速通过迷宫, 而模仿专家的机器人因为物理原因或环境改变, 行驶速度相对较慢甚至难以完成任务. 因此, 模仿者与专家之间的最优策略存在差异. 但是, 专家样本中仍然具有帮助机器人走出迷宫的信息可以利用.

利用只包含目标状态信息的样本集合, Fu等人^[119]提出VICE (variational inverse control with events)算法. 与传统逆向强化学习算法通过最大化累积奖赏模仿专家策略不同, VICE算法以最大化目标状态在未来发生概率为目标. 因为只需提供目标状态信息, VICE算法极大降低了专家样本的采集难度, 提高了在实际任务中的算法性能, 但与专家交互查询信息方法的引入, 增加了算法的训练时间.

与VICE算法不同, Ibarz等人^[120]仍然通过最大化累积奖赏模仿专家策略且专家样本需提供只包含状态信息的专家轨迹, 但在训练过程中需以权重形式人工标定对产生轨迹的偏好. 通过调整奖赏函数, 最大化带偏好标记轨迹的累积奖赏. 为解决离线模仿学习中的领域自适应问题, Jiang等人^[121]提出一种通过最大化专家策略轨迹(只包含状态信息)概率模仿专家策略的算法.

为解决专家采样环境与学习者应用环境不一致问题, Liu等人^[122]抛弃专家样本中的动作信息, 只学习专家状态轨迹, 以此提出了基于状态对齐的模仿学习算法(state alignment based imitation learning, SAIL). 专家示范环境与实际学习环境之间的差别会导致智能体与专家在相同状态所采取动作不同, SAIL算法将之前算法要求状态-动作对相匹配的目标改为状态分布相匹配. 另外, 为使智能体学习所得轨迹与专家轨迹相匹配, SAIL算法分别从局部状态对齐和全局状态对齐两个方面进行改进, 在局部状态对齐方面: 增加了基于状态的 $\;\beta $ -VAE模型, $\;\beta $ -VAE模型用以预测下一状态, 帮助智能体返回专家样本轨迹中. 在全局状态对齐方面: 通过计算专家样本状态分布与当前策略轨迹状态分布之间的Wasserstein距离, 给出状态转移的奖赏函数, 并用PPO算法学习最优策略.

相比于BC算法和GAIL算法, SAIL算法在状态空间一致而转移函数和动作空间不一致的问题中具有更好的效果. 但是, SAIL算法需要较高的计算量, 同时也具有较低的样本利用率.

6.4 对比分析

本节介绍了基于部分可观察、从观测中学习和基于状态信息的逆向强化学习算法. 3类算法同属状态动作信息不完全逆向强化学习算法, 且各自解决的问题存在差别, 其中基于状态信息的逆向强化学习算法可用于解决观察模仿学习问题, 但观察模仿学习算法重点研究如何利用状态为图像或视频信息的任务, 基于状态信息的逆向强化学习算法侧重研究示学体不匹配和采样环境与应用环境不一致问题.

因为传感器噪声, 或者由于人、机器或环境的干扰, 在机器控制、图像处理和观测学习等领域存在非常多的部分可观察逆向强化学习问题. 但目前对这一领域的研究尚处于起步阶段, Kitani等人^[73]的算法在处理特征问题上有些复杂, Boularias等人^[113]的算法虽然可以解决简单的实际问题但计算量较大.

观察模仿学习方法用于解决的问题为视频感知和动作控制问题. 为从只包含状态信息的专家样本中学习, 目前使用的方法包括基于模型方法、生成对抗模仿学习方法和奖赏塑形方法等. 通过将以上算法与其他(如强化学习算法)方法结合, 可以进一步提升算法性能, 目前对于这一领域的研究尚有待于深入研究.

与观察模仿学习方法不同, 基于状态信息的逆向强化学习方法的输入状态不局限于视频或图片, 另外, 基于状态信息的逆向强化学习方法不仅探索如何合理利用专家状态信息, 更注重解决专家样本采样环境与应用环境不匹配或示学体不匹配问题. 目前算法也存在一些问题, 例如, 当环境发生物理改变导致最优策略与专家策略出现差异时, 只有VICE算法适用. 另外, 专家还有其他表达目标的方式, 也可作为辅助信息协助算法模仿专家策略.

7 多智能体逆向强化学习

逆向强化学习算法应用到多智能体领域仍存在许多问题亟待解决^[123]. 在多智能体模型中, 首先, 环境相对于单个智能体在不断变化, 其次, 当前智能体所采取的最优策略与其他智能体所采取策略有关, 因此可能存在多个最优策略. 针对以上问题, Waugh等人^[124]与Kuleshov等人^[125]分别对奖赏函数的设定问题进行研究, Song等人^[126]提出基于生成对抗框架的MAGAIL (multi-agent generative adversarial imitation learning)算法. Wang等人^[127]则基于零和博弈, 探讨了示范样本由次优策略生成的多智能体问题. 但该方向仍有许多问题尚未解决, 需进一步研究^[128].

Hadfield-Menell等人^[129]提出协作逆向强化学习算法(cooperative inverse reinforcement learning, CIRL), 以解决目标统一(value alignment)问题. 在实际任务中, 由于缺少奖赏函数, 工程师为让机器实现某一目标, 通常需要手工设计奖赏函数, 其中目标统一问题是工程师需要解决的核心问题. 即让智能体学习所得最优策略与工程师所期望目标一致. 因此, 作者提出了CIRL模型, 模型中两个玩家合作游戏, 分别是智能体和人, 其中, 人知道真实奖赏函数, 而智能体只知道真实奖赏函数的先验分布. 智能体通过采取动作, 不断探索如何使人所获得的奖赏最大. 虽然智能体不知道奖赏函数, 但因为其目标与人相同, 所以实际上其和人共享一个奖赏函数, 算法的目标为, 人与智能体采取联合动作, 最大化所获得的总奖赏. 因此, 这一模型鼓励人产生更好的专家样本, 同时鼓励智能体向人学习.

Wang等人^[127]为解决随机零和博弈问题中专家示范样本非最优问题, 提出一种多智能体竞争的逆向强化学习算法. 在以往多智能体逆向强化学习算法中, 通常假设专家示范样本由最优策略产生, 并基于这一假设将多智能体问题解耦. 这一假设在简单问题中尚可满足要求, 但随着问题复杂性的增加, 基于最优策略的专家示范样本越来越难以获得. 因此该算法摒弃专家示范样本最优性假设, 只要求其尽可能最优, 并引入DNN (deep neural nets)分别表示策略函数和奖赏函数. 然后, Wang等人提出了一种对抗训练算法, 用以寻找纳什均衡策略. 总体上算法分为两个部分: 策略部分, 算法基于当前奖赏函数寻找纳什均衡策略; 奖赏部分, 通过更新奖赏函数, 缩小专家策略与纳什均衡策略之间的差距.

在多智能体问题中存在多个纳什均衡, 同时对单个智能体来说环境是非稳态的, 这导致许多模仿学习算法难以应用在多智能体模仿学习领域, Yu等人^[128]提出一个通用的多智能体对抗逆向强化学习算法(multi-agent adversarial inverse reinforcement learning), 用以解决马尔可夫决策框架下的多智能体模仿学习问题. 传统单智能体逆向强化学习算法可以看作多智能体逆向强化学习算法的特殊形式, 作者从单智能体逆向强化学习算法中的经典算法GAIL出发, 构建多智能体问题中拉格朗日对偶问题, 并对每个智能体分别分配生成器和判别器. 这一算法可以用于解决高维环境中的复杂动作模仿问题, 且合作多智能体模仿任务和竞争多智能体模仿任务皆可适用.

Zhang等人^[130]从网络安全领域出发, 指出多智能体领域存在一类问题: 在两个智能体博弈过程中, 防守者不知道其所对抗入侵者的真实目的, 而且入侵者会故意隐藏其真实目的. 之前的CIRL和MA-IRL算法无法解决这类问题, 因为对于不同示范样本, 奖赏函数会随之改变. 为解决这一问题, 作者提出了非合作逆向强化学习算法(non-cooperative inverse reinforcement learning, N-CIRL). 并将问题抽象为单方信息不对称(one-side incomplete information)的零和博弈马尔可夫问题, 两个智能体具有完全不同的目标, 只有一个智能体知道真正的奖赏函数. 算法建立N-CIRL的对偶问题, 通过线性规划求解, 其中防守者只需知道入侵者的动作和下一状态信息.

在运动分析中, 准确评估运动员能力对团队战术、运动员训练和运动员交易都十分重要, 而评估运动员能力最重要的环节是评估其采取动作的正确性. 为解决这一问题, Luo等人^[131]将多智能体逆向强化学习算法应用在专业冰球运动分析中, 提出了一种基于领域知识的逆向强化学习算法(inverse reinforcement learning method with domain knowledge, IRL-DK). IRL-DK算法通过交替学习的方式训练智能体, 将单智能体逆向强化学习算法直接用于多智能体马尔可夫问题中. 假设有A和B两支队伍, 算法首先将队伍B视为队伍A所面对环境的一部分, 然后基于单智能体马尔可夫决策过程学习队伍A的奖赏函数, 队伍B的奖赏函数也采用同样的方式学习, 两支队伍交替训练直到算法收敛. IRL-DK采用最大熵逆向强化学习算法, 且在算法中增加了基于领域知识的精确稀疏奖赏, 具体实现方式为: 在逆向强化学习算法的目标函数后额外增加一项, 该项为奖赏函数与基于领域知识的奖赏函数之间的欧式距离. 因此, 最优奖赏函数的目标既包括使智能体尽可能模仿专家策略, 又包括尽可能从基于领域知识的奖赏函数中学习. 实验证明, 相比于其他算法, IRL-DK算法取得了较好的成绩, 且对运动员的评价较为准确.

逆向强化学习方法可以有效解决多智能体领域中的奖赏函数难以设定问题. 但与多智能体强化学习相同, 多智能体逆向强化学习也存在维度爆炸、策略难以收敛和不稳定等问题, 是一个十分复杂的研究方向. 目前的研究主要集中在奖赏函数求解、专家样本非最优和其他一些应用问题. 当前算法的问题主要有以下3个: (1)依然需要人工设定基于先验知识的粗糙奖赏函数; (2)从专家样本中对每个智能体的策略进行解耦训练随着任务复杂性的增加变得越来越困难; (3)随着状态-动作空间变大, 对专家样本的需求也急剧增加. 基于以上分析, 抛弃对粗糙奖赏函数的需求、提升算法鲁棒性、提高专家样本利用率和将多智能体逆向强化学习算法应用于解决复杂大状态空间的合作或竞争问题仍有待进一步研究.

8 奖赏塑形逆向强化学习

奖赏塑形是一类以学习最优策略为前提, 对奖赏函数进行修改的方法^[132], 最早应用于强化学习算法中. 因在逆向强化学习算法中, 依然需要依据专家样本求解奖赏函数, 奖赏塑形方法在逆向强化学习领域也有广泛应用. 目前研究方法分为两类: (1)辅助奖赏塑形方法. 此类方法为加快算法收敛速度、提升算法稳定性和提高样本利用率, 重塑奖赏函数, 但无法保证依据修改后的奖赏函数, 算法可收敛至专家策略, 需借助额外信息辅助算法收敛; (2)直接奖赏塑形方法. 依据此类方法中的奖赏函数, 算法可直接求解专家策略.

8.1 辅助奖赏塑形方法

鉴于奖赏重塑方法在逆向强化学习中的广泛使用, Piot等人^[133]将状态-动作对的优势函数作为奖赏, 并将此项作为目标函数中的正则项, 进行策略优化, 但算法的主要目标仍为最大化专家策略与次优策略之间的边际. 基于该奖赏函数, Metelli等人^[134]提出一种基于二阶标准的奖赏函数筛选算法, 在算法训练过程中, 将最大化累积奖赏作为优化目标, 通过筛选具有最大信息量的奖赏函数, 引导策略梯度更新, 但算法仍需借助当前策略与专家策略之间的BC损失(行为克隆损失)保证策略收敛至专家策略. Judah等人^[135]将奖赏重塑方法应用于自动驾驶问题中, 通过重塑后的奖赏函数判断当前驾驶策略是否最优, 并提出一种新的拉格朗日优化函数求解专家策略.

Jena等人^[136]提出基于生成对抗模仿学习框架的A-GAIL (augmenting GAIL)算法, 算法的奖赏函数为 $r(s, a) = - \log (1 - D(s, a))$ , A-GAIL算法提出一种新的基于优势函数的BC损失函数, 提升了算法的样本利用率. Brantley等人^[137]提出DRIL (disagreement-regularized imitation learning)算法, 将逆向强化学习算法中奖赏函数和策略的交替更新过程缩减为一个只优化策略的过程, 以提高算法的采样效率. 首先算法通过专家样本预训练奖赏函数, 然后直接利用强化学习算法学习最优策略, 但算法依然需要借助BC损失. 基于BC损失, Reddy等人^[108]同样提出将逆向强化学习算法缩减为一个只优化策略过程的算法SQIL (soft Q imitation learning). SQIL算法直接规定专家样本的奖赏为1, 非专家样本的奖赏为0, 并通过SAC算法学习最优策略.

8.2 直接奖赏塑形方法

Finn等人^[138]将能量模型(energy based model, EBM)与GAN结合提出了一种与GAIL算法等价的GAN-GCL (generative adversarial network guided cost learning)算法. GAN-GCL算法使用EBM替代GAIL中的判别器, EBM的目标为求解区分专家策略与当前策略的能量方程, 生成器的目标为最小化当前样本与专家样本之间的能量差. 为提升奖赏函数的稳定性, Fu等人^[139]提出一种基于生成对抗模仿学习框架的AIRL (adversarial inverse reinforcement learning)算法, 其中判别器由优势函数的指数形式和策略概率组成. 在基于生成对抗模仿学习框架的算法中, 专家样本中吸收状态(轨迹结束状态)的奖赏为0, 这导致算法容易陷入局部最优. Kostrikov等人^[140]在提出的DAC算法中, 规定吸收状态的奖赏需增加一个额外奖赏, 并对所有轨迹的吸收状态进行专门训练, 使用异策略强化学习算法学习最优策略, 大大提高了算法的样本利用率. Ghasemipour等人^[141]在AIRL算法的基础上, 结合f-MAX算法^[141]提出FAIRL算法, 证明了最大化基于重塑奖赏函数的累计奖赏等价于最小化当前策略与专家策略之间占用率度量概率分布的KL散度. 为提升奖赏函数的稳定性, AIRL算法需额外引入一个只与状态有关的重塑奖赏函数, 并进行训练. 而在Ni等人^[142]提出的f-IRL算法中, 重塑奖赏函数可被直接求得. 与f-IRL算法相同, f-GAIL算法^[143]同样使用f-散度模仿专家策略, 但f-GAIL算法基于生成对抗模仿学习框架, 提升了算法的样本利用率. 此外, Balakrishnan等人^[144]利用贝叶斯优化算法, 通过高斯过程后验模型求解奖赏函数, 可以求得最优奖赏函数的集合.

Liu等人^[145]为解决IRL方法中奖赏函数求解成本高且算法训练不稳定问题, 采用能量模型对专家样本分布进行建模, 将IRL方法中更新奖赏函数和策略的迭代过程缩减为两步: (1)通过能量模型学习奖赏函数; (2)基于奖赏函数, 使用强化学习算法学习最优策略. 提高了算法的稳定性和样本利用率.

8.3 对比分析

在辅助奖赏塑形方法中, 重塑的奖赏函数通常为一个包含先验知识的简单函数, 提供当前状态-动作对在短期内的回报预测. 然而, 直接通过重塑奖赏函数进行策略学习, 很难得到具有专家策略性能的最优策略. 因此, 在算法训练过程中, 辅助奖赏塑形方法需要额外信息辅助学习, 通常使用BC损失. 但由于专家样本数量限制, 使用BC损失容易产生过拟合问题, 导致算法性能变差. 如何更有效地引导算法模仿专家策略, 提供更具泛化性的动作选择信息还有待研究.

在直接奖赏塑形方法中, 若使用奖赏函数 $r(s, a) = - \log (1 - D(s, a))$ , 算法容易陷入专家样本中的环路轨迹中, 并且在专家轨迹的吸收状态, 奖赏为0. 若使用奖赏函数 $r(s, a) = \log (D(s, a))$ , 由于奖赏函数提供的所有奖赏为负数, 导致算法学习速度变慢且训练过程容易失败. 目前的直接奖赏塑形方法主要从提升奖赏函数的准确性和提出新的目标函数缩小当前策略与专家策略的距离两个方向入手, 但都缺乏对奖赏函数收敛至最优策略和如何配合算法进行优化的理论分析和证明. 另外, 由于奖赏塑形方法可以灵活调节奖赏函数, 因此其可应用于解决状态动作信息不完全问题和高维状态-动作空间问题.

9 离线逆向强化学习

不同于目前逆向强化学习方法需要与真实或虚拟环境交互. 离线逆向强化学习方法从给定的专家样本中推断奖赏函数, 不再与虚拟环境或真实环境交互, 且不再从专家策略获取任何额外信息. 离线逆向强化学习方法用以解决难以建立准确模拟环境或从环境中获取样本的成本较高(但已采集到较为丰富样本用以离线训练)的一类问题. 这类问题普遍存在, 如健康护理、金融投资、教育和工业生产等. 目前离线逆向强化学习算法主要分为两类: 优化利用专家样本信息和解决领域自适应(domain adaptation)问题.

9.1 优化利用专家样本信息

Lee等人^[146]提出DSFN (deep successor feature network)算法, 依据学徒学习算法中所提出的定理优化当前策略, 使得当前策略中状态-动作对的特征期望逼近专家样本中的状态-动作对的特征期望, 其中, 状态-动作对的特征由编码器生成. 另外, 算法提出TRIL (transition regularized imitation learning)模型, 用以保证算法的轨迹不偏离专家样本状态-动作空间. 虽然DSFN算法在临床虚拟实验中取得了较好的效果, 但其需要较多的专家样本, 而在实际任务中收集的专家样本往往由不同水平的策略生成. 直接从既包含好样本也包含差样本的混合样本中学习, 会导致算法只能学习到性能一般的策略. 若只从好样本中学习, 但好样本数量不足以训练稳定的智能体. Liu等人^[147]提出COIL (curriculum offline imitation learning)算法, 依次从学习样本中抽样不同批次的训练样本, 因为抽样样本的大小不同, 所以通过BC算法训练的新BC智能体也具有不同性能, 算法通过KL散度让学习策略模仿具有最优性能的BC智能体策略.

9.2 解决领域自适应问题

目前逆向强化学习算法假设算法训练和测试环境相同, 然而在实际问题中, 通过专家策略收集样本的环境与实际应用的环境总会存在差异. 为解决这类领域自适应问题, Zweig等人^[148]通过理论分析证明了离线逆向强化学习算法在领域自适应问题中性能的理论上界. 但该文中对环境之间必须具有同构马尔可夫决策过程(isomorphic MDPs)的限制太过严苛, 限制了算法的实用性.

Jarrett等人^[149]使用能量模型建立只与状态有关的密度概率分布, 通过最小化与专家样本之间的状态概率分布, 学习最优策略. 另外, Jiang等人^[121]提出HIDIL (horizon-adaptive inverse dynamics)算法, 算法应用由HID (horizon-adaptive inverse dynamics)组成的一组模型预测当前策略所生成的轨迹是否为专家策略轨迹, 通过最大化专家轨迹的概率求解最优策略. 在实际任务中, 算法取得了很好的效果.

9.3 对比分析

在离线逆向强化学习方法中, 算法既没有准确的环境模型, 也无法通过与环境交互采样数据. 因此, 通过异策略预测难以准确预测特征期望, 进而导致难以获得准确的奖赏函数, 影响离线逆向强化学习算法的性能. 目前的算法主要集中于如何最大化专家样本的信息, 缺乏对如何合理采样专家样本和如何处理专家样本以更好训练智能体等方向的研究. 在领域自适应问题中, 专家在采样环境(source dynamic)的目标与智能体在目标环境(target dynamic)的目标相同, 不同之处在于采样环境的观测视角与目标环境不同或环境的物理结构不同. 目前的算法集中于如何提高不同环境中的轨迹匹配度, 但若环境的物理结构发生变化, 专家策略的轨迹也会改变, 对这一问题的研究仍有待深入. 另外Chen等人^[150]和Pulver等人^[151]为平衡自动驾驶问题中规划、性能、安全和效率问题, 将离线逆向强化学习算法应用于该领域.

10 关键问题分析

目前, 逆向强化学习领域仍然存在许多问题亟待解决, 例如: 怎样衡量当前所求奖赏函数的准确性; 怎样解决示范样本非最优问题; 怎样提高样本利用率. 本节将基于前文对这些关键问题进行总结说明.

10.1 衡量奖赏函数准确性问题

对于求得奖赏函数, 仍需筛选其中最优解. 可直接计算当前奖赏函数和真实奖赏函数之间的距离, 但真实奖赏函数难以获取且直接计算奖赏函数并不有效, 因为在某个状态的奖赏不同可能导致最后的策略差异非常大^[152]. 因此最好的方法是, 衡量当前策略与专家策略的差距. 一般通过衡量所学策略与专家策略的匹配程度实现, 即: 计算专家样本中所有状态-动作对与学习所得最优策略的状态-动作对的匹配比例, 但该方法无法衡量在关键状态策略的差异程度.

10.2 示范样本非最优问题

逆向强化学习一个重要的假设是, 专家样本由最优策略在环境中采样生成, 但在现实中存在许多高维度问题^[53], 难以大量产生专家示范样本, 同时因为问题的复杂性, 专家策略难以保证最优. 例如, 训练机器人做家务、股票交易和一些复杂游戏等. 传统逆向强化学习算法中, 保证算法最优的限制条件为: 学习所得奖赏函数对应最优策略所生成样本的特征期望尽可能与专家样本的特征期望相等. 这导致算法难以解决示范样本非最优问题.

10.3 提高样本利用率

在连续高维状态-动作空间问题或采样成本高的问题中, 通常难以大量获取专家样本, 例如, 在机械手臂与真实环境交互的问题中, 专家样本需人工示范生成, 且机械手臂容易损伤自身或周围环境, 这要求算法提高专家样本利用率和采样样本利用率. 目前逆向强化学习算法利用专家样本的方式较为单一, 一般从专家样本中随机抽取样本, 虽然已有一些基于主动学习或机器学习的算法提出, 但专家样本利用率仍有很大的提升空间. 另外, 由于逆向强化学习算法基于奖赏和策略迭代更新框架, 极大提高了算法对采样样本的需求.

表1将对前9节提到的主要算法以表格形式分析比较, 介绍算法相比之前算法的创新点, 并分析算法的优缺点和关键特性, 例如, 奖赏函数的类型、奖赏函数的选择方式、基于模型算法(model-based)或无模型算法(model-free)、算法复杂度和样本利用率等.

11 未来展望

目前该领域发展非常快, 不断有新的算法提出, 也有许多新的研究方向值得深入研究, 除前文提到的关键问题外, 以下几点可能成为未来的重点研究方向.

(1) 逆向强化学习在多专家示范样本问题中的研究

在基于生成对抗框架的模仿学习算法中, 当智能体从多个专家产生的示范样本中学习时, 只能获得其中一个专家的策略. 因此, 生成对抗模仿学习算法从单专家所产生示范样本中训练效果相比从多专家所产生示范样本中学习效果更好^[153]. 对于这类多模态问题, 如何通过对专家样本增加标签或改变判别器模型来增加算法的学习能力, 有待深入研究.

(2) 逆向强化学习在观察模仿学习问题中的研究

传统IRL算法从示范样本中学习最优策略, 这些示范样本通常包含状态信息和动作信息. 目前, 存在大量的人类作业视频^[154], 而这些视频不包含动作信息, 寻找一种新的减少IfO方法与IfD方法之间信息差的算法, 让智能体从视频中学习, 是观察模仿学习^[34]领域重要的研究方向^[155]. 另外, 如何消除示学体不匹配问题, 也是未来的研究方向.

在机械手臂和机器人模仿学习领域, 由于该类问题的采样难度大, 目前这一领域的研究一直停留在模拟环境阶段. 如何增加采样效率, 实现其在工业领域的落地, 是未来重要的研究方向^[114].

(3) 逆向强化学习在多智能体领域的研究

在多智能体领域存在多个纳什均衡, 对于每个智能体, 环境在不断改变, 因此智能体的最优策略也在不断变化, 这导致算法难以收敛. 因此, 设计一种新的模型, 最大化利用专家样本信息, 帮助智能体快速收敛至纳什均衡是该领域的研究重点.

(4) 逆向强化学习在示范样本非最优问题中的研究

目前绝大多数IRL算法假设示范样本由最优策略产生, 然而在实际任务中, 示范样本中通常包含差样本^[52]. 针对这一问题, 可通过强化学习方法继续提高策略性能^{[13, 64, 156]}. 但是, 如何筛选差样本并将其从示范样本中移除或利用差样本中的信息帮助智能体学习仍然是一个有待解决的问题^[107].

(5) 逆向强化学习在度量算法性能问题中的研究

逆向强化学习算法的目的是从示范样本中学习最优策略. 怎样度量学习所得策略与专家策略之间的相似度至关重要. 目前算法采用的方法有KL散度、欧几里得距离和Wasserstein距离^[157]等. 探索一种新的度量方式也是未来重要的研究方向^[158].

12 总　结

逆向强化学习是强化学习领域的重要研究方向之一, 也是模仿学习领域的主要实现方法, 已在汽车导航、路径推荐和机器最优控制等领域取得了令人瞩目的成果. 最近几年, 越来越多的学术界和工业界人士开始对其进行探索和研究, 现已成为模仿学习领域的一个热门研究方向.

本文详细介绍了逆向强化学习领域的关键问题、研究进展和发展方向. 通过奖赏函数构建方式将逆向强化学习算法分为基于线性奖赏函数和非线性奖赏函数的逆向强化学习算法, 以此详细阐述了最大边际逆向强化学习算法、最大熵逆向强化学习算法、最大熵深度逆向强化学习算法和生成对抗模仿学习算法等, 并分析了其优点和不足, 同时介绍了一些逆向强化学习算法的前沿研究方向, 包括状态动作信息不完全逆向强化学习、多智能体逆向强化学习、示范样本非最优逆向强化学习、指导逆向强化学习、奖赏塑形逆向强化学习和离线逆向强化学习.

通过对当今逆向强化学习算法的研究进展进行综述, 总结了当前的成就, 梳理了该领域的发展脉络. 但因为逆向强化学习是一个跨越心理学、认知科学和最优控制等领域的交叉学科, 仍然存在许多难题等待解决. 未来逆向强化学习将朝以下几个方向发展: (1)有效学习多专家样本问题; (2)在观察模仿学习领域的应用; (3)在多智能体领域的应用; (4)在示范样本非最优问题中的研究; (5)寻找更有效的度量策略相似度的方法. 随着以上问题研究的逐步深入, 相信逆向强化学习算法将会发挥越来越重要的作用, 实现DeepMind提出的“解决智能, 并用智能解决一切”的目标.