基于帕累托前沿面曲率预估的超多目标进化算法

引用本文

梁正平, 林万鹏, 胡凯峰, 明仲, 朱泽轩. 基于帕累托前沿面曲率预估的超多目标进化算法[J]. 软件学报, 2023, 34(9): 4096-4113. http://www.jos.org.cn/1000-9825/6648.htm

Liang ZP, Lin WP, Hu KF, Ming Z, Zhu ZX. Many-objective Evolutionary Algorithm Based on Curvature Estimation of Pareto Front[J]. Journal of Software, 2023, 34(9): 4096-4113(in Chinese). http://www.jos.org.cn/1000-9825/6648.htm

基于帕累托前沿面曲率预估的超多目标进化算法

梁正平 , 林万鹏 , 胡凯峰 , 明仲 , 朱泽轩

深圳大学计算机与软件学院, 广东深圳 518060

收稿时间: 2021-01-09; 修改时间: 2022-01-07; 采用时间: 2022-01-29; jos在线出版时间: 2022-10-27

基金项目: 国家重点研发计划(2021YFB2900800); 国家自然科学基金(61871272); 广东省自然科学基金(2020A1515010479, 2021A1515011911); 深圳市高等院校稳定支持(20200811181752003)

作者简介: 梁正平(1979－), 男, 博士, 副教授, CCF专业会员, 主要研究领域为计算智能, 大数据分析与应用;
林万鹏(1995－), 男, 硕士, 主要研究领域为计算智能;
胡凯峰(1993－), 男, 硕士, 主要研究领域为计算智能;
明仲(1967－), 男, 博士, 教授, CCF高级会员, 主要研究领域为软件工程, 人工智能;
朱泽轩(1981－), 男, 博士, 教授, 主要研究领域为计算智能, 机器学习, 生物信息学.

通讯作者: 梁正平, E-mail: liangzp@szu.edu.cn.

摘要: 基于分解的超多目标进化算法是求解各类超多目标优化问题的主流方法, 其性能在很大程度上依赖于所采用参考向量与真实帕累托前沿面(Pareto front, PF)的匹配程度. 现有基于分解的超多目标进化算法尚难以同时有效处理各类PF不同的优化问题. 为此, 提出了一种基于PF曲率预估的超多目标进化算法(MaOEA-CE). 所提算法的核心包括两个方面, 首先基于对PF曲率的预估, 在每次迭代过程中生成不同的参考向量, 以渐进匹配不同类型问题的真实PF; 其次在环境选择过程中, 再基于预估的曲率选择合适的聚合函数对精英解进行挑选, 并对参考向量进行动态调整, 在维护种群多样性的同时提升种群的收敛性. 为验证MaOEA-CE的有效性, 将其与7个先进的超多目标算法在3个主流测试问题集DTLZ、WFG和MaF上进行对比, 实验结果表明MaOEA-CE具有明显的竞争力.

关键词: 超多目标优化进化算法曲率预估参考向量环境选择

Many-objective Evolutionary Algorithm Based on Curvature Estimation of Pareto Front

LIANG Zheng-Ping , LIN Wan-Peng , HU Kai-Feng , MING Zhong , ZHU Ze-Xuan

College of Computer Science and Software Engineering, Shenzhen University, Shenzhen 518060, China

Abstract: The many-objective evolutionary algorithm based on decomposition is the main approach to solving many-objective optimization problems, but its performance largely depends on the matching degree between the adopted reference vectors and the real Pareto front (PF). Existing decomposition-based many-objective evolutionary algorithms can hardly deal with all kinds of many-objective optimization problems with different PF at the same time. To solve this issue, this study proposes a many-objective evolutionary algorithm based on the curvature estimation (MaOEA-CE) of PF. The core of the proposed algorithm includes two aspects: Firstly, on the basis of PF curvature estimation, different reference vectors are generated in each iteration to gradually match the real PF of different kinds of problems. Secondly, with the estimated PF curvature, the appropriate aggregation function is used to select elite solutions and dynamically adjust the generated reference vector in the environmental selection, which can improve the convergence while maintaining the diversity of the population. Moreover, MaOEA-CE is compared with seven advanced many-objective algorithms on three mainstream problem sets for testing, i.e., DTLZ, WFG, and MaF, to verify its effectiveness. The experimental results prove that MaOEA-CE has strong competitiveness.

Key words: many-objective optimization evolutionary algorithm curvature estimation reference vectors environmental selection

一般来说, 一个多目标优化问题(multi-objective optimization problem, MOP)^[1]可以用如下数学形式进行表示:

$ \begin{gathered} \min {\text{ }}F({\mathbf{x}}) = ({f_1}({\mathbf{x}}), {f_2}({\mathbf{x}}), \ldots, {f_M}({\mathbf{x}}))\; {\text{ s.t. }}\; {\mathbf{x}} \in \Omega \end{gathered} $

(1)

其中, x=(x₁, x₂, …, x_n)是决策空间 $\Omega $ 中的n维决策向量, $F({\mathbf{x}})$ 为待求解的M个目标函数. 当M大于3时, 也称为超多目标优化问题(many-objective optimization problem, MaOP)^[2]. 基于分解的进化算法对于MaOP的求解具有较大的竞争优势, 已在各类复杂的软件项目管理、路径规划、特征抽取等MaOPs的求解中得到广泛应用^[3-7]. 基于分解进化算法的核心是利用参考向量对目标空间进行划分, 将单个超多目标优化问题分解为多个单目标优化问题, 然后再进行求解. 影响此类算法性能的关键因素是所采用参考向量与待求解问题真实PF的匹配程度.

基于分解的超多目标进化算法(many-objective evolutionary algorithm based on decomposition, MaOEA/D) 中常见的参考向量生成方法包括NBI^[8], K-layer^[9]和Mixture Uniform Design (MUD)^[10]这3种类型. 其中, NBI是使用最为广泛的参考向量生成方法, 非常适合线性PF优化问题的处理. K-layer方法对于凹型PF优化问题有较好的效果. MUD方法的优势则在于支持任意数目参考向量, 但所生成参考向量的多样性不如NBI和K-layer. 总体而言, 上述3类参考向量生成方法各自适合处理一些特定的规则型PF优化问题, 对于断开、退化、偏好等不规则型PF优化问题, 由于所生成参考向量在PF上的分布不均匀, 难以取得较好的效果.

为支持不同形状PF优化问题的处理, 现有MaOEA/D类算法通常在种群进化过程中引入对参考向量进行自适应调整的策略. 根据调整过程中所使用启发式信息来源的不同^[11], 可分为随机参考向量^{[6, 12,13]}、拟合自适应参考向量^[14,15]、局部种群引导的自适应参考向量^[16,17]、局部存档引导的自适应参考向量^[18,19]、基于邻接参考向量的自适应参考向量^[20,21]和基于偏好的自适应参考向量^[22,23]等. 上述参考向量调整策略虽然在解决各类不规则PF优化问题时可取得较好的效果, 但却容易导致在处理规则PF优化问题时性能恶化^[24].

为能同时处理好不同形状的PF优化问题, 且更好地平衡种群的多样性和收敛性, 本文提出一种基于PF 曲率预估的超多目标进化算法(many-objective evolutionary algorithm based on curvature estimation of PF, MaOEA-CE). MaOEA-CE采用了一种基于曲率预估的参考向量生成方法(reference vectors based on curvature estimation, RVCE), 通过当前种群对真实PF的曲率进行预估, 生成可大致适应实际PF形状的参考向量, 并在每次迭代过程中对参考向量进行调整, 渐进匹配不同类型优化问题的真实PF. 同时, 提出了一种基于曲率预估的环境选择策略(environment selection based on curvature estimation, ESCE), 进一步基于预估的曲率选择合适的聚合函数对精英解进行挑选, 并对参考向量进行动态调整, 在维护种群多样性的同时提升种群的收敛性.

本文的主要工作和创新点如下.

(1) 提出一种新的基于曲率预估的参考向量生成方法, 该方法可在进化过程中渐进匹配各种形状的PF.

(2) 提出一种新的基于曲率预估的环境选择策略, 利用预估的曲率自适应选择聚合函数, 可较好地平衡种群的多样性和收敛性.

(3) 将MaOEA-CE与7个先进的超多目标优化算法在DTLZ、WFG和MaF问题集上进行对比实验, 对MaOEA-CE 的性能进行全面验证.

本文第1节介绍相关工作. 第2节阐述所提算法的主要内容. 第3节对实验方案、实验结果进行介绍, 并进行相关分析. 最后总结全文并对未来工作进行探讨.

1 相关工作 1.1 参考向量生成方法

MaOEA/D中常见的参考向量生成方法包括NBI^[8], K-layer^[9]和MUD^[10]. NBI通过在M– 1维的单位超平面上进行均匀采点生成参考向量, 且满足 $\displaystyle\sum\nolimits_{i = 1}^M {{f_i}} = 1$ . 由NBI生成的参考向量在线性PF优化问题上的多样性很好, 但对于凹/凸PF优化问题, 其参考向量存在稀疏不均的缺陷. K-layer首先将M –1维超平面切分成M个平面三角形, 然后在各切分子区域内通过均匀采点生成参考向量. 由K-layer生成的参考向量中心密集、边缘稀疏, 较适合处理凹型PF优化问题, 在线性和凸型PF优化问题上的多样性则不如NBI. MUD采用与NBI相同的采点方式, 然后将所采集的点转换到一个M维单纯形上, 再根据转换后的点生成参考向量. 由MUD生成的参考向量在角落区域较为稀疏, 其多样性总体较差.

1.2 参考向量调整方法

根据参考向量调整过程中所使用启发式信息来源的不同, 现有参考向量调整方法可分为如下几种类型.

(1) 随机参考向量, 不使用任何启发式信息, 而是采用随机方式对参考向量进行调整. 如MOGLS^[12]在每轮迭代过程中通过随机生成的参考向量来引导精英种群的搜索, RVEA*^[6]则周期性地剔除无效参考向量, 并采用随机方式补充新的参考向量. 此类方法的优点在于操作简单、容易实现, 但难以有效保证种群的多样性和收敛性.

(2) 拟合自适应参考向量, 通过对整个种群/存档的拟合来调整参考向量. 如paλ-MOEA/D^[14]将PF拟合在 ${f_1}^p + {f_2}^p + \ldots + {f_M}^p = 1$ 的曲面上, 同时引入HV指标^[25]对参考向量进行调整. 此类方法利用整个种群/存档的信息来估计PF的形状, 从而具有一定的稳健性, 缺陷在于要求待求解问题的PF形状满足所构建的理论模型, 否则拟合出的参考向量质量难以保障.

(3) 局部种群引导的自适应参考向量, 利用局部种群中的个体来调整参考向量. 如MOEA-AM2M^[16]将各子区域内与选定个体具有最大夹角的个体作为新参考向量, g-DBEA^[17]选择跟被删除参考向量具有最大垂直距离的个体作为新的参考向量. 此类方法是最常见的参考向量调整方法, 当种群能够贴近真实PF时可以在各种不规则PF优化问题上发挥很好的作用, 当种群与真实PF相差很远时则容易被多样性或收敛性差的个体误导.

(4) 局部存档引导的自适应参考向量, 利用局部存档中的个体来调整参考向量. 如MOEA/D-AWA^[18]首先对外部存档中的个体在当前种群内的稀疏水平值进行计算, 再根据稀疏水平值最高的个体生成新的参考向量. 此类方法的优缺点与局部种群引导的调整方法相似.

(5) 基于邻接参考向量的自适应参考向量, 依靠邻接参考向量来调整参考向量. 如A-NSGA-III^[20]选择在拥挤区域的有效参考向量周围生成新的参考向量. 该类方法能够改善种群的局部多样性, 不足之处在于较难处理退化、尖峰或长尾等PF形状的优化问题.

(6) 基于偏好的自适应参考向量, 依据偏好信息来调整参考向量. 如pMOEA/D^[22]使用期望点、保留点和偏好半径划定一块偏好区域来调整参考向量. 此类方法可以使用较小的种群来处理MaOPs, 计算代价低, 但单纯基于偏好信息容易导致种群陷入局部最优.

2 MaOEA-CE算法

本节介绍MaOEA-CE算法的主要框架和核心策略, 并对算法的复杂性进行分析.

2.1 算法框架

MaOEA-CE的伪代码如算法1所示. 首先, 初始化大小为N的种群P. 在每一轮进化过程中, 先根据当前种群信息预估PF的近似曲率p, 并利用预估的曲率p生成对应曲面上均匀分布的参考向量W. 接着采用二进制锦标赛法^[26]选择父代, 并使用模拟二进制交叉(SBX)^[27]和多项式变异(PM)^[28]变异生成子代种群. 最后基于曲率p和参考向量W对子代种群和父代种群的并集进行环境选择. 循环上述过程, 直至达到最终的进化代数, 将最后一代的精英个体组成的种群P作为输出.

算法1. MaOEA-CE算法框架.

输入: 种群大小N;

输出: 种群P.

1. 初始化种群P

2. while 未达到最大迭代次数 do

3.　根据当前种群P预估PF的曲率p

4.　根据曲率p生成参考向量W

5.　使用交叉变异生成子代O

6. 　基于p和W对P∪O进行环境选择

7. end while

8. return P

2.2 曲率预估

(1) 归一化

由于PF的缩放会影响曲率p的估算, 导致生成的参考向量不能很好地匹配真实PF的形状. 为此, 在估算种群所对应PF的曲率之前, 需对种群进行归一化处理. 本文中, 将种群P的非支配层在各个维度分量上的最小值, 作为理想点z的对应分量. 将角落解在各个维度分量上的最大值, 作为极差点znad的对应分量. 角落解为距离各个方向轴最近的个体, 其第i维分量值的计算公式如下:

$ {\mathbf{x}}_i^{{\rm{corner}}} = \{ {\mathbf{x}}|{\mathbf{x}} = \arg \min dis{t^ \bot }({\mathbf{x}}, {{\mathbf{e}}^i})\} $

(2)

其中, x为目标向量, e为各轴的单位方向向量, dist为目标向量x到轴向单位方向向量e的欧式距离.

在计算出理想点z和极差点znad后, 对目标向量各个维度进行归一化的公式如下:

$ {f_i}({\mathbf{x}}) = \frac{{{f_i}({\mathbf{x}}) - {{\textit{z}}_i}}}{{{\textit{z}}na{d_i} - {{\textit{z}}_i}}} $

(3)

(2) 估算PF的曲率

由于种群中支配个体的收敛性不如非支配个体, 若将收敛程度较差的支配个体用于曲率预估, 容易导致所估算的近似PF的曲率与真实PF存在较大差异. 为此, 本文采用2REA^[29]中提出的方法, 仅选取种群中的非支配个体, 并基于它们的L_p距离^[30]来对曲率p进行自适应估算. 其中, L_p距离的计算公式如下:

$ L({\mathbf{x|}}p) = {\left(\sum\limits_{i = 1}^M {{{({f_i}({\mathbf{x}}))}^p}} \right)^{1/p}}, \; {\text{ }}p > 0 $

(4)

曲率预估的具体过程如下: 首先将p值限定在合适的取值区域, 并基于一定间隔进行采样, 然后分别计算在每个p值下, 所有非支配个体的L_p距离对应的标准差. 由于所选p值对应的 ${f_1}^p + {f_2}^p + \ldots + {f_M}^p = 1$ 曲面越贴近非支配个体构成的近似PF, 对应的标准差越小. 故标准差最小的p值曲面最接近非支配个体所构成的近似PF, 从而可用该p值对应的 ${f_1}^p + {f_2}^p + \ldots + {f_M}^p = 1$ 曲面对当前种群进行拟合, 并将该p值作为当前种群所对应PF曲率的预估值.

2.3 根据预估曲率生成参考向量

RVCE的总体框架类似NBI^[8], 但对于参考向量各维度上的分量值, 则基于预估的PF曲率进行计算, 其伪代码如算法2所示.

算法2. 参考向量生成.

输入: 曲率p, 种群大小N;

输出: 参考向量W.

1. 使用公式(5), 公式(6)计算H, H'

2. 通过公式(7)将曲率为p的弧线段均匀划分成H份, 计算出对应的{t₀, t₁, …, t_H}

3. 根据{t₀, t₁, …, t_H}和公式(9)构建参考向量W

4. if H＜M then

5. 　通过公式(7)将曲率为p的弧线段均匀划分成H'份, 计算出对应的{t₀, t₁, …, t_H'}

6. 　根据{t₀, t₁, …, t_H'}和公式(9)构建参考向量W'

7. 　使用公式(10)将W'向内部缩放1/2

8.　 W= W∪W'

9. end if

10. return W

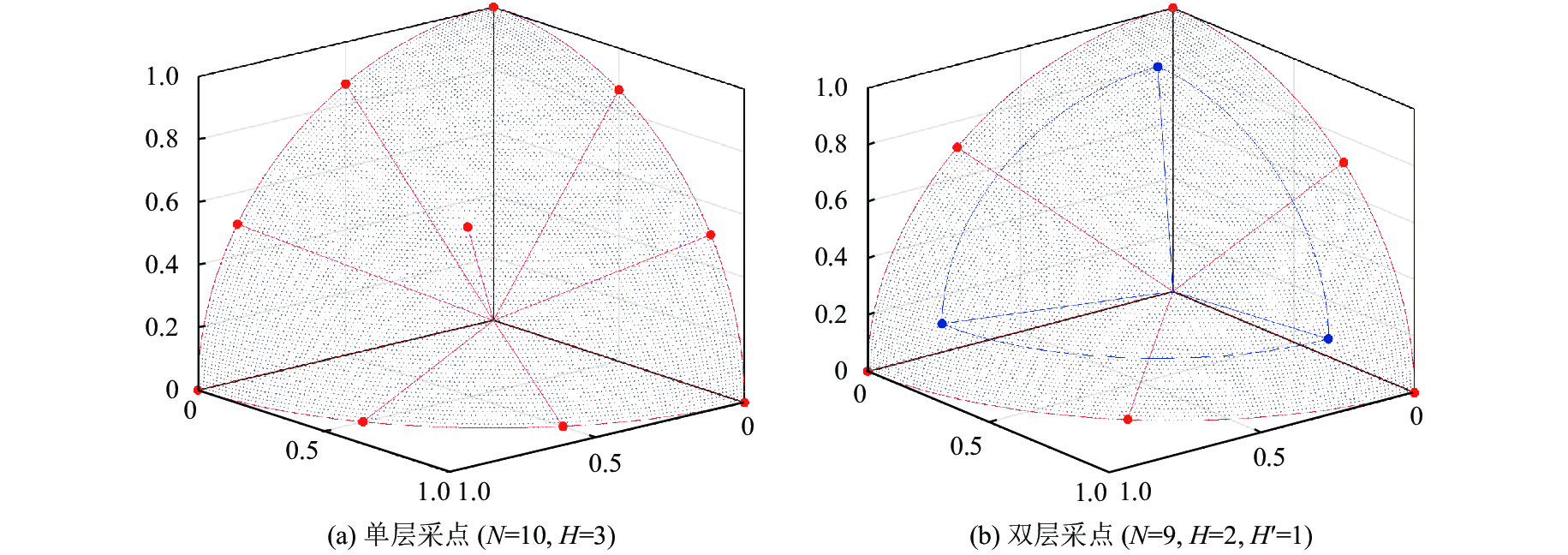
首先, 根据目标维度M和种群大小N, 使用公式(5)计算各目标维度的划分数H. 若H≥M, 使用单层采点^[8]生成全部参考向量, 如图1(a)所示, 其中的红色实心点对应生成的参考向量. 若H<M, 则使用双层采点^[4]生成全部参考向量, 如图1(b)所示, 其中红色实心点对应外层的参考向量, 蓝色实心点对应内层的参考向量, H和H'分别为外层和内层在各维度上的划分数, H'由公式(6)计算得出. 采用分层策略的原因在于对高维问题, 仅使用单层采点容易导致内部区域采点数量稀疏, 多样性难以得到保证^[5].

Fig. 1 Examples of one-layer reference vector generation method and two-layer reference vector generation method on 3-dimension problem 图 1 三维目标空间下的单层采点和双层采点示例

$ N = \left( {\begin{array}{*{20}{c}} {H + M - 1} \\ {M - 1} \end{array}} \right) $

(5)

$ N = \left( {\begin{array}{*{20}{c}} {H + M - 1} \\ {M - 1} \end{array}} \right) + \left( {\begin{array}{*{20}{c}} {H' + M - 1} \\ {M - 1} \end{array}} \right) $

(6)

其次, 将曲率为p的弧线段均匀划分成H份, 所得结果{t₀, t₁, …, t_H}作为参考向量各维度上的分量值. 其中, t₀=0, t_H=1, 其余的t_k (k∈{1, 2, …, H–1})满足以下公式:

$ \int_{{t_k}}^{{t_{k + 1}}} {{{(1 - {x^p})}^{1/p}}} dx = \frac{1}{H}\int_0^1 {{{(1 - {x^p})}^{1/p}}} dx $

(7)

对于采用单层采点的低维问题, 基于上述{t₀, t₁, …, t_H}, 即可生成如下形式的全部参考向量W:

$ \left\{ {\begin{array}{*{20}{l}} {{u_i} = (u_i^1, u_i^2, \ldots , u_i^M)} \\ {u_i^j \in \{ {t_0}, {t_1}, \ldots , {t_H}\} } \end{array}} \right. $

(8)

其中, u_i表示W中的第i个参考向量, $u_i^j$ 表示u_i在第j维上的分量值, 且满足如下公式:

$ \left\{ {\begin{array}{*{20}{l}} {{u_i} = ({t_{{k_1}}}, {t_{{k_2}}}, \ldots , {t_{{k_M}}})} \\ {{k_1} + {k_2} + \ldots + {k_M} = H} \\ {{k_l} \in \{ 0, 1, \ldots , H\} } \end{array}} \right. $

(9)

对于采用双层采点的高维问题, 还需进一步根据公式(7)将内层各弧线段均匀划分成H'份, 再根据得出的{t₀, t₁, …, t_H'}构建参考向量W'. 由于高维问题的外层采点边缘密集、内部稀疏, 为提升参考向量整体的多样性, 借鉴文献[4]中的做法, 将W'向内部缩放1/2, 以补充内部参考向量的数量. 缩放公式如下:

$ W' = \frac{1}{2}W' + \frac{1}{{2M}} $

(10)

最终, 将W和缩放后的W'合并, 即可得到高维问题的全部参考向量.

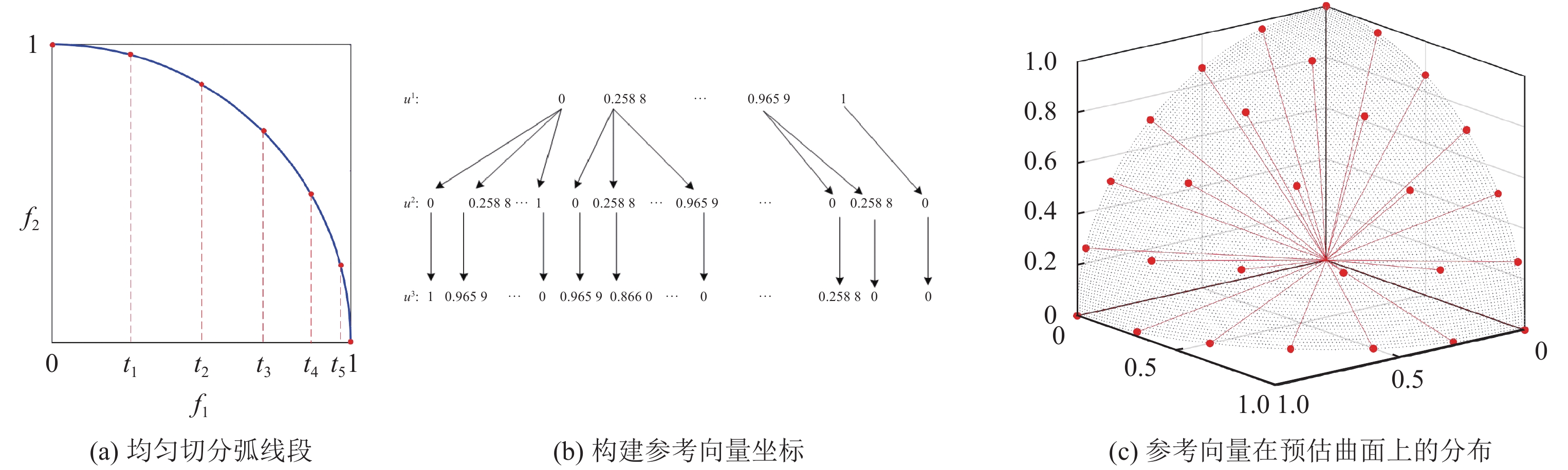
图2直观展示了RVCE在三维问题上生成参考向量的过程, 其中种群大小N设为28, 预估曲率p设为2. 根据公式(5), 可得知H为6. 由于H>M, 使用单层采点即可生成全部参考向量. 图2(a)为均匀切分弧线段的图例, 根据公式(7), {t₀, t₁, t₂, t₃, t₄, t₅, t₆}分别对应{0, 0.2588, 0.5000, 0.7071, 08660, 0.9659, 1}. 图2(b) 展示了根据公式(9)构建参考向量坐标(0, 0, 1), (0, 0.2588, 0.9659), …, (0.9659, 0.2588, 0), (1, 0 , 0)的过程, 其中u¹, u², u³分别为参考向量在第一、第二、第三维的分量. 图2(c) 展示了最终生成的参考向量, 它们均匀分布在预估曲率所对应的曲面上.

Fig. 2 Illustration of the reference vectors generation on 3-dimension problem with RVCE 图 2 RVCE在三维问题上生成参考向量的示例

RVCE基于自适应方式生成的预估曲率p, 将不同问题的真实PF用曲率不同的 ${f_1}^p + {f_2}^p + \ldots + {f_M}^p = 1$ 曲面进行拟合, 并基于该曲面生成具有良好多样性的均匀分布参考向量, 从而可较好支持各类PF优化问题的处理.

2.4 基于预估曲率进行环境选择

ESCE的核心是基于预估的曲率和所生成的参考向量, 通过自适应选择聚合函数来挑选精英解. 同时通过对参考向量的动态调整, 以更好地支持各类不规则型PF优化问题. 其伪代码如算法3所示.

算法3. 环境选择.

输入: 种群R, 种群大小N, 曲率p, 参考向量W;

输出: 精英种群P.

1. 从种群R中找出角落解放入S中

2. 归一化种群R

3. 剔除参考向量W中没有非支配解关联的参考向量

4. 根据曲率p和参考向量W从种群R中选出精英种群S' //算法4

5. S = S∪S', R = R \ S

6. if |S| > N then

7. 　在S中剔除|S|–N个局部密度最大的解

8.　 P = S

9. end if

10. if |S| < N then

11.　根据曲率p、当前精英种群S和当前种群R确定最终精英种群U //算法5

12.　 P = U

13. end if

14. return P

由于角落解覆盖空间大, 且相互间隔较远, 为确保种群整体的多样性, 首先将种群中的角落解作为默认的精英解. 接着, 对种群进行归一化, 并剔除参考向量集中没有任何非支配解关联的无效参考向量. 然后, 根据预估曲率和剩余的参考向量, 通过自适应选择聚合函数, 从种群的非支配解集中挑出聚合函数值最优的解作为精英解, 如算法4所示. 最后, 若挑选出的精英解个数大于N, 则逐一计算各精英解的局部密度^[26], 并依次删除局部密度最大的多余精英解. 若挑选出的精英解个数小于N, 则继续采用算法5, 根据预估曲率、已挑选出的精英解和余下的非支配解, 通过新生成的参考向量, 继续挑选更多的精英解, 直至精英解个数等于N.

算法4. 根据曲率和参考向量选择精英种群.

输入: 候选种群R, 曲率p, 参考向量W;

输出: 精英种群S.

1. S = []

2. for w∈W do

3.　 if p ≥ 1 then

4. 　　　计算种群R中各非支配解与参考向量w的PBI聚合函数值

5.　 else

6. 　　　计算种群R中各非支配解与参考向量w的TCH聚合函数值

7.　 end if

8. 　找出聚合函数值最优的解s

9. 　 S = S∪s

10. end for

11. return S

在算法4中, 对于每个有效参考向量, 均通过最优聚合函数值, 从非支配解中挑出一个作为环境选择的精英解. 当预估曲率p≥1时, 选择正交边界惩罚函数(PBI)^[3]作为聚合函数, 当曲率p<1时, 则选择切比雪夫函数(TCH)^[31]作为聚合函数. 原因在于相比其他聚合函数, 对于PF形状为非凸的优化问题, PBI能够在保证种群收敛性的同时提供更好的多样性^[3], 而对于PF 形状为凸的优化问题, TCH能更好地平衡种群的收敛性和多样性^[32]. 因此, 通过预估曲率对聚合函数进行自适应选择, 有利于确保在将各类PF形状拟合到 ${f_1}^p + {f_2}^p + \ldots + {f_M}^p = 1$ 曲面时, 都能根据有效参考向量选择出质量更好的精英解, 避免仅使用单种聚合函数存在的偏好, 从而有效平衡种群的收敛性和多样性.

算法5. 根据曲率和当前精英种群确定最终精英种群.

输入: 候选种群R, 当前精英种群S, 曲率p;

输出: 最终精英种群U.

1. U = S

2. while |U| < N do

3. 　计算R中各非支配解与U中所有解的最小欧式距离

4. 　找出上述最小距离中的最大值在R中对应的解x

5. 　根据曲率p和参考向量x从R的非支配解集中选出一个精英解u //算法4

6.　 U = U∪u, R = R \ u

7. 　找出种群R中收敛指标最差的解c

8.　 R = R \ c

9. end while

10. return U

在算法5中, 首先计算当前种群中各非支配解与当前精英种群中所有解的最小欧式距离, 然后将上述最小距离中的最大值在当前种群中对应的解x作为新的参考向量, 并调用算法4选出一个与预估曲率p和参考向量x对应的新的精英解u. 此后, 将所选出的精英解u, 以及当前种群中收敛性最差的解c从当前种群中删除. 依此循环, 直至最终精英种群中解的数量等于N. 为确保不同PF形状下解之间最小距离的定义更加精准, 对于解之间的距离, 同样基于预估曲率进行自适应计算. 若曲率预估过程中将PF拟合成平面, 即p=1, 则将两个解在超平面上的映射点之间的欧式距离作为解之间的距离; 若将PF拟合成凹形曲面, 即p>1, 则将两个解与原点之间构成的夹角作为解之间的距离; 若将PF拟合成凸形曲面, 即p<1, 则将两个解与极差点znad的夹角作为解之间的距离. 基于上述最小距离的最大值找出的x, 是当前种群非支配解中多样性最好的解, 因而最合适作为新的参考向量来挑选精英解. 此外, 为进一步提升种群的收敛性, 在每轮选择的最后, 均将当前剩余种群中收敛性最差的解删除. 由于分量和方法具有简单高效, 且搜索性能强等优点^[26], 此处采用分量和作为种群中各个解的收敛指标.

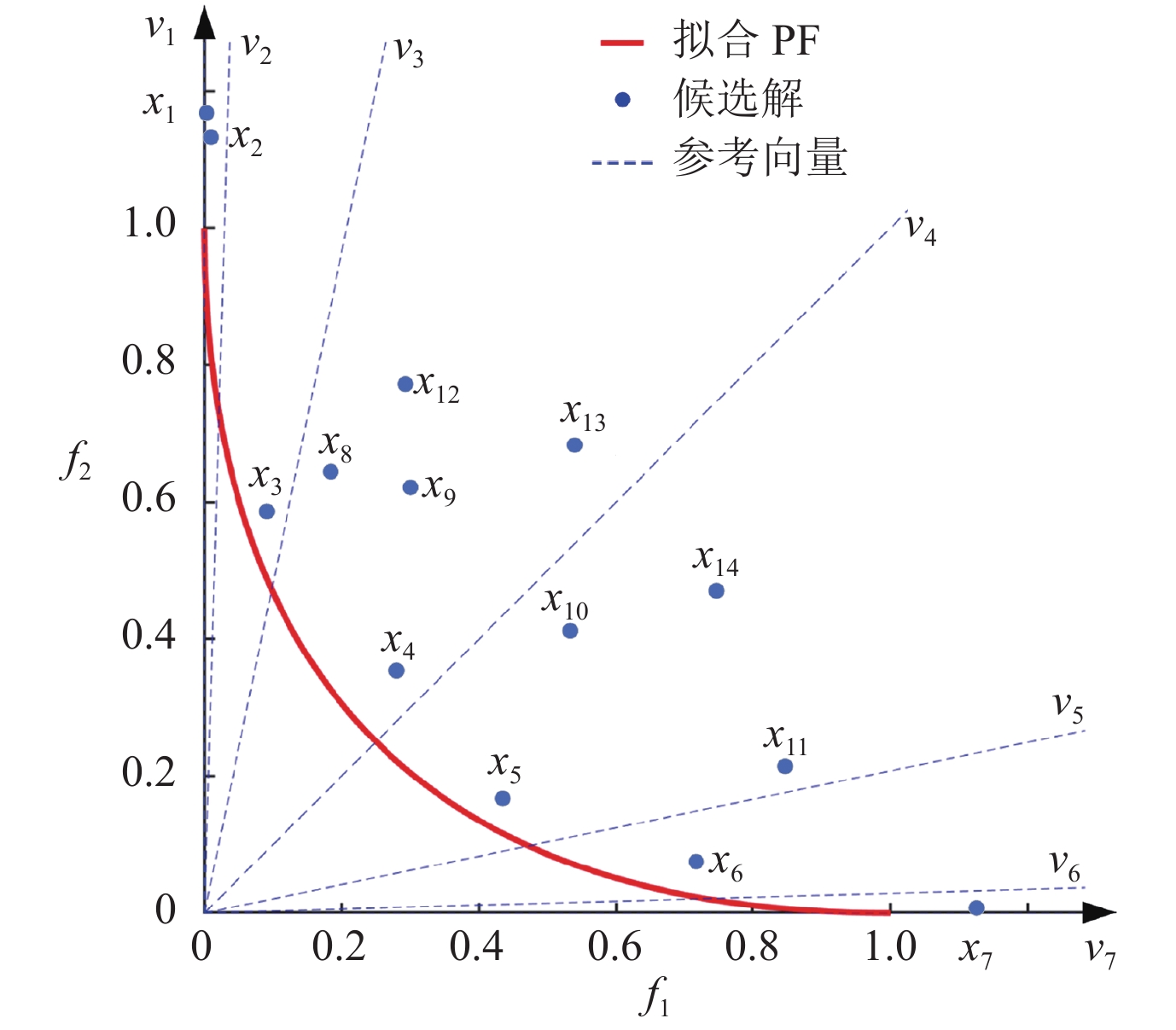
图3为二维空间中使用ESCE进行环境选择的示例. 种群大小N设为7, 红色弧线表示所拟合的PF曲线, 其曲率p=0.5, v₁–v₇为基于RVCE生成的参考向量, x₁₁–x₁₄为种群的候选解, 其中x₁–x₇为第1层非支配解, x₈–x₁₁为第2层非支配解. 从图3可见, x₁和x₇为角落解, 直接加入精英种群中. v₂和v₆没有非支配解与之关联, 从参考向量中将它们剔除. 由于p<1, 选择TCH作为聚合函数, 得到分别与剩余参考向量v₁、v₃、v₄、v₅和v₇逐一对应, 且聚合函数值最优的x₁、x₃、x₄、x₆和x₇作为新获得的精英解. 此时精英种群的大小为5, 需继续挑选精英解. 在剩余种群中, x₂和x₅为非支配解. 从图3可见, 相比x₂, x₅与当前精英种群中各个解的最小距离更大, 故将x₅作为新的参考向量. 进一步可发现相比x₂, 候选解x₅与新参考向量的TCH值更优, 将x₅加入精英种群. 之后, 从种群中剔除刚选出的精英解x₅, 以及收敛性最差的候选解x₂. 继续对剩余种群进行处理, 可发现x₉为精英解. 此时, 精英解的个数等于种群大小, 环境选择结束.

Fig. 3 Illustration of the elites selection on 2-dimension space with ESCE 图 3 ESCE在二维空间中选择精英解的示例

2.5 时间复杂度分析

曲率预估的时间复杂度为O(MN)^[29], 其中M是目标维度, N是种群大小. 算法2使用预估曲率根据公式(9)生成N个参考向量, 采用单层采点时的时间复杂度为O(N), 采用双层采点时, 考虑外层采点的缩放计算, 最坏情况下的计算量是单层采用时的两倍, 但时间复杂度依然为O(N). 子代生成中, 遗传算子SBX和PM的时间复杂度为O(DN), 其中D是决策变量的数目. 环境选择过程中, 非支配排序的时间复杂度为O(Nlog_M–2N)^[7], 非支配解与目标空间各方向轴的距离计算需消耗的时间复杂度为O(MN), 种群归一化时间复杂度为O(MN), 算法4 根据参考向量W选择精英解集需消耗的时间复杂度为O(MN|W|), 其中|W|为参考向量的个数. 由于|W|≤N, 故算法4的最坏时间复杂度为O(MN²). 对于算法5, 最坏情况下需要补充(N–M)≈N个解, 但其每次调用算法4 时仅涉及一个参考向量, 故算法5的最坏时间复杂度为O(MN²). 综上分析可知, MaOEA-CE的时间复杂度为max{O(MN²), O(DN)}.

3 实验设计与结果分析

本节在DTLZ^[32]、WFG^[33]和MaF^[34]问题集上, 将MaOEA-CE与7个先进的超多目标优化算法进行对比, 以验证MaOEA-CE的优异性能. 此外, 在不同类型的PF问题上, 分别对参考向量生成方法RVCE和环境选择策略ESCE的有效性进行验证.

3.1 实验设计

(1) 测试问题

DTLZ和WFG是MaOPs领域两组经典的测试问题集, 其中不同的测试问题具有不同的特性和PF形状. MaF是问题特性更为复杂的最新测试问题集, 对现有MaOEA算法提出了更大的挑战. 这3组测试问题集包含各种类型的PF形状, 可大致分为规则PF与不规则PF两类. 规则PF又可分为平面PF、凹曲面PF和凸曲面PF, 不规则PF问题可分为退化PF、断开PF、倒置PF、凹/凸混合PF和具有偏好的PF等. 其中, DTLZ1、MaF9和MaF14为平面PF, DTLZ2-4、WFG4-9、MaF5和MaF12-13为凹曲面PF, MaF3为凸曲面PF, DTLZ5-6、WFG3和MaF6为退化PF, DTLZ7和MaF7为断开PF, MaF1、MaF4、MaF8和MaF15为倒置PF, WFG1-2和MaF10-11为凹/凸混合PF, MaF2为具有偏好的PF.

(2) 对比算法

考虑到MaOEA-CE为基于分解的超多目标优化算法, 为对其性能进行充分验证, 选取多个基于分解的代表性算法NSGA-III^[4]、RVEA^[6]、SPEA-R^[9]、ASEA^[35]和hpaEA^[36]作为对比算法, 同时也将基于改进Pareto关系的算法NSGA-II-SDR^[37]、基于指标的算法MaOEA-IGD^[38]作为对比算法, 以更全面的验证MaOEA-CE的性能.

1) NSGA-III是MaOEA领域的经典算法, 其特点是将非支配排序与参考向量结合, 可提高算法运行效率.

2) RVEA提出了一个新颖的聚合算子APD, 该算子在进化前期偏向于收敛性而在后期侧重多样性, 可取得较好的综合性能.

3) SPEA-R提出了一种基于参考向量的密度估计方法和多样性优先的环境选择策略, 对处理高维MaOPs 具有很好的性能表现.

4) ASEA提出了一个两阶段排序的环境选择策略, 可较好地平衡种群的收敛性和多样性.

5) hpaEA提出了一种突出解选择方法, 在父代选择和环境选择过程中优先保护突出解, 可提高种群的收敛性.

6) NSGA-II-SDR提出了一种新颖的支配关系SDR, 基于候选解之间的夹角自适应选择精英解, 可较好地平衡种群的收敛性和多样性.

7) MaOEA-IGD提出了一种高效的支配比较方法, 并基于IGD指标进行环境选择, 在解决MaOP方面具有相当的竞争力.

(3) 评价指标

HV^[25]指标通过计算解集与目标空间参考点之间围成的超体积来对算法进行评估, HV值越大表示算法性能越好. 由于HV指标具有严格的帕累托相容性^[39], 可以很好地评判MaOEA的综合性能. 为了提高HV指标的计算效率, 本文采用蒙特卡罗模拟方法来计算HV指标的值. 类似文献[29], 使用10000个采样点来保证计算的准确性, 同时将参考点设为(1.5, 1.5, …, 1.5). 此外, 为验证参考向量生成方法RVCE的多样性, 本文还采用SPREAD^[40]指标对其多样性进行专门衡量.

(4) 参数设置

为确保实验的公平性, 所有算法使用相同的种群大小. 目标数M和种群数量N的具体设置如表1所示. 遗传算子SBX和PM的参数设置如表2所示. 参照文献[41], 决策变量数D统一设为100, WFG测试问题中的位置变量数设为k=M–1. 每个算法独立运行30次, 实验中的进化代数统一为2000代. 各对比算法特有的其他参数, 采用各自原始文献中设定的值. 通过计算HV指标的均值和标准差, 采用Wilcoxon秩和检验对MaOEA-CE与其他7个先进算法综合性能进行衡量. 实验结果表格中使用符号“+”“−”“≈”分别表示对比算法的性能在5%的显著水平上优于、劣于、等于MaOEA-CE, 加粗表示每个测试问题上的最佳结果.

Table 1 Setting of the population size 表 1 种群大小设置

Table 2 Parameter settings for crossover and mutation 表 2 交叉变异参数设置

3.2 实验结果与分析

(1) 算法整体性能验证与分析

表3–表5分别展示了8个算法在DTLZ、WFG和MaF测试问题集上的HV值统计结果. 可以看出, MaOEA-CE在绝大部分测试问题上都取得了最佳HV均值, 说明MaOEA-CE具有非常优异的整体性能. 下面分别介绍各个算法在3个测试问题集上的详细结果并进行分析.

Table 3 The statistical results (mean) of the HV values obtained by MaOEA-CE, NSGA-III, RVEA, SPEAR, ASEA, hpaEA, NSGAII-SDR and MaOEA-IGD on DTLZ1-7 表 3 不同算法在DTLZ1–7 上获得的HV值的统计结果 (均值)

Problem	M	MaOEA-CE	NSGA-III	RVEA	SPEA-R	ASEA	hpaEA	NSGA-II-SDR	MaOEA-IGD
DTLT1	3	9.3746E–1	9.3757E–1+	9.3758E–1+	8.9761E–1–	9.3758E–1+	9.3794E–1+	9.0603E–1–	9.2458E–1–
	5	9.9535E–1	9.9572E–1≈	9.9575E–1≈	9.8701E–1–	9.9570E–1≈	9.9596E–1+	9.7795E–1–	9.7590E–1–
	8	9.9981E–1	9.9978E–1–	9.9980E–1–	9.9831E–1–	9.9980E–1–	9.9983E–1+	9.5818E–1–	9.7182E–1–
	10	9.9999E–1	9.9940E–1–	9.9999E–1–	9.9910E–1–	9.9999E–1–	9.9999E–1≈	9.6778E–1–	9.7637E–1–
DTLZ2	3	8.2719E–1	8.2633E–1–	8.2633E–1–	8.2511E–1–	8.2632E–1–	8.2667E–1–	7.1278E–1–	8.1986E–1–
	5	9.6105E–1	9.6032E–1–	9.6032E–1–	9.5966E–1–	9.6022E–1–	9.6122E–1+	9.5620E–1–	9.6031E–1–
	8	9.9434E–1	9.9259E–1–	9.9364E–1–	9.9328E–1–	9.9360E–1–	9.8982E–1–	9.7828E–1–	9.9377E–1–
	10	9.9884E–1	9.9769E–1–	9.9864E–1–	9.9847E–1–	9.9863E–1–	9.9607E–1–	9.9831E–1–	9.9867E–1–
DTLZ3	3	8.2707E–1	8.2586E–1–	8.2599E–1–	7.6426E–1–	8.2632E–1–	8.2611E–1–	7.0900E–1–	6.9920E–1–
	5	9.6110E–1	9.6015E–1–	9.6027E–1–	8.9202E–1–	9.6031E–1–	9.6088E–1–	9.5766E–1–	9.6014E–1–
	8	9.9421E–1	9.8869E–1–	9.9359E–1–	3.6538E–1–	9.9366E–1–	9.2456E–1–	9.8530E–1–	9.9215E–1–
	10	9.9881E–1	9.9597E–1–	9.9864E–1–	1.9874E–2–	9.9860E–1–	2.2700E–1–	9.9837E–1–	9.9866E–1–
DTLZ4	3	7.7498E–1	8.0810E–1+	8.1421E–1+	8.2468E–1+	8.1995E–1+	6.5919E–1–	6.5694E–1–	7.5729E–1–
	5	9.6107E–1	9.5856E–1–	9.6023E–1–	9.5944E–1–	9.6015E–1–	9.3655E–1–	8.4979E–1–	9.5886E–1–
	8	9.9435E–1	9.9097E–1–	9.9349E–1–	9.9315E–1–	9.9363E–1–	9.8974E–1–	9.0644E–1–	9.9165E–1–
	10	9.9885E–1	9.9833E–1–	9.9864E–1–	9.9844E–1–	9.9864E–1–	9.9854E–1–	9.7358E–1–	9.9868E–1–
DTLZ5	3	4.9691E–1	4.9227E–1–	4.6895E–1–	4.8013E–1–	4.8293E–1–	4.9672E–1–	4.8459E–1–	2.7776E–1–
	5	3.9329E–1	3.7469E–1–	3.5853E–1–	2.6792E–1–	3.5169E–1–	3.2557E–1–	3.7479E–1–	3.3263E–1–
	8	3.5127E–1	3.3844E–1–	3.3362E–1–	1.1313E–1–	3.3418E–1–	1.7885E–1–	3.3921E–1–	3.2337E–1–
	10	3.4556E–1	3.3533E–1–	3.3342E–1–	8.7316E–2–	3.3355E–1–	1.5405E–1–	3.3468E–1–	3.3387E–1–
DTLZ6	3	4.9712E–1	4.8962E–1–	4.3809E–1–	4.8205E–1–	4.6560E–1–	4.9706E–1–	4.7656E–1–	2.7059E–1–
	5	3.9140E–1	3.5882E–1–	3.6385E–1–	1.1392E–1–	3.4855E–1–	2.4060E–1–	3.7179E–1–	2.9571E–1–
	8	3.4922E–1	3.3359E–1–	3.3957E–1–	1.8683E–3–	3.3414E–1–	5.0408E–2–	3.3563E–1–	3.1209E–1–
	10	3.4616E–1	3.3338E–1–	3.3633E–1–	2.4107E–4–	3.3359E–1–	9.9183E–3–	3.3355E–1–	3.2287E–1–
DTLZ7	3	5.2444E–1	5.2897E–1+	5.2457E–1+	5.2656E–1+	5.2049E–1–	5.1360E–1–	5.2203E–1–	4.3744E–1–
	5	4.8477E–1	5.3138E–1+	4.9513E–1+	5.2104E–1+	5.1085E–1+	5.2420E–1+	5.1197E–1+	4.4938E–1–
	8	4.2246E–1	4.9148E–1+	4.1973E–1≈	4.6964E–1+	3.3758E–1–	4.8455E–1+	4.3294E–1+	3.5903E–1–
	10	4.1267E–1	4.7833E–1+	4.0332E–1≈	4.6247E–1+	3.5668E–1–	4.7031E–1+	4.4377E–1+	1.8168E–1–
+ / – / ≈		－	6/21/1	4/21/3	5/23/0	3/24/1	7/20/1	3/25/0	0/28/0

Table 4 The statistical results (mean) of the HV values obtained by MaOEA-CE, NSGA-III, RVEA, SPEAR, ASEA, hpaEA, NSGAII-SDR and MaOEA-IGD on WFG1-9 表 4 不同算法在WFG1–9上获得的HV 值的统计结果 (均值)

Problem	M	MaOEA-CE	NSGA-III	RVEA	SPEA-R	ASEA	hpaEA	NSGA-II-SDR	MaOEA-IGD
WFG1	3	9.7938E–1	9.7801E–1–	9.7684E–1–	9.7826E–1–	9.7788E–1–	7.3159E–1–	9.6130E–1–	6.1760E–1–
	5	9.9975E–1	9.9972E–1–	9.9965E–1–	9.9971E–1–	9.9955E–1–	9.8959E–1–	9.9153E–1–	9.4641E–1–
	8	9.9999E–1	9.9997E–1–	9.9958E–1–	9.9999E–1≈	9.9935E–1–	9.9082E–1–	9.8679E–1–	9.2150E–1–
	10	1.0000E+0	9.9996E–1–	9.9967E–1–	1.0000E+0≈	9.9920E–1–	9.9808E–1–	9.8925E–1–	9.5552E–1–
WFG2	3	9.7425E–1	9.7270E–1–	9.7163E–1–	9.7216E–1–	9.7293E–1–	9.6980E–1–	9.5331E–1–	8.4610E–1–
	5	9.9972E–1	9.9932E–1–	9.9894E–1–	9.9932E–1–	9.9911E–1–	9.9885E–1–	9.8364E–1–	9.6925E–1–
	8	9.9995E–1	9.9956E–1–	9.9344E–1–	9.9922E–1–	9.9860E–1–	9.9756E–1–	9.8302E–1–	9.8087E–1–
	10	9.9998E–1	9.9959E–1–	9.9588E–1–	9.9945E–1–	9.9893E–1–	9.9793E–1–	9.8990E–1–	9.9243E–1–
WFG3	3	6.3751E–1	6.3354E–1–	5.9869E–1–	6.2317E–1–	6.2103E–1–	6.0309E–1–	6.2319E–1–	3.5871E–1–
	5	4.5858E–1	4.4654E–1–	4.4544E–1–	4.6348E–1+	4.6436E–1+	3.8441E–1–	4.7049E–1+	4.9643E–1+
	8	3.5167E–1	2.9941E–1–	2.2962E–2–	2.8705E–1–	2.9525E–1–	6.0218E–2–	2.9405E–1–	3.3940E–1–
	10	2.4232E–1	2.0225E–1–	0.0000E+0–	2.5487E–1+	1.9253E–1–	2.4764E–3–	1.7228E–1–	2.9590E–1+
WFG4	3	8.2712E–1	8.2630E–1–	8.2538E–1–	8.2513E–1–	8.2629E–1–	8.1789E–1–	8.2130E–1–	4.9112E–1–
	5	9.6100E–1	9.5982E–1–	9.5980E–1–	9.5999E–1–	9.5994E–1–	9.4340E–1–	9.5528E–1–	8.2800E–1–
	8	9.9411E–1	9.9210E–1–	9.9292E–1–	9.9332E–1–	9.9217E–1–	9.2108E–1–	9.9218E–1–	9.6573E–1–
	10	9.9866E–1	9.9733E–1–	9.9783E–1–	9.9842E–1–	9.9698E–1–	9.3679E–1–	9.9791E–1–	9.8333E–1–
WFG5	3	7.9661E–1	7.9603E–1–	7.9586E–1–	7.9586E–1–	7.9602E–1–	7.9326E–1–	7.9328E–1–	6.8639E–1–
	5	9.2350E–1	9.2273E–1–	9.2274E–1–	9.2264E–1–	9.2272E–1–	9.2245E–1–	9.1996E–1–	8.9242E–1–
	8	9.4983E–1	9.4914E–1–	9.4906E–1–	9.4909E–1–	9.4894E–1–	9.3390E–1–	9.4827E–1–	9.3349E–1–
	10	9.5096E–1	9.5074E–1–	9.5073E–1–	9.5077E–1–	9.5055E–1–	9.4259E–1–	9.5042E–1–	9.4237E–1–
WFG6	3	7.8783E–1	7.8891E–1≈	7.8790E–1≈	7.9605E–1+	7.9163E–1≈	7.8718E–1≈	7.8426E–1≈	4.9499E–1–
	5	9.1020E–1	9.1397E–1≈	9.1071E–1≈	9.2174E–1+	9.1491E–1≈	9.0831E–1≈	9.1222E–1≈	6.0327E–1–
	8	9.4119E–1	9.3619E–1≈	9.2784E–1–	9.5153E–1+	9.3951E–1≈	9.1932E–1–	9.4458E–1≈	7.2931E–1–
	10	9.4234E–1	9.3361E–1–	9.3172E–1–	9.4564E–1≈	9.3951E–1≈	9.2251E–1–	9.4023E–1≈	7.5567E–1–
WFG7	3	8.2691E–1	8.2614E–1–	8.2534E–1–	8.2565E–1–	8.2602E–1–	8.2607E–1–	8.2282E–1–	5.4301E–1–
	5	9.6093E–1	9.5994E–1–	9.5971E–1–	9.5995E–1–	9.5999E–1–	9.5937E–1–	9.5691E–1–	7.5777E–1–
	8	9.9426E–1	9.9332E–1–	9.9267E–1–	9.9330E–1–	9.9312E–1–	9.7086E–1–	9.9237E–1–	9.4719E–1–
	10	9.9881E–1	9.9831E–1–	9.9824E–1–	9.9850E–1–	9.9787E–1–	9.7579E–1–	9.9828E–1–	9.8229E–1–
WFG8	3	7.8698E–1	7.8189E–1–	7.8197E–1–	7.8505E–1–	7.8021E–1–	7.7789E–1–	7.7789E–1–	2.8274E–1–
	5	9.2608E–1	9.2211E–1–	9.2142E–1–	9.2625E–1+	9.1852E–1–	9.1997E–1–	9.1997E–1–	4.0027E–1–
	8	9.6906E–1	9.6459E–1–	9.4007E–1–	9.7269E–1≈	9.5890E–1–	9.4538E–1–	9.6830E–1–	9.2024E–1–
	10	9.8494E–1	9.8179E–1–	9.4638E–1≈	9.9103E–1+	9.6542E–1–	9.6759E–1–	9.9128E–1+	9.6007E–1–
WFG9	3	8.1738E–1	8.1429E–1–	8.1570E–1–	8.1531E–1–	8.2219E–1+	8.0927E–1–	8.1465E–1–	5.7273E–1–
	5	9.4138E–1	9.3823E–1–	9.4186E–1≈	9.3992E–1–	9.4883E–1+	9.3642E–1–	9.3954E–1–	5.8588E–1–
	8	9.6370E–1	9.4268E–1–	9.6111E–1≈	9.5631E–1–	9.6845E–1≈	9.4903E–1–	9.7048E–1+	6.5693E–1–
	10	9.7547E–1	9.5584E–1–	9.6513E–1–	9.6891E–1–	9.7427E–1≈	9.6036E–1–	9.7536E–1≈	8.2792E–1–
+ / – / ≈		－	0/33/3	0/31/5	7/25/4	3/27/6	0/34/2	3/28/5	2/34/0

表3为8个算法在DTLZ的7个测试问题上的HV值统计结果. 可以看出, 在DTLZ的28个测试实例中, MaOEA-CE在18个上均优于其他7个对比算法, 尤其在DTLZ3和DTLZ5–6的所有目标维度上, MaOEA-CE的性能均优于其他算法. DTLZ2–4为规则型凹曲面PF问题, 采用RVCE生成的参考向量在此类规则型问题上具有很好的多样性, 同时在ESCE中使用的PBI聚合函数能很好平衡此类凹曲面PF问题的多样性和收敛性, 因此MaOEA-CE相较于其他算法有更好的性能表现. 对于退化问题DTLZ5–6, 由于它们的PF仍可较精准地拟合到 ${f_1}^p + {f_2}^p + \ldots + {f_M}^p = 1$ 的凹曲面上, 使用RVCE依然能够生成一部分对其PF进行均匀分割的参考向量, 同时ESCE从剩余候选解中依次选择多样性最好的解作为新参考向量, 可进一步提升对种群多样性的维护, ESCE中使用的PBI聚合函数同样较好平衡了此类凹曲面PF问题的多样性和收敛性. 在DTLZ1问题上, hpaEA显示了较强的竞争力, 主要是因为hpaEA利用超平面来选择突出解, 有利于提高种群的收敛性. DTLZ7是一个凹/凸混合、断开且多模的测试问题, 将其PF拟合到 ${f_1}^p + {f_2}^p + \ldots + {f_M}^p = 1$ 曲面时存在较大的误差, 采用RVCE生成的参考向量并不能均匀分割其PF, 导致MaOEA-CE在DTLZ7上性能较差.

表4为8个算法在WFG的9个测试问题上的HV值统计结果. 可以看出, 在WFG的36个测试实例中, MaOEA-CE在24个上均优于其他7个对比算法, 特别是在WFG1–2、WFG4–5和WFG7的所有目标维度上, MaOEA-CE的性能均优于其他算法. WFG4–9为带缩放的凹曲面PF问题, 得益于RVCE生成的参考向量更加均匀, 以及ESCE中的PBI聚合函数能很好平衡此类凹曲面PF问题的多样性和收敛性, MaOEA-CE保持了较好的性能. 对于PF形状不规则的WFG1–2, 由于它们的PF 整体上仍贴近一个 ${f_1}^p + {f_2}^p + \ldots + {f_M}^p = 1$ 的凸曲面, RVCE依然能够生成可较均匀分割其PF的参考向量, 有利于种群多样性的保护, ESCE中使用的TCH聚合函数则能较好平衡此类凸曲面PF问题的多样性和收敛性. 此外, SPEA-R在WFG问题上也有相对较好的性能表现, 原因在于其环境选择过程中对凹型PF上目标点的密度估计较为准确, 有利于获得较好的多样性. hpaEA在WFG问题集上的性能相对较差, 原因在于hpaEA优先保护的突出解偏向线性平面, 而WFG绝大部分测试问题的PF为非线性曲面, 突出解保护策略不利于种群的多样性.

表5为8个算法在MaF的15个测试问题上的HV值统计结果. 可以看出, 在MaF的60个测试实例中, MaOEA-CE在32个上均优于其他7个对比算法. 其中, 在MaF1–6、MaF8–11和MaF15上, MaOEA-CE的性能表现整体优于其他7个算法. MaF7与DTLZ7是完全相同的测试问题, MaOEA-CE在MaF7上性能较差的原因与DTLZ7一致. MaF12是具有偏好、欺诈和变量相关的凹PF问题, MaF13是单峰、退化和变量相关的凹PF问题, MaF14是线性、部分变量相关和大规模的PF问题, 由于它们的问题特性非常复杂, 使用 ${f_1}^p + {f_2}^p + \ldots + {f_M}^p = 1$ 曲面对它们真实PF的拟合不够准确, 导致使用RVCE生成的参考向量在PF上的分布并不均匀, 从而对MaOEA-CE的性能造成较重大影响. hpaEA和NSGA-II-SDR在MaF12–14上的性能相对更优, 原因在于二者分别通过突出解和改进Pareto支配关系来提升种群的收敛性, 在一定程度上提升了算法在难收敛问题上的性能. MaOEA-IGD在MaF的所有测试实例上, 绝大部分处于劣势, 原因在于该算法的收敛性能不佳.

Table 5 The statistical results (mean) of the HV values obtained by MaOEA-CE, NSGA-III, RVEA, SPEAR, ASEA, hpaEA, NSGAII-SDR and MaOEA-IGD on MaF1-15 表 5 不同算法在MaF1–15上获得的HV 值的统计结果 (均值)

Problem	M	MaOEA-CE	NSGA-III	RVEA	SPEA-R	ASEA	hpaEA	NSGA-II-SDR	MaOEA-IGD
MaF1	3	4.9799E–1	4.8598E–1–	4.7123E–1–	4.7259E–1–	4.7208E–1–	4.9485E–1–	2.5217E–1–	2.8927E–1–
	5	1.4627E–1	1.1336E–1–	7.8370E–2–	9.0352E–2–	6.8489E–2–	1.3803E–1–	1.3384E–1–	3.2076E–2–
	8	1.0906E–2	4.0290E–3–	1.3660E–3–	2.7066E–3–	3.1157E–3–	1.0117E–2–	9.7873E–3–	1.2752E–3–
	10	1.9679E–3	5.2642E–4–	1.9348E–4–	3.2796E–4–	3.3767E–4–	1.7984E–3–	1.7527E–3–	1.4435E–4–
MaF2	3	4.5678E–1	4.5245E–1–	4.5338E–1–	4.5076E–1–	4.5095E–1–	4.5375E–1–	4.5884E–1+	3.7126E–1–
	5	4.2329E–1	4.2303E–1≈	4.0534E–1–	4.0429E–1–	4.0153E–1–	4.2312E–1≈	4.3632E–1+	3.1366E–1–
	8	4.5519E–1	4.2801E–1–	3.7168E–1–	3.9951E–1–	4.1442E–1–	4.3020E–1–	4.3662E–1–	3.2552E–1–
	10	4.6311E–1	4.3900E–1–	3.7616E–1–	3.9923E–1–	4.2919E–1–	4.4104E–1–	4.3435E–1–	3.4286E–1–
MaF3	3	9.8505E–1	9.8340E–1–	9.6485E–1–	8.6753E–1–	9.8360E–1–	9.8381E–1–	9.5516E–1–	8.8378E–1–
	5	9.9991E–1	9.9985E–1–	9.9723E–1–	8.1852E–1–	9.9874E–1–	9.9988E–1–	9.8845E–1–	9.7356E–1–
	8	9.9999E–1	9.9469E–1–	9.9787E–1–	0.0000e+0–	9.9934E–1–	7.7534E–1≈	9.9048E–1–	9.4713E–1–
	10	1.0000E+0	9.6229E–1–	9.9928E–1–	0.0000e+0–	9.9974E–1–	1.7624E–1–	9.9527E–1–	6.7725E–1–
MaF4	3	7.2548E–1	7.1482E–1–	7.0209E–1–	5.0522E–1–	7.1489E–1–	7.2012E–1–	6.8641E–1–	4.1433E–1–
	5	3.4251E–1	3.0207E–1–	2.1434E–1–	1.5477E–1–	2.7559E–1–	3.4028E–1–	3.2714E–1–	9.6973E–2–
	8	4.4984E–2	3.2808E–2–	4.6900E–3–	1.9399E–2–	1.3030E–2–	4.6555E–2+	1.4404E–2–	4.6584E–3–
	10	1.2826E–2	8.4276E–3–	6.3090E–4–	3.7490E–3–	2.5650E–3–	1.2995E–2≈	2.9656E–3–	6.1820E–4–
MaF5	3	7.8529E–1	7.9609E–1+	8.1425E–1+	8.2455E–1+	8.2629E–1+	6.6712E–1–	6.8278E–1–	7.0968E–1–
	5	9.5826E–1	9.6015E–1+	9.6023E–1+	9.5931E–1+	9.6016E–1+	9.3951E–1≈	4.5073E–1–	9.1274E–1–
	8	9.9430E–1	9.9362E–1–	9.9060E–1–	9.9312E–1–	9.9364E–1–	9.8210E–1–	3.9845E–1–	9.2812E–1–
	10	9.9884E–1	9.9864E–1–	9.9794E–1–	9.9840E–1–	9.9864E–1–	9.9857E–1–	3.3333E–1–	9.5652E–1–
MaF6	3	4.9710E–1	4.9148E–1–	4.7204E–1–	4.8177E–1–	4.7538E–1–	4.9694E–1–	4.9593E–1–	2.5543E–1–
	5	3.9053E–1	3.8489E–1–	3.7607E–1–	3.7224E–1–	3.7257E–1–	3.9313E–1+	3.8721E–1–	2.8579E–1–
	8	3.5443E–1	3.4585E–1–	3.4424E–1–	2.8150E–1–	3.4284E–1–	3.5542E–1+	3.5232E–1–	2.4527E–1–
	10	3.4718E–1	3.3739E–1–	3.3804E–1–	3.3310E–1–	3.3945E–1–	1.6816E–1–	3.4630E–1–	2.6687E–1–
MaF7	3	5.2823E–1	5.2885E–1+	5.2452E–1–	5.2656E–1–	5.1686E–1–	5.0590E–1–	5.2181E–1–	4.2422E–1–
	5	4.6996E–1	5.3088E–1+	4.9530E–1+	5.2113E–1+	5.0780E–1+	5.3163E–1+	5.1138E–1+	4.5028E–1–
	8	4.2271E–1	4.9212E–1+	4.1734E–1≈	4.7006E–1+	3.3802E–1–	4.8514E–1+	4.5129E–1+	3.6332E–1–
	10	4.1122E–1	4.7762E–1+	3.9733E–1≈	4.6235E–1+	3.6186E–1–	4.7138E–1+	4.2367E–1+	1.8099E–1–
MaF8	3	5.1996E–1	5.0539E–1–	4.7047E–1–	3.6160E–1–	4.7816E–1–	4.5558E–1–	4.6674E–1–	3.1555E–1–
	5	3.1436E–1	2.9786E–1–	2.3879E–1–	2.1653E–1–	2.5939E–1–	3.2053E–1+	3.0666E–1–	1.6752E–1–
	8	1.2838E–1	1.0572E–1–	6.5197E–2–	6.5849E–2–	8.3962E–2–	1.2272E–1–	1.2628E–1–	5.2245E–2–
	10	6.7858E–2	5.7489E–2–	2.9669E–2–	3.2694E–2–	4.1377E–2–	6.9193E–2+	6.8512E–2+	2.3727E–2–
MaF9	3	9.3475E–1	9.3593E–1+	9.3584E–1+	8.3721E–1–	9.3582E–1+	9.0166E–1–	8.9191E–1–	9.2918E–1–
	5	5.8000E–1	4.2801E–1–	4.9133E–1–	2.7343E–1–	4.8674E–1–	5.7677E–1–	5.3847E–1–	3.5685E–1–
	8	2.0014E–1	1.2760E–1–	1.0444E–1–	2.9296E–3–	1.1663E–1–	1.0469E–1–	1.8491E–1–	7.2643E–2–
	10	1.0502E–1	7.2012E–2–	4.1430E–2–	2.7051E–2–	7.1224E–2–	9.4443E–2≈	1.0802E–1+	3.6124E–2–
MaF10	3	9.7935E–1	9.7783E–1–	9.7702E–1–	9.7826E–1–	9.7787E–1–	7.7177E–1–	9.6233E–1–	6.4863E–1–
	5	9.9974E–1	9.9973E–1–	9.9964E–1–	9.9972E–1–	9.9957E–1–	9.8260E–1–	9.9342E–1–	9.4515E–1–
	8	9.9999E–1	9.9997E–1–	9.9956E–1–	9.9999E–1≈	9.9931E–1–	9.9165E–1–	9.8661E–1–	8.9547E–1–
	10	1.0000E+0	9.9996E–1–	9.9965E–1–	1.0000E+0≈	9.9918E–1–	9.9840E–1–	9.9334E–1–	9.7845E–1–
MaF11	3	9.7452E–1	9.7259E–1–	9.7160E–1–	9.7218E–1–	9.7305E–1–	9.6957E–1–	9.5492E–1–	8.4863E–1–
	5	9.9974E–1	9.9934E–1–	9.9894E–1–	9.9930E–1–	9.9913E–1–	9.9887E–1–	9.8384E–1–	9.7031E–1–
	8	9.9996E–1	9.9951E–1–	9.9419E–1–	9.9932E–1–	9.9867E–1–	9.9761E–1–	9.8258E–1–	9.9088E–1–
	10	9.9998E–1	9.9962E–1–	9.9597E–1–	9.9945E–1–	9.9904E–1–	9.9781E–1–	9.8930E–1–	9.9331E–1–
MaF12	3	8.1769E–1	8.1410E–1–	8.1249E–1–	8.1345E–1–	8.2250E–1+	8.1011E–1–	8.1439E–1–	5.7944E–1–
	5	9.4157E–1	9.3810E–1–	9.4223E–1≈	9.3938E–1–	9.4936E–1+	9.3687E–1–	9.3987E–1–	5.7041E–1–
	8	9.6771E–1	9.3395E–1–	9.5396E–1≈	9.5398E–1–	9.6846E–1≈	9.4923E–1–	9.6979E–1+	6.7272E–1–
	10	9.7611E–1	9.5449E–1–	9.6421E–1–	9.6629E–1–	9.7362E–1–	9.6081E–1–	9.7568E–1≈	8.9621E–1–
MaF13	3	8.1946E–1	8.0630E–1–	8.0976E–1–	7.8134E–1–	7.8633E–1–	8.1310E–1–	8.0665E–1–	5.4095E–1–
	5	3.4000E–1	4.3333E–1+	4.4163E–1+	3.0659E–1≈	2.3448E–1–	5.4262E–1+	5.0696E–1+	2.1748E–1–
	8	2.7340E–1	2.5128E–1–	2.3716E–1–	6.5586E–2–	5.1483E–2–	3.6381E–1+	3.2646E–1+	1.6913E–1–
	10	2.4484E–1	2.3886E–1≈	1.9731E–1–	7.4218E–2–	1.2907E–1–	3.1031E–1+	2.8323E–1+	1.7397E–1–
MaF14	3	4.8254E–1	4.9241E–1≈	3.2139E–1–	4.9997E–1≈	1.4367E–1–	5.1904E–1≈	4.2558E–1–	3.9439E–1–
	5	3.9173E–1	3.4397E–1≈	4.4363E–1≈	4.4782E–1≈	0.0000E+0–	4.9931E–1≈	5.7176E–1+	3.7015E–1≈
	8	3.0330E–1	2.1658E–2–	5.7359E–1+	0.0000E+0–	2.6407E–2–	2.3519E–3–	6.8671E–1+	4.0283E–1≈
	10	1.5560E–1	1.9455E–3–	3.9095E–1+	0.0000E+0–	1.7218E–1+	9.0664E–3–	7.1243E–1+	3.5439E–1+–
MaF15	3	5.3478E–1	4.0624E–1–	1.2197E–1–	1.9904E–1–	1.3200E–1–	5.3045E–1–	3.4101E–1–	3.5516E–1–
	5	1.2881E–1	2.4554E–2–	1.4756E–1+	2.3718E–2–	7.8316E–3–	4.9786E–2–	7.8868E–2–	8.7205E–2–
	8	5.0939E–3	7.1208E–4–	5.2940E–3≈	1.5267E–4–	1.1806E–3–	8.1626E–4–	2.5359E–3–	8.4895E–4–
	10	6.8956E–4	2.0188E–5–	5.0135E–4–	2.3329E–7–	6.0210E–5–	2.4857E–5–	3.4704E–4–	8.7840E–5–
+ / – / ≈		－	8/48/4	8/46/6	5/50/5	7/52/1	11/42/7	14/45/1	1/57/2

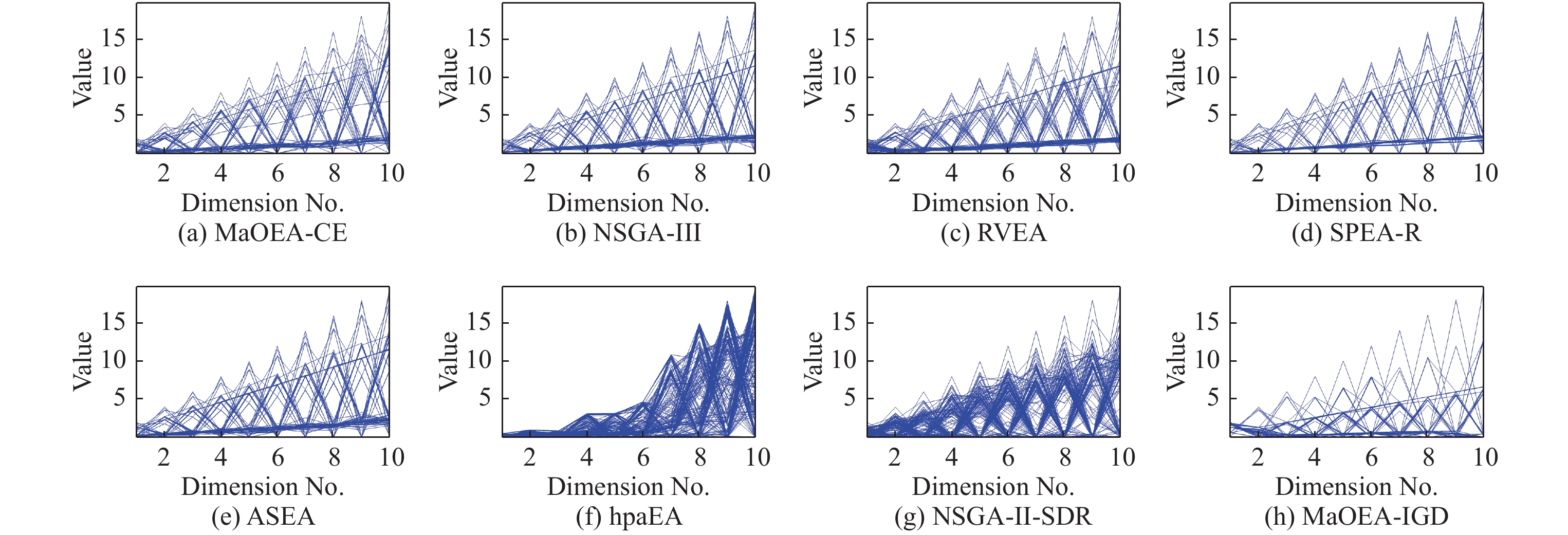
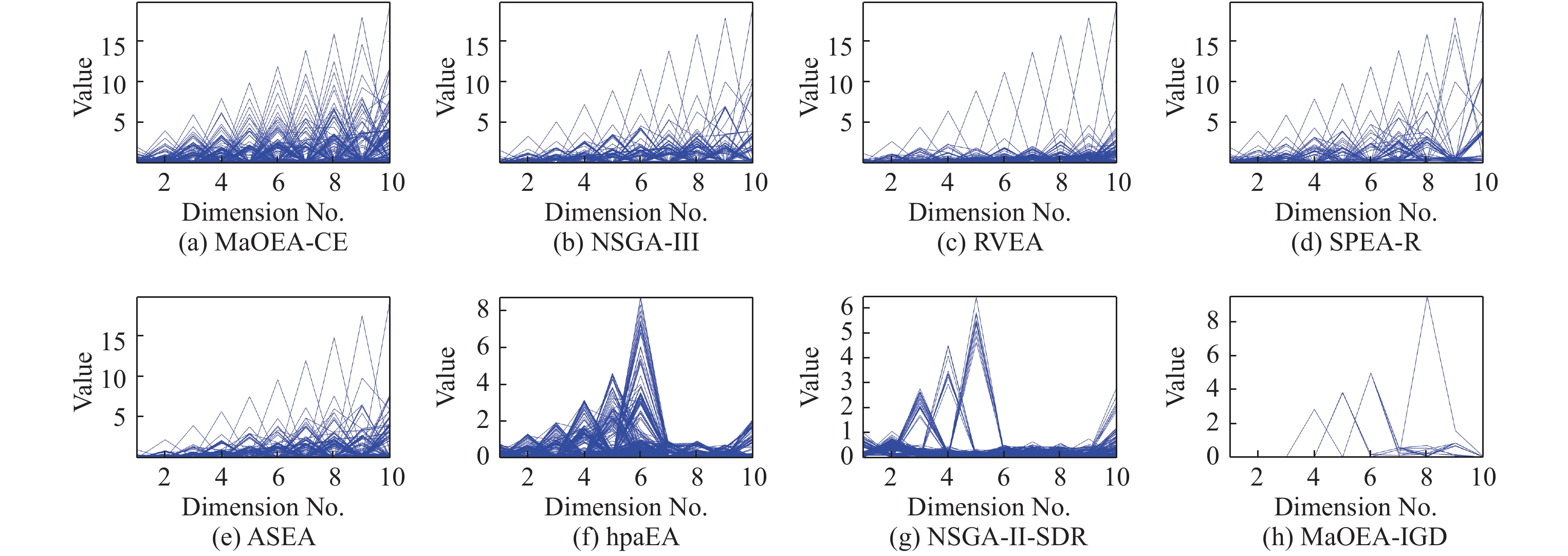
为进一步展示8个算法在处理规则型PF问题和不规则型PF问题时平衡种群收敛性和多样性的能力, 图4和图5分别给出了各算法在规则型PF问题WFG4和不规则型PF问题WFG1上, 目标维度为10时的最终种群分布图. 从图4可以看出, 在处理规则的WFG4问题时, MaOEA-CE、NSGA-III、RVEA、SPEA-R和ASEA都显示出了较好的收敛性和多样性, 但hpaEA、NSGA-II-SDR和MaOEA-IGD的多样性则较差. 从图5可以看出, 在处理不规则的WFG1 问题时, MaOEA-CE相比其他7个算法, 保持了更好的多样性和收敛性, 而NSGA-III、RVEA、SPEA-R和ASEA 存在多样性较差的情形, hpaEA, NSGA-II-SDR和MaOEA-IGD则多样性和收敛性均相对较差. 综上可见, MaOEA-CE在处理规则和不规则PF问题时都具有很强的竞争力.

Fig. 4 Solution sets of MaOEA-CE, NSGA-III, RVEA, SPEA-R, ASEA, hpaEA, NSGA-II-SDR and MaOEA-IGD on WFG4 problem with 10-objectives 图 4 不同算法在10维WFG4 问题上获得的解集

Fig. 5 Solution sets of MaOEA-CE, NSGA-III, RVEA, SPEA-R, ASEA, hpaEA, NSGA-II-SDR and MaOEA-IGD on WFG1 problem with 10-objectives 图 5 不同算法在10维WFG1 问题上获得的解集

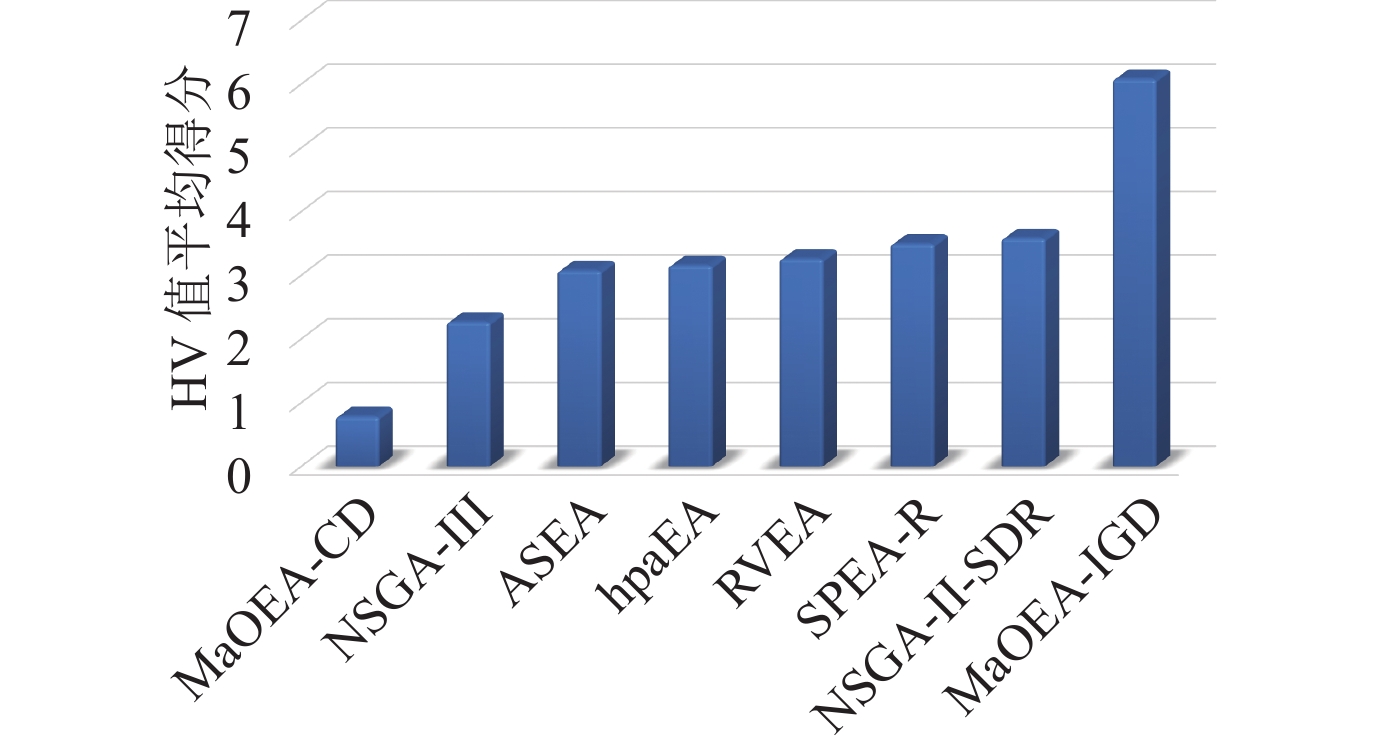
此外, 采用 $\theta $ -DEA^[7]中提出的平均得分计算方法, 图6展示了8 个算法在DTLZ、WFG和MaF的全部128个测试实例上的HV值平均得分, 得分越小, 整体性能越好. 根据图6, 可直观看出MaOEA-CE相比于其他7个算法具有非常明显的性能优势.

Fig. 6 Ranking in the average performance score in terms of HV over all test instances for the algorithms of MaOEA-CE, NSGA-III, RVEA, SPEA-R, ASEA, hpaEA, NSGA-II-SDR and MaOEA-IGD 图 6 不同算法在所有测试实例中的平均HV性能得分排名

(2) RVCE的有效性验证

为单独验证RVCE方法的有效性, 本文以经典的NSGA-III为框架, 分别将不同的参考向量生成方法RVCE、NBI、K-layer和MUD嵌入其中, 形成的新算法分别命名为NSGA-III-RVCE、NSGA-III-NBI、NSGA-III-K-layer和NSGA-III-MUD. 在7个不同形状的PF问题上对这4 个算法进行对比实验, 包括平面PF问题DTLZ1、凹曲面PF问题DTLZ2、WFG4和MaF2、凸曲面PF问题MaF3、凹/凸混合PF问题WFG1和WFG2、退化PF问题DTLZ5.

(3) ESCE的有效性验证

为单独验证ESCE策略的有效性, 用ESCE分别替换3个先进的MaOEA算法A-NSGA-III^[20]、RVEA*^[6]和hpaEA^[36]中原有的环境选择, 形成的新算法分别命名为A-NSGA-III-ESCE、RVEA*-ESCE和hpaEA-ESCE.

采用和RVCE有效性验证相同的测试问题, 表6展示了3个原算法与3个新算法的HV值统计结果. 可以发现, 在采用了ESCE策略之后, 3个新算法的性能均得到了较大程度提升. 其中, A-NSGA-III-ESCE和RVEA*-ESCE几乎在所有测试实例上的性能都得到了提升. hpaEA-ESCE在DTLZ1问题上出现了性能下滑, 原因在于hpaEA原有环境选择算子采用的突出解保护措施有利于强化种群往线性平面收敛的压力. 但对于其他非线性问题, hpaEA-ESCE则显示出了更好的性能. 综上说明ESCE具有较强的竞争力.

Table 6 The statistical results (mean) of the HV values obtained by A-NSGA-III, A-NSGA-III-ESCE, RVEA*, RVEA*-ESCE, hpaEA and hpaEA-ESCE on different test problems 表 6 不同算法在不同测试问题上的HV值的统计结果(均值)

Problem	M	A-NSGA-III	A-NSGA-III-ESCE	RVEA*	RVEA*-ESCE	hpaEA	hpaEA-ESCE
DTLZ1	3	9.3377E–1	9.3751E–1+	9.3505E–1	9.3751E–1+	9.3820E–1	9.3750E–1–
	5	9.9524E–1	9.9572E–1+	9.9523E–1	9.9575E–1+	9.9600E–1	9.9574E–1–
	8	9.9943E–1	9.9982E–1+	9.9981E–1	9.9981E–1≈	9.9984E–1	9.9980E–1–
	10	9.9772E–1	9.9999E–1+	9.9998E–1	9.9999E–1+	9.9999E–1	9.9999E–1≈
DTLZ2	3	8.2620E–1	8.2634E–1+	8.2290E–1	8.2634E–1+	8.2668E–1	8.2634E–1–
	5	9.6019E–1	9.6004E–1–	9.5885E–1	9.6000E–1+	9.6128E–1	9.6013E–1–
	8	9.8749E–1	9.9376E–1+	9.9360E–1	9.9378E–1+	9.9119E–1	9.9379E–1+
	10	9.9628E–1	9.9870E–1+	9.9859E–1	9.9870E–1+	9.9564E–1	9.9870E–1+
DTLZ5	3	4.9339E–1	4.9684E–1+	4.9662E–1	4.9689E–1+	4.9670E–1	4.9694E–1+
	5	3.7483E–1	3.8379E–1+	3.7784E–1	3.8425E–1+	3.6688E–1	3.8573E–1+
	8	3.3755E–1	3.5115E–1+	3.4321E–1	3.5229E–1+	1.7902E–1	3.5239E–1+
	10	3.3339E–1	3.4405E–1+	3.3677E–1	3.4595E–1+	1.4458E–1	3.4597E–1+
WFG1	3	9.7645E–1	9.7773E–1+	9.7468E–1	9.7741E–1+	7.6637E–1	9.7745E–1+
	5	9.9961E–1	9.9965E–1+	9.9946E–1	9.9962E–1+	9.8418E–1	9.9966E–1+
	8	9.9977E–1	9.9999E–1+	9.9111E–1	9.9999E–1+	9.9441E–1	9.9999E–1+
	10	9.9989E–1	1.0000E+0+	9.9956E–1	1.0000E+0+	9.9935E–1	1.0000E+0+
WFG2	3	9.7055E–1	9.7332E–1+	9.6861E–1	9.7345E–1+	9.6946E–1	9.7365E–1+
	5	9.9826E–1	9.9960E–1+	9.9864E–1	9.9929E–1+	9.9882E–1	9.9933E–1+
	8	9.9894E–1	9.9991E–1+	9.9712E–1	9.9981E–1+	9.9767E–1	9.9979E–1+
	10	9.9884E–1	9.9996E–1+	9.9648E–1	9.9988E–1+	9.9798E–1	9.9987E–1+
WFG4	3	8.0855E–1	8.2631E–1+	8.2169E–1	8.2632E–1+	8.2401E–1	8.2631E–1≈
	5	9.5297E–1	9.5956E–1+	9.5956E–1	9.5964E–1+	9.4029E–1	9.5958E–1+
	8	9.6134E–1	9.9346E–1+	9.8260E–1	9.9341E–1+	9.2349E–1	9.9341E–1+
	10	9.7337E–1	9.9845E–1+	9.8865E–1	9.9838E–1+	9.3472E–1	9.9838E–1+
MaF2	3	4.5057E–1	4.5691E–1+	4.5251E–1	4.5690E–1+	4.5326E–1	4.5758E–1+
	5	4.1416E–1	4.3073E–1+	4.1015E–1	4.3302E–1+	4.2443E–1	4.3478E–1+
	8	4.2143E–1	4.6468E–1+	3.8947E–1	4.6517E–1+	4.2997E–1	4.6450E–1+
	10	4.4179E–1	4.7225E–1+	3.7131E–1	4.6408E–1+	4.4293E–1	4.6468E–1+
MaF3	3	9.8121E–1	9.8335E–1+	9.8198E–1	9.8339E–1+	9.8413E–1	9.8341E–1–
	5	9.9912E–1	9.9984E–1+	9.9984E–1	9.9985E–1+	9.9990E–1	9.9985E–1–
	8	8.5212E–1	9.9999E–1+	1.0000E+0	9.9999E–1–	7.3086E–1	9.9999E–1≈
	10	9.3565E–1	1.0000E+0+	1.0000E+0	1.0000E+0+	1.5039E–1	1.0000E+0+
+ / – / ≈		－	31/1/0	－	30/1/1	－	22/7/3

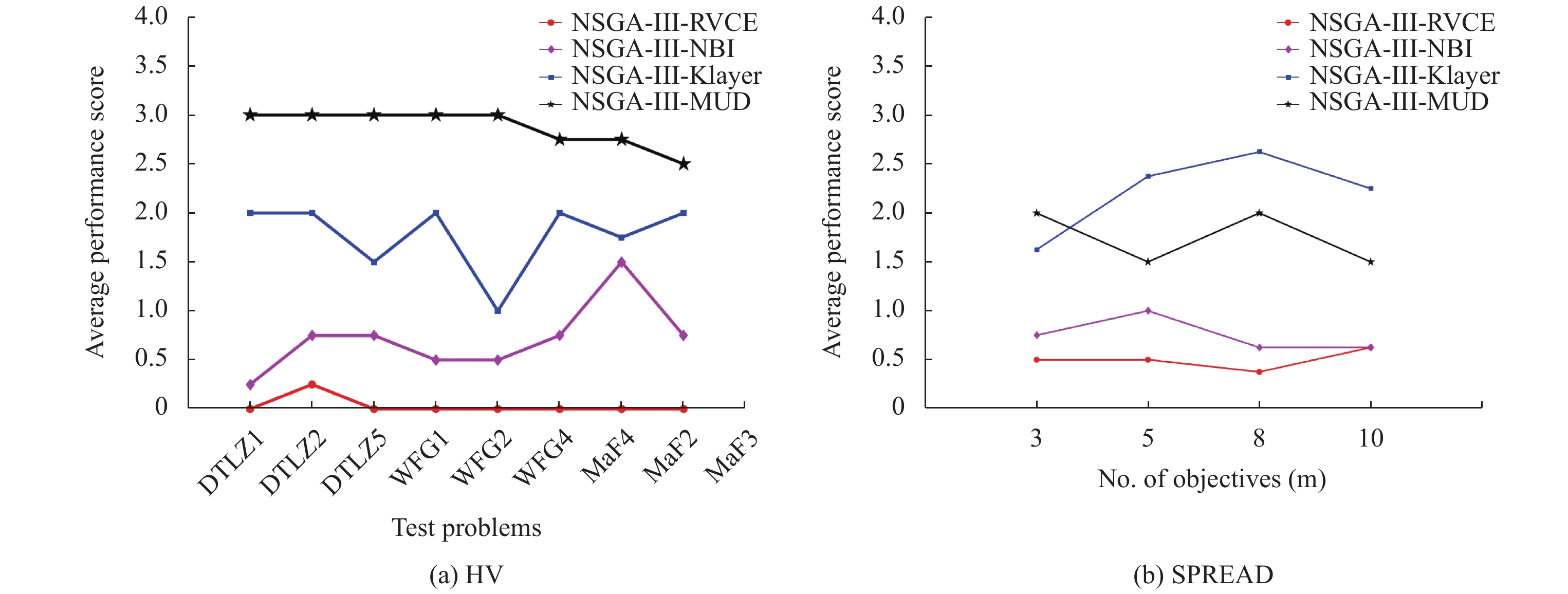
图7(a)展示了4个对比算法分别在7个测试问题上, 3、5、8、10维的平均HV值. 可以发现, 对于上述PF形状不同的各个问题, NSGA-III-RVCE均取得了最佳的整体综合性能, 说明RVCE比其他3种参考向量生成方法更具竞争力. 图7(b)展示了4个对比算法分别在3、5、8、10维度上, 7个测试问题的平均SPREAD值. 同样可以发现, NSGA-III-RVCE在不同的目标维度上都取得了第1名的成绩, 说明从低维到高维测试实例, RVCE生成的参考向量对于种群多样性的维护都最具竞争优势.

Fig. 7 Ranking in the average performance score in terms of HV on each test problem and the average performance score in terms of HV on each dimension for the algorithms of NSGA-III-RVCE, NSGA-III-NBI, NSGA-III-K-layer and NSGA-III-MUD 图 7 不同算法在各个测试问题上的平均HV性能得分排名和在不同维度下的平均SPREAD性能得分排名

4 总结与展望

为能同时处理好具有各种PF形状的优化问题, 本文提出了一种基于PF曲率预估的超多目标进化算MaOEA-CE. 通过对当前种群所对应PF的拟合, 设计了一种基于曲率的参考向量生成方法RVCE, 可较好地生成能匹配不同PF形状的参考向量, 有利于提升进化过程中种群的多样性. 同时设计了一个基于曲率的环境选择策略ESCE, 通过对聚合函数的自适应选择, 并利用种群信息对参考向量进行动态调整, 结合对收敛性最差个体的逐一剔除, 在维护种群多样性的同时提升了种群的收敛性. 与7个先进算法在DTLZ、WFG和MaF测试集上的对比实验表明, MaOEA-CE在处理各类规则PF和不规则PF时均有很强的竞争力. 未来工作中, 我们将致力于研究在难收敛和不规则PF问题上准确预估PF的能力, 从而使生成的参考向量具有更强的适应性, 以进一步提高算法的性能. 与此同时, 将本文所提算法扩展至各类带约束问题和各类实际应用问题, 具有非常重要的价值. 本文所提算法的源代码已在 https://github.com/CIA-SZU/LWP上公开.

参考文献

[1]	Zhou YM, Li ZJ, Ge JD, Li CY, Zhou XY, Luo B. Multi-objective workflow scheduling based on delay transmission in mobile cloud computing. Ruan Jian Xue Bao/Journal of Software, 2018, 29(11): 3306–3325 (in Chinese with English abstrct). http://www.jos.org.cn/1000-9825/5479.htm
[2]	Xiang Y, Zhou YR, Cai SW. Integrating preference in many-objective optimal software product selection algorithm. Ruan Jian Xue Bao/Journal of Software, 2020, 31(2): 282–301 (in Chinese with English abstrct). http://www.jos.org.cn/1000-9825/5637.htm
[3]	Zhang QF, Li H. MOEA/D: A multiobjective evolutionary algorithm based on decomposition. IEEE Trans. on Evolutionary Computation, 2007, 11(6): 712-731. [doi:10.1109/TEVC.2007.892759]
[4]	Deb K, Jain H. An evolutionary many-objective optimization algorithm using reference-point-based nondominated sorting approach, part I: Solving problems with box constraints. IEEE Trans. on Evolutionary Computation, 2014, 18(4): 577-601. [doi:10.1109/TEVC.2013.2281535]
[5]	Li K, Deb K, Zhang QF, Kwong S. An evolutionary many-objective optimization algorithm based on dominance and decomposition. IEEE Trans. on Evolutionary Computation, 2015, 19(5): 694-716. [doi:10.1109/TEVC.2014.2373386]
[6]	Cheng R, Jin YC, Olhofer M, Sendhoff B. A reference vector guided evolutionary algorithm for many-objective optimization. IEEE Trans. on Evolutionary Computation, 2016, 20(5): 773-791. [doi:10.1109/TEVC.2016.2519378]
[7]	Yuan Y, Xu H, Wang B, Yao X. A new dominance relation-based evolutionary algorithm for many-objective optimization. IEEE Trans. on Evolutionary Computation, 2016, 20(1): 16-37. [doi:10.1109/TEVC.2015.2420112]
[8]	Das I, Dennis JE. Normal-boundary intersection: A new method for generating the pareto surface in nonlinear multicriteria optimization problems. SIAM Journal on Optimization, 1998, 8(3): 631-657. [doi:10.1137/S1052623496307510]
[9]	Jiang SY and Yang SX. A strength Pareto evolutionary algorithm based on reference direction for multiobjective and many-objective optimization. IEEE Trans. on Evolutionary Computation, 2017, 21(3): 329-346. [doi:10.1109/TEVC.2016.2592479]
[10]	Tian Y, Xiang XS, Zhang XY, Cheng R, Jin YC. Sampling reference points on the Pareto fronts of benchmark multi-objective optimization problems. In: Proc. of the 2018 IEEE Congress on Evolutionary Computation. Rio de Janeiro: IEEE, 2018. 1–6.
[11]	Ma XL, Yu YN, Li XD, Qi YT, Zhu ZX. A survey of weight vector adjustment methods for decomposition-based multiobjective evolutionary algorithms. IEEE Trans. on Evolutionary Computation, 2020, 24(4): 634-649. [doi:10.1109/TEVC.2020.2978158]
[12]	Ishibuchi H, Murata T. A multi-objective genetic local search algorithm and its application to flowshop scheduling. IEEE Trans. on Systems, Man, and Cybernetics, Part C (Applications and Reviews), 1998, 28(3): 392-403. [doi:10.1109/5326.704576]
[13]	Li H, Ding M, Deng JD, Zhang QF. On the use of random weights in MOEA/D. In: Proc. of the 2015 IEEE Congress on Evolutionary Computation. Sendai: IEEE, 2015. 978–985.
[14]	Jiang SW, Cai ZH, Zhang J, Ong YS. Multiobjective optimization by decomposition with Pareto-adaptive weight vectors. In: Proc. of the 7th Int’l Conf. on Natural Computation. Shanghai: IEEE, 2011. 1260–1264.
[15]	Gu FQ, Cheung YM. Self-organizing map-based weight design for decomposition-based many-objective evolutionary algorithm. IEEE Trans. on Evolutionary Computation, 2018, 22(2): 211-225. [doi:10.1109/TEVC.2017.2695579]
[16]	Liu HL, Chen L, Zhang QF, Deb K. An evolutionary many-objective optimisation algorithm with adaptive region decomposition. In: Proc. of the 2016 IEEE Congress on Evolutionary Computation. Vancouver: IEEE, 2016. 4763–4769.
[17]	Asafuddoula M, Singh HK, Ray T. An enhanced decomposition-based evolutionary algorithm with adaptive reference vectors. IEEE Trans. on Cybernetics, 2018, 48(8): 2321-2334. [doi:10.1109/TCYB.2017.2737519]
[18]	Qi YT, Ma XL, Liu F, Jiao LC, Sun JY, Wu JS. MOEA/D with adaptive weight adjustment. Evolutionary Computation, 2014, 22(2): 231-264. [doi:10.1162/EVCO_a_00109]
[19]	De Farias LRC, Braga PHM, Bassani HD, Araújo AFR. MOEA/D with uniformly randomly adaptive weights. In: Proc. of the 2018 Genetic and Evolutionary Computation Conf. Kyoto: ACM, 2018. 641–648.
[20]	Jain H, Deb K. An evolutionary many-objective optimization algorithm using reference-point based nondominated sorting approach, Part II: Handling constraints and extending to an adaptive approach. IEEE Trans. on Evolutionary Computation, 2014, 18(4): 602-622. [doi:10.1109/TEVC.2013.2281534]
[21]	Xu H, Zeng WH, Zhang DF, Zeng XX. MOEA/HD: A multiobjective evolutionary algorithm based on hierarchical decomposition. IEEE Trans. on Cybernetics, 2019, 49(2): 517-526. [doi:10.1109/TCYB.2017.2779450]
[22]	Ma XL, Liu F, Qi YT, Li LL, Jiao LC, Deng XZ, Wang XD, Dong B, Hou ZT, Zhang YX, Wu JS. MOEA/D with biased weight adjustment inspired by user preference and its application on multi-objective reservoir flood control problem. Soft Computing, 2016, 20(12): 4999-5023. [doi:10.1007/s00500-015-1789-z]
[23]	Yu G, Zheng JH, Shen RM, Li MQ. Decomposing the user-preference in multiobjective optimization. Soft Computing, 2016, 20(10): 4005-4021. [doi:10.1007/s00500-015-1736-z]
[24]	Ishibuchi H, Setoguchi Y, Masuda H, Nojima Y. Performance of decomposition-based many-objective algorithms strongly depends on Pareto front shapes. IEEE Trans. on Evolutionary Computation, 2017, 21(2): 169-190. [doi:10.1109/TEVC.2016.2587749]
[25]	Zitzler E, Thiele L. Multiobjective evolutionary algorithms: A comparative case study and the strength Pareto approach. IEEE Trans. on Evolutionary Computation, 1999, 3(4): 257-271. [doi:10.1109/4235.797969]
[26]	Liu YP, Gong DW, Sun J, Jin YC. A many-objective evolutionary algorithm using a one-by-one selection strategy. IEEE Trans. on Cybernetics, 2017, 47(9): 2689-2702. [doi:10.1109/TCYB.2016.2638902]
[27]	Deb K, Agrawal RB. Simulated binary crossover for continuous search space. Complex Systems, 1995, 9(2): 115-148.
[28]	Deb K, Goyal M. A combined genetic adaptive search (GeneAS) for engineering design. Computer Science and Informatics, 1996, 26(4): 30-45.
[29]	Liang ZP, Hu KF, Ma XL, Zhu ZX. A many-objective evolutionary algorithm based on a two-round selection strategy. IEEE Trans. on Cybernetics, 2021, 51(3): 1417-1429. [doi:10.1109/TCYB.2019.2918087]
[30]	Jara EC. Multi-objective optimization by using evolutionary algorithms: The p-optimality criteria . IEEE Trans. on Evolutionary Computation, 2014, 18(2): 167-179. [doi:10.1109/TEVC.2013.2243455]
[31]	Li K, Zhang QF, Kwong S, Li MQ, Wang R. Stable matching-based selection in evolutionary multiobjective optimization. IEEE Trans. on Evolutionary Computation, 2014, 18(6): 909-923. [doi:10.1109/TEVC.2013.2293776]
[32]	Deb K, Thiele L, Laumanns M, Zitzler E. Scalable test problems for evolutionary multiobjective optimization. In: Abraham A, Jain L, Goldberg R, eds. Evolutionary Multiobjective Optimization: Theoretical Advances and Applications. London: Springer, 2005. 105–145.
[33]	Huband S, Hingston P, Barone L, While L. A review of multiobjective test problems and a scalable test problem toolkit. IEEE Trans. on Evolutionary Computation, 2006, 10(5): 477-506. [doi:10.1109/TEVC.2005.861417]
[34]	Cheng R, Li MQ, Tian Y, Zhang XY, Yang SX, Jin YC, Yao X. A benchmark test suite for evolutionary many-objective optimization. Complex & Intelligent Systems, 2017, 3(1): 67-81. [doi:10.1007/s40747-017-0039-7]
[35]	Liu C, Zhao Q, Yan B, Elsayed S, Ray T, Sarker R. Adaptive sorting-based evolutionary algorithm for many-objective optimization. IEEE Trans. on Evolutionary Computation, 2019, 23(2): 247-257. [doi:10.1109/TEVC.2018.2848254]
[36]	Chen HK, Tian Y, Pedrycz W, Wu GH, Wang R, Wang L. Hyperplane assisted evolutionary algorithm for many-objective optimization problems. IEEE Trans. on Cybernetics, 2020, 50(7): 3367-3380. [doi:10.1109/TCYB.2019.2899225]
[37]	Tian Y, Cheng R, Zhang XY, Su YS, Jin YC. A strengthened dominance relation considering convergence and diversity for evolutionary many-objective optimization. IEEE Trans. on Evolutionary Computation, 2019, 23(2): 331-345. [doi:10.1109/TEVC.2018.2866854]
[38]	Sun YN, Yen GG, Yi Z. IGD indicator-based evolutionary algorithm for many-objective optimization problems. IEEE Trans. on Evolutionary Computation, 2019, 23(2): 173-187. [doi:10.1109/TEVC.2018.2791283]
[39]	Zitzler E, Thiele L, Laumanns M, Fonseca CM, Da Fonseca VG. Performance assessment of multiobjective optimizers: An analysis and review. IEEE Trans. on Evolutionary Computation, 2003, 7(2): 117-132. [doi:10.1109/TEVC.2003.810758]
[40]	Xiang Y, Zhou YR, Li MQ, Chen ZF. A vector angle-based evolutionary algorithm for unconstrained many-objective optimization. IEEE Trans. on Evolutionary Computation, 2017, 21(1): 131-152. [doi:10.1109/TEVC.2016.2587808]
[41]	Wang R, Zhou ZB, Ishibuchi H, Liao TJ, Zhang T. Localized weighted sum method for many-objective optimization. IEEE Trans. on Evolutionary Computation, 2018, 22(1): 3-18. [doi:10.1109/TEVC.2016.2611642]
[1]	周业茂, 李忠金, 葛季栋, 李传艺, 周筱羽, 骆斌. 移动云计算中基于延时传输的多目标工作流调度. 软件学报, 2018, 29(11): 3306–3325. http://www.jos.org.cn/1000-9825/5479.htm
[2]	向毅, 周育人, 蔡少伟. 集成偏好的高维多目标最优软件产品选择算法. 软件学报, 2020, 31(2): 282–301. http://www.jos.org.cn/1000-9825/5637.htm