2. 华东交通大学 信息工程学院, 江西 南昌 330013
2. School of Information Engineering, East China Jiaotong University, Nanchang 330013, China
随着经济的快速发展, 国家的车辆总数、城市道路和高速公路的数量也随之不断增加, 更多的道路交通问题(交通拥堵, 交通事故等)也随之而来. 其中, 交通事故是15–29岁年轻人的首要死亡原因. 交通事故的发生会直接影响到发生事故路段的交通状况, 导致交通拥堵, 甚至造成更为严重的损失. 如何基于实时道路风险预测进行路径选择, 从而缓解交通拥堵减少交通事故的发生, 已经成为现代城市发展中亟待解决的一个热点问题[1].
目前国内外对于道路安全风险的研究方法主要分为两个方面: 一是通过模糊理论[2]、回归分析[3]、深度学习[4]等模型来预测事故的发生率、事故发生次数等相关数据并分析道路交通的安全性; 二是通过分析道路条件、交通环境因素与交通安全的关系来判断道路的安全性[5]. 道路交通安全研究已积累大量的研究成果, 由于利用的数据不同, 还存在一些不足. 如利用交通事故数据方面, 大多是事故后的统计工作, 事故发生前的风险研究相对较少.
随着智能设备的不断发展, 车联网(Internet of vehicles, IoV)系统[6]成为了解决该问题的一个热门话题. 车联网系统是一个三级客户端连接云系统, 分别包括客户端、连接和云. 但由于云计算所需要处理的交通数据非常庞大, 这样对数据分析的结果就会有所延迟, 这样的缺陷对于交通实时信息传递是致命的. 新型网络任务和场景, 如自动驾驶、安防监控等, 对于网络延时和可靠性安全性等方面的高要求使得传统网络架构难以应对, 由此边缘计算(edge computing)[7]应运而生. 边缘计算主要包含虚拟化[8]、云计算[9]和软件定义网络[10]等关键技术. 边缘计算体系结构旨在推动收集、处理与生成数据, 它是一个服务沿云到网络边缘的连续体, 在数据源头的一侧采用网络、计算、存储、应用核心能力为一体的开放平台, 就近提供最近端服务, 可以产生更快的网络服务响应, 有很大的潜力来解决数据传输延迟这一问题[11, 12].
本文提出基于道路风险评估的实时路径选择方法是在边缘计算技术的基础上实施. 交通边缘服务器将道路车流信息进行处理分析得出道路当前所处在什么样的交通状况, 通过对车辆异常信息, 车流密度等数据分析判断道路的风险性. 然后边缘服务器将这些信息集中上传至云服务器, 通过云服务器分析将得出的结果反馈给道路上的行驶车辆. 以这样的方式便可以快速实现对路面车辆的宏观调控, 提醒司机在有风险的路段小心驾驶或者避开有高风险的路段, 进而更合理地进行路径选择, 避免不良交通事件的发生.
综上, 本文的主要工作可以总结如下:
(1)针对城市交通道路的实际情况, 提出一种新的实时道路风险评估模型(real-time road risk assessment model based on edge computing, R3A-EC), 该模型利用边缘计算技术的低延迟和高可靠性对道路车辆数据进行收集和反馈. 模型综合车流信息、道路信息、车辆异常行为等数据对道路风险进行综合评估.
(2)提出一种基于道路风险评估的路径选择方法(real-time route selection method based on risk assessment, R2S-RA), 该方法结合实时道路风险评估模型, 对行驶车辆的可选路径实施新的权重计算方法, 将道路风险以及道路拥堵情况对路径规划进行统一的权重计算, 并通过最小风险贝叶斯决策进行验证, 得出具有风险的路段. 并通过得出的权重实现更好的路径选择, 使得车辆所选的路径既安全又快捷.
本文第1节介绍相关研究工作. 第2节详细介绍了基于边缘计算的道路风险实时评估模型R3A-EC. 第3节介绍基于道路风险评估的实时路径选择方法R2S-RA. 第4节将该方法在人工路网和真实的城市交通路网中进行验证, 证实其有效性和实用性. 第5节对全文进行总结, 并对未来工作进行展望.
1 相关研究为了实现城市快速路实时交通流运行安全主动风险评估, Ren等人收集了大量的交通事故数据, 通过分析交通事故发生频率的时空变化规律, 提出了一种基于递归神经网络的高精度深度学习交通事故风险预测模型用来预测某一地区交通事故发生的频率[13]. Caliendo等人研究了快速路上实时交通流数据与交通运行事故风险的关系, 利用实时快速路检测器数据可动态预估交通流运行的事故风险, 从而实现主动交通安全管理[14]. Er等人[15]提出了一种基于实时交通异常检测, 提取感兴趣车辆与增加风险因子之间关系的新型交通事故风险预测方法, 交通模型在交叉口的学习过程中, 通过跟踪每辆车来检测所有的轨迹, 然后根据道路模型进行分组, 利用混合高斯 [16]和通用路由模型对所有轨迹进行连续隐马尔可夫模型聚类[17], 得到每一组轨迹. 在提取所有的CRM并定义它们之间的关系后, 在实时交通分析过程中, 对车辆的部分运动进行评估并检测是否存在异常. Fang等人提出了一个基于驾驶员个人信息、交通违规和交通事故数据记录的驾驶员交通安全评估数据挖掘框架, 通过证据权重和信息值选择相关特征子集进行探索性数据分析, 为二进制分类器的特征选择提供了一个很好的框架, 该算法很好地实现了对驾驶员的交通安全评估[18]. 惠飞等人提出一种基于GPS数据的驾驶行为异常检测方法, 利用时间、速度、加速度、方向、转角等全局与局部特征及其对应的统计量, 构建车辆驾驶行为的特征属性, 并基于多特征对已有的商用车轨迹数据进行聚类分析得出道路风险状况[19]. 以上方法大多是对历史事故数据分析得出的结论, 对于道路交通实时风险评估较少.
为了避免交通拥堵进而更好地实现路径选择, Wan等人提出了一种基于MCS (mobile crowd sensing)技术[20]的交通状况预测新算法, 通过智能手机等平台达到对路面车辆行驶信息的收集, 并将收集到的信息上传至辅助云服务器分析道路拥堵情况, 进而实现路径选择的目的[21]. Liang等人从微观车辆的角度选择道路, 比较车辆对整个公路网交通影响程度进行排序, 减少了车辆平均行驶时间[22]. 严丽平等人提出了一种城市交通路网动态实时多路口路径选择模型, 结合车辆对前方可选路线的偏好以及可选路线的实时交通状况, 并利用自适应学习算法[23]进行博弈, 以使得各行驶车辆的动态路线选择策略达到Nash均衡[24]. Yamada 等人提出推荐新路路径的办法, 选择与行驶时间相近的路段, 并根据概率推荐车辆, 将交通流量疏散到一组相似路段上[25], 但该方法是基于静态的历史交通数据. Pan等人根据实时交通信息状况, 将车辆尽可能地分散到路况较好的路段使得没有充分利用短路径的容量, 从而使得一些车辆的行驶路程较长[26]. 以上方法大都致力于研究减少出行时间, 减少交通拥堵, 充分利用城市道路资源等, 却并未考虑到出行道路的风险问题.
为了实现交通信息数据的可靠性和低延迟传输, Garg等人将边缘服务器作为中间接口, 辅助车辆与云端数据中心间通信, 减少了终端节点访问时间和网络拥塞[27]. Yang等人提出了一种融合交通灯模型和车速模型的新型短期交通预测模型, 并考虑了边缘计算服务器有限的计算资源, 可以更有效地捕捉到交通状况的实时变化[28]. 相比传统网络架构, 边缘计算采用降低服务器和用户间距离的方式减少了网络响应时间, 同时降低了数据传输功耗和网络堵塞时间[29]. 然而在该技术的基础上对于道路安全的研究相对较少, 利用边缘计算的低延迟、高可靠及海量连接等特性来对道路进行实时风险评估是非常有意义的.
综上, 现有的交通预测评估系统缺乏对道路车辆行驶整体协调性等相关研究. 为此, 本文首次构造了一个基于边缘计算技术的道路风险实时评估模型R3A-EC, 并提出基于该模型的城市路网实时路径选择方法R2S-RA. 该模型通过实时评估道路的风险程度以及拥堵情况的方法来实现更加安全便捷的交通路径规划, 而该方法既考虑了当前道路的实时交通情况又将道路风险对路径选择的影响考虑在内, 极大地提高了道路选择的安全性和快捷性.
2 R3A-EC模型影响道路风险的因素有很多, 但绝大多数主要来自于行人、车辆和道路. 以往对城市道路风险的研究中, 众多关于车速离散度的研究通常通过判断车速的分布情况来判断交通流是否处于异常状态, 并没有考虑到城市道路车辆行为异常的情况, 而且有些模型也没有考虑到车辆所处的状态信息是否可取. 因此, 本文构造了基于边缘计算技术的道路风险实时评估模型R3A-EC, 该模型结合车流密度、道路质量以及车辆行为异常和车速离散程度对某一段道路发生事故的风险程度进行评估, 并据此对路径的选择进行优化. 该模型的优势在于它对道路上的每辆车赋予一个异常占重值, 并对这些数据做统计分析, 结合车辆车速的离散程度以及道路质量情况得出道路实时的风险程度, 并以此为基础进行实时路径选择以及对异常驾驶的司机进行提醒, 这样可以很好地避免交通事故的发生.
车辆通过智能手机等设备记录并上传车辆行驶的多项数据信息(实时速度、加速度、轨迹节点位置信息等)到距离最近的边缘服务器. 在这一过程中, 在路边临时停车以及等待交通信号灯通过的车辆状态数据均会被上传, 但这些数据对于评估道路风险存在严重的偏差影响. 因此, 本节提出的R3A-EC模型通过收集在道路上正常行驶的车辆的信息数据来对当前道路风险进行合理的评估, 并规划实时、安全、快捷的行驶路线. 基于边缘计算的实时道路信息交互框架. 第2.1节介绍了边缘计算网络架构的过程, 第2.2节介绍了基于异常车辆的道路风险评估过程, 第2.3节介绍了道路风险最小风险贝叶斯决策模型.
2.1 边缘计算网络架构为了能够快速地对道路车辆海量的实时信息进行收集和分析, 并将分析结果及时反馈给道路上的行驶车辆, 就目前国内外研究来看, 采用边缘计算技术无疑是较好的选择. 如图1所示, 边缘计算网络架构主要分为终端节点、边缘服务层和云端中心网络3层. 终端节点层主要为接入边缘服务器的移动设备, 在本文中为道路上的行驶车辆, 车辆的车载导航设备以及智能手机均可作为终端节点将道路信息传送给边缘服务器. 边缘服务器的主要任务是其作为边缘云对终端设备的信息进行融合管理以及通信等功能, 在本文中主要是对道路上行驶车辆的位置信息、速度信息以及轨迹信息进行收集并分析得到当前道路风险状态. 中心网络层只与边缘服务器进行通信, 其作用是对边缘服务器数据处理的结果进行整合, 车辆导航基于该结果实现对每辆车进行的路线规划, 避开高风险道路达到整体调控的目的. 在此过程中, 每条道路都对应其附近的一个边缘服务器, 同时作为一个风险评估单元进行独立评估, 随后边缘服务器将该结果传送给中心网络服务器, 中心网络将每条道路的风险状态汇集成为一个城市道路风险网, 之后中心网络再通过车辆导航设置好的出发地和目的地来寻找一条新的低风险、耗时低路线.
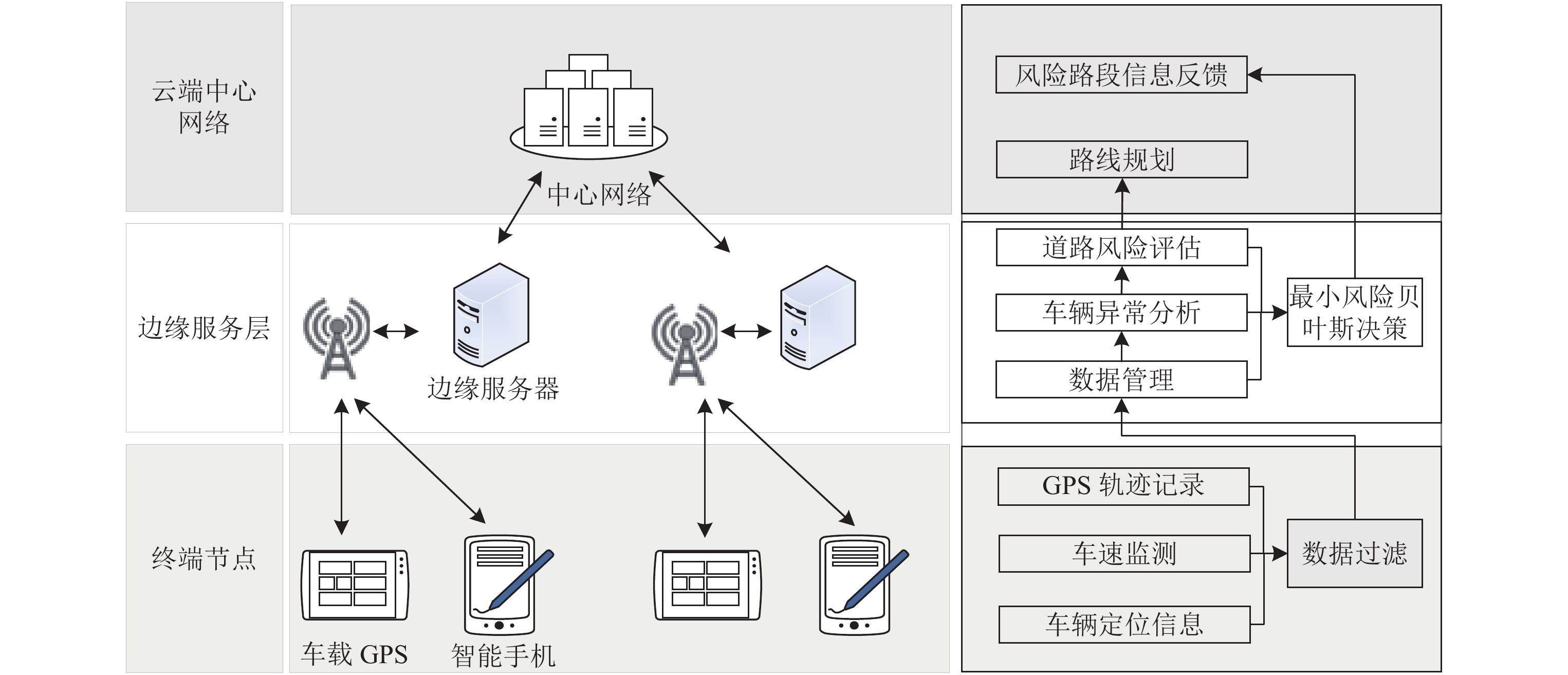
|
Fig. 1 Frame diagram of real-time road information interaction of edge service 图 1 边缘服务实时道路信息交互架构图 |
为了最大程度减少数据收集的延迟, 可以将边缘服务器基站均匀分布以达到覆盖城市每条道路的目的. 对每一个边缘服务基站进行编号, 然后对每一个基站按照就近原则分配其所管控的道路信息, 并对每条道路制定编号. 在终端节点收集信息之后进行任务分割分配, 以便于众多道路车辆的交通数据被分配到多个边缘服务器上进行管理分析, 相较于直接采用云网络服务器处理更加有效率. 数据均通过道路上车辆的感知设备进行收集并传输至边缘服务器. 然而, 道路上的车辆行为较为复杂多变, 其所收集到的数据也是复杂多样的, 其中难免存在一些不可靠的数据, 因此, 需要采用数据过滤的方式对不合格的数据进行过滤, 避免其对后续道路风险的评估以及路线的规划产生不良的影响. 比如, 当车辆在路边临时停车时, 该车辆的速度并不能作为可以依据的数据进行风险评估, 以及当车辆在等待红绿灯时的车辆速度信息也不能作为评估的依据. 通过数据过滤, 使得边缘结点上传至边缘服务器的数据更为可靠, 最后所评估的风险值也会更加准确. 随后众多边缘服务器的信息汇集至中心网络, 整个边缘服务器所覆盖的地区交通情况便可以被中心网络进行宏观上的把控, 从而可以对行驶车辆提供更加精确有效的路线选择. 这种方法还有一点优势在于随着城市交通路网的复杂而变得更加的有选择性, 对于市区外的公路或者高速路, 由于路段长度较长且可选择性较低, 因此该种方法并不适用.
2.2 基于异常车辆的道路风险评估异常车辆通常是指道路上存在的异常驾驶行为的车辆, 比如行车的车速超过道路速度限制、驾驶员紧急变换车道以及车辆频繁的加速减速等. 这些行为是导致交通事故的重要诱导因素. 因此, 异常驾驶行为的检测对于城市道路上的交通安全具有非常重要的意义. 本文主要从车辆急变道、车辆急加速急减速、车速离散程度3个角度来评估道路的风险.
对于城市路网中的每一个行驶车辆, 需要对其行驶轨迹进行记录, 本文采用的轨迹记录方法是由连续的GPS轨迹节点的集合组成, 记为
通常车辆变道时间是比较短的, 一般在3–8 s内便可以完成, 而且车辆的转向角度也是比较小的, 因此可以通过计算GPS轨迹点之间的转角来检测车辆是否发生变道行为.
当车辆的行驶方向未发生改变时, 如图2所示, 考察车辆行驶轨迹的3个结点
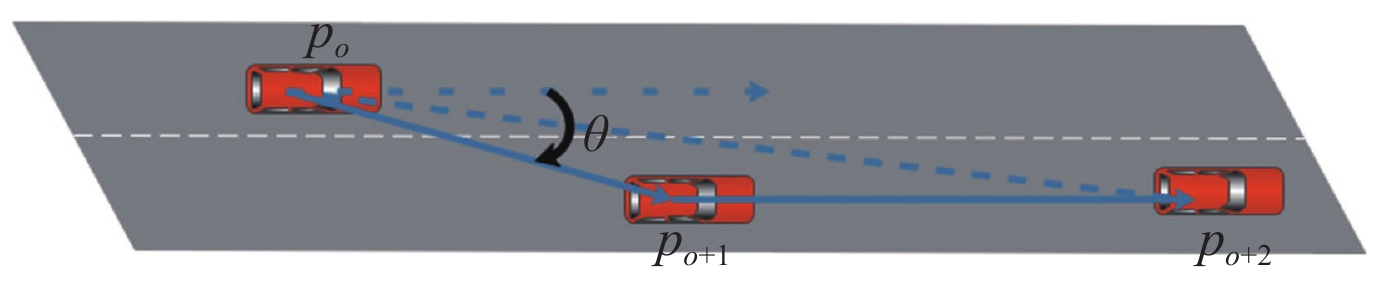
|
Fig. 2 Lane change track diagram of road vehicles 图 2 道路车辆变道轨迹图 |
| $ \theta = {\text{180}} - \arccos \frac{{d{{({p_o}, {p_{o + 1}})}^2} + d{{({p_{o + 1}}, {p_{o + 2}})}^2} - d{{({p_o}, {p_{o + 2}})}^2}}}{{2({p_o}, {p_{o + 1}})({p_{o + 1}}, {p_{o + 2}})}} $ | (1) |
该转角的角度值越大, 越能说明驾驶员行车经验缺乏或者需要紧急避让, 越容易造成道路不稳定因素, 从而可能引发交通事故. 当行驶方向发生改变时, 说明车辆正在弯道上行驶或者驶入另一条方向不同的车道, 应当放弃所测量值. 根据行业经验, 变道偏角大于15°即可判定该车辆发生变道行为. 依据行车经验, 将变道角度大于25°的车辆分类为急变道车辆. 根据车辆在过去一个周期内的行车轨迹, 统计其在道路上的急变道车辆数, 增加急变道车辆特征记为B.
2.2.2 急加速急减速行为分析交通运输行业规定, 急加速或者急减速并不属于违规行为, 但是在道路交通中, 经常性的该行为却是引发交通事故的重要因素. 因此在车辆行驶轨迹点的基础上可以计算出车辆加速度的变化. 根据车辆GPS轨迹结点
| $ {a_o} = \left| {{v_{o + 1}}\left. { - {v_o}} \right|} \right./\Delta t $ | (2) |
为了更好地区分不同区间急加速和急减速对路面造成的风险程度, 本文根据我国公交安保部2012年制定的急加速和急刹车判断标准, 将急加/减速按危险程度分为3个等级标准, 如表1所示.
| Table 1 Grade standards for rapid acceleration/deceleration 表 1 急加/减速等级标准 |
统计不同标准的急加/减速的车辆数目, 增加急加/减速特征
根据行业经验, 车速离散程度越大说明该路段中超车频率越高, 发生事故的可能性就越大. 对于众多车辆的车速离散程度, 本文用道路车辆速度的标准差
| $ \sigma ({v_{k, l}}) = \sqrt {\frac{1}{{{n_{k, l}}}}\sum\limits_{m = 1}^{{n_{k, l}}} {\mathop {({v_m} - {{\bar v}_{k, l}})}\nolimits^{\text{2}} } } $ | (3) |
其中,
当某一路段上的车辆速度偏离均值较大时, 可以判定该车的车速存在异常. 对道路上的这些车辆进行如下统计. 设置:
| $ \left|{v}_{m}-{\overline{v}}_{k, l}\right|=\left\{ {\begin{array}{l}0,\;\; \left|{v}_{m}-{\overline{v}}_{k, l}\right| < \sigma ({v}_{k, l})\\ \text{1},\;\;\left|{v}_{m}-{\overline{v}}_{k, l}\right|\geqslant \sigma ({v}_{k, l})\end{array}\;\;m=(1, 2, 3, \dots , n)} \right. $ | (4) |
那么, 存在车速异常的车辆总数
| $ {U_{k, l}} = \sum\limits_{m = 1}^{{n_{k, l}}} {\left| {{v_m} - {{\bar v}_{k, l}}} \right|} $ | (5) |
道路风险同时与道路的质量也存在着一定的关系. 道路的质量与道路的风险是负相关的关系, 即道路质量越好, 发生事故的可能性相对来说就会变小, 反之发生事故的可能性就会越大. 根据城市道路各类(级)道路主要技术指标, 城市道路可分为快速路、主干道、次干道和支路4类, 而目前城市主要道路中, 快速路和主干道安全性均较高, 因此本文将两种道路统一为一类, 最终将不同类别的道路划分为3个不同质量等级标准, 对不同质量的道路赋予相应的质量参数值, 为了可以使得不同类别的道路可以降低或者增加交通风险的目的, 将可用道路的质量标准区间设置为[0.5, 2], 该值的大小体现了道路路面质量的高低, 例如道路车道数量、平坦程度以及是否存在需要躲避的障碍物之类. 不同的路段需要人为提前考察道路的质量并对其赋予相应的道路质量值
| Table 2 Road quality parameter Settings of different levels 表 2 不同级别道路质量参数设置 |
在以往对于异常行为车辆的参数设置中, 多数研究学者将正常行驶的车辆与异常行驶的车辆设置为0和1, 但不同异常行为的车辆对于交通影响的程度是不同的, 某些异常行为例如一级的急加速和急减速行为相对于急变道而言更容易造成交通事故的发生. 当多种异常行为同时存在于一个车辆的时候, 那么该车辆对于道路风险造成的影响也是非常大的. 因此对不同异常行为需要有不同的异常占重, 本文通过多组仿真实验计算得出一组较为合理的异常参数, 并据此参数来进行后续的道路风险评估. 具体参数设置如表3所示.
| Table 3 Parameter Settings of abnormal behavior 表 3 异常行为参数设置 |
表3中速度异常指的是车速偏离标准值较大的车辆所赋予的异常占重值, 此类车辆的异常仅为速度异常. 急加/减速分为3个标准, 分别赋予相应大小的异常数值. 混合异常指的是前边3种异常中有两项或者3项同时发生在同一辆车上, 记为H, 其所赋予的异常值相对较大. 设置一个较短的周期, 以一分钟的周期为例, 统计每条道路一分钟内的车辆数据作为依据, 根据以上不同的异常占重值以及道路质量参数q和车流密度
| $ {F}_{k, l}=\frac{{\displaystyle \sum _{m=1}^{{n}_{k, l}}\left|{v}_{m}-{\overline{v}}_{k, l}\right|}+{B}_{k, l}\cdot \mu +{\displaystyle \sum _{t=1}^{3}{S}_{{t}_{k, l}}\cdot {\gamma }_{t}}+{H}_{k, l}\cdot \upsilon }{n}\cdot {\rho }_{k, l}\cdot {q}_{k, l}\;\;(m=1, 2, \text{3}\text{, }\dots \text{, }nt=1, 2, 3) $ | (6) |
| $ {\rho _{k, l}} = \frac{{{n_{k, l}}}}{{{d_{k, l}}}} \times 100 $ | (7) |
其中,
基于上节道路风险的评估, 为了可以更多地了解道路交通流的风险状态, 本文采用SUMO (simulation of urban mobility)交通仿真软件对城市不同交通状态下的车速分布进行了统计, 通过逐次加入更多的车辆来模拟不同的交通状态. 本文统计了交通顺畅、正常情况以及交通繁忙3种交通流的车速分布情况, 将所统计的数据使用最小二乘法进行拟合, 结果如图3所示. 可以看出, 在城市交通中, 道路上不同车速下的车辆数目呈现正态分布, 因此可以采用最小风险贝叶斯决策来判断道路的风险状态.
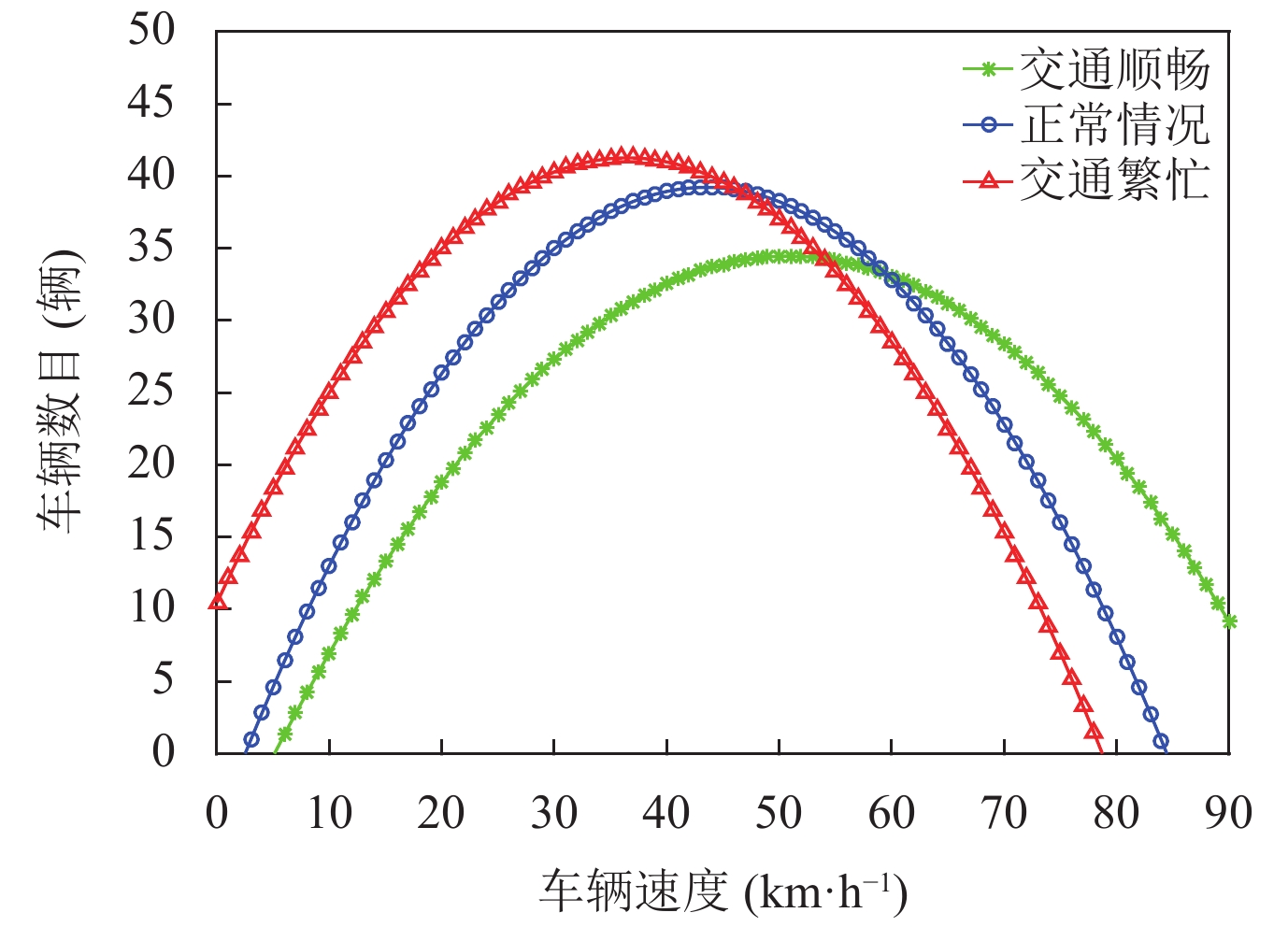
|
Fig. 3 The number of vehicles corresponding to different speeds in three traffic states 图 3 3种交通状态下不同车速对应的车辆数目 |
将某一路段的车流观测量K分为正常类
| Table 4 Minimum risk Bayesian Decision table 表 4 最小风险贝叶斯决策表 |
道路风险最小风险贝叶斯决策模型的计算步骤如下.
(1)对于先验概率, 本文通过对路面正常车辆与异常车辆的数目所占的比率对先验概率进行了估计, 分别记为
| $ p({w_1}) = 1 - \frac{{\displaystyle\sum\limits_{m = 1}^n {\left| {{v_m} - {{\bar v}_{}}} \right|} + B + \displaystyle\sum\limits_{t = 1}^3 {{S_t}} + H}}{n} $ | (8) |
| $ p({w_{\text{2}}}) = \frac{{\displaystyle\sum\limits_{m = 1}^{{n_{}}} {\left| {{v_m} - {{\bar v}_{}}} \right|} + B + \displaystyle\sum\limits_{t = 1}^3 {{S_t}} + H}}{n} $ | (9) |
(2)根据贝叶斯分类算法原理, 计算的后验概率为:
| $ p({w_1}\left| K \right.) = \frac{{p(K\left| {{w_1}} \right.)p({w_1})}}{{p(K\left| {{w_1}} \right.)p({w_1}) + p(K\left| {{w_2}} \right.)p({w_2})}} $ | (10) |
| $ p({w_{\text{2}}}\left| K \right.) = \frac{{p(K\left| {{w_{\text{2}}}} \right.)p({w_{\text{2}}})}}{{p(K\left| {{w_1}} \right.)p({w_1}) + p(K\left| {{w_2}} \right.)p({w_2})}} $ | (11) |
(3)计算决策为
| $ R({a_1}\left| K \right.) = \lambda {\text{(}}{a_1} , {w_1}{\text{)}}P{\text{(}}{w_1}\left| K \right.{\text{)}} + \lambda {\text{(}}{a_1} , {w_2}{\text{)}}P{\text{(}}{w_2}\left| K \right.{\text{)}} $ | (12) |
| $ R({a_{\text{2}}}\left| K \right.) = \lambda {\text{(}}{a_{\text{2}}} , {w_1}{\text{)}}P{\text{(}}{w_1}\left| K \right.{\text{)}} + \lambda {\text{(}}{a_{\text{2}}} , {w_2}{\text{)}}P{\text{(}}{w_2}\left| K \right.{\text{)}} $ | (13) |
(4)比较两个条件风险值的大小并做出决策.
| $ R({a_{{\textit{z}}'}}\left| K \right.) = {\min _{{\textit{z}} = 1, 2}}R\{ {a_{\textit{z}}}\left| K \right.\} $ | (14) |
通过以上步骤, 得出
由于道路的车流情况每时每刻都是在不断发生变化的, 为了能够实时地对道路风险进行评估并以此对路径进行选择, 本文采用某一路段前几分钟的交通流数据对道路进行实时风险评估, 然后根据道路风险值对道路权重进行计算, 并基于该权重值对行驶车辆进行实时低风险路径选择. 第3.1节介绍了基于道路风险的路径权重计算方法, 第3.2节介绍了R2S-RA路径选择方法的过程.
3.1 基于道路风险的路径权重计算将多个边缘服务站均匀设置于城市路网中, 如图4所示. 对每一条道路根据路口序号进行编号, 每一条道路对应一个附近的边缘服务器, 每条道路的距离用
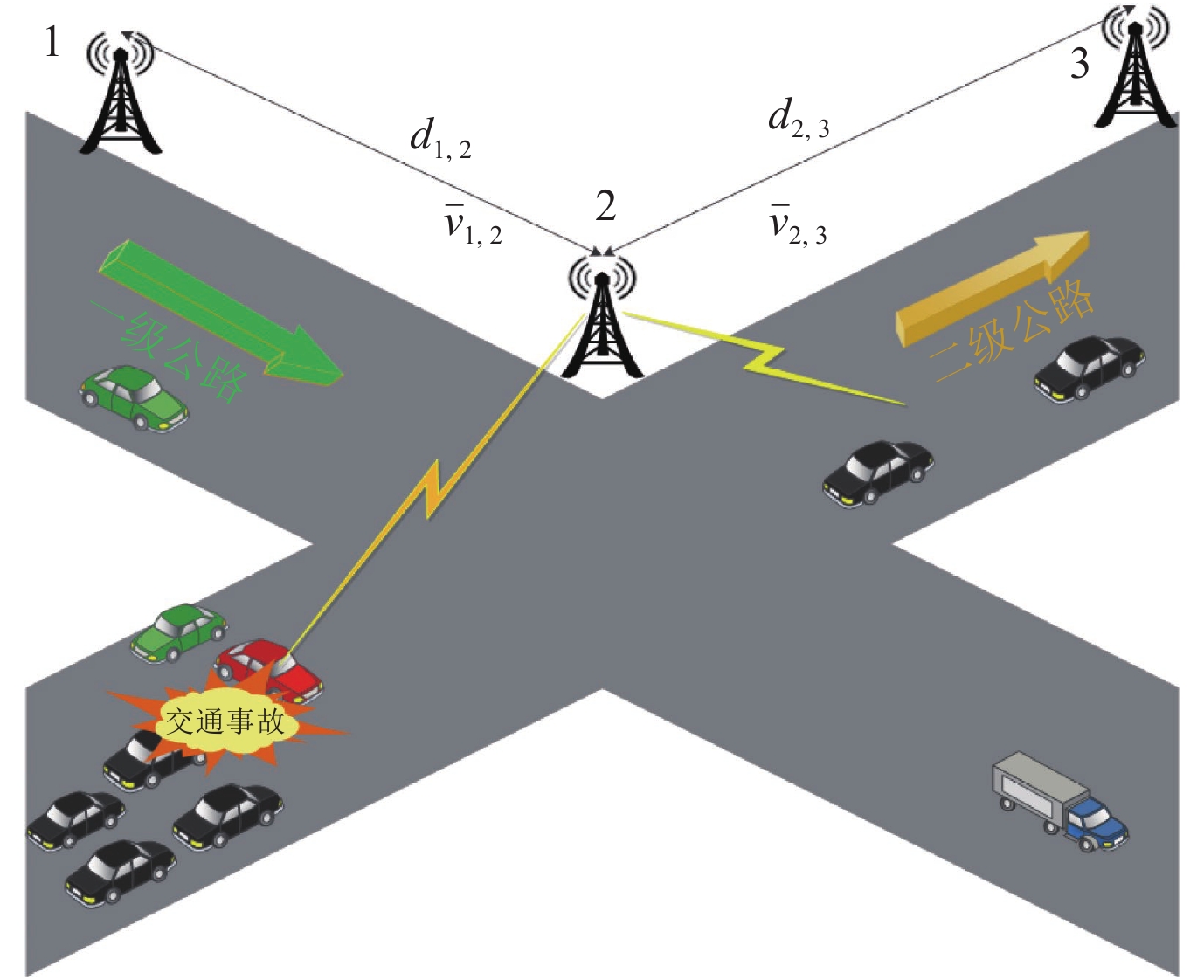
|
Fig. 4 Edge Service - Schematic diagram of road condition information 图 4 边缘服务—路况信息示意图 |
| $ {r}_{i, j}=\left\{ {\begin{array}{l}+\infty \text{, }\;交通拥堵{; }\\ \text{0}{, }\;道路通畅. \end{array} } \right.$ | (15) |
以南昌市部分区域为例. 如图5所示, 部署边缘服务器将该区域路段覆盖, 将各个交通路口连接起来形成一个路网.
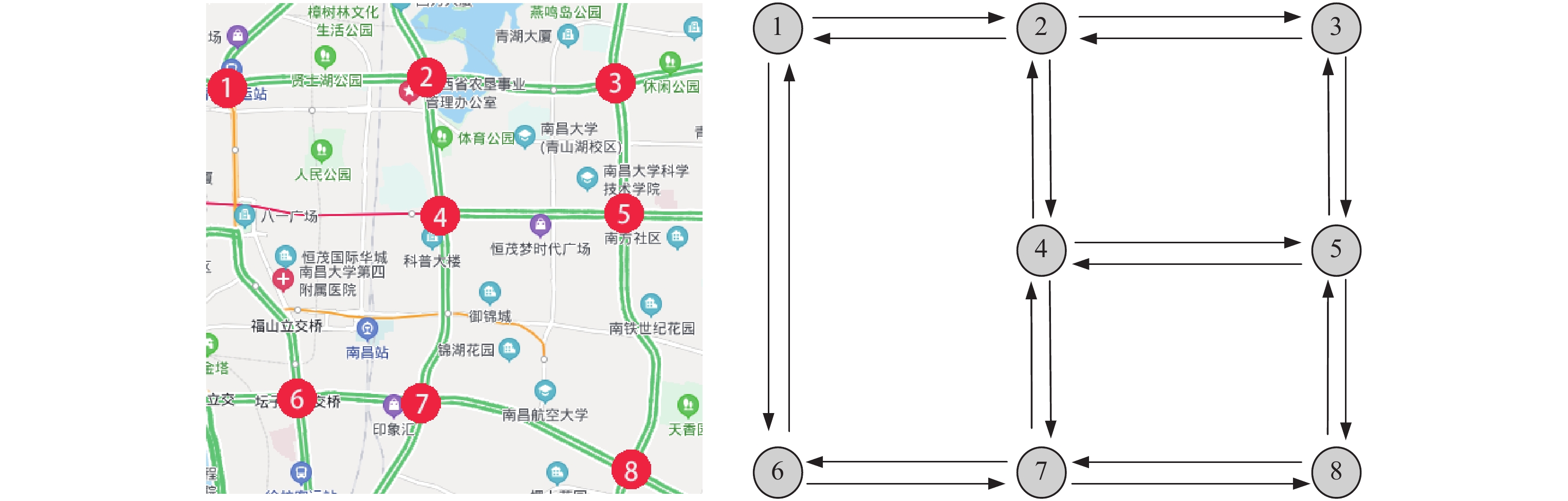
|
Fig. 5 Diagram of edge computing server deployment 图 5 边缘计算服务器部署示意图 |
| $ {\omega _{i, j}} = \frac{{{d_{i, j}} + {r_{i, j}}}}{{{{\bar v}_{i, j}}}} $ | (16) |
在这里, 该道路的基础权重是以通过该道路所需的平均时间来定义的, 但在道路的选择上, 无论是最短路径或者最短时间, 对于希望安全行驶的司机来说都不一定是最理想的道路选择方法, 结合第2节的道路风险实时评估, 设置一种低风险的路径选择方法, 选择风险较低的路段. 根据每条道路风险期望值F', 得到新的权重矩阵
| $ {F'_{i, j}} = \frac{{\displaystyle\sum\limits_{\text{1}}^T {{F_{i, j}}} }}{T} $ | (17) |
| $ {W_{i, j}} = (1 + {F'_{i, j}}){\omega _{i, j}} $ | (18) |
公式(17)和公式(18)中, T为道路的一个风险度量周期, 在计算风险时本文所使用的车辆数据为道路每分钟的数据信息, 较短时间的道路风险不能用来衡量一条路径的近期风险, 因为随着道路车辆的驶入和驶出, 道路风险处于一个动态的变化过程, 当有异常驾驶行为的车辆驶出某一条道路时, 该道路的风险会降低, 同时该车辆驶入的道路风险会增加. 道路风险符合短期不可预测、长期可预测的规律. 当道路上车辆较多时, 道路的风险水平不会因为较少异常车辆的驶入和驶出发生较大的改变; 当道路车辆较少时, 车辆密度这一因素也会使得道路风险不会因为异常车辆的驶入和驶出发生较大改变, 因此, 本文选择设定一个时间周期, 即每T分钟计算一个道路风险期望值用来衡量道路的风险状况, 所得到的新的权重值是结合每条道路通行能力以及道路安全水平来衡量的. 在计算道路权重时, 为了实现可以兼顾安全与短时两个方面, 但又不希望风险值对道路影响占比过大, 设置公式(18)进行计算, 该公式是在道路平均通行时间的基础上加入了道路风险的占比影响, 通过与其他权重计算方式进行比较, 该公式得到的权重值作为路径选择的依据更为可靠. 在目前较主流的基于群智感知(MEC)动态路径选择优化算法基础上再使用该权重值进行路径的最优选择, 得出同时兼顾安全与快捷的路径选择方案. 同时, 为了评估该模型所选择路径的可靠性, 设置公式(19)对所选路径1~
| $ \bar F' = \frac{{\text{1}}}{\psi }\sum\limits_{\text{1}}^\psi {{{F'}_{i, j}}} $ | (19) |
当行驶车辆设置好出发地和目的地的时候, 根据公式(18)计算出的路径权重得出初始路径方案. 车辆在按照初始方案行驶的过程中, 不同的道路风险会随着时间的改变而发生变化. 因此, 在给定的时间段T内会形成一个路径的更新版本, 即每T分钟获得一个新的路径. 为了达到这个目标, 首先设置参数T, 并且设置目的地距离出发地之间的距离和道路质量. 然后结合从边缘服务器获取的站点间车辆以及交通事件信息, 在车辆行驶过程中, 每T分钟更新一个从下一个站点到目的地站点的路径. 当城市交通路网状态以较高的频率变化时, 必须设置较短的时间周期T. 基于道路风险评估的实时路径选择方法R2S-RA的具体实现如算法1.
算法1. R2S-RA.
输入: 出发地和目的地;
输出: 更新后路径规划方案Path.
1. 确定城市路网各路段风险指标.
2. 执行公式(18)更新路径权重
3. 初始化路线方案Path.
4. 设置时间周期T.
5. For t=1 to T
执行公式(6)更新各路段实时风险
执行公式(17)更新路段风险期望
执行公式(18)更新路径权重
6. 获取车辆当前位置.
7. 更新路线方案Path=new Path.
End
8. If 车辆未抵达目的地 then return to 5. End
Else 算法结束.
End
4 仿真与实验分析为了验证R2S-RA方法的可行性, 本文分别基于人工路网和真实路网两种场景来进行实验. 为了评估该方法的有效性, 本文选择传统的最短路径Dijkstra算法、基于VANET的最短时间算法、基于MEC的动态路径规划算法以及双向A*最短路径优化算法与本文提出的R2S-RA方法进行对比实验, 针对车辆的行驶时间以及所选路径的平均风险进行比较, 以证实R2S-RA方法的有效性和实用性.
4.1 人工路网在人工路网实验中, 本文使用SUMO交通仿真软件对道路交通微观车辆信息进行模拟仿真. 实验中路网的设置如图6所示, 人工路网中的每条道路都是双向的, 为了更为真实的模拟现实道路的交通情况, 每条道路的长度控制在1.5–4 km之间, 道路的长度在规定范围内随机设置. 在该路网中, 边缘服务器设置在每个路口的交汇处, 每一个边缘服务器负责对固定的道路信息数据收集, 使得每一条道路均被边缘服务器所覆盖. 比如在6号交叉口处设立的服务器只对2-6和5-6两条路面的车辆信息进行收集和处理.
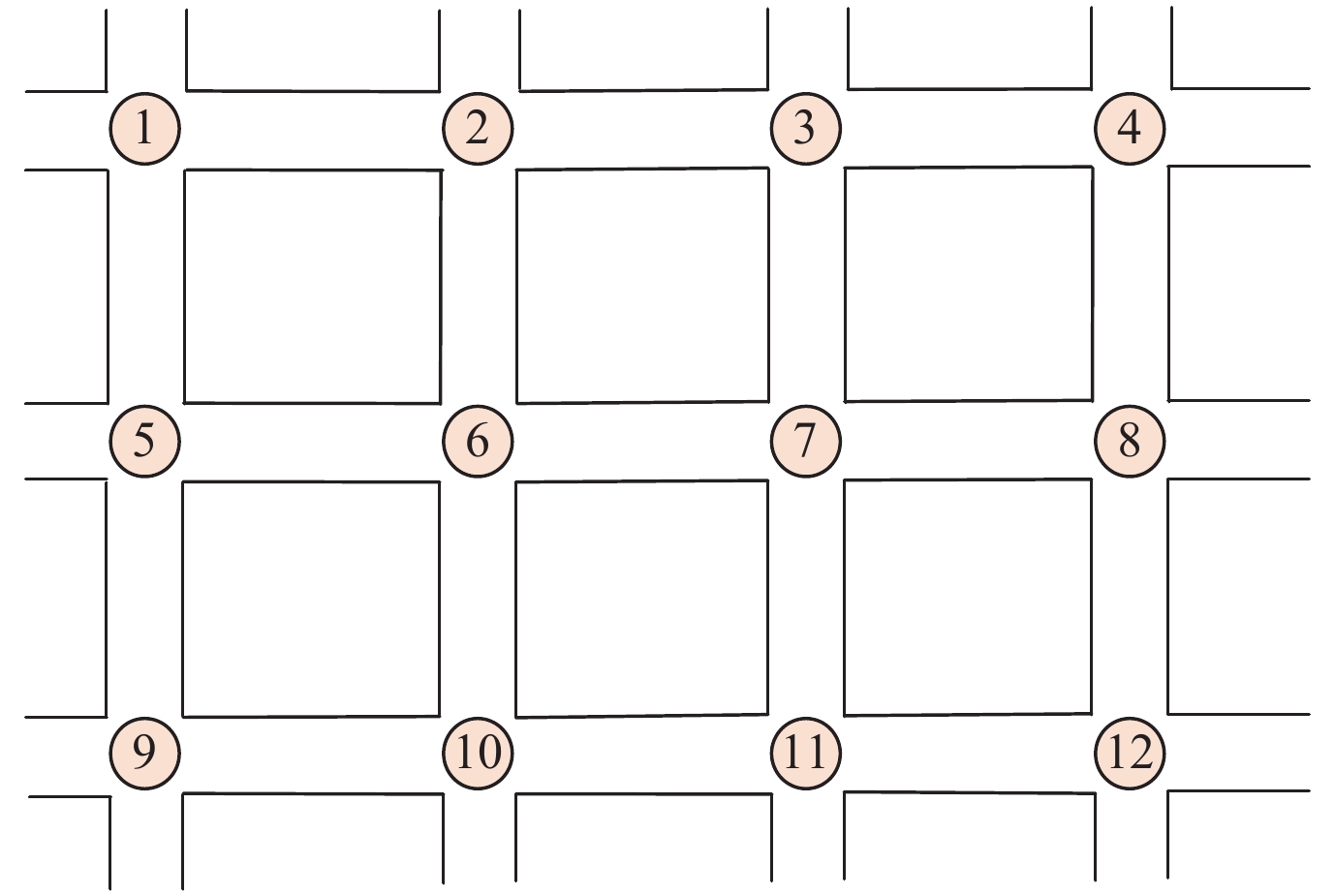
|
Fig. 6 Schematic diagram of artificial road network 图 6 人工路网示意图 |
为了对不同路径规划方法的优劣性进行比较, 在仿真实验中, 本文设置出发地站点为1, 目的地站点为12, 这样可以有更多的可选路径. 使用仿真软件在每条道路上生成车辆进行仿真以获取车辆的实时速度, 车流密度以及车辆从出发点到目的地所行驶的时间. 根据实验需要, 对其中部分车辆随机设置异常属性值, 部分仿真实验数据见表5, 该表为其中一组仿真数据, 其描述了部分路径在某一时刻的各项参数信息. 本文在人工路网场景下共设置了30组对比实验, 每次实验道路的各项参数均不相同, 道路的通行能力即道路质量是通过模拟真实路径并进行人为设置的. 在实验过程中随机在道路上增加影响原本路径规划的事故因素, 比如在某一段路设置更多的车辆使得道路拥堵, 使得该模型会根据这些信息更新一条新的路径方案使得车辆仍可以顺利到达目的地, 每一辆车根据自己设置的出发地和目的地会随着道路的风险程度以及通行能力得出相应的规划路径, 从而验证该模型在微观车辆动态路径规划的可行性. 实验设置时间周期T为5 min, 即每5 min更新一次道路的权重值作为路径选择更新的依据.
| Table 5 Part of road simulation experiment parameters 表 5 部分道路仿真实验参数 |
根据最小风险贝叶斯决策经验, 设置最小风险贝叶斯决策各个损失参数值. 经过多次实验计算结果对比, 当把有高风险路段决策为正常路段的损失函数即
| Table 6 Minimum risk Bayesian decision table 表 6 最小风险贝叶斯决策表 |
同时, 为了验证R2S-RA方法在动态路径选择方面的表现, 本实验通过设置道路车辆的数量和异常车辆信息对不同的路段设置交通拥堵、高路段风险等情况, 然后分别结合传统的最短路径Dijkstra算法、基于VANET的最短时间算法、基于MEC的动态路径规划算法以及双向A*最短路径优化算法在所选路径的行驶时间以及路径的平均风险进行了对比, 结果如图7和图8所示. 图7中曲线表示为多组路径选择车辆所需行驶的时间, 本文采用最小二乘法对不同的路径规划算法所需要的行驶时间进行拟合, 得出较为平滑的曲线, 更为直观的展示每种路径规划方法在此性能的优劣性. 图8则是对每次路径规划的路径平均风险进行对比, 通过对比相同交通流状态下不同模型选择路径的平均风险来得出不同模型路径选择的安全性. 为了避免偶然事件的发生, 每种路径规划方法均设置30组实验, 每组实验通过逐次增加车辆的数目来达到不同交通流的状态, 实验所获取的车辆行驶时间为多个车辆的平均行驶时间, 最后将所有结果绘制成图.
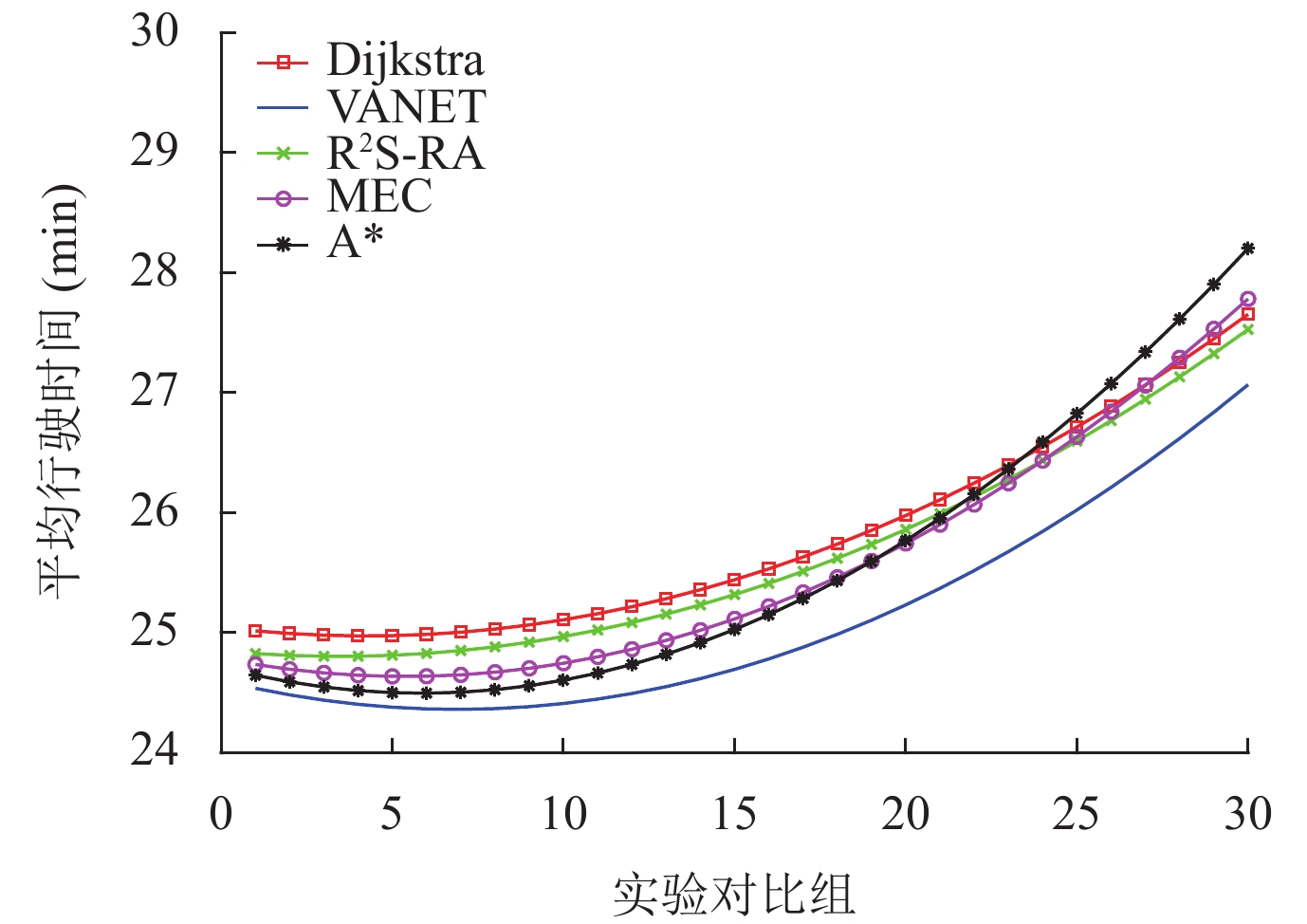
|
Fig. 7 Comparison of average travel time of different route selection methods in artificial road network 图 7 人工路网中不同路径选择方法的平均行驶时间对比图 |
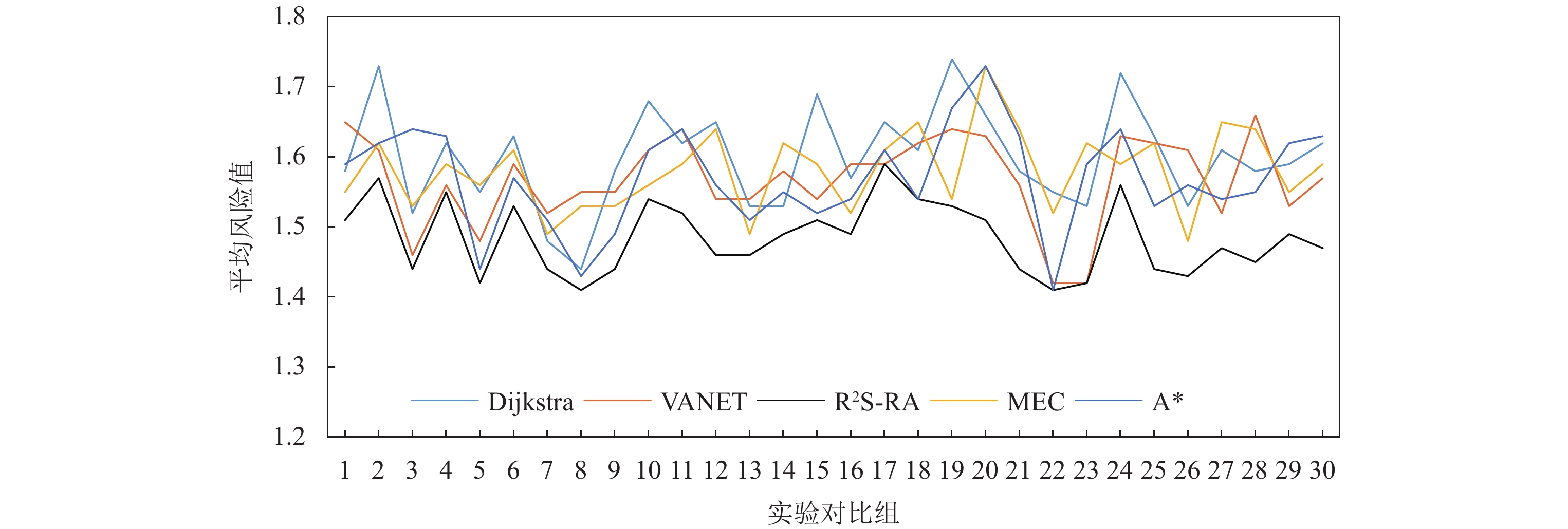
|
Fig. 8 Comparison diagram of route risks of different models in artificial road network 图 8 人工路网不同模型路径选择路径平均风险对比图 |
(1) 在人工路网中, 随着车辆数目的增多, 所有的路径规划模型在行驶时间上呈现先慢后快的增长趋势. 本文所提出的R2S-RA方法在时间上的优势相对于基于VANET最短时间路径选择方法以及基于MEC的动态路径规划算法上有一定的差距, 但随着车辆数目的增多, 这种差距也在逐渐缩小. 从选择的路径平均风险角度来看, 该方法所选的路径平均风险值均为最低, 也就是说其所选择的道路畅通性以及道路的安全性上有很大的优势, 而且最终到达目的地所使用的时间相差并不是很大. 传统最短路径Dijkstra算法和双向A*算法虽然在行驶的路程较短, 但受到道路的通行能力的影响, 最终所需要的行驶时间往往不是最少的.
(2) 在行驶过程中对道路设置多种突发状况, R2S-RA方法均可以很好地更新出相对更为安全并且较为快捷的路线, 使得最终的行驶时间在完全可以接受的范围内. 随着路段的增多, 该种方法可以有更多的道路进行选择, 可以很好地满足未来道路繁杂的场景. 这种路径选择方式对于行车经验不足的司机来说是非常友好的.
4.2 真实路网为了验证R2S-RA方法在现实城市路网中的实用性, 本文以南昌市重要交通区域为例, 设置真实城市路网, 如图9所示.

|
Fig. 9 Real road network in some areas of Nanchang 图 9 南昌市部分地区真实路网 |
使用OSM (open street map)地图服务将该区域的主要道路导入SUMO交通仿真软件中进行车辆路径规划的模拟仿真, 同样通过设置道路车辆的数目来模拟不同时间段的交通流状态. 设置车辆的出发地和目的地, 统计车辆在路径规划过程中所行驶的时间并与现实中导航工具的预估时间进行比较, 通过调整车辆数量使得两者差距接近, 这样该仿真工具可以很大程度上模拟现实城市的道路交通. 为了验证道路质量在该模型中的影响情况, 通过实地考察对每条道路赋予不同道路质量参数值, 如表7所示. 边缘服务器的部署(1–25)覆盖所有道路, 为了验证真实路网采用该模型选择路线的可行性, 本文主要采用主干道道路车辆信息进行仿真实验.
| Table 7 Road quality parameters of different routes in real road network 表 7 真实路网中不同路径的道路质量参数 |
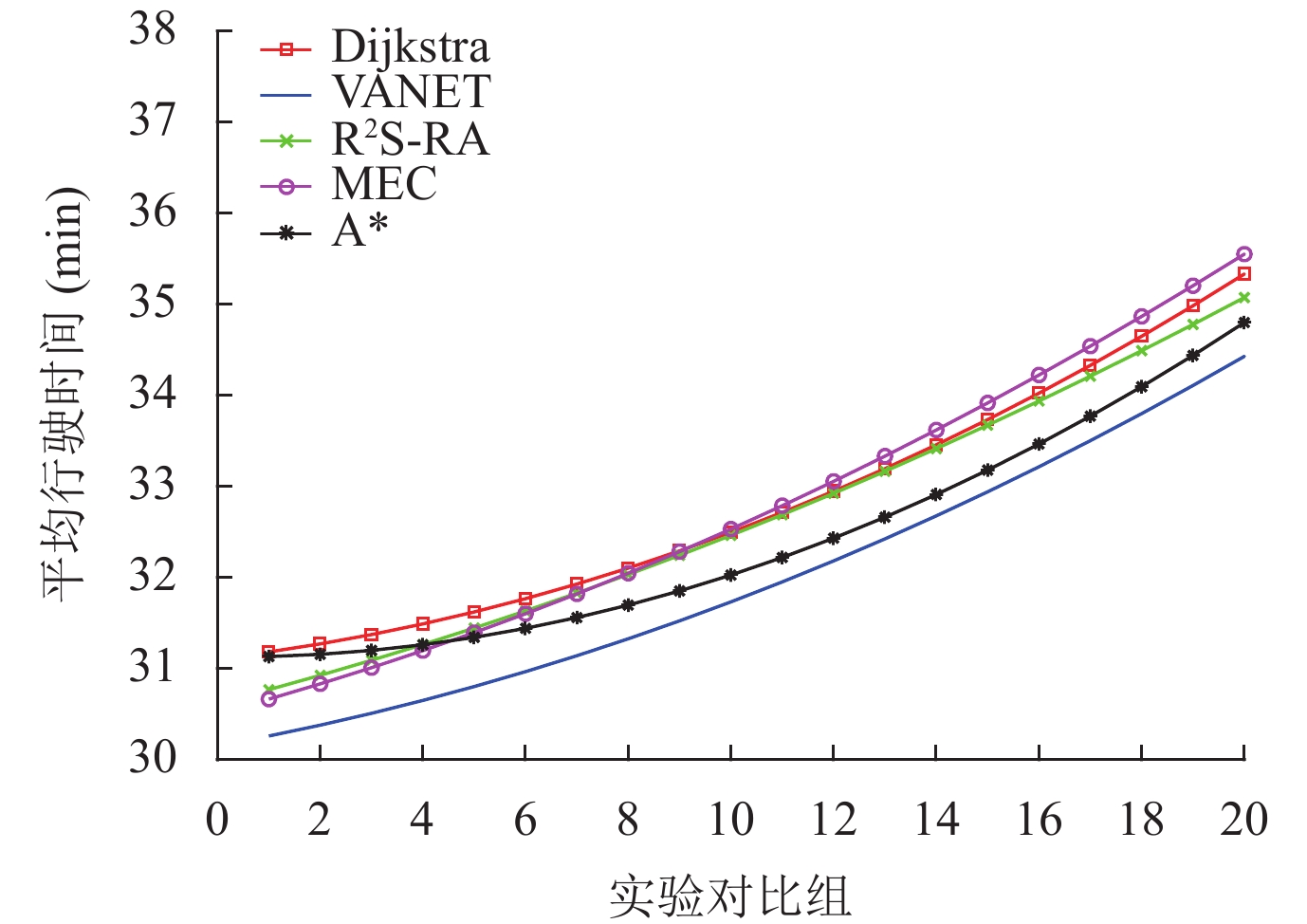
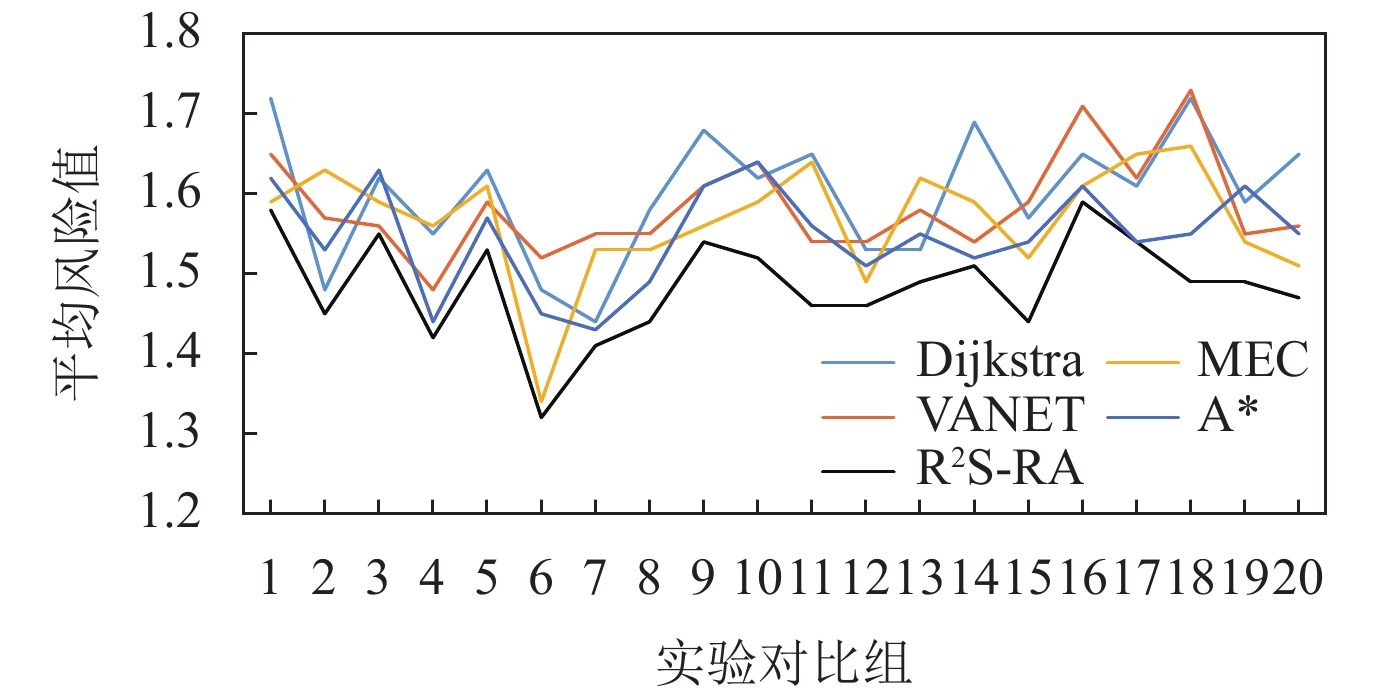
与人工路网实验相似, 为了使得路径选择多样性, 分别设置出发地和目的地为站点1和站点25, 根据南昌市区9:00–10:00、12:00–13:00以及16:00–18:00这3个不同时间段的实际交通情况, 调整仿真实验中道路的车辆数目与之相匹配, 并在每条道路设置存在异常行为的车辆. 设计与传统的最短路径Dijkstra算法、基于VANET的最短时间算法、基于MEC的动态路径规划算法以及双向A*最短路径优化算法进行对比实验. 实验共设置20组, 每组实验所设置的车辆数量设置与人工路网一致为逐次递增, 达到不同交通状态环境下进行仿真. 同样, 在实验中随机对部分道路设置交通拥堵事件来验证R2S-RA路径动态路径选择的可行性, 每一组实验均统计不同模型下多辆车(本文中设置车辆数为20)从初始地到目的地的平均行驶时间. 最后对最终的统计结果采用最小二乘法进行拟合对比, 对每组实验所选道路的平均风险进行计算并进行对比, 得出平均行驶时间对比图以及平均风险对比图, 如图10和图11所示.
|
Fig. 10 Comparison of average travel time of different route selection methods in real road network 图 10 真实路网中不同方法的路径选择平均行驶时间对比图 |
|
Fig. 11 Route risk comparison diagram of route selection for different models in real road network 图 11 真实路网中不同路径选择方法的路径风险对比图 |
从图10和图11的实验结果可以看出, 在真实城市路网中, 由于不同道路的距离差异较大, 且道路复杂程度较高, 在车辆平均行驶时间的对比上较人工路网的趋势有所不同, 随着道路车辆数目的递增, 其呈现匀速增长的趋势. 但从整体来看R2S-RA方法在不同交通状态的情况下所行驶的时间与基于VANET最短时间算法下行驶时间上的差值完全在可以接受的范围. 而在不同方法下选择的路径风险平均值对比图中, R2S-RA方法所选择的路径风险值均是处于最低水平, 与人工路网环境下的实验结果相较一致.
5 结 论为了减少交通事故以及交通拥堵事件的发生, 本文提出了基于边缘计算技术的道路风险实时评估模型R3A-EC, 该模型从道路车辆的异常行为出发, 利用边缘计算技术对行驶中的车辆信息进行收集并对道路风险进行实时评估, 再利用最小风险贝叶斯决策模型进一步验证判断. 同时, 本文基于R3A-EC模型设计了对城市路网中的车辆进行实时路径选择的方法R2S-RA. 最后通过大量对比实验, 得出以下结论.
(1) R2S-RA方法相较于目前多种路径选择算法, 在行驶的时间总体上要大于以最短时间目的的路线选择算法, 但该方法兼顾了道路安全与出行时间两个优势, 使得在对路径的选择上更加安全合理, 尤其是行车经验不足的新手司机. 这样的路径选择方式会大大减少道路交通事故以及交通拥堵的发生.
(2) 当存在某一条道路风险极低, 道路状况非常好, 但由于路段距离较长, 如果选择该路段会使得最终的行驶时间大大增加的情况, R2S-RA方法会很好地放弃这种路段的选择, 使得最后的行驶时间在较优的范围内.
未来的研究工作将围绕以下两个方面进行展开:
(1) 实验中增大路径距离的差异性, 改进对道路权重的衡量方法.
(2) 考虑交通灯对车辆路径选择时间上的影响.
致谢 我们真诚地向对本文工作给予支持和建议的审稿人、主编、编辑、同行、同学和老师表示感谢.
| [1] |
Schrank D, Eisele B, Lomax T. 2012 Urban Mobility Report. Texas: Texas A & M University, 2012.
|
| [2] |
Driss M, Saint-Gerand T, Bensaid A, Benabdeli K, Hamadouche MA. A fuzzy logic model for identifying spatial degrees of exposure to the risk of road accidents (Case study of the Wilaya of Mascara, Northwest of Algeria). In: Proc. of the 2013 Int’l Conf. on Advanced Logistics and Transport. Sousse: IEEE, 2013. 69–74.
|
| [3] |
Tae SK, Jeong GU, Hyuck JP. Risk assessment of the road cut slopes in Gyeoungnam based on multiple regression analysis. The Journal of Engineering Geology, 2007, 17(3): 393-404.
|
| [4] |
Alrajhi M, Kamel M. A deep learning model for predicting and visualizing the risk of road traffic accidents in Saudi Arabia: A tutorial approach. Int’l Journal of Advanced Computer Science and Applications, 2019, 10(11): 475-483.
[doi:10.14569/IJACSA.2019.0101166] |
| [5] |
Moosavi S, Samavatian MH, Parthasarathy S, Teodorescu R, Ramnath R. Accident risk prediction based on heterogeneous sparse data: New dataset and insights. In: Proc. of the 27th ACM SIGSPATIAL Int’l Conf. on Advances in Geographic Information Systems. Chicago: ACM, 2019. 33–42.
|
| [6] |
Dandala TT, Krishnamurthy V, Alwan R. Internet of Vehicles (IoV) for traffic management. In: Proc. of the 2017 Int’l Conf. on Computer, Communication and Signal Processing (ICCCSP). Chennai: IEEE, 2017. 1–4.
|
| [7] |
Shi WS, Cao J, Zhang Q, Li YHZ, Xu LY. Edge computing: Vision and challenges. IEEE Internet of Things Journal, 2016, 3(5): 637-646.
[doi:10.1109/JIOT.2016.2579198] |
| [8] |
Morabito R, Cozzolino V, Ding AY, Beijar N, Ott J. Consolidate IoT edge computing with lightweight virtualization. IEEE Network, 2018, 32(1): 102-111.
[doi:10.1109/MNET.2018.1700175] |
| [9] |
Li L, Zhang XY, Liu KY, Jiang F, Peng J. An energy-aware task offloading mechanism in multiuser mobile-edge cloud computing. Mobile Information Systems, 2018, 2018: 7646705.
[doi:10.1155/2018/7646705] |
| [10] |
Zhao P. Application of edge computing network based on Software-defined Network (SDN). Mechanical & Electrical Engineering Technology, 2019, 48(27): 143-145, 234(in Chinese with English abstract).
[doi:10.3969/j.issn.1009-9492.2019.07.049] |
| [11] |
Shi WS, Dustdar S. The promise of edge computing. Computer, 2016, 49(5): 78-81.
[doi:10.1109/MC.2016.145] |
| [12] |
He L, Ota K, Dong MX. Learning IoT in edge: Deep learning for the internet of things with edge computing. IEEE Network, 2018, 32(1): 96-101.
[doi:10.1109/MNET.2018.1700202] |
| [13] |
Ren HL, Song Y, Wang JW, Hu YC, Lei JZ. A deep learning approach to the citywide traffic accident risk prediction. In: Proc. of the 21st Int’l Conf. on Intelligent Transportation Systems (ITSC). Maui: IEEE, 2018. 3346–3351.
|
| [14] |
Caliendo C, Guida M, Parisi A. A crash-prediction model for multilane roads. Accident Analysis & Prevention, 2007, 39(4): 657-670.
[doi:10.1016/j.aap.2006.10.012] |
| [15] |
Er U, Yüksel S, Aköz Ö, Karslıgil ME. Traffic accident risk analysis based on relation of common route models. In: Proc. of the 21st Int’l Conf. on Pattern Recognition. Tsukuba: IEEE, 2013. 2561–2564.
|
| [16] |
Bouwmans T, El Baf F, Vachon B. Background modeling using mixture of gaussians for foreground detection—A survey. Recent Patents on Computer Science, 2008, 1(3): 219-237.
[doi:10.2174/1874479610801030219] |
| [17] |
Porikli F M. Trajectory distance metric using Hidden Markov Model based representation. In: Proc. of the 6th IEEE Int’l Workshop on Performance Evaluation of Tracking and Surveillance. 2004.
|
| [18] |
Fang AF, Qiu CL, Zhao L, Jin YJ. Driver risk assessment using traffic violation and accident data by machine learning approaches. In: Proc. of the 3rd IEEE Int’l Conf. on Intelligent Transportation Engineering (ICITE). Singapore: IEEE, 2018. 291–295.
|
| [19] |
Hui F, Peng N, Jing SC, Zhou Q, Jia S. Driving behavior clustering and abnormal detection method based on agglomerative hierarchy. Computer Engineering, 2018, 44(12): 196-201(in Chinese with English abstract).
[doi:10.19678/j.issn.1000-3428.0050708] |
| [20] |
Li JL, Yuan Q, Yang FC. Crowd sensing and service in Internet of vehicles. ZTE Technology Journal, 2015, 21(6): 6-9(in Chinese with English abstract).
[doi:10.3969/j.issn.1009-6868.2015.06.002] |
| [21] |
Wan JF, Liu JQ, Shao ZH, Vasilakos AV, Imran M, Zhou KL. Mobile crowd sensing for traffic prediction in Internet of vehicles. Sensors, 2016, 16(1): 88.
[doi:10.3390/s16010088] |
| [22] |
Liang ZL, Wakahara Y. A route guidance system with personalized rerouting for reducing traveling time of vehicles in urban areas. In: Proc. of the 17th Int’l IEEE Conf. on Intelligent Transportation Systems. Qingdao: IEEE, 2014. 1541–1548.
|
| [23] |
He YH, Xia ZZ. A self-adaptive learning algorithm for BP network. Systems Engineering-Theory & Practice, 2000, 20(1): 93-98(in Chinese with English abstract).
[doi:10.12011/1000-6788(2000)1-93] |
| [24] |
Yan LP, Hu WB, Wang H, Qiu ZY, Du B. Dynamic real-time algorithm for multi-intersection route selection in urban traffic networks. Ruan Jian Xue Bao/Journal of Software, 2016, 27(9): 2199–2217 (in Chinese with English abstract). http://www.jos.org.cn/1000-9825/5063.htm
|
| [25] |
Yamada K, Ma JS, Fukuda D. Simulation analysis of the market diffusion effects of risk-averse route guidance on network traffic. Procedia Computer Science, 2013, 19: 874-881.
[doi:10.1016/j.procs.2013.06.117] |
| [26] |
Pan J, Popa IS, Zeitouni K, Borcea C. Proactive vehicular traffic rerouting for lower travel time. IEEE Trans. on Vehicular Technology, 2013, 62(8): 3551-3568.
[doi:10.1109/TVT.2013.2260422] |
| [27] |
Garg S, Singh A, Kaur K, Aujla GS, Batra S, Kumar N, Obaidat MS. Edge computing-based security framework for big data analytics in VANETs. IEEE Network, 2019, 33(2): 72-81.
[doi:10.1109/MNET.2019.1800239] |
| [28] |
Yang SR, Su YJ, Chang YY, Huang HN. Short-term traffic prediction for edge computing-enhanced autonomous and connected cars. IEEE Trans. on Vehicular Technology, 2019, 68(4): 3140-3153.
[doi:10.1109/TVT.2019.2899125] |
| [29] |
Zhang Z, Zhang XQ, Zuo DC, Fu GD. Research on target tracking application deployment strategy for edge computing. Ruan Jian Xue Bao/Journal of Software, 2020, 31(9): 2691–2708 (in Chinese with English abstract). http://www.jos.org.cn/1000-9825/5938.htm
|
| [10] |
赵攀. 基于软件定义网络(SDN)机边缘计算网络的应用. 机电工程技术, 2019, 48(27): 143-145, 234.
[doi:10.3969/j.issn.1009-9492.2019.07.049] |
| [19] |
惠飞, 彭娜, 景首才, 周琪, 贾硕. 基于凝聚层次的驾驶行为聚类与异常检测方法. 计算机工程, 2018, 44(12): 196-201.
[doi:10.19678/j.issn.1000-3428.0050708] |
| [20] |
李静林, 袁泉, 杨放春. 车联网群智感知与服务. 中兴通讯技术, 2015, 21(6): 6-9.
[doi:10.3969/j.issn.1009-6868.2015.06.002] |
| [23] |
何耀华, 夏志忠. BP网络的快速自适应学习算法. 系统工程理论与实践, 2000, 20(1): 93-98.
[doi:10.12011/1000-6788(2000)1-93] |
| [24] |
严丽平, 胡文斌, 王欢, 邱振宇, 杜博. 城市路网多路口路径动态实时选择方法. 软件学报, 2016, 27(9): 2199–2217. http://www.jos.org.cn/1000-9825/5063.htm
|
| [29] |
张展, 张宪琦, 左德承, 付国栋. 面向边缘计算的目标追踪应用部署策略研究. 软件学报, 2020, 31(9): 2691–2708. http://www.jos.org.cn/1000-9825/5938.htm
|



