The Chinese Meteorological Society
Article Information
- Xiaolan LI, Yongqiang YU, Hailong LIU, Pengfei LIN. 2017.
- Sensitivity of Atlantic Meridional Overturning Circulation to the Dynamical Framework in an Ocean General Circulation Model. 2017.
- J. Meteor. Res., 31(3): 490-501
- http://dx.doi.org/10.1007/s13351-017-6109-3
Article History
- Received June 16, 2016
- in final form November 9, 2016
2. College of Earth Science, University of Chinese Academy of Sciences, Beijing 100049
Atlantic meridional overturning circulation (AMOC) is an important component of the global ocean circulation system, characterized by warm and saline surface water from low latitudes or the Southern Ocean moving northward to high latitudes, and cold water flowing southward to low latitudes at depth. AMOC plays a significant role in transporting heat northward. At 24°–26°N, ocean circulation carries approximately 1.3 PW (1 PW = 1015 W) of heat northward, accounting for 25% of total northward heat transport at these latitudes by global air–sea systems (Hall and Bryden, 1982; Trenberth et al., 2001; Johns et al., 2011). Due to this poleward heat transport, the climate of the northern North Atlantic and northwestern Europe is particularly warmer than other areas of the same latitude (Rahmstorf and Ganopolski, 1999). Consequently, if AMOC weakens, the northward transport of heat will decrease, which can influence the climate of regional and remote areas, e.g., ENSO (El Niño–Southern Oscillation) variability (Timmermann et al., 2005), the position of the ITCZ (intertropical convergence zone; Vellinga and Wood, 2002), Atlantic ecosystems (Schmittner, 2005), and sea level changes of the North Atlantic (Levermann et al., 2005).
Because of AMOC’s important influence on climate, in order to better understand the part played by AMOC in climate systems, a joint UK–US RAPID–MOCHA (Rapid Climate Change–Meridional Overturning Circulation and Heat flux Array) observing system was established in April 2004 to continuously monitor the AMOC at 26.5°N (Cunningham et al., 2007). However, the dataset produced by this observing system is too short, and thus understanding AMOC relies heavily on climate models. Climate models can simulate the basic structure of the AMOC reasonably, but its strength and depth vary considerably among models (Zhang and Wang, 2013; Kostov et al., 2014; Song et al., 2014). Similar discrepancies can also be found in ocean hindcasts. Forced by results from the second phase of the Coordinated Ocean–ice Reference Experiments (CORE II; Large and Yeager, 2009), that is, the same atmospheric forcing, ocean models show the maximum AMOC as varying between 8 and 28 Sv (1 Sv = 106 m3 s–1), and the penetration depth also changes among models (Danabasoglu et al., 2014). These inconsistent values in AMOC strength are related to the dynamical framework and physical parameterization of the model. A number of studies have focused on improvements in physical parameterizations. For example, Danabasoglu et al. (1994) first used the mesoscale eddy parameterization of Gent and McWilliams (1990) and showed that meridional overturning circulation expanded in the North Atlantic. By using a new overflow parameterization representing density driven flows, the North Atlantic deep water (NADW) penetrated deeper and was stronger north of 40°N (Danabasoglu et al., 2010; Yeager and Danabasoglu, 2012). Other studies have emphasized the dynamical framework of models, including model resolution (Bryan et al., 2006) and the grid coordinate system, for example, using a tripolar or dipolar grid (Murray, 1996) instead of a latitude–longitude grid. However, despite a tripolar grid having been applied in many ocean general circulation models, such as MOM4 (Modular Ocean Model, version 4; Griffies et al., 2005) and POP2 (Parallel Ocean Program, version 2; Smith et al., 2010; Danabasoglu et al., 2012), no study has discussed the sensitivity of the AMOC to the choice of grid coordinate system in an ocean model.
Earlier ocean models utilize the latitude–longitude grid coordinate system, as does LICOM [State Key Laboratory of Numerical Modeling for Atmospheric Sciences and Geophysical Fluid Dynamics/Institute of Atmospheric Physics (LASG/IAP) Climate Ocean Model (Liu et al., 2012)], which is the ocean component of the FGOALS [Flexible Global Ocean–Atmosphere–Land System (Bao et al., 2013; Li et al., 2013)] climate model, also developed at LASG/IAP. The convergence of meridians at the North Pole can lead to polar singularity, and two ways can be used to overcome this problem: an artificial island at the North Pole and several surrounding circles of latitude (Pacanowski et al., 1993), or a zonal filter at high latitudes (Bryan et al., 1975). LICOM uses both methods. Nevertheless, it cannot simulate transpolar drift, due to the island at the North Pole, and shows biases in the high latitudes of the North Atlantic (Liu et al., 2004; Yu et al., 2011) and in the Arctic Ocean (Liu et al., 2012). Efforts have been made to improve the simulation in the North Atlantic and the Arctic Ocean by removing the island at the North Pole (Yu, 1997; Liu et al., 2006; Huang et al., 2014). However, this has not fundamentally solved the problem.
In this paper, a new method is introduced to avoid polar singularity, by changing the dynamical framework in LICOM. The traditional grid coordinate system of LICOM is the latitude–longitude grid and, in order to maintain the stability of numerical solution, a 1-2-1 low-pass filter at high latitudes and an artificial island at the North Pole and surrounding latitudes are adopted. Improvements using the new version of LICOM with a tripolar grid without any zonal filter and island are presented in this study. The tripolar grid has three poles—one located at the South Pole, as in the original version, but the other two located in two continental regions: northern Russia and northern Canada (Murray, 1996). The approach can eliminate the polar singularity induced by the latitude–longitude grid and yield a more uniform grid distance in the Arctic Ocean than that in the traditional latitude–longitude grid. In the tripolar grid, the artificial island at the North Pole and zonal filter at high latitudes become unnecessary, because the maximum and minimum of the grid distance is 131 and 27 km, respectively, compared to 111 and 6 km in the latitude–longitude grid.
The rest of the paper is organized as follows. Section 2 describes LICOM, the experimental design, and the method for calculating meridional stream function. The mean state of AMOC according to the two versions of LICOM and the causes are detailed in Section 3. Section 4 concludes the study.
2 Experimental design and methodology2.1 Experimental designIn order to evaluate the sensitivity of AMOC to the dynamical framework of the ocean model, two numerical experiments are carried out with LICOM2.0—one using the latitude–longitude grid (hereinafter referred to as Lat_1), and the other (its revised version) using a tripolar grid (hereinafter referred to as Tri). The main differences in model configuration between the latitude–longitude version and the tripolar version lie in the zonal filter and topography. Therefore, in order to isolate the individual contribution from the zonal filter, we design another sensitivity experiment, named Lat_2, with an enhanced filter on both temperature and salinity, to further detect the effect of the zonal filter on AMOC. Furthermore, because the effect of temperature and salinity variation on density change is opposite, another two sensitivity experiments are conducted, with an enhanced filter on temperature (Lat_2_T) and salinity (Lat_2_S), respectively.
All five experiments are based on LICOM2.0, which is a stand-alone model, forced by climatological wind and heat flux from CORE data (Large and Yeager, 2004). Precipitation, evaporation, and river runoff are also from the observational dataset of Large and Yeager (2004). Because LICOM2.0 is a stand-alone model, when the simulated temperature is lower than the ice point (–1.8°C), it is simply set to the freezing point of sea water. Furthermore, the sea surface salinity (SSS) is restored to the observations with a timescale of 30 days. Other details of LICOM 2.0 can be found in Liu et al. (2012).
Although all five experiments share the same source code, such as the same subgrid parameterization schemes, the topographical data and the horizontal grid distribution are different. The zonal filter option at high latitudes switches on in the four latitude–longitude grid experiments (Lat_1, Lat_2, Lat_2_T, and Lat_2_S), and off in the experiment Tri. The construction of the tripolar grid in experiment Tri is the same as suggested by Murray (1996), and the finite difference schemes are redesigned based on the same idea in LICOM2.0 (Yu et al., 2016, personal communication). The horizontal resolution of LICOM is approximately 1° × 1°, with a refinement of 0.5° between 10°S and 10°N, but the total number of horizontal grid points is 360 × 196 in the latitude–longitude grid and 360 × 218 in the tripolar grid. The vertical resolution is identical in the five experiments, with the equivalent depth of 10 m in the upper 150 m.
All three Lat_2 series experiments are based on Lat_1, with an enhanced filter on both the frequency and the spatial domain. In the latitude–longitude version of LICOM, the zonal filter is employed to both the temperature or salinity and their temporal tendency with different frequency. The frequency of the zonal filter in Lat_1 is every 5 days for temperature or salinity, whereas it is every 12 h in the three Lat_2 series experiments. The frequency of the filter for the temperature or salinity tendency is the same in the four latitude–longitude experiments, and it is applied in each time step. The expanded domain of the filter starts from 58°N in the three Lat_2 series experiments, whereas it is from 63°N in Lat_1. Details are provided in Table 1.
| Experiment | Filter frequency for temperature or salinity | Filter frequency for temperature or salinity tendency | Spatial domain of the filter for temperature | Spatial domain of the filter for salinity | Use island near the North Pole |
| Lat_1 | Every 5 days | Each time step | 63°N | 63°N | Yes |
| Tri | N/A | N/A | N/A | N/A | N/A |
| Lat_2 | Every 12 h | Each time step | 58°N | 58°N | Yes |
| Lat_2_T | Every 12 h | Each time step | 58°N | 63°N | Yes |
| Lat_2_S | Every 12 h | Each time step | 63°N | 58°N | Yes |
All five experiments are integrated for 500 model years. At the beginning, there are fast adjustments in AMOC (see Fig. S1 in supplemental material of the online version). When the experiments reach an equilibrium state at about 150 years, the AMOC variability becomes very weak, since the forcing fields of the experiments are the climatological mean state. In our analysis, the last 100 years from 401 to 500 model years are selected. In addition, the temperature and salinity data from PHC3.0 [Polar Science Center Hydrographic Climatology, version 3; updated from Steele et al. (2001)] are adopted in this study.
2.2 Calculation of meridional stream functionGenerally, the meridional stream function is used to represent the AMOC. Two methods can be used to calculate the stream function. One uses the meridional velocity v integrated zonally and vertically, and the other uses the vertical velocity w integrated zonally and meridionally. In essence, the results of the stream function are the same. Traditionally, the stream function can usually be estimated using the following formula:
| $\psi \left({z, y} \right) = \iint {v{\rm d}x{\rm d}z, } $ | (1) |
where v is the meridional velocity and ψ is the meridional stream function integrated zonally from the eastern boundary of the Atlantic basin to the western one. However, the axes of the tripolar grid coordinates are not parallel to the zonal or meridional direction in the northern high latitudes. Rotation of the coordinates is involved, which causes non-conservation of mass if v is used to calculate AMOC; thus, we use w to calculate ψ, as suggested by Smith et al. (2010):
| $\psi \left({z, y} \right) = \iint {w{\rm d}x{\rm d}y}, $ | (2) |
where y is an artificial latitude. Specifically, we first determine how many grids are located between two adjacent artificial latitudes, and then add them up and integrate meridionally from 31°S to 90°N, and vertically. Note that the strength of the stream function at 31°S is estimated by integrating the meridional velocity v zonally and vertically through the basin. The four latitude–longitude grid experiments also use w to estimate the stream function, but the results are almost the same as that calculated from v.
The algorithm of meridional freshwater transport is similar to AMOC, while the meridional heat transport (MHT) is different. The original calculation of MHT uses vt integrated zonally and vertically, where v is the meridional flow and t is the potential temperature. However, the new algorithm first calculates the advection tendency of every grid point, integrates zonally and vertically, and then integrates from south to north to gain a value every latitude. Note that the latitude is also an artificial one.
3 Results3.1 Mean state of AMOCThe annual mean AMOC simulated by the five experiments is presented in Fig. 1. All experiments successfully capture the wind-driven cells in the upper 500 m of the tropical ocean and the NADW below 500 m. However, an anticlockwise circulation exists in subpolar to polar regions in the four latitude–longitude grid experiments, while such circulation does not exist in Tri. The causes of this circulation are still unknown. A possible reason may be related to the application of an artificial island at the North Pole in the latitude–longitude grid experiments, which cannot simulate the transpolar drift.
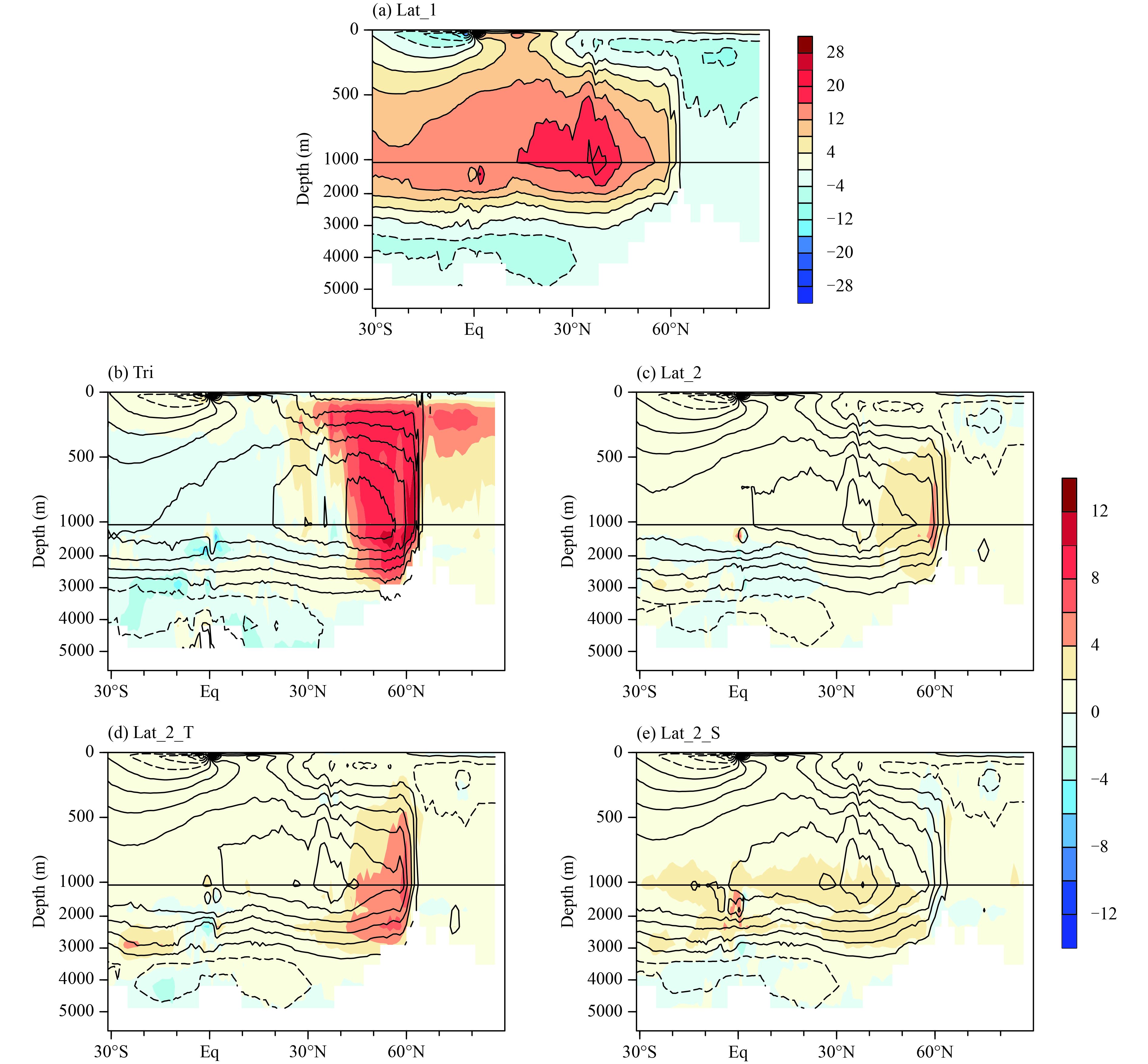
|
| Figure 1 Annual mean AMOC (Sv; 1 Sv = 106 m3 s–1) from (a) Lat_1, (b) Tri, (c) Lat_2, (d) Lat_2_T, and (e) Lat_2_S (see Section 2.1 and Table 1 for details of these experiments). The contours in (b–e) indicate the simulated AMOC, and the color shading shows the differences between each experiment and Lat_1. The contour interval is 4 Sv. |
Another discrepancy can also be seen in Fig. 1, insofar as Tri simulates the strongest NADW, with its main body located further northward. Compared with Lat_1, the experiments with an enhanced filter also show stronger NADW, especially Lat_2_S. In order to identify the source of NADW, we divide it into two parts: formation of deep water in the Labrador Sea, and that in the Greenland–Iceland–Norwegian (GIN) seas (Cheng et al., 2011). The deep-water formation rate in the GIN seas is defined as the maximum of the stream function in the vertical direction at 63°N, where the boundary of the GIN seas and the North Atlantic lies. The deep-water formation rate in the Labrador Sea is the difference between the AMOC strength (referred to here as the maximum of the stream function between 20° and 60°N, under 500 m) and the deep-water formation rate in the GIN seas. As shown in Table 2, the deep-water formation in the GIN seas and the Labrador Sea both contribute to NADW in Tri, whereas the deep-water formation region is mainly in the Labrador Sea in the other four latitude–longitude grid experiments. The maximum deep-water formation in the Labrador Sea occurs in Lat_2_S.
| Experiment | Maximum AMOC at 26.5°N (Sv) | AMOC strength (Sv) | Deep-water formation rate in the GIN seas (Sv) | Deep-water formation rate in the Labrador Sea (Sv) |
| Lat_1 | 18.5 | 22.2 | –0.11 | 22.2 |
| Tri | 18.0 | 22.8 | 8.96 | 13.84 |
| Lat_2 | 19.9 | 23.6 | 1.64 | 21.96 |
| Lat_2_T | 20.3 | 23.6 | 0.52 | 23.08 |
| Lat_2_S | 21.1 | 24.5 | 0.76 | 23.74 |
In addition, we compare the simulated AMOC with the observed one estimated from the RAPID observation system along 26.5°N (Cunningham et al., 2007; Johns et al., 2011). Compared to the RAPID estimate of 18.5 Sv (Johns et al., 2011), the experiments with an enhanced filter simulate larger northward transport across 26.5°N, especially Lat_2_S (21.1 Sv), compared with Tri (18.0 Sv).
Given the fact that the stream function maximum is located at approximately 1000 m, Fig. 2 presents the stream function changes with latitude at 1000 m. As shown, the stream function maximum in the four experiments with the latitude–longitude grid is located at 38°N, whereas in Tri it occurs at 47°N. Furthermore, Tri simulates a larger stream function than the other four experiments between 42° and 65°N. This is consistent with the conclusion drawn from Fig. 1, that is, that the main part of the NADW is located further northward in Tri. As for the four latitude–longitude grid experiments, the magnitude of the stream function in the experiments, from large to small, follows the order Lat_2_T, Lat_2, Lat_2_S, and then Lat_1. In addition, we calculate the AMOC in potential density (referenced to 2000 m) space in the four latitude–longitude grid experiments (see Fig. S2 in supplemental material ofthe online version). The results show that the maximum AMOC is shifted to the subpolar region at about 55°N, but the maximum value center is all around 1036.8 kg m–3, which is similar to results in the depth space.
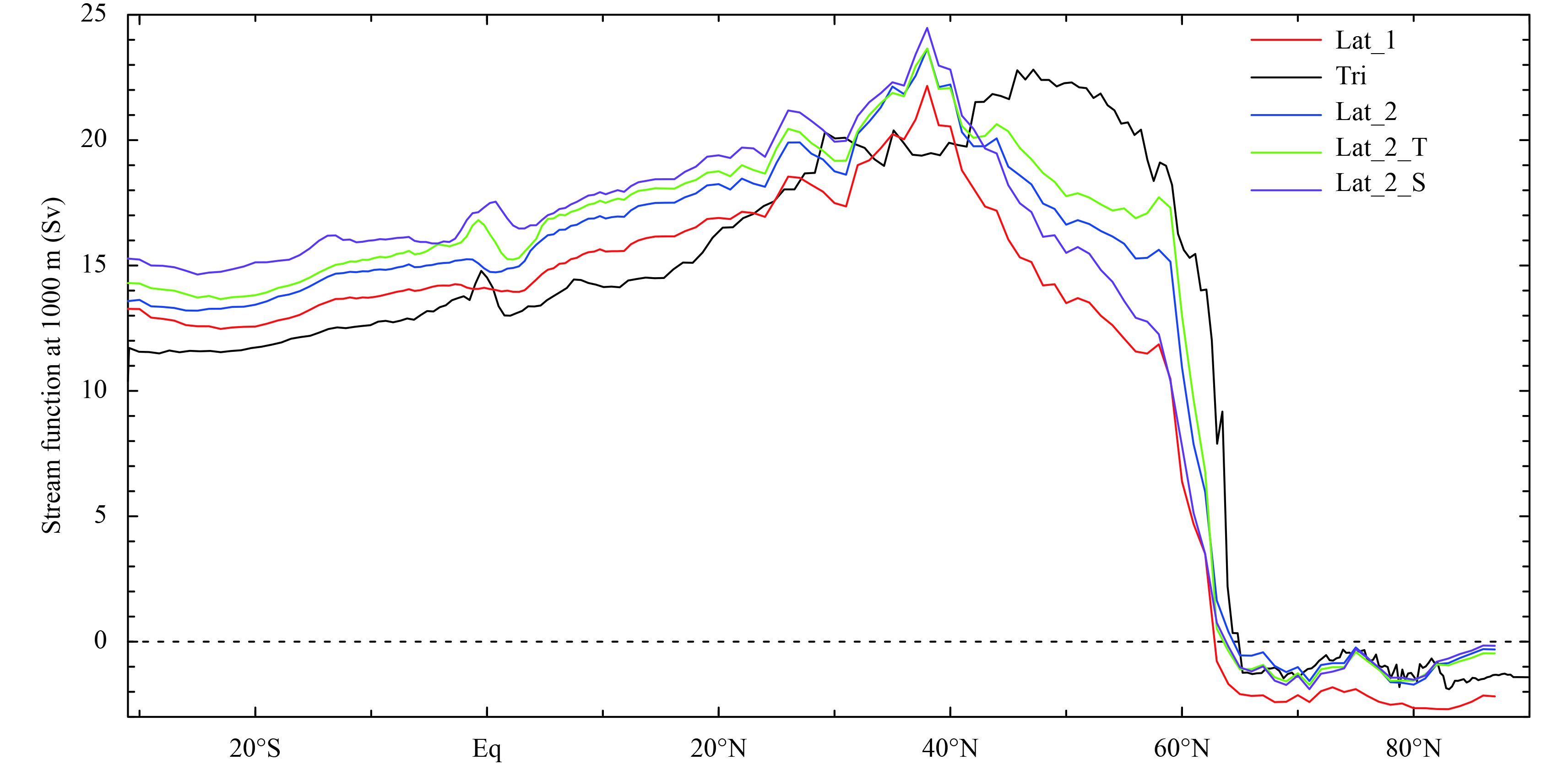
|
| Figure 2 Variation of the stream function (Sv) at 1000 m with latitude in experiment Lat_1 (red), Tri (black), Lat_2 (blue), Lat_2_T (green), and Lat_2_S (purple). See Section 2.1 and Table 1 for details of these experiments. |
The formation of NADW is associated with the process by which warm and salty water masses transport from low to high latitudes, and then cool down and sink in particular regions due to increased density, caused by atmospheric forcing. The changes in density can be attributed to the variation in temperature and salinity. Figure 3 presents the annual mean SST over the North Atlantic Ocean in February, when the strongest deep convection occurs. Compared with the latitude–longitude grid experiments, Tri simulates warmer SST in the central eastern area of the GIN seas, and the cold biases are much improved (Fig. 3c). One reason for this is the lack of a zonal filter in Tri, so that SST increases in the eastern basin of the ocean. This is also illustrated by the results from the intensified filter experiments. Because of the strengthened filter, the SST along the eastern coast of the ocean decreases, amplifying the cold biases between observation and the experiments in the GIN seas (Figs. 3d–f). Notice that the SST biases are different in the Labrador Sea in the three intensified filter experiments, with Lat_2_S showing the most bias, followed by Lat_2, and then Lat_2_T. The other reason may be associated with the different topographies between the latitude–longitude and tripolar grid versions, for example, the artificial island near the North Pole being applied in the former but not in the latter. Observational current in the Arctic Ocean is strong at the surface and weak in the deep ocean, and there is no obvious overturning cell in the Arctic Ocean. However, because of the island near the North Pole in the latitude–longitude grid experiments, a counterclockwise overturning cell, with a maximum of about 8 Sv, is simulated in all four latitude–longitude grid experiments (Fig. 1). In contrast, the correct topography around the North Pole in Tri avoids simulating a false overturning cell in the Arctic.

|
| Figure 3 SST (°C) in February from (a) PHC3.0 (Polar Science Center Hydrographic Climatology, version 3), (b) Lat_1, (c) Tri, (d) Lat_2, (e) Lat_2_T, and (f) Lat_2_S (see Section 2.1 and Table 1 for details of these experiments). The contours in (b–f) indicate the simulated SST, and the color shading shows the differences between each experiment and PHC3.0. |
The annual mean SSS over the North Atlantic in February is shown in Fig. 4. Similar to the distribution of SST, the SSS bias is also improved in Tri in the GIN seas (Fig. 4c), suggesting more saline water masses entering into the GIN seas. In addition, the SSS biases in the three strengthened filter experiments (Figs. 4d–f) are also similar to the SST biases (Figs. 3d–f) in the Labrador Sea. Lat_2_S shows the largest positive salinity anomaly (approximately 0.5 psu), with Lat_2 at 0.2 psu and Lat_2_T close to that observed.

|
| Figure 4 As in Fig. 3, but for sea surface salinity (psu). |
From the distribution of SST and SSS, Tri simulates an improved SST and SSS in the GIN seas. Furthermore, salinity plays a dominant role in deep-water formation in the GIN seas. For the three experiments with an enhanced filter, the convection is damped over the GIN seas and the deep-water formation is strengthened over the Labrador Sea. However, Lat_2_S simulates a larger SST (Fig. 3f) and SSS (Fig. 4f) in the Labrador Sea, whereas Lat_2_T does not. This indicates the impacts on SST and SSS are different by expanding the spatial domain of the filter on temperature and salinity, respectively. In the Labrador Sea, a strengthened filter on temperature (Lat_2_T) increases the SST that weakens the convection, whereas an enhanced filter on salinity (Lat_2_S) increases the SSS that strengthens the convection. In turn, strengthened convection increases the SST in Lat_2_S in the Labrador Sea (Fig. 3f).
3.2.2 Zonally averaged temperature and salinityAMOC comprises northward flow in the upper ocean and southward flow in the deep ocean. Therefore, the spatial distribution of temperature and salinity in the subsurface and deep ocean (here, 300–1500 m) may also contribute to AMOC. Figure 5 presents the zonally averaged temperature in February, in which the warm biases in Tri (Fig. 5c) are much smaller than in the latitude–longitude grid experiments (Figs. 5b, d–f) below 300 m in the subtropical regions. More obvious improvements in salinity can also be seen in subtropical regions, with positive biases of less than 0.8 psu (Fig. 6c), compared to almost 1.5 psu in the four latitude–longitude grid experiments. Furthermore, negative biases above 500 m are also improved in Tri in subpolar to polar regions. This can be attributed to more saline water masses entering the subpolar regions in Tri, leading to enhanced density. Thus, deep convection strengthens and more deep water forms in high latitudes. At depth, deep water moves southward and decreases the positive biases of temperature and salinity at low latitudes. In brief, removing the zonal filter and artificial island near the North Pole are two important reasons why the AMOC is improved in experiment Tri.
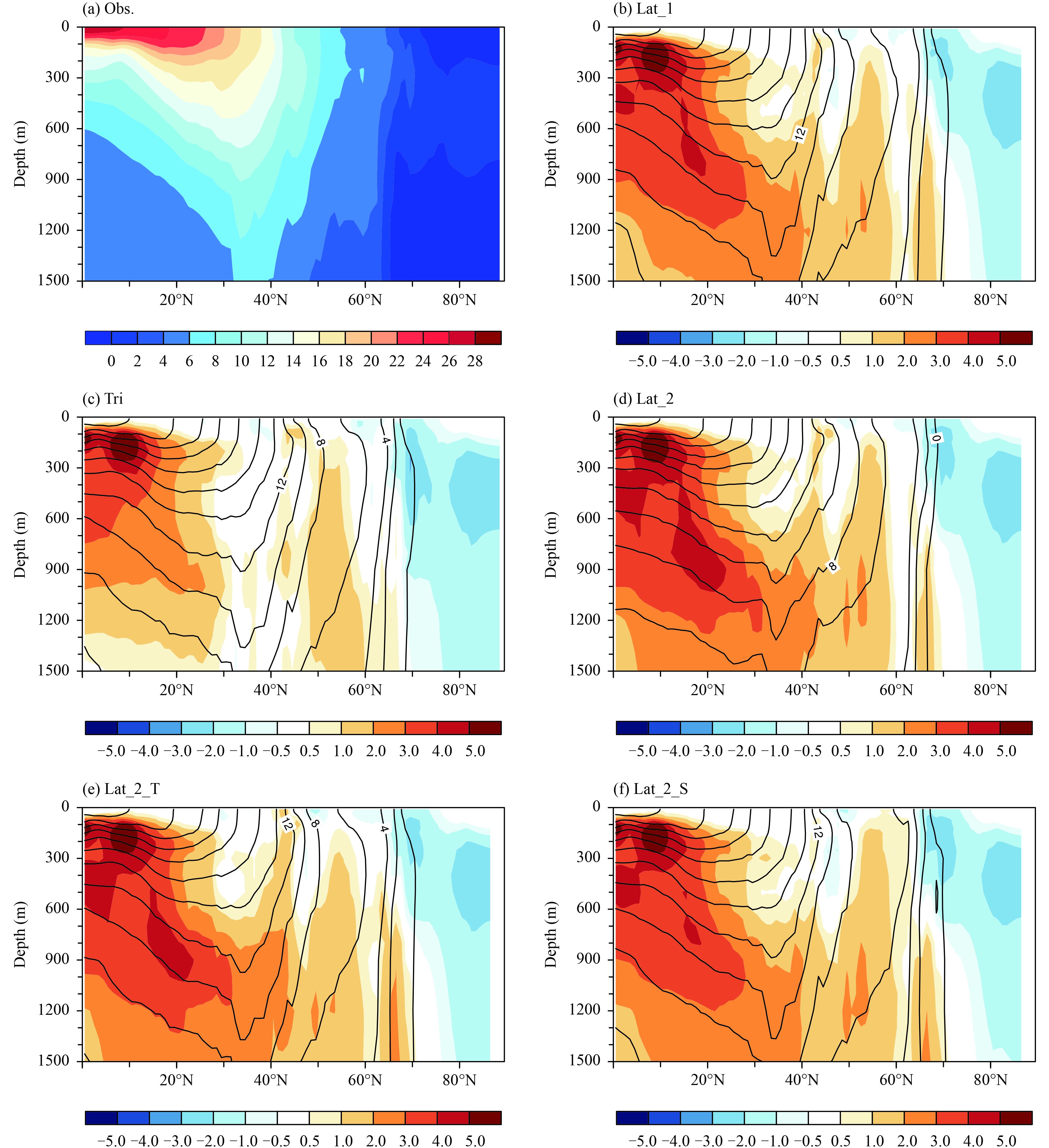
|
| Figure 5 Zonally averaged potential temperature (°C) in February from (a) PHC3.0 (Polar Science Center Hydrographic Climatology, version 3), (b) Lat_1, (c) Tri, (d) Lat_2, (e) Lat_2_T, and (f) Lat_2_S (see Section 2.1 and Table 1 for details of these experiments). The contours in (b–f) indicate the simulated temperature, and the color shading shows the differences between each experiment and PHC3.0. |
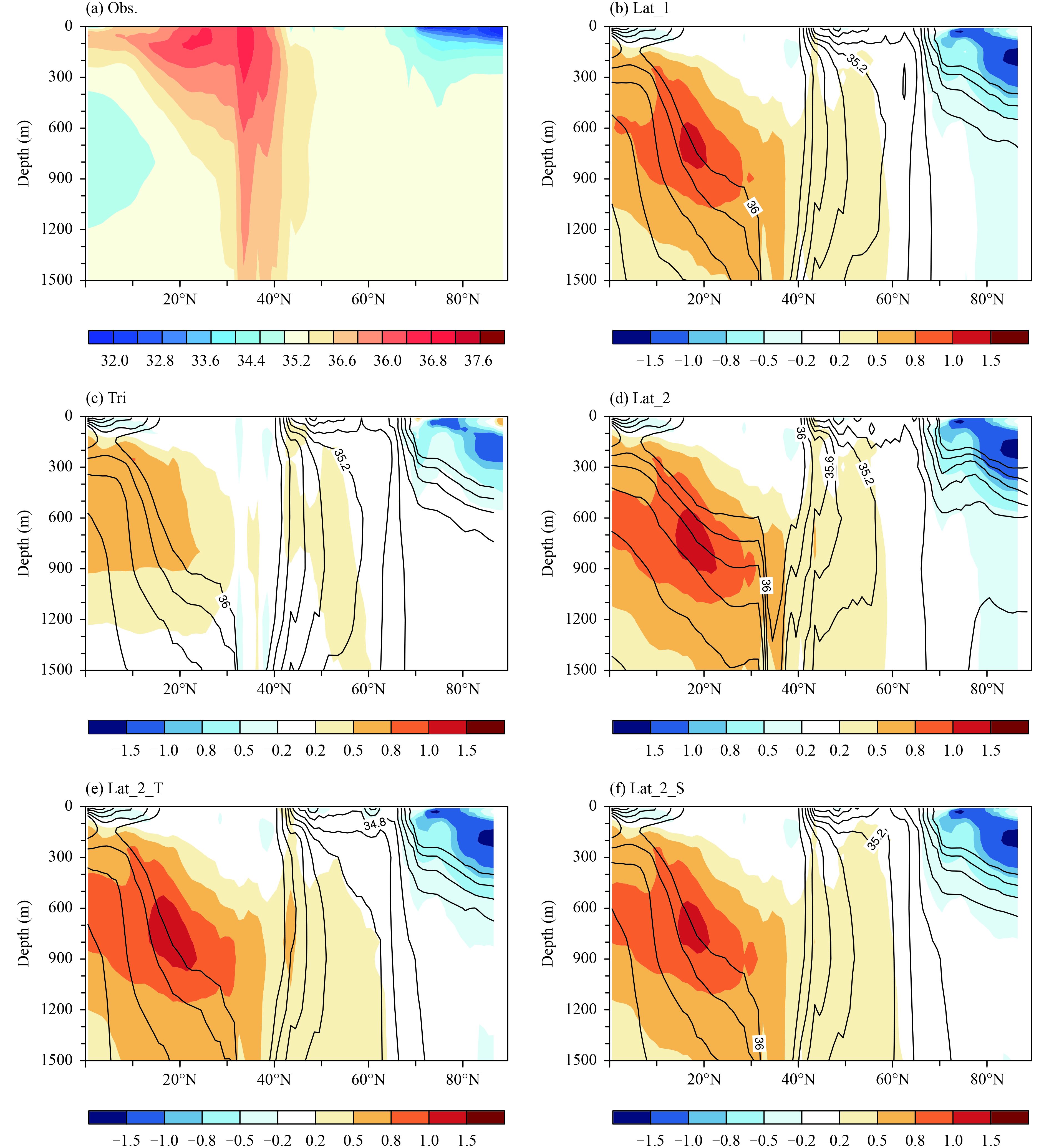
|
| Figure 6 As in Fig. 5, but for salinity (psu). |
The changes in AMOC are closely related to horizontal currents; surface currents and barotropic stream function (BSF) in the North Atlantic in February are illustrated in Fig. 7. Because the AMOC is a typical baroclinic overturning circulation, with opposite meridional velocity in the upper and deep ocean, as shown in Fig. 1, obvious changes in surface currents can be found, whereas the vertical mean BSF shows no significant changes in Fig. 7. The difference in currents between Tri and Lat_1 demonstrates that the currents in Tri are stronger than in Lat_1 (Fig. 7b), especially the west boundary current and the consistent northward flow in the GIN seas. This should be associated with the removal of the zonal filter in Tri. Without the filter, the zonal temperature and salinity will enhance, leading to a strengthened northward geostrophic current. The realistic current near the North Pole, for example, transpolar drift, may also contribute to the stronger flow in Tri.

|
| Figure 7 (a) Climatological mean barotropic stream function (BSF; color-shaded; Sv) and surface current (vectors; m s–1) in February from Lat_1. (b–e) Differences in BSF (color-shaded; Sv) and surface current (vectors; m s–1) between Lat_1 and (b) Tri, (c) Lat_2, (d) Lat_2_T, and (e) Lat_2_S. |
Because AMOC has an important influence on global climate, it is a key index in evaluating state-of-the-art climate models. Most CMIP3 and CMIP5 models are able to simulate AMOC’s structure well, but its strength differs among models (Zhang and Wang, 2013; Kostov et al., 2014; Song et al., 2014), which is related to the dynamic framework and physical parameterizations of the ocean model. Therefore, in order to evaluate the sensitivity of AMOC strength to an ocean model’s dynamical framework, two experiments are carried out in the present study using LICOM—one with the original latitude–longitude grid, and the other with a revised tripolar grid. Three additional experiments are also carried out using an enhanced filter, which is one of the differences between the latitude–longitude grid and tripolar grid, to explore the effect of the zonal filter on AMOC strength.
By dividing the deep-water formation region into the Labrador Sea and GIN seas, we analyze how deep-water formation in these two regions contributes to the simulated AMOC in each of the numerical experiments. Among the five experiments, Tri simulates the strongest NADW, with its main part located further northward in the GIN seas; meanwhile, the three enhanced-filter experiments also show larger NADW than Lat_1, due to enhanced deep-water formation, mainly in the Labrador Sea. Strong convection in the deep-water formation regions is related to strengthened density, which results from low temperature or high salinity. In Tri, more warm saline water masses enter the GIN seas, and salinity plays a dominant role in the convection. One reason for this is the lack of zonal filter in Tri, as the zonal gradient of temperature and salinity are increasing, leading to a strengthening of the north geostrophic flow. Thus, more saline waters are transported to the GIN seas, which strengthens the convection and causes them to sink. At depth, it is transported southward with cold water, decreasing the positive subsurface temperature and salinity biases in the subtropical regions. The other reason may be the topography, in that there is no island at the North Pole in Tri. In the three enhanced filter experiments, warm and saline water is suppressed from propagating northward and accumulating in the Labrador Sea, especially the experiment with the strengthened salinity filter.
Acknowledgements. The authors would like to thank Prof. Jun Cheng of Nanjing University of Information Science & Technology and the two anonymous reviewers for their valuable suggestions and helpful comments.
| Bao Q., Lin P. F., Zhou T. J., et al.,2013: The flexible global ocean–atmosphere–land system model, spectral version 2: FGOALS-s2. Adv. Atmos. Sci., 30, 561–576. DOI:10.1007/s00376-012-2113-9 |
| Bryan F. O., Danabasoglu G., Nakashiki N., et al.,2006: Response of the North Atlantic thermohaline circulation and ventilation to increasing carbon dioxide in CCSM3. J. Climate, 19, 2382–2397. DOI:10.1175/JCLI3757.1 |
| Bryan K., Manabe S., Pacanowski R. C., 1975: A global ocean–atmosphere climate model. Part II: The oceanic circulation. J. Phys. Oceanogr., 5, 30–46. DOI:10.1175/1520-0485(1975)005<0030:AGOACM>2.0.CO;2 |
| Cheng J., Liu Z., He F., et al.,2011: Impact of North Atlantic–GIN Sea exchange on deglaciation evolution of the Atlantic meridional overturning circulation. Clim. Past, 7, 935–940. DOI:10.5194/cp-7-935-2011 |
| Cunningham S. A., Kanzow T., Rayner D., et al.,2007: Temporal variability of the Atlantic meridional overturning circulation at 26.5°N. Science, 317, 935–938. DOI:10.1126/science.1141304 |
| Danabasoglu G., McWilliams J. C., Gent P. R., 1994: The role of mesoscale tracer transports in the global ocean circulation. Science, 264, 1123–1126. DOI:10.1126/science.264.5162.1123 |
| Danabasoglu G., Large W. G., Briegleb B. P., 2010: Climate impacts of parameterized Nordic Sea overflows. J. Geophys. Res., 115, C11005. DOI:10.1029/2010JC006243 |
| Danabasoglu G., Bates S. C., Briegleb B. P., et al.,2012: The CCSM4 ocean component. J. Climate, 25, 1361–1389. DOI:10.1175/JCLI-D-11-00091.1 |
| Danabasoglu G., Yeager S. G., Bailey D., et al.,2014: North Atlantic simulations in Coordinated Ocean-ice Reference Experiments phase II (CORE-II). Part I: Mean states. Ocean Model., 73, 76–107. DOI:10.1016/j.ocemod.2013.10.005 |
| Gent P. R., McWilliams J. C., 1990: Isopycnal mixing in ocean circulation models. J. Phys. Oceanogr., 20, 150–155. DOI:10.1175/1520-0485(1990)020<0150:IMIOCM>2.0.CO;2 |
| Griffies S. M., Gnanadesikan A., Dixon K. W., et al.,2005: Formulation of an ocean model for global climate simulations. Ocean Sci., 1, 45–79. DOI:10.5194/os-1-45-2005 |
| Hall M. M., Bryden H. L., 1982: Direct estimates and mechanisms of ocean heat transport. Deep-Sea Res., 29, 339–359. DOI:10.1016/0198-0149(82)90099-1 |
| Huang W. Y., Wang B., Li L. J., et al.,2014: Improvements in LICOM2. Part II: Arctic circulation. J. Atmos. Oceanic Technol., 31, 233–245. DOI:10.1175/JTECH-D-13-00064.1 |
| Johns W. E., Baringer M. O., Beal L. M., et al.,2011: Continuous, array-based estimates of Atlantic Ocean heat transport at 26.5°N. J. Climate, 24, 2429–2449. DOI:10.1175/2010JCLI3997.1 |
| Kostov Y., Armour K. C., Marshall J., 2014: Impact of the Atlantic meridional overturning circulation on ocean heat storage and transient climate change. Geophys. Res. Lett., 41, 2108–2116. DOI:10.1002/2013GL058998 |
| Large, W. G., and S. G. Yeager, 2004: Diurnal to Decadal Global Forcing for Ocean and Sea-Ice Models: The Data Sets and Flux Climatologies. NCAR Technical Note NCAR/TN-460+STR, Boulder, USA, 105 pp. |
| Large W. G., Yeager S. G., 2009: The global climatology of an interannually varying air–sea flux data set. Climate Dyn., 33, 341–364. DOI:10.1007/s00382-008-0441-3 |
| Levermann A., Griesel A., Hofmann M., et al.,2005: Dynamic sea level changes following changes in the thermohaline circulation. Climate Dyn., 24, 347–354. DOI:10.1007/s00382-004-0505-y |
| Li L. J., Lin P. F., Yu Y. Q., et al.,2013: The flexible global ocean–atmosphere–land system model, grid-point version 2: FGOALS-g2. Adv. Atmos. Sci., 30, 543–560. DOI:10.1007/s00376-012-2140-6 |
| Liu, H. L., Y. Q. Yu, W. Li, et al., 2004: Manual for LASG/IAP Climate System Ocean Model. Science Press, Beijing, China, 108 pp. (in Chinese) |
| Liu H. L., Lin P. F., Yu Y. Q., et al.,2012: The baseline evaluation of LASG/IAP climate system ocean model (LICOM) version 2. Acta Meteor. Sinica, 26, 318–329. DOI:10.1007/s13351-012-0305-y |
| Liu X. Y., Liu H. L., Zhang X. H., et al.,2006: Experiments of a reduced grid in LASG/IAP world ocean general circulation models (OGCMs). J. Trop. Meteor., 12, 9–15. |
| Murray R. J., 1996: Explicit generation of orthogonal grids for ocean models. J. Comput. Phys., 126, 251–273. DOI:10.1006/jcph.1996.0136 |
| Pacanowski, R. C., K. W. Dixon, and A. Rosati, 1993: The GFDL Modular Ocean Model Users Guide. Geophysical Fluid Dynamics Laboratory Ocean Group Tech. Rep. 2, Princeton, USA, 46 pp. |
| Rahmstorf S., Ganopolski A., 1999: Long-term global warming scenarios computed with an efficient coupled climate model. Clim. Change, 43, 353–367. DOI:10.1023/A:1005474526406 |
| Schmittner A., 2005: Decline of the marine ecosystem caused by a reduction in the Atlantic overturning circulation. Nature, 434, 628–633. DOI:10.1038/nature03476 |
| Smith, R. D., P. W. Jones, B. Briegleb, et al., 2010: The Parallel Ocean Program (POP) Reference Manual: Ocean Component of the Community Climate System Model (CCSM) and Community Earth System Model (CESM). Los Alamos National Laboratory Tech. Rep., Santa Fe, USA, 141 pp. |
| Song Y., Yu Y. Q., Lin P. F., 2014: The hiatus and accelerated warming decades in CMIP5 simulations. Adv. Atmos. Sci., 31, 1316–1330. DOI:10.1007/s00376-014-3265-6 |
| Steele M., Morley R., Ermold W., 2001: PHC: A global ocean hydrography with a high quality Arctic Ocean. J. Climate, 14, 2079–2087. DOI:10.1175/1520-0442(2001)014<2079:PAGOHW>2.0.CO;2 |
| Timmermann A., An S.-I., Krebs U., et al.,2005: ENSO suppression due to weakening of the North Atlantic thermohaline circulation. J. Climate, 18, 3122–3139. DOI:10.1175/JCLI3495.1 |
| Trenberth K. E., Caron J. M., Stepaniak D. P., 2001: The atmospheric energy budget and implications for surface fluxes and ocean heat transports. Climate Dyn., 17, 259–276. DOI:10.1007/PL00007927 |
| Vellinga M., Wood R. A., 2002: Global climatic impacts of a collapse of the Atlantic thermohaline circulation. Clim. Change, 54, 251–267. DOI:10.1023/A:1016168827653 |
| Yeager S. G., Danabasoglu G., 2012: Sensitivity of Atlantic meridional overturning circulation variability to parameterized Nordic Sea overflows in CCSM4. J. Climate, 25, 2077–2103. DOI:10.1175/JCLI-D-11-00149.1 |
| Yu, Y. Q., 1997: Design of ocean–sea ice–atmosphere coupling scheme and numerical simulation of interdecadal climate variability. Ph. D. dissertation, Institute of Atmospheric Physics, Chinese Academy of Sciences, Beijing, China, 130 pp. (in Chinese) |
| Yu Y. Q., Zheng W. P., Wang B., et al.,2011: Versions g1.0 and g1.1 of the LASG/IAP flexible global ocean–atmosphere– land system model. Adv. Atmos. Sci., 28, 99–117. DOI:10.1007/s00376-010-9112-5 |
| Zhang L. P., Wang C. Z., 2013: Multidecadal North Atlantic sea surface temperature and Atlantic meridional overturning circulation variability in CMIP5 historical simulations. J. Geophys. Res. Oceans, 118, 5772–5791. DOI:10.1002/jgrc.20390 |
 2017, Vol. 31
2017, Vol. 31


