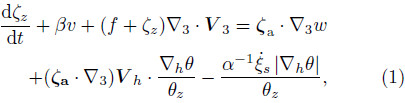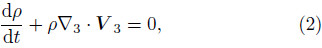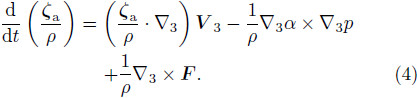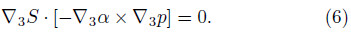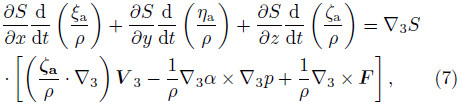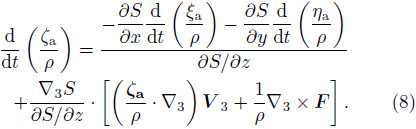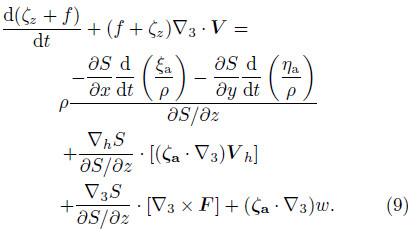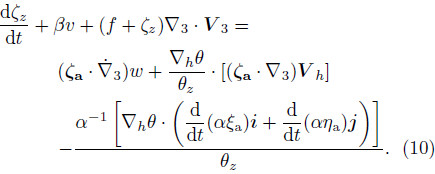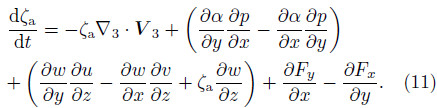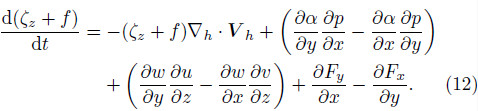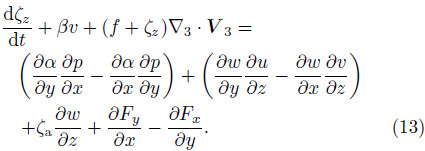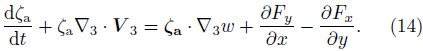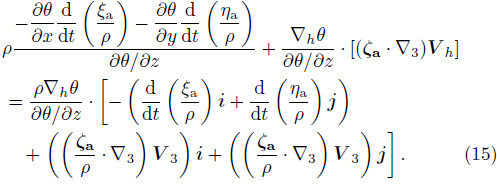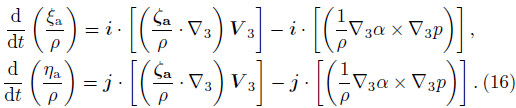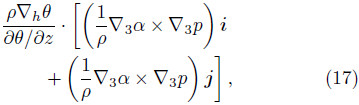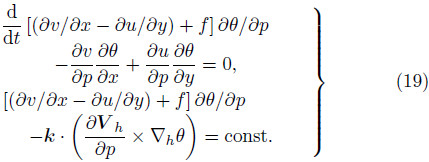The Chinese Meteorological Society
Article Information
- WANG Xiuming, ZHOU Xiaogang, TAO Zuyu, LIU Hua . 2016.
- Discussion on the Complete-Form Vorticity Equation and Slantwise Vorticity Development
- J. Meteor. Res., 30(1): 67-75
- http://dx.doi.org/10.1007/s13351-016-5040-3
Article History
- Received May 4, 2015;
- in final form November 11, 2015
2 Physical School of Peking University, Beijing 100871
The atmospheric momentum equations describethe basic theoretical relations in atmospheric dynamics.The vertical vorticity equation obtained from thehorizontal momentum equation summarizes the generalrules of synoptic-scale motion of the atmospherein the form of a quasi-horizontal vortex; it is thusan important theoretical basis for weather forecasting, and is referred to as the classical vertical vorticityequation. This classical vertical vorticity equationis derived only from the atmospheric momentumequations,excluding the thermodynamic energy equation.Only when the thermodynamic equation is includedcan vortex motion of the atmosphere be completelydescribed(Liu and Liu, 2011). The potentialvorticity equation,deduced from the vorticity equation,thermodynamics equation, and continuity equation,is an expression that can comprehensively takeinto account the functions of dynamics and thermodynamics.Wu and Liu(1998,1999) and Wu(2001)deduceda vertical vorticity equation related to thermodynamicfactors,starting from the potential vorticityexpression through complex mathematical transforms, and the potential vorticity conservation equation wasincluded. This vertical vorticity equation was namedthe complete-form vertical vorticity tendency equation,or complete-form vorticity equation. One term in the equation is called the “slantwise term”,whichis correlated to the ratio between the horizontal gradient and vertical gradient of potential temperature.Wu and Liu(1999) and Wu(2001)believed thisto be a new term compared to the classical verticalvorticity equation. The vertical vorticity development(slantwise vorticity development),causedby isentropic surface tilt,was discussed on the basisof the complete-form vorticity equation. Thereafter,the complete-form vorticity equation and slantwisevorticity development have been applied in analysesof subtropical highs,frontal cyclones,tropical cyclones, and Meiyu frontal severe rainfall(Li and Duan, 1999; Ma et al., 2002; Jiang et al., 2004; Wang et al., 2007; Wang et al., 2010; Li et al., 2013). Wu et al.(2013)further introduced the concept of generalizedslantwise vorticity development,which is a coordinateindependent framework of vorticity development includingslantwise vorticity development.
Chen(2006)pointed out that there are someshortcomings in this complete-form vorticity equation.For example, Wu(2001)did not discuss whether theclassical vertical vorticity equation and the completeformvorticity equation are consistent with each otherwhen the isentropic surface is tilting. The completeformvorticity equation derived from the potential vorticityequation cannot accurately reflect the impact ofthe solenoidal term on the change in vertical vorticity.Moreover,it overestimates the slantwise vorticityforcing effect on the development of vertical vorticity.
To discuss the issues mentioned above and betterunderst and the complete-form vorticity equation,we deduce an expression that is consistent with thecomplete-form vorticity equation,on the basis of thethree-dimensional(3D)vorticity equation and themathematical deformation of entropy function. Then,based on the new equation and its deduction,we examinethe consistency of the complete-form vorticityequation and its classical counterpart, and further analyzehow to better underst and the complete-form vorticityequation and its solenoidal term,as well as theslantwise vorticity development.
2. Complete-form vertical vorticity equation
The expression of Ertel potential vorticity(Ertel, 1942a,b)in the height coordinate is  ,in an adiabatic atmosphere is
,in an adiabatic atmosphere is 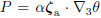 ,whereζa is the absolute vorticity,θs is ploytropic temperature, and θ is potential temperature. Starting fromthe adiabatic Ertel potential vorticity expression,wecan easily obtain the following equation:
,whereζa is the absolute vorticity,θs is ploytropic temperature, and θ is potential temperature. Starting fromthe adiabatic Ertel potential vorticity expression,wecan easily obtain the following equation:
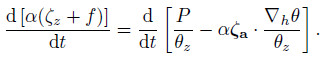
Wu(2001)deduced the z-coordinate vorticityequation in the following form through a seriesof mathematical transformations and named it thecomplete-form vorticity equation:
where ζz is the vertical component of relative vorticityin the z-coordinate system; β is the Rossby parameter;f is the Coriolis parameter; θz = ∂θ/∂z is the partialderivative of potential temperature to z; α is specificvolume; S is the unit vector along the direction of ∇hθ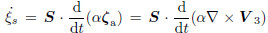 ,inwhich V3 is the 3D absolute velocity vector,v is they component of velocity, and d/dt is the total timederivative operator,which means
,inwhich V3 is the 3D absolute velocity vector,v is they component of velocity, and d/dt is the total timederivative operator,which means 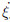 s is related to thehorizontal vorticity varying with time. The second and third terms on the right-h and side are jointly namedthe “baroclinic term”,while the second term alone iscalled the “slantwise term” and the first term is the“twisting term”.
s is related to thehorizontal vorticity varying with time. The second and third terms on the right-h and side are jointly namedthe “baroclinic term”,while the second term alone iscalled the “slantwise term” and the first term is the“twisting term”.
The other two different forms of the completeformvertical vorticity equation are(Wu,2001)
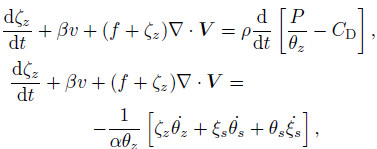
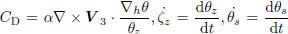 .Here,the PV conservation,or dP/dt = 0 is used in asubtle way so that the vertical vorticity changing withtime is not on the right-h and side of the equation. Wu(2001)believed that the key difference between the complete-form vorticity equation and the classical verticalvorticity equation is that the former contains the“baroclinic term”,which is related to the isentropicsurface tilt. Thus,severe weather,which is closely relatedto static stability and atmospheric baroclinicity,can be interpreted. When the isentropic surface tiltsmore,the contribution of the slantwise term to thedevelopment of vertical vorticity is far more than thestretching term and twisting term derived from theclassical vertical vorticity equation. Here,the jointstretching term and twisting term is in fact the firstterm on the right-h and side of Eq.(1),i.e.,ζa•∇3w.
.Here,the PV conservation,or dP/dt = 0 is used in asubtle way so that the vertical vorticity changing withtime is not on the right-h and side of the equation. Wu(2001)believed that the key difference between the complete-form vorticity equation and the classical verticalvorticity equation is that the former contains the“baroclinic term”,which is related to the isentropicsurface tilt. Thus,severe weather,which is closely relatedto static stability and atmospheric baroclinicity,can be interpreted. When the isentropic surface tiltsmore,the contribution of the slantwise term to thedevelopment of vertical vorticity is far more than thestretching term and twisting term derived from theclassical vertical vorticity equation. Here,the jointstretching term and twisting term is in fact the firstterm on the right-h and side of Eq.(1),i.e.,ζa•∇3w.
In order to better underst and the complete-formvorticity equation,a new complete-form vorticityequation is derived based on the 3D vorticity vectorequation in the height coordinate.
The form of the continuity equation in the z coordinateis
where ρ is density and V 3 is the 3D velocity vector.The form of the 3D vorticity equation in the zcoordinate is(Lü and Peng,1990)
where ζa = ∇ × V 3 + 2Ω is the absolute vorticity,F is frictional force, and α is specific volume. In Eq.(3),the first term on the left-h and side is the rateof variation of the absolute vorticity field; the secondterm denotes the vorticity advection; the third term isthe 3D divergent term,which describes the stretchingof vorticity as a result of flow compressibility; and thefourth term is the twisting term. The first term on theright-h and side is the solenoidal term, and the secondterm is the frictional term.Taking Eq.(2)into Eq.(3)for the 3D divergentterm, and multiplying Eq.(3)with 1/ρ,the followingequation is then obtained:
Equation(4)is the total time derivative equation ofthe ratio of the absolute vorticity to density,which isnamed the ratio vorticity.Entropy is a crucial concept in classical thermodynamics(Liu et al., 2007). The thermodynamics equationcan be expressed with entropy function as(Lü et al., 2004)
where S = cp ln θ is the entropy function,θ =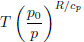 is potential temperature,
is potential temperature,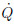 is the diabaticheating rate, and T is temperature. SinceS is a function of p and ρ,i.e.,S = S(ρ,p),
is the diabaticheating rate, and T is temperature. SinceS is a function of p and ρ,i.e.,S = S(ρ,p),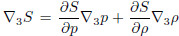 , and the solenoidal vectoris −∇3α×∇3p. Therefore,
, and the solenoidal vectoris −∇3α×∇3p. Therefore,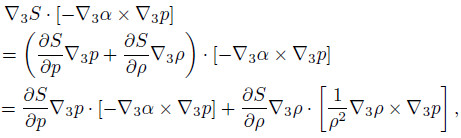
Next,we apply the operator ∇3S to Eq.(4), and the equation changes into
where ξa,ηa, and ζa are components in the x,y, and zdirections,respectively,of the absolute vorticity, and ζa = ζz + f. According to Eq.(6),we can eliminatethe second term on the right-h and side of Eq.(7),which means the solenoidal term is not explicitly includedin Eq.(7). Then,Eq.(7)can be rewrittenasThe left-h and side of Eq.(8)can be written as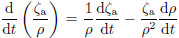 . Then,by taking Eq.(2)into the left-h and side and multiplying both sides byρ,Eq.(8)can be expressed asBy replacing S with θ,ignoring the effect of friction, and recalling that
. Then,by taking Eq.(2)into the left-h and side and multiplying both sides byρ,Eq.(8)can be expressed asBy replacing S with θ,ignoring the effect of friction, and recalling that 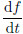 = βV and ∂θ/∂z can be writtenas θz,Eq.(9)can be rewritten as
= βV and ∂θ/∂z can be writtenas θz,Eq.(9)can be rewritten as
Taking note that the third term on the right-h and side of Eq.(10)can be written as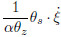 , and comparingEq.(10)with Eq.(1),which was put forwardby Wu(2001),we see that the two equations shareexactly the same form. Here,the entropy functionS is used first,because it is considered to start fromthe general thermodynamic equation, and only for anideal gas undergoing an adiabatic process,the ErtelPV can be expressed as αζa ·∇θ(Ertel, 1942a,b; Wu,1990). The difference between Eq.(10)(or Eq.(1)) and Eq.(9)lies in the fact that Eq.(10)is limited toan adiabatic process; thus,Eq.(9)is a more generalexpression of the complete-form vorticity equation.
, and comparingEq.(10)with Eq.(1),which was put forwardby Wu(2001),we see that the two equations shareexactly the same form. Here,the entropy functionS is used first,because it is considered to start fromthe general thermodynamic equation, and only for anideal gas undergoing an adiabatic process,the ErtelPV can be expressed as αζa ·∇θ(Ertel, 1942a,b; Wu,1990). The difference between Eq.(10)(or Eq.(1)) and Eq.(9)lies in the fact that Eq.(10)is limited toan adiabatic process; thus,Eq.(9)is a more generalexpression of the complete-form vorticity equation.
When the isentropic surface is tilting,thecomplete-form vorticity equation has the “baroclinicterm” related to the isentropic surface tilt. However,whether or not the two equations are accordant whenthe isentropic surface is tilting has not been discussed.We believe that,even though their forms are different,the complete-form vertical vorticity equation and the classical vertical vorticity equation should be consistentin essence. We illustrate this in the followingsubsections through comparative analysis of the twoequations.
3.1 Classical vertical vorticity equationIn the z coordinate,the 3D absolute vorticity vectoris written as ζa = ξai+ηaj+ζak. By applying theoperator k to Eq.(3),the vertical vorticity equationcan be obtained,which is
The first term on the right-h and side of Eq.(11)can be further decomposed into
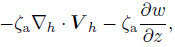
 can be eliminated and Eq.(11)can be further expressed as
can be eliminated and Eq.(11)can be further expressed as
Equation(12)is the classical vertical vorticityequation. The total derivative of absolute vorticity ison its left-h and side. The first term on its right-h and side is the horizontal divergence term; the second termis the solenoidal term,which is the vertical componentof the 3D solenoidal term; the third term is the twistingterm; and the fourth term is the frictional term. Itis important to note that,compared to the fourth termon the left-h and side of Eq.(3),i.e.,the 3D twistingterm,the twisting term of Eq.(12)is its vertical component, and  is eliminated together with the 3Ddivergence term.
is eliminated together with the 3Ddivergence term.  is usually called the stretchingterm,but in essence it is one part of the twisting term.
is usually called the stretchingterm,but in essence it is one part of the twisting term.
By converting the left-h and side of Eq.(12)intoa form consistent with the left-h and side of Eq.(10),it becomes
To compare the complete-form vorticity equation and classical vertical vorticity equation is in fact acomparison of Eqs.(10) and (13). Furthermore,it isimportant to note that the second term on the righth and side of Eq.(13)is just the vertical component ofthe twisting term of Eq.(3). The comparison revealsthat the classical vertical vorticity equation containsthe solenoidal term,while the complete-form verticalvorticity equation does not; but,the “baroclinic term”,correlated to the isentropic surface tilt,is added,whichrefers to the second and third terms on the right-h and side of Eq.(10). If the “baroclinic term” in Eq.(10)isproven to be the solenoidal term in Eq.(13),we can beconvinced that the complete-form vorticity equationis the same as the classical vorticity equation. Thus,having illustrated the consistency of the two equationswhen the isentropic surface is horizontal,we next focuson the relationship between the “baroclinic term” and solenoidal term when the isentropic surface is tilting.
When the isentropic surface is horizontal,∇3S isvertical to the 3D solenoidal vector based on Eq.(6);thus,the 3D solenoidal vector remains in the horizontaldirection,i.e.,the vertical component of the 3Dsolenoidal term is zero, and there is no solenoidal termin Eq.(13). At this moment,∇hθ = 0,∇hθ/θz = 0, and the first and second terms on the right-h and sideof Eq.(10)are zero. Therefore,when the isentropicsurface is horizontal,Eq.(10)becomes
Obviously,Eq.(14)contains no “baroclinicterm”, and Eq.(13)contains no solenoidal term either;thus,the forms of the two equations,i.e.,thecomplete-form vertical vorticity equation and the classicalvertical vorticity equation,are accordant.
It can be proven that when the isentropic surfaceis tilting,the “baroclinic term” of the complete-formvorticity equation is the solenoidal term in the classicalvertical vorticity equation,regardless of the effectof friction. The “baroclinic term” in Eq.(10)can berewritten as
Applying i· and j· to Eq.(4),we can respectivelyobtain the following equations:
Substituting Eq.(16)into Eq.(15),the “baroclinicterm” can be expressed as
and Eq.(6)can be rearranged to
Hence,the “baroclinic term” in Eq.(17)can bewritten as [k•(∇3α ×∇3p)],which is the solenoidalterm in the classical vertical vorticity equation. Thismeans that the “baroclinic term” is equal to thesolenoidal term. Therefore,we draw the conclusionthat,regardless of whether the isentropic surface ishorizontal or tilting,the complete vertical vorticityequation is always consistent with the classical verticalvorticity equation.
The development of synoptic-scale weather disturbanceis often referred to as cyclogenesis—a termthat emphasizes the role of relative vorticity in the developmentof synoptic-scale systems(Holton,2004).Atmospheric baroclinicity contributes to the generation and development of weather systems(disturbances),which was first proposed by Jaw(1946). Jaw(1946)indicated that,since the effect of the solenoidalfield destabilizes the disturbance of zonal circulation,the planetary wave is unstable in a baroclinic atmosphere.The solenoidal term in the classical verticalvorticity equation is the term to measure the strengthof baroclinicity. The more solenoids in a unit area,thestronger the baroclinicity. If the “baroclinic term” expressesthe atmospheric baroclinicity,the “baroclinicterm” should be equal to the solenoidal term. Thevorticity equation in isobaric coordinates contains nosolenoidal term. It contains inexplicitly in the divergenceterm. There is no solenoid on the isobaric surface, and the isopycnal on the isobaric surface is theisotherm. Consequently,the denser the isotherms onthe isobaric surface(the greater the temperature gradients),the more solenoids are reflected in the unitarea vertically, and the stronger the baroclinicity.
3.3 Underst and ing of the complete-form vorticityequationBased on the deviation of Eq.(10),the completeformvorticity equation can be obtained through amathematical transform of multiplying Eq.(4)by∇3θ, and it is actually the deformation of the followingexpression:
It can be seen that the complete-form vorticityequation is only the mathematical decompositionform that the total time derivative of the ratio of 3Dabsolute vorticity to density projects in the 3D entropy(potential temperature)gradient. Actually,Eq.(18)is one part for deducing the PV equation,i.e., . On this basis,the PV equation canbe obtained by adding
. On this basis,the PV equation canbe obtained by adding 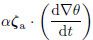 ,i.e.,the transformationof the thermodynamics equation.
,i.e.,the transformationof the thermodynamics equation.
The third term on the right-h and side of Eq.(10)is,in fact,obtained by moving the second and thirdterms on the left-h and side of Eq.(18)to its righth and side. It contains not only the variation in horizontalvorticity with time,but also the change in densitywith time and the horizontal gradient of entropy.Wu(2001)believed this term to be about the changein horizontal vorticity with time,involving other dynamicfactors,but he did not discuss it any further.According to Eq.(16),the change in the ratio of horizontalvorticity results from the horizontal componentof the solenoidal term and twisting term,while thehorizontal twisting term is counteracted by the secondterm on the right-h and side of Eq.(10),which meansthat the second and third terms in Eq.(10)are correlated.The second term on the right-h and side of Eq.(10),which is the “slantwise term”,is connected withthe projection of the 3D twisting term on the horizontalsurface.
In addition,from the physics viewpoint,when theleft-h and side of an equation is written in the form ofthe total time derivative of a physical quantity, and theright-h and side is the spatial distribution function ofvariables,which is not related to time,the term on theright-h and side can be regarded as the forcing term,enabling diagnosis of the change in the physical quantityon the left-h and side with time. This is convenientfor analysis of its physical forces as well as diagnosiswith observational data. The right-h and side of Eq.(13)does not contain a time change item,so the forcingterm on the right-h and side can be used to analyzethe tendency of vertical vorticity. In the completeformvorticity equation(Eq.(1)or Eq.(10)),thetotal time derivative operator for horizontal vorticityis contained on the right-h and side of the equation,so the change in the ratio of horizontal vorticity withtime is required.
4. “Slantwise term” and baroclinicityThe contribution of the “slantwise term” is very important to the development of vertical vorticity, and it is far more than the twisting term and stretchingterm of the classical vertical equation when the isentropicsurface has a larger tilting angle(Wu,2001).The discussion in Section 3.2 made it clear that thebaroclinic term of the complete-form vorticity equationis equal to the solenoidal term of the classical verticalvorticity equation,which is the projection of the3D solenoidal term in the vertical direction. Becausethe 3D solenoidal term is parallel to the isentropic surface,the more tilted the isentropic surface,the biggerthe projection of the 3D solenoidal term in the verticaldirection, and the less capable it is to neglect itsimpact on vertical vorticity. Therefore,the solenoidalterm or the “baroclinic term” is very important in thevicinity of atmospheric fronts.
It is a fact that the erupting development of verticalvorticity often appears near a frontal system asa consequence of the existence of isentropic surfacetilt,vertical wind shear, and a low-level jet, and thiswas the purpose of the work of Wu and Liu(1999) and Wu(2001),who tried to use the “slantwise term”in a theoretical explanation. From the above discussionin this paper,we have learned that,in fact,the“slantwise term” cannot explain the solenoidal termcontribution, and it is canceled by the other terms onthe right-h and side of the equation.
In synoptic analysis(in the isobaric coordinates),the isentropic surface is the same as the isotherm surface.Inside air masses,temperature varies slightlyon the isobaric surface,the incline of the isentropicsurface is very small(nearly horizontal), and the magnitudeis about one thous and th of a degree. In thefrontal area,with a larger horizontal difference in temperaturebetween cold and warm air masses,the inclineof the isentropic surface is large,at one hundredthof a degree. In isobaric chart synoptic analysis,the isotherm line is a constant potential temperatureline. The density of isotherm lines on the isobaricchart refers to the degree of tilt of the isentropic surface.Therefore,the impact of so-called(isentropicsurface)tilting vorticity development(or tilting vorticityforcing)on vertical vorticity is the forcing effectof the baroclinicity on vertical vorticity changes(Ma et al., 2002).
The classical vorticity equation cannot diagnosethe forcing effect of the baroclinicity because it cannotdescribe the thermodynamic process explicitly,whichis the reason why the PV is introduced. The PV isobtained by the vector vorticity equation and the thermodynamicenergy equation, and it has a conservativeproperty in the absence of diabatic and frictional processes.Hoskins(2003)pointed out in the PV thinkingtheory that the interaction of PV anomalies athigh levels, and potential temperature anomalies atlow levels,contributes to cyclogenesis, and this is analternative method for diagnosing the development ofdisturbance in a baroclinic atmosphere(the developmentof a vortex system or atmospheric circulation),which is called the initial value approach to cyclogenesis(Holton,2004).
Zhou et al.(2011)investigated the expressionof PV equations, and the expression in the isobaric and isentropic coordinates,with two approaches—onestarting from the 3D vector momentum equation,continuityequation, and thermodynamic equation, and the other directly from the corresponding scalar momentumequations. The results showed that the formsof PV expression obtained by different methods aredifferent in the isobaric coordinate. The PV equationderived from the p-coordinate scalar momentum equationsis the strict PV equation in nature. Under adiabatic and frictionless conditions,the form of the PVconservation expression deduced from the p-coordinatescalar momentum equations changes into:
From the expression of PV in the p-coordinate,Eq.(19),it can be seen that the PV contains theeffects of isentropic surface tilt,the vertical shear ofhorizontal winds, and static stability and vertical vorticity.Under the quasi-geostrophic model,the PV hasthe characteristic of inversion given a suitable bound ary. The distribution of PV determines the geopotentialheight distribution, and then the distributionof temperature and geostrophic wind. The relationshipbetween the vorticity field and the PV field is notimmediate. The positive PV anomaly reinforces therelative vorticity,which comes from the balance adjustmentunder a certain balance constraint, and correspondingly,the atmosphere near the PV anomaly isadjusted(Hu,2003). Based on Eq.(19),it is easyto calculate the PV anomaly by the absolute vorticity,static instability,vertical wind shear, and horizontalgradient of potential temperature; but where there isa PV anomaly,it is impossible to tell which part isfrom vertical vorticity stretching and which is frombaroclinicity.Mesoscale frontal rainb and s are closely connectedto cyclogenesis, and the PV thinking can explain cyclogenesis(the development of a synoptic vortex systemin a baroclinic atmosphere). However,it cannot explainthe cross-frontal circulation associated with theconcentrated frontal rainb and ,as it crosses the isentropicsurface beyond the scope of the PV thinking.
5. ConclusionTo take into account the influence of the thermodynamicfactor,the complete-form vorticity equationwas derived out of PV by Wu and Liu(1999) and Wu(2001). In this study,starting from the vorticity vectorequation, and combining the continuity equation and multiplying the 3D entropy gradient,we havederived and obtained the same complete-form vorticityequation. Seen from the process of deduction,the complete-form vorticity equation is the mathematicaldecomposition and deformation of the totaltime derivative of the ratio of 3D absolute vorticity todensity, and projects onto the 3D entropy(potentialtemperature)gradient. The complete-form vorticityequation is consistent with the classical vertical vorticityequation in nature,regardless of whether ornot the isentropic surface is tilting. The “baroclinicterm” of the complete-form vorticity equation is thesolenoidal term of the classical vorticity equation. Inaddition,the two items of the “baroclinic term” arenot independent of one another.
The impact of so-called(isentropic surface)tiltingvorticity development on vertical vorticity is theforcing effect of the baroclinicity on vertical vorticitychanges. The “slantwise term” in the complete-formvorticity equation is connected to the horizontal twistingterm, and it is counteracted by other terms on theright-h and side of the equation. It affects the totalderivative of horizontal vorticity,thus influencing thevertical vorticity again.
The thermodynamic factor in the classical verticalvorticity equation of the p-coordinate is implied inthe divergence term,so it cannot be directly used toanalyze the effect of baroclinicity on vertical vorticity.Perhaps we can depend on PV thinking; and thePV expression,which is derived from the scalar formof the momentum equations in isobaric coordinates,should be adopted when calculating PV.
| Chen Zhongming, 2006: Comparison of the different forms of vertical vorticity tendency equation. J. Nanjing Univ. (Natl. Sci.), 42, 535-542. (in Chinese) |
| Ertel, H., 1942a: Ein neuer hydrodynamischer Wirbelsatz. Meteor. Z., 59, 277-281. |
| Ertel, H., 1942b: Ein neuer hydrodynamischer Erhaltungssatz. Naturwissenschaften, 30, 543-544. |
| Holton, J. R., 2004: An Introduction to Dynamic Meteorology, Fourth Edition. Elsevier Academic Press, San Diego, 228-230 pp. |
| Hoskins, B., 1997: A potential vorticity view of synoptic development. Meteor. Appl., 4, 325-334. |
| Hoskins, B. J., M. A. Pedder, and D. W. Jones, 2003: The omega equation and potential vorticity. Quart. J. Roy. Meteor. Soc., 129, 3277-3303. |
| Hu Bowei, 2003: Some opinions about the “potential vorticity thinking” and its application. J. Nanjing Inst. Meteor., 26, 111-115. (in Chinese) |
| Jaw, J.-J., 1946: The formation of the semipermanent centers of action in relation to the horizontal solenoidal field. J. Meteor., 3, 103-114. |
| Jiang Yongqiang, Chen Zhongyi, Zhou Zugang, et al., 2004: Slantwise vorticity development and meso-β scale low vortex. J. PLA Univ. Sci. Technol., 5, 81-87. (in Chinese) |
| Li Na, Ran Lingkun, Zhou Yushu, et al., 2013: Diagnosis of the frontogenesis and slantwise vorticity development caused by the deformation in the Beijing “7.21” torrential rainfall event. Acta Meteor. Sinica, 71, 593-605. (in Chinese) |
| Li Ying and Duan Xu, 1999: Slantwise vorticity development and severe precipitation in winter over Yunnan. J. Nanjing Inst. Meteor., 22, 705-710. (in Chinese) |
| Liu Chongjian, Liu Ying, and Xu Hui, 2007: Entropy flow and the evolution of the atmospheric systems. Chinese J. Atmos. Sci., 31, 1251-1256. (in Chinese) |
| Liu Shida and Liu Shikuo, 2011: Dynamics of Atmospheric Eddy. China Meteorological Press, Beijing, 41-42 pp. (in Chinese) |
| Lü Meizhong and Peng Yongqing, 1990: Tutorial of the Dynamical Meteorology. China Meteorological Press, Beijing, 131-132 pp. (in Chinese) |
| Lü Meizhong, Hou Zhiming, and Zhou Yi, 2004: Dynamic Meteorology. China Meteorological Press, Beijing, 22-23 pp. (in Chinese) |
| Ma Leiming, Qin Zenghao, Duan Yihong, et al., 2002: Case study on the impact of atmospheric baroclinicity to the initial development of Jianghuai cyclone. Acta Oceanol. Sinica, 24(S1), 95-104. (in Chinese) |
| Wang Ying, Wang Yuan, Zhang Lixiang, et al., 2007: The development of slantwise vorticity near a weakened tropical cyclone. J. Trop. Meteor., 23, 47-52. (in Chinese) |
| Wang Ziqian, Zhu Weijun, and Duan Anmin, 2010: A case study of snowstorm in Tibetan Plateau induced by Bay of Bengal storm: Based on the theory of slantwise vorticity development. Plateau Meteor., 29, 703-711. (in Chinese) |
| Wu Guoxiong, 2001: Comparison between the completeform vorticity equation and the traditional vorticity equation. Acta Meteor. Sinica, 59, 385-392. (in Chinese) |
| Wu, G. X., and H. Z. Liu, 1998: Vertical vorticity development owing to down-sliding at slantwise isentropic surface. Dyn. Atmos. Oceans, 27, 715-743. |
| Wu Guoxiong and Liu Huanzhu, 1999: Complete form of vertical vorticity tendency equation and slantwise vorticity development. Acta Meteor. Sinica, 57, 1-14. (in Chinese) |
| Wu Guoxiong, Zheng Yongjun, and Liu Yimin, 2013: Dynamical and thermal problems in vortex development and movement. Part II: Generalized slantwise vorticity development. Acta Meteor. Sinica, 27, 15-25. |
| Wu Rongsheng, 1990: Atmospheric Dynamics. China Meteorological Press, Beijing, 85-86 pp. (in Chinese) |
| Zhou Xiaogang, Liu Shijun, Wang Xiuming, et al., 2011: An investigation into the expression of potential vorticity in the common meteorological coordinate systems. Acta Phys. Sinica, 60, 059201. (in Chinese) |
 2016, Vol. 30
2016, Vol. 30