自流式注射法是一种新型施药技术，主要利 用蒸腾拉力将注入树体内的药物运输到叶片中^[1]，具有药剂吸收率高、见效快、无污染、设备价格 低、易于使用等优点^{[2, 3]}。

自流式注射法的核心问题之一是对树体吸收 药液量的研究。在实际操作中常存在如下问题： 若药剂稀释倍数过大，则药液不能完全被树体吸 收；若稀释倍数过小，则高浓度的药液易对树体 产生药害。因此，目前已有不少研究拟通过明确 影响树体吸收量的因素来调控其吸收量，以减少 药害的发生^{[4, 5, 6, 7, 8, 9]}。但目前尚未见关于在特定时间内 依据某一变量定量计算苹果树体吸收量方面的研 究报道。

本研究以纯水为注射液，在 7-11 月期间对注 射时的初始流速、注射过程中流速及树体吸收量 进行了连续的动态观察，旨在明确苹果树体有效 吸收期并建立初始流速 v₀ 与有效吸收期内树体对注射液吸收量的回归方程，以期为估测苹果树对 其他药剂的吸收量提供参考。

所用苹果树为河北农业大学标本园内 15 年生 盆栽树，品种为嘎拉，其主干直径为 13～15 cm； 供试药剂用纯水代替；仪器主要有自流式枝干注 射器 (广州东莞市倍特包装材料有限公司) 及充电 式电钻 (上海日立电动工具有限公司)。

试验地点为河北 农业大学标本园，时间为 2014 年 7 月至 11 月，每月进行 1 次试验，均于无风、晴天的 9:00 am 开 始。于树体基部钻 2 个孔径 3 mm、深 3 cm 的注 射孔，将 500 mL 纯水注入带有刻度的注射袋中，挂在离钻孔 120 cm 高的位置。分别于试验开始后0、3、6、9、12、24、27、30、33、36、48、72 及 96 h 使用秒表记录输液器滴壶中滴落 1 滴液体的 时间，并通过计算每时段注射袋中水平液面的刻 度差记录该时段的吸收量，树体在 0～96 h 内的吸 收量计为总吸收量。同时记录温度。试验重复 6 次。

利用 SPSS 17.0 统计软件对测试数据 进行回归分析，将各个相邻观测时间对应的流速 及 v₀ 与有效吸收期内树体吸收量分别作散点分布 图，由散点分布图形式确立回归模型和回归方 程。

按 1.2.1 节方法进 行注射试验，记录初始流速 v₀ 与 48 h 内树体的吸 收量。将 v₀ 代入 1.2.2 节所建立的回归方程中，计算出树体 48 h 的吸收量，并将其与实际测定的 记录值进行对比，计算差异率，筛选最佳回归方 程。

通过秒表测出滴壶中滴落 1 滴液体的时间 (t)，计算出 60 s 内滴落的液滴数 (S)：S = 60/t；已知 1 滴液体的体积为 0.05 mL，由此可得 1 滴液体滴 落时间与流速的转化公式 (1)：

其中，v = 流速 (mL/min)，S = 60 s 内滴落的液滴数，t = 1 滴液体滴落的时间 (s)。

差异率 (D) 计算公式见式 (2)：

其中，S_j = 吸收量计算值(mL)，S_c = 吸收量实 测值(mL)。

数据采用 Excel 进行整理、计算和绘图，通过SPSS 17.0 数据分析软件进行差异显著性分析。

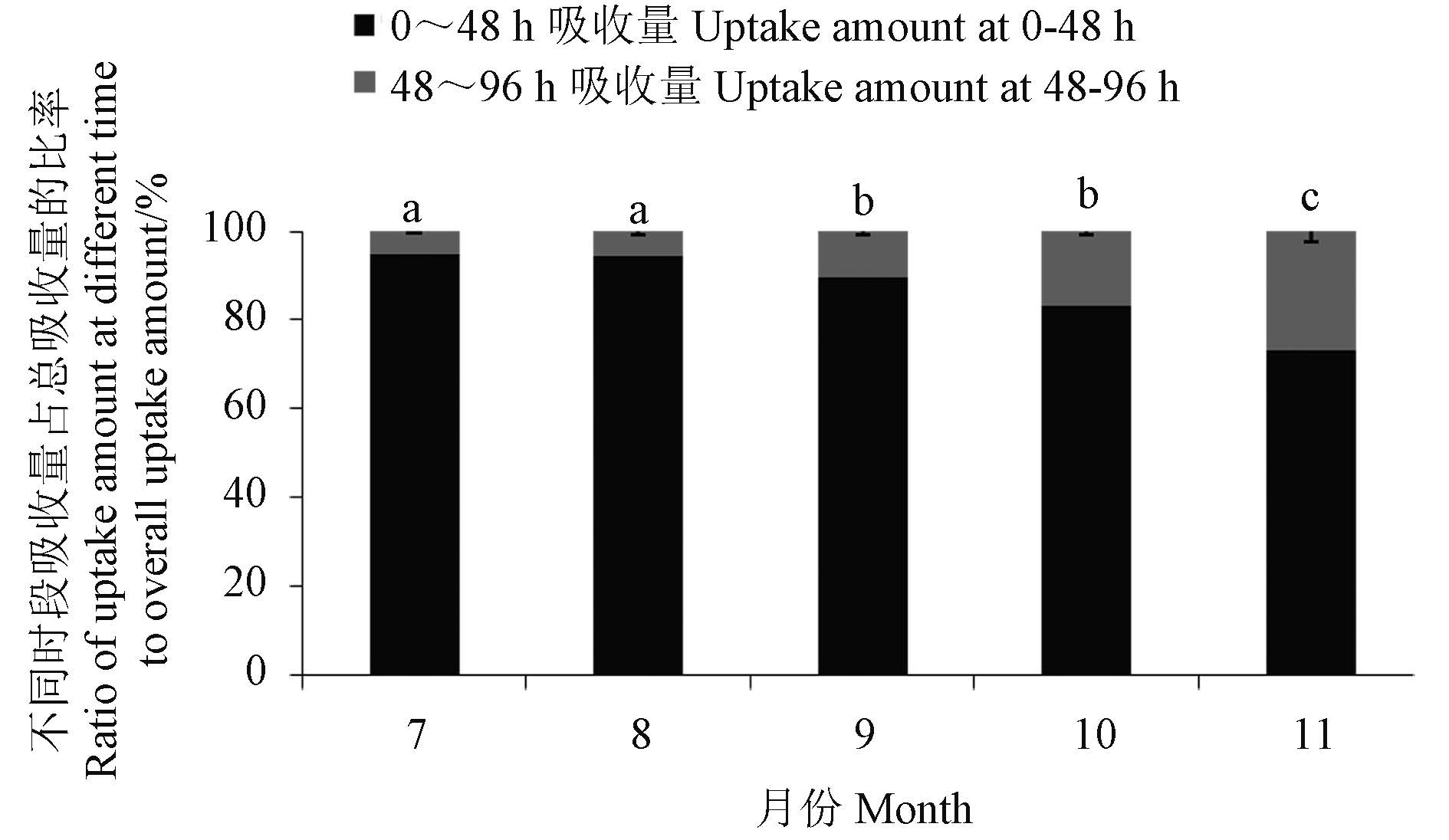
结果表明，开始注射后不同时间段内苹果树 体吸收量占总吸收量 (0～96 h 内吸收量) 的百分比 存在显著差异。由图 1 可知：在 7-11 月份，注射 开始后 0～48 h 苹果树体吸收量占总吸收量的 80% 左右，显著高于开始注射后 48～96 h 期间的 吸收量，说明树体吸收注射液的主要时间段是在 开始注射后 0～48 h，因此将开始注射后 0～48 h 定为有效吸收期；此外，树体 48～96 h 吸收量占 总吸收量的比率随月份的推移而逐渐增加，其中 11 月份处理组 48～96 h 吸收量占总吸收量的 26.5%，显著高于其他月份。

图 1

Fig. 1

注：相同小写字母表示数据在 5% 水平差异不显著。 Note: The same lowercase letters indicate the data no significant difference at P = 0.05 level. 图 1 树体不同月份 0～48 h 及 48～96 h 吸收量占总吸收量的比率 Fig. 1 The ratio of uptake amount at 0-48 h and 48-96 h with different months to overall uptake amount in trees

由表 1 可知，不同月份相邻观测时间与 对应的流速间存在极显著的一元线性关系和幂函 数曲线关系，且一元线性回归方程与幂函数曲线 回归方程的决定系数 (R²) 均在 0.8 以上。

表 1 (Table 1)

表 1 相邻观测时间与对应流速间的回归方程 Table 1 Regression equations of adjacent observation time corresponding to the flow speed 指标 * Factor* vx 回归方程 Regression equations 一元线性回归 One-factor liner regression 一元函数对应的决定系数 R2 of one-factor liner regression 幂函数曲线回归 Exponent function regression 幂函数对应的决定系数 R2 of exponent function regression v0 v3 = 1.298v0 + 0.2** 0.921 v3 = 1.213v01.077** 0.947 v3 v6 = 0.842v3 – 0.058** 0.965 v6 = 0.768v31.025** 0.975 v6 v9 = 0.334v6 + 0.034** 0.858 v9 = 0.394v60.912** 0.963 v9 v12 = 0.295v9 + 0.084** 0.846 v12 = 0.372v90.705** 0.801 v12 v24 = 3.562v12 – 0.008** 0.875 v24 = 3.017v120.950** 0.865 v24 v27 = 1.036v24 + 0.076** 0.950 v27 = 1.144v240.920** 0.966 v27 v30 = 0.59v27 + 0.079** 0.956 v30 = 0.72v270.947** 0.979 v30 v33 = 0.437v30 – 0.012** 0.963 v33=0.405v300.995** 0.976 v33 v36 = 0.492v33** 0.995 v36 = 0.475v330.975** 0.992 v36 v48 = 3.841v36 – 0.011** 0.996 v48 = 3.662v361.020** 0.963 注：vx 表示注射开始后 x h 时的流速；** 表示回归方程在 1% 水平呈极显著回归关系。 Note: vx means the flow speed x hours after injection；** Means the coefficient of regression significant at the level of P = 0.01.

表 1 相邻观测时间与对应流速间的回归方程 Table 1 Regression equations of adjacent observation time corresponding to the flow speed

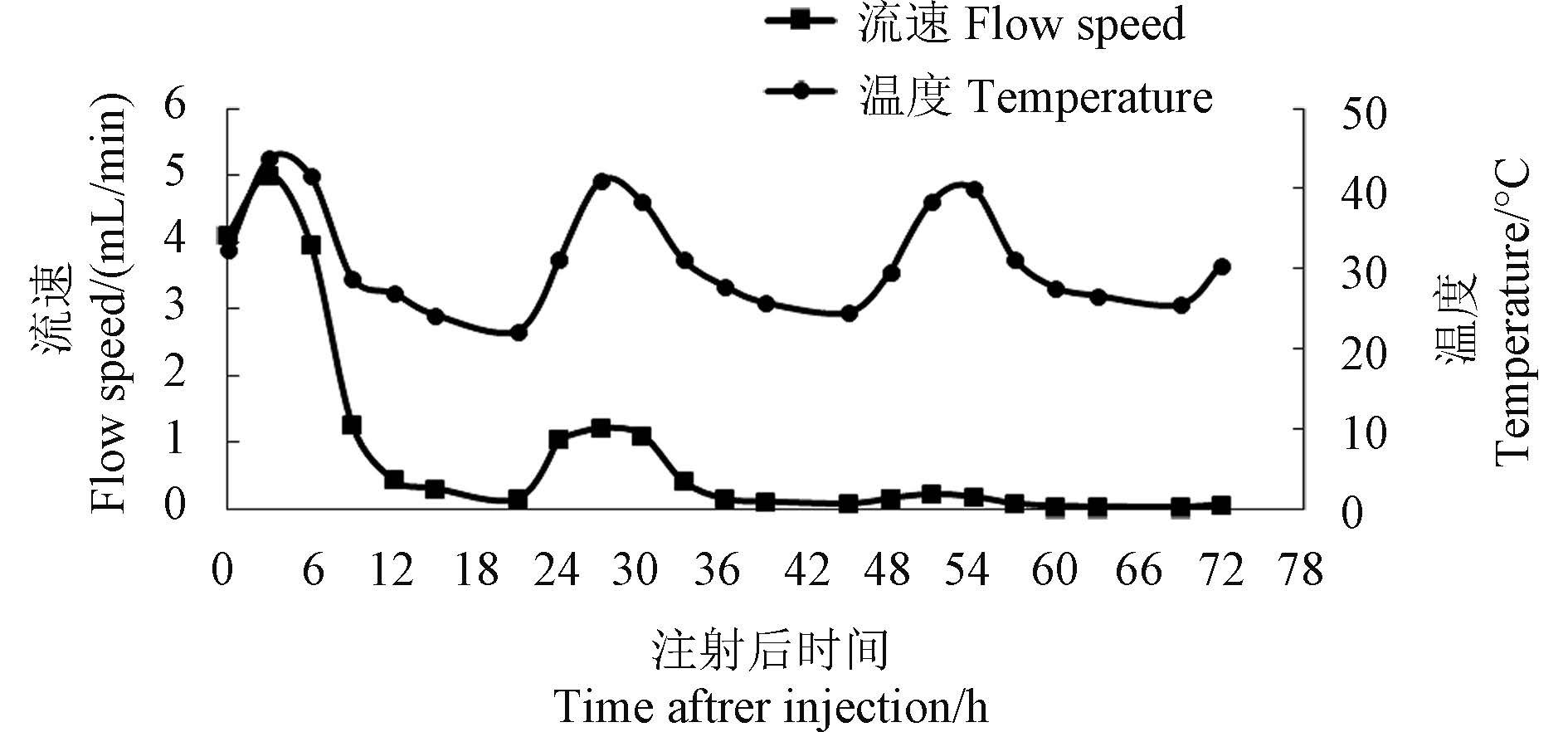
在开始注射后 72 h 内，7 月份处理组中温度对流速均具有一定的影响 (图 2 )，且流速的变化曲线与温度变化曲线在 0～72 h 内具有正相关性：温度上升时流速亦上 升，温度下降则流速也下降。

图 2

Fig. 2

图 2 7 月份处理组温度对流速的影响 Fig. 2 Influence of temperature on the flow speed in July

测定结果表明，7-11 月 试验期间，初始流速 v₀ 与其 48 h 内吸收量之间存 在极显著的一元线性关系和幂函数曲线关系 (P = 0.01)。其中，一元线性回归方程为 y = 819.058v₀ - 60.540，R² = 0.758；幂函数曲线回归方程为 y = 813.543v₀ ^0.816，R² = 0.778。

将测试结果代入所建立 方程中，分别计算出苹果树体 48 h 内的吸收量，并将实测吸收量与计算值进行比较，计算差异 率。由表 2 可知：在初始流速为 0～1 mL/min 时，采用一元回归方程计算所得吸收量与实际吸 收量的差异率显著高于采用幂函数方程计算的差异率；在初始流速为 2～4 mL/min 时，幂函数方 程的差异率显著高于一元回归方程；在初始流速 为 1～2 mL/min 时，则采用一元回归方程与幂函 数方程的差异率无显著差异。但无论采用一元回 归方程还是幂函数方程，计算所得吸收量与实测吸收量的差异率均较大，都在 20%～30% 之间。

表 2 (Table 2)

表 2 吸收量实测值与方程计算值比较 Table 2 Comparison of the actual measured value and calculated value on uptake 初始流速 Initial speed, v0/(mL/min) 差异率 Difference ratio/% 一元线性回归函数 One-factor liner regression 幂曲线回归函数 Exponent function regression 0～1 27.37 b 23.88 a 1～2 28.51 a 29.52 a 2～4 20.61 a 27.53 b 注：数据后相同小写字母表示同行数据在 5% 水平差异不显著。 Note: The same lowercase letters after data indicate the data in the same line compared with no significant difference at P = 0.05 level.

表 2 吸收量实测值与方程计算值比较 Table 2 Comparison of the actual measured value and calculated value on uptake

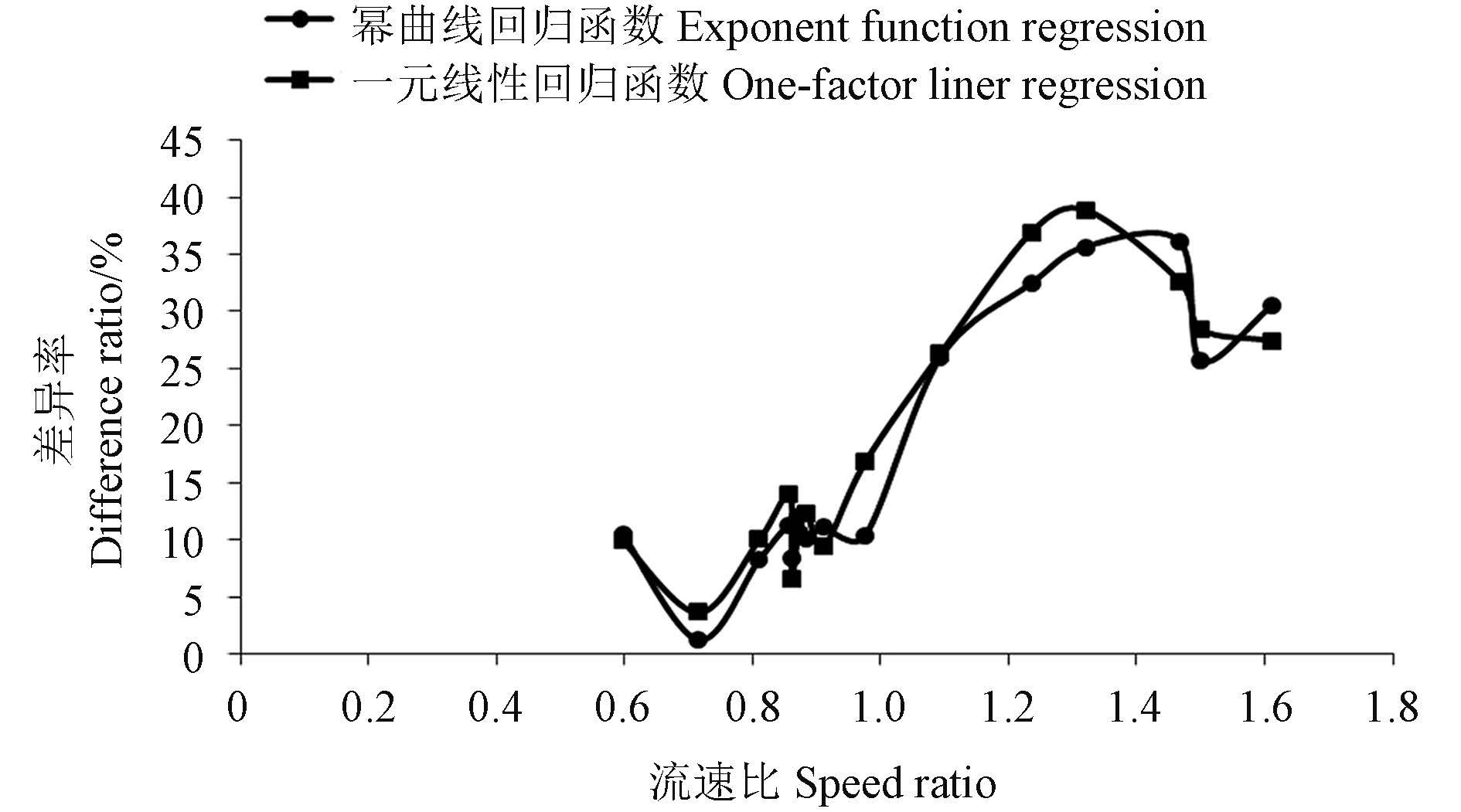
2.3 节中对回归方程的检验表明，样本实测值 与方程计算值的差异率均大于 20%。为降低差异 率，通过对数据的分析，发现差异率大小与初始 流速 v₀ 和 v₃ 的比值 (流速比，v₀/v₃) 有关，因此进 一步就各样本吸收量差异率与其流速比的关系进 行了分析。由图 3 可知：当流速比在 0.6～1 时，一元回归函数与幂函数方程的差异率均小于 20%，且两类函数的变化趋势相似；当流速比在 1～1.6 时，两函数方程的差异率均大于 20%。说 明流速比是影响差异率的主要原因，且该值为 1 是差异率大于 20% 的临界值。

图 3

Fig. 3

图 3 流速比对吸收量实测值与方程计算值差异率的影响 Fig. 3Influence of speed ratio on difference ratio between the actual measured and calculation value about absorption

测定结果表明，7-11 月试验期间，初始流速 v₀ 与注射开始后 48 h 内苹果 树体的吸收量之间存在极显著的一元线性关系和 幂函数曲线关系 (P = 0.01)。当流速比 (v₀/v₃) 为 0.6～1 时，一元线性回归方程为 y = 842.832v₀ - 26.732，R² = 0.824，幂函数曲线回归方程为 y = 877.427v₀ ^0.705，R² = 0.774；当流速比为 1～1.6 时，一元线性回归方程为 y = 528.460v₀ + 69.395，R² = 0.966，幂函数曲线回归方程为 y = 588.696v₀ ^0.955，R² = 0.972。

按初始流速 v₀ 的范围及 流速比，分别将 v₀ 代入所建立的方程中，计算 48 h 内苹果树体的吸收量，比较实测吸收量与方 程计算值的差异率。由表 3 可知，区分流速比 后，采用一元函数回归方程与幂函数回归方程时 的差异率均小于 15%。其中，当流速比为 0.6～1 时，初始流速为 0～1 mL/min，一元函数与幂函数 方程的差异率无显著性差异，初始流速为 1～ 4 mL/min，则一元函数方程的差异率显著低于幂 函数方程；当流速比为 1～1.6 时，一元函数与幂 函数方程的差异率无显著性差异。

表 3 (Table 3)

表 3 区分流速比时吸收量实测值与方程计算值比较 Table 3 Comparison of actual measured value and calculated value on uptake based on the speed ration 初始流速 Initial speed，v0/ (mL/min) 差异率 Difference ratio/% 流速比为 0.6～1 Speed ratio between 0.6 and 1   流速比为 1～1.6 Speed ratio between 1 and 1.6 一元回归函数 One-factor liner regression 幂曲线回归函数 Exponent function regression 一元回归函数 One-factor liner regression 幂曲线回归函数 Exponent function regression 0～1 6.53 a 5.57 a   7.13 a 4.48 a 1～2 2.72 a 6.74 b   3.96 a 3.84 a 2～4 9.21 a 12.57 b   4.22 a 5.61 a 注：数据后相同小写字母表示同行数据在 5% 水平差异不显著。 Note: The same lowercase letters after data indicate the data in the same line compared with no significant difference at P = 0.05 level.

表 3 区分流速比时吸收量实测值与方程计算值比较 Table 3 Comparison of actual measured value and calculated value on uptake based on the speed ration

研究发现，苹果树体吸收药液的主要时间段 是在开始注射后 0～48 h，因此以开始注射后 0～48 h 为有效吸收期。其原因可能是由于树体对 伤口存在自我修复能力，注射过程中，树体破损 的伤口慢慢恢复，导致后期药液进入树体的阻力 逐渐增大，树体对药液的吸收量减少。同时也发 现，开始注射后 48～96 h 期间树体吸收量占总吸 收量的比率随试验月份的推移而逐渐增大，这可 能是因为 7～8 月份时树体的新陈代谢较旺盛，其 自我修复能力较强，而 11 月份时树体即将进入休 眠状态，新陈代谢较缓慢，其自我修复能力下 降，对破损组织的修复较慢，因此导致 11 月份处 理组树体 48～96 h 吸收量占总吸收量的比率显著 高于其他月份的现象。

本研究还发现，不同月份处理，相邻观测时 间点与药液流速之间具有极显著的一元函数与幂 函数关系。其原因是由于注射过程中流速随温度 的变化而变化：温度上升时流速升高，温度下降 时流速亦下降，相邻观测时间点之间温度的规律性变化导致了流速呈规律性变化。根据这种相邻 观测时间对应流速间的规律性变化，笔者猜测某 一时间点流速与吸收量之间亦可能存在某种规律 性。

药液流速比 (v₀/v₃) 是影响回归方程估测吸收 量准确性的关键因素之一。本研究发现，同一天 注射的样本中，既有 v₀ > v₃ 的情况，也有 v₀ < v₃ 的情况。这可能是由树体自身的差异性导致的： 不同树体内的自然存水情况不同，当蒸腾拉力一 定时，若树体内存水较少，则其负压相对较大，此时树体吸收药液的动力既有树体内的负压又有 外界的蒸腾拉力，因此流速较快。一般情况下，注射开始后 3 h (12:00 am) 时的温度较初始注射时 (9:00 am) 高，虽然 12:00 am 时外界的蒸腾拉力大 于 9:00 am 时的蒸腾拉力，但由于已经过 3 h 的吸 收，树体内存水已趋于饱和，负压可能消失，此 时的吸收动力仅为蒸腾拉力，因此流速 v₃ 可能小 于初始流速 v₀；若树体内本身存水较多，则负压 较小，当树体内负压与外界蒸腾拉力之和小于 12:00 am 时的蒸腾拉力时，即会出现 v₀ < v₃ 的情 况。同时当 v₀ 一定，v₃ > v₀ 时，初始注射时间 (9:00 am) 至注射开始后 3 h (12:00 am) 的吸收量会大于流速比值小时对应的吸收量。由于开始注射 至 3 h 时的流速较其他时段快，且此阶段的吸收量 在 48 h 内吸收量中所占的比重亦较大，因此需依 据不同的 v₀/v₃ 比值建立相应的拟合方程，从而保 证方程计算的结果更加贴近树体实际吸收量。