2. 三峡大学电气与新能源学院,湖北 宜昌 443002
2. College of Electrical Engineering and New Energy, China Three Gorges University, Yichang 443002, China
不断扩张的电力系统规模和持续增长的电力需求,导致电力系统运行的稳定裕度逐渐降低,越发接近其稳定极限[1-2]。当遇到严重的故障时,当前电力系统可能会失去暂态稳定性,引起级联停电或大停电事故[3]。为了保护电力系统免受暂态失稳所带来的负面影响,需要对电力系统的运行状态进行在线暂态稳定分析。
电力系统暂态稳定分析的目的是对电力系统的运行状况进行实时监测,以便系统运行人员及时掌握系统运行信息[4]。时域仿真[5] (Time Domain Simulation,TDS)是一种经典的暂态稳定分析方法,利用微分代数方程组对电力系统进行建模,通过数值积分法求解给定故障下的系统响应,并基于是否违反预定义的安全准则来确定系统的安全状态。然而,TDS计算繁琐,不适用于复杂的电力系统。随着人工智能的快速发展,极限学习机[6-7] (Extreme Learning Machine,ELM)、决策树[8] (Decision Tree,DT)、逻辑回归[9] (Logistic Regression,LR)和支持向量机[10-11] (Support Vector Machine,SVM)等机器学习方法被广泛应用于电力系统暂态稳定分析领域,但这些方法存在泛化能力不强及应用于高维数据时预测精度不足等问题。
本文提出了一种基于皮尔逊相关系数[12](Pear- son Correlation Coefficient,PCC)和核极限学习机[13](Kernel Extreme Learning Machine,KELM)的电力系统暂态稳定分析方法。该方法利用PCC对高维数据进行降维,并利用泛化性能更好,精度更高的KELM模型进行预测。在新英格兰10机39节点系统上的测试结果表明该方法可有效应用于电力系统暂态稳定分析领域。
1 输入特征选择输入特征的选择对于机器学习模型输出结果的准确性至关重要。随着电力系统的广域互联和新能源渗透率的不断提高,电力系统的规模和复杂度持续增加,使得电力系统的运行特征数量急剧增加[14]。
用于电力系统暂态稳定分析的特征主要包括母线电压幅值和相角、负荷的有功功率和无功功率、发电机的有功功率和无功功率、分流器的无功功率、线路的有功功率和无功功率、线路的视在功率以及线路的有功损耗和无功损耗[15]。对于基于机器学习的电力系统暂态稳定分析方法,过多的输入特征不仅不利于提高机器学习模型的预测精度,还会增加模型的计算负担,严重影响计算效率[16]。
为提高模型计算速度,本文通过特征选择方法对上述特征进行数据降维,以筛选出与电力系统暂态稳定指标相关性较强的关键特征作为机器学习模型的输入,特征选择方法主要用构建暂态稳定裕度(Transient Stability Margin,TSM)来表征系统的稳定程度,并使用PCC选出与TSM相关性较强的关键特征。
1.1 TSMTSM可以表示电力系统当前运行点到安全边界的距离,其通常被用来描述电力系统的暂态稳定程度[17]。本文使用故障的临界切除时间(Critical Clearing Time,CCT),式中记为tCCT;实际切除时间(Actual Clearing Time,ACT),式中记为tACT,构建TSM,式中记为TSM,如式(1)所示:

|
(1) |
TSM为-1~1范围内的连续值,设置T′SM为TSM的临界值,若TSM>T′SM,则判定电力系统当前的运行状态为稳定,并且TSM越大,稳定程度越高;反之,则判定电力系统当前的运行状态为不稳定。根据不同电力系统不同的安全需求,T′SM可以被灵活设置。
1.2 PCCPCC是一种衡量两变量之间线性相关性的量化指标。本文采用PCC来计算电力系统运行特征与TSM之间的相关性P,计算如式(2)所示:
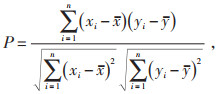
|
(2) |
式中:n为样本数量;xi为特征;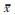
| 表 1 P值的相关性 Table 1 Correlation of P-value |
根据每个特征与TSM之间的P值,对所有特征进行降序排序,选取前20个P值较大的关键特征作为机器学习模型的输入,所选特征与TSM之间的相关程度如图 1所示。由图 1可知,本文所选取的关键特征与TSM之间的相关性均大于0.75,说明其对电力系统暂态稳定分析十分重要。以所选关键特征作为机器学习模型的输入,不仅可以得到较为准确的评估结果,还可以显著降低机器学习模型的计算负担,提高暂态稳定分析的速度,满足在线应用的实时性需求。

|
| 图 1 关键特征与TSM的相关性 Figure 1 Correlation between key characteristics and TSM 图中:1~20表示本文所选取的关键特征,21表示对应的TSM值,颜色越亮表示相关性越强。 |
KELM是基于ELM提出的改进算法,将核函数引入到ELM中,改善了隐藏神经元随机赋值所产生的泛化性和稳定性不足等问题,提高了模型的预测性能[18],其基本结构如图 2所示。

|
| 图 2 KELM结构图 Figure 2 The structure diagram of KELM 图中:K(x1, x2),…,K(xi, xj)为不同的核函数;β为隐含层的输出权值;F(x)为KELM模型的输出。 |
ELM是一种单隐含层前馈神经网络,其输出矩阵T可表示为:

|
(3) |
式中:H为隐含层输出矩阵。
将网络训练转换为线性系统求解的问题,根据式(3)可得:
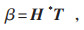
|
(4) |
式中:H* 为H的摩尔-彭罗斯广义逆矩阵,可通过正交投影或者奇异值分解来获取,即:

|
(5) |
为增强ELM的稳定性,引入正则化系数C和单位矩阵I,则输出权值的最小二乘解为:

|
(6) |
由于ELM在训练时,每次所得到的H* 是不同的,因此每次获取的隐含层输出权值β也是不确定的,模型的输出结果会出现随机波动。为提高ELM的稳定性和泛化能力,将核函数引入到ELM中,核矩阵Ω可定义为:

|
(8) |
式中:xi和xj为输入的特征,h(x) 为隐含层输出函数。
由上述公式可得,KELM的输出为:
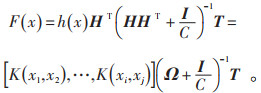
|
(8) |
将KELM引入电力系统暂态稳定分析领域,通过构建基于KELM的电力系统暂态稳定预测模型建立电力系统关键运行特征与TSM之间的映射关系,以此实现对电力系统当前运行状况的实时暂态稳定分析。
2.2 暂态稳定分析流程基于PCC和KELM的电力系统暂态稳定分析流程如图 3所示,主要包含3个阶段,分别为离线训练、模型更新和在线应用。

|
| 图 3 暂态稳定分析流程 Figure 3 Flow chart of transient stability analysis 图中:PMU为相量测量装置,Phasor Measurement Unit。 |
首先,利用电力系统仿真软件PSS/E生成仿真数据以建立包含电力系统运行特征与相应TSM的初始数据集。为了扩大初始数据集的规模、增强KELM模型的适用性,在生成仿真数据时对发电和负荷水平增加一定程度的扰动。然后,基于PCC特征选择方法筛选出与TSM相关性较强的关键特征,并将其与相应的TSM合并建立关键数据集。其次,使用五折交叉验证法对KELM模型进行训练,随机选取80%的数据作为训练集,其余数据作为测试集。其中关键特征作为KELM模型的输入,TSM作为KELM模型的输出,通过模型训练建立输入与输出之间的映射。最后,根据训练好的模型在测试集上的性能测试结果对模型进行参数调整。
2.2.2 模型更新电力系统的运行条件很难保持不变。当系统运行条件发生改变(如负荷调度、检修等)时,离线阶段训练好的KELM模型可能无法适应电力系统新的运行工况,导致模型预测准确性大幅度下降,以至于无法满足在线暂态稳定分析的准确性要求。为此,需要根据新的工况生成新的训练样本对KELM模型进行再训练以提高KELM模型的适应性。
2.2.3 在线应用当PMU实时测量数据被输送到训练好的KELM模型中时,该模型可以立刻给出电力系统当前运行状态的暂态稳定分析结果。若系统当前运行状态被判定为稳定,则继续对系统进行监测;否则,将发出警报提醒系统运行人员采取相应的预防控制措施。
2.3 模型性能评价指标本文采用残差平方误差[19]R2和均方根误差[20] RMSE来评价KELM预测模型的性能,计算公式见式(9)和式(10):
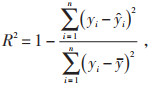
|
(9) |

|
(10) |
式中:ŷi为特征在KELM模型中的TSM预测值。
R2的取值范围为(0,1),R2越大,预测模型性能越好[21]。RMSE表示预测值与实际TSM之间的差异,取值范围为(0,+∞),RMSE越小,表明预测值越接近实际值,预测模型性能越好[22]。
3 算例分析在图 4所示的新英格兰10机39节点系统中进行KELM模型性能测试。该系统包含39条母线(1—39),10台发电机(G1—G10),46条传输线,以及19个负荷节点[23]。计算机配置为:Intel Core i5- 9300 2.40 GHz、16.0 G RAM。

|
| 图 4 新英格兰10机39节点系统 Figure 4 New England 10-machine 39-bus system |
首先,利用电力系统仿真软件PSS/E进行数据仿真,并通过python程序实现仿真自动化,使用MATLAB对潮流报表进行特征提取。其次,基于PCC对电力系统运行特征进行选择,筛选出与TSM高度相关的关键特征。最后,生成了3820个样本。随机选取80%的样本对KELM模型进行训练,其余的样本用于测试。训练和测试均重复5次,直到评价指标的平均值和标准偏差稳定为止。测试结果如表 2所示。
| 表 2 KELM模型性能测试结果 Table 2 The performance test results of KELM model |
由表 2可知,KELM模型的预测准确率和对测试样本的预测时间均满足电力系统暂态稳定分析的要求。
3.2 模型性能比较为分析KELM模型的有效性,将其与ELM、DT、LR和SVM模型进行性能对比测试。所有评估模型均基于Pytorch框架实现,模型参数使用默认参数。在测试中,所有模型均使用相同的训练集和测试集,测试结果如表 3所示。
| 表 3 不同模型的性能测试 Table 3 Performance test results for different models |
由表 3可知,相较于DT、LR和SVM模型,KELM模型具有更加优越的预测性能。预测值十分接近实际值,在进行电力系统暂态稳定分析时,结论更可靠。ELM模型与KELM模型的预测性能比较接近,但KELM模型的泛化能力更强,更加适用于复杂多变的电力系统中。
3.3 训练集规模对模型性能的影响训练集的规模往往也会影响机器学习模型的预测性能。为研究不同训练集大小对模型预测性能的影响,使用不同比例的原始训练集对KELM模型进行训练,然后在同一测试集上进行测试,测试结果如表 4所示。
| 表 4 不同规模训练集下的模型性能 Table 4 Model performance under different scale training sets |
由表 4可知,训练集规模越大,KELM模型预测性能越高,30%的原始训练集就足以训练一个合格的预测模型(R2>0.9)。系统运行人员可以根据实际需求选择合适的训练集大小,以节省训练时间。
4 结束语本文提出了一种基于PCC和KELM的电力系统暂态稳定分析方法,该方法利用PCC探索电力系统运行特征与TSM之间的相关性,选择相关性较高的关键特征作为KELM预测模型的输入,对KELM模型进行训练获取关键特征与TSM之间的映射关系。在新英格兰10机39节系统中对其进行了性能测试,结果表明,相比其他机器学习模型,本方法具有更优越的预测性能,更加适用于电力系统暂态稳定分析领域。
| [1] |
侯博, 程晓磊, 王渊, 等. 基于PSS/E的异步联网对蒙西电网西电东送能力的影响分析[J].
内蒙古电力技术, 2018, 36(6): 1-5 HOU Bo, CHENG Xiaolei, WANG Yuan, et al. Analysis for Influence of Asynchronous Interconnection on West-To-East Power Transmission in West Inner Mongolia Power Grid[J]. Inner Mongolia Electric Power, 2018, 36(6): 1-5 (  0) 0)
|
| [2] |
魏文兵, 毛钧毅, 荣娜, 等. 采用随机矩阵与CNN的暂态电压稳定快速评估[J].
电网与清洁能源, 2020, 36(11): 68-76 WEI Wenbing, MAO Junyi, RONG Na, et al. Fast Evaluation of transient voltage stability using random matrix and convolutional neural network[J]. Advances of Power System & Hydroelectric Engineering, 2020, 36(11): 68-76 (  0) 0)
|
| [3] |
YAN Rong, GENG Guangchao, JIANG Quanyuan, et al. Fast transient stability batch assessment using cascaded convolutional neural networks[J].
IEEE Transactions on Power Systems, 2019, 34(4): 2802-2813 DOI:10.1109/TPWRS.2019.2895592 (  0) 0)
|
| [4] |
韩天森, 陈金富, 李银红, 等. 电力系统稳定评估机器学习可解释代理模型研究[J].
中国电机工程学报, 2020, 40(13): 4122-4131 HAN Tiansen, CHEN Jinfu, LI Yinhong, et al. Study on interpretable surrogate model for power system stability evaluation machine learning[J]. Proceedings of the CSEE, 2020, 40(13): 4122-4131 (  0) 0)
|
| [5] |
高昆仑, 杨帅, 刘思言, 等. 基于一维卷积神经网络的电力系统暂态稳定评估[J].
电力系统自动化, 2019, 43(12): 18-26 GAO Kunlun, YANG Shuai, LIU Siyan, et al. Transient stability assessment for power system based on one-dimensional convolutional neural network[J]. Automation of Electric Power Systems, 2019, 43(12): 18-26 (  0) 0)
|
| [6] |
ZHANG Yuchen, XU Yan, DONG Zhaoyang, et al. Intelligent early warning of power system dynamic insecurity risk: toward optimal accuracy earliness tradeoff[J].
IEEE Transactions on Industrial Informatics, 2017, 13(5): 2544-2554 DOI:10.1109/TII.2017.2676879 (  0) 0)
|
| [7] |
张翌晖, 张元胜, 文立斌, 等. 基于多RBF-ELM集成模型的电力系统暂态稳定评估[J].
武汉大学学报(工学版), 2021, 54(9): 852-859 ZHANG Yihui, ZHANG Yuansheng, WEN Libin, et al. Power system transient stability assessment based on multi-radial basis function-extreme learning machine integrated model[J]. Engineering Journal of Wuhan University, 2021, 54(9): 852-859 (  0) 0)
|
| [8] |
朱利鹏, 陆超, 黄河, 等. 基于广域时序数据挖掘策略的暂态电压稳定评估[J].
电网技术, 2016, 40(1): 180-185 ZHU Lipeng, LU Chao, HUANG He, et al. Wide-area time series data mining based transient voltage stability assessment[J]. Power System Technology, 2016, 40(1): 180-185 (  0) 0)
|
| [9] |
聂鼎, 范黎涛, 王科, 等. 基于AHP的多因素中压配网线路风险量化评估方法研究[J].
电工技术, 2021(4): 52-54 NIE Ding, FAN Litao, WANG Ke, et al. Research on AHP-based multi-factor medium voltage distribution network line risk quantitative assessment method[J]. Electric Engineering, 2021(4): 52-54 (  0) 0)
|
| [10] |
田芳, 周孝信, 于之虹. 基于支持向量机综合分类模型和关键样本集的电力系统暂态稳定评估[J].
电力系统保护与控制, 2017, 45(22): 1-8 TIAN Fang, ZHOU Xiaoxin, YU Zhihong. Power system transient stability assessment based on comprehensive SVM classification model and key sample set[J]. Power System Protection and Control, 2017, 45(22): 1-8 (  0) 0)
|
| [11] |
刘信彤, 辛业春, 王长江, 等. 基于Smo-PinSVM的含新能源电力系统暂态稳定评估[J].
太阳能学报, 2021, 42(5): 98-104 LIU Xintong, XIN Yechun, WANG Changjiang, et al. Transient stability assessment in bulk power grid with renewable energy using Smo-PinSVM[J]. Acta Energiae Solaris Sinica, 2021, 42(5): 98-104 (  0) 0)
|
| [12] |
Benesty J, Chen J, Huang Y. On the importance of the Pearson correlation coefficient in noise reduction[J].
IEEE Transactions on Audio, Speech, and Language Processing, 2008, 16(4): 757-765 (  0) 0)
|
| [13] |
HUANG G B. An insight into extreme learning machines: random neurons, random features and kernels[J].
Cognitive Computation, 2014, 6(3): 376-390 (  0) 0)
|
| [14] |
刘俊, 王旭, 孙惠文, 等. 采用FJPD互信息的电力系统暂态稳定性预测特征选择分析[J].
智慧电力, 2018, 46(10)78-85, 95 LIU Jun, WANG Xu, SUN Huiwen, et al. Feature selection analysis of power system transient stability prediction using FJPD mutual information[J]. Smart Power, 2018, 46(10)78-85, 95 (  0) 0)
|
| [15] |
张雅婷, 刘颂凯, 张磊, 等. 针对数据缺失的电力系统暂态稳定评估方法[J].
电力系统及其自动化学报, 2023, 35(3): 59-68 ZHANG Yating, LIU Songkai, ZHANG Lei, et al. A transient stability assessment method for power systems with data missing[J]. Proceedings of the CSU-EPSA, 2023, 35(3): 59-68 (  0) 0)
|
| [16] |
刘炼, 王强, 陈浩. 基于改进随机森林的电力系统暂态稳定评估[J].
科学技术与工程, 2022, 22(11): 4367-4374 LIU Lian, WANG Qiang, CHEN Hao. Transient stability assessment of power system based on improved random forest[J]. Science Technology and Engineering, 2022, 22(11): 4367-4374 (  0) 0)
|
| [17] |
刘书池, 刘颂凯, 张磊, 等. 考虑样本不平衡的电力系统鲁棒暂态稳定评估[J].
智慧电力, 2022, 50(7)16-22, 73 LIU Shuchi, LIU Songkai, ZHANG Lei, et al. Robust transient stability assessment of power system considering sample imbalance[J]. Smart Power, 2022, 50(7)16-22, 73 (  0) 0)
|
| [18] |
徐永海, 涂菁菁, 尹忠东. 基于核极限学习机的风光容量配置研究[J].
电测与仪表, 2019, 56(9): 73-80 XU Yonghai, TU Qingqing, YIN Zhongdong. The capacity selection of wind photovoltaic power generations based on KELM method[J]. Electrical Measurement & Instrumentation, 2019, 56(9): 73-80 (  0) 0)
|
| [19] |
晏光辉, 刘颂凯, 张磊, 等. 基于迁移学习的智能静态电压稳定评估方案[J].
电测与仪表, 2022, 59(2): 92-99 YAN Guanghui, LIU Songkai, ZHANG Lei, et al. Intelligent static voltage stability assessment scheme based on transfer learning[J]. Electrical Measurement & Instrumentation, 2022, 59(2): 92-99 (  0) 0)
|
| [20] |
陈康, 王泽, 郭永吉. 基于grcForest模型的风电并网系统暂态电压稳定评估[J].
智慧电力, 2023, 51(1): 31-37 CHEN Kang, WANG Ze, GUO Yongji. Transient voltage stability assessment of wind power grid-connected system based on grcForest model[J]. Smart Power, 2023, 51(1): 31-37 (  0) 0)
|
| [21] |
韩朋, 张晓琳, 张飞, 等. 基于AM-LSTM模型的超短期风电功率预测[J].
科学技术与工程, 2020, 20(21): 8594-8600 HAN Peng, ZHANG Xiaolin, ZHANG Fei, et al. Ultra-short-term wind power prediction based on AM-LSTM model[J]. Science Technology and Engineering, 2020, 20(21): 8594-8600 (  0) 0)
|
| [22] |
伍骏杰, 张倩, 陈凡, 等. 计及误差修正的变分模态分解-长短期记忆神经网络短期负荷预测[J].
科学技术与工程, 2022, 22(12): 4828-4834 WU Junjie, ZHANG Qian, CHEN Fan, et al. Short-term load forecasting with error correction and variational mode decomposition-long short-term memory[J]. Science Technology and Engineering, 2022, 22(12): 4828-4834 (  0) 0)
|
| [23] |
李嘉敏, 杨红英, 闫莉萍, 等. 样本不平衡情况下的电力系统暂态稳定集成评估方法[J].
电力系统自动化, 2021, 45(10): 34-41 LI Jiamin, YANG Hongying, YAN Liping, et al. An integrated evaluation method for transient stability of power systems with unbalanced samples[J]. Automation of Electric Power Systems, 2021, 45(10): 34-41 (  0) 0)
|
 2023, Vol. 41
2023, Vol. 41





